Surface Tension of High Temperature Liquids Evaluation with a Thermal Imaging Furnace

Abstract

At high temperature, the reactivity of liquid metals, salts, oxides, etc. often requires a container-less approach for studying composition-sensitive thermodynamic properties, such as component activities and surface tension. This experimental challenge limits access to essential properties, and therefore our understanding of molten systems. Herein, a thermal imaging furnace (TIF) is investigated as a mean of container-less study of molten materials via the formation of pendant drops. In situ optical characterization of a liquid metal drop is proposed through the use of a conventional digital camera. We report one possible method for measuring surface tension of molten systems using this pendant drop technique in conjunction with an image analysis procedure. Liquid copper was used to evaluate the efficacy of this method. The surface tension of liquid copper was calculated to be 1.159 $\pm \ 0.043$ N$\text {m}^{-1}$ at $1084\pm 20$ $^{\circ }\mathrm {C}$, in agreement with published values.

Introduction

Knowledge of the basic thermodynamic information and physical properties of the liquid state of materials, such as molten metals or alloys, molten oxide and molten intermetallic compounds, is relatively poorly developed, when compared with the breadth of data available for materials systems near room temperature. These data include, and are not limited to, the Gibbs energy, component activities, surface tension, melting temperature, and vapor pressure. The absence of this sort of information constrains the use and study of materials, not only for molten systems but also for the solid state, since many of these materials are employed at temperatures in the vicinity of $T_\text {fus}$.

This lack of high temperature liquid state data can be attributed to the experimental challenges that accompany measurements of melting temperature, surface tension, etc. Of primary concern is the reactivity of molten materials at high temperature, as small amounts of impurities can significantly change the measured values of the quantities stated above. The issue of sample contamination from a holder or stage may be addressed by adopting a container-less approach to the study of molten systems. The pendant drop technique is one such method. For this technique, a rod of the material is suspended in a furnace, and localized melting at one end is induced to form a stable liquid drop. For example, pendant drops were recently used to measure Gibbs energy in molten alumina at temperatures in excess of 2000 $^{\circ }\mathrm {C}$ [1].

The pendant drop technique is particularly conducive to the study of liquid surface tension due to the known dependence of the equilibrium drop shape on the two forces acting on the drop: gravity and surface tension. Previous studies have used the pendant drop technique to measure the surface tension of liquid metals [2,3,4] and refractory oxides [5,6,7]. With regards to the experimental setup for liquid metals at high temperature, the approaches to date have employed either refractory oxide capillaries to contain the liquid metal, which are unsuitable for high melting temperature metals, or electron beam or induction melting, which can only be used with electronically conductive liquids and may induce unwanted vibrations [8]. Both issues may be addressed by using a thermal imaging furnace (TIF) with an optical heating source.

In this paper we describe a method for measuring surface tension using a TIF in conjunction with an image analysis procedure that employs an open-source drop shape optimization program (OpenDrop [9]). To our knowledge, this is one of the first studies reporting an experimental setup suitable for surface tension measurements from container-less pendant drops of both liquid metal and nonmetal compounds at high temperatures. Copper was chosen as a model test liquid for evaluating the TIF measurement apparatus, as its surface tension is well-studied, but the approach may be used for higher melting temperature metals and compounds as well. Herein, the results for liquid Cu are presented.

Background

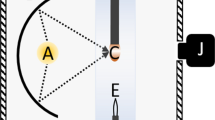
The relationship between the drop shape and surface tension ($\gamma$) is defined mathematically by the mean curvature of the drop

$$\begin{aligned} \frac{\mathrm {d}\phi }{\mathrm {d}s} + \frac{\sin \phi }{x} = \frac{\Delta P}{\gamma } = \frac{\Delta \rho g \left( h - z \right) }{\gamma }. \end{aligned}$$

(1)

Equation (1) is the Young-Laplace equation in cylindrical coordinates (see Fig. 1) where $\phi$ is the tangent angle and s is the arc length with origin at $x=0$. $\Delta P$, the pressure difference across the drop interface, may be expressed as $\Delta \rho g \left( h - z \right)$ where $\Delta \rho$ is the difference in density between the drop and the surrounding medium, g is the gravitational acceleration, and $z = h$ defines the height at which $\Delta P = 0$.

Fig. 1

Coordinate system for defining the shape of pendant drops

Equation (1) may be nondimensionalized by normalizing the coordinates with respect to the capillary length ${L_c = \sqrt{\gamma / \Delta \rho g}}$ (e.g., $\overline{x}=x/L_c$), yielding

$$\begin{aligned} \frac{\mathrm {d}\phi }{\mathrm {d}\overline{s}} = \left( \overline{h} - \overline{z} \right) - \frac{\sin \theta }{\overline{x}}. \end{aligned}$$

(2)

The complete set of equations describing the family of pendant drop shapes is then given by Eq. (2) and Eqs. (3–7)

$$\begin{aligned} \frac{\mathrm {d}\overline{x}}{\mathrm {d}\overline{s}} = \cos \phi \left( \overline{s}\right) \end{aligned}$$

(3)

$$\begin{aligned} \frac{\mathrm {d}\overline{z}}{\mathrm {d}\overline{s}} = \sin \phi \left( \overline{s}\right) \end{aligned}$$

(4)

$$\begin{aligned} \overline{x} = {\left\{ \begin{array}{ll} 0 &{} \overline{s}=0 \\ \overline{a} &{} \overline{s}=\overline{s}_0 \end{array}\right. } \end{aligned}$$

(5)

$$\begin{aligned} \overline{z} = {\left\{ \begin{array}{ll} -\overline{d} &{} \overline{s}=0 \\ 0 &{} \overline{s}=\overline{s}_0 \end{array}\right. } \end{aligned}$$

(6)

$$\begin{aligned} \phi = {\left\{ \begin{array}{ll} 0 &{} \overline{s}=0 \\ \chi &{} \overline{s}=\overline{s}_0 \end{array}\right. } \end{aligned}$$

(7)

where $\overline{a}$ is the nondimensionalized rod radius, $\overline{d}$ is the nondimensionalized depth of the drop, $\overline{s}_0$ is the nondimensionalized arc length at $\overline{z}=0$, and $\chi$ is the tangent angle at the solid-liquid interface ($\overline{s}=\overline{s}_0$). A numerical solution of the drop shape ($\overline{x}(s)$, $\overline{z}(s)$) may be obtained by renormalizing the domain with respect to $\overline{s}_0$.

The Bond number

$$\begin{aligned} Bo = \Delta \rho g R^2_0 / \gamma = \left( R_0 / L_c\right) ^2 \end{aligned}$$

(8)

is a dimensionless quantity that is a measure of the relative influence of gravity to that of surface tension on the drop shape [10, 11]. $R_0$ is the radius of curvature at $s = 0$. For an axisymmetric drop (this analysis is only true for axisymmetric drops) $R_0 = R_1 (0) = R_2 (0)$ where $R_1(s)$ and $R_2(s)$ are the principal radii of curvature. Large values of Bo are associated with drops of low sphericity. Small values of Bo indicate that the drop shape is largely controlled by surface tension. As a consequence, drops with small Bond numbers are relatively insensitive to d (drop growth). The error associated with measured values of $\gamma$ is therefore much greater for drops with small Bo, as most drops will exhibit only small deviations from sphericity, which are difficult to capture with precision. Berry et al. [9] provides a detailed analysis of this phenomenon. Practically speaking, it is advantageous, therefore, to carry out experiments in which the pendant drops that form have Bond numbers that are as large as possible. Figure 2 provides some sense of the relation between rod diameter, drop size, and Bond number. Plotted are curves of Bo as a function of $\overline{d}$ for a range of nondimensionalized rod radii, $\overline{a}$, from 0.2 to 1.5. The dashed line is the locus of maximum drop volume. For perspective, we may look at typical liquid metals, which have capillary lengths near $5\ \text {mm}$. For a $2.5\ \text {mm}$ radius rod (a typical rod size for use in the TIF), the Bond number for a liquid metal drop close to its maximum volume is approximately 0.45. From the analysis by Berry et al., it can be concluded that such a measurement, if performed, would yield values of the surface tension without significant error when computed via a curve fitting optimization. This of course does not take into account other sources of experimental uncertainty, such as sample contamination and vibrations.

Fig. 2

Bond number (Bo) as a function of the nondimensionalized drop depth ($\overline{d}=d/L_c$) for a range of nondimensionalized rod radii ($\overline{a}=a/L_c$). The dashed line is the locus of maximum drop volume. The maximum drop volume is a point of unstable equilibrium, and values of Bo and $\overline{d}$ beyond this point to do not represent physically-realizable static drop shapes

The calculation of $\gamma$ from pendant drop shapes was first conducted by Andreas et al. [12] and later expanded upon by Fordham [13]. In this approach, a shape factor $S=r_s/r_e$ is determined for the drop image, where $r_e$ is the drop radius at its widest point and $r_s$ is the drop radius at $z=2r_e - d$. From the Bond number equation ($Bo = \Delta \rho g R^2_0 / \gamma$) a term $H(S)=4Bo(r_e/R_0)^2$ is defined, and values of $\gamma$ may be calculated from reported tables of H as a function of S. The principal deficiency of this approach is the relatively large error incurred by the high sensitivity of the calculated $\gamma$ to the single quantity $r_e$. For a $1\ \%$ error in $r_e$, the uncertainty in $\gamma$ may be as large as $20\ \%$ [14]. Nevertheless, the approach of Andreas and Fordham remains a standard analytical method for calculating surface tension from pendant drop images.

Greater precision in the determination of $\gamma$ was achieved by the development of computer optimization programs for fitting the entirety of the drop profile to the theoretical drop shape [9, 15, 16]. In this method, the surface tension is calculated by minimizing an objective function of the unknown parameters governing the drop shape:

$$\begin{aligned} \mathop {\text {argmin}}\limits _\nu = \sum ^N_{n=1} \left[ e\left( u_n,\nu \right) \right] ^2,\ \nu \equiv f\left( Bo, R_0, x(s_0), z(s_0),...\right) \end{aligned}$$

(9)

where $e\left( u_n,\nu \right)$ is the distance between point $u_n$ on the measured drop profile and the nearest point on the theoretical drop curve $\nu$, which is a function of several unknown parameters, invariably including the Bond number, $R_0$, and the position of the drop apex. For a detailed perspective, see Rotenburg et al. [16] and Berry et al. [9].

Experimental Methods

Sample Preparation

Copper rods (Goodfellow $99.95\ \%$ O.F.H.C., $\varnothing = 5\,\text {mm}, 100\,\text {mm}$ length) were degreased with anhydrous acetone and placed in a 3 M nitric acid bath at room temperature for 30 s before being rinsed with deionized water. They were then dried and immediately stored in Ar.

Fig. 3

a Xenon lamp. b Ellipsoidal mirror. c Liquid drop. d Sample rod. e Stainless steel sample holder. f stainless steel rod. g Quartz tube with window. h Welding glass. i Camera. j Threaded steel cap. k TIF

Furnace Operation

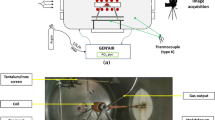
A TIF (Crystal Systems Corp., model TX-12000-I-MIT-PC) equipped with four Xe lamps (12 kW total) was used to form the pendant drops, a schematic of which is presented in Fig. 3. The metal rod was held in place by a stainless steel set-screw sample holder fixed to the upper shaft, which provides rotation and z-axis displacement via external stepper motors with sub-millimeter precision. In this way, deviations from drop axisymmetry were minimized. Sealing for the upper shaft was provided by an Ultra-Torr fitting. A quartz tube (Technical Glass Products, $\varnothing = 50\ \text {mm}$) sealed with Viton O-rings provided a gas-tight environment for the rod. The quartz tube was manufactured with a 23 mm flat circular pane positioned at the z-position of the furnace hot-zone and was oriented to face the welding glass viewing port on the furnace enclosure through which images were taken. The images were captured using a tripod-mounted camera (Canon Inc., EOS Rebel T5i DSLR) equipped with a zoom lens (Canon Inc., EF-S 18–135 mm).

Prior to heating, the interior of the quartz tube was evacuated and refilled with Ar gas (Airgas Inc., UHP Ar $>99.999\ \%$). This purge operation was carried out a minimum of three times, after which an Ar flow rate of 200 mL $\text {min}^{-1}$ was established using a digital mass flow controller (Tylan General Inc., FC-260V). The lamps were then powered and the rotating (3 rpm) rod positioned so that its free end was located in the furnace hot-zone. The lamp power was increased by $1\ \%$ per minute until melting was observed. The temperature was measured with a type C thermocouple in the vicinity of the drop, with the uncertainty being within 50 $^{\circ }\mathrm {C}$ of $T_\text {fus} = 1084\ ^{\circ }\mathrm {C}$. At this point rotation was stopped. Once the liquid copper drop was stable and of sufficient size, photographs were taken with the following image capture settings: 400 ISO, 1/30 s shutter speed, and f/5.6. An example of such an image is presented in Fig. 4a. If, at some point the drop detached from the rod, the rod end was refrozen and the lamp power ramp-up was carried out again.

Image Processing

The raw images were processed using Wolfram Mathematica 11. After cropping the images, an edge-detection algorithm was applied to isolate the drop profile as shown in Fig. 4b and c. The drop outline was then filled white (Fig. 4d). The processed images were subsequently analyzed with the open-source tensiometry software OpenDrop [9], which applies a drop shape optimization routine to calculate the apparent surface tension from the measured drop shape.

Fig. 4

a Raw drop image, cropped from the original photograph. b Image after passing through the Mathematica edge detection function. c The drop profile after removal of extraneous edges. d Final drop profile to be used with the OpenDrop program

Results and Discussion

The calculated surface tension for liquid copper is 1.159 $\pm \ 0.043\,$N$\text {m}^{-1}$ at a temperature of within 50 $^{\circ }\mathrm {C}$ of $T_\text {fus}$ (1084 $^{\circ }\mathrm {C}$). The error is the statistical uncertainty from 36 drop images. The value we calculate is in agreement with previously published values [17]. These are shown in Fig. 5. Our value is slightly lower than the typically accepted value of 1.3 N$\text {m}^{-1}$. The discrepancy may be due to surface active impurities such as oxygen, as some oxide was observed on the drop surface during the measurements.

Fig. 5

Comparison of published values [17] for the surface tension of liquid copper with the value calculated in this study

Conclusion

A procedure for measuring surface tension from pendant drops using an optical TIF in conjunction with an open source tensiometry program OpenDrop was described. This is the first study employing a setup suitable for measuring the surface tension of both electronically conductive liquids and nonmetal liquids such as molten oxides. Liquid copper was chosen was a suitable candidate metal for evaluating this methodology. We report a value of 1.159 $\pm \ 0.043\,$N$\text {m}^{-1}$ for the surface tension of liquid copper at its melting point, in agreement with published values.