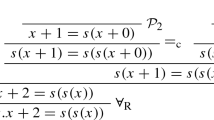Keywords

1 Introduction

The implicational fragment of propositional intuitionistic logic can be defined by two axiom schemes:

$$\begin{aligned}&K: ~~~~~ A\rightarrow \left( B\rightarrow A\right) \\&S: ~~~~~ \left( A\rightarrow \left( B\rightarrow C\right) \right) \rightarrow \left( \left( A\rightarrow B\right) \rightarrow \left( A\rightarrow C\right) \right) \\ \end{aligned}$$

and the modus ponens inference rule:

$$MP: ~~~~~ A,~A \rightarrow B ~\vdash ~ B.$$

Our interest in theorem provers for this minimalist logic fragment has been triggered by its relation, via the Curry-Howard isomorphism, to the inverse problem, corresponding to inferring types for lambda terms, type inhabitation. In its simplest form, the Curry-Howard isomorphism [1, 2] connects the implicational fragment of propositional intuitionistic logic and types in the simply typed lambda calculus. A low polynomial type inference algorithm associates a type (when it exists) to a lambda term. Harder (PSPACE-complete, see [3]) algorithms associate inhabitants to a given type expression with the resulting lambda term (typically in normal form) serving as a witness for the existence of a proof for the corresponding tautology in implicational propositional intuitionistic logic. As a consequence, a theorem prover for implicational propositional intuitionistic logic can also be seen as a tool for program synthesis, as implemented by code extraction algorithms in proof assistants like Coq [4].

This provides a simple and effective testing mechanism: by using as input the type of a lambda term known to have as an inhabitant the term itself. While only providing “positive examples” - formulas known to be tautologies, this is becoming increasingly difficult with size, as the asymptotic density of typable terms in the set of closed lambda terms has been shown to converge to 0 [5]. As a consequence, even our best generators [6], based on Boltzmann samplers, are limited to lambda terms in normal form of about size 60–70, given the very large number of retries needed to filter out untypable terms.

Thus, besides generating large simply typed lambda terms, we will need to devise testing methods also ensuring correct rejection of non-theorems and termination on arbitrary formulas.

This will lead us to a stepwise refinement from simpler to more efficient equivalent provers. We will start from a known, proven to be sound and complete prover as a first step, and use a test-driven approach to improve its performance and scalability while having soundness and completeness as invariants. As even small, apparently obvious changes in sound and complete provers can often break these properties, one must chose between writing a formal proof for each variant or setting up an extensive combinatorial and random testing framework, able to ensure correctness, with astronomically low chance of error, “at the push of a button”.

We chose the second approach. Besides the ability to also evaluate scalability and performance of our provers, our combinatorial generation library, released as open source software, has good chances to be reused as a testing harness for other propositional solvers, (e.g., SAT, ASP or SMT solvers) with structurally similar formulas.

Our combinatorial testing framework comprises generators for

  • simply typed lambda terms (in normal form) and their types

  • formulas of the implicational subset of propositional calculus, requiring

    • generation of binary trees with internal nodes labeled with

    • generation of set partitions helping to label variables in leaf position.

For quick correctness tests we build all-formula generators. Total counts for formulas of a given size for tautologies and non-tautologies provide an instant indicator for high-probability correctness. It also provides small false positives or negatives, helpful to explain and debug unexpected behavior.

For performance, scalability and termination tests, in the tradition of QuickCheck [7, 8] we build random formula generators, with focus on ability to generate very large simply typed lambda terms and implicational formulas.

While our code at (https://github.com/ptarau/TypesAndProofs), covers a few dozen variants of implicational as well as full propositional provers, we will describe here a few that win on simplicity and/or scalable performance.

Notations and Assumptions. As we will use Prolog as our meta-language, our notations will be derived as much as possible from its syntax (including token types and operator definitions). Thus, variables will be denoted with uppercase letters and, as programmer’s conventions final s letters indicate a plurality of items (e.g., when referring to the content of \(\varGamma \) contexts). We assume that the reader is familiar with basic Prolog programming, including, besides the pure Horn clause subset, well-known builtin predicates like memberchk/2 and select/3, elements of higher order programming (e.g., call/N), and occasional use of CUT and if-then-else constructs.

Lambda terms are built using the function symbols a/2 = application, l/2 = lambda binder, with a logic variable as first argument and expression as second, as well as logic variables representing the variables of the terms.

Type expressions (also seen as implicational formulas) are built as binary trees with the function symbol and logic variables at their leaves.

The Paper Is Organized as Follows. Section 2 overviews the LJT sequent calculus for implicational propositional intuitionistic logic. Section 3 describes, starting with a direct encoding of the LJT calculus as a Prolog program, derivation steps leading to simpler and faster provers. Section 4 describes our testing framework. Section 5 overviews related work and Sect. 6 concludes the paper.

2 Proof Systems for Implicational Propositional Intuitionistic Logic

Initially, like for other fields of mathematics and logic, Hilbert-style axioms were considered for intuitionistic logic. While simple and directly mapped to SKI-combinators via the Curry-Howard isomorphism, their usability for automation is very limited. In fact, their inadequacy for formalizing even “hand-written” mathematics was the main trigger of Gentzen’s work on natural deduction and sequent calculus, inspired by the need for formal reasoning in the foundation of mathematics [9].

Thus, we start with Gentzen’s own calculus for intuitionistic logic, simplified here to only cover the purely implicational fragment, given that our focus is on theorem provers working on formulas that correspond to types of simply-typed lambda terms.

2.1 Gentzen’s LJ Calculus, Restricted to the Implicational Fragment of Propositional Intuitionistic Logic

We assume familiarity with basic sequent calculus notation. Gentzen’s original LJ calculus [9] (with the equivalent notation of [10]) uses the following rules.

$$\begin{aligned}&LJ_1:~~~~\frac{~}{A,\varGamma ~\vdash ~ A}\\&LJ_2:~~~~\frac{A,\varGamma ~\vdash ~ B}{\varGamma ~\vdash ~ A\rightarrow B}\\&LJ_3:~~~~\frac{A \rightarrow B,\varGamma ~\vdash ~ A ~~~~ B,\varGamma ~\vdash ~ G}{A \rightarrow B, \varGamma ~\vdash ~ G}\\ \end{aligned}$$

As one can easily see, when trying a goal-driven implementation that uses the rules in upward direction, the unchanged premises on left side of rule \(LJ_3\) would not ensure termination as nothing prevents A and G from repeatedly trading places during the inference process.

2.2 Roy Dyckhoff’s LJT Calculus, Restricted to the Implicational Fragment of Propositional Intuitionistic Logic

Motivated by problems related to loop avoidance in implementing Gentzen’s LJ calculus, Roy Dyckhoff [10] splits rule \(LJ_3\) into \(LJT_3\) and \(LJT_4\).

$$\begin{aligned}&LJT_1:~~~~\frac{~}{A,\varGamma ~\vdash ~ A}\\&LJT_2:~~~~\frac{A,\varGamma ~\vdash ~ B}{\varGamma ~\vdash ~ A\rightarrow B}\\&LJT_3:~~~~\frac{B,A,\varGamma ~\vdash ~ G}{A \rightarrow B,A,\varGamma ~\vdash ~ G}\\&LJT_4:~~~~\frac{D \rightarrow B,\varGamma ~\vdash ~ C \rightarrow D ~~~~ B,\varGamma ~\vdash ~ G}{ \left( C \rightarrow D \right) \rightarrow B,\varGamma ~\vdash ~ G }\\ \end{aligned}$$

This avoids the need for loop checking to ensure termination as one can identify a multiset ordering-based size definition that decreases after each step [10]. The rules work with the context \(\varGamma \) being a multiset, but it has been shown later [11] that \(\varGamma \) can be a set, with duplication in contexts eliminated.

As it is not unusual with logic formalisms, the same calculus had been discovered independently in the 50’s by Vorob’ev and in the 80’s–90’s by Hudelmaier [12, 13].

3 The Test-Driven Prover Derivation Process

Starting from this calculus, we will describe our “test-driven” derivation process for simpler and/or more efficient provers that will be validated at each step by our testing framework described in the next section.

3.1 An Executable Specification: Dyckhoff’s LJT Calculus, Literally

Roy Dyckhoff has implemented the LJT calculus as a Prolog program.

We have ported it to SWI-Prolog as a reference implementation (see https://github.com/ptarau/TypesAndProofs/blob/master/third_party/dyckhoff_orig.pro). However, it is a fairly large (420 lines) program, partly because it covers the full set of intuitionistic connectives and partly because of the complex heuristics that it implements.

This brings up the question if, in the tradition of “lean theorem provers”, we can build one directly from the LJT calculus, in a goal oriented style, by reading the rules from conclusions to premises.

Thus, we start with a simple, almost literal translation of rules \(LJT_1 \ldots LJT_4\) to Prolog with values in the environment \(\varGamma \) denoted by the variable Vs.

figure c

Note the use of select/3 to extract a term from the environment (a nondeterministic step) and termination, via a multiset ordering based measure [10]. An example of use is:

figure d

Note also that integers can be used instead of atoms, flexibility that we will use as needed.

Besides the correctness of the LJT rule set (as proved in [10]), given that the prover has passed our tests, it looks like being already quite close to our interest in a “lean” prover for the implicational fragment of propositional intuitionistic logic. However, given the extensive test set (see Sect.  4) that we have developed, it is not hard to get tempted in getting it simpler and faster, knowing that the smallest error will be instantly caught.

3.2 Concentrating Nondeterminism into One Place

We start with a transformation that keeps the underlying implicational formula unchanged. It merges the work of the two select/3 calls into a single call, observing that their respective clauses do similar things after the call to select/3. That avoids redoing the same iteration over candidates for reduction.

figure e

This results on our tests (see Sect. 4 for details) in an improvement on a mix of tautologies and non-tautologies, in exchange for a slowdown on formulas known to be tautologies.

3.3 Implicational Formulas as Nested Horn Clauses

Given the equivalence between: \(B_1 \rightarrow B_2 \ldots B_n \rightarrow H\) and (in Prolog notation) H :- \(B_1,B_2, \ldots , B_n\), (where we choose H as the atomic formula ending a chain of implications), we can, recursively, transform an implicational formula into one built form nested clauses, as follows.

figure f

Note also that the transformation is reversible and that lists (instead of Prolog’s conjunction chains) are used to collect the elements of the body of a clause.

figure g

This suggests transforming provers for implicational formulas into equivalent provers working on nested Horn clauses.

figure h

A first improvement, ensuring quicker rejection of non-theorems is the call to memberchk in the 3-rd clause to ensure that our goal G is the head of at least one of the assumptions. Once that test is passed, the 3-rd clause works as a reducer of the assumed hypotheses. It removes from the context a clause and it removes from its body a formula , to be passed to , with the remaining context. Should be atomic, we succeed if and only if it is already in the context. Otherwise, we closely mimic rule \(LJT_4\) by trying to prove , after extending the context with the assumption . Note that in both cases the context gets smaller, as does not contain the anymore. Moreover, should the body end up empty, the clause is downgraded to its atomic head by the predicate trimmed/2. Also, by having a second select/3 call in the third clause of ljh, will give ljh_imp more chances to succeed and commit.

Thus, besides quickly filtering out failing search branches, the nested Horn clause form of implicational logic helps bypass some intermediate steps, by focusing on the head of the Horn clause, which corresponds to the last atom in a chain of implications.

The transformation brings to hprove/1 an extra 66% performance gain over bprove/1 on terms of size 15, which scales up to run as much as 29 times faster on terms of size 16.

3.4 Propagating Back the Elimination of Non-matching Heads

We can propagate back to the implicational forms used in bprover the observation made on the Horn-clause form that heads (as computed below) should match at least one assumption.

figure r

We can apply this to bprove/1 as shown in the 3-rd clause of lje, where we can also prioritize the assumption found to have the head G, by placing it first in the context.

figure s

This brings the performance of eprove within a few percents of hprove.

3.5 Extracting the Proof Terms

Extracting the proof terms (lambda terms having the formulas we prove as types) is achieved by decorating in the code with application nodes a/2, lambda nodes l/2 (with first argument a logic variable) and leaf nodes (with logic variables, same as the identically named ones in the first argument of the corresponding l/2 nodes).

The simplicity of the predicate eprove/1 and the fact that this is essentially the inverse of a type inference algorithm (e.g., the one in [14]) help with figuring out how the decoration mechanism works.

figure t

Thus, lambda nodes decorate implication introductions and application nodes decorate modus ponens reductions in the corresponding calculus. Note that the two clauses of ljs_imp provide the target node T. When seen from the type inference side, T is the type resulting from cancelling the source type S and the application type \(S \rightarrow T\).

Calling sprove/2 on the formulas corresponding to the types of the S, K and I combinators, we obtain:

figure u

4 The Testing Framework

Correctness can be checked by identifying false positives or false negatives. A false positive is a non-tautology that the prover proves, breaking the soundness property. A false negative is a tautology that the prover fails to prove, breaking the completeness property. While classical tautologies are easily tested (at small scale against truth tables, at medium scale with classical propositional provers and at larger scale with a SAT solver), intuitionistic provers require a more creative approach, given the absence of a finite truth-value table model.

As a first bootstrapping step, assuming that no “gold standard” prover is available, one can look at the other side of the Curry-Howard isomorphism, and rely on generators of (typable) lambda terms and generators implicational logic formulas, with results being checked against a trusted type inference algorithm.

As a next step, a trusted prover can be used as a “gold standard” to test both for false positives and negatives.

4.1 Finding False Negatives by Generating the Set of Simply Typed Normal Forms of a Given Size

A false negative is identified if our prover fails on a type expression known to have an inhabitant. Via the Curry-Howard isomorphism, such terms are the types inferred for lambda terms, generated by increasing sizes. In fact, this means that all implicational formulas having proofs shorter than a given number are all covered, but possibly small formulas having long proofs might not be reachable with this method that explores the search by the size of the proof rather than the size of the formula to be proven. We refer to [14] for a detailed description of efficient algorithms generating pairs of simply typed lambda terms in normal form together with their principal types. The code we use here is at: https://github.com/ptarau/TypesAndProofs/blob/master/allTypedNFs.pro

4.2 Finding False Positives by Generating All Implicational Formulas/Type Expressions of a Given Size

A false positive is identified if the prover succeeds finding an inhabitant for a type expression that does not have one.

We obtain type expressions by generating all binary trees of a given size, extracting their leaf variables and then iterating over the set of their set partitions, while unifying variables belonging to the same partition. We refer to [14] for a detailed description of the algorithms.

The code describing the all-tree and set partition generation as well as their integration as a type expression generator is at:

https://github.com/ptarau/TypesAndProofs/blob/master/allPartitions.pro.

We have tested the predicate lprove/1 as well as all other provers derived from it for false negatives against simple types of terms up to size 15 (with size defined as 2 for applications, 1 for lambdas and 0 for variables) and for false positives against all type expressions up to size 7 (with size defined as the number of internal nodes).

An advantage of exhaustive testing with all formulas of a given size is that it implicitly ensures coverage: no path is missed simply because there are no paths left unexplored.

4.3 Testing Against a Trusted Reference Implementation

Assuming we trust an existing reference implementation (e.g., after it passes our generator-based tests), it makes sense to use it as a “gold standard”. In this case, we can identify both false positives and negatives directly, as follows:

figure v

When specializing to a generator for all well-formed implication expressions, and using Dyckhoff’s dprove/1 predicate as a gold standard, we have:

figure w

To test the tester, we design a prover that randomly succeeds or fails.

figure x

We can now test lprove/1 and badprove/1 as follows:

figure y

A more interesting case is when a prover is only guilty of false positives. For instance, let’s naively implement the intuition that a goal is provable w.r.t. an environment Vs if all its premises are provable, with implication introduction assuming premises and success achieved when the environment is reduced to empty.

figure z

As the following test shows, while no tautology is missed, the false positives are properly caught.

figure aa

4.4 Random Simply-Typed Terms, with Boltzmann Samplers

Once passing correctness tests, our provers need to be tested against large random terms. The mechanism is similar to the use of all-term generators.

We generate random simply-typed normal forms, using a Boltzmann sampler along the lines of that described in [6]. The code variant, adapted to our different term-size definition is at:

https://github.com/ptarau/TypesAndProofs/blob/master/ranNormalForms.pro. It works as follows:

figure ab

Interestingly, partly due to the fact that there’s some variation in the size of the terms that Boltzmann samplers generate, and more to the fact that the distribution of types favors (as seen in the second example) the simple tautologies where an atom identical to the last one is contained in the implication chain leading to it [5, 15], if we want to use these for scalability tests, additional filtering mechanisms need to be used to statically reject type expressions that are large but easy to prove as intuitionistic tautologies.

4.5 Random Implicational Formulas

The generation of random implicational formulas is more intricate.

Our code combines an implementation of Rémy’s algorithm [16], along the lines of Knuth’s algorithm R in [17] for the generation of random binary trees at https://github.com/ptarau/TypesAndProofs/blob/master/RemyR.pro with code to generate random set partitions at:

https://github.com/ptarau/TypesAndProofs/blob/master/ranPartition.pro.

We refer to [18] for a declarative implementation of Rémy’s algorithm in Prolog with code adapted for this paper at:

https://github.com/ptarau/TypesAndProofs/blob/master/RemyP.pro.

As automatic Boltzmann sampler generation of set partitions is limited to fixed numbers of equivalence classes from which a CF- grammar can be given, we build our random set partition generator that groups variables in leaf position into equivalence classes by using an urn-algorithm [19]. Once a random binary tree of size N is generated with the constructor labeling internal nodes, the \(N+1\) leaves of the tree are decorated with variables denoted by successive integers starting from 0. As variables sharing a name define equivalence classes on the set of variables, each choice of them corresponds to a set partition of the \(N+1\) nodes. Thus, a set partition of the leaves {0,1,2,3} like {{0},{1,2},{3}} will correspond to the variable leaf decorations

$$\begin{aligned} 0,1,1,2 \end{aligned}$$

The partition generator works as follows:

figure ad

Note that the list of labels it generates can be directly used to decorate the random binary tree generated by Rémy’s algorithm, by unifying the list of variables Vs with it.

figure ae

The combined generator, that produces in a few seconds terms of size 1000, works as follows:

figure af

Note that we use Prolog’s tabling (a form of automated dynamic programming) to avoid costly recomputation of the (very large) Sterling numbers in the code at: https://github.com/ptarau/TypesAndProofs/blob/master/ranPartition.pro.

4.6 Testing with Large Random Terms

Testing for false positives and false negatives for random terms proceeds in a similar manner to exhaustive testing with terms of a given size.

Assuming Roy Dyckhoff’s prover as a gold standard, we can find out that our bprove/1 program can handle 20 terms of size 50 as well as the gold standard.

figure ag

In fact, the size of the random terms handled by bprove/1 makes using provers an appealing alternative to random lambda term generators in search for very large (lambda term, simple type) pairs. Interestingly, on the side of random simply typed terms, limitations come from their vanishing density, while on the other side they come from the known PSPACE-complete complexity of the proof procedures.

4.7 Scalability Tests

Besides the correctness and completeness test sets described so far, one might want also ensure that the performance of the derived provers scales up to larger terms. Given space constraints, we only show here a few such performance tests and refer the reader to our benchmarks at: https://github.com/ptarau/TypesAndProofs/blob/master/bm.pro.

Time is measured in seconds. The tables in Fig. 1 compare several provers on exhaustive “all-terms” benchmarks, derived from our correctness test.

Fig. 1.
figure 1

Performance of provers on exhaustive tests (faster ones in the right table)

Full size image

First, we run them on the types inferred on all simply typed lambda terms of a given size. Note that some of the resulting types in this case can be larger and some smaller than the sizes of their inhabitants. We place them in the column Positive - as they are known to be all provable.

Next, we run them on all implicational formulas of a given size, set to be about half of the former (integer part of size divided by 2), as the number of these grows much faster. We place them in the column Mix as they are a mix of provable and unprovable formulas.

The predicate hprove/1 turns out to be an overall winner, followed closely by eprove/1 that applies to implicational forms a technique borrowed from hprove/1 to quickly filter out failing search branches.

Testing exhaustively on small formulas, while an accurate indicator for average speed, might not favor provers using more complex heuristics or extensive preprocessing, as it is the case of Dyckhoff’s original dprove/1.

We conclude that early rejection via the test we have discovered in the nested Horn clause form is a clear separator between the slow provers in the left table and the fast ones in the right table, a simple and useful “mutation” worth propagating to full propositional and first order provers.

As the focus of this paper was to develop a testing methodology for propositional theorem provers, we have not applied more intricate heuristics to further improve performance or to perform better on “human-made” benchmarks or compare them on such tests with other provers, as there are no purely implicational tests among at the ILTP library [20] at http://www.iltp.de/. On the other hand, for our full intuitionistic propositional provers at https://github.com/ptarau/TypesAndProofs, as well as our Python-based ones at https://github.com/ptarau/PythonProvers, we have adapted the ILTP benchmarks on which we plan to report in a future paper.

5 Related Work

The related work derived from Gentzen’s LJ calculus is in the hundreds if not in the thousands of papers and books. Space constraints limit our discussion to the most closely related papers, directly focusing on algorithms for implicational intuitionistic propositional logic, which, as decision procedures, ensure termination without a loop-checking mechanism.

Among them the closest are [10, 11], that we have used as starting points for deriving our provers. We have chosen to implement the LJT calculus directly rather than deriving our programs from Roy Dyckhoff’s Prolog code. At the same time, as in Roy Dyckhoff’s original prover, we have benefitted from the elegant, loop-avoiding rewriting step also present in Hudelmaier’s work [12, 13]. Similar calculi, key ideas of which made it into the Coq proof assistant’s code, are described in [21].

On the other side of the Curry-Howard isomorphism, the thesis [22], described in full detail in [23], finds and/or counts inhabitants of simple types in long normal form. But interestingly, these algorithms have not crossed, at our best knowledge, to the other side of the Curry-Howard isomorphism, in the form of theorem provers.

Using hypothetical implications in Prolog, although all with a different semantics than Gentzen’s LJ calculus or its LJT variant, go back as early as [24, 25], followed by a series of \(\lambda \)Prolog-related publications, e.g., [26]. The similarity to the propositional subsets of N-Prolog [25] and \(\lambda \)-Prolog [26] comes from their close connection to intuitionistic logic. The hereditary Harrop formulas of [26], when restricted to their implicational subset, are much easily computable with a direct mapping to Prolog, without the need of theorem prover. While closer to an LJ-based calculus, the execution algorithm of [25] uses restarts on loop detection instead of ensuring termination along the lines the LJT calculus. In [27] backtrackable linear and intuitionistic assumptions that mimic the implication introduction rule are used, but they do not involve arbitrarily deep nested implicational formulas.

Overviews of closely related calculi, using the implicational subset of propositional intuitionistic logic are [11, 28].

For generators of random lambda terms and related functional programming constructs we refer to [7, 8]. We have shared with them the goal of achieving high-probability correctness via automated combinatorial testing. Given our specific focus on propositional provers, we have been able to use all-term and all-formula generators as well as comparison mechanisms with “gold-standard” provers. We have also taken advantage of the Curry-Howard isomorphism between types and formulas to provide an initial set of known tautologies, usable as “bootstrapping mechanism” allowing to test our provers independently from using a “gold-standard”.

6 Conclusions and Future Work

Our code base at https://github.com/ptarau/TypesAndProofs provides an extensive test-driven development framework built on several cross-testing opportunities between type inference algorithms for lambda terms and theorem provers for propositional intuitionistic logic.

It also contains the code of the provers presented in the paper together with several other provers and “human-made” test sets.

Our lightweight implementations of these theoretically hard (PSPACE-complete) combinatorial search problems, are also more likely than provers using complex heuristics, to be turned into parallel implementations using multi-core and GPU algorithms.

Among them, provers working on nested Horn clauses outperformed those working directly on implicational formulas. The fact that conjunctions in their body are associative and commutative also opens opportunities for AND-parallel execution.

Given that they share their main data structures with Prolog, it also seems interesting to attempt their partial evaluation or even compilation to Prolog via a source-to-source transformation. At the same time, the nested Horn clause provers might be worth formalizing as a calculus and subject to deeper theoretical analysis. We plan future work in formally describing the nested Horn-clause prover in sequent-calculus as well as exploring compilation techniques and new parallel algorithms for it. A generalization to nested Horn clauses with conjunctions and universally quantified variables seems also promising to explore, especially with grounding techniques as used by SAT and ASP solvers, or via compilation to Prolog.