Keywords

Introduction

Gold–copper (Au–Cu) alloy [1,2,3] is widely used for brazing filler metal, dental material and decoration due to its high wettability, excellent corrosion resistance and fascinating color. A large amount of waste Au–Cu alloy will be produced in China and overseas every year with the increasing consumption of Au–Cu alloy in electronics, aerospace and function materials filed. Au is precious metal, which can be used for investment and value preservation, or as an ornament, and Cu has good conductivity and is widely used in the power industry. The separation and recovery of Au and Cu from waste Au–Cu alloy in an environmentally sound manner, therefore, is of great practical significance not only for recovery of precious metals but also for conservation of mineral resources.

Vacuum distillation [4,5,6] is recognized as one of the most advanced and clean technologies for the separation of various kinds of alloys. It has the advantages of short flowsheet, zero discharge compared to other traditional smelting methods (e.g., pyre-refining and electro-refining). It can avoid the shortcomings of other smelting methods.

Reliable VLE data are essential for the design of different processes, such as vacuum distillation of alloys. It is difficult to determine the VLE of alloy systems by experiments because of the complexity and strong cohesiveness of metal vapor. In contrast, model prediction is a convenient and economic approach to obtain VLE data of alloy systems. Activity coefficients are indispensable for VLE prediction. The MIVM [7] proposed by Tao has been widely used to predict the activity coefficients of alloy systems [8,9,10,11,12,13,14], and good results have been achieved. However, the practical application of the MIVM has been greatly hindered by the complex calculation process of coordination numbers and lack of molar volumes of some components in liquid state (e.g., C, Ta, V2O5, Cu2S, CaSiO3, etc.). Tao [15] simplified the MIVM reasonably for expanding its application range. However, the simplified MIVM (SMIVM ) has not been used for the prediction of activity of Au–Cu alloy and VLE of alloy systems. Moreover, the authors did not find any reported VLE data for the binary Au–Cu alloy system. The Au–Cu alloy , therefore, was selected to demonstrate the utility and reliability of SMIVM in vacuum distillation in order to provide a rigorous model for quantitatively predicting the distribution of components of Au–Cu alloy in vacuum distillation. This will provide an intuitive and simple way to analyze the product compositions’ dependence of temperature and system pressure in vacuum distillation. The optimum technique parameters can also be obtained from VLE phase diagram .

The purpose of this study was to predict the activities of the components of Au–Cu alloy using the SMIVM ; the comparison between the calculated results and experimental data was carried out for validation purpose. The VLE phase diagrams of Au–Cu alloy in vacuum distillation were also predicted based on the SMIVM and VLE theory.

Simplified Molecular Interaction Volume Model

According to the MIVM, the molar excess Gibbs energy G Em of the liquid mixture i − j can be expressed as [7]

$$ \begin{aligned} \frac{{G_{\text{m}}^{\text{E}} }}{RT} & = x_{i} \ln \left( {\frac{{V_{{{\text{m}}i}} }}{{x_{i} V_{{{\text{m}}i}} + x_{j} V_{{{\text{m}}j}} B_{ji} }}} \right) + x_{j} \ln \left( {\frac{{V_{{{\text{m}}j}} }}{{x_{j} V_{{{\text{m}}j}} + x_{i} V_{{{\text{m}}i}} B_{ij} }}} \right) \\ & \quad - \frac{{x_{i} x_{j} }}{2}\left( {\frac{{Z_{i} B_{ji} \ln B_{ji} }}{{x_{i} + x_{j} B_{ji} }} + \frac{{Z_{j} B_{ij} \ln B_{ij} }}{{x_{j} + x_{i} B_{ij} }}} \right) \\ \end{aligned} $$
(1)

where xi and xj are the molar fractions of components i and j, Zi and Zj are first coordination numbers, Vmi and Vmj are the molar volumes of the components i and j in liquid phase, respectively, R is the universal gas constant, and Bij and Bji are the pair-potential energy interaction parameters.

The coordination numbers are defined as follows [7]:

$$ Z_{i} = \frac{{4\sqrt {2\pi } }}{3}\left( {\frac{{r_{mi}^{3} - r_{0i}^{3} }}{{r_{mi} - r_{0i} }}} \right)\rho_{i} r_{mi} \exp \left( {\frac{{\Delta H_{mi} (T_{mi} - T)}}{{Z_{c} RTT_{mi} }}} \right) $$
(2)

Zc = 12 is the close-packed coordination, and ΔHmi is the melting enthalpy. ρi= Ni/Vi = 0.6022/Vmi is the molecular number density, r0i and rmi are the beginning and first peak values of radial distance near its melting point, respectively. Vmi is the molar volume in cm3 mol−1, and Tmi is the melting temperature in Kelvin.

With the help of the thermodynamic relation (∂G Em /∂xi)T,p,xj≠i = RT lnγi, the activity coefficients of components of a binary mixture i − j can be derived, respectively, from Eq. (1) as follows:

$$ \begin{aligned} \ln \gamma_{i} & = \ln \left( {\frac{{V_{{{\text{m}}i}} }}{{x_{i} V_{{{\text{m}}i}} + x_{j} V_{{{\text{m}}j}} B_{ji} }}} \right) + x_{j} \left( {\frac{{V_{{{\text{m}}j}} B_{ji} }}{{x_{i} V_{{{\text{m}}i}} + x_{j} V_{{{\text{m}}j}} B_{ji} }} - \frac{{V_{{{\text{m}}i}} B_{ij} }}{{x_{j} V_{{{\text{m}}j}} + x_{i} V_{{{\text{m}}i}} B_{ij} }}} \right) \\ & \quad - \frac{{x_{j}^{2} }}{2}\left( {\frac{{Z_{i} B_{ji}^{2} \ln B_{ji} }}{{(x_{i} + x_{j} B_{ji} )^{2} }} + \frac{{Z_{j} B_{ij} \ln B_{ij} }}{{(x_{j} + x_{i} B_{ij} )^{2} }}} \right) \\ \end{aligned} $$
(3)
$$ \begin{aligned} \ln \gamma_{j} & = \ln \left( {\frac{{V_{{{\text{m}}j}} }}{{x_{j} V_{{{\text{m}}j}} + x_{i} V_{{{\text{m}}i}} B_{ij} }}} \right) - x_{i} \left( {\frac{{V_{{{\text{m}}j}} B_{ji} }}{{x_{i} V_{{{\text{m}}i}} + x_{j} V_{{{\text{m}}j}} B_{ji} }} - \frac{{V_{{{\text{m}}i}} B_{ij} }}{{x_{j} V_{{{\text{m}}j}} + x_{i} V_{{{\text{m}}i}} B_{ij} }}} \right) \\ & \quad - \frac{{x_{i}^{2} }}{2}\left( {\frac{{Z_{j} B_{ij}^{2} \ln B_{ij} }}{{(x_{j} + x_{i} B_{ij} )^{2} }} + \frac{{Z_{i} B_{ji} \ln B_{ji} }}{{(x_{i} + x_{j} B_{ji} )^{2} }}} \right) \\ \end{aligned} $$
(4)

It can be seen from Eq. (2) that the calculation of coordination number is complicated. Furthermore, the molar volumes Vmi are also difficult to find out from literature. This has greatly hindered the promotion and application of the MIVM. Recently, Tao [15] reported that the difference of component coordination numbers has negligible impact on the prediction accuracy of the MIVM. However, the prediction effect is somehow better when Z is close to 10. Therefore, the values of both Zi and Zj will be set as 10 in this study for simplification purpose.

In addition, the molar volume of component i in the liquid state, viz., Vmi, can be replaced by its molar volume in solid state Vi because the density difference of a substance in the liquid state and solid state is usually small.

Consequently, Eqs. (3) and (4) can be simplified, respectively, as Eqs. (5) and (6),

$$ \begin{aligned} \ln \gamma_{i} & = 1 + \ln \left( {\frac{{V_{i} }}{{x_{i} V_{i} + x_{j} V_{j} B_{ji} }}} \right) - \frac{{x_{i} V_{i} }}{{x_{i} V_{i} + x_{j} V_{j} B_{ji} }} - \frac{{x_{j} V_{i} B_{ij} }}{{x_{j} V_{j} + x_{i} V_{i} B_{ij} }} \\ & \quad - 5x_{j}^{2} \left( {\frac{{B_{ji}^{2} \ln B_{ji} }}{{(x_{i} + x_{j} B_{ji} )^{2} }} + \frac{{B_{ij} \ln B_{ij} }}{{(x_{j} + x_{i} B_{ij} )^{2} }}} \right) \\ \end{aligned} $$
(5)
$$ \begin{aligned} \ln \gamma_{j} & = 1 + \ln \left( {\frac{{V_{j} }}{{x_{j} V_{j} + x_{i} V_{i} B_{ij} }}} \right) - \frac{{x_{i} V_{j} B_{ji} }}{{x_{i} V_{i} + x_{j} V_{j} B_{ji} }} - \frac{{x_{j} V_{j} }}{{x_{j} V_{j} + x_{i} V_{i} B_{ij} }} \\ & \quad - 5x_{i}^{2} \left( {\frac{{B_{ij}^{2} \ln B_{ij} }}{{(x_{j} + x_{i} B_{ij} )^{2} }} + \frac{{B_{ji} \ln B_{ji} }}{{(x_{i} + x_{j} B_{ji} )^{2} }}} \right) \\ \end{aligned} $$
(6)

It can be seen from Eqs. (5) and (6) that the coordination number of pure component was not involved in the SMIVM . The SMIVM , therefore, will be more convenient than the MIVM in practical application.

VLE Calculation Method

The fugacity of each component in the vapor phase and liquid phase is equal when the system reaches equilibrium. Since vacuum distillation is usually carried out at less than 10 Pa (e.g., 5 Pa), the vapor phase can be regarded as an ideal gas, while the liquid phase is regarded as the actual solution. The actual solution is usually modified by inserting a factor γ into Raoult’s law, and a much more realistic equation for VLE can then be expressed as follows [16]:

$$ y_{i} p = x_{i} \gamma_{i} p_{i}^{\text{sat}} \quad \left( {i = 1,2,\, \ldots ,\,N} \right) $$
(7)

where p sat i is the saturated vapor pressure of pure component i at temperature T, p the system pressure ; xi and yi are the mole fraction of component i in the liquid phase and vapor phase, respectively; γi is the activity coefficient of component i in the liquid phase.

For a binary alloy system i − j,

$$ x_{i} + x_{j} = 1;\quad y_{i} + y_{j} = 1 $$
(8)
$$ p = p_{i}^{\text{sat}} \gamma_{i} x_{i} + p_{j}^{\text{sat}} \gamma_{j} x_{j} = p_{i}^{\text{sat}} \gamma_{i} x_{i} + p_{j}^{\text{sat}} \gamma_{j} (1 - x_{i} ) $$
(9)

Connecting Eqs. (7) and (9), xi and yi can be obtained as follows:

$$ x_{i} = \frac{{p - p_{j}^{\text{sat}} \gamma_{j} }}{{p_{i}^{\text{sat}} \gamma_{i} - p_{j}^{\text{sat}} \gamma_{j} }} $$
(10)
$$ y_{i} = \frac{{p_{i}^{\text{sat}} \gamma_{i} x_{i} }}{p} $$
(11)

Results and Discussion

Activity

In order to check the reliability of the SMIVM and to make the calculation representative, the activities of components of Au–Cu liquid alloy were calculated using the SMIVM .

The binary parameters Bji and Bij can be calculated from Eqs. (5) and (6) using the Newton–Raphson methodology if the infinite dilute activity coefficient, i.e., γ ∞ i and γ ∞ j are known. The calculation process is far more convenient than the MIVM because the calculation of Zi and Vmi was not involved in the SMIVM . The γ ∞ i and γ ∞ j [17] of Au–Cu binary liquid alloy are listed in Table 1.

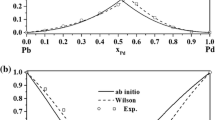
Table 1 The parameters of binary liquid Au–Cu alloy [17]
Full size table

Substituting the binary parameters Bji, Bij and Vi, Vj into Eqs. (5) and (6), the activities of components of Au–Cu alloy can be obtained, as shown in Fig. 1.

Fig. 1
figure 1

Comparison of the predicted activity of SMIVM (lines) with experimental data (symbols) of Au–Cu alloy

Full size image

It can be seen from Fig. 1 that the calculated activities are consistent with the experimental data. This confirms that the prediction of activities of Au–Cu alloy using the SMIVM is reliable. In order to make a more strict verification, the average relative deviations Si and the average standard deviations Si* were also calculated based on Eqs. (12) and  (13), respectively, and the result is shown in Table 2.

Table 2 The average relative deviations Si and the average standard deviations Si*of activity of components in Au–Cu alloy calculated using the SMIVM
Full size table
$$ S_{i} = \pm \frac{100}{n}\sum\limits_{i = 1}^{n} {\left| {\frac{{a_{i,\exp } - a_{{i,{\text{cal}}}} }}{{a_{i,exp} }}} \right|} $$
(12)
$$ S_{i}^{ *} = \pm \left[ {\frac{1}{n}\sum\limits_{i = 1}^{n} {\left[ {a_{i,\exp } - a_{{i,{\text{cal}}}} } \right]}^{2} } \right]^{1/2} $$
(13)

where ai,exp is the experimental data of activity , and ai,cal is the calculated data of the SMIVM , and n is the number of data points.

It can be seen from Table 2 that the average relative deviations and the average standard deviations were smaller than ±0.5528% and  ±0.0100, respectively, for the selected Au–Cu alloy system, which further confirms that the simplification of the MIVM in this work is reasonable, and the SMIVM is reliable for predicting the activity coefficients of components of Au–Cu alloy .

VLE of Au–Cu Alloy

For Au–Cu alloy , the general procedure for obtaining a T − x(y) diagram is realized using an iterative algorithm [4]. Substituting the corresponding γ, p and psat at different temperatures into Eqs. (10) and (11), the content of Au in the vapor phase and liquid phase can be obtained. The T − x(y) phase diagram of Au–Cu alloy can then be obtained, as shown in Fig. 3a. The saturated vapor pressure of Au and Cu can be calculated from the vapor pressure equation shown in Table 3 [18], as shown in Fig. 2.

Table 3 The equations for saturated vapor pressure of Au and Cu [18]
Full size table
Fig. 2
figure 2

Saturated vapor pressure of Au and Cu

Full size image

The calculation of p − x(y) diagram is somewhat similar to that of T − x(y) diagram, and the value of γ can be calculated from Eqs. (5) and (6) by setting a serious of value for x at a certain system temperature. Substituting these values into Eq. (9), the system pressure p can be obtained, respectively, and yAu can be obtained from Eq. (11). As a result, p − x(y) diagram of Au–Cu alloy system can be established, as shown in Fig. 3b.

Fig. 3
figure 3

VLE phase diagram of Au–Cu alloy : a T − x(y) diagram at 5 Pa; b p − x(y) diagram at 1700 K

Full size image

The comparison of the saturated vapor pressure of components of alloys at the same temperature can be used as a rough guide in predicting which one should exhibit preferential evaporation. As can be seen from Fig. 2 that the saturated vapor pressure of Cu was larger than that of Au, which indicates that Cu will evaporate into the vapor phase, Au concentrates in the liquid phase. Although the method of comparison of the saturated vapor pressure of components of Au–Cu alloy is really simple and convenient, the saturated vapor pressure cannot be used to predict the separation degree and the product composition in vacuum distillation.

It can be seen from Fig. 3a that the content of Cu in the vapor phase ranges from 0.3513 to 0.0126 and the content of Au in the liquid phase ranges from 0.9000 to 0.9980, while the temperature increases from 1809 to 1834 K at 5 Pa.

In addition, an optimal experimental condition of the vacuum process can be obtained from the VLE phase diagrams. For example, based on the T − x(y) phase diagram , if the purity of Au we wanted is higher than 0.998, then the distillation temperature at 5 Pa must be higher than 1834 K while the content of Cu in vapor phase will be less than 0.013.

Furthermore, the lever rule [19] can be used in the VLE phase diagram to determine the moles of residues and volatiles at a fixed temperature and pressure (e.g., T = 1700 K, p = 5 Pa). A tie line was plotted in the T − x(y) diagram which across the vapor and liquid curves to point P and Q, respectively, as shown in Fig. 3a. The compositions of P and Q are yP and xQ, respectively, after the system reaches equilibrium. Assuming the mole fraction of Au in the initial alloy is xM, the moles of residues and volatiles, i.e., nl and ng, can then be obtained, respectively, from the following level rule equations:

$$ n_{l} = \frac{{x_{M} - y_{P} }}{{x_{Q} - y_{P} }}n = \frac{{\left| {PM} \right|}}{{\left| {PQ} \right|}}n $$
(14)
$$ n_{g} = \frac{{x_{Q} - x_{M} }}{{x_{Q} - y_{P} }}n = \frac{{\left| {QM} \right|}}{{\left| {PQ} \right|}}n $$
(15)

where n is the total amount of substance of initial alloy, \( \left| {PM} \right| \), \( \left| {QM} \right| \) and \( \left| {PQ} \right| \) are the length of the line segment PM, QM and PQ, respectively.

It is very useful in quantitatively predicting the distribution of the components and the separation degree of alloys in vacuum distillation. The VLE phase diagrams can be used to choose the operational conditions and the needed products under specified conditions. The present calculation is helpful to get more reliable results in vacuum distillation due to the thermodynamic data is scarce.

Conclusions

In this work, the activities of components of Au–Cu liquid alloy were calculated using the SMIVM . The comparison shows that the calculated results are in good agreement with the experimental data, indicating that the SMIVM is very reliable for calculating the activity of Au–Cu alloy . Meanwhile, The VLE phase diagrams of Au–Cu alloy were calculated based on VLE theory and the SMIVM . The temperature–composition (T − x(y)) and pressure –composition (p − x(y)) phase diagrams can be used to quantitatively predict the products composition in vacuum distillation, and to choose the optimal process parameters , which provides an efficient and convenient way to guide the actual production of vacuum metallurgy.