1 Introduction

There is an increasing demand on reliability and safety of industrial systems subject to potential process abnormalities and component faults [1]. Electrical motors are one of the most used machines in the industry. Generally, they are critical components in automation processes. Therefore, questions related to their protection against failures have received great attention [2,3,4,5,6]. Condition monitoring and predictive maintenance of induction motors may lead to significant improvements of availability, quality, and productivity of production lines. Detecting faults in incipient stage is of utmost importance since functional failures may quickly occur after the initial development of a fault.

A major part of induction motor faults occurs in the stator windings [2, 7]. The inter-turns short-circuit is a primary fault that happens after insulation breakdown. Among the main reasons for insulation fail are high stator core or winding temperatures; slack core lamination, slot wedges, and joints; loose bracing for end winding; contamination due to chemical reactions, moisture, or dirt; electrical discharges due to aging of the insulating material; and leakage in cooling systems. After primary faults, the motor degradation process increases, and more serious failures, such as phase-to-phase and phase-to-ground short-circuits, appear. Usually, these types of faults result in irreversible motor damage. However, if inter-turns faults are detected at incipient stage, the faulty phase winding may, for example, be replaced, which significantly reduces financial losses and increases operational safety. Among the benefits detection systems can bring to industry are motor life extension, idling periods reduction, unnecessary disconnections avoiding, manpower scheduling at the fault moment, repair cost minimization, human security improvement, components storage reduction, and minimization of losses.

During the last three decades, computational intelligence methods have been a promising direction for solutions of pattern recognition issues. Neural Networks and Hybrid Systems have been successfully applied to detecting different kinds of faults in electrical machines [8,9,10,11,12]. A difficulty of applying neural networks to condition monitoring systems, as well as to the vast majority of real-world engineering applications, concerns the selection of a suitable network structure and connection parameters. A proper selection of these is essential to lead the network to achieve a reasonable fault detection performance. Some of these parameters, viz., the number of hidden layers and the number of neurons per layer, are frequently set from a trial-and-error approach performed by a human designer. This may be an exhaustive task that can take a considerable amount of time [12]. Efforts for making neural network design more sophisticated and less human dependent is underway, especially considering information from particular application domains.

A drawback of using neural networks for fault detection, including feedforward, recurrent, convolutional, and deep networks and deep models in general [13], is the use of first- or second-order deterministic optimization algorithms for training. Since the backpropagation (BP) algorithm was discussed by Rumelhart et al. [14], researchers quite often resort to first-order learning methods and variations. Since the nature of first-order methods is to converge locally, it can be demonstrated that its solution is highly dependent on random initial weights and rarely is the global solution. Several variations of first-order optimization methods were compared to Quasi-Newton, Non-Derivative Quasi-Newton, Gauss–Newton, and Secant methods by Chen and Sheu [15]; Evolutionary Strategies and Genetic Algorithm by [16, 17]; Bayesian Regularization, Modified Levenberg–Marquardt, and Simulated Annealing in [18]; Bee and Ant Colony by [19, 20]; Adaptive Differential Evolution in [21]; and Particle Swarm by [22, 23]. All these training methods could lead a neural model to achieve better performance in terms of learning efficiency, training time, easiness-of-use, and accuracy in a class of problems.

The present study focuses on the development of architectures and weights of feedforward neural networks using different learning algorithms, viz., a properly designed genetic algorithm and an online incremental algorithm. The former produces an evolutionary neural network (EANN), while the latter generates an evolving fuzzy granular neural network (EGNN). The purpose of the neural networks is to detect and determine the number of shorted-turns in the stator windings of induction machines. The problem is formulated as a multiclass classification problem. Real dynamic environment subject to mechanical asymmetries, voltage unbalance, and measurement noise is taken into consideration.

Evolving the EANN architecture includes finding a suitable number of hidden layers and neurons per layer—being these the parameters that largely affect its generalization ability. An overly complex neural model may overfit the data and thus exhibit poor generalization, whereas a simple model may be insufficient to represent nonlinear correlations among features. GA takes into account the development of both, parameters and structure of the neural network. The main reasons for the choice of GA as learning method are: (1) GA operates on codified parameters. It results in a search for local minima independently of the continuity of error functions or the existence of derivative; (2) the search toward the best solution starts from a set of points deployed in the search space (global search–populational strategy). Thus, the probability that the solution gets stuck on local minima is minimized; (3) the search toward the best solution utilizes genetic operators, which are stochastic in nature, instead of deterministic; and (4) GA automatizes the trial-and-error approach to set up structural parameters.

EGNN encodes a set of fuzzy rules in its structure. Therefore, neural processing conforms with that of a fuzzy inference system [24]. The network is equipped with fuzzy neurons, which perform aggregation functions, and with an incremental algorithm for learning from a data stream. Fuzzy granules and rules are created gradually according to new information discovered from the data. Evolving systems from data streams is an active and promising research topic [25,26,27,28,29,30,31,32,33,34,35]. In particular, EGNN provides: (1) computational tractability and scalability with the number of samples and attributes; (2) improved interpretability and transparency by means of granular local models and linguistic rules; and (3) reduced cost of data processing in relation to non-evolving methods. EGNN has shown to be extremely general and able to outperform state-of-the-art evolving methods and models, including evolving classifiers [24, 36, 37].

Section 2 outlines a general framework for electrical machine fault detection assisted by the genetic neural classifier, EANN, and the incremental neurofuzzy classifier, EGNN. Section 3 addresses GA learning and describes the genetic operators for recombining, mutating, and selecting architectures and connection weights of a feedforward network. Incremental learning from data streams and development of a neurofuzzy granular network are given in Sect. 4. EANN and EGNN performance on detecting incipient faults in induction machines and discussions about genetic and incremental learning are reported in Sect. 5. True conditions of actual industrial practice, namely, different load and speed conditions, voltage unbalance, and noisy environment, are analyzed. Section 6 concludes the chapter and presents some ideas for further investigation.

2 Electrical Machine Fault Detection

A general view of the electrical machine fault detection system is shown in Fig. 1. Voltage, current, and rotor speed measurements are obtained from induction motors and properly placed sensors. The data are preprocessed and attribute vectors whose values are related to the healthy state of the machines are obtained. The Acquisition and Data Treatment module also disposes the machines’ state variables to the Parameters Estimation, Optimization, and Faults Simulator modules. The latter includes faulty samples in the Database. Therefore, the database is composed of healthy and faulty data vectors. Faulty samples are related to different incipient fault severities, i.e., from 1 to 3 shorted-turns in the stator windings; different locations, i.e., stator phases a, b, and c; and different operating points and levels of noise. For EANN, a percentage of randomly selected samples are admitted for training, while the rest is used for testing. The Genetic Algorithm module develops the EANN architecture and its weights. It elects the best architecture and its respective best vector of weights according to a fitness function. On the other hand, a neurofuzzy EGNN structure is evolved from scratch by means of an incremental learning algorithm. In this case, training and testing are not separated procedures. In other words, EGNN provides an output—a classification for the input data sample—and then, the input–output pair is used for training. Online learning proceeds in a per-sample incremental basis. A diagnosis report is generated by both EANN and EGNN.

Fig. 1
figure 1

General view of the electrical machine fault detection and classification system

Full size image

A description of the system modules is given below:

  • Acquisition and data treatment → This module measures voltage, current, and rotor speed signals from induction machines. The number of motors connected to the system is limited by the number of I/O channels. The acquired data are preprocessed. Offsets are removed, and magnitude correction factors are applied. Low pass filters minimize noise and slot effect. Other calculations such as active and reactive power, power factor, rotor slip, and sequential components are carried out. The data are displayed on the interface prior to being saved in a file repository.

  • Parameters estimation module → No load and blocked rotor tests are required to be performed to obtain fundamental machine parameters if the corresponding datasheet is not available. Additionally, online parameter estimation algorithms, namely, Recursive Least Squares and Extended Kalman Filter, operate in parallel to adapt key parameters required by the inter-turns fault simulator model. Updated parameters are important to reflect the actual condition of the motor and avoid false positives. The most significant parameters considered for adaptation over time are the mutual inductance, rotor resistance, and equivalent resistance and inductance. Refer to [7, 38] for further descriptions.

  • Optimization module → This module provides further refinement of the parameters used by the fault simulator model. The Conditional Gradient method, also known as the Frank–Wolfe algorithm [39], is employed to optimize certain parameters, viz., the magnetizing and leakage inductances of the stator windings and the stator resistance. The objective is to allow the fault simulator to better reproduce the actual state variables. The objective function (OF) is the sum of the square error between the estimated and actual stator currents, voltage–current displacement angles, and rotor speed. Taken the derivative of the OF with respect to the states, we obtain a linearized OF for the application of the method. At each iteration, steps on the motor model parameters are given as an attempt to minimize the OF. If the OF value increases, the step on the parameters is rejected. The smaller the OF value, the more accurate the estimated states.

  • Fault simulator module → The state-space model of induction motors is changed mainly to allow simulations of turn-to-turn short-circuit in the stator windings. Moreover, changeable loads, voltage unbalance, noise, and winding asymmetries can be simulated. For completeness of this study, the key formulas are succinctly presented below. Refer to [7, 38, 40] for detailed information.

    The dynamic equations of an induction motor in state variables are

    $$\displaystyle \begin{aligned}{}[\dot{I}_{abcsr}]=[L]^{-1}\left[[V_{abcsr}]-\left[[R]+[\dot{L}]\right][I_{abcsr}]\right] {} \end{aligned} $$
    (1)

    where [L] and [R] are 6 × 6 inductance and resistance matrices; [V abcsr] and [I abcsr] are 6 × 1 stator and rotor voltage and current matrices in the abc frame of reference. \([\dot {I}_{abcsr}]\) can be calculated by the fourth-order Runge–Kutta algorithm. The model is complemented by mechanical equations:

    $$\displaystyle \begin{aligned} \begin{array}{rcl} T_{e} = \frac{P}{2}(i_{abcs})^T \frac{\partial}{\partial \theta_r} [L_{sr}^{\prime}] i_{abcr}^{\prime} {} \end{array} \end{aligned} $$
    (2)
    $$\displaystyle \begin{aligned} \begin{array}{rcl} \omega_{r} = \frac{P}{2}\int{\frac{T_{e}-T_{l}}{J}} {} \end{array} \end{aligned} $$
    (3)

    where T e is the electromagnetic torque; P the number of poles; θ r the electrical angular displacement; \([L_{sr}^{\prime }]\) and \(i_{abcr}^{\prime }\) the inductances and currents referred to the stator; ω r is the rotor speed; T l the load torque; and J the inertia.

    In a condition of stator shorted-turns, inductances are calculated from:

    $$\displaystyle \begin{aligned} \begin{array}{rcl} L_{(1-k)} = (1-k)^2L {} \end{array} \end{aligned} $$
    (4)
    $$\displaystyle \begin{aligned} \begin{array}{rcl} L_{k} = k^2L {} \end{array} \end{aligned} $$
    (5)
    $$\displaystyle \begin{aligned} \begin{array}{rcl} L_{k(1-k)} = (1-k)L {} \end{array} \end{aligned} $$
    (6)

    where k is the percentage of turns in short-circuit; L (1−k) refers to the inductance of the winding fraction without fault; and L k is the inductance of the faulty part of the winding. The latter equation refers to the mutual inductance between the part of the winding without fault and the other phases, including rotor phases. Refer to [7, 38] to comprehend how exactly the elements of the matrix L are changed due to shorted-turn faults.

    A fault requires the inductance matrix to be rewritten in seven dimensions, with three lines and columns representing the fraction of the stator phases without fault, a line and column representing the fraction of the faulty stator phase, and three lines and columns representing the rotor phases. Similarly, the resistance matrix is rewritten as a seven-dimension matrix considering:

    $$\displaystyle \begin{aligned} \begin{array}{rcl} R_{(1-k)} = (1-k)R {} \end{array} \end{aligned} $$
    (7)
    $$\displaystyle \begin{aligned} \begin{array}{rcl} R_{k} = kR {} \end{array} \end{aligned} $$
    (8)

    where R (1−k) and R k are the resistances of the winding fraction without and with fault. Naturally, the resistance matrix is diagonal.

  • Database → The database consists of input–output samples that are useful to train and test neural network classification models. The abc stator currents, voltage–current displacement angles per phase, and rotor speed are used in this study as input attributes to the neural classifiers. Several other attributes are available such as the dq0 and sequential components of voltages, currents, and magnetic fluxes [40]. The output variable is a class, which is associated to the number of stator shorted-turns per phase. Therefore, the neural classification models consist of a map f : X → Y  so that \(X \in \mathbb {R}^7\) and \(Y \in \mathbb {N}\). As new data samples are available, the neural classification models can be updated if needed.

  • EANN-GA → A feedforward neural network for each induction machine being monitored is considered. The network structure and connection weights are evolved via a specially designed genetic algorithm. EANN may have one or two hidden layers. While an inner loop deals with optimization over the parameter space, an outer loop concerns with searching for a potentially optimal solution over the structure space. After the learning process, the best network architecture and its best vector of parameters are chosen. Section 3 addresses phenotype representation; initialization of populations; recombination, mutation, and selection operators; fitness evaluation; and the stopping criteria adopted.

  • EGNN-IL → A neurofuzzy network able to learn gradually from a data stream is developed for each induction machine. EGNN self-adapts its granular structure and connection weights by means of a recursive procedure. Different fuzzy neurons to perform aggregation of values through the network can be chosen. Additionally, attribute weighting is an inherent characteristic of the network due to its modular structure. In general, EGNN can handle fuzzy, interval, and numerical data as well as prediction, control, and classification problems. This study focuses on numerical data processing and fault classification only. Section 4 describes how granules, rules, and weights are adapted on the fly.

  • Diagnosis report → A diagnosis report may be displayed at any time. The report includes statistical summaries of electrical machines, graphics of specific state variables and parameters, evolution of error indices and fault patterns, and neural network classification performance.

The condition monitoring system can manage several induction machines in field applications simultaneously. As the development of inter-turn faults takes some time, constant (uninterrupted) supervision of machines is not mandatory and, therefore, a single microcomputer and a switching scheme among machines and corresponding neural classifiers is, in general, acceptable. Otherwise, distributed computing may be taken into consideration. The monitoring response time is usually short, and microcomputer availability is high since offline training of EANN classification models can be performed apart from online data processing whereas EGNN online adaptation is carried out in a matter of milliseconds, as discussed in the next sections. As a numerical example, if 10 induction motors are monitored, then switching the corresponding neural classifiers in 10-s intervals is enough.

3 Genetic Algorithm for Neural Network Learning

This section describes a genetic method for developing the architecture and setting the parameters of a feedforward neural network. Fundamentally, the genetic algorithm performs the following steps:

  • Genetic representation or codification of potential solutions;

  • Definition of initial parameters. These include population size, relative elitism, penalty factors, mutation rate, and training stop criteria;

  • Initialization of the population with a priori knowledge about the expected behavior of the neural network;

  • Application of genetic operators, i.e., mutation, recombination, and selection operators, over individuals of the population;

  • Evaluation of the fitness of the individuals of a population;

  • Post-processing of the fittest individual.

The GA learning procedure is shown in the flowchart of Fig. 2. In the figure, the inner loop evolves Ω generations of weights individuals, whereas the outer loop evolves α generations of architectures individuals (global search). The fittest architecture individual and its respective fittest weights are found. Post-processing concerns searching for better solutions on the parameter space, close to the fittest vector of weights for a specific architecture (local search). In the figure, W and A are related to the weights and architectures populations, respectively. Learning is guided by an error-and-model-compactness-based fitness function.

Fig. 2
figure 2

General view of the genetic algorithm for developing the architecture and adapting the parameters of a feedforward neural network for fault detection

Full size image

3.1 Initialization and Parameterization

A schematic representation of the basic processing units of the evolutionary neural network is illustrated in Fig. 3. In the figure, x j and w j refer to the j-th input and connection weight, respectively; b is the bias; net is the weighted sum of the inputs, and φ(.) is a sigmoidal logistic function, which gives the output y.

Fig. 3
figure 3

Schematic representation of a neuron of the evolutionary neural network

Full size image

From prior knowledge about the neural network learning problem, we want the nonlinear functions φ(.) of all neurons to be initially triggered within their unsaturated regions, i.e., net≅0 for sigmoid functions. Otherwise, the network would barely differentiate input data at the very beginning of the learning process, which could lead a rougher and slower adaptation. For example, if the error backpropagation algorithm is considered, a mechanism to accelerate learning convergence is to set small random initial weights. Similarly, in real genetic programming, the allele (range of possible values) of genes (elements) of chromosomes (candidate solutions) representing weight vectors can be initially adjusted to small random values around 0, e.g., [−0.01, 0.01], yielding the same result.

Some remarks about the EANN learning algorithm include: (1) initial architectures and weights populations consist of 20 individuals each. We consider the Pittsburgh approach, i.e., all architecture and weight vectors compete with each other to be the fittest solution; (2) the algorithm is elitist. The fittest solution in previous generations is preserved for the next generations. The elitist approach ensures that the overall best individual remains in the population independently of the application of genetic operators; and (3) the number of individuals that compose the populations of architectures and weights is constant over generations. Although recombination operators make the populations double in size, a selection operator reduces the populations to the half.

Notice that GA global heuristic search tends to find a “good” solution by exploiting a highly dimensional parameter space whose error surface contains several hills, valleys, and plateaus. However, such solution may not be locally optimal. There are some hybrid techniques proposed in the literature for post-processing the solution through local search methods, e.g., [41, 42]. In this study, local search using a gene mutation operator is employed. Details are addressed in the subsequent sections.

3.2 Phenotype Representation

Mapping phenotypes into genotypes is crucial in the development of GA-based models, especially in constrained optimization problems. For instance, mutation and recombination operators may produce infeasible solutions. Care must be taken in both representation of individuals and definition of genetic operators. Undesirable effects such as requirement of extra manipulations of chromosomes, more complex objective functions, and premature convergence of the population may be immediate outcomes of an inadequate representation.

Encoding in GA is the form in which chromosomes and genes are expressed. There are basically two types of encoding, binary and real. The former was widely discussed, while the latter fits continuous optimization problems better and therefore is adopted in the present study. Several successful applications of real codification may be found in the literature, e.g., [17, 43].

Let P and G be phenotypic (behavioral) and genotypic (informational) spaces, respectively [44]. Phenotypes representing feedforward neural network architectures and weight vectors are encoded into genotypes by a direct mapping M P→G. Genotypes are assumed to be haploid chromosomes as shown in Fig. 4. Chromosomes associated to architectures are composed of a pair of genes, A and B, which refer to the number of neurons in the first and second hidden layers of EANN. In case gene A or B is zero, then the underlying EANN has a single hidden layer. The range of values, i.e., the allele, that each gene of the architecture chromosomes may assume is [0, 99], while the allele of weight chromosomes is [−1, 1].

Fig. 4
figure 4

Phenotype–genotype codification of architectures and weights

Full size image

The length of a weight chromosome:

$$\displaystyle \begin{aligned} \begin{array}{rcl} L = I A + A B + B O, {} \end{array} \end{aligned} $$
(9)

is variable. It depends on the values of the genes of the corresponding architecture chromosome, A and B, and on the number of inputs, I, and outputs, O, of the underlying neural network.

3.3 Recombination Operator

Defining the most appropriate recombination operator for different sorts of applications is a hard problem and an open issue. We examine common recombination operators in anomaly detection scenarios, viz., Arithmetic, Multipoint, and Local Intermediate Crossover. These operators can be either sexual or global. In the sexual form, only parents are involved on the generation of offspring. Conversely, in the global form, the whole population may contribute to generate offspring. In this study, we opt for the sexual form of recombination. In other words, 20 parents generate 20 children in each iteration of the algorithm.

3.3.1 Arithmetic Crossover

This operator is particularly suited for constrained numerical optimization problems with convex feasible region Ξ C. Let c n, n = 1, …, N, represent the n-th individual of a population. As a consequence of two individuals, c n1 and c n2, belong to Ξ C, convex combinations of c n1 and c n2 also belong to Ξ C. This ensures that Arithmetic Crossover produces only valid offspring.

Formally, two parent chromosomes are linearly combined to produce two offspring according to:

$$\displaystyle \begin{aligned} \begin{array}{rcl} Son_1 = a ~ Parent_1 + (1- a) ~ Parent_2 \end{array} \end{aligned} $$
(10)
$$\displaystyle \begin{aligned} \begin{array}{rcl} Son_2 = (1 - a) ~ Parent_1 + a ~ Parent_2 \end{array} \end{aligned} $$
(11)

where a is a random value chosen before each crossover operation. As an example, consider a random list of parents, see Fig. 5. Each operation produces two children whose genes inherit a combination of the parent genes.

Fig. 5
figure 5

Arithmetic crossover operator

Full size image

3.3.2 Multipoint Crossover

In multipoint crossover, children inherit sets of successive genes from two randomly selected parents. p randomly selected points along the chromosomes of the parents divide them into p + 1 parts. Then, genes of each father are exchanged to generate offspring. An intuitive example of a p-point crossover operator is shown in Fig. 6. Similar to other crossover operators, the population doubles in size after multipoint recombination. The recombination potential, exploratory power, and learning progress of a GA using p-point crossover are discussed in [45].

Fig. 6
figure 6

Multipoint crossover operator

Full size image

3.3.3 Local Intermediate Crossover

Local intermediate crossover is particularly useful when convergence to a unique solution is expected. In this operator, the average values of the genes of randomly selected parents are inherited by the single offspring, that is:

$$\displaystyle \begin{aligned} \begin{array}{rcl} c^{\prime}_{n1} = \frac{c_{n1} + c_{n2}}{2} ~. \end{array} \end{aligned} $$
(12)

Local intermediate crossover implies that sons receive inheritance of both parents equally. Clearly, if intermediate recombination is applied often, then the chromosomes become similar. This may lead to premature convergence of the population, especially when no other operator, such as mutation, is used to keep population diversity. Two crossover lists with 10 matches each are considered in this study to generate 20 children for the next generation.

3.4 Mutation Operator

Mutation operations involve single individuals, in contrast to recombination. This type of operator assures that there is always a probability of reaching any point within the search space. Usually, when the current solution of the problem is far from being the best according to a fitness function, a higher mutation rate can be employed as an attempt to find better solutions farther from the current ones. On the other hand, when the current solution is close from being the best, a low mutation rate can be adopted. This approach leads to search for solutions in promising regions.

Mutation commonly does not produce offspring. The mutated individuals remain in the population for later breeding. An individual c n has its corresponding mutated value \(c_n^{\prime }\) from \(c_n^{\prime } = m(c_n)\), where m(.) is a mutation function. Gaussian and random mutation operators are considered for analysis.

3.4.1 Gaussian Mutation

Gaussian mutation is frequently applied in real-coded GA. This is mainly because it supports fine-tuning of solutions. Chromosomes c n of an individual have their corresponding mutated values \(c_n^{\prime }\) from:

$$\displaystyle \begin{aligned} \begin{array}{rcl} c_n^{\prime} = c_n \pm M ~, \end{array} \end{aligned} $$
(13)

where M is a normal density function N(mean, Γ) with mean = 0 and standard deviation, Γ.

Gaussian mutation is applied gene-to-gene, with a gene mutation probability rate between 1% and 10%, directly proportional to the fitness of the chromosome.

3.4.2 Random Mutation

Random mutation is a member of the class of random search optimization methods. Features that make this operator useful are the enhancement of processing speed and nonsusceptibility to local minima. Randomness is generally controlled to ensure convergence while allowing enough freedom for a complete coverage of the search space.

Random mutation creates a random solution \(c_n^{\prime }\) at the vicinity of the current solution c n using a uniform probability distribution such that all genes of the newest individual \(c_n^{\prime }\) are within [−1, 1] and [0, 99] for weight and architecture chromosomes, respectively. The mutated genes should remain feasible with respect to these bounds. The free change of mutated genes may give rise to better solutions. Better solutions are maintained, while worse ones are rejected. Similar to the Gaussian mutation, random mutation is applied gene-to-gene with a changing probability rate from 1% to 10%. Mutated values are given as:

$$\displaystyle \begin{aligned} \begin{array}{rcl} c_n^{\prime} = c_n + r ~, {} \end{array} \end{aligned} $$
(14)

where r is a random value in [−0.1, 0.1] for weight individuals; and a random value in [−5, 5] rounded to an integer for the case of architecture individuals.

3.4.3 Post-Processing Based on Local Random Mutation

Post-processing neural network parameters can be done from different local search methods. Local mutation is a simple and fast approach to try to improve the solution found so far. With the EANN architecture defined, the basic idea is to change some genes of the current weight solution using random mutation in a specific way.

Mutation probability rate is restricted to 10% per gene, and r ∈ [−0.1, 0.1], as in (14). Whenever a gene is changed, the fitness of the new solution is immediately calculated, and the new value of the gene is either accepted or ignored. New weight solutions are evaluated twice, considering c n + r and c n − r. This approach promotes a local search for a better solution around the current best solution and parallel to the axes of the search space.

3.5 Fitness Function

GA mimics the principle of natural selection. A fitness measure is used to choose relatively fitter individuals in a population to evolve. The higher the fitness of an individual, the higher its survival probability [44].

To determine the fitness of weight chromosomes, we use

$$\displaystyle \begin{aligned} \begin{array}{rcl} F(c_n) = \gamma (\tau_{train}^\xi + \tau_{test}^\zeta) ~, {}\vspace{-2pt} \end{array} \end{aligned} $$
(15)

where F(c n) is the fitness of the chromosome c n; ξ and ζ are parameters defined according to the emphasis on training and testing performance; τ train and τ test refer to the neural network learning and generalization ability:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \tau_{train} = \frac{C_{train}} {C_{train} + W_{train}} ~, \end{array} \end{aligned} $$
(16)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \tau_{test} = \frac{C_{test}} {C_{test} + W_{test}} ~, \end{array} \end{aligned} $$
(17)

where C and W are the amount of correct and wrong classifications. In addition:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \gamma = e^{-k L} {} \end{array} \end{aligned} $$
(18)

is a penalty factor for large network architectures; L, calculated as in Eq. (9), is the length of a weight chromosome; and 0 < k < 1 is a constant.

The fitness of an architecture chromosome is the greatest fitness of weight chromosomes of the current generation. Naturally, F should be maximized.

3.6 Selection Operator

Selection is the operation in which individuals are chosen for later breeding. First, individuals are chosen to enter a mating pool. Operators should ensure that individuals with higher fitness have greater probability of being selected for mating, but those individuals with lower fitness still have a probability of being chosen. Having some probability of choosing worse individuals is important to assure that the search process is global and it does not simply converge to the nearest local minimum.

The original GA uses selection proportional to the fitness usually implemented with Roulette Wheel [44]. To better control the selective pressure of individuals and to avoid premature convergence, Tournament selection is considered [46].

3.6.1 Tournament Selection

Tournament selection is an alternative to fitness-proportional selection. Empirical results suggest that the tournament method can perform better and be faster than roulette selection [44, 46]. Moreover, it attenuates the selection pressure.

The operator considers the number of wins of an individual in H matches against H random opponents of the population—a one-against-one approach. The winner of a match is the individual with the best fitness compared to the direct opponent.

We use H = 5 in such a way that individuals winning at least three matches remain for the next generation. The procedure continues until the mating pool is full, i.e., 20 out of 40 individuals are selected. The selective pressure provided by the tournament operator is weak since a good diversity of individuals may remain in the population. Parents and children may compose the next generation.

3.6.2 Elitism

Elitism consists in maintaining the fittest individual of the population. This strategy ensures that the best solution found so far is retained. While this strategy could be applied more broadly, e.g., selecting the 2 or 3 best solutions, overuse can lead to premature convergence to a suboptimal solution. Tournament selection, as described in the previous section, is inherently an elitist approach.

3.7 Stopping Criteria

Training stopping criteria is an important issue in evolutionary modeling. Early termination may generate poor solutions, whereas late termination might cause overfitting. The proposed GA is terminated if one of the following is reached:

  • Maximum number of architecture generations, α;

  • Maximum number of weight generations, Ω;

  • Acceptable fitness reached, \(F(c_n^*) > \varXi \);

  • Maximum number of weight generations without replacing the fittest c n, δ.

In the latter case, the solution has attained a plateau such that iterations have no longer produced better results.

4 Incremental Algorithm for Neurofuzzy Network Learning

EGNN is a neurofuzzy granular network constructed incrementally from an online data stream [24, 36]. Although its learning algorithm can process mixtures of fuzzy, interval, and numerical data, this study focuses on numerical data only. Additionally, the network can play the role of a regressor, predictor, controller, or classifier [47, 48]. We emphasize EGNN for fault detection and classification. Particularly, evolving classification is a research topic under broad discussion. A number of methods have been developed with focus on typicality and eccentricity data analytics [49], robustness of Takagi–Sugeno fuzzy models [50], local strategies to smooth parameter changes [51], self-organization of fuzzy models [52], ensembles of models [53], scaffolding fuzzy type-2 models [54], semi-supervision [55], interval granular computing models [56], and on applications such as fault detection in wind turbines [57] and monitoring of waste-water treatment processes [58].

The basic processing elements of EGNN are fuzzy neurons. Its architecture encodes a set of fuzzy rules, and neural processing conforms with a fuzzy inference system. The network architecture results from a gradual construction according to new information. The consequent part of an EGNN rule may be composed of a linguistic and a functional term. Independently of the choice of fuzzy neuron, network parameters, and properties of input–output data, the linguistic term of the rule consequent produces a granular output, while the functional term gives a pointwise output. In the present study, we are interested in the pointwise output only, which is a class. Learning in EGNN means to fit new data into local granular models recursively. Granules, neurons, and connections can be added, adapted, removed, and combined. Therefore, the network captures new information from data streams and adapts itself to a new scenario.

4.1 Numerical and Fuzzy Data

Fuzzy data arise from expert knowledge, inaccurate measurements, variables that are hard to be precisely quantified, perceptions, and when preprocessing steps introduce uncertainty in numerical data. A fuzzy datum x j has the following form:

$$\displaystyle \begin{aligned} \begin{array}{rcl} x_j(z)=\left\{\begin{array}{cl} \phi_j, & ~ z \in ~[\underline{\underline{x}}_j,\underline{x}_j[ \\ 1, & ~ z \in ~[\underline{x}_j,\overline{x}_j] \\ \iota_j, & ~ z \in ~ ]\overline{x}_j,\overline{\overline{x}}_j] \\ 0, & ~ \mathrm{otherwise} \end{array}\right. {} \end{array} \end{aligned} $$
(19)

where z is a real number in X j. If the fuzzy datum x j is normal (x j(z) = 1 for at least one \(z \in \Re \)) and convex (x j(κz 1 + (1 − κ)z 2) ≥ min(x j(z 1), x j(z 2)), \(z^1, z^2 \in \Re \), κ ∈ [0, 1]), then it is a fuzzy interval [59]. In particular, if:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \phi_j &\displaystyle =&\displaystyle \frac{z-\underline{\underline{x}}_j}{\underline{x}_j-\underline{\underline{x}}_j} \mathrm{ ~ and} \end{array} \end{aligned} $$
(20)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \iota_j &\displaystyle =&\displaystyle \frac{\overline{\overline{x}}_j-z}{\overline{\overline{x}}_j-\overline{x}_j}, \end{array} \end{aligned} $$
(21)

then the fuzzy datum (19) has trapezoidal membership function and can be represented by the quadruple \(( \underline { \underline {x}}_j, \underline {x}_j,\overline {x}_j,\overline {\overline {x}}_j)\). If \( \underline {x}_j = \overline {x}_j\), the fuzzy datum is a fuzzy number. Numerical data arise if \( \underline { \underline {x}}_j = \underline {x}_j = \overline {x}_j = \overline {\overline {x}}_j\).

4.2 Network Architecture

Let x = (x 1, …, x n) be an input vector and y the output. Consider that the data stream (x, y)[h], h = 1, …, is measured from an unknown function f. Inputs x j and output y can be fuzzy data in general and numerical data in particular.

Figure 7 shows a four-layer EGNN model. The input layer receives x [h]. The granular layer consists of a set of granules \(G^i_j\), j = 1, …, n; i = 1, …, c, stratified from the input data. Fuzzy sets \(G_j^i\), i = 1, …, c, form a fuzzy partition of the j-th input domain, X j. A granule \(G^i= G^i_1 \times \cdots \times G^i_n\) is a fuzzy relation, i.e., a multidimensional fuzzy set in X 1 ×⋯ × X n. Thus, G i has membership function \(G^i(x) = min\{G_1^i(x_1),\cdots ,G_n^i(x_n)\}\) in X 1 ×⋯ × X n. Granule G i may have a companion local function p i. For classification, we use a 0-th-order function:

$$\displaystyle \begin{aligned} \begin{array}{rcl} p^i(\hat{x}_1,\ldots,\hat{x}_n) = \hat{C}^i, {} \end{array} \end{aligned} $$
(22)

where \(\hat {C}^i\) is the estimated class.

Fig. 7
figure 7

Evolving neurofuzzy network architecture

Full size image

Define \(\hat {x}_j\) as the midpoint of \(x_j = ( \underline { \underline {x}}_j, \underline {x}_j,\overline {x}_j,\overline {\overline {x}}_j)\). Thus:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathrm{mp}(x_j) = \hat{x}_j = \frac{\underline{x}_j+\overline{x}_j}{2}. \end{array} \end{aligned} $$
(23)

Naturally, if the input data are numerical, then \(\hat {x}_j = x_j\).

Similarity degrees \(\widetilde {x}^{i} = (\widetilde {x}^{i}_1, \ldots , \widetilde {x}^{i}_n)\) are the result of matching between input x = (x 1, …, x n) and fuzzy sets \(G^i = (G_1^i,\ldots ,G_n^i)\). In general, data and granules are trapezoidal objects. A convenient similarity measure to quantify the match between a sample and the current knowledge is

(24)

This measure returns \(\widetilde {x}_j^i=1\) for identical trapezoids and reduces linearly as any numerator term increases. Naturally, measure (42) can be applied to numerical data. In this case, \( \underline { \underline {x}}_j = \underline {x}_j = \overline {x}_j = \overline {\overline {x}}_j\) [24, 48].

The aggregation layer is composed of fuzzy neurons A i, i = 1, …, c. A fuzzy neuron A i combines weighted similarity degrees \((\widetilde {x}^{i}_1 w^{i}_1, \ldots , \widetilde {x}^{i}_n w^{i}_n)\) into a single value o i, which refers to the level of activation of rule R i. The output layer processes (o 1, …, o c) using a fuzzy neuron A f. A f performs the maximum S-norm in this study. The class C i∗ associated to the most active rule R i∗ is the network output.

Under assumption on specific weights and types of neurons, fuzzy rules extracted from the EGNN classifier, as described in this study, are of the type:

$$\displaystyle \begin{aligned} R^i:\text{ IF (}x_1\text{ is }G_1^i\text{ ) AND }\ldots\text{ AND (}x_n\text{ is }G_n^i\text{ ) THEN }(\hat{y} \text{ is } \hat{C}^i\text{ )}. \end{aligned}$$

As: (1) fuzzy sets \(G^i_j ~ \forall i, j,\) are time varying; (2) a diversity of aggregation functions can be used in the neural body A i; and (3) fuzzy granules overlap in the input space, thus the class separation surface provided by an EGNN model is nonstationary and can be highly nonlinear.

4.3 Fuzzy Neuron

Fuzzy neurons are neuron models based on aggregation operators. EGNN may use different types of aggregation neurons to perform information fusion. Generally, there is no guideline to choose a particular aggregation operator to construct a fuzzy neuron [60].

Aggregation operators A : [0, 1]n → [0, 1], n > 1, combine input values in the unit hypercube [0, 1]n into a single value in [0, 1]. They must satisfy the following properties: (1) monotonicity in all arguments, i.e., given \(x^1 = (x^1_1, \ldots , x^1_n)\) and \(x^2 = (x^2_1, \ldots , x^2_n)\), if \(x^1_j \leq x^2_j ~\forall j\) then A(x 1) ≤ A(x 2); and (2) boundary conditions: A(0, 0, …, 0) = 0 and A(1, 1, …, 1) = 1. The classes of aggregation operators considered in this study are summarized below. See [59, 60] for a detailed coverage.

4.3.1 Triangular Norm and Conorm

T-norms (T) are commutative, associative, and monotone operators on the unit hypercube whose boundary conditions are T(α, α, …, 0) = 0 and T(α, 1, …, 1) = α, α ∈ [0, 1]. An example of T-norm is the minimum operator:

(25)

which is the strongest T-norm because:

$$\displaystyle \begin{aligned} \begin{array}{rcl} ~~ T(x) \leq T_{min}(x) ~~ \mathrm{for any} ~ x \in [0,1]^n. \end{array} \end{aligned} $$
(26)

The minimum is idempotent, symmetric, and Lipschitz-continuous. Further examples of T-norms include the product:

$$\displaystyle \begin{aligned} \begin{array}{rcl} T_{prod}(x) = \prod_{j=1}^n x_j,\vspace{-3pt} \end{array} \end{aligned} $$
(27)

and the Lukasiewicz T-norm:

$$\displaystyle \begin{aligned} \begin{array}{rcl} T_L (x)= \max(0,\sum_{j=1}^n x_j - (n-1)),\vspace{-3pt} \end{array} \end{aligned} $$
(28)

which are non-idempotent, but Lipschitz-continuous aggregation operators.

S-norms (S) are operators on the unit hypercube which are commutative, associative, and monotone. S(α, α, …, 1) = 1 and S(α, 0, …, 0) = α are the boundary conditions of S-norms.

S-norms are stronger than T-norms. The maximum operator:

(29)

is the weakest S-norm, that is:

$$\displaystyle \begin{aligned} \begin{array}{rcl} S(x) \geq S_{max}(x) \geq T(x), ~ \mathrm{for any} ~ x \in [0,1]^n.\vspace{-3pt} \end{array} \end{aligned} $$
(30)

The maximum is idempotent, symmetric, and Lipschitz-continuous.

4.3.2 Neuron Model

Let \(\widetilde {x} = (\widetilde {x}_1, \ldots , \widetilde {x}_n)\) be a vector of membership degrees of a sample x = (x 1, …, x n) in the fuzzy sets G = (G 1, …, G n). Let w = (w 1, …, w n) be a weight vector such that:

$$\displaystyle \begin{aligned} \begin{array}{rcl} w_j \in [0,1], ~ j = 1,\ldots,n. \end{array} \end{aligned} $$
(31)

Product T-norm is used to perform synaptic processing, while an aggregation operator A is used to fuse the individual results of synaptic processing. The output of a fuzzy aggregation neuron is

$$\displaystyle \begin{aligned} \begin{array}{rcl} o = A(\widetilde{x}_1 w_1, \ldots, \widetilde{x}_n w_n). \end{array} \end{aligned} $$
(32)

A fuzzy neuron produces a diversity of nonlinear mappings between neuron inputs and output depending on the choice of weights w and aggregation operator A. The fuzzy neuron model is shown in Fig. 8.

Fig. 8
figure 8

Fuzzy neuron model

Full size image

4.4 Granular Region

The support and the core of trapezoidal membership function \(G^i_j\) are

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathrm{supp}(G^i_j) &\displaystyle =&\displaystyle [\underline{\underline{g}}^i_j,\overline{\overline{g}}^i_j], {} \end{array} \end{aligned} $$
(33)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathrm{core}(G^i_j) &\displaystyle =&\displaystyle [\underline{g}^i_j,\overline{g}^i_j].\vspace{-3pt} \end{array} \end{aligned} $$
(34)

The midpoint and width of \(G^i_j\) are given by:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathrm{mp}(G^i_j) &\displaystyle =&\displaystyle \frac{\underline{g}^i_j+\overline{g}^i_j}{2}, \end{array} \end{aligned} $$
(35)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathrm{wdt}(G^i_j) &\displaystyle =&\displaystyle \overline{\overline{g}}^i_j - \underline{\underline{g}}^i_j.\vspace{-3pt} \end{array} \end{aligned} $$
(36)

The maximal allowed expandable width of fuzzy sets \(G_j^i\) is denoted by ρ, i.e., wdt\((G^i_j) \leq \rho \), j = 1, …, n; i = 1, …, c. Let the expansion region of a fuzzy set \(G^i_j\) be

$$\displaystyle \begin{aligned} \begin{array}{rcl} E^i_j &\displaystyle =&\displaystyle \left[\mathrm{mp}(G^i_j) - \frac{\rho}{2}, \mathrm{mp}(G^i_j) + \frac{\rho}{2}\right]. {}\vspace{-3pt} \end{array} \end{aligned} $$
(37)

It follows that wdt\((G^i_j) \leq \) wdt\((E^i_j)\) ∀j, i. Values of ρ allow different representations of the same problem at different levels of detail.

4.5 Granularity Adaptation

A balance between parametric and structural adaptation is a key to capture changes of time-varying systems. The procedure described below reconciles parametric and structural changes in EGNN.

The value of ρ affects the granularity and accuracy of models. In practice, ρ ∈ [0, 1] settles the size of expansion regions (37) and the need to either create or adapt rules to fit a new sample. EGNN starts learning with an empty rule base and with no a priori knowledge of data properties. In this case, it is worth to initialize ρ at an intermediate value, e.g., ρ [0] = 0.5.

Let r be the number of rules created in h r steps. If the number of rules grows faster than a rate η, i.e., r > η, then ρ is increased:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \rho(\mathrm{new}) &\displaystyle =&\displaystyle \left( 1 + \frac{r}{h_r} \right) \rho(\mathrm{old}). {}\vspace{-3pt} \end{array} \end{aligned} $$
(38)

Equation (38) acts against outbursts of growth since large rule bases increase model complexity and worsen generalization. If the number of rules grows at a rate smaller than η, i.e., r ≤ η, then ρ is decreased:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \rho(\mathrm{new}) &\displaystyle =&\displaystyle \left( 1 - \frac{(\eta-r)}{h_r} \right) \rho(\mathrm{old}).\vspace{-3pt} \end{array} \end{aligned} $$
(39)

If ρ = 1, then EGNN is structurally stable, but unable to capture abrupt changes. Conversely, if ρ = 0, then EGNN overfits the data causing excessive model complexity. Adaptability is reached from intermediate values.

Reducing ρ may require a reduction of larger granules to fit them to the new requirement. In this case, the support of \(G^i_j\) is narrowed as follows:

Cores \([ \underline {g}_j^i,\overline {g}_j^i]\) are handled similarly. Time-varying granularity is useful to avoid guesses on how fast and how often the data stream properties change.

4.6 Developing Granules

Granules are created if the support of at least one entry of (x 1, …, x n) is not enclosed by expansion regions \((E^i_1, \ldots , E^i_n)\), i = 1, …, c. This is the case that granules G i cannot expand beyond the limit ρ to fit the sample. Otherwise, if x [h] is placed inside an E i, but the class \(C^{[h]} \neq \hat {C}^{i}\), then a new granule G c+1 should be created.

A new granule G c+1 is formed by fuzzy sets \(G^{c+1}_j\) whose parameters match the sample:

$$\displaystyle \begin{aligned} \begin{array}{rcl} G^{c+1}_j = (\underline{\underline{g}}_j^{c+1}, \underline{g}_j^{c+1}, \overline{g}_j^{c+1}, \overline{\overline{g}}_j^{c+1}) = (\underline{\underline{x}}_j, \underline{x}_j, \overline{x}_j, \overline{\overline{x}}_j). \end{array} \end{aligned} $$
(40)

The consequent p c+1 is associated to a class, \(\hat {C}^{c+1} = C^{[h]}\).

Adaptation of granules consists in expanding or contracting the support and the core of fuzzy sets \(G^i_j\). Granule G i is adapted if a sample falls within its expansion region, i.e., if supp\((x_j) \subset E^i_j\), j = 1, …, n, and C [h] is the same as \(\hat {C}^{i}\). In situations in which more than one granule encloses the sample, adapting only one of them is enough to guarantee data inclusion. In particular, we may choose G i such that i = arg max(o 1, …, o c), i.e., G i has the highest activation level.

Adaptation proceeds depending on where the input datum x j is placed in relation to the fuzzy set \(G^i_j\):

The first and last rules perform support expansion, and the second and seventh rules execute core expansion. The remaining cases concern core contraction.

Operations on core parameters, \( \underline {g}^i_j\) and \(\overline {g}^i_j\), require adjustment of the midpoint of the respective fuzzy sets:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathrm{mp}(G^i_j)\mathrm{(new)} = \frac{\underline{g}^i_j \mathrm{(new)} + \overline{g}^i_j \mathrm{(new)}}{2}. \end{array} \end{aligned} $$
(41)

As a result, support contraction may happen in two occasions:

4.7 Adapting Connection Weights

Weights \(w^i_j \in [0,1]\) represent the importance of the j-th attribute of \(G_j^i\) to the neural network output. If \(w_j^i=1\), then the output is not affected. A relatively lower value of \(w_j^i\) discounts the impact of the respective attribute. The procedure described below assigns lower weight values to less helpful attributes.

If a granule G c+1 is created, weights are set as \(w^{c+1}_j = 1\), ∀j. If it is known a priori that different attributes have different importance, then values for \(w^{c+1}_j\) can be chosen in a way to reflect that.

Weights \(w^i_j\), j = 1, …, n, corresponding to the most active granule G i, i = arg max(o 1, …, o c), are updated from:

$$\displaystyle \begin{aligned} \begin{array}{rcl} w^i_j(\mathrm{new}) = w^i_j(\mathrm{old}) - \beta^i \widetilde{x}^{i}_j |\epsilon|. {} \end{array} \end{aligned} $$
(42)

where \(\widetilde {x}^{i}_j\) is the similarity between \(x^{i}_j\) and \(G^{i}_j\); β i depends on the number of right (R i) and wrong (W i) classifications so far provided by G i according to:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \beta^i = \frac{W^i}{R^i+W^i}; \end{array} \end{aligned} $$
(43)

and

$$\displaystyle \begin{aligned} \begin{array}{rcl} \epsilon^{[h]} = C^{[h]} - \hat{C}^{[h]} \end{array} \end{aligned} $$
(44)

is the current estimation error. Equation (42) penalizes the j-th attribute of G i in the next iterations if the estimated class is wrong.

4.8 Learning Algorithm

The learning algorithm to evolve EGNN is given below:

————————————————————————————

BEGIN

Select a type of neuron for the aggregation layer;

Set parameters ρ [0], h r, η, c = 0;

Read input sample x [h], h = 1;

Create granule G c+1, neurons A c+1, A f, and respective connections;

For h = 2, … do

Read and feedforward x [h] through the network;

Compute rule activation levels (o 1, …, o c);

Aggregate activation values using A f to get an estimation \(\hat {C}^{[h]}\);

// The class C [h] becomes available;

Compute output error \(\epsilon ^{[h]} = C^{[h]} - \hat {C}^{[h]}\);

If x [h] is not within expansion regions E i∀i or 𝜖 [h] ≠ 0

Create granule G c+1, neuron A c+1, and connections;

Else

Adapt the most active granule G i∗, i ∗ = arg max(o 1, …, o c);

Adapt weights \(w^{i*}_j ~ \forall j\);

If h = αh r, α = 1, 2, …

Adapt model granularity ρ;

END

————————————————————————————

5 Results and Discussion

Experimental results on electrical machine fault detection and classification using neural networks trained via genetic (EANN) and incremental (EGNN) algorithms are shown in this section. First, individual results for each neural classifier and discussions considering different initial parameters and operators are presented. Then, general comparisons and statistical analyses are performed. We look forward to concise models and high accuracy and processing speed.

5.1 Preliminaries

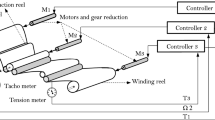
The dataset was generated from the validated mathematical model described in Sect. 2. An induction motor properly designed for insertion of stator shorted-turns and the experimental setup for model validation are shown in Fig. 9. Stator phase windings were fractionated such that short-circuits on a number of turns could be imposed externally (see white wires on the top of the motor).

Fig. 9
figure 9

Instrumental setup and motor external connections

Full size image

The characteristics of the underlying induction motor are: power, 5 Hp; voltage (Y), 127 V; poles, 4; stator turns per phase, 84; inertia, 0.00995 J m2; rated torque, 2.1 kgf m; rated speed, 1715 RPM; stator resistance, 0.730  Ω; rotor resistance, 0.360 Ω; stator and rotor leakage inductance, 0.006 H; and mutual inductance 0.027 H. Table 1 shows the conditions of shorted-turns in the stator windings and a summary of the 10-class balanced classification problem. The dataset contains 350 7-attribute samples. The attributes are the abc stator currents, voltage–current displacement angles, and the rotor speed. Voltage unbalance in the 3-phase system (127 ± 10 V), current measurement noise (± 0.1 A), and variable load ([0, 6] Nm) were considered to generate 35 samples that represent each of the 10 classes.

Table 1 Classes of the 10-class balanced classification problem
Full size table

Offline learning methods, such as EANN, use 200 random samples for training and 150 samples for testing. Data stream learning methods, such as EGNN, employ a sample-per-sample testing-before-training approach.

5.2 Genetic EANN for Fault Detection

Genetic mutation and recombination operators are compared in this section within the framework of electrical machine fault detection. Additionally, the overall performance of the detection system using the GA-based neural network is given.

First, the effect of applying arithmetic, multipoint, and local intermediate recombination operators is evaluated assuming the other GA operators fixed. Figure 10 illustrates the evolution of the average and best fitness of the population over the generations using the different recombination operators. For 500 generations of weight individuals, arithmetic crossover provided the overall fittest individual and the highest average fitness.

Fig. 10
figure 10

Comparison between crossover operators

Full size image

A second experiment concerns the evaluation of Gaussian and random mutation operators with all other GA operators fixed. Figure 10a shows the detection system performance under different Gaussian mutation rates. The fittest individual was reached under an 8% mutation rate, while the best average fitness was obtained under a 5% rate. Figure 11b shows the result for random mutation under distinct mutation rates. Random mutation under a 5% rate generated the fittest individual and the highest average fitness.

Fig. 11
figure 11

Comparison between mutation operators under different probability rates. (a) Gaussian mutation. (b) Random mutation

Full size image

Genetic operators that generated the fittest individual, i.e., arithmetic crossover and random mutation under a 5% rate, were chosen for subsequent experiments. In addition, k = 0.9 in Eq. (18). We evaluated neural network architectures considering recombination, mutation, tournament selection with elitism, and post-processing based on local random mutation. Figure 12a presents the development of various EANN architectures over the generations. In a small amount of architecture generations—30 generations, an 88.77% accuracy on fault detections was reached by the architecture [7; 21; 5; 1]. This notation indicates the number of neurons in the input, first and second hidden, and output layers, respectively.

Fig. 12
figure 12

General results for inter-turns fault detection using EANN. (a) Evolution of the fitness/accuracy of EANN architectures over time. (b) Performance comparison between a deterministic error-backpropagation-based MLP neural network and EANN, which carries out a global search for parameters prior to local search using genetic operators

Full size image

In a further experiment, the fault detection system using the trained EANN with 21 and 5 neurons in the hidden layers was subject to different sets of test data. Datasets were built considering different maximum levels of voltage unbalance and measurement noise (zero-mean white noise) on current waveforms. Each dataset contains 150 samples, which are used to test the EANN—being 15 samples of each class. Figure 12b shows the performance of EANN and that of a Multilayer Perceptron MLP neural network for detecting stator inter-turns short-circuit. The MLP neural network has similar architecture as that of EANN, but was trained via backward propagation of errors—a gradient descent optimization method. Conversely, GA carried out a global search for parameters prior to the typical local search, which supports deterministic methods such as the backpropagation algorithm.

Notice from Fig. 12b that EANN outperformed MLP in all situations. For example, in a less noisy environment with balanced voltages, close to the right upper corner of the graph, the detection system using EANN achieved 94.67% of correct classifications against 91.33% of the MLP neural network. The total training time for ten thousand epochs of the MLP backpropagation algorithm was about 19 min, while the time to evolve 30 architecture generations with 20 individuals each, 50 weight generations with 20 individuals each, and post-processing the fittest solution was about 55 min. In general, EANN provided greater robustness to voltage unbalance, variable loads, and measurement noise as shown by the 16% gap between the accuracy surfaces in the left lower corner of Fig. 12b.

5.3 Incremental EGNN for Fault Detection

A neurofuzzy EGNN classifier was evolved based on a data stream from the induction machine. The network uses seven input attributes, viz., abc stator currents, voltage–current displacement angles, and rotor speed. 350 samples, one at a time, became available for testing and training. No data is available before EGNN learning starts, and no data is stored during the learning process.

The initial parameters for the learning algorithm are ρ [0] = 0.7, h r = 30, and η = 1. First, different types of aggregation neurons A i ∀i, viz., minimum, product, and Lukasiewicz were evaluated. The output neuron A f performs S max aggregation. A summary of the results from 10 runs obtained using the different aggregation neurons A i is shown in Table 2. The average number of rules during the iterations and the total processing time are also shown.

Table 2 Evaluation of different types of EGNN fuzzy aggregation neurons
Full size table

Notice that the EGNN construction that uses product T prod and maximum S max fuzzy neurons in the aggregation and output layers, respectively, performed better than the other configurations using approximately from 12 to 13 granules. EGNN learning algorithm alone, disregarding any other acquisition and data processing procedure, can handle 2906 samples per second in the worst case.

The need to calculate effective values of the voltage and current, and phase angle based on a 60-Hz power system imposes a limit on the provision of input samples to the network. If the effective values are calculated using half-wave cycle, then a maximum of 120 input data samples per second are available for EGNN processing. Therefore, the bottleneck of the fault detection system in terms of processing capacity is certainly not imposed by the classifier so that parallel programming environments are needless.

For gradual and small changes of attribute values, the learning algorithm adapts the parameters of granules and connections. EGNN is able to handle new classes and abrupt changes on the data stream, e.g., due to the development of a fault, load change, or voltage unbalance. In these cases, the algorithm creates additional granules, connections, and neurons to maintain its accuracy.

Figure 13 depicts a typical behavior of the T prod − S max EGNN model using ρ [0] = 0.7, h r = 30, and η = 3. The figure shows that the accuracy of the classifier increases quickly along with an increase in the number of rules during the first iterations. EGNN makes use of approximately 12.7 rules with a maximum of 16 rules to support a 94.5% classification accuracy on this simulation. After about 70 time steps, the performance of the EGNN classifier achieved a quasi-steady state in spite of recurrent structural and parametric updates.

Fig. 13
figure 13

EGNN classification accuracy and number of rules during the learning steps

Full size image

Nonstationary decision boundaries drawn by EGNN granules during the progress of inter-turns short-circuit in the stator phases A, B, and C are illustrated in Figs. 14, 15, and 16, respectively. Granular regions representing a healthy and faulty induction machine are visible in the first quadrant of the figures since in previous iterations the neural network was exposed to samples of all classes provided by the Fault Simulator model. After the occurrence of a shorted-turn in one of the stator windings, the neural network changed structurally and parametrically to fit the new samples, which reflect the fault occurrence. Therefore, as the number of shorted-turns evolves from 1 to 3 turns, the granular regions related to the underlying faulty winding expand toward the other regions. Samples bringing information about the faulty class predominate in the data stream.

Fig. 14
figure 14

EGNN classification boundaries during the development of a fault in stator phase A: (a) healthy induction machine. Boundaries after (b) 1, (c) 2, and (d) 3 shorted-turns

Full size image
Fig. 15
figure 15

EGNN classification boundaries during the development of a fault in stator phase B: (a) healthy induction machine. Boundaries after (b) 1, (c) 2, and (d) 3 shorted-turns

Full size image
Fig. 16
figure 16

EGNN classification boundaries during the development of a fault in stator phase C: (a) healthy induction machine. Boundaries after (b) 1, (c) 2, and (d) 3 shorted-turns

Full size image

5.4 Comparative Analyses and Discussion

The evolutionary EANN and evolving fuzzy granular EGNN neural networks were able to detect shorted-turns in the stator windings of an induction machine with a reasonable degree of success. While EGNN achieved a 96.28% best accuracy using product T prod and maximum S max fuzzy neurons in the aggregation and output layers, EANN reached a 94.67% best correct classification rate in a similar scenario using arithmetic crossover, random mutation, tournament selection, and subsequent local search based on local random mutation.

Both learning methods, genetic and incremental, addressed issues such as convergence to a local optimum, dependence on initial parameters and trial-and-error approach on choosing an architecture for the neural classifier. To shed light on these issues, a Multilayer Perceptron MLP neural network with the same structure as that of the fittest EANN, but trained with a gradient algorithm, was used for comparison. The MLP classifier achieved a 91.33% success rate on fault classification.

While from one side the accuracy of the evolutionary EANN, evolving EGNN, and non-evolving MLP classifiers are relatively close to each other (within a 5% range) for the underlying problem, from the other side the time spent by the learning algorithms to provide such performance was about 55 min, 19 min, and 0.1 s, respectively, for the offline genetic, error backpropagation, and online incremental algorithm. Notice that MLP and EANN would certainly benefit from parallel processing, whereas EGNN supports the volume of data in question.

The main point on time and space complexity is that the parameter space of neural networks is usually very large and in principle of undefined dimension. Online incremental learning is based on a bottom-up approach that starts from scratch and considers new neurons and connections (dimensions in the parameter space) only if necessary. The size of the neural network model is controlled by the granularity adaptation mechanism. Moreover, recursive formulas do not require accumulation of samples and multiple passes over the same data, but a data stream and a single scan of the samples. This explains the enormous difference on computational complexity of the algorithms and supports incremental learning from sequential data as a mainstream of research to deal with complex and big data applications.

The effectiveness of the mathematical model to simulate shorted-turns in the stator windings of electrical machines, real genetic programming, and of the evolving fuzzy granular approach for condition monitoring and pattern classification was verified in this study. The fault simulation model, together with the identification and optimization algorithms, is an important alternative tool for destructive tests. Moreover, fault simulation allowed a variety of practical situations to be incorporated and considered as entries of the dataset. Therefore, the neural classifiers could be trained to be immune to voltage unbalance and load change situations.

6 Conclusion

Early detection of incipient fault conditions in induction machines, such as the turn-to-turn short-circuit fault, is of utmost importance because functional failures may occur minutes or hours after the initial development. The faulty winding should be restored or replaced to prevent complete loss of the motor. Operational hazards as well as significant financial losses can be avoided if the machine is stopped for maintenance.

In this study, learning methods are proposed to evolve architectures and weights of a feedforward neural network aiming at fault detection and classification. In particular, genetic and incremental learning methods are addressed producing, respectively, evolutionary EANN and evolving EGNN models. Both neural models were able to detect shorted-turns successfully. EGNN achieved a 96.28% accuracy using product T prod and maximum S max fuzzy neurons, whereas EANN reached a 94.67% accuracy on correct classification using arithmetic crossover, global and local random mutation, and tournament selection. Issues such as convergence to local optima, dependence on initial parameters, and choice of a neural architecture by trial and error were overcome. Moreover, a Multilayer Perceptron MLP model trained with a gradient algorithm was considered to highlight the advantages of performing global search for parameters prior to local search. The MLP classifier achieved a 91.33% accuracy. The striking difference concerns the time spent to produce such results, which was about 55 min, 19 min, and 0.1 s, respectively, for the genetic, gradient, and online incremental algorithms. Bottom-up incremental learning from scratch takes into account new neurons and connections (dimensions in the parameter space) only if necessary for a better classification accuracy.

The effectiveness of a mathematical model to simulate shorted-turns in the stator windings was verified (validated) in this and related studies. The fault simulation model, together with the identification and optimization algorithms briefly presented, is an important alternative tool for destructive tests. Moreover, fault simulation granted a diversity of practical situations to be incorporated into datasets. Therefore, the neural classifiers could be trained to be immune to voltage unbalance and load change situations.

Further work will address methods to control the specificity of information granules in evolving granular neurofuzzy networks; linguistic data approximation, and missing data imputation due to sensor malfunction or saturation. In addition to sensor faults, airgap eccentricity and multi-fault models based on dq0 and sequential components will be approached.