Keywords

1 Drug Resistance Problem

Every organism attempts to survive in hostile conditions by making minor modifications in its life cycle. Though these modifications are observed phenotypically, genetic reshuffling and alterations are the underlying cause of these changes. Although we are unable to accurately explain this phenomenon and its initiation, we have been able to use this observed knowledge and empirically derive explanations for such modifications. However, it may not always be necessary to know all the details regarding genetic modifications, so long as we can correctly, at least empirically, understand such observations, and put it to effective use to predict and understand the drug resistance problem. Often the enzymes in the biochemical pathways undergo mutations to improve the survival rate of the organism by either improving the protein function or catalytic efficiency and stability to escape the inhibitory action of the drug. In the latter case, the motive for modifying the drug target is to ensure that drug binding is weakened. Moreover, the mutations are such that substrate binding is unaffected or minimally affected. Most of the computational methods employed to study the mechanism of drug resistance , attempt to understand the differences in the binding patterns of the substrate and the drug molecule, i.e. understanding the “ substrate-envelope hypothesis ”. Here, we present an overview of those computational methods that employ free energy of binding as a tool to gauge the differences in the binding of the substrate and the drug molecule before and after mutation .

In the Sect. 1, we discuss the driving force for resistant mutations and throw some light on the different mechanisms by which drug resistance can occur. In Sect. 2, we present a brief overview of molecular dynamics, thermodynamics of protein–ligand binding, and various methods for computing the free energy of binding. The last section, Sect. 3, has a detailed discussion on various free energy-based methods used to understand and predict the target site mutations leading to loss in drug binding .

1.1 Overview of the Mechanisms of Drug Resistance

The drug-induced selection pressure [1,2,3,4] is the major driving force for infectious organisms to try to evade the effects of drugs. One of the primary moves that any organism will adopt is to disrupt the action of drug molecules by one or more possible mechanisms. To show its effect, the drug must enter the cells and find its target protein. As a primary defence mechanism against drugs, the organism may down regulate the expression of influx channels that enable the entry of the drug, resulting in a decreased concentration build-up within the cell. Another strategy that hinders the build-up of the drug inside the cell is the upregulation of the expression of efflux channels/pumps that facilitate the egress of the drug molecules. These strategies are often very difficult to understand owing to the complicated pathways involved in the upregulation or downregulation of various proteins associated in the regulation of traffic to and from the cell. This attribute is difficult to study using computational techniques that use free energy -based methods . Target site mutations [5,6,7,8] that lead to disruption in the drug binding without significant loss of the protein function [9, 10] is another mechanism of drug resistance . Such mutations can be studied using computer simulations that enable us to estimate the free energy difference between the drug binding to the mutant and the wild-type protein. An essential factor to consider while understanding target site mutation is the fitness cost associated with the mutational change. This can be estimated by the change in the free energy of binding of the natural ligands /substrates; for example, a drop in their binding energy indicates that substrate binding is impeded, which this leads to increased fitness cost . This means the enzyme now must expend more energy to carry out the same reaction. Hence, we can assume that such mutations are seldom seen, and if at all they occur, a compensatory mutation(s) will be seen to counter the detrimental effects of those mutations [11, 12]. Another strategy adopted by organisms is to increase the production of drug-metabolizing enzymes that modify the drugs to their inactive form eventually leading to their elimination. A classic example of this is the inactivation of penicillin by the enzyme β-lactamase .

1.2 Overview of Computational Methods to Study Drug Resistance

Broadly , computer-assisted methods used to study drug resistance can be classified into two categories based on the information they require and the output they return. The first category of methods requires only 1D sequence data as input and the output is generally a classification type , i.e. the test sequence is classified as a resistant or a non-resistant sequence. Thus, the methods grouped under this class are collectively called as “sequence-based” methods [13]. The workflow of these methods is akin to machine learning or QSAR type classification methods. In a nutshell, sequence-based methods require sequences with the corresponding biological activity data (Ki or IC50 or any other suitable numerical value) for the drug under study. Such data can be curated from databases like HIVDB (for HIV resistance, curated and maintained by Stanford University; [14, 15]) CancerDR (for cancer resistance, curated by CSIR Institute of Microbial Technology and OSDD, India; [16]), tuberculosis resistance mutation database (curated and maintained by various departments and schools with Harvard University; [17], and many other such databases . The data is then split into training and test sets to develop and validate the predictive models . The advantage of such methods is that it is not necessary to know the tertiary structure of the protein or the drug-receptor interactions. Therefore, sequence-based methods are computationally inexpensive and large amount of data can be trained to obtain decent quality predictive models in a short time. However, they suffer from two major drawbacks; (1) a lot of a priori information on drug-resistant mutations is needed to train/develop predictive models and (2) no mechanistic insights or atomistic details can be obtained.

The drawbacks seen in the sequence-based methods are efficiently overcome by structure-based methods [13, 18, 19]. Further, structure-based methods are the methods of choice when atomistic details are desired. However, these additional details come at an added computational cost and require high-resolution protein structures to be able to make accurate and reliable predictions . However, unlike the sequence-based methods, they do not require large a priori information on mutations; on the contrary, they can be applied to systems where no data on mutation is available. To assess the binding stability which is the basis for predictions, these methods employ either empirical scoring functions that implicitly try to reflect the free energy of binding or use techniques that compute the free energy of binding per se. Molecular docking -based methods use empirical scoring functions to find the best docking conformations, and these methods are computationally less expensive. Therefore, they can be applied to assess many protein–ligand complexes. The ligand can be docked to various mutant proteins to predict their binding strength before and after mutations, and this will allow one to understand the effect of the mutation on the binding strength. The accuracy of docking-based methods relies on the accuracy of the scoring function, and they are best suited for rank ordering of compounds rather than computing the absolute free energy of binding. The major issue with docking-based methods is that most docking programs treat proteins as rigid entities, and therefore, mutations in highly flexible protein–ligand systems are poorly understood [19]. However, in recent times there have been several attempts to incorporate protein flexibility in molecular docking [20]. This has largely improved the enrichment scores. Due to the limited scope of this chapter, such docking methods will not be discussed here and have been treated elsewhere [21,22,23,24,25]. Molecular dynamics-based methods can incorporate flexibility in the protein–ligand complexes, and in most cases, are the methods of choice as a conformational sampling tool to explore the phase space accessible to the system under study. The conformations sampled are used to compute the free energy change. However, the drawback of MD-based methods is the computational cost, which is several magnitudes higher compared to docking-based methods.

Another critical issue that must be addressed about the structure-based methods is, how fast predictions can be made, in addition to how reliable are the predictions. These methods find application in drug discovery programs , wherein additional filters can be placed to weed out molecules likely to encounter a high level of resistance or assist in suitably modifying leads to inhibit the mutant proteins. Drug discovery itself is an extremely lengthy and expensive process, and an additional filter like resistance should be economical in terms of time as well as money. Moreover, such methods should also assist medicinal chemists during lead optimization stages to identify potential groups that will help evade drug resistance and avoid late-stage failures that lead to huge financial losses.

2 Molecular Dynamics Simulations and Free Energy Calculations

2.1 Overview of MD and Conformational Sampling Methods

Computer simulations are very useful in predicting changes in molecular properties brought about by alterations in an atom or a group of atoms, particularly, amino acid residues. Therefore, they find good application in predicting the effect of mutations on drug binding at the active site or elsewhere. Protein design experiments clarify the effect of a mutation on drug or substrate binding , thereby facilitating prediction of drug-resistant mutations. This way the program can be used to select all mutations wherein drug binding is hampered and substrate binding is either improved or [26].

In case of free energy calculations, molecular dynamics (MD) simulations are the most commonly used technique to generate conformational ensembles . Hence, it is rightly called as one of the main toolkits for theoretically studying biological molecules (Hansson et al. [27], Binder et al. [28]. MD calculates the time-dependent behaviour of particles or atoms, by numerical integration of Newton’s second law of motion and predicts the future positions and momenta. MD simulations have provided detailed information on the fluctuations and conformational changes of proteins and nucleic acids upon drug/substrate binding . As a result, it is now routinely used to investigate the structure, dynamics and thermodynamics of biological molecules and their complexes. MD simulations have an advantage in that, starting from an X-ray or NMR solved structure, it can provide insights into the dynamic nature of biomolecules that are inaccessible to experiments. To accurately simulate the behaviour of molecules, one must be able to account for the thermal fluctuations and the environment-mediated interactions arising in diverse and complex systems (e.g., a protein-binding site or bulk solution). This depends on how accurately the force fields represent the atoms and treats the non-bonded interactions. A complete account of force fields can be found in the review by Pissurlenkar et al. [29]. However, most of the biological events occur at timescales that are not routinely reachable by classical MD simulations, for example, protein folding occurs in the timescale of few seconds, whereas drug binding and unbinding occur in the timescale of few microseconds to milliseconds. The routine timescale that is feasible using high-end servers equipped with graphic processing units [30,31,32] and distributed grid computing [33, 34], is few tens of microseconds, that is nearly 1/100th of the timescale required to study protein folding . Conventional MD suffers from the severe limitation that it is extremely difficult to sample high-energy regions and surmount energy barriers, leading to inaccuracies in free energy calculations.

The limitations of classical MD simulations have motivated the development of new conformational sampling algorithms that facilitate the sampling of conformational space that is inaccessible to classical MD simulation. The simplest way to encourage the system to sample the high-energy regions on the phase space is to increase the target temperature [35]. This leads to increased kinetic energy of the system that enables it to surmount these barriers. However, it has been argued by many, that such elevated temperatures (~400 K and above) lead to physiologically unrealistic states that may severely distort the results; however, such methods have been found to be advantageous in improving the sampling efficiency during MD simulations. Another method that uses elevated temperature to enhance the sampling is the replica-exchange molecular dynamics (parallel tempering, [36, 37]). In this approach, several replicas are simulated in parallel at different temperatures. At appropriate intervals, the replicas switch temperatures with the nearest replica, and this exchange is governed by the Metropolis acceptance criteria. However, all these methods do not prohibit the system from revisiting the same conformational space. This problem was resolved by adding the memory concept in molecular dynamics (local elevation method [38] Metadynamics [39]) uses Gaussian potentials that discourage the system from sampling the same conformational space. These are few of the most commonly used methods to tackle sampling problems in molecular dynamics, a complete account on enhanced sampling algorithms can be found elsewhere [40,41,42,43,44].

2.2 An Overview of Thermodynamics of Protein–Ligand Binding

Molecular interactions , between the ligand and receptor, are primarily non-covalent in nature and governed by attractive and repulsive forces. In drug design experiments, the goal is always to optimize the attractive interactions and reduce the repulsive ones [45,46,47]. Moreover, these associations are temporary, and the lifespan of such complexes are governed by the off rates (Koff) or the dissociation constant (Kd), both of which indicate the binding strength of a ligand to its protein counterpart. In the realm of thermodynamics, binding is governed by enthalpic and entropic components [48] given by Eq. 1.

$$ \Delta G = \Delta H - T\Delta S $$
(1)

where ∆G is the binding free energy ; ∆H is enthalpy ; ∆S is entropy and T is the temperature in Kelvin.

The association is favourable, i.e. spontaneous when the ∆GGibbs is negative and unfavourable otherwise. All the binding and pre-binding (recognition and pre-organization) events in biomolecular associations are either enthalpy (∆H) driven or entropy (∆S) driven. The enthalpic component represents several types of non-covalent interactions like electrostatic , van der Waals , ionic, hydrogen bonds and halogen bonds, while the entropic components reflect the contribution to binding due the dynamics or flexibility of the system. Computing the enthalpic component of binding has reached far heights, in terms of methods available for calculating the aforementioned type of interactions. However, till date, calculation of the entropic component is extremely difficult, and the algorithms are computationally very demanding.

The Gibbs equation is more relevant in biochemistry for calculating the free energy and is given by Eq. 2:

$$ \Delta G_{\text{Gibbs}} = - RT\,\ln K_{d} $$
(2)

where ∆GGibbs is Gibbs free energy , R is universal gas constant , T is the temperature in Kelvin, Kd is the dissociation constant . Equations 1 and 2, along with the Born–Haber cycle [46] (Fig. 1) form the basis for the development of the methods used to compute the free energy binding. The two main methods are Free energy perturbation (FEP) and Thermodynamics Integration (TI), both of which will be dealt with in the subsequent Sect. 2.3.2. However, measuring the dissociation constants from simulations is a daunting task; nevertheless, computing the partition functions from the molecular simulations is relatively easy. Hence, the ratios of the partition functions can be used to estimate the free energy of binding, which is given by Eq. 2a,

$$ \Delta G = - k_{\text{B}} T\, \ln \frac{{Q_{\text{PL}} }}{{Q_{\text{P}} Q_{\text{L}} }} $$
(2a)

where kB is the Boltzmann constant , T is the temperature in Kelvin, Q is the partition function with subscripts PL, P and L indicating protein–ligand complex, protein, and ligand, respectively. This section presents a summary of thermodynamics, which is imperative for understanding the application and methods developed to compute binding free energy . More elaborate discussions on the thermodynamics of protein–ligand binding can be found in the reviews by Bronowska [48], and Homans [46].

Fig. 1
figure 1

Thermodynamic or Born–Haber cycle for the receptor-ligand binding

Full size image

2.3 Methods to Compute Free Energy Binding

Free energy is a quantity that can be measured for systems such as liquids or flexible macromolecules with several minimum energy configurations separated by high-energy barriers. However, its computation is far from trivial and the associated quantities such as entropy and chemical potential are also difficult to calculate. More so, the free energy cannot be accurately determined from classical molecular dynamics or Monte Carlo simulations due to their inability to sample adequately from the high-energy regions of the phase space, which also make important contributions to the free energy. However, the free energy differences (ΔΔG) are rather simple to compute. The free energy binding for the non-covalent association of two molecules (protein and ligand in this case) may be written as follows:

$$ \Delta G_{\text{bind}} = G_{\text{complex}} - \left( {G_{\text{protein}} + G_{\text{ligand}} } \right) $$
(3)

The binding event is an additive interaction of many events [49,50,51,52], for example solvation energy (Gsol), conformational energy (Gconf), energy due to interaction with residues in the vicinity (Gint), and energy associated with different types of motions (translational, rotational and vibrational, Gmotion). The classical binding free energy equation now can be rewritten as follows:

$$ \Delta G_{\text{bind}} = G_{\text{sol}} + G_{\text{conf}} + G_{{\text{int} }} + G_{\text{motion}} $$
(4)

Directly computing the free energy from an MD or MC simulation is not trivial; hence, the following methods have been formulated. Broadly, the methods used for computing free energy are classified as partitioning-based methods or end-state free energy methods and non-partitioning-based methods. The partitioning-based methods partition the binding energy into various components as shown in Eq. 4; however, this method has been highly criticized [53] stating that it is physically unreal to partition the free energy into components.

2.3.1 End-State Free Energy Methods or Partitioning-Based Methods

The human body majorly comprises of water; hence, it is imperative to carefully include the solvation effects while computing the free energy of binding. More importantly, water plays a crucial role in ligand recognition and in the binding phenomenon. In computational chemistry, the methods for incorporation of solvent are divided into three groups: (i) continuum electrostatic methods/implicit solvent , (ii) explicit solvent models with microscopic detail and (iii) hybrid approaches. Historically, the continuum electrostatic methods were among the first to consider the solvent effect, and they still represent very popular approaches to evaluate solvation free energies , especially in quantum chemistry . Polarizable continuum model (PCM, [54]), COnductor-like Screening MOdel (COSMO, [55]) and SMD solvation model [56] are few popular models for treating solvent effects implicitly in quantum chemistry . Continuum solvation methods are computationally economical; however, the frictional drag of the solvent is highly underestimated and as a consequence may drive the system to non-physical states . Moreover, solvent–solvent and solute–solvent interactions are inadequately treated, posing a danger of underestimating the effects of such interactions. The explicit treatment of solvent enables one to consider the solvent–solvent and solute–solvent interactions . This prohibits the systems from visiting non-physical states due to the inclusion of the dampening effect shown by the solvent atoms. The principal drawback of explicit solvent models is the number of atoms to be considered in the system leading to increased computational cost. However, with the help of GPU-based acceleration, this drawback, now, is hardly any cause for worry.

The end-state free energy methods use the conformations extracted from an MD or MC simulation, wherein the system is simulated by explicitly defining the solvent. However, while solving the GB or PB equation, the solvent is implicitly treated by defining the external dielectric constant for water (for most drug design cases) and a suitable internal dielectric constant [57,58,59,60,61].

2.3.1.1 Molecular Mechanics-Poisson Boltzmann/Generalized Born Surface Area (MM-PB/GB-SA)

The MM-GBSA [62,63,64,65] approach employs molecular mechanics -based energy calculations and the generalized Born model to account for the solvation effects in the calculation of the free energy . Similarly, the MM-PBSA [66,67,68] approach solves the linear or nonlinear Poisson–Boltzmann equation [69,70,71], to account for the solvation electrostatics , whereas the MM part is calculated as in MM-GBSA from the derivative of the force field equations. Both these approaches are parameterized such that they partition the energy components into various terms, and the net free energy change is the sum of these individual terms (Coulomb, vdW, solvation, etc.). MM-PBSA has gained considerable attention for estimating the binding free energies of molecular complexes due to its exhaustive nature of computing the solvation electrostatics by iteratively solving the PB equation, whereas the GB method does not involve any rigorous and iterative procedure and hence is faster. However, this does not necessarily guarantee that the MM-PBSA method always outperforms MM-GBSA method. In MM-PB(GB)SA methods, MD- or MC-derived conformational ensembles are used to compute the “average” free energy of a state and this is approximated as follows:

$$ \left\langle G \right\rangle = \left\langle {E_{\text{MM}} } \right\rangle + \left\langle {G_{{{\text{PBSA}}/{\text{GBSA}}}} } \right\rangle - T\left\langle {S_{\text{MM}} } \right\rangle $$
(5)

where the angular bracket <> indicates average over the MD/MC conformations, EMM is the molecular mechanics energy that typically includes bond, angle, torsion, van der Waals , and electrostatic terms (see Eqs. 7c and 7d) and is evaluated with no or extremely large (virtually infinite) non-bonded cut-off limit. The second term is solved as mentioned in the preceding stanza and it forms the crux of this method. The last term T <SMM>, is the solute entropy , which is estimated by quasi-harmonic analysis [72, 73] of the trajectory or by normal mode analysis [74,75,76].

The following equation (Eq. 6) shows how the binding free energy is computed from the energies of the ligand , protein, and its complex over all the MD or MC snapshots. However, the snapshots can be obtained in two possible ways—one is called the single trajectory approach and other is the multiple trajectory approach. In the single trajectory approach, only the protein–ligand complex is simulated, and the snapshots for the protein, ligand and the complex are extracted by defining appropriate atom numbers from the parameter and coordinate file. However, in the multiple trajectory approach, three separate simulations are performed, one each for the protein, ligand and protein–ligand complex.

$$ \left\langle {\Delta G_{\text{bind}} } \right\rangle = \left\langle {G_{\text{complex}} } \right\rangle - \left( { \left\langle {G_{\text{protein}} } \right\rangle - \left\langle {G_{\text{ligand}} } \right\rangle } \right) $$
(6)

Furthermore, Eq. 1 is modified to accommodate solvation electrostatics and hydrophobic terms as shown in Eq. 5. Here, Eqs. 7a–7d give the computation of the individual terms,

$$ \Delta G_{\text{bind}} = \Delta E_{\text{MM}} + \Delta G_{\text{sol}} - T\Delta S $$
(7a)
$$ \Delta G_{\text{sol}} = \Delta G_{{{\text{sol}} - {\text{elect}}}} + \Delta G_{\text{nonpolar}} $$
(7b)
$$ \Delta E_{\text{MM}} = \Delta E_{\text{int}} + \Delta E_{\text{elect}} + \Delta E_{\text{vdW}} $$
(7c)
$$ \Delta E_{\text{int}} = \Delta E_{\text{bond}} + \Delta E_{\text{angle}} + \Delta E_{\text{torsion}} $$
(7d)

Here, ∆EMM is computed in the gas phase using classical force fields , ∆Gsol is computed using PBSA or GBSA method, ∆Gsol-elect is computed using PB or the GB method, and the ∆Gnonpolar is computed by the solvent accessible surface area (SA). While employing the single trajectory approach, Eq. 7d generally cancels out and hence makes negligible contribution to the binding energy .

2.3.1.2 Linear Interaction Energy (LIE)

Linear interaction energy [77,78,79] is similar to the MM-PB/GB-SA method with regard to the partitioning of the electrostatic and van der Waals terms (polar and non-polar contribution, respectively,); however, the use of the weighting parameter for electrostatic and van der Waals interactions, is unique to this method. LIE measures the binding energy by estimating the difference in the interaction energies of the ligand in the solvent (unbound state) and in the protein environment (bound state). Hence, to obtain these interactions, two separate MD simulations are performed. In one simulation, only the ligand is placed in the solvent (mostly water) and in the other, the protein–ligand complex is placed in the solvent. The formulation of this method is based on deriving the linear response approximation from converged ensemble interactions, most often extracted from well-equilibrated trajectories from the MD simulation of the ligand with its surroundings (solvent or protein).

The mathematical formula for computing free energies using LIE method is given in Eq. 8

$$ \Delta G_{\text{bind}} = \alpha \left[ {\left\langle {E_{\text{coul}}^{{{\text{L}} - {\text{S}}}} } \right\rangle_{\text{PL}} - \left\langle {E_{\text{coul}}^{{{\text{L}} - {\text{S}}}} } \right\rangle_{\text{L}} } \right] + \beta \left[ {\left\langle {E_{\text{vdW}}^{{{\text{L}} - {\text{S}}}} } \right\rangle_{\text{PL}} - \left\langle {E_{\text{vdW}}^{{{\text{L}} - {\text{S}}}} } \right\rangle_{\text{L}} } \right] $$
(8)

where the angular bracket <> indicates ensemble over the MD trajectory, \( E_{\text{coul}}^{{{\text{L}} - {\text{S}}}} \) and \( E_{\text{vdW}}^{{{\text{L}} - {\text{S}}}} \) are electrostatic and van der Waals interactions between the ligand and its medium in the vicinity (PL—protein–ligand complex; L—ligand in solvent), and α is the weighting parameter for electrostatic interactions, which is most often set to 0.5 [78]. This value is assumed due to the linear response of the surroundings to the electrostatic field and was validated using more extensive computations on the ions (Na+ and Ca2+) in water [80]. β is the weighting parameter for van der Waals interactions and is set to 0.16−0.18 [81], which is a subject of much debate owing to the difficulty in estimating the vdW’s contribution to the free energy of binding. However, these values are obtained by empirical fitting the experimental binding free energies. Moreover, the linear response of the vdW term is assumed by observing the linear trend in the interaction of the hydrocarbons with the solvent (water) that depends on the number of carbons in a hydrocarbon.

2.3.2 Non-partitioning-Based Methods

In non-partitioning methods, there is no partitioning of the free energy into various components. Statistical mechanics plays a crucial role in deriving the relationship between the free energy of a system and the ensemble average of the Hamiltonian that describes the system. These methods are far more accurate than the previously mentioned end-state free energy methods, but at the same time, are computationally very demanding. Hence, while dealing with a large dataset of molecules against a particular protein target, it is worthwhile to screen the molecules using a fast method like high-throughput virtual screening [82, 83], followed by a flexible docking -based screening, then use an end-state free energy method, and finally employ the non-partitioning methods to study few tens of molecules. Here, we will present a brief discussion on FEP and TI methods along with their mathematical treatment, and then move on to explain the idea behind alchemical free energy predictions.

2.3.2.1 Free Energy Perturbation (FEP) and Thermodynamic Integration (TI)

Most of the methods for free energy calculations are generally formulated in terms of estimating the relative free energy differences, ΔG, between two equilibrium states, or binding of two similar ligands to a common target. The free energy difference between the two states I and II can be formally obtained by Zwanzig’s formula [84, 85].

$$ \Delta G = G_{\text{II}} - G_{\text{I}} = \beta^{ - 1} \ln e^{{\left( { - \beta \Delta {\text{V}}} \right)}}_{\text{I}} $$
(9)

Here, \( \beta = \left( {k_{B} T} \right)^{ - 1} \)

This represents a sampling of the differences in potentials (ΔV) of the two states using Monte Carlo or molecular dynamics simulation over the potential of state I. To ensure the convergence of these calculations, it is recommended that the potentials of the two systems should thermodynamically overlap. For satisfying this condition, correct conformations must be selected, which is a daunting task, and hence, to achieve this, a multistep process is usually implemented. A path between the states I and II is defined by introducing a set of intermediate potential energy functions that are constructed as linear combinations of the initial (I) and final (II) state potentials and these intermediate states are non-physical states (Eq. 10).

$$ V_{m} = \left( {1 - \lambda_{m} } \right)V_{\text{I}} - \lambda_{m} V_{\text{II}} $$
(10)

where the transition from one state to another is discretized into many points (m = 1,…,n), each represented by a separate potential energy function that corresponds to a given value of λ, such that λm varies from 0 to 1. Here, zero indicates the pure initial state of the system and one indicates pure final state of the system. The total free energy , thus, can be obtained by summing over the intermediate states along the λ variable.

$$ \Delta G = G_{\text{II}} - G_{\text{I}} = - \beta^{ - 1} \mathop \sum \limits_{m = 1}^{n - 1} \ln \langle^{{\left[ { - \beta \left( {V_{m + 1} - V_{m} } \right)} \right]}}\rangle_{m} $$
(11)

This approach is known as free energy perturbation (FEP) where Δλm = λm−1 − λm; hence, it can be written as

$$ \Delta G = - \beta^{ - 1} \mathop \sum \limits_{m = 1}^{n - 1} \ln \langle e^{{\left[ { - \beta \Delta V\Delta \lambda_{m} )} \right]}}\rangle_{m} $$
(12)

Since the potential difference can also be described as the derivative of the potential with respect to λm, Eq. 12 can also be written as,

$$ \Delta G = - \beta^{ - 1} \mathop \sum \limits_{m = 1}^{n - 1} \ln \langle e^{{\left[ { - \beta \frac{{\partial V_{m} }}{{\partial \lambda_{m} }}\Delta \lambda_{m} )} \right]}}\rangle_{m} $$
(13)

Now, expansion of the Eq. 13 by the Taylor expansion series gives Eq. 14,

$$ \Delta G = \mathop \sum \limits_{m = 1}^{n - 1} \langle e^{{\left[ { - \beta \frac{{\partial V_{m} }}{{\partial \lambda_{m} }}\Delta \lambda_{m} )} \right]}}\rangle_{m} $$
(14)

wherein 0 → λ can instead be written as an integral over λ

$$ \Delta G = \mathop \smallint \limits_{0}^{1} \langle \beta \frac{\partial V\left( \lambda \right)}{\partial \lambda }\rangle_{\lambda } {\text{d}}\lambda $$
(15)

Equation 15 is usually referred to as the thermodynamic integration (TI) method for calculating the free energy change [86, 87]. In the early days of free energy simulations, the TI approach was synonymous with the slow-growth method [88]. In the slow-growth method, the value of λ is changed at each time step during the MD simulation. While this method was claimed to be more efficient than the discrete FEP formulation, nowadays, a “non-continuous” change in λ is a better choice (50–100 discrete points are usually recommended). This facilitates equilibration at each point, the addition of extra points at any time, and use of any pattern of spacing between the λ-points, to optimize the efficiency.

2.3.2.2 Alchemical Free Energy Perturbation

Here , the free energy is computed by transforming a molecule from one state (bound-solvated) to another state (unbound-solvated) through several physically unrealistic states, that are called as alchemical states , hence the name “Alchemical Free energy ” [89, 90]. This method is regarded as one of the apt methods to study the effect of mutations on the drug binding affinity (Fig. 2). The total free energy change in a thermodynamic cycle in any alchemical transformation is equal to zero.

Fig. 2
figure 2

Thermodynamics cycle for computing alchemical free energy binding. Image reproduced from Wang et al. [91] [open-access article distributed under the terms of the Creative Commons Attribution License (CC BY)]

Full size image
$$ \Delta G_{1} - \Delta G_{4} - \left( {\Delta G_{2} - \Delta G_{3} } \right) = 0 $$
(16a)
$$ \Delta G_{1} - \Delta G_{4} = \Delta G_{2} - \Delta G_{3} $$
(16b)

3 Application of Computational Methods to Understand Drug-Resistant Mutations

3.1 Computational Mutation Scanning

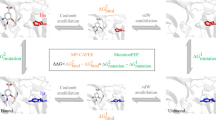
Computational mutation scanning [92] is a useful method to explore the sensitivity to changes in the composition of the amino acid in a protein-binding site (Fig. 3). In computational mutation scanning , the wild-type amino acid residue is mutated to another amino acid in the binding pocket or elsewhere. However, the most widely practised method is to mutate any amino acid residue to an alanine, since it is the simplest amino acid with a side chain (not glycine because it is devoid of a side chain). Hence, this method is equivalent to the experimental “alanine-scanning mutagenesis”, which is a powerful tool to investigate and confirm the important interactions in the protein–protein interface and protein–ligand interactions. In computational alanine scanning, all atoms from the Cβ carbon atom of the amino acid under study are replaced by three hydrogen atoms to convert it to an alanine. After the mutation , the change in the binding energy is estimated either using docking with an appropriate scoring function or by MM-PBSA or MM-GBSA to compute ΔΔG (Eq. 17c). By scanning with alanine at various positions in the binding cavity , important residues can be identified, as mutating an important amino acid will drastically decrease the binding energy.

$$ \Delta G_{\text{bind}}^{\text{Wild}} = \Delta G_{\text{complex}}^{\text{Wild}} - \Delta G_{\text{receptor}}^{\text{Wild}} - \Delta G_{\text{ligand}} $$
(17a)
$$ \Delta G_{\text{bind}}^{\text{Mut}} = \Delta G_{\text{complex}}^{\text{Mut}} - \Delta G_{\text{receptor}}^{\text{Mut}} - \Delta G_{\text{ligand}} $$
(17b)
$$ \Delta \Delta G = \Delta G_{\text{bind}}^{\text{Mut}} - \Delta G_{\text{bind}}^{\text{Wild}} = \left[ {\Delta G_{\text{complex}}^{\text{Mut}} - \Delta G_{\text{complex}}^{\text{Wild}} } \right] - \left[ {\Delta G_{\text{receptor}}^{\text{Mut}} - \Delta G_{\text{receptor}}^{\text{Wild}} } \right] $$
(17c)
Fig. 3
figure 3

Thermodynamic cycle for computing free energy change between mutated and wild-type protein

Full size image

In the context of predicting drug-resistant mutations , one must perform alanine scanning in the binding site on two complexes, i.e. with the substrate bound complex and the inhibitor-bound complex. The change in the binding energy after mutation is computed for both the systems, viz., for inhibitor and the substrate. A decrease in the binding affinity for the inhibitor with negligible or no change in the binding affinity for the substrate indicates a hotspot amenable to resistant mutation , these spots are termed as “mutational hotspots ”. The method follows the substrate-envelope hypothesis [93,94,95], which states that there is a large fitness cost that needs to be paid if one mutates an amino acid residue that is involved in substrate binding . Mutating such amino acids could lead to impaired enzyme function resulting in the death of an organism. This can be put to appropriate use by developing inhibitors that completely overlap in the substrate binding region, leading to a lower predisposition towards developing drug resistance [96,97,98,99].

However, a major drawback in alanine scanning is that when mutating a large amino acid residue to alanine one can only study the effect of decreasing the side chain or loss of charged groups in the binding site. It is difficult to understand the resistant mutation , wherein there is a change in charged amino acid residue, for example, arginine replacing aspartate or a large amino acid replaces a small amino acid residue. Nevertheless, computational alanine scanning has been successfully used to predict mutational hotspots .

Hao et al. [100] reported a modification of computational alanine scanning (CAS), named computational mutation scanning (CMS) to study drug resistance in six HIV-1 protease inhibitors. This protocol is an improvised version of the classical CAS that enables a geometry optimization step and incorporates entropy calculations by means of normal model analysis. Using a single trajectory approach and modifying the standard MM-PBSA protocol, to allow for mutations with other amino acid residues, they computed the change in the binding affinities (ΔΔG) of 77 drug-mutant combinations (includes single and double mutants). They obtained promising results with ~83% consistency with the experimental observations, demonstrating that the prowess of the method lies in identifying the binding hotspots. However, Hao et al., do not report the change in the binding affinity for various substrates, from which they could have investigated the substrate-envelope hypothesis for the HIV-1 protease. This could have led to interesting findings facilitating our understanding about those mutations that would lead to a decrease in the enzyme function, either leading to the death of the organism or compelling a compensatory mutation to counter the lethal effects of any mutation. This information can be used to unravel the role and need for double, triple or even multiple mutations.

Tse and Verkhivker [101] used CAS along with residue interaction network to elucidate the effects of inhibitor binding on the network of residues in ABL kinase. They showed the utility of this combination in deducing the critical networks of amino acid residues and the changes that follow upon inhibitor binding, using a selective kinase inhibitor (nilotinib ) and two promiscuous (bosutinib and dasatinib) kinase inhibitors. The changes in the interaction networks in the enzyme holds key hints to unravel the mystery of how drug-resistant mutations are seen for ABL kinase inhibitors. Moreover, the mutations that occur far from the binding site can also be explained, since a mutation far off from the site can affect drug binding through a cascade of events that eventually percolate into the binding site through the changes in the residue interaction network . CAS followed by MM-PBSA added the energetic component to locate the hotspots that could lead to drug resistance in the kinase inhibitors

3.2 MM-PB(GB)-SA

MM-GBSA or MM-PBSA are two widely used free energy methods employed to understand the effects of mutations on the drug binding affinity, moreover, these methods are successful in predicting likely mutations leading to drug resistance . These methods are able to predict due to their amenability to decompose the free energy into its components at the residue level that leads to better understanding of the effect of mutations on drug binding . Lethal effects of the V82F/I84V double mutation in HIV-1 protease on amprenavir were demonstrated using MM-PBSA approach on snapshots obtained from the well-equilibrated protein–ligand complex [102]. It was reported that amprenavir lost its binding affinity due to distortions in the binding site, hence weakening many favourable interactions (ΔΔG = 3.73 kcal/mol). Such a distortion of the binding site was previously observed and attributed to the rapid flap movements seen in this double mutant which is absent in the wild-type HIV-1 protease [103]. Furthermore, newer inhibitors, that are very close structural analogues of amprenavir , like TMC126 (ΔΔG = 2.01 kcal/mol) and TMC114 (darunavir, ΔΔG = 3.45 kcal/mol) were also seen to be affected by these mutations , though to a lesser extent than amprenavir . Despite structural distortions in the binding site, it had no effect on the substrate binding , and hence, the catalytic process was unhindered.

Hou et al. [104] combined MM-GBSA with the positional variability approach, to modify Kollman’s FV value [105] to give a new scoring function also called FV (Free energy /Variability) score. Using the FV score, they evaluated the binding of six substrates that are hydrolysed by HIV-1 protease and confirmed Kollman’s [105] observation that drug-resistant mutations are more likely to occur at less conserved regions. The FV score reported by Hou et al. comprises two components, one that reflects the binding energetics at the per-residue level, obtained by MM-GBSA , and the second component is the sequence variability that represents the conservation of amino acids at each position. Using this score, one can identify amino acid residues that are crucial for substrate and inhibitor binding, and thus classify the residues that are exclusively involved in substrate binding and those that are exclusive for inhibitor binding. Such a classification when coupled with the positional variability of amino acid residues can extract those positions with low conservation and exclusivity for inhibitor binding; such positions are highly amenable to mutations leading to drug resistance . Employing this method Hou et al. confirmed their previous observation [102] that the V82F/I84V double mutations are lethal for many FDA approved HIV-1 protease inhibitors, whereas TMC126 is still active against this mutant.

3.3 Vitality Analysis

One of the primary drawbacks of the aforementioned methods to predict drug-resistant mutations is their inability to accurately estimate the binding affinity for the substrate molecule(s). The fitness cost of the mutation can be estimated by gauging the change in the binding affinity of the substrate to its enzyme target; any perturbation in the substrate binding is likely to affect the function of the enzyme. Therefore, computing the catalytic efficiency of the enzyme before and after mutation will enable us to understand the fitness cost . Pioneering work in this line was done by Gulnik et al. [1]. In this work, they have determined the catalytic efficiency (Eq. 18a) of HIV-1 protease following few active and non-active site mutations . This principle was incorporated in terms of free energy change by Warshel et al., and they employed this method (Eq. 18b) to computationally predict the likely mutations that could potentially abolish drug binding leading to drug resistance . This method is aptly named as “Vitality approach” wherein higher vitality values indicate that the resistance is more likely as there is little chance of increase in the catalytic efficiency of the enzyme. The basic workflow adopted by Warshel et al. [106, 107] is to estimate the change in the drug binding before and after mutation , depicted in the first part of Eq. 18b and then estimate the catalytic efficiency by determining the binding of the substrate by modelling the transition state (TS) conformation of the enzyme, depicted in the second part of Eq. 18b. However, the challenge of employing this method to predict likely mutations is that a thorough knowledge of the catalytic mechanism of the enzyme is essential. Nonetheless, this method is far more accurate and truly predictive in nature. This is exemplified by the fact that Warshel et al. successfully used this method on six clinical agents active against HIV-1 protease.

$$ {\text{Vitality value}} = \frac{{\left( {\frac{{K_{i} k_{\text{cat}} }}{{K_{m} }}} \right)_{\text{mutant}}}}{{\left( {\frac{{K_{i} k_{\text{cat}} }}{{K_{m} }}} \right)_{\text{WT}}}} $$
(18a)
$$ \ln \frac{{\gamma_{M} }}{{\gamma_{N} }} \cong \frac{1}{\text{RT}} \left( {\Delta \Delta G_{\text{bind}}^{N \to M} \left( {\text{drug}} \right) - \Delta \Delta G_{\text{bind}}^{N \to M } \left( {\text{TS}} \right)} \right) $$
(18b)

where Ki = inhibition constant ; kcat = constant that defines the turnover rate of an enzyme-substrate complex to the product; Km = Michaelis constant .

4 Concluding Remarks

This chapter describes important computational methods that have been proven extremely helpful in gaining insights into mutations leading to drug resistance . We have attempted to introduce methods used to compute the free energy of binding along with their mathematical formulations, practical implementation and pros and cons of such methods. Finally, we have discussed a few applications of such methods to study drug resistance.