A More Efficient AOA Method for 2D and 3D Direction Estimation with Arbitrary Antenna Array Geometry

Abstract

Direction of arrival (DOA) estimation is currently an active research topic in array signal processing applications. Thus, a more efficient method with better accuracy than the current subspace angle of arrival (AOA) methods is proposed in this paper. The proposed method is called subtracting signal subspace (SSS), which exploits the orthogonality between the signal subspace (SS) and the array manifold vector (AMV). A novel approach applied to the pseudospectrum extracts the correct peaks and removes the sidelobes perfectly. The principle working of the proposed algorithm is given and mathematical model derived. The computational burden of the new method is also presented and compared with other methods. The SSS algorithm is implemented with both linear and planar antenna arrays. An intensive Monte Carlo simulation is conducted and compared with other popular AOA methods to verify the effectiveness of the SSS algorithm.

1 Introduction

Localization-based techniques are growing in importance for applications such as mobile communications [1], radar applications [2] and medical services [3]. Estimating directions of arrival (DOA) of signals incoming from different directions on an array of spatially distributed antennas or sensors is one of the most important factors in array signal processing. Capon [4], Multiple signal classification (MUSIC) [5], Estimation of Signal Parameters via Rotational Invariance Technique (ESPRIT) [6] and Propagator [7] are well-known AOA estimation techniques. Massive multiple input multiple output (MIMO) technology is a promising physical layer candidate for the fifth generation (5G) due to its probable advantages such as high energy efficiency, high spectral efficiency and high spatial resolution. An efficient and accurate AOA method is desirable when integrated with massive MIMO in order to minimize the required computational burden in addition to improving the quality of service (QoS) provided by mobile communication operators [8]. It also emphasizes the performance of the beamforming technology, for instance, when the directions of the desired signals and interference signals are estimated accurately, a suitable beamforming algorithm can be applied to enhance the gain of the useful signals and suppress the noise and interference [9]. Generally, obtaining limited hardware cost with large array aperture cause serious challenges for real-time signal processing and parameter estimation.

Thus, several efforts have been made towards reducing the complexity through avoiding the high computational demanding spectra search array. Root-MUSIC technique [10] was proposed to reduce the computational complexity of the MUSIC method by finding the roots of an involved polynomial, which are associated with directional signals. This method is a less computational burden and faster than MUSIC since it does not need an extensive searching through the manifold vector. The main limitation of this method is applicable only to uniform linear arrays. Other attempts have been achieved using specific shapes of the array geometry in order to minimize the degrees of freedom (FOM) in the spectral search process [11, 12]. An efficient-computational subspace method was developed for 2D DOA estimation utilizing an L-shaped array [13]. This method obtains the noise subspace by rearranging the elements of the covariance matrix into three vectors to decrease the computational complexity. An efficient AOA method called Maximum Signal Subspace (MSS) was suggested in [14] to estimate DOAs; it is based on the orthogonality between the antenna array steering vector and the eigenvector which corresponding to the largest eigenvalue. However, it is also applicable only for uniform linear antenna arrays. Recently, a low complexity angle of arrival method called Propagator Direct Data Acquisition (PDDA) [15] has been proposed to estimate the direction of the received signals directly from the received data without the need to construct the covariance matrix, compute the inverse of a matrix, or apply the EVD approach. This, in turn, reduces the computational complexity significantly. The PDDA method is dependent on calculating the propagator vector which represents the cross-correlation between the measurement data from the first element and the other antenna elements.

In this work, we propose a more computational efficient AOA method to compute the directions of arrival signals with any type of antenna array geometry. The proposed method could be a good alternative to the MUSIC method specifically in massive MIMO technology. The SSS method based on the orthogonality between signal subspace and the manifold array vector. A wide range of scenarios with intensive Monte Carlo simulation is performed and the results verified the effectiveness of the SSS method in both 2D and 3D estimation applications. It is also compared with some of the well-known AOA methods and the obtained results show that its superiority. The remainder of this paper is organized as follows. The signal model for DOA estimation with arbitrarily configured arrays is presented in Sect. 2. Section 3 gives the principle working of the proposed approach in addition to the complexity analysis. Section 4 presents numerical simulations with wide scenarios to demonstrate the effectiveness of the proposed method as well as to verify the theoretical analysis. The results are discussed and compared with other AOA methods. In Sect. 5, the conclusions of this work are summarized.

Throughout this paper, lowercase letters are used for scalar quantities whereas boldface lowercase and uppercase letters denote vectors and matrixes respectively. Superscripts, (·)^T, (·)^H and E{.} refer to transpose, conjugate transpose and the expected value respectively. The operator $(\bar{a})$ is a unit vector, I_M is the M × M identity matrix and ||·|| is a matrix or vector norm.

2 DOA Signal Model

Consider P signals arriving from different directions impinging on an M element antenna array, as depicted in Fig. 1. Then, the total received signal, $\varvec{X}\left( t \right)$, that includes directions both of elevation angle $\left( {\theta_{k} } \right)$ and azimuth angle $\left( {\phi_{k} } \right)$, corrupted by AWGN, is given as described below:

Fig. 1.

M-element arbitrary antenna array receiving P signals from different directions.

$$ \varvec{X}\left( \varvec{t} \right) = \varvec{A}(\theta ,\phi )\,\varvec{S}\left( t \right) + \varvec{N}\left( t \right) $$

(1)

where $\varvec{S}\left( \varvec{t} \right) = \left[ {\varvec{s}_{1} \left( t \right),\varvec{s}_{2} \left( t \right), \ldots ,\varvec{s}_{P} \left( t \right)} \right]^{T}$ is the (P × L) incident signals, L is the number of snapshots, $N\left( t \right) = \left[ {\varvec{n}_{1} \left( t \right),\varvec{n}_{2} \left( t \right), \ldots ,\varvec{n}_{\varvec{M}} \left( t \right)} \right]$ is an array of AWGN for each channel and $\varvec{A}(\theta ,\phi )$ is the steering matrix for P vectors it is defined as follows:

$$ \varvec{A}(\theta ,\phi ) = \left[ { \varvec{a}(\theta_{1} ,\phi_{1} ) \varvec{a}(\theta_{2} ,\phi_{2} ) \ldots \,\, \ldots \varvec{a}(\theta_{P} ,\phi_{P} ) } \right] $$

(2)

From Fig. 1, the unit vector, $\varvec{u}_{k}$, that includes the directions of $\theta_{k}$ and $\phi_{k}$ for any arrival signal is given as follows:

$$ \varvec{u}_{k} = \cos \phi_{k} \sin \theta_{k} \bar{a}_{x} + \sin \phi_{k} \sin \theta_{k} \bar{a}_{y} + \cos \theta_{k} \bar{a}_{z} $$

(3)

where $\bar{a}_{x} ,\bar{a}_{y}$ and $\bar{a}_{z}$ are unit vectors for Cartesian co-ordinates. The unit vector $\varvec{v}_{\varvec{i}}$ is the distance from a reference antenna element to the ith element and it is given as follows:

$$ \varvec{v}_{\varvec{i}} = r_{i} \cos \varphi_{i} \bar{a}_{x} + r_{i} \sin \varphi_{i} \bar{a}_{y} ,i = 1,2, \ldots ,M. $$

(4)

The phase angle $(\varphi_{i} )$ between a reference element and the others is defined as follows:

$$ \varvec{\varphi }_{\varvec{i}} = \frac{2\pi }{M}\left( {i - 1} \right) $$

(5)

The projection angle $(\alpha_{ik} )$ between a reference elements and the ith elements as shown in Fig. 1 due to the incident plane waves can be calculated from the dot product between unit vectors $v_{i}$ and $u_{k}$ as described below:

$$ \begin{array}{*{20}c} {\alpha_{ik} = \cos^{ - 1} \left( {\frac{{v_{i} .u_{k} }}{{\left\| {v_{i} } \right\|.\left\| {u_{k} } \right\|}}} \right)} \\ {\alpha_{ik} = \cos^{ - 1} \left( {\sin \theta_{k} \cos (\phi_{k} - \varphi_{i} )} \right)} \\ \end{array} $$

(6)

Once the above angle is computed, the time difference of arrival $(\tau_{ik} )$ of the kth signal between the reference element and the others can be calculated as in the following equation:

$$ \begin{array}{*{20}c} {\tau_{ik} = r\,\cos \alpha_{ik} = r\,\cos \left( {\cos^{ - 1} \left( {\sin \theta_{k} \cos (\phi_{k} - \varphi_{i} )} \right)} \right)} \\ {\tau_{ik} = r\,\sin \theta_{k} \cos (\phi_{k} - \varphi_{i} )} \\ \end{array} $$

(7)

Next, the corresponding phase difference $(\psi_{ik} )$ for each $(\tau_{ik} )$ can be determined:

$$ \psi_{ik} = \beta .\tau_{ik} = \frac{2\pi }{\lambda }r\,\sin \theta_{k} \cos (\phi_{k} - \varphi_{i} ) $$

(8)

$\beta = \frac{2\pi }{\lambda }$ is the spatial frequency, $r$ is the distance between the reference element and ith element, $d$ is the separation between adjacent elements. Then, the steering vector for an arbitrary geometry can be calculated:

$$ \varvec{a}(\theta_{k} ,\phi_{k} ) = \left[ {\begin{array}{*{20}c} {e^{{ - j\psi_{1k} }} } & {\begin{array}{*{20}c} {e^{{ - j\psi_{2k} }} } & \cdots & \cdots \\ \end{array} } & {e^{{ - j\psi_{Mk} }} } \\ \end{array} } \right] $$

(9)

The array covariance matrix (CM) is given by:

(10)

Complete knowledge of covariance matrix, $\varvec{R}_{xx}$, may not be supposed; instead, the sample-average estimated array input matrix can be used to construct CM as follows:

(11)

3 The Proposed AOA Method

The fundamental idea of this algorithm is applying the EVD approach to the CM or SVD to the received signal data and then sorting the eigenvalues in ascending way. Due to the orthogonal complementarity of the signal subspace (SS) and noise subspace (NS), DOAs can be estimated either from NS such as MUSIC or from SS such as ESPRIT. For computational reasons, SS is preferred since its dimension usually is much smaller than NS. This means the computational burden of the SSS method in the pseudo-spectrum construction stage using SS is much less compared to MUSIC. Further, SS is more efficient to use than NS. The SSS method is based on the orthogonality between the SS and the AMV as shown in Fig. 2.

Fig. 2.

The orthogonality between SS and AMV.

Applying Eigenvalue decomposition (EVD) approach to and then sorting the eigenvalues in a descending way yields:

(12)

Where ${\varvec{\Sigma}}_{{\varvec{SS}}} = \left[ {\uplambda_{1} ,\quad\uplambda_{2} ,\quad \ldots \, \ldots ,\quad\uplambda_{P} } \right]$ is a vector with dimension (1 × P) and it represents the largest P eigenvalues; the corresponding eigenvectors of ${\varvec{\Sigma}}_{{\varvec{SS}}}$ are:

$$ \varvec{Q}_{{\varvec{SS}}} = \left[ {\varvec{q}_{1} ,\quad \varvec{q}_{2} ,\quad \ldots \quad \ldots ,\quad \varvec{q}_{\varvec{P}} } \right] $$

(13)

Whereas ${\varvec{\Sigma}}_{{\varvec{NS}}} = \left[ {\uplambda_{P + 1} ,\quad\uplambda_{{{\text{P}} + 2}} ,\quad \ldots \,\, \ldots ,\quad\uplambda_{\text{M}} } \right]$ is a vector with (1 × M–P) size and represents the lowest P eigenvalues; the coresponging eigenvectors of ${\varvec{\Sigma}}_{{\varvec{NS}}}$ are:

$$ \varvec{Q}_{{\varvec{NS}}} = \left[ {\varvec{q}_{P + 1} \quad \varvec{q}_{P + 1} , \ldots \, \ldots ,\quad \varvec{q}_{M} } \right] $$

(14)

Then, the spatial spectrum of the SSS method can be constructed below formula;

$$ \varvec{P}_{{\varvec{ss}}} \left( \theta \right) = \left\| {\varvec{a}\left( \theta \right)\,\varvec{Q}_{{\varvec{SS}}} } \right\|^{2} $$

(15)

In order to extract the actual peaks and remove the sidelobe efficiently, we propose the following novel approach; firstly, normalise the pseudospectrum of the above equation using the maximum value:

$$ \varvec{P}_{{\varvec{Norm}}} \left( \theta \right) = \varvec{P}_{{\varvec{ss}}} \left( \theta \right)/max\left( {\varvec{P}_{{\varvec{ss}}} \left( \theta \right)} \right) $$

(16)

Next, to obtain narrower nulls towards DOAs and minimize the side-lobe levels significantly, subtract $\varvec{P}_{{\varvec{Norm}}} \left( \theta \right)$ from unity as follows:

$$ \varvec{P}_{\varvec{S}} \left( \theta \right) = 1 - \varvec{P}_{{\varvec{Norm}}} $$

(17)

Finally, apply the following formula to obtain peaks in the DOA signals,

$$ \varvec{P}_{{\varvec{SSS}}} \left( \theta \right) = \frac{1}{{\varvec{P}_{\varvec{S}} \left( \theta \right) + \varepsilon }} $$

(18)

where is $\varepsilon = 1/\uplambda_{1}$ a small scalar value added to avoid possible singularities. The needed number of computational operations to construct the pseudospectrum for SSS and other AOA methods was calculated and presented in Table 1.

Table 1. The required computational burden of the SSS method vs. other AOA methods.

where $J_{\theta }$ and $J_{\varnothing}$ denote the iteration numbers for elevation and azimuth planes respectively. Based on the above arguments, the proposed method gives lower computational burden than the other AOA methods in the spatial spectrum construction stage. Thus, the SSS method will be more efficient to implement with the massive MIMO technology compared to the above-presented AOA algorithms. This, in turn, will minimize the execution time and the required memory storage significantly.

4 Simulation Results and Discussion

A computer simulation is performed with many scenarios to validate the theoretical claims of the proposed method.

4.1 The 2D Estimation of the SSS Method Using Linear Arrays

Firstly, the performance estimation of the proposed method is studied with the variation of the SNR at the antenna array output. Five different values of SNR is set namely: SNR = –20 dB, –10 dB, 0 dB, 10 dB, 20 dB and each SNR three plane waves are assumed arriving from 0⁰, 30⁰, and –50⁰. A uniform linear array (ULA) consisting of ten elements (M = 10) with spacing d = 0.5 $\uplambda$ between each adjacent elements is used; the number of snapshots is taken L = 100. The performance estimation of the proposed method under these conditions is illustrated Fig. 3, it can be seen from this graph that the SSS method produces sharp peaks towards the directions of arrival signals with high resolution through the whole tested SNR range. However, the SNR effect on the performance estimation is clear where the produced peaks became narrow and accurate with increase in SNR and vice versa.

Fig. 3.

The performance of the SSS algorithm with different SNR.

Secondly, the performance estimation of the SSS method is examined under various angular separations between AOAs. Seven signals are assumed incident on ULA with these directions $[(\uptheta_{1} ,\uptheta_{2 \, } \,\text{ = }\,\uptheta_{1} + \Delta\uptheta_{\text{j}} ,(\uptheta_{3} ,\uptheta_{4} \,\text{ = }\,\uptheta_{3} + \Delta\uptheta_{\text{j}} ,\uptheta_{5 \, } \,\text{ = }\,\uptheta_{3} - \Delta\uptheta_{\text{j}} ),(\uptheta_{6} ,\uptheta_{7} \,\text{ = }\,\uptheta_{6} + \Delta\uptheta_{\text{j}} )]$, where θ₁ = –50°, θ₂ = 0°, θ₃ = 30° and $\Delta\uptheta_{\text{j}}$ is the angular separation between each pair of AOAs. Three $\Delta\uptheta_{\text{j}}$ are considered namely: $\Delta\uptheta = [1^{^\circ } ,2^{^\circ } ,3^{^\circ } ]$, M = 20, SNR = 10 dB, L = 100 and d = 0.5 λ. 100 Monte Carlo trials for each $\Delta\uptheta_{\text{j}}$ are conducted and a cumulative distribution function (CDF) is plotted for five steps of $\Delta\uptheta_{\text{j}}$. The performance separation of SSS is shown in Fig. 4 and the percentage of detection of the AOAs at each step of $\Delta\uptheta = [1^{^\circ } ,1.5^{^\circ } ,2^{^\circ } ,2.5^{^\circ } ]$ is 0.60, 0.76, 0.98 and 100 respectively. These results reflect the strength and effectiveness of the new method.

Fig. 4.

The performance estimation and detection of the SSS method with different angular separations.

4.2 The 3D Estimation of the SSS Method Using Planar Arrays

The second scenario presents two simulation examples: the former assumes ten signals are incident from different $\theta$ and $\phi$ angles on a uniform rectangular array (URA) with (10 × 10) antenna elements. The other simulation parameters are L = 2048 and SNR is set to 20 dB and d = 0.5 $\uplambda$. The latter emulates 25 signals impinging on URA with (16 × 16) antenna elements. The actual directions of received signals are generated randomly and indicated by red lines. The performance estimation of the SSS algorithm for the first and second scenario is depicted in Fig. 5 and Fig. 6 respectively. As can be seen from these graphs, the SSS method estimated DOAs accurately with less computation complexity in the scanning process stage compared to the MUSIC and other AOA methods as shown in Table 2.

Fig. 5.

The 3D performance estimation of the SSS method with P = 10, M = [10 × 10].

Fig. 6.

The 3D performance estimation of the SSS method with P = 25, M = [16 × 16].

Table 2. The required computational operations comparison between the SSS method and other AOA methods.

4.3 The Performance Estimation Comparison with Other AOA Methods

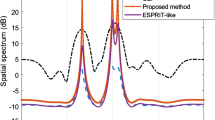
The final scenario compares the estimation accuracy of the SSS method with four common AOA techniques namely: Capon, Min-Norm, MUSIC and ESPRIT. The comparison tests the collected number of snapshots (L) for received signals and thus a simulation is run with seven different number of snapshots namely: L = [1, 3, 5, 10, 20, 50, 100, and 200]. For each L, 1000 Monte Carlo simulation is carried out to generate three AOAs randomly within angular space [90°–90°]. The other simulation parameters are M = 10, SNR = 10 dB, and d = 0.5λ. The average root mean square error (ARMSE) is calculated and then plotted as given in the below Fig. 7.

Fig. 7.

The SSS performance estimation comparison with other methods.

$$ {\text{ARMSE}} = \frac{1}{K}\sum\nolimits_{j = 1}^{K} {\sqrt {\frac{1}{P}\sum\nolimits_{k = 1}^{P} {\left[ {\left( {\theta_{k} - \widehat{\theta }_{k} } \right)^{2} } \right]} } } $$

(19)

As can be seen from this figure, the SSS method gives the best estimation resolution among the presented methods especially at a single and fewer number of snapshots.

5 Conclusion

A new high precision technique based on the orthogonality between SS and AMV has been proposed in this paper to estimates the directions of incident signals. The DOA model has been presented and the antenna array steering vector derived for an arbitrary array geometry. The principle and the mathematical model of the SSS method have been also given and demonstrated with many numerical examples for both 2D and 3D estimation applications. The performance estimation of the SSS method was compared with popular AOA algorithms using extensive Monte Carlo simulation and the results verified it has the highest resolution among them. The SSS method is applicable for any type of array configuration and gives less computational burden in the scanning process stage than MUSIC and other well-known AOA algorithms.