Keywords

1 Introduction

Many studies have been carried out to understand the behavior of smoke in closed places in order to escape people in places where there is fire. In an emergency situation, fires can be classified as accidental or intentional, with the dispersion varying according to the material that suffers the combustion process [7].

In a fire associated with the combustion phenomenon, four dangerous situations appear in general: heat, flames, insufficiency of oxygen and smoke. Of these four factors, smoke is one that causes very serious damage to people life [7]. Considering a fire situation in an environment in which it does not have any type of alarm or signaling, when people smell the smoke, they will instinctively look for the nearest exit. However, the smoke will hinder the vision causing tearing, in addition to causing respiratory symptoms such as coughing and suffocation. Smoke can cause panic, because it occupies a large volume of the environment, making it difficult for people to move in an evacuation [7]. There is great importance in conducting studies of the behavior of smoke to prevent deaths in fires caused by their inhalation.

Building projects should include active and passive measures to facilitate the escape of people, but prior simulation of an emergency situation minimizes the chances of fatality. Therefore, the objective of this paper is to propose a model to simulate the dispersion of smoke in an environment using potential fields and cellular automata. Cellular automata represent evolutionary systems that from an initial random configuration, each component of the system has its evolution based on the current situation of its neighbors and a set of rules that are the same for all components [12]. Potential field is an array or field of vectors that represent the space. The main idea of this method is to establish a potential field of attractive forces around the target point and a potential field of repulsive forces around obstacles. The sum of all forces determines the subsequent direction and velocity of the movement [4], and a new potential field is established called the artificial potential field [14].

In this work, a new application for potential fields is proposed, being joined to cellular automata to describe the dispersion of the smoke in a closed environment. We simulate an emergency situation causing the crowd evacuation in which each person is modeled as an autonomous agent using multiagent simulation [13].

The paper is organized as follows. In the next section the related works to the proposed method are presented. The details of the model are introduced in Sect. 3. The simulation results are analyzed in Sect. 4. At last the final considerations is given.

2 Related Works

Pessoli [6] proposes a methodology to simulate the transport of light pollutants under the action of wind fields in complex environments. The method consists of dividing the advective diffusion equation into two components, one laminar and other tubular. The internal modules of the model are programmed in C, for the external modules it was used the MATLAB® interpolation tool and for the calculation of the wind fields in the entire environment was used a CFD (Computational Fluid Dynamics).

The potential fields method has been commonly used in obstacle prevention because its modelling is simple. However, the method brings substantial deficiencies. Koren and Borenstein [4] present a rigorous mathematical analysis to identify the problems inherent in the potential fields method. As a result, the authors define a differential equation that combines the robot and the environment in a unified system.

Silva et al. [10] show the importance of respecting the indications of the ABNTFootnote 1 standard for emergency situations. For validate it, two scenarios were modeled using NetLogo software: a scenario where it uses real data from the Kiss nightclub in Santa Maria/RS (Brazil), at the time of the tragedy in 2013; and a second scenario for the Kiss nightclub respecting the ABNT standard. Considering the data obtained from the evacuations in the two scenarios, it was possible to note that the application of emergency exit signs, together with the number of doors and their correct dimensions, make evacuation considerably more effective.

Helbing et al. [3] model the evacuation of pedestrians in a panic situation using particle systems. It uses a social forces model that influences the behavior of pedestrians to investigate the mechanisms of panic and interference by uncoordinated movement in crowds.

Zheng et al. [15] propose a model to study the dynamics of evacuation of pedestrians with influence of fire and the smoke dispersion. The direction of smoke dispersion is from top to bottom, which leaves less size to pedestrians movement, and pedestrians’ movement behavior is divided into three stages: normal walking, curved walk and crawling. The influence of fire and smoke on the movement of pedestrians is modeled by the field of fire floor and the field of smoke floor.

Hardt et al. [2] propose a computational model for real-time simulation of the large-scale flow of smoke or gas in large environments, depending of a given configuration of obstacles and a field of winds. A discrete approach was adopted for wind transport and diffusion mechanisms, allowing simple and efficient simulation.

The work of Pax and Pavón [5] proposes an architecture of agents for internal scenarios, looking for performance and flexibility in the individual behavior of the agents. It keeps the crowd effects and allows the modeling of rich and heterogeneous behaviors for each agent.

In this section some related models to the proposal of this paper were presented. A specific discussion will be given in Sect. 4.1.

3 The Model

3.1 The Potential Fields Model

Considering a simple case, we can assume an element (e.g., a robot or an agent) being a point that is influenced by the potential field 2D. If we assume a differentiable potential field function U(q), we can find the related artificial force F(q) acting at the position \(q=(x,y)\) [9]. We have:

$$\begin{aligned} F (q) = -\nabla U(q)\text{, } \text{ where } \nabla U(q)= \left[ \begin{array}{l} \frac{\partial U}{\partial x}, \frac{\partial U}{\partial y} \end{array} \right] \end{aligned}$$
(1)

denotes the gradient vector of U in the q position. The potential field that acts on the element is the sum of the attractive field with the repulsive field:

$$\begin{aligned} U(q) = U_{att}(q) + U_{rep}(q). \end{aligned}$$
(2)

The attractive potential can be defined as a parabolic function:

$$\begin{aligned} U_{att}(q) = \frac{1}{2}k_{att}.\rho _{goal}^{2}(q), \end{aligned}$$
(3)

where \(k_{att}\) is a positive scale factor and \(\rho _{goal}(q)\) indicates the Euclidean distance \(\left\| q-q_{goal} \right\| \). Since this potential is differentiable:

$$\begin{aligned} F_{att}(q) = - \nabla U_{att}(q) = -k_{att}.\rho _{goal}(q)\nabla \rho _{goal}(q) = -k{att}.(q-q_{goal}). \end{aligned}$$
(4)

The repulsive potential should be strong when the element is close to the obstacle, but it should not influence when the element is far from the obstacle. We can define it as:

$$\begin{aligned} U_{rep}(q)=\left\{ \begin{array}{cc} \frac{1}{2}k_{rep}\left( \frac{1}{\rho (q)}-\frac{1}{\rho _{0}}\right) ^{2} &{}\text{, } \text{ if } \rho (q)\le \rho _{0}\\ 0 &{}\text{, } \text{ if } \rho (q)>\rho _{0}\\ \end{array} \right. . \end{aligned}$$
(5)

The \(k_{rep}\) constant is a scaling factor, \(\rho (q)\) is the distance of q to the obstacle and \(\rho _{0}\) is the distance of influence of the obstacle. The repulsive potential function \(U_{rep}\) is positive or zero, and it tends to infinity when the element approaches the obstacle. If the boundary of the obstacle is convex and differentiable in parts, \(\rho (q)\) is differentiable everywhere in the free configuration space. We can define a repulsive force as:

$$\begin{aligned} F_{rep} = -\nabla U_{rep}(q), \end{aligned}$$
(6)
$$\begin{aligned} F_{rep} = \left\{ \begin{array}{cc} k_{rep}\left( \frac{1}{\rho (q)}-\frac{1}{\rho _{0}}\right) \frac{1}{\rho ^{2}(q)}\frac{q-q_{obstacle}}{\rho _{0}} &{}\text{, } \text{ if } \rho (q)\le \rho _{0}\\ 0 &{}\text{, } \text{ if } \rho (q)>\rho _{0}\\ \end{array} \right. . \end{aligned}$$
(7)

In this way, the resultant force is:

$$\begin{aligned} F(q) = F_{att}(q) + F_ {rep}(q), \end{aligned}$$
(8)

which acts on the element and it is influenced by attractive and repulsive forces, directing the element away from the obstacles towards to the target [9].

3.2 The Potential Field Model Adapted for Smoke Dispersion

This work creates a model to simulate the dispersion of smoke in an environment using the concept of potential fields associated with cellular automata. From this model, we simulated an emergency situation causing an evacuation of people based on multiagent system. The Fig. 1 shows the diagram of the methodology and the following subsections present their steps.

Fig. 1.
figure 1

Proposed methodology.

Full size image

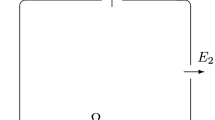
Potential fields are typically used for agent movement models. In this work, a new application for the concept is proposed, being used to describe the dispersion of the smoke in a closed environment. For that, it was necessary to make some adjustments in the equations of the potential fields, then it could be used in this new application. In the original definition of potential fields, it is considered only a possible target for the agent to reach and obstacles can be more than one in the environment. In our application, the equations were modified so that it was possible to have a single obstacle (fire) with several possible targets (doors). With this, the obstacle generates a force of repulsion while each target generates its force of attraction. Considering the Vector Agent position being \(\overrightarrow{q}=(q_{x},q_{y})\), the Vector Target position being \(\overrightarrow{a}=(a_{x},a_{y})\) and the Vector Obstacle position being \(\overrightarrow{o}=(o_{x},o_{y})\), the artificial potential field for the dispersion of the smoke is obtained through the following equations:

Attractive Potential

$$\begin{aligned} U_{a}(q)=\frac{1}{2}k_{a}\frac{1}{\parallel \overrightarrow{q} - \overrightarrow{a}\parallel ^{2}}. \end{aligned}$$
(9)

The \(k_{a}\) constant is how much the field deforms near the target point.

Attraction Force

$$\begin{aligned} \overrightarrow{F}_{a}(q)=-\nabla U_{a}(q)=-\left[ \frac{\partial U_{a}}{\partial q_{x}}\widehat{i}+\frac{\partial U_{a}}{\partial q_{y}}\widehat{j}\right] =-\left[ A_{a}\widehat{i}+B_{a}\widehat{j}\right] . \end{aligned}$$
(10)

Calculating \(A_{a}\), we have:

$$\begin{aligned} A_{a}=\frac{1}{2}k_{a}\left[ \frac{2a_{x}-2q_{x}}{[(q_{x}-a_{x})^{2}+(q_{y}-a_{y})^{2}]^{2}}\right] . \end{aligned}$$
(11)

Calculating \(B_{a}\), we have:

$$\begin{aligned} B_{a}=\frac{1}{2}k_{a}\left[ \frac{2a_{y}-2q_{y}}{[(q_{x}-a_{x})^{2}+(q_{y}-a_{y})^{2}]^{2}}\right] . \end{aligned}$$
(12)

Repulsive Potential

$$\begin{aligned} U_{r}(q)=\left\{ \begin{array}{ccc} C_{r} &{}\text{, } \text{ if } &{}{\small d(q,o)\le inf}\\ 0 &{}\text{, } \text{ if }&{}{\small d(q,o)> inf}\\ \end{array} \right. , \end{aligned}$$
(13)
$$\begin{aligned} \text{ where } C_{r} = \frac{1}{2}k_{r}\left( \frac{1}{d(q,o)}-\frac{1}{inf}\right) ^{2}. \end{aligned}$$
(14)

The \(k_{r}\) constant is how much the field deforms near the obstacle point, d(q, o) is the Euclidean distance of the agent to the obstacle and inf is the distance of influence of the obstacle.

Calculating \(C_{r}\), we have:

$$\begin{aligned} C_{r}=\frac{1}{2}k_{r}\left[ \frac{1}{(o_{x}-q_{x})^2+(o_{y}-q_{y})^{2}} -\frac{2}{inf\sqrt{(o_{x}-q_{x})^2+(o_{y}-q_{y})^2}}+\frac{1}{inf^{2}}\right] . \end{aligned}$$
(15)

Repulsion Force

$$\begin{aligned} {\overrightarrow{F}}_{r}(q)=-\nabla U_{r}(q)=-\left[ \frac{\partial U_{r}}{\partial q_{x}}\widehat{i}+\frac{\partial U_{r}}{\partial q_{y}}\widehat{j}\right] .\quad \text{ Therefore, } \end{aligned}$$
(16)
$$\begin{aligned} {\overrightarrow{F}}_{r}(q)=-\left[ \frac{\partial C_{r}}{\partial q_{x}}\widehat{i}+\frac{\partial C_{r}}{\partial q_{y}}\widehat{j}\right] =-\left[ D_{r}\widehat{i}+E_{r}\widehat{j}\right] . \end{aligned}$$
(17)

Calculating \(D_{r}\), we have:

$$\begin{aligned} D_{r}=\frac{1}{2}k_{r}\left[ \frac{2o_{x}-2q_{x}}{[(o_{x}-q_{x})^2+(o_{y}-q_{y})^2]^{2}}+\frac{2}{inf}\left( \frac{1}{2[(o_{x}-q_{x})^2+(o_{y}-q_{y})^2]^{\frac{3}{2}}}-2q_{x}+2o_{x}\right) \right] . \end{aligned}$$
(18)

Calculating \(E_{r}\), we have:

$$\begin{aligned} E_{r}=\frac{1}{2}k_{r}\left[ \frac{2o_{y}-2q_{y}}{[(o_{x}-q_{x})^2+(o_{y}-q_{y})^2]^{2}}+\frac{2}{inf}\left( \frac{1}{2[(o_{x}-q_{x})^2+(o_{y}-q_{y})^2]^{\frac{3}{2}}}-2q_{y}+2o_{y}\right) \right] . \end{aligned}$$
(19)

Resultant Force

$$\begin{aligned} \text{ Finally, } F(q) = - \sum _{i=1}^{n} {\overrightarrow{F}}_{a_{i}}(q) + \overrightarrow{F}_{r}(q). \end{aligned}$$
(20)

The model potential field is defined from its attracting points which are the exit doors and a repulsive point that is the origin of the fire. The smoke is generated at the point of repulsion, it starting gradually and moves according to the vectors generated by the potential field. Table 1 shows the steps of the smoke dispersion, that is an approximation of Fick’s Second Law [8], where Fick’s Laws are diffusion mass transport equations. The second Fick law associated to potential fields defines the rules used in the cellular automata necessary to define how smoke can spread through of building.

Table 1. Smoke dispersion rules.
Full size table

3.3 Calibrating Parameters for the Simulations

The Table 2(a) shows some simulations using one door and the focus of the smoke, varying the parameters door constant \((k_{a})\), smoke constant \((k_{r})\), and smoke influence (inf), which are part of the equations of the potential field. Analyzing each column of Table 2(a), it is possible to see that there is no change in the size of the smoke dispersion by varying the parameters \(k_{a}\) and \(k_{r}\). However, when analyzing each line of Table 2(a), it is possible to see that there is a change in the size of the smoke dispersion by varying the parameter inf, and it is possible to say that the most relevant variable in the formation of the smoke is the influence of the smoke. In this way, an average value for the variables was chosen for our experiments: door constant equal to 5, smoke constant equal to 5, and smoke influence equal to 5. After defining the values of the constant parameters, the smoke dispersion was simulated with 1, 2, 3 and 4 doors, in ticks 11, 15, 21 and 25, as shown in Table 2(b).

Table 2. (a) Simulations with one door and the focus of smoke, varying the parameters door constant \(k_{a}\), smoke constant \(k_{r}\) and influence of smoke inf. (b) Simulations with 1–4 doors, in ticks 11, 15, 21 and 25.
Full size table

3.4 Crowd Evacuation Model

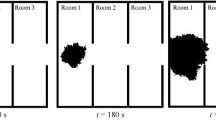
In order to simulate a crowd emergency situation with the dispersion of smoke, the NetLogo software was used to implement the case study. The simulation environment implemented by Silveira [11] in the NetLogo was used, which is an simple evacuation model where an environment with a crowd is created, and people leave by the nearest door using Euclidean Distance. The environment has a square configuration, with 61\(\,\times \,\)61 grid, as shown in Table 3, which it is possible to choose the agents or the vectors of the potential field to be shown, but it is always possible to see the dispersion of smoke. In the modeled environment, people are created in random positions and move randomly until they recognize the smoke. When this happens, agents identify the closest exit, calculated by the Euclidean Distance. These agents have the ability to communicate with others when they feel the smoke in the environment (this ability could be ON or OFF).

Table 3. Interfaces.
Full size table

4 Results Analysis

In the simulations performed with the model some parameters were their values fixed and some parameters varied their values, as shown in Table 4. The initial population size in the simulations was chosen, and it increases gradual, to facilitate the analysis of the results. For each configuration of values, five simulations were performed, and the average, the standard deviation and the percentage of people that left or died in relation to the initial amount of people in the environment were calculated.

Table 4. Parameters.
Full size table

In this section, we analyze the results obtained from the simulations to evaluate the influence of communication in an emergency situation with different populations of people in an environment. The focus of our work is to understand the used techniques, without a concern about computational performance. In the Table 5(a), (b) and (c) are the values obtained from these simulations.

Table 5. Simulations: (a) population 35 agents, (b) population 150 agents, and (c) population 600 agents (L: people who have left; D: people who died; %: percentage of people who left or died in relation to the total number of people).
Full size table

In a general way, it is possible to see that the more doors, the lower the percentage of dead, as established by the Brazilian standard NBR 9077 [1]. With a population of 35 agents (Table 5(a)) having communication and three or four doors the values of people who left were better, but as it is a small population, people are far from each other to communicate. An example, which we can see in the Table 5(a), when we have four doors, with communication came out 83% of the people, while without communication came 79%. When analyzing the Table 5(b) with 150 agents, in the simulations with communication, people’s exit results are better, with this it is understood that communication has more impact in the process of evacuation people. An example, which we can see in the Table 5(b), when we have four doors, with communication 82% of people left and without communication 77% of people left. And with 600 agents (Table 5(c)), it is possible to see that in the simulations when there are many people in the environment, we obtained better results when we have four doors without communication, because there are many people in the simulation and they simply leave the environment, before identifying the fire or be warned from the fire. An example, which we can see in the Table 5(c), when we have four doors, without communication 60% of people left, while with communication 53% of people left.

4.1 Smoke Dispersion Methods Comparison

Zheng et al. [15] simulate the evacuation dynamics of pedestrians with the influence of fire and the smoke dispersion. The smoke dispersion is from top to bottom, as time goes on, less space as to people walk in the environment as a normal way. In this way, this work considers three ways to people movement: normal walking, curved walk, and crawling. The Fig. 2(a) shows the simulation performed, where, in the middle of the room happens the fire in the red color; the smoke in shades of gray (the stronger the more smoke); people in a normal walking are in blue; people in a curved walk are in green; and people in crawling are in cyan. There are two evacuation doors on the left at the room.

Using our model to represent the same scenario presented in [15], we obtained the results presented in the Fig. 2(b), where the smoke is represented in shades of gray and two doors on the left in yellow; and the potential field vectors are in red. It is possible to see that our approach could reproduce the smoke dispersion for this scenario, with a more “realist” way, because the form of smoke is less symmetric (drop form), differently of the results in [15], which only uses the neighborhood to disperse the smoke.

Fig. 2.
figure 2

(a) The results of the work in [15]. (b) Our results using the same scenario. (Color figure online)

Full size image

Hardt et al. [2] simulate in real time the large-scale smoke or gas flow in large environments, where there are one obstacle (yellow circle) and a wind field. The Fig. 3(a) shows the sequence of laminar wind images, using a diffusion coefficient equal to 0.2.

Using our model to represent the same scenario in [2], we obtain the results presented in Fig. 3(b), that shows the images sequence of the smoke with diffusion coefficient equal to 0.2. In this model, the obstacle is the blue circle, and the attractor is the door in the right side of the environment (in yellow). Our scenario has just one attractor to cause the dissipation of smoke, whereas the proposed method in [2] uses a wind field (whole field acts as attractors, using a flow velocity). Therefore, the smoke shape is different: the dispersion in our model is wider in the initial point and finer at the end point, near the door.

Fig. 3.
figure 3

(a) The results in [2]. (b) Our results using the same scenario. (Color figure online)

Full size image

5 Final Considerations and Further Works

This paper presented a new model to simulate the dispersion of smoke in closed environments, using potential fields associated to the concept of cellular automata, and modeling an emergency situation using multiagent-based simulation. The results of our experiments showed that using the potential fields in the modeling of smoke dispersion, generally, brings a good approximation of what happens in reality. For example, when there is a single door and a single focus of fire that generates smoke, it tends to move toward the door forming a drop, having its rounded part in the focus of the fire and narrowing in the vicinity of the door. Modeling the evacuation of people in an emergency situation was taken into consideration communication between people, to know if its influence is significant in an emergency situation. If the people know about the smoke, the amount of agents that leave the environment is significant. It is notice that people live longer when they talking each other about the emergency situation.

As future work, we intend to generate complex scenarios with obstacles within the environment (e.g., with walls, tables, and chairs), add emergency signals (according NBR 9077 [1]), and model real scenarios such as the Kiss Nightclub [10]. Other improvements will be proposed in the concept of potential fields to model the agents movement, as well as apply the concepts of roadmaps (path planning). In this way, people will not only look for the nearest path but rather the safest. Finally, another work is ensured the conservation of mass in the smoke dispersion.