Predictive Run-Time Verification of Discrete-Time Reachability Properties in Black-Box Systems Using Trace-Level Abstraction and Statistical Learning

Abstract

Run-time Verification (RV) has become a crucial aspect of monitoring black-box systems. Recently, we introduced $\mathcal {P}{} \textit{revent}$, a predictive RV framework, in which the monitor is able to predict the future extensions of an execution, using a model inferred from the random sample executions of the system. The monitor maintains a table of the states of the prediction model, with the probability of the extensions from each state that satisfy a safety property.

The size of the prediction model directly influences the monitor’s memory usage and computational performance, due to the filtering techniques used for run-time state estimation, that depends on the size of the model. Hence, achieving a small prediction model is key in predictive RV.

In this paper, we use symmetry reduction to apply abstraction, that, in the absence of a model in black-box systems, is performed on the observation space. The symmetry relation is inferred based on k-gapped pair model, that lumps symbols with similar empirical probability to reach a set of target labels on a set of samples. The obtained equivalence classes on the observation space are used to abstract traces that are used in training the prediction model.

We demonstrate the soundness of the abstraction, in the case that the generating abstract model is a deterministic Discrete-Time Markov Chain (DTMC). We use Hidden Markov Models (HMMs) to handle the abstraction-induced non-determinism by learning the distribution of a hidden state variable. We implemented our approach in our tool, $\mathcal {P}{} \textit{revent}$, to empirically evaluate our approach on the Herman’s randomised self-stabilising algorithm. Our results show that the inferred abstraction significantly reduces the size of the model and the training time, without a meaningful impact on the prediction accuracy, with better results from the HMM models.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Run-time Verification (RV) [28] has become a crucial element in monitoring and analysing safety aspects of black-box stochastic systems [29, 39], where there is almost surely a non-zero probability of failure. In RV, a monitor checks the current execution, that is a finite prefix of an infinite path, against a given property, typically expressed in Linear Temporal Logic (LTL) [36], that represents a set of acceptable infinite paths. If any infinite extension of a prefix belongs (does not belong) to the set of infinite paths that satisfy the property, the monitor accepts (resp. rejects) the prefix. However, if the monitor is not able to reach a verdict with the given prefix because it can be extended to satisfy or violate the property, the monitor outputs unknown [5].

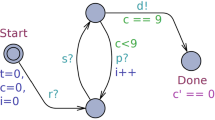
We introduced the predictive RV framework [3], where the monitor finitely extends the prefix based on a prediction model that is trained on the set of independent and identically distributed (iid) sample traces. This gives the monitor the ability to detect a monitorable [14] property’s satisfaction/violation before its occurrence. In this paper, we propose inferring trace-level abstraction to reduce the size of the prediction model. Our focus is on the discrete-time reachability properties, specified as target labels on the observation space $\varSigma$. The maximum length of the extensions is specified as the prediction horizon (Fig. 1).

Fig. 1.

Overview of predictive RV with abstraction.

Abstraction. The key idea in our abstraction is to decrease the size of the observation space by extracting symbols that have similar transient probability [24] to reach the target labels. Therefore, our approach can be seen as a form of symmetry reduction [23] on the observation space that is implemented at the trace-level [33]. We use k-gapped pair model [13] to detect the symbols that have similar empirical probability to reach the target symbols within k steps. The symbols that have probability zero are considered irrelevant in the prediction. The symmetrical symbols are then lumped into equivalence partition over the observation space to convert the traces of the training set into abstract traces.

Learning. If there is no non-determinism in the generating model of the abstract traces, given that the property is a bounded reachability LTL formula, any learning technique to infer the deterministic model, such as Aalergia [30], suffices to provide the prediction model that in the limit is as accurate as the actual model. However, the trace-level abstraction may induce non-determinism in the trained model [33]. We use Hidden Markov Model [37] (HMM) to infer the induced non-determinism by the abstraction, and compare the results with the deterministic as well as the actual model [30]. We train an HMM using Baum-Welch algorithm [37], that is an approximation to find the parameters of the HMM that maximizes the likelihood of the training data.

Reachability Analysis and Monitor Construction. The monitor in our framework is the result of a bounded reachability analysis on the prediction model. We use Prism [34] to perform the probabilistic bounded reachability analysis on the prediction model. The monitor is implemented as a lookup table, where each entry is a combination of three elements: an integer variable t, a state of the prediction model, and the probability that from that state the system reaches the states with the target labels, within t steps. The value of t is constrained by the prediction horizon that is expected from the prediction model.

State Estimation. Given that the original DTMC is deterministic, the system state can be determined by the observed path u. However, if the prediction model is non-deterministic, the state of the system needs to be estimated [40] based on the prefix u. Any filtering techniques [38] can be exploited to estimate the state at run-time. If the size of the model is large, approximate techniques such as the Viterbi algorithm [3, 43] can be applied too. Since the purpose of the current paper is to reduce the size of the prediction model, and also for evaluation purposes, we apply a direct approach and compute the posterior probability distribution of the states in the prediction model after observing u, using Forward-Backward algorithm [37].

The output of the monitor is the probability that from the estimated state s the system reaches the target labels within at most h steps. This probability is retrieved from the probability table after estimating the current state. Respectively, the size of the prediction model dictates both the size and the computational overload of the monitor.

In summary, our paper makes the following contributions:

• define trace-level abstraction as a symmetry relation in the observation space, and infer it using k-gapped pair model

• resolve non-determinism induced by the abstraction using hidden state variable

• demonstrate the validity of our approach on a distributed randomized algorithm, by showing the significant reduction in the prediction models with minimum impact on the prediction accuracy.

The rest of the paper is organized as follows: in Sect. 2 we introduce our running example, followed by preliminaries in Sect. 3, and a brief description of the prediction procedure in Sect. 4. In Sect. 5 we explain the trace-level abstraction using symmetry relation on the observation space and our algorithm to infer the symmetry. Learning deterministic models, and some theoretical guarantee, as well as learning non-deterministic models are described in Sect. 6. We conclude the paper by discussing the results of our case study in Sect. 7.

2 Running Example

We use the die example [34] as the running example throughout the paper. This example demonstrates the simulation of throwing a fair 6-sided die with flipping a fair coin [22]. Let C be the output of the flipped coin ($C\in \{ii,hh,tt\}$), where hh, tt display head and tail, resp., and ii is a special symbol to indicate the initial state of the coin. Also, let D be the output of the simulated die ($D\in \{0,\dots ,6\}$), where $1,\dots ,6$ is the simulated output of the die, and 0 shows that the coin needs to be flipped again, and the output of the die is not determined yet. The coin needs to be flipped at least three times to simulate observing a number on the die. We define $\varSigma _{die}:C\times D$ as the observation space, that denotes the output of the coin and the die in the process.

Fig. 2.

The learned model of the die example from 1000 samples used as the prediction model.

Suppose checking the reachability property eventually the outcome of the die is either “1” or “6”, at run-time, which translates to the LTL property , based on the symbols in the defined observation space. Any (infinite) execution paths with the prefix u : (ii, 0)(tt, 0)(hh, 0)(hh, 6) satisfies $\varphi$. However, the result on the prefix $u':(ii,0)(tt,0)(hh,0)(tt,0)$ is unknown [6], as it can be extended to an infinite path that satisfies $\varphi$ (e.g., (ii, 0)(tt, 0)(hh, 0) $(tt,0)(hh,0)(hh,6)^{\omega }$), or an infinite path that violates $\varphi$ (e.g., $(ii,0)(tt,0)(hh,0)(tt,0)(tt,0)(tt,5)^{\omega }$).

To deal with the inconclusive results due to unknown extensions [5], we provide the monitor with a prediction model to extend the prefix and generate the results based on the probability of the extensions that satisfy the given property. In the die example, the model in Fig. 2 is created from 1000 iid samples, with which the monitor is able to compute the probability of all the extensions that satisfy $\varphi$ (the shaded states). We limit the length of the extensions to some boundary, which we call the prediction horizon.

3 Preliminaries

In this section, we briefly introduce definitions and notations. A probability distribution over a finite set S is a function $P: S \rightarrow [0,1]$ such that $\sum _{s \in S}P(s) = 1$. We use $X_{1:n}$ to denote a sequence $x_1,x_2,\dots ,x_n$ of values of a random variable X, and use u and w to, respectively, denote a finite and an infinite path.

Discrete-Time Markov Chains (DTMC).

Definition 1

(DTMC). A Discrete-Time Markov Chain (DTMC) is a tuple $\mathcal {M}:(S, \varSigma , \pi , \mathbf {P}, L)$, where S is a non-empty finite set of states, $\varSigma$ is a non-empty finite alphabet, $\pi : S \rightarrow [0,1]$ is the initial probability distribution over S, $\mathbf {P}: S\times S \rightarrow [0,1]$ is the transition probability, such that for any $s \in S$, $P(s, \cdot )$ is a probability distribution, and $L:S\rightarrow \varSigma$ is the labeling function.

Let $\mathcal {M}$ be a DTMC. The sequence $\sigma _0\sigma _1\dots$ is an execution path on $\mathcal {M}$ iff $\mathbf {P}(s_i,s_{i+1})>0$, where $L(s_i) = \sigma _i, i \ge 0$. An execution path can be finite or infinite. The probability measure on the execution paths is defined using cylinder sets [24]. We deal with finite paths in the remaining of the paper. We denote by $Path_k(\sigma )$ the set of all finite execution paths of length k that start with $\sigma$. In the following, we define the finite extension of a path.

Definition 2

(Finite Extensions of a Path). Let $\sigma _0\sigma _1\cdots \sigma _n$ be a finite execution path on a DTMC. The set of finite extensions of u is denoted by $Ext_u$ and defined as follows:

$$ Ext_u = \{u\in Path_k(\sigma _{n}) | k \ge 0\} $$

We denote by $Ext^{\le h}_u$, if $k \le h$ in Definition 2.

Definition 3

(Deterministic State). State $s \in S$ of a DTMC is called deterministic iff for all $\sigma \in \varSigma$, there exists at most one $s'\in S$ such that $\mathbf {P}(s,s')>0$ and $L(s')=\sigma$.

Definition 4

(Deterministic DTMC [30]). A DTMC is deterministic iff:

• There exists $s_{init} \in S$ such that $\pi (s_{init}) = 1$.

• For all $s \in S$, s is deterministic.

Hypothesis Testing. Let X be some random variable with unknown mean $\mu$ and variance $\sigma ^2$. Let $x_1,\dots ,x_n$ be iid random samples of X, with mean $\bar{X}$ and variance $v^2$. A two-sided null hypothesis test enables us to check $H_0:|\mu -\bar{X}|=0$. According to the central theorem [15], as the number of samples grows $|\mu -\bar{X}|$ follows a student’s t-distribution [15]. Therefore using confidence $\alpha$ and the t-distribution we are able to accept $H_0$, if $\frac{|\bar{X}-\mu |}{\tfrac{\sqrt{v}}{n}} \le t_{n-1,\alpha }$.

4 Prediction as Quantitative Bounded Reachability Analysis

Let $\mathcal {M}$ be a DTMC, $\mathcal {G} \subseteq \varSigma$ be the set of target labels of some goal states in $\mathcal {M}$, and $\mathcal {L}(\mathcal {G})$ be the set of finite execution paths on $\mathcal {M}$ that end with $\sigma \in \mathcal {G}$. The monitor’s purpose is to estimate the probability of all the extensions of length at most h that satisfy . In a discrete-time setting, the variable h is a positive integer, which we call the prediction horizon. Computing the probability of the satisfying extensions is achieved by performing a bounded reachability analysis on the prediction model.

Let $u \notin \mathcal {L}(\mathcal {G})$ be the execution on $\mathcal {M}$ observed so far, and $Ext_u$ be the set of finite extensions of u. The output of the monitor is the probability measure of the set of the paths of length at most h that satisfy , i.e.,

$$\begin{aligned} Pr(\mathcal {C}), \text { where } \mathcal {C}=\{v \in Ext^{\le h}_u | uv \in \mathcal {L}(\mathcal {G})\}) \end{aligned}$$

(1)

Suppose also that s is the state corresponding to the last label in u, which is obtained by some state estimation technique [3, 21, 40]. As u expands, the new state is consequently estimated at run-time.

The probability (1) can be obtained by recursively computing the transient probability in $\mathcal {M}$ [24]: starting from s the probability of being at state $s'$ after h steps, such that $L(s') \in \mathcal {G}$. We can effectively turn computing the transient probability into checking the following quantitative PCTL property [17, 24]:

(2)

Due to multiplications of large and typically sparse matrices, the calculation of (2) is not practical during run-time [24]. As a result, we use Prism [34] to execute the quantitative reachability analysis [4] on all the states of $\mathcal {M}$ off-line, and store the values in a look-up table. The size of the table is $O(|\mathcal {M}|)$ [3], where $|\mathcal {M}|$ is the size of the prediction model. Subsequently, reducing the size of the model results in a smaller look-up table, in addition to the performance improvement due to a faster state estimation.

In our example, $\mathcal {G}_{\varphi } = \{(tt,1),(hh,1),(hh,6),(tt,6)\}$. Using the model in Fig. 2, the monitor is able to retrieve the value of , where $s_{u'}$ is the state of the model after generating $u'$. For instance, , which translates to the probability of all the extensions of length at most 20, that terminate with the labels where the outcome of the die is 6 or 1.

5 Trace-Level Abstraction by Inferring Symmetry in the Observation Space

We use a finite partitioning of the observation space, $\varSigma$, to achieve the trace-level abstraction in the form of a projection. The abstract traces are then used to train the prediction models, which ideally have smaller sizes than the model trained from the concrete traces, but are good enough approximates.

The simplest abstraction is to divide the observation space into two partitions, the atomic propositions that appear in the target labels and the non-target labels [33], i.e., $\mathcal {G}$, and $\varSigma -\mathcal {G}$, which we denote by $\varSigma _{\bar{\mathcal {G}}}$. The projection $R_{\mathcal {G}}:\varSigma \rightarrow \{gg,nn\}$ simply maps a symbol of a path to the symbol gg, if it is a target label, i.e., $R(\sigma ) = gg$ iff $\sigma \in \mathcal {G}$, and to the symbol nn otherwise. Consider $\mathcal {G}_\varphi$ and the traces u and $u'$. The projection of u and $u'$, using the projection relation $R_{\mathcal {G}_\varphi }$, are respectively, $\tilde{u}:(nn)(nn)(nn)(gg)$ and $\tilde{u'}:(nn)(nn)(nn)(nn)$.

The projection $R_{\mathcal {G}}$ may collapse the non-target symbols, that have a non-zero probability to reach a target label within some bounded steps, with symbols that never reach the target labels, i.e., have probability zero. For instance, compare the symbols (hh, 0) and (hh, 4). The former appears immediately before the target label (hh, 6) often in a simulated path; whereas the latter has no appearance before any of the target labels (see Fig. 2). Both are replaced with nn in $R_{\mathcal {G}}$, thus the predictive information from (hh, 0) and (hh, 4) are combined.

The key insight in our abstraction method is to not only detect the symbols with no significant correlation with the target labels, but also recognize the ones that have similar empirical probability to reach the target labels within a fixed number of steps, and collapse them together. As a result, we leverage the notion of symmetry [23] on the observation space to recognize the symbols with similar prediction power and lump them into the same partition. We define the symmetry relation with respect to reaching the target labels. More specifically, we say two symbols are symmetrical iff the probability measure of a fixed length path, that starts from either symbols and ends with some target labels, is equal.

Let $\mathcal {M}$ be a deterministic DTMC. Let $P_k: \varSigma _{\bar{\mathcal {G}}} \rightarrow \varSigma _{\bar{\mathcal {G}}}$ be the permutations on the non-target labels, such that $Pr(Path^{\mathcal {G}}_k(P_k(\sigma ))) = Pr(Path^{\mathcal {G}}_k(\sigma ))$ for all $\sigma \in \varSigma _{\bar{\mathcal {G}}}$, and some fixed integer $k > 0$, where $Path^\mathcal {G}_k(.) = Path_k(.) \cap \mathcal {L}(\mathcal {G})$. A group of permutations defined by $P_k$ on $\varSigma _{\bar{\mathcal {G}}}$ provides an equivalence relation (so-called the orbits) on $\varSigma _{\bar{\mathcal {G}}}$ that with $\mathcal {G}$ defines the equivalence classes over the observation space. We denote by $\varSigma _k$ the abstract alphabet set that contains a unique representative symbol for each partition, and by $R_k:\varSigma \rightarrow \varSigma _k$ the corresponding projection that maps each symbol to its rep. in the abstract alphabet.

Let $\mathcal {M}_k$ be the quotient of $\mathcal {M}$, where $\varSigma$ is replaced with $\varSigma _k$, and $L_k:S\rightarrow \varSigma _k$ such that $L_k(s)=R_k(L(s))$. Given that $\mathcal {M}_k$ is deterministic, we can show that $\mathcal {M}_k$ is bisimilar to $\mathcal {M}$. Therefore bounded predictions from any state in both models are equal (see Theorem 1). In the case that $\mathcal {M}_k$ is non-deterministic, we employ a hidden state variable to infer the non-determinism imposed by abstraction (see Sect. 6.2).

In the remainder, we use k-gapped pair model (Sect. 5.1) combined with hypothesis testing (Sect. 5.2) to infer $R_k$, and consequently, $\varSigma _k$.

5.1 k-gapped Pair Model

The k-gapped pair model [13] has been successfully applied in mining biological sequences [20], and in context-dependent text prediction [11]. We use the k-gapped pair model to extract the predictive symbols with respect to the target labels in the training set.

A k-gapped pair model is a triplet $(\sigma ,\sigma ',k)$, where $\sigma ,\sigma ' \in \varSigma$, and $k\ge 0$ is an integer that indicates the number of steps (gaps) between $\sigma$ and $\sigma '$. If $k=0$ the k-gapped pair is equivalent to a bigram [31].

The k-gapped occurrence frequency of the symbols $\sigma$ and $\sigma '$, is the frequency that $\sigma$ appeared within exactly k steps before $\sigma '$ over the sample path. Assuming that $\sigma '\in \mathcal {G}$, we use the sum of k-gapped occurrence frequency of a given symbol over all the target labels in the sample set, and define it as the k-prediction support. Algorithm 1 shows computing k-prediction support of symbol $\sigma$. Symbols $\sigma _j$ and $\sigma _{j+k+1}$ are the $j^{th}$ and $(j+k+1)^{th}$ symbols of the sample path $u_i$ in each iteration of the loop in line 3, and in line 5 is the indicator function that returns 1 if $\sigma _i = \sigma$ and $\sigma _{i+k+1}=\sigma '$; and 0 otherwise. The output of Algorithm 1 is the vector $[F_{u_1}\dots F_{u_m}]$, the k-prediction support values of each sample path for symbol $\sigma$.

The k-prediction support of $\sigma$ is essentially the empirical estimation of $Pr(Path^{\mathcal {G}}_k(\sigma ))$. Under the assumption that $F_{u_1},\dots , F_{u_m}$ is covariance-stationary [16], i.e., the mean is time-invariant and the autocovarinace function depends only on the distance k, both of which hold if the samples are iid, and the underlying generating model is a deterministic DTMC, we are able to use hypothesis testing to extract $R_k$.

5.2 Using Hypothesis Testing to Extract Symbols with Equivalent Prediction Support

Algorithm 2 demonstrates the procedure of extracting the abstract alphabet set, based on the symmetry between the k-prediction support of the symbols. The algorithm receives the sample set, the alphabet set, the set of target labels, and k, as inputs, and infer $R_k$, by generating the partitions $V_1,\dots ,V_t$.

The algorithm iterates over the symbols not considered in any equivalence classes, that are stored in $\mathcal {R}$ (the loop in lines 5–17). In each iteration, the symbol with the maximum k-prediction support score is found in $\mathcal {R}$ and stored in $\sigma _{max}$ with its score in $F_{max}$ (line 6). The score 0 indicates that there is no path of length k to any target labels from the symbols in $\mathcal {R}$ and we can end the procedure (line 7); otherwise, the symbols with statistically similar k-prediction support score to $\sigma _{max}$ are extracted from $\mathcal {R}$, and inserted in $V_t$ (for loop in 9–13). The statistical testing is conducted via the function HypothesisTesting, which performs a two-sided hypothesis t-test to check $H_0:F_{max}-F_{\sigma }=0$. Depending on the number of samples, a proper confidence is chosen to test $H_0$.

Algorithm 2 terminates, if there is no more symbol to classify, i.e., $\mathcal {R}=\emptyset$, or if all the remaining symbols in $\mathcal {R}$ have no k-prediction support. We dedicate a representative symbol for each extracted partition, including $\mathcal {G}$ and $\mathcal {R}$ if it is not empty, and define $R_k$ accordingly.

At worst, a total number of $O(|\varSigma |^2)$ comparisons is required to extract the abstract alphabet set. Given that the size of the actual model is at least as large as $|\varSigma |$, storing the entire vector of k-prediction support score for all symbols is impractical for large models. In fact, to make the usage of memory independent of the size of the alphabet, the computation of F in Algorithm 1 is performed on-the-fly, which only depends on the size of sample data. Compared to inferring the abstract alphabet from a model that is trained from the concrete traces, our approach is more memory-efficient.

Table 1 demonstrates the k-prediction support of the symbols (tt, 0) and (hh, 0), for $k=0,1,2$, over 1000 samples. The equivalence classes obtained by Algorithm 2 for $k=2$, where $R_2(\sigma _g)=gg, \sigma _g\in \mathcal {G}_{\varphi }, R_2(\sigma _v)=v1, \sigma _v\in V_1 = \{(ii,0),(hh,0),(tt,0)\}, R_2(\sigma _n)=nn, \sigma _n\in \mathcal {R}=\varSigma _{die}-\mathcal {G}_{\varphi }-V_1$. Notice that according to the original model in Fig. 2 the probability of reaching any of the labels in $\mathcal {G}_\varphi$ from (ii, 0), (hh, 0), (tt, 0) in 3 steps (within 2 gaps) is equal.

Table 1. The k-prediction support of all the symbols except the target labels, (hh, 6) and (tt, 1), for $k=0,1,2$, obtained from 1000 sample paths of the die example (scale $\times 10^{-3}$).

Fig. 3.

The learned deterministic DTMC from the abstract traces using the alphabet $\{gg,v1,nn\}$ using 2-prediction support.

6 Learning

6.1 Learning Deterministic DTMC

Amongst probably almost correct (PAC) techniques to train deterministic DTMCs [42], state-merging algorithms [9], are known to be effective. We use Aalergia [1, 30], that generates a frequency prefix tree acceptor (FPTA) from the training data, and then applies data-dependent compatibility criterion, parameterized by $\alpha$, to merge the states of the FPTA, and finally transforms it into a DTMC by normalizing the frequencies. The learned model converges to the generating deterministic DTMC, $\mathcal {M}$, in the limit for any $\alpha >1$ [33]. Figure 3 depicts the learned model from the abstract traces, based on the extracted symbols in Table 1.

In the following, we demonstrate the correctness of the predictions made by the deterministic DTMC trained from the abstract traces.

Theorem 1

Let $\mathcal {M}_k:(S,\varSigma _k,\pi ,\mathbf {P},L_k)$ be the representation of $\mathcal {M}$, where the states are relabelled based on the symbols in $\varSigma _k$. Suppose $\mathcal {G}\subseteq \varSigma$ is the set of target symbols, and $'gg'$ is their representative symbol in $\varSigma _k$. Also let $\mathcal {M}^\#:(\tilde{S}, \varSigma _k, \tilde{\pi }, \tilde{\mathbf {P}}, \tilde{L})$ be the learned model from the samples of $\mathcal {M}_k$, using any PAC learning algorithm. Then, under the assumptions of the convergence of the learning algorithm,

(3)

Proof

Notice that since prediction in our setting is a bounded LTL property, (3) is valid for the initial state, regardless of whether $\mathcal {M}_{k}$ is deterministic or not (see Theorem 1 in [33]). If $\mathcal {M}_{k}$ is a deterministic DTMC, the states of the trained model $\mathcal {M}^\#$, almost surely bisimulates the states of $\mathcal {M}_{k}$ in the limit (see Theorem 1 in [30]). As a result, under the assumptions of the convergence of the learning algorithm, (3) is followed.   $\square$

6.2 Learning Non-deterministic DTMC Using HMM

A Hidden Markov Model (HMM) specifies the distribution of a sequence as the joint distribution of two random variables: the hidden state variable, and the observation variable. More particularly, an HMM is the joint distribution over $X_{1:n}$, the sequence of the state variable, and $Y_{1:n}$, the sequence of observations (both with identical lengths). The joint distribution is such that $Pr(y_i\mid X_{1:i}, Y_{1:i}) = Pr(y_i\mid x_i)$ for $i\in [1,n]$, i.e., the current observation is conditioned only on the current state, and $Pr(x_i\mid X_{1:i-1}, Y_{1:i-1}) = Pr(x_i\mid x_{i-1})$ for $i\in [1,n]$ i.e., the current state is only conditioned on the previous hidden state. We use $\pi$ to denote the initial probability distribution over the state space, i.e., $Pr(x_1) = \pi (x_1)$. As a result, an HMM can be defined with three distributions:

Definition 5

(HMM). A finite discrete Hidden Markov Model (HMM) is a tuple $\mathcal {H}:(S, \varSigma , \pi , T, O)$, where S is the non-empty finite set of states, $\varSigma$ is the non-empty finite set of observations, $\pi : S \rightarrow [0,1]$ is the initial probability distribution over S, $T: S\times S \rightarrow [0,1]$ is the transition probability, and $O:S\times \varSigma \rightarrow [0,1]$ is the observation probability. We use $\varTheta _{\mathcal {H}}$ to denote $\pi$, T, and O.

In our setting, observations are the symbols of the abstract alphabet, $\varSigma _k$, and hidden states are the states of the generating model, i.e., the deterministic DTMC. The random hidden state variable creates an extra degree of freedom which allows to distinguish states that emit the same symbol but have different joint probability distributions.

Notice that the PAC learning of an HMM is a hard problem under cryptographic assumptions [10, 41] because the probability distribution over the state sequence X is unknown, therefore, the likelihood function does not have a closed form [41]. Subsequently, approximate algorithms, such as Expectation-Maximization (EM) [8], are employed. Training an HMM using EM is known as the Baum-Welch algorithm [37] (BWA), which calculates the parameters of the HMM by finding the maximum likelihood of the sample data. BWA requires the number of hidden states in a finite state HMM as an input, or hyper-parameter. The hyper-parameters are typically chosen based on some criterion that prevents overfitting (e.g., Bayesian Information Criterion (BIC) [12]).

To run the reachability analysis on the HMM, $\mathcal {H}:(S, \varSigma , \pi , T, O)$, we adopt the direct method in [45] to create an equivalent DTMC, $\mathcal {M}_H:(S\times \varSigma ,\varSigma ,\pi (s,.),\mathbf {P}$ $,L(.,\sigma ))$, where $\mathbf {P}((s,\sigma ),(s',\sigma '))=T(s,s')\times O(s',\sigma ')$.

Figure 4 displays the non-deterministic DTMC and the trained HMM over the abstract traces obtained by $R_2$ from Table 1. The DTMC in Fig. 4a is similar to the DTMC in Fig. 2, except that the states are relabeled using $R_2$ (see Sect. 5.2). Relabeling the model creates non-determinism as the sequence (v1, v1, v1) corresponds to several state sequences in the model. The HMM in Fig. 4b is obtained by training HMM that has 4 hidden states. Each hidden state corresponds to the set of states in the DTMC in Fig. 4a with the same labels. There are two hidden states associated with (v1) to distinguish between the states of the model in Fig. 4a that reach the target states (labelled (gg)) with different joint probabilities.

Fig. 4.

Training non-deterministic DTMC using HMM.

7 Case Study: Randomised Self-Stabilising Algorithm

We use Herman’s self-stabilising algorithm [18] to experiment our approach in $\mathcal {P}{} \textit{revent}$.¹ The algorithm provides a protocol for N identical processes (N is odd) in a token ring network, with unidirectional synchronous communication. Starting from an arbitrary configuration, the network will eventually converge to a defined stable state within a finite number of steps. The token is infinitely circulated in the ring amongst the processes in a fair manner. The stable state is defined as such that there is exactly one process that has the token. The process i has a local Boolean variable $x_i$. If $x_i = x_{i-1}$ there is a token with process i, in which case process i randomly chooses to set $x_i$ to the next value or leave it unchanged (i.e., equal to $x_{i-1}$).

The observation space for a ring with N processes has $2^{N}$ symbols, each representing the values of the local variable in each process. The observation space maps one-to-one to the state space of the corresponding DTMC. We are interested in monitoring the property which translates into the target symbols in which only one process has the same label as its left neighbour, i.e., there exists only one i such that $x_i = x_{i-1}$. The monitoring procedure throughout our experiments is performed off-line; however, in principle the on-line monitoring procedure would be the same, except that the execution path keeps expanding as the system continues running.

We collected 1000 iid samples from the DTMC using Prism simulation tool [34]. The length of the samples is constrained by a maximum, and is distributed uniformly. We first run Algorithm 2 to extract the predictive symbols for the target symbols specified by $\varphi _{stable}$. We replaced the symbols of the sampled traces based on the found partitioning, and performed the training algorithms to learn a deterministic DTMC as well as an HMM. The number of states in the HMM is chosen so that it is comparable to the size of the learned DTMC.

Prediction Evaluation: Using the values obtained from the actual models, we use Mean-Square Prediction Error (MSPE) [15] to measure the performance of the predictions by each model. The evaluation is conducted on a separate iid sample from the training samples, where the following is computed for each instance i that the prediction is made (i.e., a target label is not still observed):

(4)

where s is the state in the actual DTMC, and $\hat{s}$ is the state in the prediction model, estimated using Forward-Backward algorithm [37]. The Forward-Backward algorithm computes the posterior probability of the state space given the observation u, i.e., $Pr(X_n=s\mid u,\varTheta )$, where n is the length of u. We define MSPE as the average of (4), i.e., $\tfrac{1}{t}\sum _{i=1}^t\varepsilon _i^2$ where t indicates the number of points on the sample where a prediction is made.

Table 2. The prediction results of different models on 100 random samples.

Table 2 summarizes our results of three different prediction models compared to the prediction results obtained from the original model for $N\in \{5,7,9,11\}$, $k=0$ (a bigram model), and prediction horizon equal to one step. The size of the original model is identical to the size of the alphabet, as there is exactly one state corresponding to the valuation of the local variables in each process. We used Aalergia [1] to train DTMC from both the concrete and abstract traces, and Matlab HMM toolbox to train the HMMs. The training was performed on an Ubuntu 17.10 machine with 24 GB RAM. Training a DTMC from concrete traces was aborted for $N=11$ due to lack of memory, as the length of the FPTAs grows exponentially with the size of the alphabet. The trained DTMCs from abstract traces have significantly smaller size in direct relation to the size of the inferred abstract alphabet, and consequently a shorter training time. This result is consistent with the fact that the actual model is highly symmetrical with respect to the stable states, i.e., the probability of reaching the stable states from the states within an equivalence class in one step is equal.

The sizes of the trained HMMs are determined by the BIC score, and the size of their equivalent DTMCs are shown in parentheses. As we can see an HMM with comparable size is substantially more accurate in making predictions than a DTMC. The state estimation also benefits from the small size of the HMM with virtually no computational overhead. Since the prediction horizon is formulated as an upper-bound, the probability of an accepting extension increases as the prediction horizon increases, which in turn results in a lower MSPE. However, as depicted in Fig. 5a trained HMM has lower error-rate even for shorter range of predictions, e.g., for $h=5$, the MSPE of the HMM is 0.03$e-$02 as opposed to 0.85$e-$2 for the DTMC.

Figure 5b demonstrates the prediction results of the DTMC trained from concrete traces, and the traces abstracted by k-prediction support, using $k=0,5,10$. The prediction results are from the initial state, and as we can see, the models learned from abstract traces almost follow the values of the actual model. The best result belongs to $k=10$, which echos the maximum expected time to reach a stable state, i.e., that the path to the target symbols from the initial state is of length at most about 9.

Fig. 5.

The experiment results for abstract models in the Herman algorithm.

8 Related Work

To the best of our knowledge our approach is novel in terms of applying learning and abstraction to predictive RV, and using HMM to handle non-determinism at the trace level. Xian Zhang et al. [46] introduce a predictive LTL semantics definition, that is applied on white-box systems (i.e., using the control flow graphs), to find the extensions that evaluate an LTL formula to true or false. Martin Leucker [27] follows the same idea and extends the semantics and the monitor construction for when an over-approximation of the program is given. Our approach works on black-box systems and finds the probability of the extensions that satisfy a reachability property based on the sample executions of the system that form a probabilistic model. Furthermore, we define the abstraction by inferring a projection function over the observation space using the sample executions.

Sistla et al. [39] propose an internal monitoring approach (i.e., the property is specified over the hidden states) using specification automata and HMMs with infinite states. Learning an infinite-state HMM is a harder problem than the finite HMMs, but does not require inferring the size of the model [7].

Nouri et al. [33] use abstraction and learning to expedite statistical model checking [25]. Their approach is the probabilistic variant of black box checking [35] in which the inferred model, in the form of definite finite automata (DFA), is checked against some properties. In our case, we use abstraction to obtain a smaller prediction model for predictive RV. In [33] the atomic propositions in the property are used for abstracting the traces. We perform a statistical analysis on the traces to obtain partitions that leave the prediction probability intact. We also use HMM to handle the potential non-determinism introduced by the abstraction.

Aichernig and Tappler [2] employ black box checking in the context of reachability analysis of stochastic systems with controllable inputs. They use Markov Decision Process (MDP), an extension of a Markov chain with non-deterministic choices, as a model that is trained from random samples. They use the inferred MDP to obtain an adversary with which they collect new samples and incrementally train new MDPs. LAR [44] is a combination of probabilistic model learning and counterexample guided abstraction refinement (CEGAR) [19]. These approaches are orthogonal to our technique and it is straightforward to extend the training to other models such as MDP, and apply probabilistic CEGAR to obtain a model that guarantees checking affirmative properties.

9 Conclusion

We propose inferring a projection relation from a random set of samples to abstract traces that are used in building prediction models to monitor a discrete-time reachability property. Our inference technique is based on finding a symmetrical relation between the symbols of the alphabet, using k-gapped pair model, and lumping them into same equivalence classes. We use the abstract traces to train deterministic DTMC as well as HMM to handle the possible non-determinism induced by abstraction. We show that the prediction results remain intact with the model trained from abstract traces, under the condition that the generating DTMC of the abstract traces is deterministic and under the constraints of the learning algorithm. We evaluated our approach on a distributed randomized algorithm, and demonstrated that in general the trained HMM from the abstract traces is more accurate than the trained DTMCs.

Our approach is most effective on the systems with large observation space, and where the model benefits from symmetry in the probability of reaching some states. The statistical analysis of the traces proposed in this paper to reduce the observation space requires enough number of executions with the target labels to reliably detect similar symbols. If the target labels indicate some rare events (e.g., error with very low probability), techniques such as [26] are required to simulate enough traces with target labels. The trained model from such simulated sample traces need to be adjusted.

Lastly, an implementation of $\mathcal {P}{} \textit{revent}$ with the application of on-line learning methods (such as state merging or splitting techniques [32]) is necessary to apply the framework to the real-world scenarios.