Abstract
Radiative transfer provides a complete description of absorption, scattering, and radiation of light in a multiple scattering medium (Chandrasekhar 1960; Ishimaru 1999; Van de Hulst 2012). Consequently, radiative transfer is important for several applications such as neutron transport (Bell and Glasstone 1970; Case and Zweifel 1967; Lewis and Miller 1984), astrophysics (Peraiah 2002; Sobolev 2017), geophysics (Tsang et al. 1985; Mobley 1994; Kirk 1994; Thomas and Stamnes 2002; Kokhanovsky 2006b; Marshak and Davis 2005; Mishchenko et al. 2006; Mishchenko 2014), heat transfer (Modest 2013), biomedical optics (Welch et al. 2011; Wang and Wu 2012), and computer graphics (Jensen 2001).
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
1 Introduction
Radiative transfer provides a complete description of absorption, scattering, and radiation of light in a multiple scattering medium (Chandrasekhar 1960; Ishimaru 1999; Van de Hulst 2012). Consequently, radiative transfer is important for several applications such as neutron transport (Bell and Glasstone 1970; Case and Zweifel 1967; Lewis and Miller 1984), astrophysics (Peraiah 2002; Sobolev 2017), geophysics (Tsang et al. 1985; Mobley 1994; Kirk 1994; Thomas and Stamnes 2002; Kokhanovsky 2006b; Marshak and Davis 2005; Mishchenko et al. 2006; Mishchenko 2014), heat transfer (Modest 2013), biomedical optics (Welch et al. 2011; Wang and Wu 2012), and computer graphics (Jensen 2001). Applying radiative transfer theory is challenging for practical problems, because exact solutions of the radiative transfer equation (RTE) are known only for special cases (Case and Zweifel 1967). Even computational methods for radiative transfer require specialized methods (Lewis and Miller 1984; Gao and Zhao 2009) that can be challenging to implement and require substantial computational resources. For these reasons, accurate approximations of solutions of the RTE, and of the RTE itself, are valuable for gaining physical insight.
Boundary layer theory provides a systematic method to solve singularly perturbed boundary value problems (Bender and Orszag 2013; Hinch 1991; Miller 2006). Larsen and Keller (1974) introduced boundary layer theory for general initial-boundary value problems for the RTE. In RTE boundary layer theory, one seeks the asymptotic solution of the RTE in the regime of a strongly-scattering medium. However, it is a rather different approach from that taken in asymptotic radiative transfer theory (ARTT), which has been reviewed by Kokhanovsky (2006a). In the asymptotic limit of strong multiple scattering, the solution of a boundary value problem for the RTE is written as a sum of an interior solution and boundary layer solutions. The interior solution is governed by the diffusion approximation. The boundary layer solutions correct for errors made by the diffusion approximation near the boundary. Through a systematic perturbation theory, one can determine all of the subproblems required to compute the interior and boundary layer solutions. Moreover, boundary layer theory provides a procedure for computing boundary conditions for the diffusion approximation. The result is a uniformly valid asymptotic approximation to the solution of the RTE that is accurate over the entire domain.
The challenge in applying boundary layer theory to problems of practical interest lies in explicitly computing the boundary layer solutions from which boundary conditions for the diffusion approximation are computed. Habetler and Matkowsky (1975) have applied boundary layer theory to initial-boundary value problems with isotropic scattering in one spatial dimension. For that problem, one can compute the boundary layer solutions explicitly using the singular eigenfunctions described by Case and Zweifel (1967). Malvagi and Pomraning (1991), and Pomraning and Ganapol (1995) have applied boundary layer theory to more general RTE problems by using an approximate variational method to compute the boundary layer solutions. Recently, the authors and their collaborators have used numerical methods in conjunction with boundary layer theory to solve various RTE problems (Kim 2011; Kim and Moscoso 2011; Rohde and Kim 2012, 2014, 2017; Lehtikangas et al. 2012; Şahin-Biryol and Ilan 2014; Dark and Kim 2017). Using numerical methods to compute boundary layer solutions has opened up the use of boundary layer theory to RTE problems of practical interest.
Another approximation, called two-flux theory, is a particularly simple, and intuitive approximation of the RTE in a plane-parallel medium. Its origin traces back to Schuster (1905) in 1905 and Schwarzschild (1906) in 1906. However, it gained popularity due to the works of (Kubelka and Munk 1931; Kubelka 1948). As a result, two-flux theory is often called Kubelka–Munk theory. This theory has found extensive use for various applications (e.g., see the review by Philips-Invernizzi et al. (2001), largely due to its simplicity.
Two-flux theory models light fluxes traveling in forward and backward directions. Absorption and scattering in the medium are quantified using absorption and scattering coefficients, typically denoted by K, and S, respectively. One major challenge in two-flux theory lies in connecting these coefficients to fundamental quantities in radiative transfer. Many studies (Brinkworth 1972; Gate 1974; Nobbs 1985; Star et al. 1988; Vargas and Niklasson 1997; Molenaar et al. 1999; Yang and Kruse 2004; Yang et al. 2004; Yang and Miklavcic 2005; Edström 2007; Thennadil 2008; Neuman and Edström 2010; Myrick et al. 2011; Kokhanovsky 2007) have addressed the theoretical basis for two-flux theory and its applicability to interpret measured data. Sandoval and Kim (2014) derive two-flux theory using a systematic perturbation analysis of the double-spherical harmonics method of order one in the limit of strong multiple scattering. This perturbation method is similar to what is done in boundary layer theory.
In this paper, we review boundary layer theory and two-flux theory and draw connections between them. In particular, we derive two-flux theory using the interior solution from boundary layer theory governed by the diffusion approximation. This derivation is more elementary than the one done by Sandoval and Kim (2014). Consequently, it provides the framework needed to understand that two-flux theory is simply a reformulation of the diffusion approximation. We use the double-spherical harmonics method (Case and Zweifel 1967; Lewis and Miller 1984; Aronson 1986) to compute boundary layer solutions which, in turn, provide an efficient and effective method for computing boundary conditions for the diffusion approximation. We use the boundary conditions for the diffusion approximation to derive boundary conditions for two-flux theory. We call this model the asymptotic two-flux theory, because it is asymptotically accurate for strongly-scattering media. In addition, by considering the double-spherical harmonics method of order one, we draw its equivalence to four-flux theory and its connection to boundary layer theory. Through these connections, we develop valuable insights into radiative transfer problems in strongly-scattering media.
By comparing results by boundary layer theory and two-flux theory with direct numerical solutions of the full RTE, we show their respective scope of applicability. Boundary layer theory gives a uniformly-valid asymptotic approximation meaning that it is accurate throughout the entire domain with an a-priori error bound. In contrast, two-flux theory is not a uniformly valid asymptotic approximation– its accuracy depends on the boundary conditions prescribed. For standard boundary conditions based on the in-going flux at the boundary, two-flux theory is accurate near the boundaries, but inaccurate in the interior of the medium. When boundary conditions for two-flux theory are prescribed in a manner consistent with boundary layer theory, we find that it is accurate in the interior of the medium, but not near the boundaries. Both boundary layer and two-flux theories are valid for strongly scattering media where scattering is not too sharply forward peaked.
The remainder of this paper is as follows. In Sect. 2 we discuss the RTE in a plane-parallel slab, and describe all of the physical quantities in that problem. In Sect. 3, we give explicit results for the spectrum of the scattering operator in the RTE. These results are used throughout the analysis that follows. We describe boundary layer theory for the RTE in Sect. 4 including all of the details in deriving the interior and boundary layer solutions. In Sect. 5 we describe the double-spherical harmonics method used to compute the boundary layer solutions which, in turn, provides a method to compute boundary conditions for the diffusion approximation governing the interior solution. We summarize the results from boundary layer theory using the double-spherical harmonics method in a procedure to compute the asymptotic approximation in Sect. 6. In Sect. 7 we give a new derivation of two-flux theory based on the interior solution from boundary layer theory. In doing so, we are able to identify its limitations and prescribe boundary conditions consistent with boundary layer theory leading to the asymptotic two-flux theory. We show computational results comparing all of these approximations in Sect. 8. Additionally, Sect. 8 discusses the relationship between four-flux theory and the double-spherical harmonics method of order one. We discuss the extension of two-flux theory for the RTE in three dimensions in Sect. 9. Section 10 gives our conclusions.
2 Radiative Transfer in a Plane-Parallel Slab
Consider a uniformly absorbing and scattering medium contained in a plane-parallel slab. When a continuous source of light penetrates into this medium, be it from incident radiation and/or emanating from the surface, the light’s radiance (or specific intensity),  , can be described by the radiative transfer equation (RTE) (Chandrasekhar 1960),
, can be described by the radiative transfer equation (RTE) (Chandrasekhar 1960),

Here, the spatial coordinates parallel to the slab surface are \((x,y)\in \mathbb {R}^2\), and the coordinate normal to the slab surface is \(z \in (z_1, z_2)\). The direction cosines \(\varOmega _{1}\), \(\varOmega _{2}\), and \(\varOmega _{3}\) are the components of  , which is a vector on the unit sphere \(S^{2}\). The absorption and scattering coefficients are denoted by \(\kappa _{a}\) and \(\kappa _{s}\), respectively. The scattering operator L is defined by
, which is a vector on the unit sphere \(S^{2}\). The absorption and scattering coefficients are denoted by \(\kappa _{a}\) and \(\kappa _{s}\), respectively. The scattering operator L is defined by

where \(p(\cdot )\) is called the scattering phase function. In a bounded domain, boundary conditions prescribe the radiance for all directions pointing into the domain (Case and Zweifel 1967; Ishimaru 1999). In general, boundary conditions take the form


where  and
and  prescribe the radiance entering the medium at \(z = z_{1}\) and \(z = z_{2}\), respectively, and \(\hat{z}\) denotes the unit vector pointing along the z-axis in the positive sense. We can consider boundary conditions that take into account reflections due to a refractive index mismatch. All of the results that follow can take these reflecting boundary conditions into account. However, they complicate the analysis without providing any additional insight, so we do not consider them here.
prescribe the radiance entering the medium at \(z = z_{1}\) and \(z = z_{2}\), respectively, and \(\hat{z}\) denotes the unit vector pointing along the z-axis in the positive sense. We can consider boundary conditions that take into account reflections due to a refractive index mismatch. All of the results that follow can take these reflecting boundary conditions into account. However, they complicate the analysis without providing any additional insight, so we do not consider them here.
We assume axi-symmetry so that \(b_{1} = b(\mu )\) where \(\mu = \cos \theta \) and \(\theta \) is the inclination angle made with respect to the z-axis. Moreover, we assume the radiance enters the medium on \(z=z_1\) uniformly in (x, y). That light is the only source in the problem, so that \(b_{2} = 0\) on the surface \(z=z_2\). Furthermore, we assume that the scattering is rotationally invariant and depends only on the angle made between the incident and scattering directions, so that  . In this case, the solution of this boundary-value problem is uniform in (x, y) and azimuthally symmetric, i.e., \(I = I(z,\mu )\). For this case, I is governed by the one-dimensional RTE
. In this case, the solution of this boundary-value problem is uniform in (x, y) and azimuthally symmetric, i.e., \(I = I(z,\mu )\). For this case, I is governed by the one-dimensional RTE
where the azimuthally-integrated scattering operator is (henceforth, the tilde on \(\tilde{L}\) is dropped)
The redistribution function h in (4) is defined in terms of the scattering phase function as
and normalized according to
Equation (4) is to be solved in \(z_{1}< z < z_{2}\) subject to the boundary conditions
It is convenient to define the non-dimensional distance variable, called the optical depth,
Making the transformation of variable from z to \(\tau \) and introducing the albedo,
we find that (4) becomes
The albedo defined in (10) satisfies \(0 < \varpi _{0}\le 1\), with \(\varpi _{0}= 1\) corresponding to conservative scattering in which \(\kappa _{a} = 0\).
3 Legendre Polynomial Expansion and the Spectrum of the Scattering Operator
The Legendre polynomials are a sequence of orthogonal polynomials, \(P_1(\mu )\), \(P_2(\mu )\), \(\ldots \). They arise as a special case of spherical harmonics (Courant and Hilbert 2008) for azimuthally invariant functions. These polynomials satisfy the orthogonality relation
with \(\delta _{mn}\) denoting the Kronecker delta. The sequence \(\{P_n(\nu )\}, n=0,1,2,\ldots \) is complete in the \(L_2\) sense. In our analysis we shall frequently refer to the first two Legendre polynomials, which are \(P_{0}(\mu ) = 1\) and \(P_{1}(\mu )= \mu \). We shall also make use of the recursion relation
Because the redistribution function (6) is inherently rotationally invariant, it can be expanded in Legendre polynomials as
where the coefficients are
Because the scattering phase function is normalized according to (7), it follows that the first coefficient of (15) is \(g_{0} = 1\). The second coefficient \(g_{1}\) is called the anisotropy factor or mean cosine, which we denote by \(g_{1} = g\). It is given by
The spectrum of the operator L, given in (5), plays a key role in our analysis. In light of (14), we find that
It follows that \(P_{n}(\mu )\) is an eigenfunction of L with eigenvalue \(1 - g_{n}\). For the standard redistribution functions considered in the literature, all the eigenvalues are simple and decreasing, i.e., \(g_n > g_{n+1}\) for all n. Since \(g_{0} = 1\), the lowest eigenvalue of L is zero. All the other eigenvalues are positive because \(g_{n} < 1\) for \(n > 0\) (Sobolev 2017; Kim and Keller 2003). To summarize, L is a non-negative operator and the isotropic function, \(P_0(\mu ) = 1\), spans its nullspace. The spectrum asymptotes to one since \(g_{n} \rightarrow 0\) as \(n \rightarrow \infty \). It also follows from (16) that the first non-zero eigenvalue of L is \(1-g\), i.e.,
4 Boundary Layer Theory and the Diffusion Approximation
Boundary layer theory for radiative transfer is an asymptotic theory for highly-scattering and weakly-absorbing media. There are three characteristic length scales in (4): the characteristic absorption length, \(\ell _{a} = \kappa _{a}^{-1}\), the scattering mean-free path, \(\ell _{s} = \kappa _{s}^{-1}\), and the thickness of the slab, \(\ell _{z} = z_{2} - z_{1}\). The highly-scattering and weakly-absorbing regime corresponds to \(\ell _{s} \ll \ell _{z} \ll \ell _{a}\). To make this precise, we introduce the small, dimensionless parameter \(0 < \varepsilon \ll 1\) and set
where \(\alpha \) is a rescaled absorption coefficient. We make the change of variables
Henceforth, the tilde sign will be dropped. Substituting (20), (19a), and (19b) into (4), we obtain
Equation (21) is to be solved in \(0< z < 1\) subject to boundary conditions
We remark that in terms of (19a) and (19b), the single scattering albedo (10) is
Thus, the albedo for this scaling is near unity, i.e., \(1-\varpi _{0}= {\mathscr {O}}(\varepsilon ^2)\). It is well-known that the diffusion approximation is valid in this regime. The diffusion approximation asserts that the radiance becomes nearly isotropic deep inside the medium due to strong multiple scattering. In what follows, we derive the diffusion approximation using perturbation methods.
We seek the solution of (21) subject to boundary conditions (22) in the asymptotic limit as \(\varepsilon \rightarrow 0^{+}\). If we were to naïvely take the limit of (21) as \(\varepsilon \rightarrow 0^{+}\), the derivative term in (21) vanishes and the resulting equation could not satisfy boundary conditions (8). In fact, the solution of this boundary value problem rapidly changes near the boundaries \(z = 0\) and \(z = 1\). For this reason, (21) is called a singularly perturbed equation. To address this, we seek its solution as the sum
with \(\varPhi \) denoting the interior solution and \(\varPsi ^{(1)}\) (resp. \(\varPsi ^{(2)}\)) denoting the boundary layer solution near \(z = 0\) (resp. \(z=1\)). In what follows, we seek to find \(\varPhi \), \(\varPsi ^{(1)}\), and \(\varPsi ^{(2)}\) using perturbation methods.
4.1 Interior Solution
We seek the asymptotic expansion for the interior solution in the form
Substituting (25) into (21) and collecting like-powers of \(\varepsilon \), we find that
We recall from Sect. 3 that \(P_{0}(\mu )\) spans the nullspace of L. Therefore, the general solution of (26a) is
where \(\rho _{0}(z)\) is an undetermined function of z. Substituting (27) into (26b) and recalling that \(P_1(\mu )=\mu \) gives
Equation (28) is a linear, non-homogeneous Fredholm integral equation of the second kind. Its solution can be decomposed as the sum of the homogeneous solution \(\phi _{1}^{H}\) and the particular solution \(\phi _{1}^{P}\). Following the analysis of (26a), \(\phi _{1}^{H} = \rho _{1}(z) P_{0}(\mu )\) where \(\rho _{1}(z)\) is an undetermined function of z. The condition for the solvability of the nonhomogeneous problem, \(L\phi = f\), with f denoting a general nonhomogeneous term, is given by
In other words, the right-hand side of (28) (i.e., the non-homogeneous term) must be orthogonal to the nullspace of L. Because \(P_{1}(\mu )\) is orthogonal to \(P_{0}(\mu )\) [see (12)], in this case, solvability condition (29) is automatically satisfied. Recall that \(L P_{1}(\mu ) = ( 1 - g ) P_{1}(\mu )\). Substituting \(\phi _{1}^{P} = C P_{1}(\mu ) \rho _{0}'(z)\) into (28), we find that \(C = -1/(1 - g)\). It follows that
Substituting (27) and (30) into (26c) with \(n = 2\), we obtain
Applying the recursion relation (13) with \(n = 1\) yields
Applying solvability condition (29) to the right-hand side of (32) leads to
Equation (33) is called the diffusion equation. It gives the leading order asymptotic behavior of the radiance in the interior of the medium.
It is instructive and useful to obtain higher-order corrections to the diffusion approximation. To this end, we substitute (33) into (32) and obtain
From spectral equation (17), we have \(L P_{1} = (1 - g) P_{1}\) and \(L P_{2} = (1 - g_{2}) P_{2}\). Substituting these into (34) we find that
with \(\rho _{2}(z)\) an undetermined function of z. Substituting (30) and (35) into (26c) with \(n = 3\), we find that
Applying the recursion relation (13) with \(n = 1\) and \(n = 2\) leads to
Applying solvability condition (29) to the right-hand side of (37) yields
Remarkably, (38) is the same as (33). We can continue on to determine \(\phi _{3}\). The result will be a linear combination of \(P_{3}(\mu )\), \(P_{2}(\mu )\), and \(P_{1}(\mu )\) with coefficients involving derivatives of \(\rho _{1}\) and \(\rho _{0}\) and the homogeneous solution, \(P_{0}(\mu ) \rho _{3}(z)\), with \(\rho _{3}(z)\) an undetermined function of z. By substituting that result into the equation for \(\phi _{4}\) and ensuring its solvability, we will find that \(\rho _{2}\) satisfies the same diffusion equation as \(\rho _{0}\) and \(\rho _{1}\).
Thus far, we have obtained an \({\mathscr {O}}(\varepsilon ^2)\) approximation of the interior solution as
with \(\rho _{0}\), \(\rho _{1}\), and \(\rho _{2}\) satisfying the diffusion equations
These diffusion equations are to be solved in \(0< z < 1\). However, this perturbation analysis does not provide a method to determine boundary conditions for (40). To address this, we analyze the boundary layer solutions.
4.2 Boundary Layer Solutions
The boundary layer solution \(\varPsi ^{(1)}\) (resp. \(\varPsi ^{(2)}\)) is a special solution of (21) that decays rapidly in a region of thickness \({\mathscr {O}}(\varepsilon )\) about \(z = 0\) (resp. \(z=1\)), called the boundary layer, and is exponentially small outside of this region.
To determine \(\varPsi ^{(1)}\), we introduce the stretched variable \(z = \varepsilon Z\) and set \(\varPsi ^{(1)}(\mu ,Z) = I(\mu ,\varepsilon Z)\). Rewriting (21) in terms of Z and \(\varPsi ^{(1)}\), we obtain
Substituting (24) into the boundary condition (8a), neglecting terms involving \(\varPsi ^{(2)}\), and solving for \(\varPsi ^{(1)}\) leads to
We are able to neglect terms involving \(\varPsi ^{(2)}\) in (42) because it is constructed to decay rapidly in a region of thickness \({\mathscr {O}}(\varepsilon )\) about \(z = 1\). Hence, it will be exponentially small near \(Z = 0\). Using (39) to \({\mathscr {O}}(\varepsilon )\) yields
However, to ensure asymptotic matching with the interior solution, we also require that
which is called the asymptotic matching condition or the radiation condition. Thus, (41) is to be solved in the half space, \(Z > 0\), subject to boundary condition (42) and radiation condition (44). We seek an asymptotic solution of the form
Substituting (45) into (41), (43), and (44), and collecting like-powers of \(\varepsilon \), we obtain at \({\mathscr {O}}(1)\)
and at \({\mathscr {O}}(\varepsilon )\)
The problems (46) and (47) determine the boundary layer solution in the boundary layer near \(z = 0\) up to \({\mathscr {O}}(\varepsilon ^{2})\).
Similarly, we can derive corresponding problem for the boundary layer solution \(\varPsi ^{(2)}\) in the boundary layer near \(z=1\). For that case, we introduce the stretched variable \(z = 1 - \varepsilon \tilde{Z}\) and set \(\varPsi ^{(2)}(\mu ,\tilde{Z}) = I(\mu ,1 - \varepsilon \tilde{Z})\) which satisfies
Substituting (24) into the boundary condition (8b), neglecting terms involving \(\varPsi ^{(1)}\), and solving for \(\varPsi ^{(2)}\) leads to
Using (39) to \({\mathscr {O}}(\varepsilon )\) yields
We require for asymptotic matching that
We seek an asymptotic solution of the form
and find that at \({\mathscr {O}}(1)\)
and at \({\mathscr {O}}(\varepsilon )\)
4.3 Boundary Conditions for the Diffusion Approximation
The boundary layer solutions satisfy conservative (no absorption), one-dimensional RTEs. These problems cannot be solved analytically, in general. We will show how to compute them numerically in the following section using the double-spherical harmonics method. However, let us suppose here that we have the surface Green’s function \(G_{s}(Z,\mu ;\mu ')\) satisfying
Using this surface Green’s function, the solution of
is given as
While the solution given in (57) satisfies (56a) and boundary condition (56b), it does not satisfy an asymptotic matching condition of the form \(\psi \rightarrow 0\) as \(Z \rightarrow \infty \). We observe that a \(\psi = \text {constant}\) is a solution of (56a). This constant mode is the only one that does not vanish as \(Z \rightarrow \infty \). Therefore, we must remove the constant mode from the solution to ensure asymptotic matching. Let the operator \({\mathscr {G}}_{s}^{0}\) be the part of \({\mathscr {G}}_{s}\) that maps the boundary data b to the constant mode. To ensure asymptotic matching, we must have the boundary data satisfy
Let
It follows from applying \({\mathscr {G}}_{s}^{0}\) to the right-hand side of (46b) and setting that result to zero that
This result sets the boundary condition for \(\rho _{0}\) on \(z = 0\). Doing the same procedure on (47b), we obtain
which sets a boundary condition for \(\rho _{1}(0)\).
Let \(\tilde{G}_{s}(Z,\mu ;\mu ')\) satisfy
Then the solution of
is given as
In fact, \(\tilde{G}_{s}(\tilde{Z},\mu ;\mu ') = G_{s}(\tilde{Z},-\mu ;-\mu ')\). Let \(\tilde{{\mathscr {G}}}_{s}^{0}\) be defined for \(\tilde{G}_{s}\) analogously to how \({\mathscr {G}}_{s}^{0}\) is defined for \(G_{s}\). It follows from applying \(\tilde{{\mathscr {G}}}_{s}^{0}\) to the right-hand side of (53b) and setting that result to zero, we obtain
This result sets a boundary condition for \(\rho _{0}\) on \(z = 1\). Doing the same procedure on (54b), we find that
which sets a boundary condition for \(\rho _{1}\) on \(z = 1\).
Through this analysis of the boundary layer solutions, we are able to determine boundary conditions for the diffusion approximation. To summarize these results, we have
and
Since \(\rho _{0}\) and \(\rho _{1}\) satisfy the same diffusion equation, we introduce \(\rho = \rho _{0} + \varepsilon \rho _{1}\) which satisfies
This form satisfies the diffusion equation with Robin boundary conditions that are typically used for the diffusion approximation. Here, the coefficients, \(\beta _{0}\) and \(\beta _{1}\) and boundary data \(\bar{b}\) are computed from the boundary layer problems defined above to ensure asymptotic matching.
5 Double-Spherical Harmonics Method
The double-spherical harmonics method is an efficient numerical method for computing solutions of the RTE (Case and Zweifel 1967; Lewis and Miller 1984; Aronson 1986). We discuss this method for solving boundary layer problems: (46), (47), (53), and (54). By doing so, we obtain a method to compute the coefficients needed for the boundary conditions of the diffusion approximation. In particular, we study the conservative, one-dimensional RTE
subject to boundary condition
We will consider conditions required to satisfy the asymptotic matching condition:
The solution of (72) is discontinuous for \(\mu = 0\) on \(Z = 0\), i.e., on the boundary along the direction that is tangent to the boundary. This discontinuity decays exponentially away from the boundary due to scattering and absorption, so it does not affect the well-posedness of this problem. However, its presence introduces a computational difficulty. We address this issue by introducing the half-range specific intensities,
Substituting (75) into (72) and (5) leads to the coupled system
with the boundary condition
In (76) the half-range integral operators: \(H_1\) and \(H_2\), are defined by
Since scattering is assumed to be rotationally invariant (see (6)), it follows that \(h(-\mu ,-\mu ') = h(\mu ,\mu ')\) and \(h(\mu ,-\mu ') = h(-\mu ,\mu ')\). These symmetries have been used in deriving (76).
Let
denote the normalized Legendre polynomial mapped to the half range, \(0 < \mu \le 1\). For the double-spherical harmonics method, we expand \(\psi ^{\pm }\) as
The objective is to determine the coefficients \(u_{n}^{\pm }(z)\). Substituting (80) into (76), multiplying this by \(\tilde{P}_{m}(\mu )\), integrating with respect to \(\mu \) over \(0 < \mu \le 1\), and using the half-space orthogonality relation,
we obtain the system of equations and boundary conditions for \(\{ u_{n}^{\pm } \}\) as
The matrices M, \(H^{(1)}\), and \(H^{(2)}\) are given by
System (82) is to be solved for each \(m = 0, 1, \ldots \). When we truncate this infinite system at \(m = N\), we obtain a finite dimensional system suitable for numerical computations. This truncation yields the double-spherical harmonics of order N approximation,
which we denote by \(DP_{N}\). The objective is to determine the \(N+1\) coefficients \(u_{n}^{\pm }(Z)\) for \(n = 0, 1, \ldots , N\).
Two useful properties of the half-range Legendre polynomials (79) assist in solving this problem. First, the matrices M, \(H^{(1)}\), and \(H^{(2)}\) are symmetric. Second, from the theory of generalized Fourier series, it follows that (84), in which \(u^{\pm }_{n}\) for \(n = 0, 1, \ldots , N\) satisfy (82), gives the optimal (in the least-squares sense) polynomial approximation of degree N for \(\psi _{\pm }\). In fact, the advantage of using the half-range specific intensities, \(\psi _{\pm }\), over the full-range specific intensity, \(\psi \), is that former are continuous functions everywhere in their domain of definition. This ensures faster convergence for \(\psi _{\pm }\) as the number of modes N increases since only smoothness over the half-range is required.
Let

denote the vectors of the coefficients corresponding to (80). Using this notation, the problem (82) can be written in matrix notation as


where \(\mathbb {I}\) is the \((N+1)\times (N+1)\) identity matrix and the entries of the vector  are defined according to
are defined according to
We call (86) the \(DP_{N}\)problem for the half space. This is a \(2(N+1) \times 2(N+1)\) system of equations along with boundary conditions. In what follows, we analyze this system.
5.1 The Generalized Eigenvalue Problem for the \(DP_{N}\)System
We seek a solution of (86) in the form

where \(\lambda \) is an eigenvalue and  its associated eigenvector, where, for convenience, we introduce the notation
its associated eigenvector, where, for convenience, we introduce the notation  , where the superscript T denotes the transpose. Substituting (88) into (86a) leads to the \(2(N+1) \times 2(N+1)\) generalized eigenvalue problem
, where the superscript T denotes the transpose. Substituting (88) into (86a) leads to the \(2(N+1) \times 2(N+1)\) generalized eigenvalue problem

We establish several important results regarding this problem.
-
Property 1. (Symmetry) If \(\lambda \) is an eigenvalue of (89) with eigenvector
 , then \(-\lambda \) is an eigenvalue with eigenvector
, then \(-\lambda \) is an eigenvalue with eigenvector  . This property follows from the invariance of (89) under the transformations: \(\lambda \rightarrow -\lambda \),
. This property follows from the invariance of (89) under the transformations: \(\lambda \rightarrow -\lambda \),  , and
, and  .
. -
Property 2. (Orthogonality) If \(\lambda \) is an eigenvalue of (89) with eigenvector
 and \(\nu \) is an eigenvalue with eigenvector
and \(\nu \) is an eigenvalue with eigenvector  , they satisfy the orthogonality relation
, they satisfy the orthogonality relation  (90)
(90)This property follows from left-multiplying (89) for the eigen-triple
 by
by 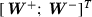 ; left-multiplying (89) for the eigen-triple
; left-multiplying (89) for the eigen-triple 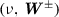 by
by  , and taking the difference between the resulting equations. The terms involving \(H^{(1)}\) and \(H^{(2)}\) vanish, because these matrices are symmetric. A corollary of Property 2 is that eigenvectors corresponding to different eigenvalues are M-orthogonal to each other in the sense that
, and taking the difference between the resulting equations. The terms involving \(H^{(1)}\) and \(H^{(2)}\) vanish, because these matrices are symmetric. A corollary of Property 2 is that eigenvectors corresponding to different eigenvalues are M-orthogonal to each other in the sense that  (91)
(91) -
Property 3. (Nullspace) Zero is an eigenvalue with multiplicity two and only one (proper) corresponding eigenvector. The nullspace also has a one-dimensional generalized eigensolution. In terms of the full-range radiance, the general solution associated with the nullspace is
$$\begin{aligned} \psi = a_{0} + b_{0} \left( Z - \frac{\mu }{1 - g} \right) ~, \end{aligned}$$(92)where \(a_{0}\) and \(b_{0}\) are scalar constants. In terms of the half-range vectors, the generalized eigenvector solution corresponding to (92) is
 (93)
(93)where
 is the unit vector in the “direction” associated with the isotropic half-range Legendre polynomial \(\tilde{P}_{0}=1\) and
is the unit vector in the “direction” associated with the isotropic half-range Legendre polynomial \(\tilde{P}_{0}=1\) and  (94)
(94)is the first column of M, whose entries correspond to the expansion of the coefficients of the functions \(\psi _{\pm } = \pm \mu \) in the half-range Legendre polynomials. This property can be understood as follows. Recall that L has a zero eigenvalue with an associated isotropic eigenfunction i.e., \(L P_{0}(\mu ) = 0\). In terms of the half-range intensities, this isotropic eigenfunction corresponds to \(\psi _{+} = \psi _{-} = a_{0} \tilde{P}_{0}(\mu )\) with \(a_{0}\) denoting a scalar constant. It follows that the vectors of expansion coefficients are given by
 . Hence, the constant \(a_0\) in (92) is in the nullspace. By inspection, the second term in (92) is also a solution of this problem. This implies that the second term in (93) is a generalized eigensolution in the nullspace. Indeed, by Property 1, the zero eigenvalue has multiplicity two.
. Hence, the constant \(a_0\) in (92) is in the nullspace. By inspection, the second term in (92) is also a solution of this problem. This implies that the second term in (93) is a generalized eigensolution in the nullspace. Indeed, by Property 1, the zero eigenvalue has multiplicity two.
5.2 Solving the \(DP_{N}\)Problem
We proceed to formally solve the \(DP_{N}\)problem (86). Recall that (93) is the nullspace solution of the \(DP_{N}\)eigenvalue problem (89) and that all the other eigenvalues come in opposite-sign pairs, \(\lambda _{-j}=-\lambda _j\), for \(j = 1, 2, \ldots N\), with associated eigenvectors  and
and  , respectively. The general solution of (86a) is
, respectively. The general solution of (86a) is

where \(a_j\), and \(b_j\) for \(j = 0, 1, \ldots , N\) are coefficients to be determined. Requiring that (95) remain bounded for all \(Z > 0\) leads to setting \(b_{0} = b_{1} = \ldots = b_{N} = 0\). Therefore,

Requiring that (96) satisfy the boundary condition (86b), we obtain

Equation (97) is a linear system for the coefficients \(a_j\), \(j=0, 1, \ldots , N\), which can be readily solved. The solution of (72) is then obtained from (96) and the \(DP_{N}\)expansion (80).
We can formally write the solution of (97) as  , where
, where  denotes the vector of expansion coefficients and \(\varGamma \) denotes the inverse of the matrix whose first column is
denotes the vector of expansion coefficients and \(\varGamma \) denotes the inverse of the matrix whose first column is  and whose subsequent columns are
and whose subsequent columns are  for \(j = 1, \ldots , N\), i.e.,
for \(j = 1, \ldots , N\), i.e.,

The matrix \(\varGamma \) gives the mapping from the boundary data to the coefficients making up the solution of (97). Let  denote the first row of \(\varGamma \). It follows that
denote the first row of \(\varGamma \). It follows that

Therefore, the inner product of  with the boundary data is the mapping from the boundary data to the only non-decaying mode of (96). This operation is precisely the \(DP_{N}\)approximation of the operator \({\mathscr {G}}_{s}^{0}\) introduced in Sect. 4.3.
with the boundary data is the mapping from the boundary data to the only non-decaying mode of (96). This operation is precisely the \(DP_{N}\)approximation of the operator \({\mathscr {G}}_{s}^{0}\) introduced in Sect. 4.3.
For boundary layer solutions about \(z = 1\), we need to solve
subject to
By replacing \(\mu \) with \(-\mu \), we obtain the same problem as (72) subject to boundary condition (73). It follows that \(DP_{N}\)solution is

with the vector of coefficients,  defined as
defined as  with
with
Note that  and
and  are switched in (102) from what appears in (96) due to the replacement of \(\mu \) by \(-\mu \).
are switched in (102) from what appears in (96) due to the replacement of \(\mu \) by \(-\mu \).
6 Procedure for Computing the Asymptotic Approximation of Boundary Layer Theory
We now have all of the components needed to evaluate the uniformly valid asymptotic approximation of the RTE in the strong-scattering regime. In what follows, we summarize the results from above in a procedure to evaluate the asymptotic approximation valid to \({\mathscr {O}}(\varepsilon ^{2})\).
To compute the asymptotic approximation of the solution to
for a specified redistribution function subject to boundary conditions
we follow the procedure given below.
-
1. Interior solution
-
a. For the \(DP_{N}\)method, set N and compute (83a), (83b), (83c), (87), and (94) using Gauss quadrature to obtain M, \(H^{(1)}\), \(H^{(2)}\),
 , and
, and  , respectively.
, respectively. -
b. Construct and solve generalized eigenvalue problem (89) for the eigenvalues \(\lambda _{\pm j}\) and eigenvectors
 , for \(j=0, 1, 2, \ldots N\).
, for \(j=0, 1, 2, \ldots N\). -
c. Use the solution from Step 1(b) to compute the matrix \(\varGamma \) given in (98) and set
 to be its first row.
to be its first row. -
d. Compute the coefficients
 (106a)
(106a) (106b)
(106b) (106c)
(106c) -
e. Using the results from Step 1(d), solve the diffusion approximation given by (71) to obtain \(\rho (z)\).
-
f. Compute the half-range interior solutions,
$$\begin{aligned} \varPhi _{\pm }(z,\mu ) = \rho (z) \mp \varepsilon \mu \rho '(z)/(1 - g), \end{aligned}$$(107)for \(z \in (0,1)\), and \(\mu \in (0,1]\).
-
-
2. Boundary layer solutions
-
a. Compute the coefficients
 (108)
(108) (109)
(109) -
b. Using the results from Step 2(a), compute
 (110)
(110) (111)
(111) -
c. Using the results from Step 2(b), compute the half-range boundary layer solutions
$$\begin{aligned} \psi _{\pm }^{(1)}(z,\mu )= & {} \sum _{n = 0}^{N} u_{n}^{\pm }(z) \tilde{P}_{n}(\mu )~,\end{aligned}$$(112)$$\begin{aligned} \psi _{\pm }^{(2)}(z,\mu )= & {} \sum _{n = 0}^{N} \tilde{u}_{n}^{\pm }(z) \tilde{P}_{n}(\mu )~. \end{aligned}$$(113) -
3. Asymptotic approximation
Compute the asymptotic approximation of the half-range specific intensities,
$$\begin{aligned} I_{\pm }(z,\mu ) = \varPhi _{\pm }(z,\mu ) + \psi _{\pm }^{(1)}(z,\mu ) + \psi _{\pm }^{(2)}(z,\mu )~, \end{aligned}$$(114)for \(z \in [0,1]\), and \(\mu \in (0,1]\).
We call (114) the uniformly valid asymptotic approximation of the boundary layer theory to \({\mathscr {O}}(\varepsilon ^{2})\). It gives an approximation to the solution of the RTE in the entire domain with an error that scales as \({\mathscr {O}}(\varepsilon ^{2})\). The interior solution \(\varPhi _{\pm }\) is derived from the diffusion approximation. The boundary layer solutions \(\psi _{\pm }^{(1)}\) and \(\psi _{\pm }^{(2)}\) give corrections to the diffusion approximation near boundaries \(z = 0\) and \(z = 1\), respectively.
7 Deriving Two-Flux Theory
Using the results from boundary layer theory discussed above, we derive two-flux theory. To do so, we introduce the half-range fluxes,
Multiplying \(\mu \) to (107) and integrating with respect to \(\mu \), we find that the associated fluxes are
Equation (116) establishes a relationship between \(F_{\pm }\) and the diffusion approximation.
Adding and subtracting the two equations in (116) for \(F_\pm \), we get
Differentiating (117) with respect to z gives
Solving for \(\rho '\) in (117b) and substituting that result into (118a), we obtain
Substituting (71a) into the right-hand side of (118b), we obtain
Solving for \(\rho \) from (117a) and substituting into (120), we get
By adding and then subtracting (119) and (121), dividing by 2, and rearranging terms, we arrive at
System (122) can be written as
with coefficients
The equations in (123) are the two-flux equations, but written with respect to scaling given in (20). We can write them in terms of the optical depth \(\tau \), defined in (9), and use the albedo (10) to express the two-flux system as
with
Alternatively, by transforming back to the dimensional z variable using (9) and (10), we arrive at the familiar two-flux equations in dimensional form,
with
These results are the same as derived by Sandoval and Kim (2014).
We have derived the two-flux equations (127) above from computing the half-range fluxes associated with the interior solution in boundary layer theory. This derivation shows that in a strongly scattering medium, two-flux theory is entirely consistent with the diffusion approximation. In fact, it is just a reformulation of the diffusion approximation. Consequently, two-flux theory is asymptotically accurate in the interior of the medium.
7.1 Limitations of Two-Flux Theory
Two-flux theory provides a simple and intuitive picture of light propagation in a scattering medium. For that reason, it is very useful. However, it is important to point out its limitations which we list below.
-
Limitation I. Two-flux theory is only valid for one-spatial dimension for problems with azimuthal symmetry.
-
Limitation II. Two-flux theory is only accurate for high-albedo media.
-
Limitation III. Two-flux theory is only valid in the interior of the domain. This theory does not accurately determine the fluxes leaving the domain.
Limitation I is inherent in the assumption of azimuthal symmetry leading to the one-dimensional RTE (4). We discuss a possible extension to three-dimensional space in Sect. 9. Limitation II and Limitation III are manifest from our derivation of System (127) from the interior solution (107) given in terms of the solution of the diffusion approximation (71). Boundary layer theory provides an asymptotic solution in the limit as \(\varepsilon \rightarrow 0^{+}\) corresponding to \(\varpi _{0}\rightarrow 1\). Furthermore, we have learned from boundary layer theory that the interior solution requires corrections in the form of boundary layer solutions to accurately capture the intensity near the boundary.
7.2 Boundary Conditions
The two-flux equations need to be supplemented with boundary conditions. These boundary conditions are usually determined by computing the half-range fluxes from boundary conditions of the RTE in the following way. Multiplying \(\mu \) to (8a) and (8b) integrating those results with respect to \(\mu \), we find that
These boundary conditions intuitively prescribe the fluxes incident on the boundaries \(z = 0\) and \(z = 1\). However, if we consider the fact that the two-flux equations are derived directly from the interior solution given by the diffusion approximation, these boundary conditions may not be appropriate. In boundary layer theory, this interior solution requires the addition of boundary layer solutions to correct it near the boundaries. We call the solution of the two-flux equations given by (123) with boundary conditions (129) naïve two-flux theory.
As an alternative to boundary conditions (129) in naïve two-flux theory, we derive boundary conditions consistent with those given in (71b) from boundary layer theory. Substituting (117) into (71b), we find that
In contrast to boundary conditions (129), these boundary conditions include an effective reflection at the boundary with reflection coefficient \(R = (\beta _{0} - 3 \beta _{1}/2)/(\beta _{0} + 3 \beta _{1}/2)\). Since these boundary conditions are derived from the asymptotic theory, we call the solution of the two-flux equations given by (123) with boundary conditions (130) asymptotic two-flux theory.
We expect a large difference in the accuracy between the naïve and asymptotic two-flux theories. The entire solution of the two-flux equations depends on the boundary conditions. Hence, differences in boundary conditions lead to differences in the entire solution. Moreover, we identified in Limitation III that two-flux theory cannot accurately capture the fluxes leaving the domain. Naïve two-flux theory insists that the boundary conditions are the incident fluxes on the boundaries. In contrast, asymptotic two-flux theory anticipates the need for boundary layer solutions to overcome Limitation III. We investigate the differences between these different two-flux theories in the computational results.
8 Computational Results
In this section, we compare the radiative transfer theory and the approximations discussed above. We seek to solve the RTE (21) with \(\alpha =1\) for different values of \(\varepsilon \) (or the albedo), and the Henyey-Greenstein redistribution function, defined as (Van de Hulst 2012)
where, in (131a), E(k) is the complete elliptic integral of the second kind, defined as
evaluated with \(k = 2\gamma / |\beta + \gamma |\). The redistribution function (131) is obtained from the three-dimensional Henyey-Greenstein scattering phase function, defined as

using the integral defined in (6).
In particular, we consider (21) in the domain \(0< z < 1\) with the boundary conditions
Upon solution of this problem, we compute the half-range fluxes
8.1 Comparison of Approximations
We compute the approximations of the problem (21) with boundary conditions (134) using the following three theories.
-
Naïve two-flux theory [(123) with boundary conditions (129)];
-
Asymptotic two-flux theory [(123) with boundary conditions (130)];
-
Boundary layer theory [Procedure given in Sect. 6].
In particular, we study \(F_{\pm }(z)\) computed from all of these theories over \(0 \le z \le 1\).
To begin with, we solve this problem with \(\varepsilon =0.01\), which corresponds to \(\varpi _{0}\approx 0.9999\) [see (23)], and \(g=0.4\), which corresponds to a moderately forward-scattering medium. We solve this problem using the \(DP_{N}\)method with \(N=12\). We use 501 grid points in z, and evaluate the integrals in (131) using the 128 point Gauss-Legendre quadrature rule. In what follows, we denote the solution thus obtained the \(DP_{12}\) solution. To validate using this method, we compared results from the \(DP_{12}\) solution to those from a highly resolved computation using the discrete ordinate method with the double-Gauss quadrature rule (see Thomas and Stamnes 2002, for example). This method has been shown to be pointwise convergent (Keller 1960). Through those comparisons, we have found that for this problem, the \(DP_{12}\) solution has a maximum relative error that is less than \(10^{-6}\). For this reason, we consider the \(DP_{12}\) solution as the benchmark, to which all other approximations evaluated here are compared.
Let \(F_{\pm }(z)\) denote to the benchmark (\(DP_{12}\)) solutions and let \(\tilde{F}_{\pm }(z)\) denote the approximate solutions. In what follows we refer to the absolute maximum errors, the relative maximum errors, and the root-mean square (RMS) errors of the solutions. These errors are defined as
respectively, where \(\{z_i\}_{i=1}^{N_z}\) denote the discrete points along the z direction.
Comparison between the \(DP_{12}\) solution (solid), the naïve two-flux solution (dots), and asymptotic two-flux solution (dashes). Here \(\varepsilon =0.01\) (\(\varpi _{0}\approx 0.9999\)) and \(g=0.4\). Panels (a) and (b) show \(F_+\) and \(F_-\), respectively. The bottom row of panels “zoom in” on the solutions inside the boundary layer near \(z = 0\)
Figure 1 shows a comparison between the \(DP_{12}\), naïve two-flux, and asymptotic two-flux solutions. The top row of plots show these solutions for \(0 \le z \le 1\). The bottom row of plots show these solutions near the boundary at \(z = 0\). The \(DP_{12}\) solution changes rapidly near the boundary at \(z=0\) corresponding to the boundary layer. Because the solution itself is very small near \(z = 1\), the rapid change near the boundary \(z=1\) is not apparent in Fig. 1. Regardless, neither the naïve nor the asymptotic two-flux solutions accurately capture these rapid changes near the boundary. The naïve two-flux solution is accurate at the boundaries, but not away from them. The absolute error made by the the naïve two-flux solution for \(F_{+}(1)\) is \(4.224 \times 10^{-4}\) and for \(F_{-}(0)\) is \(8.689 \times 10^{-4}\). Even though it captures the qualitative behavior of \(F_{\pm }(z)\) over \(0< z < 1\), it exhibits a large quantitative error. In contrast, the asymptotic two-flux solution accurately approximates the \(DP_{12}\) solution for \(0< z < 1\), but makes a substantial error at the boundary layer near \(z=0\).
The relative maximum error of the naïve two-flux solution is 0.0930. This maximum error is attained in the interior of the domain. The relative maximum error of the asymptotic two-flux solution is 0.0988. This maximum error is attained at \(z=0\). From the results in Fig. 1, we observe that the asymptotic two-flux theory is accurate over a much larger portion of the domain than the naïve two-flux theory. This difference is captured better by the RMS error. The RMS error of the naïve two-flux solution is 0.0136, whereas, the RMS error of the asymptotic two-flux theory is 0.00163. With respect to the the RMS error, the asymptotic two-flux theory is an order of magnitude more accurate than the naïve two-flux theory.
Figure 2 shows a comparison between the half-range interior solutions, \(\varPhi _{\pm }\), boundary layer solutions, \(\varPsi ^{(1)}_\pm +\varPsi ^{(2)}_\pm \), and the uniformly valid asymptotic solution of boundary layer theory, which is the sum given in (114). Here, we see how the boundary layer solutions correct the interior solution near the boundaries. They are exponentially small in the interior of the domain. Consequently, they do not interfere with the approximation made by the interior solution there. Because the boundary layer solutions take care of the boundary conditions and the rapid change in the solution near the boundaries, they free the interior solution from having to satisfy boundary conditions it is not capable of satisfying which, in turn, allows it to accurately capture the solution in the interior of the domain. It is in this way that boundary layer theory provides a uniformly accurate approximation throughout the entire domain.
Comparison between the interior solution (dots), the boundary layer solution (solid), and uniformly valid asymptotic solution (dashes) of boundary layer theory, for the same problem as in Fig. 1. The bottom row of panels “zoom in” on the solutions inside the boundary layer near \(z = 0\)
Figure 3 shows a comparison between the solutions computed using \(DP_{12}\), the uniformly valid asymptotic solution of boundary layer theory, and asymptotic two-flux theory. Since asymptotic two-flux theory is consistent with the diffusion approximation, it is equivalent to the interior solution in boundary layer theory. The interior solution does not satisfy the boundary conditions prescribed with the RTE, so it makes a significant error near the boundary \(z=0\). On the other hand, because boundary layer theory corrects the diffusion approximation by including boundary layer solutions near each of the boundaries, it provides a uniformly valid asymptotic approximation for all \(0 \le z \le 1\). In particular, these boundary layer solutions accurately capture the rapid change in the solution near \(z = 0\) and \(z = 1\). In particular, the relative maximum error of the uniformly valid asymptotic approximation is approximately \(8.343 \times 10^{-4}\) with an RMS error of \(1.135 \times 10^{-4}\). As a result, the uniformly valid asymptotic approximation and the \(DP_{12}\) solution are indistinguishable to the eye. These results clearly show that boundary layer theory provides a very accurate approximation over the whole domain. It is vastly superior over both of the two-flux theories, as well as the diffusion approximation, since it includes the boundary layer solutions that take into account the rapid changes near the boundaries.
Comparison between the \(DP_{12}\) solution (dots), the uniformly valid asymptotic approximation (dashes), and the asymptotic two-flux theory (solid) for the same problem as in Fig. 1. The bottom row of panels “zoom in” on the solutions inside the boundary layer near \(z = 0\)
The derivation of two-flux theory indicates that it is valid only in the interior of the domain of a strongly scattering medium. The results shown here indicate that asymptotic two-flux theory is more accurate than the naïve two-flux theory everywhere except near the boundaries. If one only considers the fluxes exiting the domain, it appears that the naïve two-flux theory provides a more accurate approximation. However, using the naïve two-flux theory in this way is problematic because it achieves this approximation at the expense of a substantial error everywhere else. In contrast, boundary layer theory provides a uniformly accurate approximation over the entire domain. Moreover, it is substantially more accurate.
8.2 Dependence on the Albedo
We now consider the accuracy of these approximations for different values of \(\varepsilon \), which is directly related to the albedo through (23). In particular, we compute the relative errors of the different approximations with \(g=0.4\) for \(0.001 \le \varepsilon \le 0.25\) corresponding to \(0.94< \varpi _{0}< 1\). According to (23), \(1 - \varpi _{0}= {\mathscr {O}}(\varepsilon ^{2})\) and so is the error of the asymptotic theory. The results in Fig. 4 show that the relative errors of both the naïve and asymptotic two-flux theories are approximately 10%. In contrast, the error of the uniformly valid asymptotic solution of boundary layer theory scales as \({\mathscr {O}}(1-\varpi _{0})\) as predicted by the asymptotic theory.
Log-log plot of the errors of the naïve two-flux solution (dots), the asymptotic two-flux solution (dashes), and the uniformly valid asymptotic solution (solid) as functions of \(1-\varpi _{0}\). All other parameters are the same as in Fig. 1
8.3 Dependence on the Anisotropy Factor
The only other parameter in this problem besides the albedo, \(\varpi _{0}\), is the anisotropy factor, g. The results shown in Sect. 8.1 were for \(g=0.4\) corresponding to mildly anisotropic scattering. We now consider the accuracy of these approximations for different values of g in Eq. (131). According to the uniformly valid asymptotic theory, the error is \({\mathscr {O}}(\varepsilon ^{2})\). Thus, the leading order behavior of the error is given by \(C \varepsilon ^{2}\), where C is some constant that is independent of \(\varepsilon \) (and consequently, \(\varpi _{0}\)). However, it may depend on g. In what follows, we seek to determine the dependence of C on g.
Figure 5 shows the relative errors of the naïve and asymptotic two-flux theories, and the uniformly valid asymptotic solution of boundary layer theory. These results show that the errors for both the naïve and asymptotic two-flux theories are approximately 10% over all values of g. In contrast, the error of the uniformly valid asymptotic solution of boundary layer theory is two order of magnitude smaller or less for \(0 \le g \le 0.9\ \). However, it appears to increase and become large as \(g \rightarrow 1\).
a Log plot of the errors of the naïve two-flux solution (dots), the asymptotic two-flux solution (dashes), and the uniformly valid asymptotic solution (solid) as functions of the anisotropy parameter g. All other parameters are the same as in Fig. 1
8.4 Forward-Peaked Scattering
The results shown in Fig. 5 are for \(\varepsilon \) held fixed at \(\varepsilon = 0.01\). Boundary layer theory ensures that the error of the asymptotic solution will decrease quadratically as \(\varepsilon \rightarrow 0\) for any fixed value of g. It does not account for sharply forward-peaked scattering corresponding to the asymptotic limit, \(g \rightarrow 1\). With sharply forward-peaked scattering, the transport mean-free path, \(\ell _{tr} = 1/[\kappa _{s} (1 - g)]\), is much larger than the scattering mean-free path, \(\ell _{s} = 1/\kappa _{s}\), since \(g \approx 1\). In this parameter regime, there is a wide separation between the scattering and diffusion length scales. As a result, anisotropic, sharply forward-peaked scattering inhibits the onset of the diffusion limit. Many more multiple scattering events are required for the radiance to become nearly isotropic compared with the mildly anisotropic scattering case. It follows that the penetration depth for the onset of the diffusion limit is much larger for this case. At intermediate penetration depths, the character of highly anisotropic scattering is different and requires additional considerations. Larsen (1999) gives an asymptotic analysis of this problem leading to useful asymptotic expansions for the scattering operator.
Same as Fig. 1 for \(g=0.9\,\)
To investigate the case of anisotropic forward-peaked scattering, we show results for \(g = 0.9\). In Fig. 6, we compare the \(DP_{12}\), naïve two-flux, and asymptotic two-flux solutions just as we have done in Fig. 1 for the \(g=0.4\) case. The overall qualitative behaviors are the same as for \(g = 0.4\). However, we observe here larger errors made by both the naïve and asymptotic two-flux solutions. The errors for \(F_{-}\) are larger than those for \(F_{+}\). The relative maximum error of the naïve two-flux solution is 0.0913 and the relative maximum error of the asymptotic two-flux solution is 0.1022. The RMS errors are 0.0157 and 0.0040 for the naïve and asymptotic two-flux solutions, respectively.
In Fig. 7 we show comparisons with the \(DP_{12}\) solution, the uniformly valid asymptotic solution of boundary layer theory, and asymptotic two-flux theory, just as Fig. 2 for the \(g = 0.4\) case. Here, we find that these approximations are not as accurate as they were for the \(g = 0.4\) case. The aforementioned errors of the asymptotic two-flux solution carry over to the asymptotic solution of boundary layer theory. In particular, the larger errors for \(F_{-}\) affect the boundary layer solution which, in turn, exhibits a noticeable error in the lower right plot of Fig. 6. The relative maximum error for the boundary layer theory asymptotic approximation is 0.0190 and the RMS error is 0.0030.
Same as Fig. 3 with \(g = 0.9\)
Just as Fig. 5 indicates, we have found that the performance of all approximations is worse for \(g = 0.9\). The behavior of the error of the asymptotic solution of boundary layer theory will decrease quadratically with \(\varepsilon \). However, for this chosen value of \(\varepsilon = 0.01\) and \(g = 0.9\), we find that the error is much larger than the case when \(g = 0.4\).
8.5 Four-Flux Theory and the \(DP_{1}\) Approximation
Two-flux theory is valid only in the interior of the domain. The eigenvalues of (123) are given by
where we have used (124). Note that these eigenvalues correspond exactly to those for the diffusion equation given in (71a). This result is not surprising since two-flux theory is derived from the interior solution governed by the diffusion approximation.
An improvement over two-flux theory, called four-flux theory, incorporates an additional length scale in the problem. This length scale is smaller than that given in (136) and, from what we now understand from boundary layer theory, attempts to resolve the rapid changes of the solution near the boundaries. Rather than give a phenomenological method to determine this additional length scale, we consider the \(DP_{N}\)method with \(N = 1\), which we call the \(DP_{1}\) approximation.
If we apply the \(DP_{1}\) approximation to (21), we obtain a \(4 \times 4\) system. By Property 1 of generalized eigenvalue problem (89), the \(DP_{1}\) approximation will produce 2 distinct length scales corresponding to the 2 distinct ± pairs of eigenvalues. One of those length scales corresponds to (136). The other length scale is the additional length scale in four-flux theory. It is one eigenmode that seeks to approximate the boundary layer solutions. For this reason, we call the four-flux solutions the results from computing the half-range fluxes \(F_{\pm }\) from the solution of the \(DP_{1}\) system.
Comparison between the \(DP_{12}\) solution (dotted blue), the uniformly valid asymptotic approximation (dashed red), and four-flux solution (solid black) for the same problem as in Fig. 1. The bottom row of panels “zoom in” on the solutions inside the boundary layer near \(z = 0\)
Figure 8 shows a comparison of results computed using \(DP_{12}\), the boundary layer solution, and four-flux theory. Here, we see that the four-flux solution captures the rapid changes in the solution near the boundaries better than the two-flux solution does. The maximum relative error made by the four-flux solution is 0.0129 and the RMS error is 0.00185. This maximum relative error is 7 times smaller than those for the naïve and asymptotic two-flux solutions. This RMS error is an order of magnitude smaller than that for the naïve two-flux solution, but of the same order as the RMS error for the asymptotic two-flux solution. However, boundary layer theory provides a vastly better approximation than four-flux theory.
Four-flux theory provides a substantial improvement over two-flux theory through the inclusion of an additional length scale. Rather than seeking to derive this length scale phenomenologically, we consider instead computing the half-range fluxes from the \(DP_{1}\) approximation. The \(DP_{1}\) approximation has 2 distinct length scales: one corresponds to the two-flux/diffusion length scale given in (136), and the other attempts to resolve the rapid changes near the boundaries. Although four-flux theory qualitatively captures the rapid changes in the solution near the boundaries, it is less accurate than the asymptotic approximation derived from boundary layer theory.
9 Extension of Two-Flux Theory for Three-Dimensional Radiative Transfer
Many physical problems of interest require solving the three-dimensional RTE. For this reason, it is tempting to seek a two-flux theory for the three-dimensional RTE. Such a theory may be used to study beam propagation and scattering in a plane-parallel medium, for example. However, Limitation I in Sect. 7.1 states that two-flux theory is only valid for one-spatial dimension for problems with azimuthal symmetry. Nonetheless, using the connection between two-flux theory and the diffusion approximation established above, we can develop what amounts to a two-flux theory for the three-dimensional RTE.
The diffusion equation in three dimensions is given by
where we have introduced the diffusion coefficient \(D = [3 ( 1 - g )]^{-1}\), for convenience, and \(\nabla ^{2}_{\perp } = \partial _{xx}^{2} + \partial _{yy}^{2}\) denoting the transverse Laplacian. In boundary layer theory for the three-dimensional RTE, the interior solution is given by

The half-range fluxes associated with this interior solution can be calculated as
Thus, we find that
By taking the partial derivative with respect to z, we obtain
From these results, we find that
The system given in (142) gives the 3D two-flux equations. Perhaps this 3D extension to two-flux theory is useful for some applications, but since it is entirely consistent with the diffusion approximation, one may as well consider solving the 3D diffusion approximation instead.
10 Conclusions
We have discussed approximations to the RTE in strongly scattering medium. In particular, we have discussed boundary layer theory and two-flux theory. Both of these theories have connections to the \(DP_{N}\)method which we also explain. By investigating the connections between these two approximations and the \(DP_{N}\)method, we have gained valuable insight into each of them.
Boundary layer theory gives a systematic perturbation method to compute the solution of the RTE in the limit as the albedo approaches one. It gives the solution as the sum of the interior solution and the boundary layer solutions. The interior solution is governed by the diffusion approximation. The boundary layer solutions satisfy a conservative, one-dimensional RTE in a half space. By requiring that boundary layer solutions satisfy asymptotic matching conditions, we derive boundary conditions for the diffusion approximation. Since we cannot solve the boundary layer problems analytically, we have used the \(DP_{N}\)method to solve them. This method also provides a convenient method to impose asymptotic matching which, in turn, provides a simple method for computing the coefficients in the boundary conditions for the diffusion approximation. The result of boundary layer theory is a uniformly valid asymptotic approximation that is accurate over the entire domain with a precisely defined error bound. Numerical results show that this asymptotic solution is very accurate over the entire domain.
Two-flux theory provides a simple and intuitive picture of light scattering and absorption in one spatial dimension. However, it has lacked a systematic theoretical framework to derive its coefficients and boundary conditions. Here, we have derived two-flux theory using the interior solution from boundary layer theory. By doing so, we have determined that two-flux theory is just a reformulation of the diffusion approximation. Consequently, it is accurate only for describing light that has penetrated deep into a strongly scattering medium. It is not accurate near boundaries or sources. This connection allows for the explicit determination of the coefficients. Specifically, we have found that the scattering coefficient is \(S = 3 \kappa _{s} (1 - g) /4 - \kappa _{a} (1 - 3 g)/4\), and the absorption coefficient is \(K = 2 \kappa _{a}\). These results provide a useful connection between two-flux theory and the fundamental quantities in radiative transfer. However, just as the boundary conditions for the diffusion approximation can be problematic, so are those for two-flux theory. Here, we have derived boundary conditions for two-flux theory that are consistent with the results in boundary layer theory for the interior solution. By doing so, we have introduced the asymptotic two-flux theory. In contrast to naïve two-flux theory that uses the fluxes incident on the boundary as boundary data, the asymptotic two-flux theory has been shown to be more accurate in the interior of the domain away from boundaries. However, despite the fact that the naïve two-flux theory makes large errors in the interior of the domain, it approximates the fluxes exiting the domain at the boundaries better than the asymptotic two-flux theory.
Two-flux theory can be improved by adding another length scale that takes into account the rapid change of the solution near the boundaries. The result is called four-flux theory. Here, we have drawn a connection between four-flux theory and the \(DP_{N}\)method with \(N = 1\). Numerical results show that four-flux theory computed from \(DP_{1}\) provides an significant improvement over two-flux theory. However, four-flux theory is substantially less accurate than boundary layer theory.
Finally, we consider two-flux theory for three-dimensional radiative transfer problems. We have derived this three-dimensional two-flux theory from three-dimensional boundary layer theory just as we have done for one-dimensional problems. This result provides some insight into how two-flux theory extends to three-dimensional problems. However, since it is a reformulation of the diffusion approximation, it is perhaps unnecessary to consider it for practical problems.
The close connections discussed here between boundary layer theory, two-flux theory, and the \(DP_{N}\)method in strongly scattering media provides valuable insight into radiative transfer problems. Specifically, by drawing the connection between the diffusion approximation and two-flux theory, we have explicitly determined the coefficients in the two-flux equations. Additionally, the challenge in applying the diffusion approximation near boundaries should serve as caution in applying two-flux theory there, as well. Having these connections established should be useful to other researchers considering these approximations for problems of practical interest.
References
Aronson R (1986) \(P_{N}\) versus double-\(P_{N}\) approximations for highly anisotropic scattering. Transport Theor Stat 15(6–7):829–840
Bell GI, Glasstone S (1970) Nuclear reactor theory. Van Nostrand Reinhold Co, New York
Bender CM, Orszag SA (2013) Advanced mathematical methods for scientists and engineers I: asymptotic methods and perturbation theory. Springer Science & Business Media, Berlin
Brinkworth B (1972) Interpretation of the Kubelka-Munk coefficients in reflection theory. Appl Opt 11(6):1434–1435
Case KM, Zweifel PF (1967) Linear transport theory. Addison-Wesley, Reading
Chandrasekhar S (1960) Radiative transfer. Dover, New York
Courant R, Hilbert D (2008) Methods of mathematical physics, Vol. 2: differential equations. Wiley, New York
Dark JP, Kim AD (2017) Asymptotic theory of circular polarization memory. J Opt Soc Am A 34(9):1642–1650
Edström P (2007) Examination of the revised Kubleka-Munk theory: considerations of modeling strategies. J Opt Soc Am A 24(2):548–556
Gao H, Zhao H (2009) A fast-forward solver of radiative transfer equation. Transp Theory Stat Phys 38(3):149–192
Gate L (1974) Comparison of the photon diffusion model and Kubleka-Munk equation with the exact solution of the radiative transport equation. Appl Opt 13(2):236–238
Habetler G, Matkowsky B (1975) Uniform asymptotic expansions in transport theory with small mean free paths, and the diffusion approximation. J Math Phys 16(4):846–854
Hinch EJ (1991) Perturbation methods. Cambridge University Press, Cambridge
Ishimaru A (1999) Wave propagation and scattering in random media. Wiley-IEEE-Press, New York
Jensen HW (2001) Realistic image synthesis using photon mapping. A K Peters Ltd., Natick
Keller HB (1960) On the pointwise convergence of the discrete-ordinate method. J Soc Ind Appl Math 8(4):560–567
Kim AD (2011) Correcting the diffusion approximation at the boundary. J Opt Soc Am A 28(6):1007–1015
Kim AD, Keller JB (2003) Light propagation in biological tissue. J Opt Soc Am A 20(1):92–98
Kim AD, Moscoso M (2011) Diffusion of polarized light. Multiscale Model Simul 9(4):1624–1645
Kirk JT (1994) Light and photosynthesis in aquatic ecosystems. Cambridge University Press, Cambridge
Kokhanovsky A (2006a) Asymptotic radiative transfer. In: Light scattering reviews. Springer, Berlin, pp 253–289
Kokhanovsky AA (2006b) Cloud optics. Springer, Berlin
Kokhanovsky AA (2007) Physical interpretation and accuracy of the Kubelka-Munk theory. J Phys D 40(7):2210
Kubelka P (1948) New contributions to the optics of intensely light-scattering materials. Part I. J Opt Soc Am 38(5):448–457
Kubelka P, Munk F (1931) Ein Beitrag zur Optik der Farbanstriche. Z Tech Phys 12:593–601
Larsen EW (1999) The linear Boltzmann equation in optically thick systems with forward-peaked scattering. Prog Nucl Energy 34(4):413–423
Larsen EW, Keller JB (1974) Asymptotic solution of neutron transport problems for small mean free paths. J Math Phys 15(1):75–81
Lehtikangas O, Tarvainen T, Kim AD (2012) Modeling boundary measurements of scattered light using the corrected diffusion approximation. Biomed Opt Express 3(3):552–571
Lewis EE, Miller WF (1984) Computational methods of neutron transport. Wiley, New York
Malvagi F, Pomraning G (1991) Initial and boundary conditions for diffusive linear transport problems. J Math Phys 32(3):805–820
Marshak A, Davis A (2005) 3D radiative transfer in cloudy atmospheres. Springer Science & Business Media, Berlin
Miller PD (2006) Applied asymptotic analysis. American Mathematical Society, Providence
Mishchenko MI (2014) Electromagnetic scattering by particles and particle groups: an introduction. Cambridge University Press, Cambridge
Mishchenko MI, Travis LD, Lacis AA (2006) Multiple scattering of light by particles: radiative transfer and coherent backscattering. Cambridge University Press, Cambridge
Mobley CD (1994) Light and water: radiative transfer in natural waters. Academic Press, New York
Modest MF (2013) Radiative heat transfer. Academic Press, New York
Molenaar R, Jaap J, Zijp JR (1999) Determination of Kubelka-Munk scattering and absorption coefficients by diffuse illumination. Appl Opt 38(10):2068–2077
Myrick ML, Simcock MN, Baranowski M, Brooke H, Morgan SL, McCutcheon JN (2011) The Kubelka-Munk diffuse reflectance formula revisited. Appl Spectrosc Rev 46(2):140–165
Neuman M, Edström P (2010) Anisotropic reflectance from turbid media. I. theory. J Opt Soc Am A 27(5):1032–1039
Nobbs JH (1985) Kubelka-Munk theory and the prediction of reflectance. Color Technol 15(1):66–75
Peraiah A (2002) An introduction to radiative transfer: methods and applications in astrophysics. Cambridge University Press, Cambridge
Philips-Invernizzi B, Dupont D, Caze C (2001) Bibliographical review for reflectance of diffusing media. Opt Eng 40(6):1082–1092
Pomraning G, Ganapol B (1995) Asymptotically consistent reflection boundary conditions for diffusion theory. Ann Nucl Energy 22(12):787–817
Rohde SB, Kim AD (2012) Modeling the diffuse reflectance due to a narrow beam incident on a turbid medium. J Opt Soc Am A 29(3):231–238
Rohde S, Kim A (2014) Convolution model of the diffuse reflectance for layered tissues. Opt Lett 39(1):154–157
Rohde SB, Kim AD (2017) Backscattering of continuous and pulsed beams. Multiscale Model Simul 15(4):1356–1375
Şahin-Biryol D, Ilan B (2014) Asymptotic solution of light transport problems in optically thick luminescent media. J Math Phys 55(6):061, 501
Sandoval C, Kim AD (2014) Deriving Kubelka-Munk theory from radiative transport. J Opt Soc Am A 31(3):628–636
Schuster A (1905) Radiation through a foggy atmosphere. Astrophys J 21:1
Schwarzschild K (1906) On the equilibrium of the sun’s atmosphere. Nach König Gesell Wiss Göttingen Math-Phys Klasse, 195, p 41–53 195:41–53
Sobolev VV (2017) Light scattering in planetary atmospheres: international series of monographs in natural philosophy, vol 76. Elsevier, Amsterdam
Star W, Marijnissen J, Van Gemert M (1988) Light dosimetry in optical phantoms and in tissues: I. multiple flux and transport theory. Phys Med Biol 33(4):437
Thennadil SN (2008) Relationship between the Kubleka-Munk scattering and radiative transfer coefficients. J Opt Soc Am A 25(7):1480–1485
Thomas GE, Stamnes K (2002) Radiative transfer in the atmosphere and ocean. Cambridge University Press, Cambridge
Tsang L, Kong JA, Shin RT (1985) Theory of microwave remote sensing. Wiley-Interscience, New York
Van de Hulst HC (2012) Multiple light scattering: tables, formulas, and applications. Elsevier, Amsterdam
Vargas WE, Niklasson GA (1997) Applicability conditions of the Kubelka-Munk theory. Appl Opt 36(22):5580–5586
Wang LV, Hi Wu (2012) Biomedical optics: principles and imaging. Wiley, New York
Welch AJ, Van Gemert MJ et al (2011) Optical-thermal response of laser-irradiated tissue, vol 2. Springer, Berlin
Yang L, Kruse B (2004) Revised Kubelka-Munk theory. I. Theory and application. J Opt Soc Am A 21(10):1933–1941
Yang L, Miklavcic SJ (2005) Revised Kubelka-Munk theory III. A general theory of light propagation in scattering and absorptive media. J Opt Soc Am A 22(9):1866–1873
Yang L, Kruse B, Miklavcic SJ (2004) Revised Kubelka-Munk theory. II. Unified framework for homogeneous and inhomogeneous optical media. J Opt Soc Am A 21(10):1942–1952
Acknowledgements
A. D. Kim acknowledges support from the Air Force Office of Scientific Research (FA9550-17-1-0238).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Ilan, B., Kim, A.D. (2019). Radiative Transfer of Light in Strongly Scattering Media. In: Kokhanovsky, A. (eds) Springer Series in Light Scattering. Springer Series in Light Scattering. Springer, Cham. https://doi.org/10.1007/978-3-030-03445-0_2
Download citation
DOI: https://doi.org/10.1007/978-3-030-03445-0_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-03444-3
Online ISBN: 978-3-030-03445-0
eBook Packages: Earth and Environmental ScienceEarth and Environmental Science (R0)





 , then
, then  . This property follows from the invariance of (
. This property follows from the invariance of ( , and
, and  .
. and
and  , they satisfy the orthogonality relation
, they satisfy the orthogonality relation 
 by
by 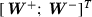 ; left-multiplying (
; left-multiplying (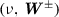 by
by  , and taking the difference between the resulting equations. The terms involving
, and taking the difference between the resulting equations. The terms involving 

 is the unit vector in the “direction” associated with the isotropic half-range Legendre polynomial
is the unit vector in the “direction” associated with the isotropic half-range Legendre polynomial 
 . Hence, the constant
. Hence, the constant  , and
, and  , respectively.
, respectively. , for
, for  to be its first row.
to be its first row.













