Abstract
Deontic Defeasible Logic (DDL) is a simple and computationally efficient approach for the representation of normative reasoning. Traditionally defeasible logics are defined proof theoretically based on the proof conditions for the logic. In this paper we present an argumentation system that corresponds to a variant of DDL. The resulting machinery is able to grasp in a natural way intuitions behind deontic reasoning with conditional norms featuring obligations, prohibitions, and (strong or weak) permissions.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Computational models of argument address defeasible claims raised on the basis of partial, uncertain and possibly conflicting pieces of information. Argumentation is pervasive in artificial intelligence, with many application domains [2].
Normative systems, and in particular legal systems, constitute a rich test bed and a major application domain for formal models of argument [13]. There, models of argument have applications ranging from case-based reasoning [14] to strategic studies in legal interactions [16, 17].
When representing and reasoning upon norms, deontic concepts such as obligation, prohibition and permission play a crucial role; and there exist some studies of deontic reasoning with formal models of argument, and a few argument-based models focus on (conditional) norms, deontic operators and their interplay [3, 4].
Besides these undertakings in deontic argumentation, many deontic formalisms have been previously designed [6]. Amongst formalisms with practical applications, DDL has been perhaps the most developed to represent and reason upon norms [8,9,10]. Moreover and interestingly, Defeasible Logic (DL) has possible interpretations in terms of arguments [7, 12, 15], but its deontic variants have received little or no consideration to construct argument-based frameworks for deontic reasoning. In this paper, we consider constructs from DDL to build a deontic argumentation system.
Contribution. Following the approach in DDL, we offer a rich formalism able to express relevant aspects of deontic reasoning, such as contrary-to-duty obligations and preferences about permissions. The deontic argumentation framework is described in the remainder of the paper.
2 Deontic Argumentation System
This section presents the deontic argumentation system. We first specify its language, then arguments are constructed. Eventually, the justification and rejection of arguments are defined.
2.1 Language
The following definitions provide the building blocks of our formalism:
-
literals and modalities ;
-
preference operators for obligations and permissions.
-
constitutive and deontic rules.
The attention is restricted to a simple propositional language with atomic negation and supplemented with a set of deontic operators  where
where  indicates an obligation, and
indicates an obligation, and  a permission.
a permission.
Definition 1
A literal is a plain literal iff it is an atomic proposition p or the negation of an atomic proposition, i.e., \(\lnot p\). A literal is a deontic literal iff it has either the form  or
or  or
or  or
or  where \(l \) is a plain literal. A literal is either a plain literal or a deontic literal.
where \(l \) is a plain literal. A literal is either a plain literal or a deontic literal.
Notation 1
Given a set of literals \(\mathcal {L}\), the set of plain literals in \(\mathcal {L}\) is denoted as \(\mathrm {Lit} _\mathcal {L}\) and the set of modal literals as \(\mathrm {ModLit} _\mathcal {L}\). However, in the remainder, the set of literals may be left implicit, and we may omit the subscript \(\mathcal {L}\).
We introduce two preference operators, \(\otimes \) for obligations and \(\odot \) for permissions. These operators are used to build chains of preferences, called \(\otimes \)- and \(\odot \)-expressions. Intuitively, an \(\otimes \)-expression such as \(l_1 \otimes l_2 \otimes \ldots \otimes l_n\) indicates that the obligation that \(l_1\) is preferred to the one that \(l_2\), which is preferred to \(l_3\) etc.
Definition 2
Let \(\oslash \in \{ \otimes , \odot \}\). An \(\oslash \)-expression is defined as follows:
-
1.
every literal \(l \in \mathrm {Lit} \) is an \(\oslash \)-expression;
-
2.
if A is an \(\oslash \)-expression and \(c_1, \dots , c_k \in \mathrm {Lit} \), then \(A \oslash c_1 \oslash \dots \oslash c_k\) is an \(\oslash \)-expression;
-
3.
nothing else is an \(\oslash \)-expression.
Notation 2
Given a set of literals \(\mathcal {L}\), the set of \(\oslash \)-expressions defined by \(\mathcal {L}\) is denoted \(\mathrm {Pref} _{\oslash , \mathcal {L}}\) or simply \(\mathrm {Pref} _{\oslash }\) if \(\mathcal {L}\) is left implicit.
Definition 3
Let \(\mathrm {Lbl}\) be a set of arbitrary labels. A set of rules \( Rul \) is a well-formed set of rules over a set of literals \(\mathcal {L}\) iff:

such that

Rules with an arrow \(\Rightarrow \) are defeasible rules, while rules with an arrow  are so-called defeaters which are essentially used to specify exceptions to defeasible rules. A defeasible rule can be used to support its consequent, whereas a defeater does not support its consequent.
are so-called defeaters which are essentially used to specify exceptions to defeasible rules. A defeasible rule can be used to support its consequent, whereas a defeater does not support its consequent.
Notation 3
The set of antecedents of a rule r is denoted \(\mathrm {A} (r)\), and \(\mathrm {C} (r)\) denotes its consequent. Other abbreviations are, for example,  , and \( Rul [b]\) to denote the set of rules whose consequent is b, and \( Rul _{\mathrm {d}} [b]\) the set of defeasible rules whose consequent is b.
, and \( Rul [b]\) to denote the set of rules whose consequent is b, and \( Rul _{\mathrm {d}} [b]\) the set of defeasible rules whose consequent is b.
Consequents of rules can be incompatible, and such incompatibilities are captured though complementary literals.
Notation 4
The complementary of a literal q is denoted by \( \sim q\); if q is a positive literal p, then \( \sim q\) is \(\lnot p\), and if q is a negative literal \(\lnot p\), then \( \sim q\) is p.
Definition 4
Let \(l\in \mathrm {Lit} \cup \mathrm {ModLit} \) denote a literal. A set of literals is a set of complementary literals of l, denoted \(\mathrm {Compl} (l)\), iff:
-
if \(l=p\in \mathrm {Lit} \) then \(\mathrm {Compl} (l) = \{ \sim l\}\);
-
 ,
,  ,
,  ,
, 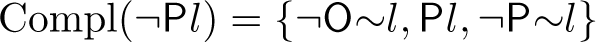 .
.
As usual, we can define a superiority relation between rules to determine their relative strength in case of conflict. As shown in [1], we can disregard the superiority relation in the discussion, since modular transformations exist that empty this relation while maintaining the same conclusions in the language [8]. This result holds both for ambiguity blocking and ambiguity propagating DL [7]. It also applies to deontic extensions of DL (including the one with \(\otimes \) and \(\odot \) operators), by means of the notion of inferiorly defeated rules [11].
2.2 Arguments and Attacks
Defining the notion of argument in the current context is not obvious. The complexity mainly resides in the richness of the language (especially the presence of the operators \(\otimes \) and \(\odot \)) and in the constructive nature of the introduction of modalities. The derivation of a modal literal such as  depends on the constructive provability of b using rules such as
depends on the constructive provability of b using rules such as  , and the derivation of
, and the derivation of  depends on showing that there is no proof for
depends on showing that there is no proof for  . We propose thus the following definition of arguments.
. We propose thus the following definition of arguments.
Definition 5
An argument A for a conclusion p generated from a set of rules \( Rul \) is a (possibly infinite) tree where
-
1.
the root node is labelled by literal p;
-
2.
any node is labelled by either a literal \(h\in \mathrm {Lit} \cup \mathrm {ModLit} \) or no literals;
and such that:
-
1.
if the node labelled by h has children \(h_1 , \dots , h_n\) \((n> 0)\), then all arcs connecting \(h_1 , \dots h_n\) to h are labelled by exactly one rule \(r \in Rul \) with \(\mathrm {A} (r) = \{b_1, \dots , b_n\}\) such that \(h_1=b_1, \dots , h_n=b_n\), and either
-
(a)
if
 and \(\mathrm {C} (r) = c_{1} \otimes \cdots \otimes c_{m}\) then
and \(\mathrm {C} (r) = c_{1} \otimes \cdots \otimes c_{m}\) then  (\(1\le k \le m\));
(\(1\le k \le m\)); -
(b)
if
 and \(\mathrm {C} (r) = c_{1} \odot \cdots \odot c_{m}\) then
and \(\mathrm {C} (r) = c_{1} \odot \cdots \odot c_{m}\) then  (\(1\le k \le m\));
(\(1\le k \le m\)); -
(c)
if \(r \in Rul ^c_{\mathrm {d}}\) then \(h =\mathrm {C} (r)\);
-
(d)
if
 then
then  is the root of the argument;
is the root of the argument; -
(e)
if \(r \in Rul ^c_{\mathrm {dft}}\) then \(h= p = \mathrm {C} (r)\) is the root of the argument;
-
(a)
-
2.
if the node labelled by h has no children (i.e. h is a leaf node), then either
-
(a)
h is labelled by no literals;
-
(b)
\(h= {\lnot \square l}\) (\(\square \in \mathrm {Mod} \));
-
(c)
 .
.
-
(a)
The interpretation of item (d) is as follows. First of all, notice that we have to do with a case where a defeater is considered. A defeater for  with head p does not positively prove anything, but it can attack any obligation rule
with head p does not positively prove anything, but it can attack any obligation rule  supporting \(\lnot p\) (i.e., proving
supporting \(\lnot p\) (i.e., proving  ). Conceptually, this means that the defeater can be a reason for stating that p is not obligatory, i.e., that
). Conceptually, this means that the defeater can be a reason for stating that p is not obligatory, i.e., that  is the case. Notice, also, that such a defeater—as any defeater here, and as done in standard argumentation semantics for DL [7]—can only label arcs leading to a root. In the modal case, this makes the interaction among arguments simple, as the concept of derivation for a negative modal literal depends on the relation between the argument considered and other arguments attacking the former one. Hence—as we will see—that
is the case. Notice, also, that such a defeater—as any defeater here, and as done in standard argumentation semantics for DL [7]—can only label arcs leading to a root. In the modal case, this makes the interaction among arguments simple, as the concept of derivation for a negative modal literal depends on the relation between the argument considered and other arguments attacking the former one. Hence—as we will see—that  is justified depends on the absence of successful arguments whose conclusion is
is justified depends on the absence of successful arguments whose conclusion is  .
.
Remark 1
Item (b) of the last condition where the modality \(\square \) is a permission  captures the case where the conclusion l as strong permission—i.e. a permission derived from a rule with
captures the case where the conclusion l as strong permission—i.e. a permission derived from a rule with  —is defeated (as we will see later). If the modality \(\square \) is an obligation
—is defeated (as we will see later). If the modality \(\square \) is an obligation  , then it captures the case where a weak permission is put forward. Similarly, the last item (c) of condition (2) captures the case where a weak permission is assumed. In both cases, such a weak permission is not directly expressed in a specific deontic rule and cannot be constructively reflected in the tree-structure. In this sense, such nodes can only be leaf nodes.
, then it captures the case where a weak permission is put forward. Similarly, the last item (c) of condition (2) captures the case where a weak permission is assumed. In both cases, such a weak permission is not directly expressed in a specific deontic rule and cannot be constructively reflected in the tree-structure. In this sense, such nodes can only be leaf nodes.
Example 1
Suppose we have the following rule set:

Then, we can build an argument as in Fig. 1. \(\square \)
We may employ some auxiliary terminology.
-
A supportive argument is a finite argument in which no defeaters are used.
-
An argument is positive iff no defeater is used in it.
-
A constitutive argument is an argument where all rules are constitutive rules.
-
Any literal/modal literal labelling any node of an argument A is a conclusion of A.
Definition 6
Let A denote any argument with height \(j\ge 1\) for any literal p.Footnote 1 The top subargument of A, denoted \(A^t\), is the top subargument of A with height 1. Let us use \(R(A^t)\) to denote the rule associated with the arcs arriving at the root of \(A^t\).
On the basis of arguments, we provide the core notion of the approach —argument agglomeration set— which gathers all arguments that are strictly needed to accept an argument. Such agglomeration set caters for two cases:
-
when nodes are labelled by rule conclusions, in case of \(\otimes \)- or \(\odot \)-expressions in the head of rules such as \(a\otimes b\) and \(p\odot q\), the fact that
 or
or  label nodes means that a and
label nodes means that a and  have been concluded;
have been concluded; -
when leaf nodes are labelled modal literals such as
 we fall in the case discussed in Remark 1; even here, conditions external to the single argument at stake must be checked, which is required to verify that such an argument is justified.
we fall in the case discussed in Remark 1; even here, conditions external to the single argument at stake must be checked, which is required to verify that such an argument is justified.
Definition 7
Let \(A\in Args \) be an argument such that for every node h of A labelled by a modal literal  ,
,  ,
,  or
or  , the arcs leading to h are labelled by
, the arcs leading to h are labelled by
-
(for literals such as
 ) \(r: b_1, \dots , b_n \Rightarrow c_{1} \otimes \cdots \otimes c_{m}\) and \(l = c_k\) (\(1\le k \le m\)), and
) \(r: b_1, \dots , b_n \Rightarrow c_{1} \otimes \cdots \otimes c_{m}\) and \(l = c_k\) (\(1\le k \le m\)), and -
(for literals such as
 ) \(r: b_1, \dots , b_n \Rightarrow d_{1} \odot \cdots \odot d_{m}\) and \(l = d_k\) (\(1\le k \le m\)).
) \(r: b_1, \dots , b_n \Rightarrow d_{1} \odot \cdots \odot d_{m}\) and \(l = d_k\) (\(1\le k \le m\)).
An argument agglomeration set \(\mathrm {Aggl}(A)\subseteq Args \) w.r.t. A is a smallest set of arguments such that \(A \in \mathrm {Aggl}(A)\) and:
-
for each (leaf) node labelled
 or
or  ,
,-
there is an argument \(B\in \mathrm {Aggl}(A)\) whose conclusion is
 ;
; -
\(\mathrm {Aggl}(B) \subseteq \mathrm {Aggl}(A)\);
-
-
for each node labelled \(c_j\) (\(1\le j < k\)),
-
there is an argument \(C\in \mathrm {Aggl}(A)\) whose conclusion is \(\lnot c_j \in \mathrm {Compl} (c_j)\);
-
\(\mathrm {Aggl}(C) \subseteq \mathrm {Aggl}(A)\);
-
-
for each node labelled \(d_j\) (\(1\le j < k\)),
-
there is an argument \(D\in \mathrm {Aggl}(A)\) whose conclusion is
 ;
; -
\(\mathrm {Aggl}(D) \subseteq \mathrm {Aggl}(A)\).
-
Remark 2
The agglomeration set of any argument A gathers all arguments that are strictly needed to accept the construction of A. Thus, the agglomeration set of A can be viewed as a single argument where special arcs connect nodes in A labelled by modal literals obtained by rules supporting \(\oslash \)-expressions.
Example 2
Suppose the following rules:

Then, we can build the following argumentsFootnote 2:

which agglomerate as illustrated in Fig. 2.
Eventually, arguments supporting complementary literals attack each other.
Definition 8
An argument A attacks an argument B iff
-
1.
there exists a node of B labelled by m, and
-
2.
there exists a node of A labelled by \(l \in \mathrm {Compl} (m)\).
A set of arguments S attacks an argument B iff there is an argument A in S that attacks B.
2.3 Justified and Rejected Arguments
The justification of arguments has been thoroughly studied in the literature, and multiple semantics have been proposed. As we are dealing with DL, we resort to the argumentation semantics for variants of DL as presented in [7].
The usual definition of accepted arguments is slightly adapted to embrace argument agglomeration sets.
Definition 9
An argument A is an accepted argument w.r.t a set of arguments S iff A is finite, and every argument attacking any argument in any \(\mathrm {Aggl}(A)\) is attacked by S.
From accepted arguments, and similarly as [5], we can define justified arguments using a ‘characteristic function’.
Definition 10
Let \( Args \) be a set of arguments. The deontic justification characteristic function of \( Args \) is a function \(J_i: \mathrm {pow}( Args ) \rightarrow \mathrm {pow}( Args )\) such that:
-
\(J_0 = \emptyset \), and
-
\(J_{i+1} = \{A\in Args \mid A \text { is } \text {accepted } \text {w.r.t. } J_i \}\).
Definition 11
Let \( Args \) be a set of arguments. The set of justified arguments of \( Args \) is \( JArgs = \bigcup _{i=1}^{\infty } J_i\).
Definition 12
Let \( Args \) be a set of arguments. A literal is a justified literal if it is a conclusion of a supportive argument in \( JArgs \).
Once justified arguments and literals are established, rejected arguments and literals can be determined. We first define rejected arguments with respect to a generic set of arguments which is then instantiated as a set of justified arguments.
Definition 13
An argument A is a rejected argument by a set of arguments S iff either
-
1.
a proper subargument B of A is in S, or
-
2.
B is attacked by a finite argument.
Definition 14
Let T be a set of arguments. The deontic rejection characteristic function of \( Args \) is a function \(R_i (T): \mathrm {pow}( Args ) \rightarrow \mathrm {pow}( Args )\) such that
-
\(R_0 (T)= \emptyset \), and
-
\(R_{i+1} (T) = \{A\in Args \mid A \text { is rejected by } R_i (T) \text { and } T\}\).
Definition 15
The set of rejected arguments w.r.t. T is \( RArgs = \bigcup _{i=1}^{\infty } R_i (T)\). An argument is rejected if it is rejected w.r.t. \( JArgs \).
From justified and rejected arguments with respect to justified arguments, we define rejected literals.
Definition 16
A literal l is a rejected literal by T iff there is no supportive argument for l in \( Args - RArgs (T)\). A literal l is rejected if it is rejected by \( JArgs \).
In reference to the above definition, we can note that the set of justified arguments \( JArgs \) is included in \( Args - RArgs ( JArgs )\). Furthermore, some arguments in \( Args - RArgs (T)\) may be neither justified nor rejected. Consequently, a literal may be neither justified nor rejected. In this case, we may say that the status of the literal is undetermined.
Example 3
Let us suppose two arguments A and B attacking each other. Argument A supports literal \(\mathsf {a}\), while argument B supports literal \(\lnot a\). The set of justified arguments is empty, and thus the set of rejected arguments is empty. Consequently, literals a and \(\lnot a\) are neither justified nor rejected. Their status is undetermined. \(\square \)
3 Conclusion
A deontic rule-based argumentation framework has been devised to capture normative knowledge and reasoning upon it. To do so, we have been inspired by works in DDL and extended the argumentation machinery developed in [7].
The main source of difficulties resided in the introduction of modal and deontic-preference operators. In particular, the introduction of modalities required to significantly modify the concept of argument and the basic system of [7]. Indeed, the derivation of a modal literal such as  depends on the constructive provability of b using rules such as
depends on the constructive provability of b using rules such as  , and the derivation of
, and the derivation of  requires that there is no proof for
requires that there is no proof for  . We have thus devised argument agglomeration sets which, to the best of our knowledge, have no counterparts in the argumentation literature.
. We have thus devised argument agglomeration sets which, to the best of our knowledge, have no counterparts in the argumentation literature.
Notes
- 1.
As usual, the height of an argument is the number of edges on the longest path between the root and a leaf node.
- 2.
Arrows indicate the type of rule used.
References
Antoniou, G., Billington, D., Governatori, G., Maher, M.J.: Representation results for defeasible logic. ACM Trans. Comput. Logic 2, 255–287 (2001)
Atkinson, K., et al.: Towards artificial argumentation. AI Mag. 38(3), 25–36 (2017)
Beirlaen, M., Heyninck, J., Straßer, C.: Structured argumentation with prioritized conditional obligations and permissions. J. Log. Comput., exy005 (2018)
Beirlaen, M., Straßer, C.: A structured argumentation framework for detaching conditional obligations. CoRR abs/1606.00339 (2016)
Dung, P.M.: On the acceptability of arguments and its fundamental role in nonmonotonic reasoning, logic programming and n-person games. Artif. Intell. 77(2), 321–358 (1995)
Gabbay, D., Horty, J., Parent, X., van der Meyden, R., van der Torre, L. (eds.): Handbook of Deontic Logic and Normative Systems. College Publications, London (2013)
Governatori, G., Maher, M.J., Antoniou, G., Billington, D.: Argumentation semantics for defeasible logic. J. Log. Comput. 14(5), 675–702 (2004)
Governatori, G., Rotolo, A.: BIO logical agents: norms, beliefs, intentions in defeasible logic. Auton. Agents Multi-Agent Syst. 17(1), 36–69 (2008)
Governatori, G., Rotolo, A., Calardo, E.: Possible world semantics for defeasible deontic logic. In: Ågotnes, T., Broersen, J., Elgesem, D. (eds.) DEON 2012. LNCS (LNAI), vol. 7393, pp. 46–60. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-31570-1_4
Governatori, G., Rotolo, A., Sartor, G.: Temporalised normative positions in defeasible logic. In: Proceedings of the 10th International Conference on Artificial Intelligence and Law, pp. 25–34. ACM (2005)
Lam, H.-P., Governatori, G.: What are the necessity rules in defeasible reasoning? In: Delgrande, J.P., Faber, W. (eds.) LPNMR 2011. LNCS (LNAI), vol. 6645, pp. 187–192. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20895-9_17
Lam, H.P., Governatori, G., Riveret, R.: On ASPIC\(^{+}\) and defeasible logic. In: Baroni, P. (ed.) Proceedings of 6th International Conference on Computational Models of Argument. IOS Press, Amsterdam (2016)
Prakken, H., Sartor, G.: Law and logic: a review from an argumentation perspective. Artif. Intell. 227, 214–245 (2015)
Prakken, H., Wyner, A.Z., Bench-Capon, T.J.M., Atkinson, K.: A formalization of argumentation schemes for legal case-based reasoning in ASPIC\(^+\). J. Log. Comput. 25(5), 1141–1166 (2015)
Riveret, R., Governatori, G., Rotolo, A.: Argumentation semantics for temporal defeasible logic. In: Proceedings of the 3rd Starting AI Researchers’ Symposium, pp. 267–268. IOS Press (2006)
Riveret, R., Prakken, H., Rotolo, A., Sartor, G.: Heuristics in argumentation: a game-theoretical investigation. In: Proceedings of the 2nd International Conference on Computational Models of Argument, pp. 324–335. IOS Press (2008)
Sartor, G., Rudnianski, M., Rotolo, A., Riveret, R., Mayor, E.: Why lawyers are nice (or nasty): a game-theoretical argumentation exercise. In: Proceedings of the 12th International Conference on Artificial Intelligence and Law, pp. 108–117. ACM (2009)
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this paper
Cite this paper
Governatori, G., Rotolo, A., Riveret, R. (2018). A Deontic Argumentation Framework Based on Deontic Defeasible Logic. In: Miller, T., Oren, N., Sakurai, Y., Noda, I., Savarimuthu, B.T.R., Cao Son, T. (eds) PRIMA 2018: Principles and Practice of Multi-Agent Systems. PRIMA 2018. Lecture Notes in Computer Science(), vol 11224. Springer, Cham. https://doi.org/10.1007/978-3-030-03098-8_33
Download citation
DOI: https://doi.org/10.1007/978-3-030-03098-8_33
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-03097-1
Online ISBN: 978-3-030-03098-8
eBook Packages: Computer ScienceComputer Science (R0)





 ,
,  ,
,  ,
, 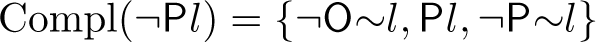 .
. and
and  (
( and
and  (
( then
then  is the root of the argument;
is the root of the argument; .
.
 or
or  label nodes means that a and
label nodes means that a and  have been concluded;
have been concluded; we fall in the case discussed in Remark
we fall in the case discussed in Remark  )
)  )
)  or
or  ,
, ;
; ;
;