On the Variance of Internode Distance Under the Multispecies Coalescent

Abstract

We consider the problem of estimating species trees from unrooted gene tree topologies in the presence of incomplete lineage sorting, a common phenomenon that creates gene tree heterogeneity in multilocus datasets. One popular class of reconstruction methods in this setting is based on internode distances, i.e. the average graph distance between pairs of species across gene trees. While statistical consistency in the limit of large numbers of loci has been established in some cases, little is known about the sample complexity of such methods. Here we make progress on this question by deriving a lower bound on the worst-case variance of internode distance which depends linearly on the corresponding graph distance in the species tree. We also discuss some algorithmic implications.

This work was supported by funding from the U.S. National Science Foundation DMS-1149312 (CAREER), DMS-1614242 and CCF-1740707 (TRIPODS). We thank Tandy Warnow for suggesting the problem and for helpful discussions.

1 Introduction

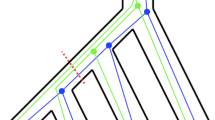
Species tree estimation is increasingly based on large numbers of loci or genes across many species. Gene tree heterogeneity, i.e. the fact that different genomic regions may be consistent with incongruent genealogical histories, is a common phenomenon in multilocus datasets that leads to significant challenges in this type of estimation. One important source of incongruence is incomplete lineage sorting (ILS), a population-genetic effect (see Fig. 1 below for an illustration), which is modeled mathematically using the multispecies coalescent (MSC) process [14, 19]. Many recent phylogenetic analyses of genome-scale biological datasets have indeed revealed substantial heterogeneity consistent with ILS [3, 6, 27].

Standard methods for species tree estimation that do not take this heterogeneity into account, e.g. the concatenation of genes followed by a single-tree maximum likelihood analysis, have been shown to suffer serious drawbacks under the MSC [20, 23]. On the other hand, new methods have been developed for species tree estimation that specifically address gene tree heterogeneity. One popular class of methods, often referred to as summary methods, proceed in two steps: first reconstruct a gene tree for each locus; then infer a species tree from this collection of gene trees. Under the MSC, many of these methods have been proven to converge to the true species tree when the number of loci increases, i.e. the methods are said to be statistically consistent. Examples of summary methods that enable statistically consistent species tree estimation include MP-EST [12], NJst [11], ASTRID [26], ASTRAL [15, 16], STEM [8], STEAC [13], STAR [13], and GLASS [17].

Here we focus on reconstruction methods, such as NJst and ASTRID, based on what is known as internode distances, i.e. the average of pairwise graph distances across genes. Beyond statistical consistency [1, 7, 11], little is known about the data requirement or sample complexity of such methods (unlike other methods such as ASTRAL [24] or GLASS [17] for instance). That is, how many genes or loci are needed to ensure that the true species tree is inferred with high probability under the MSC? Here we make progress on this question by deriving a lower bound on the worst-case variance of internode distance. Indeed the sample complexity of a reconstruction method depends closely on the variance of the quantities it estimates, in this case internode distances. Our bound depends linearly on the corresponding graph distance in the species tree which, as we explain below, has possible implications for the choice of an accurate reconstruction method.

The rest of the paper is structured as follows. In Sect. 2, we state our main results formally, after defining the MSC and the internode distance. In Sect. 3, we discuss algorithmic implications of our bound. Proofs can be found in Sect. 4.

2 Definitions and Results

In this section, we first introduce the multispecies coalescent. We also define the internode distance and state our results formally.

Fig. 1.

An incomplete lineage sorting event (in the rooted setting). Although 1 and 2 are more closely related in the rooted species tree (fat tree), 2 and 3 are more closely related in the rooted gene tree (thin tree). This incongruence is caused by the failure of the lineages originating from 1 and 2 to coalesce within the shaded branch. The shorter this branch is, the more likely incongruence occurs.

Multilocus Evolution Under the Multispecies Coalescent. Our analysis is based on the multispecies coalescent (MSC), a standard random gene tree model [14, 19]. See Fig. 1 for an illustration. Consider a species tree $(\mathcal {S},\varGamma )$ with n leaves. Here $\mathcal {S}= (\mathcal {V},\mathcal {E},r)$ is a rooted binary tree with vertex and edge sets $\mathcal {V}$ and $\mathcal {E}$ and where each leaf is labeled by a species in $\{1,\ldots ,n\}$. We refer to $\mathcal {S}$ as the species tree topology. The branch lengths $\varGamma = (\varGamma _e)_{e\in E}$ are expressed in so-called coalescent time units. We do not assume that $(\mathcal {S},\varGamma )$ is ultrametric (see e.g. [25]). Each gene¹ $j = 1,\ldots , m$ has a genealogical history represented by its gene tree $\mathcal {T}_j$ distributed according to the following process: looking backwards in time, on each branch e of the species tree, the coalescence of any two lineages is exponentially distributed with rate 1, independently from all other pairs; whenever two branches merge in the species tree, we also merge the lineages of the corresponding populations, that is, the coalescent proceeds on the union of the lineages; one individual is sampled at each leaf. The genes are assumed to be unlinked, i.e. the process above is run independently and identically for all $j = 1,\ldots ,m$. More specifically, the probability density of a realization of this model for m independent genes is

$$\begin{aligned}&\prod _{j=1}^m \prod _{e\in E} \exp \left( -\left( {\begin{array}{c}O_j^{e}\\ 2\end{array}}\right) \left[ \gamma _j^{e, O_j^{e}+1} - \gamma _j^{e, O_j^{e}}\right] \right) \times \prod _{\ell =1}^{I_j^{e}-O_j^{e}} \exp \left( -\left( {\begin{array}{c}\ell \\ 2\end{array}}\right) \left[ \gamma _j^{e, \ell } - \gamma _j^{e, \ell -1}\right] \right) , \end{aligned}$$

where, for gene j and branch e, $I_j^{e}$ is the number of lineages entering e, $O_j^{e}$ is the number of lineages exiting e, and $\gamma _j^{e,\ell }$ is the $\ell ^{th}$ coalescence time in e; for convenience, we let $\gamma _j^{e,0}$ and $\gamma _j^{e,I_j^{e}-O_j^{e}+1}$ be respectively the divergence times (expressed in coalescence time units) of e and of its parent population (which depend on $\varGamma$). We write $\{\mathcal {T}_j\}_j \sim \mathcal {D}_{\mathrm {s}}^{m}[\mathcal {S},\varGamma ]$ to indicate that the m gene trees $\{\mathcal {T}_j\}_j$ are independently distributed according to the MSC on species tree $\mathcal {S},\varGamma$. To be specific, $\mathcal {T}_j$ is the unrooted gene tree topology—without branch lengths—and we remark that, under the MSC, $\mathcal {T}_j$ is binary with probability 1. Throughout we assume that the $\mathcal {T}_j$’s are known and were reconstructed without estimation error.

Internode Distance. Assume we are given m gene trees $\{\mathcal {T}_j\}_j$ over the n species $\{1,\ldots ,n\}$. For any pair of species x, y and gene j, we let $d^j_\mathrm {g}(x,y)$ be the graph distance between x and y on $\mathcal {T}_j$, i.e. the number of edges on the unique path between x and y. The internode distance between x and y is defined as the average graph distance across genes, i.e.

$$\begin{aligned} \hat{\delta }_{\mathrm {int}}^{m}(x,y) = \frac{1}{m} \sum _{j=1}^m d^{\mathcal {T}_j}_\mathrm {g}(x,y). \end{aligned}$$

Under the MSC, the internode distances $(\hat{\delta }_{\mathrm {int}}^{m}(x,y))_{x,y}$ are correlated random variables whose joint distribution depends in the a complex way on the species tree $(\mathcal {S},\varGamma )$. Here follows a remarkable fact about internode distance [1, 7, 11]. Let $\bar{\delta }_{\mathrm {int}}(x,y)$ be the expectation of $\hat{\delta }_{\mathrm {int}}^{m}(x,y)$ under the MSC and let $\mathcal {S}_{\mathrm {u}}$ be the unrooted version of the species tree $\mathcal {S}$. Then $(\bar{\delta }_{\mathrm {int}}(x,y))_{x,y}$ is an additive metric associated² to $\mathcal {S}_{\mathrm {u}}$ (see e.g. [25]). In particular, whenever $\mathcal {S}_{\mathrm {u}}$ restricted to species x, y, w, z has quartet topology xy|wz (i.e. the middle edge of the restriction to x, y, w, z splits x, y from w, z), it holds that³

$$\begin{aligned} \bar{\delta }_{\mathrm {int}}(x,w)+\bar{\delta }_{\mathrm {int}}(y,z) = \bar{\delta }_{\mathrm {int}}(x,z) + \bar{\delta }_{\mathrm {int}}(y,w) \ge \bar{\delta }_{\mathrm {int}}(x,y) + \bar{\delta }_{\mathrm {int}}(w,z). \end{aligned}$$

This result forms the basis for many popular multilocus reconstruction methods, including NJst [11] and ASTRID [26], which apply standard distance-based methods to the internode distances

$$\begin{aligned} (\hat{\delta }_{\mathrm {int}}^{m}(x,y))_{x,y}. \end{aligned}$$

Main Results. By the law of large numbers, for all pairs of species x, y

$$\begin{aligned} \hat{\delta }_{\mathrm {int}}^{m}(x,y) \rightarrow \bar{\delta }_{\mathrm {int}}(x,y), \end{aligned}$$

with probability 1 as $m \rightarrow +\infty$, a fact that can be used to establish the statistical consistency (i.e. the guarantee that the true specie tree is recovered as long as m is large enough) of internode distance-based methods such as NJst [11]. However, as far as we know, nothing is known about the sample complexity of internode distance-based methods, i.e. how many genes are needed to reconstruct the species tree with high probability—say $99\%$—as a function of some structural properties of the species tree—primarily the number of species n and the shortest branch length f? We do not answer this important but technically difficult question here, but we make progress towards its resolution by providing a lower bound on the worst-case variance of internode distance. Let $d_\mathrm {g}^{\mathcal {S}_{\mathrm {u}}}(x,y)$ denote the graph distance between x and y on $\mathcal {S}_{\mathrm {u}}$.

Theorem 1

(Lower bound on the worst-case variance of internode distance). There exists a constant $C > 0$ such that, for any integer $n \ge 4$ and real $f > 0$, there is a species tree $(\mathcal {S},\varGamma )$ with n leaves and shortest branch length f such that the following holds: for all pairs of species $\ell ,\ell '$ and all integers $m \ge 1$, if $\{\mathcal {T}_j\}_j \sim \mathcal {D}_{\mathrm {s}}^{m}[\mathcal {S},\varGamma ]$ then

$$\begin{aligned} \mathbf {Var}\left[ \hat{\delta }_{\mathrm {int}}^{m}(\ell ,\ell ')\right] \ge C \frac{d_\mathrm {g}^{\mathcal {S}_{\mathrm {u}}}(\ell ,\ell ')}{m}, \end{aligned}$$

(1)

and, furthermore,

$$\begin{aligned} \max _{\ell ,\ell '} \mathbf {Var}\left[ \hat{\delta }_{\mathrm {int}}^{m}(\ell ,\ell ')\right] \ge C \frac{n}{m}, \end{aligned}$$

(2)

In words, there are species trees for which the variance of internode distance scales as the graph distance—which can be of order n—divided by m. The proof of Theorem 1 is detailed in Sect. 4.

3 Discussion

How is Theorem 1 related to the sample complexity of species tree estimation methods? The natural approach for deriving bounds on the number of genes required for high-probability reconstruction in distance-based methods is to show that the estimated distances used are sufficiently concentrated around their expectations—provided that m is large enough as a function of n and f (e.g. [2, 9]; but see [22] for a more refined analysis). In particular, one needs to control the variance of distance estimates.

Practical Implications. Bound (2) in Theorem 1 implies that to make all variances negligible the number of genes m is required to scale at least linearly in the number of species n. In contrast, certain quartet-based methods such as ASTRAL [15, 16] have a sample complexity scaling only logarithmically in n [24].

On the other hand, Bound (2) is only relevant for those reconstruction algorithms using all distances, for instance NJst which is based on Neighbor-Joining [2, 10]. Many so-called fast-converging reconstruction methods purposely use only a strict subset of all distances, specifically those distances within a constant factor of the “depth” of the species tree. Refer to [9] for a formal definition of the depth, but for our purposes it will suffice to note that in the case of graph distance the depth is at most of the order of $\log n$. Hence Bound (1) suggests it may still possible to achieve a sample complexity comparable to that of ASTRAL—if one uses a fast-converging method (within ASTRID for instance).

The Impact of Correlation. Theorem 1 does not in fact lead to a bound on the sample complexity of internode distance-based reconstruction methods. For one, Theorem 1 only gives a lower bound on the variance. One may be able to construct examples where the variance is even larger. In general, analyzing the behavior of internode distance is quite challenging because it depends on the full multispecies coalescent process in a rather tangled manner.

Perhaps more importantly, the variance itself is not enough to obtain tight bounds on the sample complexity. One problem is correlation. Because $\hat{\delta }_{\mathrm {int}}^{m}(x,y)$ and $\hat{\delta }_{\mathrm {int}}^{m}(w,z)$ are obtained using the same gene trees, they are highly correlated random variables. One should expect this correlation to produce cancellations (e.g. in the four-point condition; see [25]) that could drastically lower the sample complexity. The importance of this effect remains to be studied.

Gene Tree Estimation Error. We pointed out above that quartet-based methods such as ASTRAL may be less sensitive to long distances than internode distance-based methods such as NJst. An important caveat is the assumption that gene trees are perfectly reconstructed. In reality, gene tree estimation errors are likely common and are also affected by long distances (see e.g. [9]). A more satisfactory approach would account for these errors or would consider simultaneously sequence-length and gene-number requirements. Few such analyses have so far been performed because of technical challenges [4, 5, 18, 21].

4 Variance of Internode Distance

In this section, we prove Theorem 1. Our analysis of internode distance is based on the construction of a special species tree where its variance is easier to control. We begin with a high-level proof sketch:

• Our special example is a caterpillar tree with an alternation of short and long branches along the backbone.

• The short branches produce “local uncertainty” in the number of lineages that coalesce onto the path between two fixed leaves. The long branches make these contributions to the internode distance “roughly independent” along the backbone.

• As a result, the internode distance is, up to a small error, a sum of independent and identically distributed contributions. Hence, its variance grows linearly with graph distance.

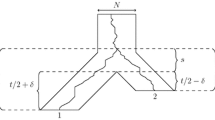
Setting for Analysis. We fix the number of species n and we assume for convenience that n is even.⁴ Recall also that f will denote the length of the shortest branch in coalescent time units. We consider the species tree $(\mathcal {S}, \varGamma )$ depicted in Fig. 2. Specifically, $\mathcal {S}$ is a caterpillar tree: its backbone is an $n-1$-edge path

Fig. 2.

The species tree used in the analysis.

$$(a,w_1), (w_1,z_1), (z_1,w_2), (w_2,z_2), \ldots , (w_{\frac{n-2}{2}},z_{\frac{n-2}{2}}),(z_{\frac{n-2}{2}},r)$$

connecting leaf a to root $r = w_{n/2}$; each vertex $w_i$ on the backbone is incident with an edge $(w_i,x_i)$ to leaf $x_i$; each vertex $z_i$ on the backbone is incident with an edge $(z_i,y_i)$ to leaf $y_i$; root r is incident with an edge (r, b) to leaf b. Each edge of the form $e = (w_i,z_i)$ is a short edge of length $\varGamma _e = f$, while all other edges are long edges of length $g = 4 \log n$.

Proof of Theorem 1

Recall that our goal is to prove that for all pairs of species $\ell ,\ell '$ and all integers $m \ge 1$, if $\{\mathcal {T}_j\}_j \sim \mathcal {D}_{\mathrm {s}}^{m}[\mathcal {S},\varGamma ]$ then

$$\begin{aligned} \mathbf {Var}\left[ \hat{\delta }_{\mathrm {int}}^{m}(\ell ,\ell ')\right] \ge C \frac{d_\mathrm {g}^{\mathcal {S}_{\mathrm {u}}}(\ell ,\ell ')}{m}. \end{aligned}$$

To simplify the analysis, we detail the argument in the case $\ell = a$ and $\ell ' = b$ only. The other cases follow similarly.

We first reduce the computation to a single gene. Recall that

$$\begin{aligned} \hat{\delta }_{\mathrm {int}}^{m}(a,b) = \frac{1}{m} \sum _{j=1}^m d^{\mathcal {T}_j}_\mathrm {g}(a,b). \end{aligned}$$

Lemma 1

(Reduction to a single gene). For any m, it holds that

$$\begin{aligned} \mathbf {Var}\left[ \hat{\delta }_{\mathrm {int}}^{m}(\ell ,\ell ')\right] = \frac{1}{m} \mathbf {Var}\left[ d^{\mathcal {T}_1}_\mathrm {g}(a,b)\right] . \end{aligned}$$

Proof

Because the $\mathcal {T}_j$’s are independent and identically distributed, it follows that

$$\begin{aligned} \mathbf {Var}\left[ \hat{\delta }_{\mathrm {int}}^{m}(\ell ,\ell ')\right]&= \mathbf {Var}\left[ \frac{1}{m} \sum _{j=1}^m d^{\mathcal {T}_j}_\mathrm {g}(a,b)\right] = \frac{1}{m^2} \sum _{j=1}^m \mathbf {Var}\left[ d^{\mathcal {T}_j}_\mathrm {g}(a,b)\right] = \frac{1}{m} \mathbf {Var}\left[ d^{\mathcal {T}_1}_\mathrm {g}(a,b)\right] , \end{aligned}$$

as claimed.

We refer to the 2-edge path $\{(w_i,z_i), (z_i,w_{i+1})\}$ as the i-th block. The purpose of the long backbone edges is to create independence between the contributions of the blocks. To make that explicit, let $\mathcal {F}_i$ be the event that, in $\mathcal {T}_1$, all lineages entering the edge $(z_i,w_{i+1})$ have coalesced by the end of the edge (backwards in time). And let $\mathcal {F}= \cap _i \mathcal {F}_i$.

Lemma 2

(Full coalescence on all blocks). It holds that

$$\begin{aligned} \mathbf {P}[\mathcal {F}] \ge 1 - 1/n. \end{aligned}$$

Proof

By the multiplication rule and the fact that $\mathcal {F}_i$ only depends on the number of lineages entering $(w_i,z_i)$, we have

$$\begin{aligned} \mathbf {P}[\mathcal {F}]&= \prod _i \mathbf {P}[\mathcal {F}_i\,|\,\mathcal {F}_{1} \cap \cdots \cap \mathcal {F}_{i-1}] = \left( \mathbf {P}[\mathcal {F}_1]\right) ^{n/2-1} \ge 1 - (n/2-1) \left( 1- \mathbf {P}[\mathcal {F}_1]\right) . \end{aligned}$$

It remains to upper bound $\mathbf {P}[\mathcal {F}_1^c]$. We have either 2 or 3 lineages entering $(z_1,w_2)$. In the former case, the failure to coalesce has probability $e^{-g}$, i.e. the probability that an exponential with rate 1 is greater than g. In the latter case, the failure to fully coalesce has probability at most $e^{-3(g/2)} + e^{-g/2}$, i.e. the probability that either the first coalescence (happening at rate 3) or the second one (happening at rate 1) takes more than g / 2. Either way this gives at most $\mathbf {P}[\mathcal {F}_1^c] \le 2 e^{-g/2}$. With $g = 4 \log n = 2 \log n^2$ above, we get the claim.

We now control the contribution from each block. Let $X_i$ be the number of lineages coalescing into the path between a and b on the i-th block. Conditioning on $\mathcal {F}$, we have $X_i \in \{1,2\}$ and we have further that all $X_i$’s are independent and identically distributed. This leads to the following bound.

Lemma 3

(Linear variance). It holds that

$$\begin{aligned} \mathbf {Var}\left[ d^{\mathcal {T}_1}_\mathrm {g}(a,b)\right] \ge \frac{n-2}{2} \,\mathbf {Var}\left[ X_1\big | \mathcal {F}_1\right] \,\mathbf {P}[\mathcal {F}]. \end{aligned}$$

Proof

By the conditional variance formula, letting $\mathbbm {1}_\mathcal {F}$ be the indicator of $\mathcal {F}$,

$$\begin{aligned} \mathbf {Var}\left[ d^{\mathcal {T}_1}_\mathrm {g}(a,b)\right]&\ge \mathbf {E}\left[ \mathbf {Var}\left[ d^{\mathcal {T}_1}_\mathrm {g}(a,b)\big | \mathbbm {1}_\mathcal {F}\right] \right] \ge \mathbf {Var}\left[ d^{\mathcal {T}_1}_\mathrm {g}(a,b)\big | \mathcal {F}\right] \mathbf {P}[\mathcal {F}]. \end{aligned}$$

On the event $\mathcal {F}$, it holds that

$$\begin{aligned} d^{\mathcal {T}_1}_\mathrm {g}(a,b)&= \sum _{i} X_i. \end{aligned}$$

Moreover, conditioning on $\mathcal {F}$ makes the $X_i$’s independent and identically distributed. Hence we have finally

$$\begin{aligned} \mathbf {Var}\left[ d^{\mathcal {T}_1}_\mathrm {g}(a,b)\right]&\ge \frac{n-2}{2} \,\mathbf {Var}\left[ X_1 \big | \mathcal {F}\right] \,\mathbf {P}[\mathcal {F}] \ge \frac{n-2}{2} \,\mathbf {Var}\left[ X_1 \big | \mathcal {F}_1\right] \,\mathbf {P}[\mathcal {F}], \end{aligned}$$

where we used the fact that $X_1$ depends on $\mathcal {F}$ only through $\mathcal {F}_1$.

The final step is to bound the contribution to the variance from a single block.

Lemma 4

(Contribution from a block). It holds that

$$\begin{aligned} \mathbf {Var}\left[ X_1\big | \mathcal {F}_1\right] = \frac{1}{3}e^{-f}\left( 1 - \frac{1}{3}e^{-f}\right) = \frac{2}{9}\left( 1 - \varTheta (f)\right) , \end{aligned}$$

for f small, where we used the standard Big-Theta notation.

Proof

As we pointed out earlier, conditioning on $\mathcal {F}_1$, we have $X_1 \in \{1,2\}$. In particular $X_1 - 1$ is a Bernoulli random variable whose variance $\mathbf {P}\left[ X_1 - 1 = 1\big | \mathcal {F}_1\right] (1- \mathbf {P}\left[ X_1 - 1 = 1\big | \mathcal {F}_1\right] )$ is the same as the variance of $X_1$ itself. So we need to compute the probability that $X_1 = 2$, conditioned on $\mathcal {F}_1$. There are four scenarios to consider (depending on whether or not there is coalescence in the short branch $(w_1,z_1)$ and which coalescence occurs first in the long branch $(z_1,w_2)$), only one of which produces $X_1 = 1$:

• No coalescence occurs in $(w_1,z_1)$ and the first coalescence in $(z_1,w_2)$ is between the lineages coming from $x_1$ and $y_1$. This event has probability $\frac{1}{3}e^{-f}$ by symmetry when conditioning on $\mathcal {F}_1$.

Hence $\mathbf {P}\left[ X_1 = 2\big | \mathcal {F}_1\right] = 1 - \frac{1}{3}e^{-f}$.

By combining Lemmas 1, 2, 3 and 4, we get that

$$\begin{aligned} \mathbf {Var}\left[ \hat{\delta }_{\mathrm {int}}^{m}(\ell ,\ell ')\right] \ge \frac{1}{m} \times \frac{n-2}{2} \times \frac{1}{3}e^{-f}\left( 1 - \frac{1}{3}e^{-f}\right) \times \left( 1 - \frac{1}{n}\right) . \end{aligned}$$

Choosing C small enough concludes the proof of the theorem.

5 Conclusion

To summarize, we have derived a new lower bound on the worst-case variance of internode distance under the multispecies coalescent. No such bounds were previously known as far as we know. Our results suggest it may be preferable to use fast-converging methods when working with internode distances for species tree estimation. The problem of providing tight upper bounds on the sample complexity of internode distance-based methods remains however an important open question.