Abstract
It seems widely accepted that human reasoning cannot be modeled by means of classical logic. Psychological experiments have repeatedly shown that participants’ answers systematically deviate from the classical logically correct answers. Recently, a new computational logic approach to modeling human syllogistic reasoning has been developed which seems to perform better than other state-of-the-art cognitive theories. We take this approach as starting point, yet instead of trying to model the human reasoner, we aim at identifying clusters of reasoners, which can be characterized by reasoning principles or by heuristic strategies.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
1 Introduction
In recent years, a new cognitive theory based on the Weak Completion Semantics (WCS) has been developed. It has its roots in the ideas first expressed by Stenning and van Lambalgen [12], but is mathematically sound [5], and has been successfully applied to various human reasoning tasks. An overview can be found in [4]. Hence, it was natural to ask whether the WCS is competitive in syllogistic reasoning and how it performs with respect to the cognitive theories evaluated in the meta-analysis by Khemlani and Johnson-Laird [7]. Syllogisms are one of the oldest kinds of logical argument that date back to Aristotle. They are especially important in the field of Psychology, as they can be easily understood, yet they are sophisticated enough to require non-trivial reasoning. According to [7], an established theory for human syllogistic reasoning is a necessary step towards a unified cognitive theory of reasoning.
A syllogism consists of two premises and a conclusion. The syllogistic reasoning task is then: given the two premises, what conclusions are valid? Consider the following pair of syllogistic premises:

The premises can be interpreted as quantified statements. In first-order logic (FOL), some c are not a follows from these premises. However, according to [7], the majority of participants in experimental studies either concluded some c are not a or answered that no valid conclusion follows. Yet, these two responses exclude each other, i.e., it is unlikely that the participants who answered no valid conclusion are the same ones who answered some c are not a, and vice versa.
The possible quantifiers and figures of the premises are shown in Tables 1 and 2: Each premise can have one of four quantifiers called moods. The entities can appear in four different orders called figures. Thus we can abbreviate the example from above which consists of moods A and O and figure 3 with A O3.
In [8], cognitive principles under the WCS for modeling the logical form of the representation of quantified statements in human reasoning are identified. The approach achieved a match of 89% with respect to the conclusions given by the participants and based on the data reported in [7]. This result stands out, as the best of the twelve other state-of-the-art cognitive theories achieved only a match of 84%.
While reasoning with conditionals, humans seem to take certain assumptions for granted which, however, are not stated explicitly in the task description. As psychological experiments show, these assumptions seem not to be arbitrary but instead are systematic in the sense that they are repeatedly made by participants. Furthermore, some assumptions appear in various experiments, whereas other assumptions are only made in very few experiments or only by some participants. In order to identify and structure these assumptions, we view them as principles that are either applied or ignored by the participants who have to solve the task. As starting point, we take the syllogistic reasoning approach presented in [8]. However, a drawback of this approach is that only the matching with respect to the aggregated data is considered, i.e., the approach models the human reasoner. However, the above example and other examples such as cases of the Wason selection task reported in [9], serve as indication that the human reasoner does not exist, but instead we might better search for clusters of human reasoners. These clusters might be expressed by principles, i.e., some clusters might apply some principles that are not applied by other clusters. We also take into account the assumption that some humans do not reason at all to solve syllogistic reasoning tasks. We believe that they use heuristic strategies [13, 14] and present a way to combine them within the WCS.
The paper is structured as follows: In Sect. 2 we present the principles for the representation of quantified statements, motivated by findings from cognitive science and philosophy of language. The WCS and the encoding of quantified statements within this approach are introduced in Sects. 3 and 4. In Sect. 5, the clusters and heuristics are discussed and an overall evaluation of the WCS is presented. In Sect. 6, we give an overview of our implementation of computing the conclusions that are drawn depending on the applied principles.
2 Principles About Quantified Statements
Eight principles for developing a logical form of quantified statements are presented. They originate from [1, 8] except of the principles in Sects. 2.5 and 2.8.
2.1 Quantified Statements as Conditionals (conditionals)
Independent of the quantifiers mood, we formalize any relation between two objects of a quantified statement by means of a conditional such that the first object is the antecedent and the second object is the conclusion in the conditional. For instance, the statement All a are b is expressed as \(\forall X (a(X)~\rightarrow ~b(X))\).
2.2 Licenses for Inferences (licenses)
Given the quantified statement all a are b, a license for this inference can then be expressed by all a that are not abnormal, are b [12]. Given the previous formalization of this statement as \(\forall X (a(X) \rightarrow b(X))\), we extend this conditional by conjoining a(X) together with an abnormality predicate: \(\forall X (a(X) \wedge \lnot ab(X) \rightarrow b(X))\). Further, nothing is abnormal with respect to X, i.e., \(\lnot ab(X)\) is assumed.
2.3 Existential Import and Gricean Implicature (import)
Humans understand quantifiers differently due to a pragmatic understanding of the language. For instance, in natural language, humans normally do not quantify over things that do not exist. Consequently, all a implies some a exists. This appears to be in line with human reasoning and has been called the Gricean implicature [3]. It corresponds to what sometimes in literature is also called existential import.
2.4 Unknown Generalization (unknownGen)
Humans seem to distinguish between some y are z and some z are y, as the results reported by [7] show. Nevertheless, if we would represent some y are z by \(\exists X (y(X) \wedge z(X))\) then this is semantically equivalent to \(\exists X (z(X) \wedge y(X))\) because conjunction is commutative in FOL. Likewise, humans seem to distinguish between some y are z and all y are z. Accordingly, if we only observe that an object o belongs to y and z then we do not want to conclude both, some y are z and all y are z. In order to distinguish between some y are z and all y are z, we introduce the following principle: If we know that some y are z, then there must not only be an object \(o_1\), which belongs to y and z but there must be another object \(o_2\), which belongs to y and for which it is unknown whether it belongs to z.
2.5 Deliberate Generalization (deliberateGen)
If all of the principles introduced so far are applied to an existential premise, the only object about which an inference can be made is the one resulting from the existential import principle. This is because the abnormality introduced by the licenses for inferences principle and according to the unknown generalization principle has to be false for the object introduced by existential import, but it is unknown for other objects. There is, however, evidence that some humans still draw conclusions in such circumstances [7]. We believe that they do not take into account abnormalities regarding objects that are not related to the premise.
2.6 Converse Premise (converse)
Although there seems to be some evidence that humans distinguish between some y are z and some z are y (see the results reported in [7]) we propose that premises of the form Iab imply Iba and vice versa. If there is an object which belongs to y and z, then there is also an object which belongs to z and y. Similarly, we apply this principle for the E mood.
2.7 Search Alternative Conclusions to NVC (searchAlt)
Our hypothesis is that when participants are faced with a NVC conclusion (no valid conclusion), they might not want to accept this conclusion and proceed to check whether there exists unknown information that is relevant. This information may be explanations about the facts coming either from an existential import or from unknown generalization. We use only the first as source for observations, as they are used directly to infer new information.
2.8 Contraposition (contraposition)
In FOL, a conditional statement of the form \(\forall (X) (a(X) \rightarrow b(X))\) is logically equivalent to its contrapositive \(\forall (X) (\lnot b(X) \rightarrow \lnot a(X))\). This contraposition also holds for the syllogistic moods A and E. There is evidence in [7] that some of the participants make use of this equivalence when solving syllogistic reasoning tasks. We believe that when they encounter a premise with the mood A (e.g., all a are b), then they might reason with the contrapositive conditional as well.
3 Weak Completion Semantics
3.1 Contextual Logic Programs
Contextual logic programs are (data) logic programs extended by the truth-functional operator \(\mathsf {ctxt}\), called context [2]. Contextual (logic) program clauses are expressions of the forms \(A \leftarrow L_1 \wedge \ldots \wedge L_m \wedge \mathsf {ctxt}(L_{m+1}) \wedge \ldots \wedge \mathsf {ctxt}(L_{m+p})\) (called rules), \(A \leftarrow \top \) (called facts), \(A \leftarrow \bot \) (called negative assumptions)Footnote 1 and \(A \leftarrow \mathsf {U}\) (called unknown assumptions), where A is an atom and the \(L_i\) with \(1 \le i \le m+p\) are literals. A is called head and \(L_1 \wedge \ldots \wedge L_m \wedge \mathsf {ctxt}(L_{m+1}) \wedge \ldots \wedge \mathsf {ctxt}(L_{m+p})\) as well as \(\top , \bot \) and \(\mathsf {U}\), standing for true, false and unknown respectively, are called body of the corresponding clauses. A contextual program, denoted by \(\mathcal P\), is a finite set of contextual program clauses. \(\mathsf {g}\mathcal{P}\) denotes the set of all ground instances of clauses occurring in \(\mathcal{P}\). A is defined in \(\mathsf {g}\mathcal{P}\) iff \(\mathsf {g}\mathcal{P}\) contains a rule or a fact with head A. A is undefined in \(\mathsf {g}\mathcal{P}\) iff A is not defined in \(\mathsf {g}\mathcal{P}\). The set of all atoms that are undefined in \(\mathsf {g}\mathcal{P}\) is denoted by \(\mathsf {undef}(\mathcal{P})\). The definition of A in \(\mathsf {g}\mathcal{P}\) is defined as \(\mathsf {def}(A,\mathcal{P}) = \{ A \leftarrow {\textit{Body}}\mid A \leftarrow {\textit{Body}}\text { is a rule or a fact occurring in } \mathsf {g}\mathcal{P}\}\). \(\lnot A\) is assumed in \(\mathsf {g}\mathcal{P}\) iff \(\mathsf {g}\mathcal{P}\) contains a negative assumption with head A, \(\mathsf {g}\mathcal{P}\) does not contain an unknown assumption with head A, and \(\mathsf {def}(A,\mathcal{P}) = \emptyset \). We omit the word contextual when we refer to programs, if not stated otherwise.
3.2 Three-Valued Łukasiewicz Logic Extended by \(\mathsf {ctxt}\) Connective
We consider the three-valued Łukasiewicz logic together with the \(\mathsf {ctxt}\) connective, for which the corresponding truth values are \(\top \), \(\bot \) and \(\mathsf {U}\), meaning true, false and unknown, respectively. A three-valued interpretation I is a mapping from the set of logical formulas to the set of truth values \(\{ \mathbf {\top }, \bot , \mathsf {U}\}\), represented as a pair \(I~=~\langle I^\mathbf {\top },I^\bot \rangle \) of two disjoint sets of atoms: \(I^\mathbf {\top }= \{A \mid A \text { is mapped to } \mathbf {\top }\text { under } I\}\) and \(I^\bot = \{A \mid A \text { is mapped to } \bot \text { under } I \}\). Atoms which do not occur in \(I^\mathbf {\top }\cup I^\bot \) are mapped to \(\mathsf {U}\). The truth value of a given formula under I is determined according to the truth tables in Table 3. \(I(F) = \top \) means that a formula F is mapped to true under I. A three-valued model \(\mathcal{M}\) of \(\mathcal{P}\) is a three-valued interpretation such that \(\mathcal{M}(A \leftarrow {\textit{Body}}) = \mathbf {\top }\) for each \(A \leftarrow {\textit{Body}}\in \mathsf {g}\mathcal{P}\). Let \(I = \langle I^\top , I^\bot \rangle \) and \(J = \langle J^\top , J^\bot \rangle \) be two interpretations. \(I \subseteq J\) iff \(I^\top \subseteq J^\top \) and \(I^\bot \subseteq J^\bot \). I is the least model of \(\mathcal{P}\) iff for any other model J of \(\mathcal{P}\) it holds that \(I \subseteq J\).
3.3 Integrity Constraints
A set of integrity constraints \(\mathcal{IC}\) consists of clauses of the form \(\mathsf {U}\leftarrow {\textit{Body}}\), where \({\textit{Body}}\) is a conjunction of literals and \(\mathsf {U}\) denotes the unknown. Hence, an interpretation maps an integrity constraint to \(\top \) iff \({\textit{Body}}\) is either mapped to \(\mathsf {U}\) or \(\bot \). Given an interpretation I and a set of integrity constraints \(\mathcal{IC}\), I satisfies \(\mathcal{IC}\) iff all clauses in \(\mathcal{IC}\) are true under I.
3.4 Forward Reasoning: Least Fixed Point of \(\varPhi _\mathcal{P}\)
For a given \(\mathcal{P}\), consider the following transformation: 1. For each ground atom A which occurs as head of a clause in \(\mathsf {g}\mathcal{P}\), replace all clauses of the form \(A \leftarrow {\textit{Body}}_1, \ldots , A \leftarrow {\textit{Body}}_m\) occurring in \(\mathsf {g}\mathcal{P}\) by \( A \leftarrow {\textit{Body}}_1 \vee \ldots \vee {\textit{Body}}_m\). 2. Replace all occurrences of \(\leftarrow \) by \(\leftrightarrow \). The obtained ground set of equivalences is called the weak completion of \(\mathcal{P}\) or \( wc \mathcal{P}\). Consider the following semantic operator, which is due to Stenning and van Lambalgen [12]: Let \(I = \langle I^\top ,I^\bot \rangle \) be an interpretation. \(\varPhi _\mathcal{P}(I) = \langle J^\top ,J^\bot \rangle \), where

[5] showed that the weak completion of non-contextual programs always has a least model under Łukasiewicz logic, which can be obtained as the least fixed point of \(\varPhi _{\mathcal{P}}\). However, for programs with the \(\mathsf {ctxt}\) operator this property only holds if the programs do not contain cycles [2]. In this paper, let \(\mathcal{M}_\mathcal{P}\) denote the least fixed point of \(\varPhi _{\mathcal{P}}\). We define  iff \(\mathcal{M}_\mathcal{P}(F) = \top \).
iff \(\mathcal{M}_\mathcal{P}(F) = \top \).
3.5 Backward Reasoning: Explanations by Means of Abduction
An abductive framework  consists of a program \(\mathcal{P}\), a set \(\mathcal{A}\) of abducibles, a set \(\mathcal{IC}\) of integrity constraints, and the entailment relation
consists of a program \(\mathcal{P}\), a set \(\mathcal{A}\) of abducibles, a set \(\mathcal{IC}\) of integrity constraints, and the entailment relation  . The set of abducibles is \(\mathcal{A}=\{ A \leftarrow \top \mid A \in \mathsf {undef}(\mathcal{P}) \} \ \cup \ \{ A \leftarrow \bot \mid A \in \mathsf {undef}(\mathcal{P}) \hbox { and } \lnot A \hbox { is not assumed in } \mathsf {g}\mathcal{P}\}\). Let
. The set of abducibles is \(\mathcal{A}=\{ A \leftarrow \top \mid A \in \mathsf {undef}(\mathcal{P}) \} \ \cup \ \{ A \leftarrow \bot \mid A \in \mathsf {undef}(\mathcal{P}) \hbox { and } \lnot A \hbox { is not assumed in } \mathsf {g}\mathcal{P}\}\). Let  be an abductive framework and the observation \(\mathcal{O}\) a set of literals. \(\mathcal{O}\) is explainable in
be an abductive framework and the observation \(\mathcal{O}\) a set of literals. \(\mathcal{O}\) is explainable in  iff there exists an \(\mathcal{E}\subseteq \mathcal{A}\), such that
iff there exists an \(\mathcal{E}\subseteq \mathcal{A}\), such that  for all \(L \in \mathcal {O}\) and \(\mathcal {P} \cup \mathcal {E}\) satisfies \(\mathcal{IC}\). \(\mathcal {E}\) is then called explanation for \(\mathcal{O}\) given \(\mathcal{P}\) and \(\mathcal{IC}\). We restrict \(\mathcal{E}\) to be minimal, i.e. there does not exist any other explanation \(\mathcal{E}' \subseteq \mathcal{A}\) for \(\mathcal{O}\) such that \(\mathcal{E}' \subseteq \mathcal{E}\).
for all \(L \in \mathcal {O}\) and \(\mathcal {P} \cup \mathcal {E}\) satisfies \(\mathcal{IC}\). \(\mathcal {E}\) is then called explanation for \(\mathcal{O}\) given \(\mathcal{P}\) and \(\mathcal{IC}\). We restrict \(\mathcal{E}\) to be minimal, i.e. there does not exist any other explanation \(\mathcal{E}' \subseteq \mathcal{A}\) for \(\mathcal{O}\) such that \(\mathcal{E}' \subseteq \mathcal{E}\).
Among the minimal explanations, it is possible that some of them entail a certain formula F while others do not. There exist two strategies to determine whether F is a valid conclusion in such cases. F follows credulously, if it is entailed by at least one explanation. F follows skeptically, if it is entailed by all explanations. Due to previous results on modeling human reasoning [4], skeptical abduction seems to be adequate.
Here, observations, are specified as \(\mathcal {O}_\mathcal {P} = \{ A \mid A \leftarrow \top \in \mathsf {def}(A, \mathcal{P}) \}\). Usually, this set is further restricted by considering only facts that result from the application of certain principles. The idea is to find an explanation for each observation \(A \in \mathcal{O}_\mathcal{P}\) after the fact \(A \leftarrow \top \) has been removed from \(\mathsf {g}\mathcal{P}\).
3.6 Encoding of Quantified Statements
Negation by Transformation \(\varvec{(}{\mathbf {\mathsf{{transformation}}}}\varvec{).}\) The logic programs we consider do not allow heads of clauses to be negative literals. A negative conclusion \(\lnot p(X)\) is represented by introducing an auxiliary formula \(p'(X)\) together with the clause \( p(X) \leftarrow \lnot p'(X)\) and the integrity constraint \(\mathsf {U}\leftarrow p(X) \wedge p'(X)\). This is a widely used technique in Logic Programming. Applying the principle licenses introduced in Sect. 2.2, the first clause is extended to \(p(X) \leftarrow \lnot p'(X) \wedge \lnot ab_{npp}(X)\) and the assumption \( ab_{npp}(X) \leftarrow \bot \) is added.
No Derivation Through Double Negation \(\varvec{(}{\mathbf {\mathsf{{doubleNeg}}}}\varvec{).}\) A positive conclusion can be derived from double negation using two conditionals under the WCS. It appears to be the case that humans do not reason in such a way (see [7]). Hence, we block them with the help of abnormalities.
4 Quantified Statements as Logic Programs
Based on the principles and encoding aspects presented in Sects. 2 and 3.6, we encode the quantified statements into logic programs. The programs are specified using the predicates y and z and depend on the figures shown in Table 2, where yz can be replaced by ab, ba, cb, or bc. Here, all principles regarding a premise are applied. However, we will later assume different clusters of reasoners, some of which do not apply certain principles (see Sect. 5). The clauses associated with principles that are not applied are removed for such clusters.
4.1 All y Are z (Ayz)
All y are z is represented by \(\mathcal{P}_{Ayz}\), which consists of the following clauses:

As contraposition has been applied, we have to add the integrity constraint \(\mathsf {U}\leftarrow y(X) \wedge y'(X)\). We obtain \(\mathcal{M}_{\mathcal{P}_{Ayz}} = \langle \{y(o),z(o)\}, \{ab_{yz}(o)\} \rangle \). Remember that we want to construct pairs of syllogistic premises. Sometimes, if a premise of A mood is combined with a premise of E or O mood (see Sects. 4.2 and 4.4), then \(z'(X)\) appearing in the body of the fourth clause becomes the negation of z(X). Otherwise, any ground instance of \(z'(X)\) is unknown and, consequently, \(\mathsf {ctxt}(z'(X))\) is false in this case. The necessity of the fourth clause and the usage of the \(\mathsf {ctxt}\) operator is discussed in the example presented in Sect. 5.2.
4.2 No y Is z (Eyz)
No y is z is represented by \(\mathcal{P}_{Eyz}\), which consists of the following clauses:

The integrity constraints \(\mathsf {U}\leftarrow z(X) \wedge z'(X)\) and \(\mathsf {U}\leftarrow y(X) \wedge y'(X)\) must be added. Iterating \(\varPhi _{\mathcal{P}_{Eyz}}\) we obtain \(\mathcal{M}_{\mathcal{P}_{Eyz}} = \langle \big \{y(o_1), z'(o_1), z(o_2), y'(o_2)\big \},\) \(\{ab_{ynz}(o_1), ab_{nzz}(o_1), z(o_1), ab_{zny}(o_2), ab_{nyy}(o_2), y(o_2)\} \rangle \).
4.3 Some y Are z (Iyz)
Some y are z is represented by \(\mathcal{P}_{Iyz}\), which consists of the following clauses:

We obtain \(\mathcal{M}_{\mathcal{P}_{Iyz}}= \langle \{y(o_1), y(o_2), z(o_1)\}, \{ab_{yz}(o_1)\} \rangle \). One should observe that \(ab_{yz}(o_2)\) is an unknown assumption in \(\mathcal{P}_{Iyz}\) and, hence, \(\mathcal{M}_{\mathcal{P}_{Iyz}}(z(o_2)) = \mathsf {U}\).
4.4 Some y Are Not z (Oyz)
Some y are not z is represented by \(\mathcal{P}_{Oyz}\) which consists of the following clauses:

We have to add the integrity constraint \(U \leftarrow z(X) \wedge z'(X)\) and obtain \(\mathcal{M}_{\mathcal{P}_{Oyz}} = \langle \{y(o_1), y(o_2), z'(o_1)\},\{ab_{ynz}(o_1), ab_{nzz}(o_1), ab_{nzz}(o_2), z(o_1) \} \rangle \).
4.5 Entailment of Conclusions from Pairs of Syllogistic Premises
Based on the applied principles of the previous section, we specify when \(\mathcal{M}_\mathcal{P}\) entails a conclusion, where yz is to be replaced by ac or ca.
-

 iff there exists an object o such that
iff there exists an object o such that 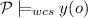 and for all objects o we find that if
and for all objects o we find that if  then
then  .
. -

 iff there exists an object \(o_1\) such that
iff there exists an object \(o_1\) such that  and for all objects \(o_1\) we find that if
and for all objects \(o_1\) we find that if 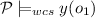 then
then  and there exists an object \(o_2\) such that
and there exists an object \(o_2\) such that  and for all objects \(o_2\) we find that if
and for all objects \(o_2\) we find that if  then
then  .
. -
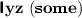
 iff there exists an object \(o_1\) such that
iff there exists an object \(o_1\) such that  and there exists an object \(o_2\) such that
and there exists an object \(o_2\) such that  and
and  and there exists an object \(o_3\) such that
and there exists an object \(o_3\) such that  and there exists an object \(o_4\) such that
and there exists an object \(o_4\) such that  and
and  .
. -

 iff there exists an object \(o_1\) such that
iff there exists an object \(o_1\) such that  and there exists an object \(o_2\) such that
and there exists an object \(o_2\) such that 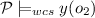 and
and  .
. -
 When no previous conclusion can be derived, no valid conclusion holds.
When no previous conclusion can be derived, no valid conclusion holds.
4.6 Accuracy of Predictions
We have nine different answer possibilities for each of the 64 pairs of syllogistic premises: Aac, Eac, Iac, Oac, Aca, Eca, Ica, Oca and NVC. For every pair of syllogistic premises, we define two lists of length nine for the predictions of the WCS and for the participants’ answers, where the first element represents Aac, the second element represents Eac, and so forth. When Aac is predicted under the WCS (or the majority’s conclusions) for a given pair of syllogistic premises, then the value of the first element of this list is a 1, otherwise it is a 0, and the same holds for the other eight elements in the list. Given

the matching percentage of this pair of syllogistic premises is then computed by \({\sum _{i=1}^{9} \textsc {comp}(i)}/{9}\).
5 Clusters and Heuristics
We understand clusters of human reasoners in terms of principles or heuristics. Each cluster is a group of humans that applies the same principles or heuristics. When identifying such clusters, e.g., among the participants in [7], the principles or heuristics used by a single cluster should lead to a significant answer for the pair of syllogistic premises in question. As the answers of all participants have been accumulated in the meta-analysis, the combined answers of all clusters should exactly correspond to the significant answers for that pair of syllogistic premises.
5.1 Basic Principles
Basic principles are assumed to be applied by all reasoners, regardless of any cluster. These are conditionals, licenses, import, and unknownGen. Note that they are not necessarily applicable to every pair of syllogistic premises: unknownGen may only be used for premises with an existential mood.
5.2 Advanced Principles and Clusters
Advanced principles are assumed by some but not all humans, making them the starting point for clusters. Advanced principles considered in this paper are converse, deliberateGen, contraposition, and searchAlt, but there may exist more. When two individuals differ in the sense that one applies such a principle and the other one does not, we assume that they belong to different clusters.
As an example, consider A O3 introduced in Sect. 1. According to the encoding described in Sect. 4, \(\mathcal{P}_{\textsf {A}\textsf {O}3,\text {basic}}\) represents the logic program for A O3, where only the basic principles are applied:

We obtain

The highlighted atoms are relevant for conclusions: NVC follows. Note that \(ab_{ab}(o_i)\) is false for all \(o_i\), \(1 \le i \le 3\). If additionally contraposition is used,

is considered that has another clause where \(ab_{ab}(X)\) is in the head. We obtain

Again, the relevant atoms are highlighted. \(\mathcal{M}_{\mathcal{P}_{\textsf {A}\textsf {O}3,\textsf {contra}}}\) entails the conclusion Oca: As \(c(o_2)\) is true, \(b'(o_2)\) is true, therefore \(\mathsf {ctxt}(b'(o_2))\) is true. This in turn makes \(ab_{ab}(o_2)\) true, and accordingly \(b(o_2)\) has to be false. But then, \(a'(o_2)\) can be derived true, which finally makes \(a(o_2)\) false.
One should observe that \(b'(o_1)\) is unknown in \(\mathcal{M}_{\mathcal{P}_{\textsf {A}\textsf {O}3,\textsf {contra}}}\). Hence, \(\mathsf {ctxt}(b'(o_1))\) is false and, consequently, \(ab_{ab}(o_1)\) is false as well. Together with \(a(o_1)\) being true we obtain that \(b(o_1)\) is true. The latter is needed to correctly implement the first premise, all a are b, in A O3. Without the \(\mathsf {ctxt}\) operator, \(b'(o_1)\) would be unknown and, consequently \(ab_{ab}(o_1)\) as well as \(b(o_1)\) would be unknown as well violating the premise all a are b.
Assuming two clusters of people whose reasoning process differs in the application of the contraposition principle, we unite the conclusions predicted for the clusters and obtain \(\{ \textsf {O}\text {ca}, \textsf {NVC}\}\). These are exactly the significant answers reported in [7].
In order to represent the principles leading to a conclusion, multinomial processing trees (MPTs) [11] are used. They have been suggested for modeling cognitive theories because they represent cognitive processes as probabilistic procedures, thus being able to predict multiple answers and even their quantitative distribution [10]. We set the latent states (inner nodes) of the MPTs to the decisions whether to use certain principles and put the corresponding conclusions in the leaves. The MPT for A O3 based on the clustering described above is presented in Fig. 1. The parameter \(p_\textsf {contraposition}\) models the probability that an individual applies the contraposition principle and, therefore, belongs to the corresponding cluster. It can be trained from experimental data with algorithms like expectation-maximization [6]. Note that the MPT in Fig. 1 is not complete in the sense that it cannot predict all possible conclusions for A O3. This issue is addressed below.
5.3 Heuristic Strategies
Some theories suggest that some humans do not reason at all to solve syllogistic reasoning tasks, but rely on heuristics such as the atmosphere bias [14] or the matching bias [13]. Such heuristics are simple rules that state what conclusions are likely depending on certain features of the premises, e.g., mood or figure. Some of the participants’ answers presented in [7], that are given by a small amount of people (less then 5%), but also some significant ones, are not (yet) explainable by the WCS. A plausible explanation for that is that these people simply guess or use one of the heuristics mentioned below (educated guess).
A generative approach to model this behavior can be based on MPTs. The MPT for a random guess can lead to all nine conclusions. MPTs for a particular heuristic strategy only take into account the valid conclusions under the corresponding theory. For the atmosphere bias, universal and affirmative conclusions are excluded when one of the premises is existential or negative, respectively. In the case of identical moods, the conclusion must have this mood as well. For the matching bias, the following order from the most to the least conservative quantifier is defined on moods:
A conclusion may not be answered if it is less conservative than one of the premises with respect to that order. We have also observed biased conclusions in the data of [7] that may be explained by the following heuristic strategy: F or almost all pairs of syllogistic premises with Fig. 1, Xac is answered, while the answer Xca is not given at all, where X is the least conservative mood from the premises that is still allowed under the matching strategy (O is preferred over I).
As an alternative to generating the answers given by a cluster of guessers using MPTs, the following inverse process can be considered: predictions of the WCS that are not in accordance with a particular heuristic strategy are not given by a cluster using that strategy. In the filtering approach, these conclusions are suppressed in the predictions. If no conclusion remains, NVC is answered instead. As it is likely that some participants do not use logic [13], such clusters must be modeled under the WCS by using the generative or the filtering approach. As a consequence, MPTs can construct a prediction for all answer possibilities.
5.4 A Clustering Approach
Based on the principles and heuristic strategies described above, the participants of [7] have been partitioned into three reasoning clusters and two clusters applying heuristic strategies:
-
1.
Basic principles, searchAlt, and converse for I.
-
2.
Basic principles, converse for I and deliberateGen.
-
3.
Basic principles, converse for I, E, and contraposition for A.
-
4.
Matching strategy.
-
5.
Biased conclusions in figure 1.
Abduction was only used in one cluster because of the computational effort it requires. Although it would be interesting to model this principle for different clusters, the impact would be very small. This is because converse is the only advanced principle that adds existential imports, which we currently consider as atoms for observations. According to the results of [8], abduction has the same results independent of whether only the converse I mood or both the converse I and E mood are used. The matching strategy was implemented using the filtering approach. The biased conclusions in figure 1 heuristics was implemented using the generative approach such that its prediction overwrites the answers of other clusters, except NVC.
5.5 Evaluation
We evaluate the predictions of the WCS based on the clustering approach described in Sect. 5.4. For that, we combine the answers of all clusters and compared them with both the data of humans and the predictions of other cognitive theories presented in [7]. In that study, the results of six psychological experiments on syllogistic reasoning were aggregated and compared with twelve well-known cognitive theories. In Table 4, it can be seen that the WCS predicts the same answers for A O3 as the majority of humans, but some other theories fail to do so. For the overall evaluation, the accuracy is computed as described in Sect. 4.6. Here the WCS clearly stands out against the other theories, but to be fair, we must also admit that we compare a relatively new theory to the best theories of 2012. The WCS predicts the participants’ answers in [7] correctly for 32 out of the 64 pairs of syllogistic premises. For 20 cases there is one incorrect prediction, for 11 cases there are two and for one case there are three mismatches. The overall match between the predictions of the WCS and the answers of the participants is 92%.
6 Implementation
The goal of our implementation is to automate the process of evaluating a certain clustering. This is crucial, because as stated above, the number of possible clusterings grows exponentially with the number of principles. We want to be able to evaluate new candidates for an optimal clustering as fast as possible.
We have developed a modular, declarative implementation, which consists of two parts: An implementation of the \(\varPhi _{\mathcal{P}}\) operator to compute the least fixed point of a given program \(\mathcal{P}\), and a framework that generates logic programs from an abstract representation of principles and evaluate the entailed conclusions.
6.1 Computing the Least Fixed Point of \(\varPhi _\mathcal{P}\)
The least fixed point of \(\varPhi _\mathcal{P}\) is computed in Prolog. The implementation receives a program \(\mathcal {P}\) – written in Prolog – as input and processes it in two phases. The output is an interpretation \(\langle I^\top , I^\bot \rangle \) of \(\mathsf {wc}\,\mathcal {P}\) represented as two lists corresponding to \(I^\top \) and \(I^\bot \). The input program \(\mathcal {P}\) is first grounded to obtain \(\mathsf {g}\mathcal{P}\) and, secondly, computes the least fixed point of \(\varPhi _\mathcal{P}\) starting with the empty interpretation \(\langle \emptyset , \emptyset \rangle \). Recall that \(\varPhi _\mathcal{P}\) operates directly on \(\mathsf {g}\mathcal{P}\). The context operator is implemented such that contextual logic programs can be handled. However, there is a problem: if a contextual logic program \(\mathcal {P}\) contains a cycle, then the least fixed point of \(\varPhi _\mathcal {P}\) may not exist. Consider the following quantified statements:
Assume that additionally to the basic principles we apply for each quantified statement the advanced principles converse, deliberateGen, and contraposition. The corresponding program consists of the following clauses:

Consider the highlighted atoms: Note the cycle \(b'> c> c'> b> ab_{ab} > b'\) where \(A > B\) if A is an atom in the head of a rule and B is an atom that occurs in the body of that rule. As \(b'\) is an argument of the context operator and is part of the cycle, this program does not admit a least fixed point. When modeling clusters, we must ensure that the logic program resulting from the applied principles do not contain such cycles. This is guaranteed for the clusters given in Sect. 5.4.
6.2 Computing the Predictions for a Cluster of Reasoners
The evaluation of a cluster is written in Haskell. A run consists of four phases:
-
1.
Generate program \(\mathcal{P}\) of the pair of syllogistic premises using the principles.
-
2.
Call the Prolog implementation to compute the least fixed point of \(\varPhi _\mathcal{P}\).
-
3.
Extract the conclusions entailed by the least fixed point of \(\varPhi _\mathcal{P}\).
-
4.
Compare the conclusions with the participants’ answers and output score.
The Haskell program contains definitions of datatypes for all entities occurring in the programs, i.e., truth values, atoms, literals, and clauses. These entities are built recursively on each other and have functions for conversion into Prolog. Principles are implemented as functions that return their corresponding clause representation. The source code of the unknownGen principle is as follows:

where the first line states that the principle is applied to negative moods (I and O) and the second line states that the clause has the form \(y(prf\mathrm {ug}) \leftarrow \top \), where prf is an identifier for objects of the clause. Using this abstraction, clusters are written as lists of ‘principle functions’ and are thus valid Haskell source code by themselves. As an example, consider the definition of the basic cluster which uses the basic principles and the converse principle for mood I:

Here,  is defined as list of principles (those we called basic in Sect. 5.1). Of course, one consequence is that the user of our implementation has to be familiar with Haskell. However, there are two main advantages of using Haskell source code as a representation. Firstly, many principles are part of a certain subset of the pair of syllogistic premises (e.g., the unknown generalization principle is used for all premises with an existential mood). These connections can be modeled precisely and without redundancy in source code. This can be seen in the example above, where
is defined as list of principles (those we called basic in Sect. 5.1). Of course, one consequence is that the user of our implementation has to be familiar with Haskell. However, there are two main advantages of using Haskell source code as a representation. Firstly, many principles are part of a certain subset of the pair of syllogistic premises (e.g., the unknown generalization principle is used for all premises with an existential mood). These connections can be modeled precisely and without redundancy in source code. This can be seen in the example above, where  is implemented as a function that takes a principle as argument and returns the corresponding principle for the converse premise. Secondly, because Haskell is a compiled language, the representation of the pair of syllogistic premises itself is compiled. Therefore, a representation is automatically checked and the program does not crash due to an error, which would not be the case if e.g., a string representation was used.
is implemented as a function that takes a principle as argument and returns the corresponding principle for the converse premise. Secondly, because Haskell is a compiled language, the representation of the pair of syllogistic premises itself is compiled. Therefore, a representation is automatically checked and the program does not crash due to an error, which would not be the case if e.g., a string representation was used.
The Prolog representation of the program results from a function converting sets of clauses to a string and is written into a file. Then, the Prolog implementation of the previous program is called to compute the least fixed point of \(\varPhi _\mathcal{P}\), which is again written to a file. After completion that file is parsed and the conclusions are extracted with respect to the definitions given in Sect. 4.5. Our heuristic filters—implemented as post-processing functions—are applied to these conclusions. This process is done for all 64 pairs where the conclusions are compared with the participants’ answers and the score of the cluster is computed.
Until now, we have only described the evaluation of a single cluster, although a clustering consists of the combined answers of all clusters. For this purpose, a list of clusters is specified, where the program computes the predictions for each cluster, combines them, and compares the results with the participants’ answers.
7 Conclusions
We have successfully extended the approach in [1, 8] by introducing two new principles and by applying a clustering approach to model individual differences in human reasoning. This takes into account that some people may not reason at all, but guess or apply heuristic strategies. The clustering presented in Sect. 5.4 is currently the best one but possibly not the optimal one. However, due to the combinatorial explosion,Footnote 2 it is difficult to find the global optimum. Furthermore, programs based on certain principles considered for some moods, might not have a least fixed point, as they contain cycles with respect to the \(\mathsf {ctxt}\) operator. This must be taken into account when selecting the principles for a clustering. Finally, we have applied multinomial processing trees to model that different principles lead to different conclusions. This information is lost if the data containing the predictions for all clusters is aggregated. If we would have more insight about the patterns participants opted for, we could model single pair of syllogistic premises by multinomial process trees instead of fitting them to the overall results.
Future work might allow us to identify and understand why humans within a cluster come to certain conclusions. Accordingly, if it is known which principles they apply, it should be possible to predict their answers.
Notes
- 1.
Under WCS, the negative assumption will become \(A \leftrightarrow \bot \) and, hence, A has to be false. This can, however, be overwritten by other rules and facts (defeating the assumption).
- 2.
For n principles, there are up to \(2^n\) possible clusters. Additionally, it is unknown if the current set of principles is already complete.
References
Costa, A., Dietz Saldanha, E.-A., Hölldobler, S.: Monadic reasoning using weak completion semantics. In: Hölldobler, S., Malikov, A., Wernhard, C. (eds.) Proceedings of the Young Scientist’s Second International Workshop on Trends in Information Processing (YSIP2) 2017, pp. 45–54. CEUR Workshop Proceedings (2017)
Dietz Saldanha, E.-A., Hölldobler, S., Pereira, L.M.: Contextual reasoning: usually birds can abductively fly. In: Balduccini, M., Janhunen, T. (eds.) LPNMR 2017. LNCS (LNAI), vol. 10377, pp. 64–77. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-61660-5_8
Grice, H.P.: Logic and conversation. In: Cole, P., Morgan, J.L. (eds.) Syntax and Semantics, vol. 3. Academic Press (1975)
Hölldobler, S.: Weak completion semantics and its applications in human reasoning. In: Furbach, U., Schon, C. (eds.) Proceedings of the Workshop on Bridging the Gap between Human and Automated Reasoning on the 25th International Conference on Automated Deduction, CEUR Workshop Proceedings, vol. 1412, pp. 2–16. CEUR-WS.org. (2015)
Hölldobler, S., Kencana Ramli, C.D.P.: Logic programs under three-valued Łukasiewicz semantics. In: Hill, P.M., Warren, D.S. (eds.) ICLP 2009. LNCS, vol. 5649, pp. 464–478. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-02846-5_37
Hu, X., Batchelder, W.H.: The statistical analysis of general processing tree models with the em algorithm. Psychometrika 59(1), 21–47 (1994)
Khemlani, S., Johnson-Laird, P.N.: Theories of the syllogism: a meta-analysis. Psychol. Bull. 138, 427–457 (2012)
Costa, A., Dietz Saldanha, E.-A., Hölldobler, S., Ragni, M.: A computational logic approach to human syllogistic reasoning. In: Gunzelmann, G., Howes, A., Tenbrink, T., Davelaar, E.J. (eds.) Proceedings of the 39th Annual Conference of the Cognitive Science Society, Austin, TX, 2017, pp. 883–888. Cognitive Science Society (2017)
Ragni, M., Dietz, E.-A., Kola, I., Hölldobler, S.: Two-valued logic is not sufficient to model human reasoning, but three-valued logic is: a formal analysis. In: Schon, C., Furbach, U. (eds.) Proceedings of the Workshop on Bridging the Gap between Human and Automated Reasoning co-located with 25th International Joint Conference on Artificial Intelligence IJCAI, CEUR Workshop Proceedings, vol. 1651, pp. 61–73. CEUR-WS.org. (2016)
Ragni, M., Singmann, H., Steinlein, E.-M.: Theory comparison for generalized quantifiers. In: CogSci (2014)
Riefer, D.M., Batchelder, W.H.: Multinomial modeling and the measurement of cognitive processes. Psychol. Rev. 95(3), 318–339 (1988)
Stenning, K., van Lambalgen, M.: Human Reasoning and Cognitive Science. A Bradford Book. MIT Press, Cambridge (2008)
Wetherick, N.E., Gilhooly, K.J.: ‘Atmosphere’, matching, and logic in syllogistic reasoning. Curr. Psychol. 14(3), 169–178 (1995)
Woodworth, R.S., Sells, S.B.: An atmosphere effect in formal syllogistic reasoning. J. Exper. Psychol. 18(4), 451 (1935)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this paper
Cite this paper
Dietz Saldanha, EA., Hölldobler, S., Mörbitz, R. (2018). The Syllogistic Reasoning Task: Reasoning Principles and Heuristic Strategies in Modeling Human Clusters. In: Seipel, D., Hanus, M., Abreu, S. (eds) Declarative Programming and Knowledge Management. WFLP WLP INAP 2017 2017 2017. Lecture Notes in Computer Science(), vol 10997. Springer, Cham. https://doi.org/10.1007/978-3-030-00801-7_10
Download citation
DOI: https://doi.org/10.1007/978-3-030-00801-7_10
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-00800-0
Online ISBN: 978-3-030-00801-7
eBook Packages: Computer ScienceComputer Science (R0)






 iff there exists an object o such that
iff there exists an object o such that 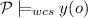 and for all objects o we find that if
and for all objects o we find that if  then
then  .
.
 iff there exists an object
iff there exists an object  and for all objects
and for all objects 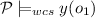 then
then  and there exists an object
and there exists an object  and for all objects
and for all objects  then
then  .
.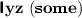
 iff there exists an object
iff there exists an object  and there exists an object
and there exists an object  and
and  and there exists an object
and there exists an object  and there exists an object
and there exists an object  and
and  .
.
 iff there exists an object
iff there exists an object  and there exists an object
and there exists an object 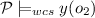 and
and  .
. When no previous conclusion can be derived, no valid conclusion holds.
When no previous conclusion can be derived, no valid conclusion holds.