1 Introduction

Collective behaviors of animals and other agents can be described by general principles based on a few typical classes despite their variety and richness of details [25]. At large there are two methods of modeling. Microscopic models abstract individual behaviors but represent properties of each member of the animal group, such as position, direction, and internal states. Examples are swarm models from physics, such as the Vicsek model and similar ones [3, 15, 24], and models focusing on the agents’ energy reserve, their random walks, and more complex behaviors (e.g., taxis behaviors), such as so-called Brownian agents [12, 21, 22]. Macroscopic models abstract away individual agents and reduce the state space to only a few variables, such as densities or sizes of groups that are in a certain state (cf. population models). Examples are from biology [13, 17, 19, 26], physics and mathematics [1, 3, 4], and swarm robotics [5, 16, 18, 20]. In this context, systems showing collective motion are represented to a large extent by only two distributions: a spatial and a directional distribution. Basically these two distributions are equivalent in their significance for effective collective motion because both physical proximity and coordination in velocities are necessary [25]. However, the directional distribution may have an assumed higher significance in the literature, especially in one-dimensional systems [2, 25, 26].

Examples for microscopic models are models of self-propelled particles (SPP) that define each particle’s motion influenced by neighboring particles [2, 26]. Examples for macroscopic models are Fokker–Planck models that describe global features of collective behaviors, such as velocity distributions and spatial distributions [9, 11, 26]. The model of Yates et al. [26], in particular, models the velocity distribution of particles based on a Fokker–Planck equation with estimated diffusion and drift coefficients based on experimental data and simulation data, whereas “the drift coefficient represents the mean rate of change of the average velocity” [26]. It turns out that such drift coefficients are time-variant and seem to depend on another state variable of the system following an exponential function (\(1-\exp (-t)\)) [6, 10, 23]. We identify a relevant graph-theoretic feature of the graph that is induced by the robots’ positions and their perceivable neighborhoods. This main feature is the size of the largest connected component of this graph, which is the largest subgraph in which all pairs of nodes are connected by paths. Time-invariant features are always of interest in mathematical modeling and so are they here, too. These time-invariant features may be used to formulate concise and precise models of collective motion.

2 Microscopic and Macroscopic Models

We introduce two models: a microscopic model of self-propelled particles (SPP) and a macroscopic model of swarm populations.

2.1 Microscopic Model: SPP

We define a time-discrete microscopic model as a 1-d SPP model of N particles moving on a circle of circumference \(U=1\) without units (i.e., periodic boundary conditions). The number of particles N can also be interpreted as particle density \(\rho =N/U=N\). Our model is similar to the model defined by Czirók and Vicsek [3, 10] but different in a few aspects. First, the allowed velocities are discrete. Second, particles explicitly decide to switch their direction of motion based on majority decisions. Third, noise is implemented as spontaneous switching of direction. A particle i has coordinate \(x_i\) and discrete, dimensionless velocity \(u_i\in \{-1,1\}\). The dynamics are defined by

$$\begin{aligned} x_i(t+1)= & {} x_i(t) + v_0u_i(t),\end{aligned}$$
(1)
$$\begin{aligned} u_i(t+1)= & {} {\left\{ \begin{array}{ll} G(L_i(t), R_i(t)), &{} \text {with probability }P_d\\ -u_i(t), &{} \text {with probability }P_n\\ u_i(t), &{} \text {else} \end{array}\right. }, \end{aligned}$$
(2)

where \(L_i\) is the number of neighboring particles located on the interval \([x_i-\varDelta r, x_i+\varDelta r]\) with velocities \(u_j=+1\), that is, neighbors moving counterclockwise or ‘left’. Similarly, \(R_i\) are neighboring particles with velocities \(u_j=-1\), that is, neighbors moving clockwise or ‘right’. The perception range of a particle is \(\varDelta r=0.002\) and a particle’s nominal velocity is \(v_0=0.001\) (see Table 1 for used parameters). \(P_d=0.1\) is the particle’s probability of reconsidering its direction of movement (i.e., on average an agent reconsiders its direction of motion every ten time steps). \(P_n=0.015\) is the particle’s probability of inverting its direction of movement spontaneously, hence, it implements noise. With G we implement a local majority decision

$$\begin{aligned} G(L,R) = {\left\{ \begin{array}{ll} +1, &{} L>R\\ -1, &{} R>L\\ u_r, &{} R=L \end{array}\right. }, \end{aligned}$$
(3)

with \(u_r\in \{-1,+1\}\) is a random tie breaker choosing \(-1\) or \(+1\) with equal probabilities.

Table 1. Parameter settings used in simulations.
Full size table

The initial condition is a random uniform distribution for both, the particles’ coordinates \(x_i\in [0, U)\) and their velocities \(u_i\in \{-1,+1\}\). Note that despite the particles’ discrete velocities \(u_i\) the system is different from cellular automata because the particles’ (initial) positions \(x_i\) are continuous. As an effect, a particle’s neighbors are distributed continuously over its whole neighborhood interval \([x_i-\varDelta r, x_i+\varDelta r]\) but propagate through it in discrete steps.

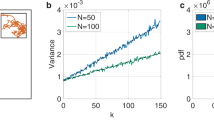
Our primary interest is the particle distribution among the two states \(u_i=\pm 1\), that is, we observe the fraction \(s_t\in [0,1]\) of particles in state \(u_i=+1\) (without loss of generality) over time t. With the settings used in this paper, s fluctuates over the whole interval \(s\in [0,1]\) for all time but with a bimodal distribution that is established after a transient (see Fig. 1a). We interpret the system states that correspond to the two peaks of this bimodal distribution as the aligned states although the particles are not completely aligned (\(s<1\) and \(s>0\)). The observed bimodal distribution is expected for effective collective motion and was reported before (e.g., see [10, 26]).

Fig. 1.
figure 1

Distributions of swarm fraction moving left \(s_t\) and swarm fraction in largest connected component \(c_t\) obtained numerically from the SPP model, \(N=42\), \(5\times 10^5\) sample simulation runs.

Full size image

2.2 Largest Component

In the following we apply a graph-theoretic interpretation of the particles’ coordinates in the SPP model. The particles are interpreted as nodes of an undirected graph. There is an edge (i, j) between particle i and j if \(d(x_i, x_j)<\varDelta r\), whereas \(d(x_i, x_j)\) gives the distance between the particles. Hence, each agent is connected by an edge to each of its neighbors, who also determine the particle’s local majority decision based on G(L, R). The largest connected component (or short: largest component) of a graph is the largest set of nodes M for which it is true that any pair of nodes out of M is connected by a path, which is a sequence of nodes that have an edge from one node to the next in the sequence. For any state of the SPP model at any time the largest component \(M_t\) can be calculated. In the following we are interested in the swarm fraction that is in the largest component \(c_t=|M_t|/N\) (|M| is the number of nodes in M). We can measure the size of the largest component as the swarm fraction \(c_t\in [0,1]\) that is part of the largest component at time step t (see Fig. 1b). The size of the largest component increases over time because aligned motion typically triggers an aggregation behavior as a side-effect [8]. Later in the simulation runs, the size of the largest component saturates at values of \(c\approx 0.8\). An interesting observation is that the swarm is aligned early at \(t\approx 500\), while the distribution of largest components stays time-variant until \(t>1000\). Hence, aligning particles is a quick process while forming a big largest component is a slow process for the tested parameter set. The used simulation software and some experiment data is available onlineFootnote 1.

2.3 Macroscopic Model

A reasonable approach is to macroscopically model trajectories \(s_t\) as a stochastic process

$$\begin{aligned} s_{t+1} = s_t + \varDelta s(s_t) + \xi _t, \end{aligned}$$
(4)

for a drift term \(\varDelta s(s_t)\) and a diffusion term \(\xi _t\) with mean \(\langle \xi \rangle =0\). This is similar to approaches based on Langevin equations and the corresponding Fokker–Planck equations [5, 18, 26]. In the following we focus on the drift term \(\varDelta s(s)\) only. Within the SPP model we can measure the mean \(\langle \varDelta s(s)\rangle \) based on averages over many realizations of the stochastic process due to

$$\begin{aligned} \langle s_{t+1}-s_t\rangle = \langle \varDelta s(s_t)+\xi _t\rangle =\langle \varDelta s(s_t)\rangle . \end{aligned}$$
(5)

The main purpose of this macroscopic model here is only to indicate the meaning of the drift coefficient \(\varDelta s(s_t)\). To keep such a macroscopic model simple, we prefer time-invariant parameters and features. In particular, the drift coefficient \(\varDelta s(s_t)\) should preferably be time-invariant. The drift term is the main driver of the system on the global level and determines whether a collective decision-making system is effective. Finding and using time-invariant coefficients could help to formulate a concise and precise model of collective motion.

3 Results

3.1 Time-Invariant Drift Coefficients

Measurements of \(\langle \varDelta s(s_t)\rangle \) reveal that it is time-variant during a transient (see Fig. 2a). The time-variance of the drift coefficient \(\langle \varDelta s(s_t)\rangle \) is known and was reported before [23]. In [6, 7] empirical evidence is given that \(\langle s_t\rangle \) follows an exponential function (symmetry is exploited here and values \(s<0.5\) are mapped by \(s'=1-s\)). This is also what is measured for the size of the largest component \(\langle c_t\rangle \) in the SPP model as shown in Fig. 2c (cf. Fig. 1b).

We find that measurements of the drift coefficient \(\varDelta s(s)\) are time-invariant if we measure them with respect to the size of the current largest component, that is, by defining a two-dimensional function \(\varDelta s(s, c)\) that takes the size of the largest component as an argument, too. Measurements are shown in Fig. 3. These are measurements at nine different times every 200 time steps and different sizes of the observed largest component. The noise of these measurements is because the \(5\times 10^5\) samples are now distributed over all different bins for the largest component sizes and certain component sizes are infrequently observed at certain times. Besides a few outliers the measurements indicate time-invariant behavior of \(\varDelta s(s, c)\), especially in comparison to Fig. 2a. Also see Fig. 2b showing the drift coefficient for \(\varDelta s(s, c=0.5)\), which indicates features hardly observed when measuring only \(\varDelta s(s)\). \(\varDelta s(s, c=0.5)\) has five zeros with three stable fixed points: \(s^*_1\approx 0.17\), \(s^*_2=0.5\), and \(s^*_3\approx 0.83\).

This approach of using a two-dimensional function \(\varDelta s(s, c)\) has two main advantages. First, a model of collective motion, for example similar to the Fokker–Planck model of Yates et al. [26], based on time-invariant functions could also give valid predictions for the transient if it is combined with a model for the increase of the largest component \(c_t\) over time, which can be simple (cf. Fig. 2c). Second, measurements of \(\varDelta s(s, c)\) also reveal otherwise hidden system properties that we discuss in the following.

For certain N and c, \(\varDelta s(s, c)\) has not only three but five zeros (see Fig. 2b) generating a stable fixed point at \(s=0.5\). Hence, the system may travel through state space, that drives the system away from a collective decision towards indecisiveness. This may happen not only early in the transient, as seen in Fig. 2a, but possibly also even later in the transient whenever the largest component has a relatively small size of about \(c\approx 0.5\).

Fig. 2.
figure 2

Drift coefficients and growth of synchronized group and largest component measured in the SPP model.

Full size image
Fig. 3.
figure 3

Time-invariant \(\langle \varDelta s(s, c)\rangle \) for \(N=70\) and \(t\in \{200,400,600,800,1000,\) 1200, 1400, 1600,  \(1800\}\), measured in the SPP model.

Full size image

Measured time-invariant \(\varDelta s(s, c)\) based on the sizes of largest components \(c\in \{0.29,0.48,0.83\}\) for \(N=38\) are shown in Fig. 4a. For a big largest component of \(c=0.83\) the system is sensitive to fluctuations around \(s=0.5\) because they are reinforced with positive feedback (i.e., on average a small majority grows). In contrast the system diminishes fluctuations for \(c=0.29\). This is probably because fluctuations affect almost only the connected component in which they occur, hence, effects in components due to fluctuations are almost independent from each other. With a largest component of \(c<0.5\), even the largest component is only a minority and consequently has no global effect. This is also seen in Figs. 4b and c, which give values of \(\varDelta s(s, c)\) for most measurable largest component sizes c as a map for bigger densities (\(N=42\) and \(N=70\)). Note that the tested swarm sizes of \(N\in \{38,42,70\}\) are chosen arbitrarily and represent different swarm densities (cf. [14]). Higher densities turn out to show more complexity in their system dynamics but also reduce the observed occurrence of small largest connected components (e.g., \(c<0.4\) for \(N=70\)). Figures 4b and c clearly indicate the underlying complex system dynamics of the collective motion process in contrast to mere time-averaged or steady-state measurements of \(\varDelta s(s)\). The stable fixed point at \(s=0.5\) for \(c<0.5\) is seen as well as the small interval around \(c\approx 0.5\) for which we have three stable fixed points (more clearly for \(N=70\) in panel c). For \(c>0.5\) the two remaining stable fixed points get closer to \(s=0\) and \(s=1\) respectively with increasing largest component size.

Fig. 4.
figure 4

Drift coefficient \(\langle \varDelta s(s, c)\rangle \) depending on the largest component for \(N\in \{38,42,70\}\).

Full size image

The unexpected complexity of the underlying system dynamics is prominent in Fig. 4c (\(N=70\)). It reminds one of so-called bifurcation scenarios from non-linear dynamics. For \(0.36\leqslant c\leqslant 0.41\) the system has four stable fixed points, which then collapse for \(c\approx 0.41\). For \(0.44\leqslant c\leqslant 0.54\) the system has three stable fixed points, which then collapse into a situation with four stable fixed points again for \(0.55\leqslant c\leqslant 0.59\). Starting from \(c\approx 0.6\) the system has increasingly more positive feedback and only two stable fixed points.

3.2 On the Effectivity of Collective Motion

We are interested in the necessary conditions for effective synchronization in collective motion, which we define by the existence of two stable fixed points at \(s=0.5\pm x\) for \(x>0\).

Fig. 5.
figure 5

Bifurcation diagrams obtained using the largest-component-based drift coefficients \(\varDelta s(s, c)\) measured in the SPP model.

Full size image

Based on the measurements of \(\varDelta s(s, c)\) we determine bifurcation diagrams depending on the largest component and density (similar to what is shown in Figs. 4b and c). In Fig. 5a we give the bifurcation diagram for a given density \(\rho =N=42\). Two stable fixed points are found for \(c\ge 0.54\).

We can investigate the influence of particle density \(\rho \), if we specify which largest component size we associate with each considered density (otherwise we would need to investigate a 3-d system). For this purpose we measure the largest component size in the SPP model in the steady state for a given density (data not shown). Following these measurements, we then define a simple ad-hoc model of the observed effective largest component size by \(c^*(\rho )=1/\rho ( -20.7/(1+\exp (-0.1\rho +0.9))+1.05\rho +6.2)\). We find a critical density of \(\rho _\text {crit}=28\) (Fig. 5b) for the selected parameters. For too sparse densities (\(\rho <\rho _\text {crit}\)) no big enough largest component forms that could trigger global alignment. Once the critical density \(\rho _\text {crit}\) is reached, appropriate largest components form and the collective motion is effective.

Hence, we observe bifurcations in two dimensions (largest component and density) and consequently two conditions have to be met for a collective decision to emerge. A minimum density is needed and at least the majority of the swarm has to be positioned within the largest component. These two conditions are distinguished by their priorities. With too low density, no stable largest cluster of size \(c>0.5\) forms. However, once this critical density is reached, a stable largest cluster of size \(c>0.5\) forms. Moreover, the clearness of the decision (s close to zero or one respectively) increases with increasing largest component c (see also Figs. 4b and c) and with increasing density \(\rho \). In addition, the bifurcation diagram for the borderline situation \(c=0.5\) (Fig. 5c) shows that even above the critical density \(\rho _\text {crit}=28\) but with a relatively small largest component the fixed point at \(s=0.5\) stays stable (this is observed on an interval of about \(c\in [0.43,0.56]\)) and interestingly two new unstable fixed points emerge which shows the particularity of the \(c=0.5\)-situations. Hence, we summarize that a critical density is necessary to observe a collective decision but during the transient, situations may emerge that stabilize the indecisive state \(s=0.5\) temporarily.

4 Conclusion

Based on a simple 1-d SPP model, we have investigated collective motion. Our focus was on measurements of the drift coefficient \(\varDelta s(s)\), which is time-variant but turns out to be time-invariant once we measure it relative to the size of the largest connected component. This feature of time-invariance may be used to formulate concise and precise models of collective motion. As discussed, a simple temporal model of the increase in size of the largest component can be formulated (exponential function) and can then be used to create a macroscopic model. This macroscopic model then exclusively uses time-invariant coefficients and allows to model the transient behavior of collective motion systems.

Note that the spatial distribution of particles seems to have more impact on the dynamics of collective decisions as modeled in this paper than the current state of majority stake s. Previously reported Fokker–Planck models [11, 18, 26] based on time-averaged drift coefficients may give good predictions for steady states but are of limited use for investigations of the temporal evolution of collective decisions and may also be of limited use to understand the underlying dynamics.

The drift coefficient of the velocity distribution based on sizes of the largest components is constant over time. Consequently the system dynamics of collective motion is completely described by positive feedback depending on largest components, the dynamics of largest components, and additional noise features (diffusion coefficient).

Future work includes investigating the generalization from 1-d space to 2-d, which could bring a qualitative change in the observed dynamics. Models and findings as reported here can help in swarm engineering to provoke advantageous system states, such as big largest connected components, and to increase performance of an engineered collective system. A key challenge for modeling is trying to answer the question of how the system behaviors that were measured here (e.g., drift coefficient depending on fraction of swarm within largest connected component, Fig. 4) could be predicted by an appropriate model.