Keywords

1 Introduction

Regenerative medicine is the application of treatments developed to replace tissues damaged by injury or disease. This technique creates living, functional tissues to repair or replace tissue function lost due to age, disease, damage, or congenital defects. These treatments involve the use of biochemical techniques to induce tissue regeneration directly at the site of damage or the use of transplantation techniques using stem cells or differentiated cells, either alone or as part of a bio artificial tissue [1, 2].

Although regenerative medicine is a large field and includes several topics as stem cell therapy (SCT) and synthetic organs, here we will focus primarily on tissue engineering (TE). In particular one of the most promising research areas within tissue engineering is bone substitute biomaterials (BSB) [3, 4]: complex and unique tissues, such as the bone, cartilage, and tendons that act as the internal support of the body. Since the long-term function of three-dimensional (3D) bone substitute biomaterials (BSB) is strongly dependent on adequate vascularization after grafting, it is crucial to develop imaging methods capable of providing detailed three-dimensional information on tissue structure.

However, full comprehension of the bone vascularization pathways is still hindered by limitations in the use of imaging techniques to monitor these processes. Nowadays, new advanced imaging modes are available. Upputuri et al. [5] recently classified the imaging approaches into three groups: nonoptical techniques (X-ray, magnetic resonance, ultrasound, and positron emission imaging), optical techniques (optical coherence, fluorescence, multiphoton, and laser speckle imaging), and hybrid techniques (photoacoustic imaging). In this regard, high-resolution microtomography (microCT) is able to provide much higher-resolution (∼1 μm) imaging, than ultrasound (∼30 μm) and MRI (∼100 μm), allowing the 3D visualization and quantification of microvasculature and bone tissues.

Within X-rays techniques, we will focus on X-ray phase-contrast tomography (XRPC) that overcomes limitations of conventional absorption-based X-ray imaging using alternative X-ray contrast mechanisms. In fact, conventional 2D imaging (histology, electron microscopy, etc.) produces an incomplete spatial coverage of the sample that leads to possible data misinterpretation, while standard absorption 3D computed tomographic imaging reaches insufficient resolution and contrast in soft tissue visualization. XRPCT enables the 3D imaging of biomaterial and soft tissue structures, as well as vascularization, with spatial resolution ranging from microns to tens of nanometers, without the use of contrast agents and without destructive sample preparation.

XRPCT is very promising in regenerative medicine field, due to the large penetration depth, excellent spatial and contrast resolution and simultaneous visualization of calcified and soft tissue. In particular, XRPC allows monitoring the regeneration of damaged tissues being able to discriminate between newly formed bone and connective tissue.

2 Physical Principles of X-Ray Phase-Contrast Imaging

The potentiality of X-ray phase-contrast tomography for different biomedical applications has been proved in numerous studies [6,7,8,9,10,11,12,13,14,15]. Since X-ray phase-contrast imaging (XPCI) exploits wave coherence, requirements on the X-ray source are necessary, despite some specific cases discussed in Chap. 15. In particular, highly coherent X-ray radiation from bright synchrotron sources offers great opportunities for many cutting-edge medical applications including regenerative medicine, in particular for bone regenerative engineering [2, 16,17,18]. Synchrotron-based XPCI is particularly attractive for biomedicine applications since it provides high-resolution, high signal-to-noise ratio in the image at shorter acquisition time with respect to other conventional imaging techniques. To introduce the principle of XPCI, let us start from the optical properties of an object, which can be described by

$$ n=1-\delta + i\beta, $$
(4.1)

where δ is the refractive index decrement responsible for the phase shift of X-ray wave propagating through the object and β is the extinction coefficient related with X-ray attenuation in the sample. The coefficient β is proportional to the linear attenuation coefficient μ:

$$ \mu =\frac{4\pi }{\lambda}\beta, $$
(4.2)

where λ is the wavelength of X-ray radiation.

In particular, conventional radiography is based on absorption contrast, i.e., the imaginary part of the refraction index, and it is obtained from X-rays attenuation through the object. Phase-contrast technique exploits the real part of the complex refractive index.

Radiography and tomography for biomedical application require high X-ray penetration depth in the (thick) sample, and typically hard X-rays with energies E ~ 10–100 keV are used for image formation. Due to the weak interaction of hard X-rays with matter the refractive index is close to one (|n−1| << 1). The values of both indexes δ and β are several orders of magnitude below unity (|n−1| ≈ 10−6). At energies far from absorption edges δ and β can be approximated as

$$ \delta \sim \frac{\rho_{\mathrm{a}}Z}{E^2} $$
(4.3)
$$ \beta \sim \frac{\rho_{\mathrm{a}}{Z}^4}{E^4}, $$
(4.4)

where ρa is the atomic number density of a material, Z is the atomic number, and E is the X-ray photons energy [19, 20].Taking into account Eq. (4.3) and Eq. (4.4), the phase-attenuation ratio δ/β is given by

$$ \frac{\delta }{\beta}\sim \frac{E^2}{Z^3} $$
(4.5)

In the Hard X-ray Region, the ratio of δ/β is in the range of 102–103 (Fig. 4.1) for different elements, typically contained in biological tissues. Therefore, at short wavelengths phase contrast is a predominant effect over absorption contrast. In particular, the advantage of phase contrast becomes more evident for low-absorbing materials (low atomic number Z) such as soft tissue in biological samples.

Fig. 4.1
figure 1

The phase-attenuation ratio δ/β as a function of energy. The ratio δ/β for carbon (the main constituent of biological tissue) increases by a factor of 1000 in the hard X-rays region. The term δ is related to the phase variation and the term β is responsible for X-ray attenuation

Full size image

According to Eqs. (4.3 and 4.4), phase contrast decreases slower than absorption contrast as X-ray energy increases; thus, the absorbed dose and therefore potential damage of tissues can be decreased by using higher X-ray energies [11].

3 Image Formation

Layout of image formation in a XPCI setup includes (1) X-ray radiation source and X-ray optics for shaping the beam, (2) rotation and translation stages for the sample (the sample is shifted and rotated during tomographic scan), (3) X-ray phase-contrast optical equipment (except for free-space propagation mode), and (4) detector [21].

3.1 X-Ray Source

X-ray beam from synchrotron radiation facility is used to investigate object internal structure. In synchrotron facilities, the incident beam is formed by incoherent superposition of waves emitted by synchrotron electrons bunch in the storage ring [22]. The transverse coherence of the generated X-ray radiation increases with X-rays propagation distance. Due to the small bunch size and long source-sample distance, synchrotron X-ray source has a high degree of transverse coherence. The emitted radiation has a specific energy spectrum; crystal monochromator allows to select a very narrow band of the spectrum (∆E/E ≈ 10−4) providing high degree of longitudinal coherence when it is required.

3.2 Object and Transmission Function

X-ray synchrotron radiation, approximated by a plane wave, illuminates the sample and passes through the object producing a distortion of the wave front. At the contact plane, the object is characterized by a transmission function (TF) defined as the E/E0, the input/output complex amplitudes ratio. We assume a linear relationship between the incident wavefield (input signal E0) and the transmitted wavefield (output signal E) [23]:

$$ E= TF\ {E}_0 $$
(4.6)

The transmission function TF depends on both the sample structure and the incident field. A variety of different processes participating in interaction between X-rays and sample significantly complicates the rigorous definition of TF, and some approximations are usually applied to simplify the description of X-ray transmission through the object. Commonly used approximations in phase-contrast imaging are weak object approximation, slowly varying phase approximation, and homogeneous object approximation [24, 25]. Due to the weak interaction of X-rays with matter, it is assumed that each element of the object interacts only with the incident wave and not with the refracted one, and diffraction phenomena within the scattering volume are neglected. In this case the object can be considered thin enough to treat the properties of a three-dimensional sample with a two-dimensional transmission function. In the so-called projection or thin object approximation TF is considered as a simple object projection into the contact plane [26]:

$$ TF\left(x,y\right)=A\left(x,y\right){e}^{i\phi \left(x,y\right)} $$
(4.7)

The amplitude modulation A and the phase shift ϕ are given as the integrals along the optic axis:

$$ A\left(x,y\right)={e}^{-\frac{1}{2}{\int}_{\mathrm{object}}\mu \left(x,y,z\right) dz}={e}^{-{\mu}_z} $$
(4.8)
$$ \varphi \left(x,y\right)=-\frac{2\pi }{\lambda }{\int}_{\mathrm{object}}\delta \left(x,y,z\right) dz, $$
(4.9)

where μz is the projection of the attenuation coefficient μ on the contact plane (x, y, z=0) divided by two.

Week object approximation is valid when both attenuation and phase shift in the object are small:

$$ {\mu}_z\ll 1,\kern0.5em \phi \ll 1 $$
(4.10)

For weakly interacting X-rays, the exponential function in Eq. (4.7) can be rewritten as a first term of the Taylor series expansion [27], leading to the next simple expression for TF:

$$ TF\approx 1-{\mu}_z+ i\phi $$
(4.11)

The assumption of slowly varying phase is given by the following expression:

$$ \left|\phi \left(\boldsymbol{r}+\lambda z{\boldsymbol{f}}_m\right)-\phi \left(\boldsymbol{r}\right)\right|\ll 1, $$
(4.12)

where r=(x,y) and f =(p, q) are space coordinates at the contact plane and the transverse Fourier space coordinates reciprocal to r, respectively; | fm=(pm, qm)| is the highest frequency of the object to be included in the computation, λ is wavelength. This approximation partially relaxes the strict weak object condition of Eq. (4.10). In particular Eq. (4.12) is used to solve the propagation problem for a pure phase object with zero absorption (μ = 0) and for a homogenous object with non-negligible absorption (μ ≠ 0) and δ ∝ β [28].

Homogeneous object approximation supposes that the object contains only one material and air. In the object with non-negligible absorption (μ ≠ 0), the coefficients β and δ are proportional δ ∝ β [28]. In this case the projected thickness of the object can be found from a single-distance image. More details on this issue will be discussed in Sect. 4.1.2.

4 Phase-Contrast Imaging Techniques

Since detector can only measure the intensity, the phase shift induced by the object in the X-ray beam cannot be directly revealed and therefore the phase information is lost. In order to detect the phase, different experimental approaches have been developed in order to transform the phase modulation into intensity modulation, directly detectable by the detector.

In the past years, a variety of techniques have been developed to detect phase contrast and to enhance the visibility of small and/or low contrast details in the sample image.

Phase-contrast imaging techniques can be grouped into four main categories: in-line phase-contrast imaging (ILPC), diffraction-enhanced imaging (DEI), analyzer-based imaging (ABI), and grating-based differential phase-contrast imaging (GBI) (see Fig. 4.2) [29,30,31,32,33].

Fig. 4.2
figure 2

Schematic representation of phase-contrast imaging experimental setup (a) analyzer-based imaging (ABI), (b) grating-based differential phase-contrast imaging (GBI), (c) in-line phase-contrast imaging (ILPC), (d) diffraction-enhanced imaging (DEI)

Full size image

4.1 Free Space Propagation Imaging

X-ray in-line phase-contrast imaging (ILPC) or free space propagation imaging (XPI) exploits the propagation of a coherent X-ray beam to generate image contrast [33]. The experimental setup of X-ray in-line phase-contrast imaging (XPCI) is similar to conventional radiography but with larger sample-detector distance. The layout of this method includes the in-line arrangement of an X-ray source, the sample, and an X-ray detector and does not need any additional optical element. The simple experimental setup and high stability make this technique very attractive for biomedical applications. Because of its simplicity and relatively low sensitivity to misalignments, it is suitable to be combined with tomography techniques.

4.1.1 Direct Problem: Contrast Formation

Some conventional approaches for analytical and numerical solutions of direct and inverse imaging problems in single-distance XPCI are here described.The direct problem of wave propagation aims to define the wavefield at a distance z = D, given the value of the field at the contact plane (z = 0). The sample induces both amplitude and phase variations in the transmitted field, but at the contact plane, only absorption contrast can be detected. The propagation of the wave in free space transforms phase modulation into detectable intensity variations. The image obtained is called defocused image: in fact, it is recorded out of focus due to the propagation from the sample to the detector. The defocusing distance D expresses the amount of defocusing in the image [34]:

$$ D=\frac{z_1{z}_2}{z_1+{z}_2}, $$
(4.13)

where z1 and z2 are defined in Fig. 4.3.

Fig. 4.3
figure 3

Schematic representation of the setup used to record the defocused image. The incoming plane wave is deformed by the modulation of the index of refraction inside the sample. The interference pattern is acquired by the detector

Full size image

In synchrotron facilities the distance z1 of the sample from the source is much larger than the propagation distance z2, and thus the defocusing distance Eq. (4.13) simply corresponds to the sample-to-detector distance:

$$ D\approx {z}_2, $$
(4.14)

The analytical description of wavefield evolution in space is based on the solution of Maxwell’s equations or electromagnetic wave equation in vacuum [35]. Due to the weak interaction of X-rays with matter, the typical refraction angles for hard X-rays interacting with the sample are very small. Therefore, X-ray photons of highly coherent low divergent synchrotron beam, even after scattering in the sample, are still propagating at small angle with respect to the z optical axis. This allows most theoretical analysis to adopt the paraxial approximation, which assumes \( {k}_x^2+{k}_y^2\ll {k}^2 \), where k is the wave vector number. Wave equation in the paraxial approximation for monochromatic wave has the name of homogeneous paraxial Helmholtz equation, and it is written as

$$ i\frac{\partial }{dz}E\left(x,y,z\right)-\frac{1}{2k}{\nabla}_{\perp}^2E\left(x,y,z\right)=0 $$
(4.15)

The solution of Eq. (4.15) is given by the Fresnel–Kirchhoff integral (Fresnel diffraction integral):

$$ E\left(x,y,z=D\right)=-\frac{ik\exp (ikD)}{2\pi D}{\iint}_{-\infty}^{\infty }E\left({x}^{\prime },{y}^{\prime },z=0\right)\exp \left[\frac{ik}{2D}\Big({\left(x-{x}^{\prime}\right)}^2+{\left(y-{y}^{\prime}\right)}^2\right]{dx}^{\prime }{dy}^{\prime } $$
(4.16)

Diffraction integral reveals that evolution of the diffraction pattern during the wave propagation is characterized with the length scale:

$$ {D}_{\mathrm{F}}=\frac{d^2}{\lambda }, $$
(4.17)

where d is the typical transverse linear size of the object or of the object details we want to detect.

Four different diffraction regimes can be distinguished by the parameter DF. The diffraction pattern varies with the distance D as it is shown in Fig. 4.4.

Fig. 4.4
figure 4

Schematic representation of the diffraction regions according to the distance D from the object

Full size image
  1. 1.

    At the contact plane z = D = 0 only absorbing features of the object are detectable. This is the case of classic radiography and absorption-based tomography.

  2. 2.

    At near-field region λD ≪ d2 locally object irregularities at any internal boundaries and interfaces of the sample (where the phase variation in high) form interference fringes highlighting the edges. Morphological details of the sample with low spatial frequencies are not yet subject to diffraction. In this region the diffraction regime is called edge enhancement because edges produce high contrast. The image of the sample at the detector still resembles the direct image of the real object (weak defocusing).

  3. 3.

    In the intermediate diffraction region (propagation distance D ≈ DF), the recorded image shows more evident diffraction characteristics. The image of the real sample is almost lost, and distinct interference patterns are produced. This is so-called holographic regime that can be divided into near and far holographic regime for distances D ≈ DF and D > DF, respectively.

  4. 4.

    Far field is reached increasing propagation distance up to D ≫ DF. In far field region the interference fringes cannot be associated with a specific sample edge, and the resemblance between the original and the detected image is completely lost. The intensity recorded by the detector is defined by Fraunhofer diffraction law.

The wave propagation problem can be solved in different way. The straightforward approach is the direct analytical or/and numerical solution of Eq. (4.15) or to diffraction integral Eq. (4.16). Fourier transform method (FTM) or angular spectrum method is another conventional method that has been extensively applied in the field of XPCI [27]. Another way to specify the attenuation and the phase shift in wavefield propagation relies on the transport-of-intensity equation as the solution of Eq. (4.15) [36].

We will discuss two methods commonly used in XPI: FTM-based approach and transport-of-intensity equation-based approach.

The simplest solution of Helmholtz equation Eq. (4.15) is the plane wave solution. Because of the linearity of Maxwell’s equations in vacuum, the general solution of the wave equation in free space can be obtained by linear superposition of elementary plane waves solution. This is the basis for so-called Fourier transform method (FTM) or angular spectrum method for the Helmholtz equation. The Fresnel–Kirchhoff integral Eq. (4.16) in FTM approach is given by equation [27]:

$$ E\left(x,y,z=D\right)=\exp (ikD){F}^{-1}\left[P\cdot F\left[{E}_0\left(x,y,z=0\right)\right]\right], $$
(4.18)

where F and F−1 are the 2D direct and inverse Fourier transforms, respectively, the term \( P=\exp \left[-\frac{iD\left({k}_x^2+{k}_y^2\right)}{2k}\right] \) is the Fresnel propagator. Since the propagation distance D is included in the numerator of the phase factor, the Fresnel FTM approach is more suitable for small distances D ≲ DF. For weakly interacting objects (see Eq. (4.11)) the wavefield at a distance D can be written as [27]:

$$ E\approx {F}^{-1}\left[\Delta \left(\boldsymbol{f}\right)-F\left[{\mu}_z\right]\cos \chi\ F\left[\phi \right]\ \sin \chi \right] $$
(4.19)

where Δ(f) is the delta function. According to Eq. (4.19), the amplitude and phase of the transmitted wavefield are filtered by the terms sinχ and cosχ in Fourier space. The functions sin χ and cos χ are called the phase-contrast transmission function and the amplitude contrast transmission function, respectively, (PCTF and ACTF). The terms sin χ and cos χ are shown in Fig. 4.5 as a functions of radial spatial frequency u = (χ/π)1/2 = (λD)1/2q. Equation (4.19) and Fig. 4.5 show that phase and absorption contrast are mixed in the image. They have different evolution with wavefield propagation. In the contact plane when u = 0, phase contrast in the image is near to zero, but the absorption image has maximum contrast.

Fig. 4.5
figure 5

Real (dashed) and imaginary (solid line) parts of the Fresnel transfer function as a function of the reduced spatial frequency

Full size image

As it follows from Eq. (4.19) for a pure phase object (mz = 0) in the near-field diffraction regime u= (λD)1/2 /d ≪ 1, the wavefield intensity at the detector plane is proportional to the second derivative of the phase function [37]:

$$ I\left(x,y,z=D\right)\approx 1-\frac{D}{k}{\nabla}_{\perp}^2\Phi \left(x,y\right) $$
(4.20)

Therefore high spatial frequencies originated from the edges of the object vastly contribute to the interference pattern formation. The object interference fringes delineate the edges and any internal boundary of the sample.

Increasing spatial frequency, phase, and amplitude CTFs oscillate. The functions reach the near holographic regime at u≈ (λDF)1/2 q and the far holographic regime at u> (λDF)1/2 q, respectively. As CTF oscillate around zero value, only spatial frequencies far from the zeros of the oscillating functions contribute to the image formation.

Transport-of-intensity equation (TIE) [28, 38, 39] is another common XPCI approach to describe image contrast formation in free space propagation. Writing the homogeneous paraxial Helmholtz equation (Eq. 4.15) in terms of intensity and phase of the propagating wave and taking the imaginary part of the final equation, one receives the transport-of-intensity equation:

$$ {\nabla}_{\perp}\left(I\left({r}_{\perp },z\right){\nabla}_{\perp}\left({r}_{\perp },z\right)\right)=-\frac{2\pi }{\lambda }{\partial}_zI\left({r}_{\perp },z\right) $$
(4.21)

TIE describes the intensity evolution of a paraxial monochromatic scalar electromagnetic wave on propagation, and it relates the phase and the derivative of the image intensity along propagation direction. TIE has a unique solution and does not require the phase unwrapping.

In general case TIE-based approaches in XPCI assume a short propagation distance D<DF to linearize the propagation model and finally to solve the inverse phase problem. In case of pure phase object, TIE gives the same expression for the intensity as in FTM approach (see Eq. (4.20)).

Non-negligible absorption in the sample requires addition assumptions for the sample properties such as sample material homogeneity or the weak absorption approximation. This problem will be discussed in the next Sect. 4.1.2.

4.1.2 Inverse Problem: Phase Retrieval

Propagation-based imaging combined with computed tomography enables access to a sample’s three-dimensional (3D) micro- or nanostructure. However, phase contrast, as it is discussed in Sect. 4.1.1, is not directly related with amplitude and phase of the object transmission function. The phase retrieval step must be performed to recover the sample refraction index.

The phase retrieval problem consists in the object phase estimation from intensity measurements accounting a priori information about the object. Different approaches are used to solve the phase retrieval problem [25, 40]. At distances close to the near-field regime, Fresnel and TIE-based methods are commonly used for phase shift reconstruction of objects at micro and sub micro-level resolution [28, 38–39, 41,42,43]. In Fresnel diffraction regime, holotomography method for multiple images at different propagation distances proved to be efficient for nanoscale resolution imaging [44]. In far-field zone the iterative image Fourier transform-based reconstruction algorithms are broadly applied to create high-resolution diffraction images [45].

Phase-contrast imaging in near field is particularly attractive for different medical application due to its ability to provide with acceptable resolution the richness of information about internal features and fine detail in the sample without a strong restriction on the sample dimension, as it takes place for other imaging techniques. In addition to that, this imaging technique has relative simple experimental setup and enables non-iterative implementation of single-image phase retrieval procedure.

In general, image at the detector contains both absorption and phase-contrast contribution; therefore information about δ and β is mixed. The different evolution of absorption and phase contrast in space allows to untangle these two parameters, but, generally, at least two intensity measurements at different distances or different energies are required [11]. The high radiation dose is a critical issue for biological samples since tomographic scan requires several successive sample acquisitions, while it is rotating. Multiple distance/energy measurements of the object additionally increase X-ray exposure time, and therefore the dose delivered to the sample. Thus, single-distance/energy image acquisition for each tomographic projection is preferable.

Phase reconstruction algorithms for single-distance image acquisition usually require a priori information about the object to solve the inverse problem and to ensure the unique solution for the problem.

The most common approximation about object material properties are:

  1. 1.

    Material has no absorption, or the absorption is constant [39].

  2. 2.

    Absorption and phase coefficients β and δ are proportional to each other, then a homogeneous object composed of the single material can be characterized by ratio δ/β, and the projected thickness of the sample can be found from single-distance image [28, 41–42].

Since often biological samples produce both phase and absorption contrast, the absorption contribution in the material cannot be neglected. Phase retrieval at homogeneous object approximation developed by D. Paganin [28] does not impose a strong restriction on the absorption phenomenon in the object. Moreover, it was shown that the algorithm can be applied for multi-material objects, for objects with homogeneous elemental composition, but varying density and for objects in which absorption is negligibly weak. The algorithm has been successfully applied in large number of experiments, and it gained wide recognition due to its stability with respect to noise, computational speed, and simplicity of implementation [46,47,48,49,50]. Paganin’s algorithm derivation starts with the transport intensity equation Eq. (4.21). The method assumes that an optically thin object is composed of a single material. For plane wave illumination the intensity and phase of the wavefield at the object plane is given by the projection approximation. Application of TIE in near field allows to find the reconstructed phase map of the object from the equation:

$$ \phi \left(x,y\right)=\frac{1}{2}\ln \left\{{\mathcal{F}}^{-1}\left(\frac{\mathcal{F}\left[\frac{I\left(x,y\right)}{I_0\left(x,y\right)}\right]}{\frac{\beta }{\delta }+\left[\frac{\lambda D}{4\pi}\right]\left({p}^2+{q}^2\right)}\right)\right\} $$
(4.22)

where I/I0 is the ratio between the measured intensity and the reference beam intensity, at distance z = D, F and F−1 are the 2D forward and inverse Fourier transforms, p and q are the Fourier coordinates, and D is the object–detector distance.

The Paganin’s algorithm retrieves the phase information at the contact plane from two-dimensional phase radiograph images at the detector (called projections). Application of the phase retrieval algorithm to all radiographs taken at different illumination angles of the object during tomographic scan gives a set of projected images at the contact plane, with 2D phase information. These images are combined to provide 3D internal structure of the object with appropriate tomographic reconstruction method. The most commonly used tomographic reconstruction algorithm is Filtered Back-projection (FBP) method. Different alternative non-iterative and iterative algorithms have been proposed for tomographic reconstruction. This topic is well studied in CT, and a review on this topic can be find elsewhere [51].

5 Imaging Techniques in Regenerative Medicine

Regenerative medicine holds great promise for the treatment of a multitude of diseases for which there is no cure and that present many complications. Besides replacing what is malfunctioning, the aim of regenerative medicine is to provide the elements required for in vivo repair. It allows to devise replacements that seamlessly integrate with the living body and to stimulate and support the body’s intrinsic capacities to heal itself.

Periodic monitoring of a regenerating tissue as it develops is one of the key steps as well as challenges. Clinical imaging is indispensable for characterizing damaged tissue, for measuring the efficacy of the treatment, and for monitoring adverse reactions [1]. Moreover clinical imaging is able to differentiate pathological and regenerative responses to the therapy. A growing emphasis is being placed on noninvasive in vivo imaging techniques to address concerns and limitations with traditional histological methods that are time-consuming, painful to the patients, and expensive in preclinical studies [52].

Among all the applications of regenerative engineering, we will focus on bone engineering because a deeper comprehension of bone formation process is at the basis of tissue engineering and regenerative medicine developments.

5.1 Bone Regenerative Engineering

Bone engineering aims to achieve functional recovery of damaged tissues by providing specific cell populations, alone or incorporated in biomaterial scaffolds, that enhance the body’s intrinsic healing capacity [1]. The bone is a natural composite of approximately 70% hydroxyapatite together with 30% collagen fibers in a strong, three-dimensional structure.

The traditional bone engineering (BE) approach is often described as a winning combination of cells, supportive material (scaffold), and growth factors (stem cells). Stem cells are required to establish a bridge between living tissues and scaffold materials. They have the potential to differentiate into every type of cell and tissue in the body and hold promise in the treatment of cardiovascular, neural, and connective tissue diseases. Scaffolds instead provide physical and chemical support, while damaged tissue is being regenerated [52].

Among the standard clinical imaging technologies and their function within regenerative medicine, phase-contrast tomography (PCT) is the most promising 3D imaging technique in bone tissue engineering [3], providing morphological and anatomical details for in vivo imaging.

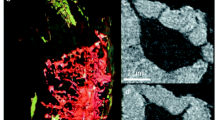
The implementation of X-ray microtomography in phase-contrast mode (XRPCT) enables the investigation of the soft connective tissues, which are invisible to the absorption contrast while are readily observed in phase contrast. Thanks to high-resolution XRPCT it is possible to obtain an exhaustive identification of the different tissues participating to the bone regeneration process, in particular collagen and mineral materials. The high spatial resolution achieved by X-ray scanning techniques allows to monitor the bone formation at the first-formed mineral deposit at the organic–mineral interface within a porous scaffold. The role of collagen matrix in the organic–mineral transition is a crucial issue for this process (Fig. 4.6).

Fig. 4.6
figure 6

Progressive deposition of hydroxyapatite crystals on collagen fibers matrix. The new-bone strats to form at the scaffold-pore interface and proceed toward the pore center where we can investigate the early steps of biomineralization process. The insets on the right corresponds to enlargements of the corresponding region marked with different colors in the image

Full size image

In fact the calcification process consists in the progressive deposition of hydroxyapatite crystals on collagen fibers [3]. Another XRPCT application in bone regenerative engineering is represented by the investigation of 3D distribution of both vessels and collagen matrix [4]. Thanks to the high quality of the images is possible to investigate the smallest micro-capillary structure without invasive contrast agent and without aggressive sample preparation.

6 Conclusion: Future Prospective

X-ray phase-contrast X-ray imaging (XPCI) is an innovative imaging technique that holds great promise for a wide range of nowadays advancing biomedical researches including bone regenerative engineering. When classical absorption does not provide sufficient contrast or demonstrates limited sensitivity, it shows great potentiality. In particularly, visualization of weakly absorbing tissue of biomedical samples or/and samples with small variations in the specimen’s density or composition [6].

Due to its unique ability XPCI allows to monitor the bone formation and identify the different tissues participating to the bone regeneration process, in particular collagen and mineral materials. Moreover it allows investigation of 3D distribution of both vessels and collagen matrix.

The ideal bone-graft substitute is biocompatible, biodegradable, osteoinductive and structurally similar to the bone. Within these parameters, a growing number of bone graft alternatives have been implemented. The strategic success lies on the delicate balance of native tissue properties addressed in a tissue substitute and its complete integration in vivo. In this sense, developing of advanced imaging techniques allows to monitor of bone regeneration processes in vivo is a crucial step in regenerative medicine.