Analysis of a Road/Tramway Intersection by the ORIS Tool

Abstract

Intelligent Transportation Systems for urban mobility aim at the grand objective of reducing environmental impact and minimize urban congestion, also integrating different mobility modes and solutions. However, the different transportation modalities may end in a conflict due to physical constraints concerned with the urban structure itself: an example is the case of intersection between a public road and a tramway right-of-way, where traffic lights priority given to trams may trigger road congestion, while an intense car traffic can impact on trams’ performance. These situations can be anticipated and avoided by accurately modeling and analyzing the possible congestion events. Typically, modeling tools provide simulation facilities, by which various scenarios can be played to understand the response of the intersection to different traffic loads. While supporting early verification of design choices, simulation encounters difficulties in the evaluation of rare events. Only modeling techniques and tools that support the analysis of the complete space of possible scenarios are able to find out such rare events. In this work, we present an analytical approach to model and evaluate a critical intersection for the Florence tramway, where frequent traffic blocks used to happen. Specifically, we exploit the ORIS tool to evaluate the probability of a traffic block, leveraging regenerative transient analysis based on the method of stochastic state classes to analyze a model of the intersection specified through Stochastic Time Petri Nets (STPNs). The reported experience shows that the frequency of tram rides impacts on the road congestion, and hence compensating measures (such as sychronizing the passage of trams in opposite directions on the road crossing) should be considered.

1 Introduction

By the year 2030, urban mobility will have changed due to sociodemographic evolution, urbanization, increase of the energy costs, implementation of environmental regulations, and further diffusion of Information and Communication Technology (ICT) applications. The demand for public and collective modes of transport will increase considerably. Part of the answer will come from the public transport that will evolve as an integrated combination of buses, cars, metros, tramways and trains [1, 13]. In general, right-of-way (ROW) is the defining characteristic of public transportation modes and we can list three ROW types:

• 1. Exclusive: Transit vehicles operate on fully separated and physically protected ROW. Tunnels, elevated structures, or at-grade tracks are such examples. This ROW type offers very high capacity, speed, reliability and safety. All heavy rail transit systems, like the Metrorail of the Washington Metropolitan Area Transit Authority, belong to this category.

• 2. Semi-Exclusive: Transit ways are longitudinally separated from other traffic, such as private vehicles and pedestrians. Light rail transit (LRT) systems, like the Florence tramway in Italy, are mostly built according to this ROW type.

• 3. Fully-Shared: Transit vehicles share ROW with other traffic, for examples buses, taxi and cars. This ROW type requires the least infrastructure investment, but operations are relatively unreliable due to roadway congestion.

Exclusive ROW needs major investment, thus often semi-exclusive or fully-shared modes are chosen. The drawback of this choice is that the different transportation modalities may end in a conflict due to physical constraints concerned with the urban structure itself. For example, this is the case of an intersection between a public road and a tramway right-of-way, where traffic lights priority given to trams may trigger road congestion, while an intense car traffic can impact on trams’ performance. These situations can be anticipated and avoided by accurately modeling and analyzing the possible congestion events. Typically, modeling tools provide simulation facilities, by which various scenarios can be played to understand the response of the intersection to different traffic loads. Simulation techniques are used to support early verification of design choices, but can analyze a limited, yet high, number of different scenarios, and encounter difficulties in the evaluation of rare events. Only modeling techniques and tools that support the analysis of the complete space of possible scenarios are able to find out such rare events [4, 7].

In this work, we present an analytical approach to model and evaluate a critical intersection for the Florence tramway, where frequent traffic blocks used to happen. This work was funded by Fondazione Cassa di Risparmio di Firenze, with the kind help of GEST¹, the company running the Florence tramway, in providing important data on which to base the study.

Fig. 1.

Map of tram route from Villa Costanza (Scandicci) to Alamanni-Stazione (Santa Maria Novella station). The route is 7720 m long with 14 tram stops.

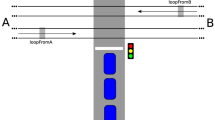
Figure 1 shows the route of line 1, which has been put in service in 2010 and links Santa Maria Novella central station to Scandicci (Florence suburbs). This line has overall good performance, with trams running regularly from the end of the line in Scandicci to almost the other end in the city center, but there is a consistent source of delay just a few meters short of the last scheduled stop, near Santa Maria Novella train station [10]. The root cause for these issues is the Diacceto-Alamanni intersection, where both via Iacopo da Diacceto, a street with dedicated tracks for tramways, and via Luigi Alamanni, a street for private transport, head to Santa Maria Novella train station.². An aerial view of this intersection is shown in Fig. 2. The darker stripe that crosses the tracks represents the (unidirectional) private traffic flow from Alamanni street that is the source of the analyzed conflict.

Fig. 2.

Aerial view of the Diacceto-Alamanni intersection.

Taking this intersection as a case study, we exploit the ORIS tool to evaluate the probability of a traffic block, leveraging regenerative transient analysis based on the method of stochastic state classes to analyze a model of the intersection specified by Stochastic Time Petri Nets (STPNs). Note that ORIS supports the analysis of models with multiple concurrent temporal parameters associated with a general (i.e., non-exponential) distribution. In particular, the model of the Diacceto Alamanni intersection includes timers associated with a deterministic value (e.g., tram interleaving period), a uniform distribution (e.g., tram delay time), and an exponential distribution (e.g., private vehicles arrival rate). The reported experience shows that the frequency of tram rides impacts on the road congestion, and hence compensating measures (e.g., sychronizing the passage of trams in opposite directions on the road crossing) should be considered.

The remainder of the paper is structured as follows. Section 2 summarises related works. Section 3 provides a short introduction to STPNs, the method of stochastic state classes, and the ORIS tool. Section 4 presents the realized model and Sect. 5 the obtained results. Finally, Sect. 6 concludes the paper.

2 Related Works

Earliest research on integrated control for traffic management at network level can be traced back to the 1970 s. The first railway timetables were planned based on the experience and knowledge of dispatchers in resolving train conflicts [17]. This manual scheduling practice proved its low efficiency with the increase of traffic congestion and exacerbated train delays.

An integrated policy for priority signals at intersections is required, given that trams operate in a semi-exclusive ROW environment. In the literature, we can find two different streams of studies: the first aiming at optimizing tram schedules without considering their effects on other traffic flows; the second aiming at manipulating the tram schedule so that trams always clear the intersection during green phases, thus reducing influences on other traffic flows. In [27], the tradeoffs between tram travel times and roadway traffic delays are explored. Literature counts several works applying different simulation techniques. Microscopic models, i.e., models in which each vehicle is modeled by itself as a particle, can be divided according to the representation of road structure in greater detail. In the continuous road model group, a base structure of road space is modeled as a continuous one dimensional (1D) link. The behavior of car agents is often implemented by applying car-following theories [26, 28, 35]. In the cell-type road model group, road space is discretized by homogeneous cells in which the behavior of car agents is expressed using transition rules such as cellular automata [19, 29]. In a queuing model group, road networks are modeled as queuing networks [2, 15]. Most commercial microscopic traffic simulators employ the continuous road model. In addition, several researchers have proposed simulation frameworks for mixed traffic of two or more models. For example, Yang et al. [32] proposed a framework for pedestrian road crossing behavior in Chinese cities in which they determined the criterion used by pedestrians to decide whether to start crossing a road after considering vehicle flows. Meanwhile, Zeng et al. [34] modeled pedestrian-vehicles interactions at crosswalks in order to minimize pedestrian-vehicle collisions.

Dobler and Lämmel [12] integrated multi-modal simulation modules to the existing framework of MATSim, a large scale traffic simulation framework based on the queuing model [8]. Their integration approach was based on locally replacing simple queue structures with continuous 2D space at sections with higher traffic flows. The behavior rules of agents in the 2D space are based on the social force model (SFM). Krajzewicz et al. [20] introduced pedestrian and bicycle agent models into SUMO, which is a widely used traffic simulator belonging to the continuous road model group [21]. Finally Fujii et al. [14] introduced an agent-based framework for mixed-traffic of cars, pedestrians and trams by using the simulator MATES [33]. To our knowledge, there is no work that leverages analytic, non simulative, techniques for the analysis of traffic models.

3 Background

In this section, we provide some background on STPNs (Sect. 3.1), the method of stochastic state classes (Sect. 3.2), and the ORIS tool (Sect. 3.3).

3.1 Stochastic Time Petri Nets

An STPN is a tuple $\langle P, T, A^-, A^+, A^{\cdot }, m_0, F, W, E, U\rangle$ where: P is the set of places; T is the set of transitions; $A^- \subseteq P \times T$, $A^+ \subseteq T \times P$ and $A^{\cdot } \subseteq P \times T$ are the sets of precondition, postcondition, and inhibitor arcs, respectively: $m_0: P \rightarrow \mathbb {N}$ is the initial marking; $F:T~\rightarrow ~{[0,1]^{[EFT_{t},LFT_{t}]}}$ associates each transition t with a Cumulative Distribution Function (CDF) $F(t):[EFT_{t}, LFT_{t}] \rightarrow [0,1]$, where $EFT_{t} \in \mathbb {Q}_{\ge 0}$ and $LFT_{t} \in \mathbb {Q}_{\ge 0} \cup \{ \infty \}$ are the earliest and latest firing time, respectively; $W: T \rightarrow {\mathbb R}_{> 0}$ associates each transition with a weight; E and U associate each transition t with an enabling function $E(t): \mathbb {N}^P \rightarrow \{true,false\}$ and an update function $U(t): \mathbb {N}^P \rightarrow \mathbb {N}^P$, which associate each marking with a boolean value and a new marking, respectively.

A place p is an input, output, or inhibitor place for a transition t if $\langle p,t \rangle \in A^-$, $\langle t,p\rangle \in A^+$, and $\langle p,t \rangle \in A^{\cdot }$, respectively. A transition t is immediate (IMM) if $EFT_{t}=LFT_{t}=0$ and timed otherwise; a timed transition t is exponential (EXP) if $F_{t}(x)=1-e^{-\lambda x}$ over $[0,\infty ]$ with $\lambda \in \mathbb {R}_{> 0}$, and general (GEN) otherwise; a general transition t is deterministic (DET) if $EFT_{t} = LFT_{t}>0$ and distributed otherwise; for each distributed transition t, we assume that $F_{t}$ is the integral function of a Probability Density Function (PDF) $f_{t}$, i.e., $F_{t}(x) = \int _0^x f_{t}(y) dy$. IMM, EXP, GEN, and DET transitions are represented by thick white, thick gray, thick black, or thin black bars, respectively.

The state of an STPN is a pair $\langle m, \tau \rangle$, where m is a marking and $\tau : T \rightarrow {\mathbb R_{\ge 0}}$ associates each transition with a time-to-fire. A transition is enabled by a marking if each of its input places contains at least one token, none of its inhibitor places contains any token, and its enabling function evaluates to true; an enabled transition t is firable in a state if its time-to-fire is equal to zero. The next transition t to fire in a state $s=\langle m, \tau \rangle$ is selected among the set of firable transitions $T_{\mathrm {f},s}$ with probability $W(t) / \sum _{t_i \in T_{\mathrm {f},s}}W(t_i)$. When t fires, s is replaced with $s' = \langle m', \tau ' \rangle$, where:

• $m'$ is derived from m by: removing a token from each input place of t, which yields an intermediate marking $m_{\mathrm {tmp}}$; adding a token to each output place of t, which yields a second intermediate marking $m'_{\mathrm {tmp}}$; and, applying the update function U(t) to $m'_{\mathrm {tmp}}$;

• $\tau '$ is derived from $\tau$ by: (i) reducing the time-to-fire of each persistent transition (i.e., enabled by m, $m_\mathrm {tmp}$ and $m'$) by the time elapsed in s; (ii) sampling the time-to-fire of each newly-enabled transition $t_n$ (i.e., enabled by $m'$ but not by $m_\mathrm {tmp}$) according to $F_{t_n}$; and, (iii) removing the time-to-fire of each disabled transition (i.e., enabled by m but not by $m'$).

3.2 The Method of Stochastic State Classes

The method of stochastic state classes [6, 18, 31] permits the analysis of STPNs with multiple concurrent GEN transitions. Given a sequence of firings, a stochastic state class encodes the marking and the joint PDF of the times-to-fire of the enabled transitions and the absolute elapsed time $\tau _{\mathrm {age}}$. Starting from an initial stochastic state class, the transient tree of stochastic state classes that can be reached within a time $t_{\mathrm {max}}$ is enumerated, enabling derivation of continuous-time transient probabilities of markings (forward transient analysis), i.e., $p_m(t):=P\{M(t)=m\}~\forall ~0\le t \le t_{\mathrm {max}}, ~\forall ~m\in \mathcal {M}$, where M(t) is the marking process describing the marking M(t) of an STPN for each time $t \ge 0$ and $\mathcal {M}$ is the set of reachable markings.

If the STPN always reaches within a bounded number of firings a regeneration, i.e., a state satisfying the Markov condition, its marking process is a Markov Regenerative Process (MRP) [9], and its analysis can be performed enumerating stochastic state classes between any two regenerations. This results in a set of trees that permits to compute a local and a global kernel characterizing the MRP behavior, enabling evaluation of transient marking probabilities through the numerical solution of Markov renewal equations (regenerative transient analysis). Trees also permit to compute conditional probabilities of the Discrete Time Markov Chain (DTMC) embedded at regenerations and the expected time spent in any marking after each occurrence of any regeneration [22], supporting derivation of steady-state marking probabilities according to the Markov renewal theory (regenerative steady-state analysis).

While stochastic state classes support quantitative evaluation of an STPN model, the set $\varOmega$ of behaviors of the STPN can be identified with simpler and more consolidated means through non-deterministic analysis of the underlying TPN model. In this case, the state space is covered through the method of state classes [11, 30], each made of a marking and a joint support for $\tau _{\mathrm {age}}$ and the times-to-fire of the enabled transitions. In this approach, enumeration of state classes starting from an initial marking provides a representation for the continuous set of executions of an STPN, enabling verification of qualitative properties of the model, e.g., guarantee, with certainty, that a marking cannot be reached within a given time bound (non-deterministic transient analysis).

3.3 ORIS Overview

ORIS [5]³ is a software tool for qualitative verification and quantitative evaluation of reactive timed systems. ORIS supports modeling and evaluation of stochastic systems governed by timers (e.g., interleaving or service times, arrival rate, timeouts) with general probability density functions (PDFs). The tool adopts Stochastic Time Petri Nets (STPNs) as a graphical formalism to specify stochastic systems, and it efficiently implements the method of stochastic state classes, including regenerative transient, regenerative steady-state and non-deterministic analysis.

The software architecture of ORIS decouples the graphical editor from the underlying analysis engines. Given the many variants of Petri net features, ORIS was developed with extensibility in mind: new features can be defined by implementing specific interfaces, so that they can be introduced in the graphical editor and made available to the analysis engines. In turn, analysis engines implement a specific interface that allows them to cooperate with the graphical interface, i.e., to collect analysis options from the user, to start/stop analysis runs, to record and display analysis logs, and to show time series and tabular results. The following analysis engines are available.

Non-deterministic Analysis is based on the theory of Difference Bound Matrix (DBM) and supports the identification of the boundaries of the space of feasible timed behaviors, producing a compact representation of the dense set of timed states that can be reached by the model [30]. The state space is displayed as a directed graph, where edges represent transition firings while nodes are state classes comprising a marking and a DBM zone of timer values. This analysis is useful to debug STPNs models and ensure that their state space M is finite.

Transient and Regenerative Analysis computes transient probabilities in Generalized Semi-Markov Processes (GSMPs) and Markov Regenerative Processes (MRPs), respectively. These methods evaluate trees where edges are labeled with transitions and their firing probabilities, while nodes are stochastic state classes [18] comprising a marking, the PDF of timers, and their support (a DBM zone). For a given time limit T, the enumeration proceeds until the tree covers the transition firings of the STPN by time T with probability greater than $1 - \epsilon$, where $\epsilon > 0$ is an error term. While standard transient analysis enumerates a single, very large tree of events, regenerative analysis avoids the enumeration of repeated subtrees rooted in the same regeneration point (where all general timers are reset or have been enabled for a deterministic time). A time step $\varDelta t$ is used to select equispaced time points where transient probabilities are evaluated (directly or by solving Markov renewal equations).

Regenerative Steady-State Analysis computes steady-state probabilities in MRPs (and thus Semi-Markov Processes (SMPs) and Continuous Time Markov Chains (CTMCs)) with irreducible state space. This method uses trees of stochastic state classes between regeneration points to compute steady-state probabilities of markings: expected sojourn times in each tree are combined with the steady-state probability of regenerations at their roots [22]. As for transient analysis, this method can be applied to STPNs allowing multiple general timers enabled in each state.

Transient Analysis Under Enabling Restriction computes transient probabilities in MRPs with at most one general transition enabled in each state [16].

ORIS engines support instantaneous (transient or steady-state) and cumulative (transient) rewards. A reward is a real-valued function of markings $r : M \rightarrow \mathbb {R}$ that is evaluated by substituting place names with the number of contained tokens in order to compute the instantaneous expected reward $I_r(t) = \sum _{i \in M} r(i)p_i(t)$ at each time t, its steady-state value $\overline{I}_r = \lim _{t \rightarrow \infty } I_r(t) = \sum _{i \in M} r(i)\overline{p}_i$ or its cumulative value over time $C_r(t) = \int _{0}^{t} I_r(t)dt$. In addition, the user can specify a stop condition, i.e., a Boolean predicate on markings such as $\mathtt {(p_0 == 1) \& \& (p_1 == 1)}$, that is used to halt the STPN. This feature can be used to compute first-passage probabilities [18] or reach-avoid objectives equivalent to bounded until operators [25].

4 Diacceto-Alamanni: An STPN Model

In this section, we describe the STPN model of the Diacceto-Alamanni intersection. Figure 3 shows the model which is composed of two submodels: the tramway submodel (blue box) and the private traffic submodel (red box).

Fig. 3.

Intersection model. The tramway submodel is highlighted by the blue box, the private traffic queue submodel is highlighted by the red one. Transitions associated with an enabling function are marked by a label “e”. (Color figure online)

4.1 Tramway Submodel

The portion of the tramway submodel in the dotted blue box represents the direction from Santa Maria Novella train station (Alamanni-Stazione), while the one in the dashed blue box represents the opposite direction. GEST provided the interleaving period of trams, which is equal to 220 s; the transition period, which models tram departures, fires a new token periodically and is enabled with continuity until place KO receives a token. Places p$0$ and p$1$ represent a tramway departing from Alamanni-Stazione and Villa Costanza, respectively. Transitions delayFromSmn and delayFromScndc represent the delays cumulated by the two trams, respectively; note that 120 s is an upper bound on the maximum delay observed in the available data set and, given that data are few and their distribution is unknown, this parameter is modeled using a uniform distribution [3].

When the tramway is approaching the intersection, dedicated wayside systems (i.e., two loops placed under the railway tracks) are activated (places Loop$01.001.1$ and Loop$01.001.2$) and the corresponding traffic lights are set to red (places setRedFromSmn and setRedFromScnd). The traffic lights are in fact set to red 5 s before the arrival of the tram at the intersection; this parameter has been provided by GEST and is modeled by the DET transitions crosslightAnticipationSmn and crosslightAnticipationScnd. Places crossingFromSmn and crossingFromScnd represent the arrival of the tram at the intersection, while transitions leavingFromSmn and leavingFromScndc account for the time needed to free the intersection. Specifically, the minimum and the maximum time needed to free the intersection are set equal to 6 s and 14 s, respectively, based on the fact that in the data set provided by GEST this temporal parameter has mean value nearly equal to 10 s and a standard deviation approximately equal to 4 s. Also in this case, given that available data are few, this parameters is modeled by a uniform distribution over the interval [6, 14] [3].

4.2 Private Transport Submodel

We model private traffic as a birth-death process with three levels of traffic congestion: specifically, places carQueue$0$, carQueue$1$, and carQueue$2$ model the condition of low, moderate, and high volume of traffic, respectively. Since we lack data on car traffic in Florence, we assume that the average traffic density is approximatively 1000 cars per hour, which is a typical value for a high traffic flow on a single lane [24], and we consider the case that the arrival/departure of two cars increases/decreases the traffic congestion level, respectively, and that the time needed to occupy the intersection is nearly half the time needed to leave it. According to this, the EXP transitions t7 and t8 have rate equal to 0.14 $\hbox {s}^{-1}$, while the EXP transitions t9 and t10 have rate equal to 0.067 $s^{-1}$.

Intuitively, the number of cars in the queue increases when the private traffic light is set to red and decreases otherwise. In order to model this behavior, transitions t$7$ and t$8$ are associated with an enabling function that evaluates to true when at least one token is present in place setRedFromSmn or in place setRedFromScnd (i.e. setRedFromSmn+setRedFromScnd>0). Conversely, transitions t$9$ and t$10$ are associated with an enabling function that evaluates to true when no token is present in places setRedFromSmn and setRedFromScnd (i.e., setRedFromSmn+setRedFromScnd==0).

4.3 Interaction Between the Tramway Submodel and the Private Transport Submodel

Road congestion may cause cars to stand for a while on the tracks after the private traffic light has turned to red, thus blocking trams. Place yellow models the private traffic light set to yellow, while place KO actually models the case that a tram ride is blocked by private vehicles on the lane. When place KO receives a token, transition stopAll becomes enabled (given that it is associated with an enabling function KO>0) and fires, depositing a token in place inhibitAll. This finally disables transitions period, leavingFromSmn, and leavingFromScndc, due to the inhibitor arcs from inhibitAll to each of these transitions.

Transitions t$13$ through t$19$ model the possibility that a tram ride is blocked by private vehicles stopping on the tracks. If the traffic congestion level is low (i.e., $carQueue0 >0$), the tram runs regularly and transition t$19$ is enabled, so that no token is deposited in place KO. If traffic congestion increases to a moderate level ($carQueue1 >0$) or to a high level ($carQueue2 >0$), transition $t13$ or transition t$14$ becomes enabled and fires, respectively. In the former case (p$3 >0$), transitions $t15$ and $t17$ fire with probability 0.3 and 0.7, respectively, given that they have weight equal to 30 and 70, respectively; in the latter case, transitions $t16$ and $t18$ fire with probability 0.4 and 0.6, respectively, given that they have weight equal to 40 and 60, respectively. In doing so, the probability of a traffic block is 0.3 and 0.4 in the case of moderate and high traffic congestion, respectively. These parameters have been estimated from tram delays observed in the data set provided by GEST.

5 Analysis and Results

In this section, we report the results obtained from the analysis of the model of Sect. 4. In all the experiments, we performed regenerative transient analysis of the model through the ORIS tool using the following parameters:

• Time limit $T= 7200\hbox { s}$ (corresponding to 2 h);

• Time step $\varDelta t= 20 \hbox { s}$.

• Error $\epsilon =0.01$;

The first experiment has been performed with average traffic density equal to 1000 cars per hour (i.e., the EXP transitions t7 and t8 have rate equal to 0.14 $\hbox {s}^{-1}$, and the EXP transitions t9 and t10 have rate equal to 0.067 $\hbox {s}^{-1}$, as shown in Fig. 3) and crosslight anticipation equal to 5 s (i.e., the value of the DET transitions crosslightAnticipationSmn and crosslightAnticipationScnd is 5 s, as also shown in Fig. 3). Figure 4 shows the probability of the private traffic queue status in a time interval of 2 h, obtained computing the instantaneous rewards “$carQueue0 >0$”, “$carQueue1 >0$”, and “$carQueue2 >0$”. Due to the high value of average traffic density, the car queue tends to be filled quite rapidly. As we can see, the reward “$carQueue2 >0$” (high traffic volume) tends to 1 s, while the rewards “$carQueue0 >0$” (low traffic volume) and “$carQueue1 >0$” (moderate traffic volume) tend to 0 s (note that the sum of tokens in places $carQueue0$, $carQueue1$, and $carQueue2$ is 1).

Fig. 4.

Transient probability of the traffic queue status.

Figure 5 shows the KO probability for different values of the crosslight anticipation parameter, obtained computing the instantaneous reward “$KO >0$”. We observe that the probability of reaching the KO state increases every 220 s for all the displayed curves, due to periodic tram departures. We also note that the probability of reaching the KO state increases when the crosslight anticipation is higher: intuitively, when the anticipation time increases, the time during which private traffic should flow away from the intersection decreases, thus degrading the queue status and consequently increasing the KO probability.

Fig. 5.

Transient probability of the KO state for different values of the crosslight anticipation parameter.

Fig. 6.

Transient probability of the KO state for different values of traffic density.

Finally, Fig. 6 shows the KO probability (obtained computing the instantaneous reward “$KO >0$”) for different values of the private traffic density. The probability of reaching the KO state increases when the traffic density is higher and reaches 0.7 in less than half an hour with extremely congested private traffic (i.e., 1500 cars per hour), while the same value is reached in more than a hour with moderately congested private traffic (i.e., 500 cars per hour).

We also argue that, for the planning of both tram timetables and traffic light timings, it is important to consider the correlation between the time of red signal, the time of green signal, and the tram headway, pointing out the need of an integrated management of the different transport systems in order to have a more robust and higher quality service. Furthermore, a more detailed analysis is needed to accurately model the behavior of private traffic during the day.

6 Conclusion

Modeling and analysis of complex intersections for the integration of private and public transport supports the evaluation of the perceived availability of public transport and the identification of robust traffic light plans and tram timetables. In this work, we presented an analytical approach to model and evaluate a critical intersection for the Florence tramway. Specifically, we used the ORIS tool to evaluate the probability of a traffic block, leveraging regenerative transient analysis based on the method of stochastic state classes to analyze a model of the intersection specified through Stochastic Time Petri Nets (STPNs). The analysis results showed a correlation between the frequency of tram rides, the traffic light plan, and the status of the queue of private vehicles, pointing out that the frequency of tram rides impacts on the road congestion. Therefore, compensating measures should be considered, such as synchronizing the passage of trams in opposite directions on the road crossing.

Within the context of modeling techniques to optimize the integration of public and private traffic, our work will go towards the following directions:

• analyze other road/tramway intersections, also considering the new tramway lines that will be opened in Florence, so as to compare differences and similarities and generalize the modeling methodology;

• improve the scalability of the approach by combining numerical solution of the tramway submodel through the ORIS tool with analytical evaluation of the traffic congestion level, which could permit to model private traffic more accurately (e.g., considering a larger number of congestion levels) without incurring in the state space explosion problem;

• evaluate to which extent the behavior of passengers and pedestrians as well as the weather conditions perturb the tramway performance, including them in the model of the road/tramway intersection [23].