Limited Evaluation Evolutionary Optimization of Large Neural Networks

Abstract

Stochastic gradient descent is the most prevalent algorithm to train neural networks. However, other approaches such as evolutionary algorithms are also applicable to this task. Evolutionary algorithms bring unique trade-offs that are worth exploring, but computational demands have so far restricted exploration to small networks with few parameters. We implement an evolutionary algorithm that executes entirely on the GPU, which allows to efficiently batch-evaluate a whole population of networks. Within this framework, we explore the limited evaluation evolutionary algorithm for neural network training and find that its batch evaluation idea comes with a large accuracy trade-off. In further experiments, we explore crossover operators and find that unprincipled random uniform crossover performs extremely well. Finally, we train a network with 92k parameters on MNIST using an EA and achieve 97.6% test accuracy compared to 98% test accuracy on the same network trained with Adam. Code is available at https://github.com/jprellberg/gpuea.

1 Introduction

Stochastic gradient descent (SGD) is the leading approach for neural network parameter optimization. Significant research effort has lead to creations such as the Adam [9] optimizer, Batch Normalization [8] or advantageous parameter initializations [7], all of which improve upon the standard SGD training process. Furthermore, efficient libraries with automatic differentiation and GPU support are readily available. It is therefore unsurprising that SGD outperforms all other approaches to neural network training. Still, in this paper we want to examine evolutionary algorithms (EA) for this task.

EAs are powerful black-box function optimizers and one prominent advantage is that they do not need gradient information. While neural networks are usually built so that they are differentiable, this restriction can be lifted when training with EAs. For example, this would allow the direct training of neural networks with binary weights for deployment in low-power embedded devices. Furthermore, the loss function does not need to be differentiable so that it becomes possible to optimize for more complex metrics.

With growing computational resources and algorithmic advances, it is becoming feasible to optimize large, directly encoded neural networks with EAs. Recently, the limited evaluation evolutionary algorithm (LEEA) [11] has been introduced, which saves computation by performing the fitness evaluation on small batches of data and smoothing the resulting noise with a fitness inheritance scheme. We create a LEEA implementation that executes entirely on a GPU to facilitate extensive experimentation. The GPU implementation avoids memory bandwidth bottlenecks, reduces latency and, most importantly, allows to efficiently batch the evaluation of multiple network instances with different parameters into a single operation.

Using this framework, we highlight a trade-off between batch size and achievable accuracy and also find the proposed fitness inheritance scheme to be detrimental. Instead, we show how the LEEA can profit from low selective pressure when using small batch sizes. Despite the problems discussed in literature about crossover and neural networks [6, 14], we see that basic uniform and arithmetic crossover perform well when paired with an appropriately tuned mutation operator. Finally, we apply the lessons learned to train a neural network with 92k parameters on MNIST using an EA and achieve 97.6% test accuracy. In comparison, training with Adam results in 98% test accuracy. (The network is limited by its size and architecture and cannot achieve state-of-the-art results.)

The remainder of this paper is structured as follows: Sect. 2 presents related work on the application of EAs to neural network training. In Sect. 3, we present our EA in detail and explain the advantages of running it on a GPU. Section 4 covers all experiments and contains the main results of this work. Finally, we conclude the paper in Sect. 5.

2 Related Work

Morse et al. [11] introduced the limited evaluation (LE) evolutionary algorithm for neural network training. It is a modified generational EA, which picks a small batch of training examples at the beginning of every generation and uses it to evaluate the population of neural networks. This idea is conceptually very similar to SGD, which also uses a batch of data for each step. Performing the fitness evaluation on small batches instead of the complete training set massively reduces the required computation, but it also introduces noise into the fitness evaluation. The second component of the LEEA is therefore a fitness inheritance scheme that combines past fitness evaluation results. The algorithm is tested with networks of up to 1500 parameters and achieves results comparable to SGD on small datasets.

Baioletti et al. [1] pick up the LE idea but replace the evolutionary algorithm with differential evolution (DE), which is a very successful optimizer for continuous parameter spaces [3]. The largest network they experiment with employs 7000 parameters. However, there is still a rather large performance gap on the MNIST dataset between their best performing DE algorithm at 85% accuracy and a standard SGD training at 92% accuracy.

Yaman et al. [15] combine the concepts LE, DE and cooperative co-evolution. They consider the pre-synaptic weights of a single neuron a component and evolve many populations of such components in parallel. Complete solutions are created by combining components from different populations to a network. Using this approach, they are able to optimize networks of up to 28k parameters.

Zhang et al. [16] explore neural network training with a natural evolution strategy. This algorithm starts with an initial parameter vector $\theta$ and creates many so-called pseudo-offspring parameter vectors by adding random noise to $\theta$. The fitness of all pseudo-offspring is evaluated and used to estimate the gradient at $\theta$. Finally, this gradient approximation is fed to SGD or another optimizer such as Adam to modify $\theta$. Using this approach, they achieve 99% accuracy on MNIST with 50k pseudo-offspring for the gradient approximation.

Neuroevolution, which is the joint optimization of network topology and parameters, is another promising application for EAs. This approach has a long history [5] and works well for small networks up to a few hundred connections. However, scaling this approach to networks with millions of connections remains a challenge. One recent line of work [4, 10, 12] has taken a hybrid approach where the topology is optimized by an EA but the parameters are still trained with SGD. However, the introduction or removal of parameters by the EA can be problematic. It may leave the network in an unfavorable region of the parameter space, with effects similar to those of a bad initialization at the start of SGD training. Another line of work has focused on indirect encodings to reduce the size of the search space [13]. The difficulty here lies in finding an appropriate mapping from genotype to phenotype.

3 Method

We implement a population-based EA that optimizes the parameters of directly encoded, fixed size neural networks. For performance reasons, the EA is implemented with TensorFlow and executes entirely on the GPU, i.e. the whole population of networks lives in GPU memory and all EA logic is performed on the GPU.

3.1 Evolutionary Algorithm

Algorithm 1 shows our EA in pseudo-code. It is a generational EA extended by the limited evaluation concept. Every generation, the fitness evaluation is performed on a small batch of data that is drawn randomly from the training set. This reduces the computational cost of the fitness evaluation but introduces an increasing amount of noise with smaller batch sizes. To counteract this, Morse et al. [11] propose a fitness inheritance scheme that we implement as well.

The initial population is created by randomly initializing the parameters of $\lambda$ networks. Then, a total of $\lambda$ offspring networks are derived from the population P. The hyperparameters $p_{E}$, $p_{C}$ and $p_{M}$ determine the percentage of offspring created by elite selection, crossover and mutation respectively. First, the $p_{E}\lambda$ networks with the highest fitness are selected as elites from the population. These elites move into the next generation unchanged and will be evaluated again. Even though their parameters did not change, the repeated evaluation is desirable. Because the fitness function is only evaluated on a small batch of data, it is stochastic and repeated evaluations will result in a better estimate of the true fitness when combined with previous fitness evaluation results. Next, $p_{C}\lambda$ pairs of networks are selected as parents for sexual reproduction (crossover) and finally $p_{M}\lambda$ networks are selected as parents for asexual reproduction (mutation). The selection procedure in both cases is truncation selection, i.e. parents are drawn uniform at random from the top $\rho \lambda$ of networks sorted by fitness, where $\rho \in \left[ 0,1\right]$ is the selection proportion.

Due to the stochasticity in the fitness evaluation, it seems advantageous to combine fitness evaluation results from multiple batches. However, simply evaluating every network on multiple batches is no different from using a larger batch size. Therefore, the assumption is made that the fitness of a parent network and its offspring are related. Then, a parent’s fitness can be inherited to its offspring as a good initial guess and be refined by the actual fitness evaluation of the offspring. This is done in form of the weighted sum

$$ f_{\text {adj}}=\left( 1-\alpha \right) \cdot f_{\text {inh}}+\alpha \cdot \text {fitness}\left( \theta ,x,y\right) , $$

where $f_{\text {inh}}$ is the fitness value inherited by the parents, $\text {fitness}\left( \theta ,x,y\right)$ is the fitness value of the offspring $\theta$ on the current batch x, y and $\alpha \in \left[ 0,1\right]$ is a hyperparameter that controls the strength of the fitness inheritance scheme. Setting $\alpha$ to 1 disables fitness inheritance altogether. During sexual reproduction of two parents with fitness $f_{1}$ and $f_{2}$ or during asexual reproduction of a single parent with fitness $f_{3}$, the inherited fitness values are $f_{\text {inh}}=\frac{1}{2}\left( f_{1}+f_{2}\right)$ and $f_{\text {inh}}=f_{3}$ respectively.

3.2 Crossover and Mutation Operators

Members of the EA population are direct encodings of neural network parameters $\theta \in \mathbb {R}^{c}$, where c is the total number of parameters in each network. The crossover and mutation operators directly modify this vector representation. An explanation of the crossover and mutation operators that we use in our experiments follows.

Uniform Crossover. The uniform crossover of two parents $\theta _{1}$ and $\theta _{2}$ creates offspring $\theta _{u}$ by randomly deciding which element of the offspring’s parameter vector is taken from which parent:

$$ \theta _{u,i}={\left\{ \begin{array}{ll} \theta _{1,i} &{} \text {with probability }0.5\\ \theta _{2,i} &{} \text {else} \end{array}\right. } $$

Arithmetic Crossover. Arithmetic crossover creates offspring $\theta _{a}$ from two parents $\theta _{1}$ and $\theta _{2}$ by taking the arithmetic mean:

$$ \theta _{a}=\frac{1}{2}\left( \theta _{1}+\theta _{2}\right) $$

Mutation. The mutation operator adds random normal noise scaled by a mutation strength $\sigma$ to a parent $\theta _{1}$:

$$ \theta _{m}=\theta _{1}+\sigma \cdot \mathcal {N}\left( 0,1\right) $$

The mutation strength $\sigma$ is an important hyperparameter that can be changed over the course of the EA run if desired. In the simplest case, the mutation strength stays constant over all generations.

We also experiment with deterministic control in the form of an exponentially decaying value. For each generation i, the mutation strength is calculated according to $\sigma _{i}=\sigma \cdot 0.99^{i/k}$, where $\sigma$ is the initial mutation strength and the hyperparameter k controls the decay rate in terms of generations.

Finally, we implement self-adaptive control. The mutation strength $\sigma$ is included as a gene in each individual and each individual is mutated with the $\sigma$ taken from its own genes. The mutation strength itself is mutated according to $\sigma _{i+1}=\sigma _{i}e^{\tau \mathcal {N}\left( 0,1\right) }$ with hyperparameter $\tau$. During crossover, the arithmetic mean of two $\sigma$-genes produces the value for the $\sigma$-gene in the offspring.

3.3 GPU Implementation

Naively executing thousands of small neural networks on a GPU in parallel incurs significant overhead, since many short-running, parallel operations that compete for resources are launched, each of which also has a startup cost. To efficiently evaluate thousands of network parameter configurations, the computations should be expressed as batch tensor¹ products where possible.

Assume we have input data of dimensionality m and want to apply a fully connected layer with n output units to it. This can naturally be expressed as a product of a parameter and data tensor with shapes $\left[ n,m\right] \times \left[ m\right] =\left[ n\right]$, which in this simple case is just a matrix-vector product. To process a batch of data at once, a batch dimension b is introduced to the data vector. The resulting product has shapes $\left[ n,m\right] \times \left[ b,m\right] =\left[ b,n\right]$. Conceptually, the same product as before is computed for every element in the data tensor’s batch dimension. Batching over multiple sets of network parameters follows the same approach and introduces a population dimension p. Obviously, the parameter tensor needs to be extended by this dimension so that it can hold parameters of different networks. However, the data tensor also needs an additional population dimension because the output of each layer will be different for networks with different parameters. The resulting product has shapes $\left[ p,n,m\right] \times \left[ p,b,m\right] =\left[ p,b,n\right]$ and conceptually, the same batch product as before is computed for every element in the population dimension.

In order to exploit this batched evaluation of populations, the whole population lives in GPU memory in the required tensor format. Next to enabling the population batching, this also alleviates the need to copy data between devices, which reduces latency. These advantages apply as long as the networks are small enough. The larger each network, the more computation is necessary to evaluate it, which reduces the gain from batching multiple networks together. Furthermore, combinations of population size, network size and batch size are limited by the available GPU memory. Despite these shortcomings, with 16 GB GPU memory this framework allows us to experiment at reasonably large scales such as a population of 8k networks with 92k parameters each at a batch size of 64.

4 Experiments

We apply the EA from Sect. 3 to optimize a neural network that classifies the MNIST dataset, which is a standard image classification benchmark with $28\times 28$ pixel grayscale inputs and $d=10$ classes. The training set contains 50k images, which we split into an actual training set of 45k images and a validation set of 5k images. All reported accuracies during experiments are validation set accuracies. The test set of 10k images is only used in the final experiment that compares the EA to SGD. All experiments have been repeated 15 times with different random seeds. When significance levels are mentioned, they have been obtained by performing a one-sided Mann-Whitney-U-Test between the samples of each experiment. The fitness function to be maximized by the EA is defined as the negative, average cross-entropy

$$\begin{aligned} -\frac{1}{n}\sum _{i=1}^{n}H\left( p_{i},q_{i}\right) =\frac{1}{nd}\sum _{i=1}^{n}\sum _{j=1}^{d}p_{ij}\log \left( q_{ij}\right) , \end{aligned}$$

(1)

where n is the batch size, $p_{ij}\in \left\{ 0,1\right\}$ is the ground-truth probability and $q_{ij}\in \left[ 0,1\right]$ is the predicted probability for the jth class in the ith example. Unless otherwise stated, the following hyperparameters are used for experiments:

$$ \begin{aligned}\text {crossover op.}&=\text {uniform}&p_{E}&=0.05&\lambda&=1000&\alpha&=1.00\\ \text {sigma adapt.}&=\text {constant}&p_{C}&=0.50&\sigma&=0.001\\ \text {batch size}&=512&p_{M}&=0.45&\rho&=0.50 \end{aligned} $$

4.1 Neural Network Description

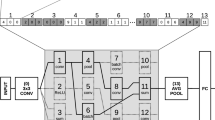
The neural network we use in all our experiments applies $2\times 2$ max-pooling to its inputs, followed by four fully connected layers with 256, 128, 64 and 10 units respectively. Each layer except for the last one is followed by a ReLU non-linearity. Finally, the softmax function is applied to the network output. In total, this network has 92k parameters that need to be trained.

This network is unable to achieve state-of-the-art results even with SGD training but has been chosen due to the following considerations. We wanted to limit the maximum network parameter count to roughly 100k so that it remains possible to experiment with large populations and batch sizes. However, we also wanted to work with a multi-layer network. We deem this aspect important, as there should be additional difficulty in optimizing deeper networks with more interactions between parameters. To avoid concentrating a large part of the parameters in the network’s first layer, we downsample the input. This way, it is possible to have a multi-layer network with a significant number of parameters in all layers. Furthermore, we decided against using convolutional layers as our batched implementation of fully connected layers is more efficient than the convolutional counterpart.

All networks for the EA population are initialized using the Glorot-uniform [7] initialization scheme. Even though Glorot-uniform and other neural network initialization schemes were devised to improved SGD performance, we find that the EA also benefits from them. Furthermore, this allows for a comparison to SGD on even footing.

4.2 Tradeoff Between Batch Size and Accuracy

The EA chooses a batch of training data for each generation and uses it to evaluate the population’s fitness. A single fitness evaluation is therefore only a noisy estimate of the true fitness. The smaller the batch size, the noisier this estimate becomes because Eq. 1 averages over fewer cross-entropy loss values. A noisy fitness estimate introduces two problems: A good network may receive a low fitness value and be eliminated during selection or a bad network may receive a high fitness value and survive. The fitness inheritance was introduced by Morse et al. [11] with the intent to counteract this noise and allow effective optimization despite noisy fitness values. However, in preliminary experiments fitness inheritance did not seem to have a positive impact on our results, so we performed a systematic experiment to explore the interaction between batch size, fitness inheritance and the resulting network accuracy. The results can be found in Fig. 1. Three key observations can be made:

First of all, the validation set accuracy is positively correlated with the batch size. This relationship holds for all tested settings of $\lambda$ and $\alpha$. This means, using larger batch sizes gives better results. Note that the EA was allowed to run for more generations when the batch size was small, so that all runs could converge. In consequence, it is not possible to compensate the accuracy loss incurred by small batch sizes by allowing the EA to perform more iterations.

Second, the validation set accuracy is also positively correlated with $\alpha$. Especially for small batch sizes, significant increases in validation accuracy can be observed when increasing $\alpha$. This is surprising as higher values of $\alpha$ reduce the amount of fitness inheritance. Instead, we find that the fitness inheritance either has a harmful or no effect.

Lastly, increasing the population size $\lambda$ improves the validation accuracy. This is important but unsurprising as increasing the population size is a known way to counteract noise [2].

Fig. 1.

Validation accuracies of 15 EA runs for different population sizes $\lambda$, fitness inheritance strengths $\alpha$ and batch sizes. Looking at the grid of figures, $\lambda$ increases from top to bottom, while $\alpha$ increases from left to right. A box extends from the lower to upper quartile values of the data, with a line at the median and whiskers that show the range of the data.

4.3 Selective Pressure

Having observed that fitness inheritance does not improve results at small batch sizes, we will now show that instead decreasing the selective pressure helps. The selective pressure influences to what degree fitter individuals are favored over less fit individuals during the selection process. Since small batches produce noisy fitness evaluations, a low selective pressure should be helpful because the EA is less likely to eliminate all good solutions based on inaccurate fitness estimates.

We experiment with different settings of the selection proportion $\rho$, which determines what percentage of the population ordered by fitness is eligible for reproduction. During selection, parents are drawn uniformly at random from this group. Low selection proportions (low values of $\rho$) lead to high selective pressure because parents are drawn from a smaller group of individuals with high (apparent) fitness. Therefore, we expect high values of $\rho$ to work better with small batches.

Table 1. Relative improvement in validation accuracy when increasing the selection proportion from $\rho =0.1$ to $\rho =0.2$ in four different scenarios. Since large population sizes are also an effective countermeasure against noise, the relative improvement decreases with increasing population sizes. The fitness noise column only depends on batch size and is included to highlight the correlation between noise and relative improvement.

Figure 2 shows results for increasing values of $\rho$ at two different batch sizes and two different population sizes. Generally speaking, increasing $\rho$ increases the validation accuracy (up to a certain degree). For a specific $\rho$ it is unfortunately not possible to compare validation accuracies across the four scenarios, because batch size and population size are influencing factors as well. Instead, we treat the relative difference in validation accuracies going from $\rho =0.1$ to $\rho =0.2$ as a proxy. Table 1 confirms that decreasing the selective pressure (by increasing $\rho$) has a positive influence on the validation accuracy.

Fig. 2.

Validation accuracies of 15 EA runs for different population sizes $\lambda$, batch sizes and selection proportions $\rho$. The first row of figures shows results for small batch sizes, while the second row shows results for large batch sizes.

4.4 Crossover and Mutation Operators

While the previous experiments explored the influence of limited evaluation, another significant factor for good performance are crossover and mutation operators that match the optimization problem. Neural networks in particular have problematic redundancy in their search space: Nodes in the network can be reordered without changing the network connectivity. This means, there are multiple equivalent parameter vectors that represent the same function mapping.

Fig. 3.

Validation accuracies of 15 EA runs with different levels of crossover $p_{C}$, crossover operators and mutation strength $\sigma$ adaptation schemes. The left column shows results using uniform crossover, while arithmetic crossover is employed for the right column.

Designing crossover and mutation operators that are specifically equipped to deal with these problems seems like a promising research direction, but for now we want to establish baselines with commonly used operators. In particular, these are uniform and arithmetic crossover as well as random normal mutation. It is not obvious if crossover is helpful for optimizing neural networks as there is no clear compositionality in the parameter space. There are many interdependencies between parameters that might be destroyed, e.g. when random parameters are replaced by those from another network during uniform crossover. Therefore, we not only want to compare the uniform and arithmetic crossover operators among themselves, but also test if crossover leads to improvements at all. This can be achieved by varying the EA hyperparameter $p_{C}$ , which controls the percentage of offspring that are created by the crossover operator. On the other hand, random normal mutation intuitively performs the role of a local search but its usefulness significantly depends on the choice of the mutation strength $\sigma$. Therefore, we compare three different adaptation schemes: constant, exponential decay and self-adaptation.

Fig. 4.

Population mean of $\sigma$ from 15 EA runs with self-adaptation turned on. The shaded areas indicate one standard deviation around the mean.

Since crossover operators might need different mutation strengths to operate optimally, we test all combinations and show results in Fig. 3. Using crossover ($p_{C}>0$) always results in significantly ($p<0.01$) higher validation accuracy than not using crossover ($p_{C}=0$), except for the case of arithmetic crossover with exponential decay. The reason for this is likely, that arithmetic crossover needs high mutation strengths but the exponential decay decreases $\sigma$ too fast. This becomes evident when examining the mutation strengths chosen by self-adaptation in Fig. 4. Compared to uniform crossover, the self-adaptation drives $\sigma$ to much higher values when arithmetic crossover is used. Overall, both crossover operators work well under different circumstances. Uniform crossover at $p_{C}=0.75$ with constant $\sigma$ achieves the highest median validation accuracy of 97.3%, followed by arithmetic crossover at $p_{C}=0.5$ with self-adaptive $\sigma$ at 96.9% validation accuracy. When using uniform crossover at $p_{C}=0.75$, a constant mutation strength works significantly ($p<0.01$) better than the other adaptation schemes. On the other hand, for arithmetic crossover at $p_{C}=0.5$, the self-adaptive mutation strength performs significantly ($p<0.01$) better than the other two tested adaptation schemes. The main drawback of the self-adaptive mutation strength is the additional randomness that leads to high variance in the training results.

4.5 Comparison to SGD

Informed by the other experiments, we want to run the EA with advantageous hyperparameter settings and compare its test set performance to the Adam optimizer. Most importantly, we use a large population, large batch size, no fitness inheritance, and offspring are created by uniform crossover in 75% of all cases:

$$ \begin{aligned}\text {crossover op.}&=\text {uniform}&p_{E}&=0.05&\lambda&=2000&\alpha&=1.00\\ \text {sigma adapt.}&=\text {constant}&p_{C}&=0.75&\sigma&=0.001\\ \text {batch size}&=1024&p_{M}&=0.20&\rho&=0.50 \end{aligned} $$

Median test accuracies over 15 repetitions are 97.6% for the EA and 98.0% for Adam. Adam still significantly ($p<0.01$) beats EA performance, but the difference in final test accuracy is rather small. However, training with Adam progresses about 10 times faster so it would be wrong to claim that EAs are competitive for neural network training. Yet, this work is another piece of evidence that EAs have potential for applications in this domain.

5 Conclusion

Efficient batch fitness evaluation of a population of neural networks on GPUs made it feasible to perform extensive experiments with the LEEA. While the idea of using very small batches for fitness evaluation is appealing for computational cost reasons, we find that it comes with the drawback of significantly lower accuracy than with larger batches. Furthermore, the fitness inheritance that is supposed to offset such drawbacks actually has a detrimental effect in our experiments. Instead, we propose to use low selective pressure as an alternative.

We compare uniform and arithmetic crossover in combination with different mutation strength adaptation schemes. Surprisingly, uniform crossover works best among all tested combinations even though it is counter-intuitive that randomly replacing parts of a network’s parameters with those of another network is helpful.

Finally, we train a network of 92k parameters on MNIST using an EA and reach an average test accuracy of 97.6%. SGD still achieves higher accuracy at 98% and is remarkably more efficient in doing so. However, having demonstrated that EAs are able to optimize large neural networks, future work may focus on the application to areas such as neuroevolution where EAs may have a bigger edge.