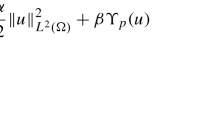Abstract
The optimal control of variational inequalities introduces a number of additional challenges to PDE-constrained optimization problems both in terms of theory and algorithms. The purpose of this article is to first introduce the theoretical underpinnings and then to illustrate various types of numerical methods for the optimal control of variational inequalities. For a generic problem class, sufficient conditions for the existence of a solution are discussed and subsequently, the various types of multiplier-based optimality conditions are introduced. Finally, a number of function-space-based algorithms for the numerical solution of these control problems are presented. This includes adaptive methods based on penalization or regularization as well as non-smooth approaches based on tools from non-smooth optimization and set-valued analysis. A new type of projected subgradient method based on an approximation of limiting coderivatives is proposed. Moreover, several existing methods are extended to include control constraints. The computational performance of the algorithms is compared and contrasted numerically.
TMS’s research was sponsored in part by the DFG grant no. SU 963/1-1 as well as Research Center matheon supported by the Einstein Foundation Berlin within project OT1.
Access provided by CONRICYT-eBooks. Download chapter PDF
Similar content being viewed by others
1 Introduction
The optimal control of variational inequalities is a natural extension of PDE-constrained optimization in which the forward problem or underlying PDE is replaced by a variational inequality or convex variational problem. There are a vast number of applications in which variational inequalities or convex variational problems are used. Perhaps the most well-known disciplines are continuum mechanics [32, 52] and mathematical image processing [67, 70, 72]. However, one also finds variational inequalities in such diverse areas as petroleum engineering [85], digital microfluidics [84], and mathematical finance [51].
Just as in PDE-constrained optimization, we are interested in optimizing or controlling the solution to variational inequalities through one or several parameters. For example, in a packaging problem, we might be interested in determining the optimal force distribution to apply to an elastic membrane in order to obtain a desired shape without passing through a fixed obstacle. In the petroleum engineering application mentioned above, one obtains a variational inequality when using the variational formulation for the steady laminar flow of drill mud modelled as a Bingham fluid. Here, one might wish to determine the optimal pressure needed to affect a desired flow regime.
Due to a lack of Fréchet (or even Gâteaux) differentiability of the control-to-state mapping, a reduced space optimization approach will require either concepts from variational analysis or approximation theory not only to prove existence of a solution but also to derive meaningful first-order optimality conditions and develop efficient numerical methods.
The theoretical and algorithmic challenges remain intact when considering a full-space approach, since the feasible set (after reformulating the variational inequality as a complementarity problem) is both non-convex and fails to satisfy the usual constraint qualifications. For example, in PDE-constrained optimization, one typically uses the Slater or Robinson-Zowe-Kurcyusz constraint qualifications, cf. [48, 77], to ensure the existence and boundedness of the set of Lagrange multipliers. In order to handle these degenerate constraints, one may take a penalty or relaxation approach, though recent work suggests that there are viable theoretical approaches to this “full-space” setting that do not rely on smoothing, see [81].
We now give a brief historical development. We caution the reader that this is only a sampling of the sizeable amount of work published over the past five decades. The purpose is merely to provide an understanding of the current motivations in theory and numerical methods, especially the ideas presented in this paper. Variational inequalities were first introduced by Signorini and solved by Fichera [29]. For this article, the early works by Brezis, Lions, and Stampacchia [18, 60] are perhaps the most relevant as they provide us with a sufficient existence and regularity theory. As a starting point for further study, we also suggest the well-known monographs by Kinderlehrer and Stampacchia and Rodrigues [53, 71]. Perhaps the earliest work on the optimal control of variational inequalities is due to Yvon, in which the adaptive penalty technique for variational inequalities (see Section 4.1) was used in order to approximate the control problem by a more tractable, parameter-dependent problem [86, 87]. This was later used by Lions [58, 59] and fully developed by Barbu [7]. The monograph by Barbu [7] contains many important results and techniques that are still used today, see also related contributions in [9,10,11,12, 50, 68, 73]. In 1976, Mignot offered an alternative to the smoothing approach by developing concepts of generalized differentiability [63]. There, he was able to prove and obtain an explicit formula for the Hadamard directional differentiability of the control-to-state mapping of the variational inequality and, with this result, derive first-order optimality conditions. This result later appeared in [64] and is rederived in [45] using techniques from variational analysis. More recent work in the control of variational inequalities has focused on the development of efficient, function-space-based numerical methods and ever more complex settings as in [2, 4, 21,22,23, 34,35,36, 39, 40, 45, 49, 56, 65, 66, 80, 83].
Parallel to the infinite-dimensional developments, a great deal of progress has been made on theory and numerical methods for finite-dimensional mathematical programs with equilibrium or complementarity constraints, as evidenced by the well-known manuscripts by Luo, Pang, and Ralph [61] and Outrata, Kočvara, and Zowe [69]. In addition to the references therein, we also mention the approaches in [3, 74], which have since been extended to infinite dimensions and are in part featured in this paper.
In reference to the existing finite-dimensional literature, recent works have begun referring to the problem class considered here as elliptic mathematical programs with equilibrium constraints (or elliptic MPECs). We will henceforth do the same for the sake of brevity.
The article is structured as follows. After introducing some necessary notation, data assumptions, and the canonical example in Section 2, we discuss sufficient conditions for the existence of a solution in Section 3. Afterwards, we give several kinds of multiplier-based first-order stationarity conditions similar to classical Karush-Kuhn-Tucker (KKT) conditions. These may or may not be first-order optimality conditions depending on the regularity and data of the given problem. For a newcomer to elliptic MPECs, this potentially puzzling array of possible stationarity conditions may seem strange. However, it is necessary to understand the gap in what is theoretically the “best” type of KKT point and what type of stationary point a given numerical method can theoretically guarantee (at least asymptotically).
Following the theoretical results in Section 3, we pass to the main focus of our discussion: numerical optimization methods for elliptic MPECs. First, in Section 4, we consider what we refer to as “regularization-based” methods. In Section 4.1, we present a typical adaptive smoothing method that makes use of approximation theory for variational inequalities and which is directly linked to the derivation of first-order stationarity conditions for the elliptic MPEC. Similarly, in Section 4.2, we use a simple penalization of the complementarity condition (in weak form) to obtain a simpler PDE-constrained optimization problem with control and state constraints. The numerical solution of the subproblems in the adaptive penalty method is thoroughly discussed for a canonical example problem and the numerical behavior is illustrated. We note that the smoothed problems become increasingly difficult to solve as the smoothing parameter tends to zero, which in part motivates the desire for “non-smooth” methods.
The structure of the non-smooth numerical methods section is devised to illustrate the parallels to some popular methods for smooth PDE-constrained optimization problems, e.g., projected-gradient methods (Section 5.1), direct solvers for the KKT system (Section 5.2), and globalization of the direct solvers via a line search (Section 5.3). There are obvious (and expected) limitations to these approaches, all of which arise from the non-smooth or degenerate nature of elliptic MPECs. Nevertheless, they indicate the possibility of inventing new efficient numerical methods beyond the adaptive smoothing/penalty paradigm, which often outperform the smooth methods in practice.
In Section 5.1, we present a new subgradient method for the reduced space problem. The choice of “subgradient” is motivated by the limiting variational calculus found, e.g., in the book by Mordukhovich [66]. We discuss the asymptotic behavior of this method and illustrate the potential for future study. Following this in Section 5.2, an active-set-based solver with feasibility restoration suggested by Hintermüller in [36] as a direct solver for the C-stationarity system is considered. Finally, in Section 5.3, we consider the so-called bundle-free implicit programming approach [46], which can be understood as a globalization of the active-set solver using a line search. We extend the latter to include control constraints. The performance of the non-smooth methods is then compared and contrasted with that of the adaptive penalty method. All numerical examples have been solved in the Julia programming language [14] version 0.5.0 on a 2016 MacBook Pro Intel(R) Core(TM) i5 @ 3.1 GHz with 16 GB 2133 MHz LPDDR3 RAM.
2 Notation, Assumptions, and Preliminary Results
In this section, we fix our notation and analytical framework. Elliptic variational inequalities and elliptic MPECs are introduced.
2.1 Norms, Inner Products, and Convergence
All spaces are based on the real number field. The Euclidean norm and scalar product on \(\mathbb {R}^m\) are denoted by |x| and x ⋅ y for \(x,y \in \mathbb {R}^m\), respectively. For \(r \in \mathbb {R}\), we denote \(\max (0,r)\) by (r)+. All other norms are denoted by ∥⋅∥X for some space X. The topological dual of X is denoted by X∗ and the dual pairing by \(\langle \cdot , \cdot \rangle _{X,X^*}\). The inner product on a Hilbert space H is denoted by (⋅, ⋅)H. Given a sequence {xk}⊂ X, we denote strong convergence to \(\overline {x} \in X\) by \(x_k \stackrel {X}{\to } \overline {x}\); for weak convergence, we use \(x_k \stackrel {X}{\rightharpoonup } \overline {x}\) and for weak-star convergence, \(x_k \stackrel {X}{\rightharpoonup ^*} \overline {x}\). In all these cases, we drop the sub- or superscripts if it is clear in context.
2.2 Extended Real-Valued Functionals and Convex Analysis
For a topological vector space U, the extended real-valued functional \(G:U \to \overline {\mathbb {R}}\) is proper if G(u) > −∞ for all u ∈ U and G(w) < +∞ for some w ∈ U. G is said to be closed or lower-semicontinuous if its epigraph
is a closed subset in the product topology on \(U \times \mathbb {R}\). Moreover, G is convex provided
For a Banach space V and \(F:V \to \overline {\mathbb {R}}\), the (convex) subdifferential of F at some point x ∈ V such that −∞ < F(x) < +∞ is defined by the potentially empty set:
If C ⊂ V , then the indicator functional iC of C is defined by
If C is non-empty, closed, and convex, then \(\mathcal {N}_C(x) := \partial i_{C}(x)\) is called the convex normal cone to C at x ∈ C. If K ⊂ V is a non-empty, closed, convex cone, then
Recall that K− referred to as the polar cone to K. For more on convex analysis, see, e.g., [25].
2.3 Function Spaces and 2-Capacity
Unless noted, \(\varOmega \subset \mathbb {R}^n\), \(n \in \left \{1,2,3\right \}\), is a non-empty, bounded, and open subset with Lipschitz boundary Γ = ∂Ω. The Lebesgue measure of \(E \subset \mathbb {R}^n\) is denoted by meas(E). For p ∈ R with 1 ≤ p < +∞, we denote the usual Lebesgue space of p-integrable functions by Lp(Ω) and the Lebesgue space of essentially bounded functionals by L∞(Ω). The norms are given by
respectively. For \(k \in \mathbb {N}\), we denote the Sobolev space of Lp-functions u with \(| D^{\alpha }u |= |(\partial ^{\alpha _1}u,\dots ,\partial ^{\alpha _n}u)| \in L^p(\varOmega )\) by Wk, p(Ω), where α = (α1, …, αn) is a multi-index with |α1| + ⋯ + |αn|≤ k and \(\partial ^{\alpha _i}u\) is the αi-th weak partial derivative of u with respect to xi, i ∈{1, 2, 3}. The Wk, p-norms are then defined by
For our discussion, the most important case is when p = 2. Here, both L2(Ω) and Hk(Ω) := Wk, 2(Ω) are Hilbert spaces with inner product defined using the norms given above. We denote the space of all H1-functions with zero trace by \(H^1_0(\varOmega )\) and its dual by H−1(Ω). It follows from the Poincaré inequality that
is an equivalent norm on \(H^1_0(\varOmega )\). See, e.g., [1] for more. Finally, recall that the 2-capacity of an arbitrary subset E ⊂ Ω is given by
cf. [6, Prop. 5.8.3]. Note that \(H^1_0\)-functions possess a representative that is continuous up to a set of positive capacity, cf. [26]. Moreover, there exist E ⊂ Ω with Cap2(E, Ω) > 0 and meas(E) = 0, e.g., the boundary of a smooth open set. Hence, an \(H^1_0\)-function in 2D is continuous across a smooth curve in the plane, but not at single points.
2.4 Elliptic Variational Inequalities
Let H be a Hilbert space and H∗ its topological dual. For this subsection, (⋅, ⋅) denotes the inner product and ∥⋅∥ the norm on H. The pairing between H and H∗ is denoted by 〈⋅, ⋅〉. Let \(a: H \times H \to \mathbb {R}\) be a bilinear form on H and A : H → H∗ the associated bounded linear operator, i.e., a(u, v) = 〈Au, v〉, u, v ∈ H. We recall that a is said to be coercive/elliptic, if there exists some constant c > 0 such that a(v, v) ≥ c∥v∥2 for all v ∈ H. Clearly, the function ∥v∥a := (a(v, v))1∕2 defines an equivalent norm on H. Let K ⊂ H be non-empty, closed, and convex and w ∈ H∗. Then, the variational problem
is called an elliptic variational inequality. Note that problems of this type are often referred to as variational inequalities of the first kind. They can be equivalently written as a generalized equation:
If we replace iK by a subdifferentiable proper closed convex functional φ, then we obtain a variational inequality of the second kind. The following is due to Lions and Stampacchia [60], see also [53]:
Theorem 1
Let \(a:H \times H \to \mathbb {R}\) be a coercive bilinear form, K ⊂ H closed and convex, and w ∈ H∗. Then, (1) possesses a unique solution S(w). Moreover, the solution mapping w↦S(w) is Lipschitz continuous: For all w1, w2 ∈ H∗, it holds that
where c is the constant of coercivity of a.
Although the solution mapping S is Lipschitz continuous, it is not necessarily differentiable. In some special cases, S is directionally differentiable. For more on variational inequalities, see, e.g., [53]. The conditions on A and K will be considered standing assumptions on the variational inequality for the rest of this article. We conclude this subsection with an example.
Example 1
In the context of (1), let \(H:= H^1_0(\varOmega )\) and H∗ = H−1(Ω). Moreover, define Ψ ∈ H1(Ω) with Ψ|Γ ≤ 0 and \(K \subset H^1_0(\varOmega )\) such that
Clearly, since \(\max (0,\varPsi ) \in H^1_0(\varOmega )\), K≠∅. Moreover, one readily shows that K is closed and convex in \(H^1_0(\varOmega )\). The setting of (1) is general enough to allow for nonsymmetric bilinear forms a(u, v), e.g.,
with appropriate assumptions on aij, bi, c. However, for our purposes it suffices to consider
Letting f ∈ H−1(Ω) and combining the above, we obtain a classical obstacle problem
If Ψ|Γ ≡ 0, then (without altering the boundary conditions), we obtain an equivalent problem:
where \(K_0 = \left \{ u \in H^1_0(\varOmega ) \left |\; u(x) \ge 0,\; \text{ a.e. } x \in \varOmega \right .\right \};\) see, e.g., [53, 71].
Of course, this set K represents perhaps the easiest kind of set that one can consider in a variational inequality. It is just one example of a so-called “polyhedric set,” a notion introduced in the mid-1970s by Haraux [33] and Mignot [63] in the context of sensitivity analysis of variational inequalities. See the recent detailed study [82] for a state-of-the-art on polyhedricity. For more general closed, convex sets, e.g.,
it is possible to prove existence, uniqueness, and continuity results under weak assumptions on Ψ. Since these sets are neither polyhedric nor cones, the differential sensitivity analysis of the solution map and subsequent derivation of optimality conditions or efficient numerical methods is extremely challenging. Elliptic MPECs with this type of constraint were considered in [45]. However, we caution the reader that the proofs for the derivation of the tangent cones are in fact erroneous. Thus, the differential sensitivity results for the solution mapping only hold under the assumption that the tangent cones do in fact have the form purported in the text.
2.5 Elliptic Mathematical Programs with Equilibrium Constraints
We present an abstract framework for a class of elliptic MPECs. Let V , H, and Z be separable Hilbert spaces such that the state space V is a dense subset of H and V ⊂ H ⊂ V∗ both algebraically and topologically. Moreover, assume that f ∈ V∗, Zad ⊂ Z is a non-empty, closed, and convex set (the set of admissible controls/decision variables), B : Z → V∗ is a bounded linear operator and \(F:U \to \overline {\mathbb {R}}\) and \(G: Z \to \overline {\mathbb {R}}\). We define an elliptic MPEC as follows:
In light of Theorem 1, we can rewrite (4) in reduced form, analogously to standard PDE-constrained optimization problems:
Here, f ∈ V∗ is fixed. Therefore, we only write S(Bz) for the solution mapping (instead of S(Bz + f)). Obtaining a meaningful full-space formulation of the optimization problem (4) is not always possible. However, if K in (1) is a cone, then we can also formulate a full-space version of the elliptic MPEC by introducing a slack variable ξ ∈ V∗:




Here, K+ := −K−. This follows from (2). Due to the presence of the complementarity condition (6d), problems of the type (6) are often referred to in the finite-dimensional literature (and more recently in the infinite-dimensional literature) as (elliptic) mathematical programs with complementarity constraints (MPCCs); see e.g., [61, 69, 74] (finite dimensions) and the recent work [81] (infinite dimensions).
Remark 1
We consider here the simplest case in which the control or decision variable z appears only on the “right-hand side” of the variational inequality. However, in many interesting applications, e.g., topology optimization [8], the control enters nonlinearly through the differential operator A, e.g., when A(z)u = −div(z∇u). In the context of elliptic MPECs, this case is scarcely covered in the literature, see [36].
We finalize this section with a canonical example of an elliptic MPEC.
Example 2
In the notation of (4), we set \(V = H^1_0(\varOmega )\), H = L2(Ω), V∗ = H−1(Ω), and Z = L2(Ω). For some ud ∈ L2(Ω), we let F be a standard tracking-type functional and G an L2-Tikhonov regularization:
For the forward problem, we choose the simplest form of the obstacle problem with Ψ ≡ 0. Then, the following is an elliptic MPEC:
Some possibilities for Zad are local bilateral constraints: − 1 ≤ w(x) ≤ 1, a.e. x ∈ Ω or global constraints such as \( \|w\|{ }_{L^2} \le 1 \).
3 Existence and Stationarity Conditions
We start this section in the abstract framework of Section 2.5. In order to provide insight into the deeper meaning of the various stationarity conditions, we ultimately restrict ourselves to the canonical example (Example 2).
3.1 Existence of a Solution
Under suitable conditions, on F, G, Zad, and B, we can use Weierstrass’s existence theorem, see, e.g., [6, Thm. 3.2.5] to prove that the reduced form MPEC has a solution. For the following result, we appeal to the monograph by Barbu [7, Chap. 3].
Theorem 2
In the context of problem (4), we assume the following:
-
1.
\(F:H \to \mathbb {R}\) is locally Lipschitz and nonnegative.
-
2.
\(G:Z \to \overline {\mathbb {R}}\)is convex, lower-semicontinuous, and for some constants κ1 > 0,\(\kappa _ 2 \in \mathbb {R}\). G(z) ≥ κ1∥z∥Z + κ2, ∀z ∈ Z
-
3.
B is completely continuous.
Then, (4), or equivalently (5), admits a solution.
Proof
By replacing G(z) with \(G(z) + i_{Z_{ad}}(z)\), the assertion follows from [7, Prop. 3.1]. In particular, we note that by Barbu [7, Lem. 3.1] the mapping (S ∘ B) : Z → V is completely continuous and, furthermore, the composite objective functional \((F \circ S \circ B):Z \to \mathbb {R}_+\) is weakly lower-semicontinuous.
Since for any z ∈ Zad, (1) has a unique solution u = S(Bz). There exists a unique \(\xi \in \mathcal {N}_K(u)\) such that ξ = Au − Bz − f. Conversely, if (z, u, ξ) satisfies (6b)–(6d), then z ∈ Zad and u = S(Bz). In other words, there is a one-to-one correspondence between the feasible set of (5) and (6). Therefore, if (4), or equivalently (5), admits a solution, then so does (6).
Corollary 1
Under the assumptions of Theorem 2 , (6) admits a solution.
Remark 2
Ignoring Theorem 2, we could also prove this assertion by appealing to [6, Thm. 3.2.5]. Indeed, under the hypotheses of Theorem 2, (6) can be viewed as an unconstrained problem in which the associated objective functional is radially unbounded, proper, and weakly lower-semicontinuous.
3.2 Primal Stationarity Conditions
In this subsection, we restrict ourselves to the setting of Example 2. As mentioned earlier, there are some situations in which the control-to-state mapping S is directionally differentiable. In particular, Mignot [63] demonstrated that the control-to-state mapping in Example 2 is directionally differentiable in the sense of Hadamard. The next result draws the parallel to PDE-constrained optimization problems.
Theorem 3
Let \((\overline {z},\overline {u})\) be a solution to (7), then the following first-order necessary optimality condition holds:
In the finite-dimensional literature, e.g., in [61, 74], primal first-order conditions of the type (8) are often referred to as B-stationarity conditions. There, the “B” comes from the fact that either the so-called Bouligand tangent cone or Bouligand differentiability is used. This motivates the next definition.
Definition 1
If \((\overline {z},\overline {u})\) is a feasible point of (7) that satisfies (8), then \((\overline {z},\overline {u})\) is B-stationary.
For the setting in (5), it is possible to derive B-stationarity conditions provided that F, G are smooth. Clearly, the main challenge is determining directional differentiability of S. Suppose for the sake of argument that \(S'(\overline {u}; du)\) is linear in du ∈ V∗. Then, we can “dualize” the B-stationarity conditions (8):
Note that the condition “\(p = S'(\overline {u})^*(u-u_d)\)” essentially means (in this ideal case) that p solves a type of adjoint equation. Using this “adjoint state” p, we could now develop solution algorithms. However, \(S'(\overline {u};du)\) is in general nonlinear ( albeit Lipschitz) in du and thus, the standard adjoint state p does not exist. As a result, there are several different types of dual/multiplier-based first-order stationarity conditions reminiscent of classical KKT conditions in nonlinear programming.
3.3 Dual Stationarity Conditions
In this subsection, we again restrict ourselves to the setting in Example 2. Furthermore, we assume that Γ is regular enough to guarantee that \(S(Bz) \in H^2(\varOmega ) \cap H^1_0(\varOmega )\) for any z ∈ Zad. This is possible if, e.g., Bz + f ∈ L2(Ω) and Ω is a convex polyhedron, cf. [18, 71]. This regularity assumption ensures that ξ ∈ L2(Ω) and, by the Sobolev embedding theorem, S(Bz) is at least Hölder continuous on Ω. We now introduce two multiplier-based first-order stationarity conditions taken from [39, 40].
Definition 2
Let z ∈ Zad and u = S(Bz) with associated slack variable ξ ∈ L2(Ω). The set \(\varOmega ^0 := \left \{x \in \varOmega \left |\; u(x) = 0 \right .\right \}\) is called the active set or coincidence set and \(I := \left \{x \in \varOmega \left |\; u(x) > 0 \right .\right \}\) the inactive set. The set \(\varOmega ^{00} := \varOmega ^0 \cap \left \{x \in \varOmega \left |\; \xi (x) = 0\right .\right \}\) is called the biactive or weakly active set and \(\varOmega ^{0+} := \varOmega ^0 \cap \left \{x \in \varOmega \left |\; \xi (x) > 0\right .\right \}\) the strongly active set.
Note that the biactive and strongly active sets are only defined up to a set of Lebesgue measure zero. In contrast, the active and inactive sets may be more finely defined up to sets of positive capacity even in less regular settings.
Definition 3
The point \((z,u,\xi ) \in L^2(\varOmega ) \times H^1_0(\varOmega ) \times L^2(\varOmega )\) is called a C-stationary point for (7) provided that there exist \(p \in H^1_0(\varOmega )\) and λ ∈ H−1(Ω) such that the following system of equations is fulfilled:
If, in addition to (9), p and λ satisfy:
then \((z,u,\xi ) \in L^2(\varOmega ) \times H^1_0(\varOmega ) \times L^2(\varOmega )\) is called an S-stationary point.
Several comments on this system are necessary. To start, we note that if K0 is replaced by the entire space \(H^1_0(\varOmega )\), then ξ, λ and the conditions (9d)–(10b) vanish and we obtain the usual first-order system for a linear-quadratic PDE-constrained optimization problem with convex control constraints. Moreover, if there is no biactive set, then both (in fact all) dual stationarity concepts coincide. Thus, biactivity is essentially the source of all difficulties in the study of MPECs. We will see later that it also relates to the Gâteaux differentiability of the control-to-state map.
Perhaps the most critical point here is the usage of almost everywhere versus quasi everywhere conditions for the multipliers. As defined above, these S-stationarity conditions are not equivalent to the necessary first-order optimality conditions in the pioneering works [63, 64]; unless certain regularity assumptions on the active/biactive/inactive sets are made. In [63, 64] (see also [43, 80]), the notion of capacity (in contrast to Lebesgue measure) is used. This is because capacity is needed for the correct representation of the tangent/contingent cone and its polar. When replacing q.e. by a.e. some conditions become stronger and others finer.
In order to see this, suppose that meas(Ω0) = 0, but Cap2(Ω0, Ω) > 0. Then, (9i) would imply λ = 0 ∈ H−1(Ω). However, when using capacity, since the test functions ϕ admit quasi-continuous representatives, requiring ϕ = 0 “quasi-everywhere” (q.e.) on Ω0 would shrink the set of test functions so that λ is not necessarily zero. Similar problems arise by requiring a.e. instead of q.e. conditions on the adjoint variables p. Indeed, if Ω0+ has measure zero, then (9h) is trivially satisfied by any p; this would not be the case if we use q.e. since \(p \in H^1_0(\varOmega )\) admits a quasi-continuous representative.
Therefore, the stationarity conditions of Mignot and Puel, see (29) below, should be considered the true strong/S-stationarity conditions for our canonical MPEC as opposed to (9)–(10). For more complex constraints in which the image space of the constraint mapping is an Lp-space, as in, e.g.,[34, 35, 45], the problems with defining active sets up to sets of capacity zero seem to be absent.
Nevertheless, (9)–(10) arose naturally through the limiting process of an adaptive penalty scheme. As such, they are highly relevant for the study of numerical methods for elliptic MPECs, especially for methods utilizing smoothing plus continuation. In contrast, it is unclear how to properly include notions of capacity into efficient numerical methods (without simplifying assumptions as in [46]).
Finally, in many complex real-world applications, it might be impossible to obtain even C-stationarity conditions of this type, due to a lack of compactness and regularity properties. For example, in the optimal control of electrowetting on dielectrics [4], Allen-Cahn [27, 28], Cahn-Hilliard [20], or Cahn-Hilliard-Navier-Stokes system with obstacle potentials [47], one can usually only derive an approximation of (9g). Here, this would be equivalent to replacing (9g) by
for sequences \(\left \{\lambda _k\right \}\) and \(\left \{p_k\right \}\) with \(\lambda _k \rightharpoonup \lambda \) and \(p_k \rightharpoonup p\).
In conclusion, the various notions of dual stationarity and the theory needed to derive them are still active areas of research. The main point here is that there is a stratification of concepts that one should also be aware of when considering the design and convergence of numerical methods. That is, it is not enough to prove that a scheme converges but also to what kind of stationary point. Of course, many of the issues involving capacity, weak topologies, products of weakly convergent sequences, and weak lim-inf or lim-sup-type sign conditions will not necessarily appear in numerical experiments.
4 Regularization-Based Methods
In this and the coming sections, we present a number of numerical optimization methods for elliptic MPECs. These are split into two classes: Methods that employ adaptive smoothing, relaxation, or penalization of the forward problem or complementarity constraints (regularization-based methods) and those that do not (non-smooth methods).
We also note that the proper discretization of elliptic MPECs using (adaptive) finite elements schemes that take into account the additional difficulties due to the inherent degeneracy/non-smoothness has only been considered in a handful of papers. For example, we mention the most recent works [16, 17, 24, 37, 62]. For our numerical study, we make use of a simple finite difference scheme to discretize the operators along with a nested grid approach to simulate mesh refinements. This allows us to easily compare the methods.
The regularization-based methods all follow a similar scheme. First, the variational inequality is approximated by a parameter-dependent semilinear elliptic PDE or the complementarity constraint is relaxed or penalized. This yields in both cases a more tractable family of approximating optimization problems. Next, the smooth PDE-constrained problems are solved, yielding a parameter-dependent KKT point. Finally, continuation is performed on the regularization parameter (passing to 0 or + ∞).
The non-smooth methods are rather different and there is still plenty of room for new ideas. We only mention here that with these methods the emphasis is placed on directly solving the original, non-smooth problem without changing the forward problem. We postpone further details until later.
4.1 An Adaptive Penalty Method
We begin in the abstract framework of Section 2.5 and present a general approximation result as found in [7, Thm. 2.2]. For a comprehensive study on the numerical analysis and approximation of variational inequalities, see, e.g., [31]. In the following, ϕ𝜖 refers to some penalty functional for the constraint K.
Definition 4
For any constant 𝜖 > 0, let \(\phi ^{\epsilon }: V \to \mathbb {R}\) such that ϕε is convex and Fréchet differentiable on V and satisfies
-
1.
There exists a C, independent of 𝜖, u with ϕ𝜖(u) ≥−C(∥u∥V + 1) for all ε > 0, u ∈ V .
-
2.
ϕ𝜖(u) → iK(u) as 𝜖 ↓ 0 for all u ∈ V .
-
3.
For all u ∈ V and for all {u𝜖} such that \(u_{\epsilon } \rightharpoonup u\) as 𝜖 ↓ 0, liminf𝜖↓0ϕ𝜖(u𝜖) ≥ iK(u).
Remark 3
See also [7, Thm 2.4] for functionals on H, which is more relevant for (13).
In the abstract setting, we approximate (1) by
We denote the approximate solution mapping by S𝜖. For the next result, we restrict ourselves to the case when A is symmetric (as in Example 2), see [7, Thm. 2.2].
Theorem 4
Let w 𝜖 → w in V∗as 𝜖 ↓ 0, then the sequence {u𝜖}⊂ V with u𝜖 := S𝜖(w𝜖) converges weakly to u = S(w) as 𝜖 ↓ 0. If in addition,
then u 𝜖 → u (strongly in V ) as 𝜖 ↓ 0.
In the setting of Example 2, one possibility for ϕ𝜖 is:
Redefining K0 for L2-functions, ϕ𝜖 in (13) is the Moreau-Yosida regularization of the indicator functional \(i_{K_0}\) with respect to the L2-topology, cf. [5, Sec. 2.7]. However, in order to solve the smoothed MPECs numerically, we will require more smoothness of ϕ𝜖 below. We now approximate (5) by:
Thus, the existence theory, optimality conditions, and numerical methods for (14) reduces to results from PDE-constrained optimization.
Turning to Example 2, we employ a smoothed plus function in (11) characterized by:
We can then prove that the approximate solution mapping S𝜖 is Fréchet differentiable. Then, for a solution (z𝜖, u𝜖), there exists an adjoint state p𝜖 ∈ V such that
holds; cf. the techniques in [57, 77].
We note here that the case of gradient constraints mentioned in (3) can also be treated using such a penalty method. However, using a standard quadratic penalty/Moreau-Yosida-type approach yields a penalized state equation of the form:
which is considerably more challenging due to the bilinear dependence on u𝜖 in the PDE and accompanying non-smooth first-order PDE.
From (16), it is possible to derive C-stationarity conditions and, under further assumptions, even S-stationarity conditions, cf. [39, 40], by passing to the limit in 𝜖. More specifically, we show that a subsequence of stationary points for (16) converges to a point that satisfies C-stationarity for (7). Therefore, if we have a numerical method that solves (16), then by performing continuation on 𝜖 ↓ 0 we have a means of numerically approximating C-stationary points (or better) for (7). This furnishes a convergence proof in function space for the “outer loop” of the method, depicted in Algorithm 4.1. For the interested reader, we provide a short discussion of the limiting arguments in Detail 5.
Algorithm 4.1 Adaptive penalty method: outer loop

Detail 5 (Sketch of the Limiting Technique)
We first note that (16a) is equivalent to
Suppose Zad is bounded, then {z𝜖}𝜖>0 is bounded in Z. Let 𝜖k ↓ 0. Then, there exists a subsequence {zl} with \(z_{l} = z_{\epsilon _{k_l}} \stackrel {Z}{\rightharpoonup }\)z⋆ ∈ Zad. Hence, \(S_{\epsilon _{k_l}}(Bz_{l}) =: u_{l} \stackrel {V}{\to } u^{\star } = S(Bz^{\star })\) by Theorem 4 due to the complete continuity of B. Therefore, \(\xi _{l} \to \xi ^{\star } := Bz^{\star } + f -Au^{\star } \in -\mathcal {N}_{K_0}(u^{\star })\), i.e., ξ⋆, u⋆ satisfy. For the adjoint state p𝜖 and multiplier λ𝜖, we test the adjoint equation (16b) with p𝜖:
for scalars c1, c2 > 0, independent of 𝜖. Since \(u_{l} \stackrel {V}{\to } u^{\star }\), {pl} is bounded in V . Hence, there exists \(\{p_{l_m}\}\) with \(p_{l_{m}}\stackrel {V}{\rightharpoonup }p^{\star }\) and, by substitution, \(\lambda _{l_m} \stackrel {V^*}{\rightharpoonup } \lambda ^{\star } = u^{\star } -u_d +A^*p^{\star }\).
Without knowledge of the best possible system, one might stop at this point; however, the theory indicates that a much more refined system is possible. We quickly demonstrate (9g). The remaining conditions (9h), (9i) require lengthy arguments that go beyond the scope of this work. Returning to (16b), it is clear that
Since A is symmetric, the bilinear form a(⋅, ⋅) is weakly lower-semicontinuous. Moreover, due to the Rellich-Kondrachov theorem, both \(u_{\epsilon } \stackrel {H}{\to } u^{\star }\), \(p_{\epsilon } \stackrel {H}{\to }p^{\star }\). Thus,
In [7], a more general setting allows a similar argument. However in general, e.g., if A is not symmetric, we only have:
as mentioned at the end of Section 3.3. □
A possible stopping rule in Algorithm 4.1 could be the residual of the C-stationarity system (9) or when a minimum value of 𝜖k+1 is reached, e.g., machine precision. Obviously, the most computationally demanding part here is step 3. Assuming that \(\mathrm {Proj}_{Z_{\mathrm {ad}}}\) is relatively simple to calculate, e.g., for local bilateral constraints, then (16) reduces to
One could then solve (20) using, e.g., a semismooth Newton method. Alternatively, an interior point approach for the projection might be employed. We briefly recall the semismooth Newton method in infinite-dimensional spaces as discussed in [19, 38, 79]. Let X, Y be Banach spaces, D ⊂ X an open subset of X, and \(\mathcal {F}:D \to Y\).
Definition 5
The mapping \(\mathcal {F}:D \subset X \to Y\) is said to be Newton-differentiable on the open subset U ⊂ D, if there exists a family of mappings \(\mathcal {G}:U \to \mathcal {L}(X,Y)\) such that
\(\mathcal {G}\) is called the Newton derivative for \(\mathcal {F}\) on U. In [38], it is shown that
for every y ∈ X and \(\delta \in \mathbb {R}\) is a Newton derivative of the \(\max (0,\cdot )\), under the condition that \(\max (0,\cdot ):L^{p}(\varOmega ) \to L^{q}(\varOmega )\) with 1 ≤ q < p ≤∞.
Therefore, if a mapping \(\mathcal {F}\) is Newton-differentiable, then using the concepts above leads to a generalized Newton step for the equation \(\mathcal {F}(x) = 0\), see, e.g., [19, 38].
Theorem 6
Suppose that \(\mathcal {F}(x^*) = 0\) and that \(\mathcal {F}\) is Newton-differentiable on an open neighborhood U of x ∗ with Newton derivative \(\mathcal {G}\) . If \(\mathcal {G}(x)\) is nonsingular for all x ∈ U and the set\(\left \{||\mathcal {G}(x)^{-1}||{ }_{\mathcal {L}(Y,X)} : x \in U\right \}\)is bounded, then the semismooth Newton iteration
converges superlinearly to x ∗ , provided that ||x0 − x∗||Xis sufficiently small.
Under the assumption that \(Z_{\mathrm {ad}} := \left \{v \in L^2(\varOmega ) \left |\; a \le v \le b, \text{ a.e. } x \in \varOmega \right .\right \}\) with a, b ∈ L2(Ω) and a < b, we can derive a semismooth Newton step for the solution of (20) in function space: Fix some \((u,p) \in H^1_0(\varOmega ) \times H^1_0(\varOmega )\) and define the following subsets of Ω:
Moreover, let Ωina := Ω ∖ (Ωa ∪ Ωb) (up to a set of Lebesgue measure zero) and define the residual \(\mathcal {F}_{\epsilon }(u,p)\) of (20) by:
Since
we can use (21) to obtain a Newton derivative \(\mathcal {G}\) for \(\mathcal {F}\):
where \(\chi _{\varOmega ^{ina}}\) is the characteristic function for the set Ωina. If (δu, δp) denotes the difference between the new iterate and the current iterate in the semismooth Newton step, then at each iteration, we solve
If we can show that \(\mathcal {G}_{\epsilon }(u,p)\) is invertible independently of (u, p) (for fixed 𝜖 > 0) so that the set \(\left \{||\mathcal {G}_{\epsilon }(u,p)^{-1}||: (u,p) \in H^1_0(\varOmega )\times H^1_0(\varOmega ) \right \}\) is bounded, then we are guaranteed to have local superlinear convergence. This leads to Algorithm 4.2.
Algorithm 4.2 Adaptive penalty method: inner loop

We conclude this subsection with a numerical experiment. This is used in part to compare to the non-smooth numerical methods in later sections.
Example 3
Let Ω = (0, 1)2, α = 1, b ≡ 0.035, a ≡ 0, and A = −Δ (associated with \(H^1_0(\varOmega )\)). Defining
we set
The example is chosen due to the nontrivial biactive set and overlap of active sets for the control and state constraints. The only change to [40, Exp. 5.1] is the addition of control constraints, which were set to ±∞ there. Concerning the discretization and solution, we use a standard five-point stencil to discretize the negative Laplace operator with finite differences. The problem is solved on a uniform mesh with 5122 grid points.
We start the algorithm at (z0, u0, ξ0) = (0, 0, 0). The stopping criterion is based on the L2-norm of the residual with stopping tolerance of 10−9. For this example, the 𝜖-update in 4.1 proved to be extremely sensitive, meaning that a reasonably aggressive update strategy, e.g., 𝜖k+1 = 𝜖k∕2 failed once \(\epsilon _{k} = \mathcal {O}(10^{-4})\). To be fair, one would normally not cold-start this algorithm on such a fine grid. Opting instead for either an adaptive FEM strategy, multigrid scheme (as in [40]), or a nested grid strategy (as in [39, 46]) would certainly improve the performance and allow for a more aggressive update strategy for the smoothing parameter. Nevertheless, we see that as the penalized problem approaches the original non-smooth non-convex problem, the nonlinear system becomes increasingly more difficult to solve (eventually even failing). See Table 1 for the convergence history and Figure 1 for plots of the solution.
Solution plots for adaptive penalty method Algorithms 4.1 and 4.2, clockwise from upper left: characteristic function \( \chi _{\varOmega ^{0}_{\star }}\) optimal control z⋆, state u⋆, multiplier λ⋆, adjoint p⋆, and multiplier ξ⋆. Notice the nontrivial biactive set for the variational inequality and the upper and lower active sets for the control constraints
4.2 An ℓ1 Penalty Method
In this subsection, we present a technique originating in the finite-dimensional MPEC literature [3]. The extension to infinite dimensions can be found here [43]. The idea is elegant in its simplicity and allows us to approximate the elliptic MPEC by a sequence of PDE-constrained optimization problems with control and state constraints. Moreover, instead of a semilinear elliptic PDE, as in the previous method, we have a linear elliptic PDE. We begin in the abstract framework of Section 2.5 under the assumption that K is a cone and then pass to the problem in Example 2.
Using an ℓ1-penalty for the condition 〈u, ξ〉 = 0, we approximate (6) by




By definition of K+, 〈u, ξ〉≥ 0. Hence, for (u, ξ) ∈ K × K+, \(\frac {1}{\epsilon }|\langle u,\xi \rangle | =\frac {1}{\epsilon }\langle u,\xi \rangle \), which yields the smooth objective \(J_{\epsilon }(z,u,\xi ):=J(z,u) + \frac {1}{\epsilon }\langle u,\xi \rangle \).
The analysis for this problem requires several technical results. Nevertheless, under appropriate regularity and boundedness assumptions, one can still show existence of a solution, consistency of the approximation, derive first-order conditions and (after passing to the limit in 𝜖) obtain a (weak) form of C-stationarity. We briefly sketch the ideas here and refer the reader to [43, Section 2] for the detailed technical analysis in the context of Example 2.
Detail 7 (Sketch of Existence and Consistency Arguments)
In addition to the assumptions in Theorem 2, let F be weakly lower-semicontinuous, Zad bounded, and A symmetric.
To show that (25) has a solution, we prove the boundedness of infimizing sequence {(zk, uk, ξk)} (despite the unboundedness of K+ and lack of coercivity of J𝜖(z, u, ξ)). Let (z0, u0, ξ0) be feasible for (6). Then, for all sufficiently large k ∈ N,
Hence, \(J(z_0,u_0) - G(z_k) \ge \frac {1}{\epsilon }\langle u_k, \xi _k\rangle \ge 0\). Since Zad is bounded, there exists a weakly convergent subsequence \(\{z_{k_l}\}\) with \(z_{k_l} \rightharpoonup z^{\star } \in Z_{\mathrm {ad}}\). Then, by the weak lower-semicontinuity of G, we have
Thus, testing (25c) with \(u_{k_l}\), we first obtain the boundedness of \(\{u_{k_l}\}\) in V and then \(\{\xi _{k_l}\}\) in V∗. Given A is symmetric, we use an argument as in (19) to prove that (along a further subsequence \(\{k_{l_m}\}\)) \(\liminf _{m} \langle u_{k_{l_m}}, \xi _{k_{l_m}}\rangle \ge \langle u^{\star },\xi ^{\star }\rangle \), where u⋆ and ξ⋆ are the weak limit points. Since K and K+ are weakly closed, u⋆ ∈ K and ξ⋆ ∈ K+. This suffices to prove that (25) has a solution. A proof for consistency of the approximation, i.e., that global optimizers {(z𝜖, u𝜖, ξ𝜖)} converge as 𝜖 ↓ 0 (at least along a subsequence) to a global optimizer {(z⋆, u⋆, ξ⋆)} of (6) can be derived analogously using the boundedness of {z𝜖}⊂ Zad and subsequently, the inequality 𝜖(J(z0, u0) − G(z𝜖)) ≥〈u𝜖, ξ𝜖〉≥ 0. □
As in Section 4.1, we restrict ourselves to the setting of Example 2 for the derivation of stationarity conditions. Here, the derivation of first-order optimality conditions requires the verification of a constraint qualification, in this case that of Robinson-Zowe-Kurcyusz, see [88]. According to Propositions 2.5 and 2.6 in [43], we have the following 𝜖-dependent first-order optimality conditions: For any solution (z𝜖, u𝜖, ξ𝜖) to (25) (under the data assumptions of Example 2), there exists a multiplier-tuple (p𝜖, 𝜗𝜖, τ𝜖) such that
In comparison, this system is much larger than (16) and contains additional information. Nevertheless, under certain boundedness assumptions, passing to the limit in 𝜖 yields, in fact, a weaker C-stationarity system, see [43, Thm. 2.9]:
To see that (28e) relates to (9h), (9i) suppose for the sake of argument that ξ⋆, p⋆, λ⋆ are merely vectors of length n and the conditions in (28e) are understood as the componentwise (Hadamard) products. Then, by complementarity, ξ⋆ ≥ 0 and \(\xi ^{\star }_i = 0\) if i is an inactive or biactive index and 〈p⋆, ξ⋆〉 = 0 in turn implies that the strongly active components of p⋆ are zero (as in (9h)). The same applies to the inactive components of λ⋆ due to 〈λ⋆, u⋆〉 = 0 (as in (9i)).
Though there is a significant gap, the derivation of (28) is related to the convergence of a function-space-based numerical method. Indeed, using known results for linear elliptic PDE-constrained optimization problems with control and state constraints, we have viable efficient algorithms that can guarantee convergence to a KKT point, which satisfies (27). By performing continuation on 𝜖 we can be assured to converge (along a subsequence) to a weak C-stationary point. Furthermore, Theorem 2.12 in [43] provides a more compelling argument.
Theorem 8 (Thm 2.12 [43])
Suppose (z𝜖, u𝜖, ξ𝜖, p𝜖, 𝜗𝜖, τ𝜖) satisfies (27) and that (z𝜖, u𝜖, ξ𝜖) is feasible for (7). Then, (z𝜖, u𝜖, ξ𝜖) is strongly stationary in the sense of Mignot and Puel, i.e., conditions (9h)–(10b) are replaced by
Since we are using an ℓ1 penalty, which often amounts to an exact penalty function, there is a good chance that a stationary point (z𝜖, u𝜖, ξ𝜖) is feasible for (7) for sufficiently small 𝜖.
Algorithm 4.3 ℓ1 penalty method: outer loop

Again we might choose as a stopping criterion the residual of C-stationarity, taking λ := 𝜖−1ξ − 𝜗 and substituting τ = 𝜖−1u − p. Since the theory only guarantees 𝜗 ∈ H−1(Ω), one will need to treat the discrete quantities carefully, cf. [43] for more details. In addition, the solution of the subproblems (25) does not reduce to the solution of a system similar to (20). Therefore, the solution of the subproblems can be more difficult than in the adaptive penalty framework. Nevertheless, the theoretical result in Theorem 8 indicates the potential of this algorithm to generate a better stationary point.
5 Non-Smooth Numerical Methods
In this section, we present several methods that do not require a smoothing or penalization of the original MPEC. We present a new approximate projected subgradient method alongside a direct solver for the C-stationarity system presented in [36] and a recent method from [46] that may serve as a globalization of the direct solver. In all of these methods, we need to solve the variational inequality (1). This can be done using the semismooth Newton methods as in [38, 41] or special monotone multigrid methods as in [55].
5.1 An Approximate Projected Subgradient Method
The subgradient method is perhaps the simplest non-smooth optimization algorithm. Suppose X is a real separable Hilbert space. Given a proper, convex, lower-semicontinuous, and subdifferentiable functional \(f: X \to \mathbb {R}\), x0 ∈ X, g0 ∈ ∂f(x0), and a sequence {νk} with νk > 0, compute a sequence of iterates {xk} according to the rule
Here, and unless otherwise noted below, we would need to apply the Riesz map to gk before using it in this iteration.
Similarly, given a non-empty, closed, and convex subset C ⊂ X the projected-gradient method replaces the previous rule by
The subgradient method was invented by N.Z. Shor in the 1970s, see [76], and although it does not guarantee descent of the objective functional and can be quite slow to converge, it still finds a wide array of applications due to its simplicity and ability to be combined with distributed algorithm techniques, as in, e.g., [78].
Consider the reduced elliptic MPEC in (5):
Since S is nonlinear, the reduced objective functional is typically non-convex. Therefore, we cannot directly apply the projected subgradient method. However, there exist a number of generalized subdifferentials for non-convex functions. In our case, we will initially make use of the limiting subdifferential (also known as the Mordukhovich subdifferential) for the reduced objective. We will restrict ourselves to the framework of Example 2. First, we recall several definitions from variational analysis, see [66].
Definition 6 (Normal Cones to Arbitrary Sets)
Let X be a Hilbert space and C ⊂ X. Then, the multifunction \(\widehat {\mathcal {N}}_{C}:X \rightrightarrows X^*\) defined by
and \(\widehat {\mathcal {N}}_C(x):=\emptyset \) for x∉C is called the regular (Fréchet) normal cone to C. The multifunction \(\mathcal {N}_{C}:X\rightrightarrows X^*\) defined by
is called the limiting (Mordukhovich) normal cone to C.
Although \(\widehat {\mathcal {N}}_{C}\) is convex, it fails to admit a satisfactory calculus needed for most non-smooth, non-convex problems. In contrast, the limiting normal cone enjoys a robust calculus. Note that for closed convex sets C, both cones agree, and in general \(\widehat {\mathcal {N}}_{C}(x) \subsetneqq \mathcal {N}_{C}(x)\). We will use the limiting normal cone to define a generalized subgradient, needed in part for our proposed numerical method.
Definition 7 (Limiting Subdifferential)
Let X be a Hilbert space, \(\phi :X \to \overline {\mathbb {R}}\), and x ∈ X such that |ϕ(x)| < +∞. The set
is called the limiting (Mordukhovich) subdifferential. If |ϕ(x)| = ∞, we set ∂ϕ(x) = ∅.
Therefore, if we know the limiting subdifferential \(\partial \mathcal {J}(z)\) in (5), then we could design a projected subgradient iteration along the lines of (30):
If \(\mathcal {J}\) were smooth, then \(\partial \mathcal {J}\) is just the gradient of the reduced objective functional, which we usually calculate in PDE-constrained optimization by solving an adjoint equation. However here, \(\mathcal {J}\) is non-smooth and non-convex. In order to obtain a generalized adjoint state for the reduced objective functional we require the so-called “coderivatives.”
Definition 8 (Coderivatives)
Let X be a Hilbert space, \(\varPhi :X \rightrightarrows X^*\), and y ∈ Φ(x), i.e., \((x,y)\in \mathop {\mathrm {Graph}}\varPhi \). The regular (Fréchet) coderivative of Φ at (x, y) is the multifunction \(\widehat {D}^*\varPhi (x,y)\colon Y^*\rightrightarrows X^*\) defined by
The limiting (Mordukhovich) coderivative D∗Φ(x, y) of Φ at \((x,y)\in \mathop {\mathrm {Graph}}\varPhi \) is similarly defined by
For example, if Φ = S𝜖 from Section 4.1, then the coderivatives coincide and we have:
i.e., \(\widehat D^*S_{\epsilon }(w,u)(w^*)\) yields the usual adjoint state p obtained by solving the associated linear elliptic PDE with − w∗ on the right-hand side.
For the tracking-type objective in Example 2, it was argued in [44, Prop. 1] that
Here, it follows from [66, Thm 4.44] that p ∈ D∗S(Bz, u)(u − ud) is a solution to the generalized adjoint equation:
where \(\xi = Bz + f - Au \in \mathcal {N}_{K_0}(u)\). Therefore, assuming that (37) were solvable, we could fashion our projected subgradient method as in Algorithm 5.4.
Algorithm 5.4 Limiting projected subgradient algorithm

Since we have no efficient means of handling \(D^* \mathcal {N}_{K_0}(u^{k+1},\xi ^{k+1})(p)\), Algorithm 5.4 is impractical, especially when we consider that subgradient methods potentially require many iterations even for favorable convex problems. We therefore propose an alternative in Algorithm 5.5. The formal derivation for the approximate generalized adjoint state is based on simple geometric observations for a related finite-dimensional setting.
Consider that the (convex) normal cone \(\mathcal {N}_{K_0}\) is generated by the (convex) subdifferential of the indicator functional \(i_{K_0}\). Since the functionals ϕ𝜖 in (13) converge in a variational sense to \(i_{K_0}\), they provide a viable candidate for approximating elements of \(\mathcal {N}_{K_0}\). Moreover, for any u ∈ V , ∇ϕ𝜖(u) = −𝜖−1(−u)+. Comparing as 𝜖 ↓ 0, it appears (at least in finite dimensions) that \( \mathop {\mathrm {Graph}} \nabla \phi ^{\epsilon } \to \mathop {\mathrm {Graph}} -\mathcal {N}_{K_0}\), see Figure 2. This behavior transfers to \(\widehat {\mathcal {N}}_{ \mathop {\mathrm {Graph}} -\mathcal {N}_{K_0}}(u,\xi )\) and \(\widehat {\mathcal {N}}_{ \mathop {\mathrm {Graph}} \nabla \phi ^{\epsilon }}(u,\xi )\), cf. Figure 2 with \(\varTheta := \mathop {\mathrm {Graph}} -\mathcal {N}_{\mathbb {R}_+}\) and \(\varLambda := \mathop {\mathrm {Graph}} \nabla \phi ^{0.1}\).
From left to right: \( \mathop {\mathrm {Graph}} \nabla \phi ^{\epsilon }\) (𝜖 = 1, 0.5, 0.1) versus \( \mathop {\mathrm {Graph}} \mathcal {N}_{ \mathbb {R}_+}\); \(\widehat {\mathcal {N}}_{ \mathop {\mathrm {Graph}} -\mathcal {N}_{ \mathbb {R}_+}}(u,\xi )\) for (u, ξ) = (1, 0), (0, 1), (0, 0); \(\widehat {\mathcal {N}}_{ \mathop {\mathrm {Graph}}\nabla \phi {0.1}}(u,\xi )\) for (u, ξ) = (1, 0), (0, 1), (0, 0)
Using the information in Figure 2, we can first calculate the limiting normal cones \(\mathcal {N}_{\varTheta }(u,\xi )\), from which we obtain: \(D^*\mathcal {N}_{\varTheta }(1,0)(p) = \{0\}, \text{ for all } p,\) and
otherwise \(D^*\mathcal {N}_{\varTheta }(0,1)(p) = \emptyset \). The most interesting case is:
Similarly, we have for all p
and
Though certainly more tractable numerically, \(D^*\mathcal {N}_{\varLambda }\) is still a set-valued mapping with non-convex images. We therefore suggest the following single-valued mapping:
where χ{u=0} is the characteristic function for the active set. This mapping coincides with the limiting coderivative \(D^*\mathcal {N}_{\varTheta }\) on the inactive set and strongly active set, whenever \(D^*\mathcal {N}_{\varTheta }\) is non-empty. On the biactive set, it is either contained in \(D^*\mathcal {N}_{\varTheta }\) or approaches it for 𝜖 ↓ 0, cf. Figure 3.
By extrapolating these ideas from this simple one-dimensional geometric study to the infinite-dimensional setting, we arrive at our proposed algorithm.
Algorithm 5.5 Approximate projected subgradient algorithm

Remark 4
In fact, − χ{u≤0}p is nothing more than the adjoint of the Newton derivative for the non-smooth Nemytskii operator \((- \cdot )_+ : H^1_0(\varOmega ) \to L^2(\varOmega )\).
Using the analytical techniques described throughout the text, we have the next result.
Theorem 9
Suppose that Z ad is bounded. Then, any sequence {(zk, uk, ξk, pk, λk)}⊂ Z × V × V∗× V × V∗generated by Algorithm5.5is bounded. Here,
Moreover, any weak accumulation point of (z⋆, u⋆, ξ⋆, p⋆, λ⋆) will be feasible for (7) and we have
Proof
Since Zad is bounded, {zk} is bounded in Z. It immediately follows that {uk} is bounded, since
and ξk = Bzk + f − Auk. Similarly, we obtain the boundedness of {pk} in V and {λk} in V∗:
and λk = ud − uk − A∗pk. Furthermore, since
the limit condition in (38) holds. Moreover, will can again show that 〈λ⋆, p⋆〉≤ 0 using the same argument as in (19) and by definition 〈λk, uk〉 = 0. Since B is compact, uk → u⋆ in V (along a subsequence). This yields 〈λ⋆, u⋆〉 = 0.
The purpose of Theorem 9 is to show that Algorithm 5.5 produces a sequence with a weak accumulation point that satisfies a kind of limiting C-stationarity system. However, the lag in indices prevents us from closing the argument by proving that {zk} fulfils (9) (regardless of whether we choose fixed, bounded, or diminishing step sizes). Nevertheless, we will see later in the bundle-free approach that a variant of our approximate adjoint equation can under certain circumstances yield descent directions for the reduced objective.
We now demonstrate the performance of the algorithm on an example with a nontrivial biactive set: Example 3. In order to assure feasibility at every step, we solve the variational inequality with the primal-dual active set (PDAS)/semismooth Newton method from [38]. Note that although the solver for the variational inequality is mesh dependent, the majority of the linear solves are done within the first four iterations, see Table 2. For a graph of the behavior of the residuals as well as plots of the solution, see Figure 4.
Clockwise from upper left: residual of strong stationarity for Algorithm 5.5, optimal control z⋆, state u⋆, multiplier λ⋆, adjoint p⋆, and multiplier ξ⋆
We again use a uniform grid with 5122 grid points and start the algorithm at (z0, u0, ξ0) = (0, 0, 0). We choose the a priori step sizes νk := (k)−1∕2 and update 𝜖k according to 𝜖k := 10−4∕2k. The inner PDAS solver stops once the residual of the non-smooth system of equations reaches a tolerance of 10−10. Though the theory does not provide a stopping criterion, we check the residual of strong stationarity, which reaches \(\mathcal {O}(10^{-9})\) after 30 iterations. The residual is calculated using a discrete approximation of the following quantity:
Despite lacking a convergence theory, the algorithm performs very well on this large-scale nontrivial problem. Indeed, counting all the free variables (z, u, ξ, etc.) there are over 106 degrees of freedom. Moreover, the presence of biactivity means that the example considered is genuinely non-smooth and non-convex. This is particularly encouraging, as the algorithm clearly outperforms the adaptive penalty method in terms of ease of implementation, size and structure of the systems of linear equations, and order of accuracy (almost reaching even strong stationarity). In particular, we note the stark contrast to the “sharpness” of the solution in comparison to the smooth method.
5.2 A Direct Solver for C-Stationarity Conditions
In this section, we adapt a method from [36] to the canonical MPEC (7). We work in the setting of Example 2 and assume that
with a, b ∈ L2(Ω), a < b. We first state the algorithm. Then, we motivate the steps of the algorithm and discuss its convergence properties.
The formal derivation of Algorithm 5.6, which we describe in detail below, follows several basic steps: Fix a control and estimate the active and inactive sets; ignoring biactivity, use (28e) to approximate (28b)–(28e) as a system of equations; solve the reduced system (including (28a)) to obtain an update; test the residual of C-stationarity, if necessary, return to 1.
Algorithm 5.6 An active-set equality-constrained newton solver w. Feasibility restoration

More specifically, suppose we are in the infinite-dimensional setting. Assuming that ξ⋆ is sufficiently regular, then Equations (28c), (28d) can be understood as the following system of smooth and non-smooth equations:
where c > 0 is some scaling constant. Since ξ⋆ ∈ L2(Ω), the Newton derivative for the plus function described at the end of Section 4.1 is not valid in this setting (since both the domain and range here must be taken as L2(Ω)). On a discrete level, this is not an issue. For some fixed z⋆, solving (40) gives a pair (u⋆, ξ⋆) along with active and inactive sets:
As in our discussion of (28), if we treat the variables u⋆, λ⋆ as finite-dimensional vectors and the complementarity condition as the pointwise product of u⋆ and λ⋆, then the complementarity condition would indicate that λ⋆ = 0 on the inactive set. Analogously, we take p⋆ = 0 on the (entire) active set, thus ignoring biactivity. Consequently the remaining sign condition in (28) holds. Finally, using the projection formula (23) along with a semismooth Newton step, we can handle the variational inequality (28a). We recall the sets
and Ωina := Ω ∖ (Ωa ∪ Ωb).
Now, supposing we want a new approximation (u⋆, z⋆, p⋆) via u⋆ + δu, z⋆ + δz, and p⋆ + δp, we consider the reduced system by eliminating the dual variables:
If we replace δz in (41d), then we get the smaller system in (δu, δp):
which is remarkably similar to the semismooth Newton step in the adaptive penalty method. Unlike the smooth methods, however, a proof of convergence remains elusive. The main culprit here is clearly the sequence \(\{\varOmega ^+_k\}\), which need not converge with respect to any notion of set convergence, e.g., Painlevé-Kuratowski or in the sense of characteristic functions.
Note also that this formally derived system is well-defined in function space provided that we have enough regularity. For example, provided that the sets Ω+(u⋆), Ω0(u⋆) are sufficiently regular, we could reduce the search for \((\delta u, \delta p) \in \mathcal {H} \times \mathcal {H}\) with \(\mathcal {H} := H^1_0(\varOmega ^+(u^{\star }))\), solve the associated weak form of (42a), (42b), and extend the solutions by zero on Ω0(u⋆).
An obvious stopping criterion for Algorithm 5.6 would be the residual of (28) up to some user-defined tolerance (as suggested in [36]). Moreover, we see that the computational effort is roughly that of the adaptive penalty method. In fact, there is much less nonlinearity here due to a lack of the penalty terms ϕε. We also mention that the MPECs in [36] are much more challenging than (7), as the controls there arise inside the differential operator. Nevertheless, the algorithm seems to perform very well, even on examples with nontrivial biactive sets.
We demonstrate the performance of Algorithm 5.6 on Example 3. As expected, Algorithm 5.6 behaves like a second-order method, see Table 3. We once again used the PDAS/semismooth Newton method in [38] to restore feasibility at every step. Moreover, since the multiplier λ is eliminated from the algorithm, we artificially reintroduce it for the calculation of the residuals.
The solutions look identical to those plotted in Figure 5. We therefore only provide images of the biactive sets for y⋆ and upper and lower active sets for z⋆. We note that this algorithm also performs quite well, reaching a residual of strong stationarity on the order of \(\mathcal {O}(10^{-8})\) within k = 5 iterations, though it never reaches \(\mathcal {O}(10^{-9})\) in contrast to the approximating subgradient algorithm. In addition, the effort to solve each step is higher, as seen in Table 4.
Plot of solutions using Algorithm 5.6. Left to right: characteristic functions \(\chi _{\varOmega ^{00}_{\star }}\)(set of all indices with \(u^{\star }_i \le \)1e−8 and \(\xi ^{\star }_i \le 0\)), \(\chi _{\varOmega ^{b}_{\star }}\) (set of all indices with \(z^{\star }_i \le b_i-\)1e−6), and \(\chi _{\varOmega ^{a}_{\star }}\) (set of all indices with \(z^{\star }_i \ge a_i+\)1e−6)
Our next non-smooth method seeks to overcome the theoretical deficiencies of Algorithm 5.5 and 5.6. In some sense, it takes a step towards bridging the gap between this active-set-based solver and the approximate projected subgradient method in the previous subsection.
5.3 The Bundle-Free Implicit Programming Method
We now present the bundle-free implicit programming approach from [46], which we extend for control constraints. In contrast to the active-set method in the previous subsection, this method is based off of B-stationarity conditions. We must therefore assume that S is directionally differentiable.
We first state the basic assumptions and the algorithm. Afterwards, we discuss the motivations for the steps and examine the convergence properties. Throughout this subsection, let \(Z_{\mathrm {ad}} := \left \{z \in L^2(\varOmega ) \left |\; a \le z \le b \right .\right \}\) with a, b ∈ L2(Ω) and a < b and assume that the variational inequality is defined as in (7). We otherwise work in the abstract framework of (6), where \( \mathcal {J}(z) := F(S(B z)) + G(z) \) and F and G are continuously Fréchet differentiable. By assumption, ξ ∈ H.
For some constant cq > 0, let q(⋅) := cq∥⋅∥2∕2 and for z ∈ Zad define the local quadratic models:
where d𝜖(⋅) is a smooth approximation of S(Bz;⋅) such that d𝜖(0) = 0. Here, we suggest letting d𝜖(w) = d, the solution to
where w ∈ V∗, 𝜖 > 0, and u = S(Bz). This is related to the true formula for d = S′(Bz;w) given by
where \( \mathcal {K}(u,\xi ): = \left \{ u \in H^1_0(\varOmega ) \left |\; d(x) \ge 0,\; \text{ q.e. } x \in \varOmega ^{0},\; d(x) = 0. \text{ a.e. }x \in \right .\right .\)\(\left .\left .\varOmega ^{0+}\right .\right \};\) see [63] (or [15, Chap. 6] for an English summary). As this formula makes use of quasi-continuity and potentially non-negligible sets of Lebesgue measure zero, it is unclear how to make direct use of the nonnegativity condition in a numerical method. To circumvent this issue, a certain regularity condition is assumed throughout (as in [46]):
-
1.
\(\varOmega ^{0} = \overline {\text{int}(\varOmega ^{0})},\)
-
2.
If m(Ω00) = 0, then cap(Ω00) = 0 or S′(Bu;Bh) = d = 0 q.e. x ∈ Ω0.
-
3.
\(\text{ If } m(\varOmega ^{00}) > 0, \text{ then } \exists \nu > 0, \exists \gamma ' > 0: \forall \gamma \ge \gamma ', d_{\gamma ,\varepsilon } \ge 0,\,a.e.\, \mathcal {A}_{\nu }\setminus \varOmega ^{0})\\ \text{where } \mathcal {A}_{\nu } := \left \{x \in \varOmega \left | \text{dist}(x,\varOmega ^{0}) < \nu \right .\right \}. \)
In light of this assumption, we speak of “negligible” biactive sets whenever m(Ω00) = 0. Note that S is in fact Gâteaux differentiable, whenever this condition holds. This once again highlights a fundamental difference between the optimal control of PDEs and variational inequalities, even for the simplest variational inequality of interest.
We also suggest the smooth approximation of the directional derivative in order to guarantee that \(p_{\epsilon } = d^{\prime }_{\epsilon }(0)^*w\) solves
and that {p𝜖}𝜖>0 is uniformly bounded in V . Notice the similarity to the approximating limiting subgradient suggested earlier.
Algorithm 5.7 A bundle-free implicit programming approach

In Algorithm 5.7, \( \mathcal {T}_{Z_{\mathrm {ad}}}(z)\) is the tangent cone to Zad at z ∈ Zad, which is defined by
We use the generalized Armijo line search (cf. [13].): Set \(\tau ^k := \beta ^{m_k} s\) where mk is the first nonnegative integer such that
where β, σ ∈ (0, 1), s > 0 and, given a step δz, we set
Since much of Algorithm 5.7 is derived from B-stationarity conditions, we restate them here:
From (47), it is clear that we can equivalently reformulate B-stationarity as:
Moreover, since \(\mathcal {J}'(z;\delta z)\) is positively homogeneous in δz, it follows that δz = 0 is a minimizer of \(\mathcal {J}'(z;\delta z)\) over \(\mathcal {T}_{Z_{\mathrm {ad}}}(z)\), whenever z is B-stationary. Finally, given that \(\mathcal {T}_{Z_{\mathrm {ad}}}(z)\) is a non-empty, closed, and convex cone, we can add the coercive quadratic form q to the definition of B-stationarity without altering the characterization, cf. the general analysis in [46, Section 2]. Therefore, if z is B-stationary, then 0 ∈ Z solves the auxiliary problem
Now, if the biactive set is negligible, then S is in fact Gâteaux differentiable. In this case, (48) has a unique solution given by
which, noting that \( \nabla \mathcal {M}(0) = B^*S'(Bz)^*\nabla F'(S(Bz)) + \nabla G(z)\), is equivalent to (??). Furthermore, in this smooth setting, we can prove the following result.
Proposition 1
Let z ∈ Zad, u = S(Bz), ξ = Au − Bz − f, and suppose that\(\mathcal {J}\)is Gâteaux differentiable at z. If z is not B-stationary, then (46) stops in a finite number of steps.
Proof
Suppose δz is given by the projection formula (??). Since δz is the unique global optimum and \(0 \in \mathcal {T}_{Z_{\mathrm {ad}}}(z)\), we have
Moreover, for any τ > 0, we have \(z(\tau ) := \mathrm {Proj}_{Z_{\mathrm {ad}}}(z-\tau \delta z)\) and since \(\mathrm {Proj}_{Z_{\mathrm {ad}}}\) is non-expansive:
Furthermore, since z ∈ Zad, \(\delta z \in \mathcal {T}_{Z_{\mathrm {ad}}}(z)\), and Zad is defined by simple pointwise bound constraints in L2(Ω), we appeal to the proof of Lemma 6.34 [15], which shows that
Finally, suppose that (46) fails for all τ > 0. Then,
On the right side of the inequality, we can estimate from below using (50):
Now, letting z(τ) = z + ττ−1(z(τ) − z) = z + τdτ, where dτ → δz by (51), we have by (49):
But, then
a contradiction, since σ ∈ (0, cq∕2).
Proposition 1 provides a justification for steps 4:–6: in Algorithm 5.7. Note that the calculation of the gradient \(\nabla \mathcal {M}^k(0)\) requires the solution of an adjoint equation. For example, in the setting of Example 2, \(\nabla \mathcal {M}^k(0) = \alpha z^k - B^*p^k\), where pk solves (here in strong form):
Turning now to the case when the biactive set is non-negligible, we can easily adjust the proof of Proposition (1) for the non-smooth setting.
Corollary 2
Let z ∈ Zad, u = S(Bz), ξ = Au − Bz − f, and suppose that δz is minimizer for (48). If z is not B-stationary, then (46) stops in a finite number of steps.
Nevertheless, whenever the biactive set is non-negligible, the directional derivative is nonlinear in δz. In particular, (48) is non-convex, which was a key assumption in the arguments. We therefore need an alternative procedure to calculate the step δz.
In Algorithm 5.7, we suggested the step \( \delta z = \mathrm {Proj}_{\mathcal {T}_{Z_{\mathrm {ad}}}(z^k)}\left [-c_q^{-1} \nabla \mathcal {M}^k_{\epsilon ^k}(0)\right ], \) which is related to the smoothed auxiliary problem using the 𝜖-dependent model \(\mathcal {M}_{\epsilon }\):
Note if the approximation was chosen so that d𝜖 → S and 0 solves (53) for all sufficiently small 𝜖 > 0 (or at least along some null sequence), then z must be B-stationary as 0 solves (48), as well. In fact, in the current setting, A is symmetric so we can use the approximation results in [7] (discussed above), see also [46], to argue that if δz𝜖 → δz weakly in L2(Ω), then
provided that B is completely continuous, e.g., when B is the embedding of L2(Ω) into H−1(Ω).
On the other hand, if there exists some \(\delta z \in \mathcal {T}_{Z_{\mathrm {ad}}}(z)\) such that \( ( \nabla \mathcal {M}_{\epsilon }(0), \delta z ) < 0, \) then by continuity, there is some η𝜖 > 0 such that \(\mathcal {M}_{\epsilon }(\eta _{\epsilon } \delta z) < 0\). Since \(\mathcal {T}_{Z_{\mathrm {ad}}}(z)\) is a cone, \(\eta _{\epsilon } \delta z \in \mathcal {T}_{Z_{\mathrm {ad}}}(z)\) and 0 does not solve (53). If this persists as 𝜖 ↓ 0, then z cannot be B-stationary.
In light of this, consider our δz update. Let \(w := d^{\prime }_{\epsilon }(0)^*F'(z) + G'(z) = \nabla \mathcal {M}_{\epsilon }(0)\) and note that
where \(\varOmega ^{a} := \left \{x \in \varOmega \left |\; z(x) = a(x) \right .\right \}\), \(\varOmega ^{b} := \left \{x \in \varOmega \left |\; z(x) = b(x) \right .\right \}\) and Ωina := Ω ∖ (Ωa ∪ Ωb). Then, using the basic properties of \(\mathrm {Proj}_{\mathcal {T}_{Z_{\mathrm {ad}}}(z)}\), we have
Assuming that the latter term is nonzero and expanding \(\mathcal {M}_{\epsilon }\) at zero in direction δz, we obtain:
We may then choose a sufficiently small η𝜖 > 0 such that
Hence, \(\mathcal {M}_{\epsilon }(\eta _{\epsilon } \delta z) \le 0\) and by definition
Therefore, if a uniform lower bound η > 0 with η𝜖 ≥ η > 0 exists, then we can prove that δz𝜖 is a descent direction for some sufficiently small 𝜖 > 0.
Proposition 2
Let z ∈ Zad, u = S(Bz), and ξ = Au − Bz − f and suppose that\(\mathcal {J}\)is only directionally differentiable at z. Furthermore, let\( \delta z_{\epsilon } = \mathrm {Proj}_{\mathcal {T}_{Z_{\mathrm {ad}}}(z)}\left [-c_q^{-1} \nabla \mathcal {M}_{\epsilon }(0)\right ] \)and assume that\( \limsup _{\epsilon \downarrow 0} ( \nabla \mathcal {M}_{\epsilon }(0),\delta z_{\epsilon }) < 0. \)If there exists an η > 0 such that\(\mathcal {M}_{\epsilon }(\eta \delta z_{\epsilon }) \le 0\)for all sufficiently small 𝜖 > 0, then there exists some\(\widehat {\epsilon } > 0\)such that\(\delta z_{\widehat {\epsilon }}\)is a descent direction for\(\mathcal {J}\)at z.
Proof
By assumption, F′(z;d𝜖(B(ηδz𝜖)) + G′(z)(ηδz𝜖) ≤−η2q(δz𝜖). Then,
Now, since \(\left \{p_{\epsilon }\right \}\) is bounded, we can show that \(\left \{\delta z_{\epsilon }\right \}\) is bounded. Hence, there is a subsequence (denoted still by 𝜖) such that \(\delta z_{\epsilon } \rightharpoonup \delta z^*\). Then, for sufficiently small \(\widehat {\epsilon } > 0\)
Hence, \( \mathcal {J}'(z; \delta z_{\widehat {\epsilon }}) \le -c_{q}\eta \|\delta z_{\widehat {\epsilon }}\|{ }^2/4, \) as was to be shown.
Since a direct verification of the hypotheses is potentially too expensive from a computational standpoint, we suggest a heuristic. Fix a lower bound \( \underline {\eta } > 0\). If \((\nabla \mathcal {M}_{\epsilon }(0),\delta z) < -q(\delta z)\) and (55) (or an approximation as in [46, Remark 3.13]) holds with η = 1 (or \(\eta = \underline {\eta }\)), we use the current δz in the line search. Thus, the “descent condition” in 9: holds. If \(-q(\delta z) \le (\nabla \mathcal {M}_{\epsilon }(0),\delta z) < 0\), then we choose η > 0 such that \(\eta q(\delta z)+ (\nabla \mathcal {M}_{\epsilon }(0),\delta z) < 0\), set δz := ηδz, update \( \underline {\eta } := \min (\eta , \underline {\eta })\), and check (55) or an approximation. Here, the descent condition also holds, but the model \(\mathcal {M}_{\epsilon }\) might be failing. If (55) fails in the latter, then we go to step 10:. Finally, if \((\nabla \mathcal {M}_{\epsilon }(0),\delta z) = 0\), then we go to step 10: . In practice, one might also attempt to circumvent the verification of (55) by using a sufficiently small 𝜖 > 0 and decreasing at every step.
This heuristic has its limitations, e.g., it cannot prohibit \( \underline {\eta } \downarrow 0\). Therefore, if it appears that this is the case, we break the while loop and go to a “robustification step” in 15:. This just means that if the quadratic model \(\mathcal {M}_{\epsilon }\) appears to be ineffective, then we should calculate a new control z by using an alternative method that is guaranteed to converge and “restart” the algorithm. For instance, we could use the adaptive penalty method in Section 4.1 (for a fixed γ, increasing each time the robustification step is used).
Finally, we recall that in the classical projected-gradient approaches, the Lipschitz continuity of the gradient of the objective is essential for convergence proofs, cf. [13]. There, one can show that the line search will always stop provided that the step size is below a certain threshold which only depends on σ and the Lipschitz modulus L. This is, of course, not possible for the control of variational inequalities as the reduced objective is non-smooth (even when the biactive set is negligible we only have Gâteaux differentiability). Therefore, we must also monitor the behavior of the accepted step sizes at each iteration. If, as with \( \underline {\eta }\), the step sizes τk appear to be rapidly decreasing with each iteration, then we also make use of a robustification step. For a full convergence proof in the case of the canonical MPEC (excluding control constraints), we refer the interested reader to [46].
We conclude by demonstrating the performance of the bundle-free method on two examples, Example 3 and the following example (adapted from [39, Ex. 6.1] by adding control constraints).
Example 4
Here, we let a ≡ 0, b ≡ 0.8 and set α = 1. In addition, we define f and ud as follows:
In order to compare to the other methods, we again use a uniform grid with 5122 grid points and start the algorithm at (z0, u0, ξ0) = (0, 0, 0) for Example 3. In contrast, we use a random starting point when solving Example 4. We start the algorithm with 𝜖0 = 10−10 and subsequently set 𝜖k+1 = 𝜖k∕2.
For Example 3 we obtain the same solution as in all the previous algorithms. Likewise, the algorithm performs very well on Example 4, see Table 5 and Figure 6. We note, however, that Example 4 (when starting with a random initial guess) is more difficult to solve. In fact, once the difference in function values becomes negligible, i.e., on the order of \(\mathcal {O}(10^{-13})\), the residual of S-stationarity stagnates at \(\mathcal {O}(10^{-7})\). Finally, one important aspect of the theory for the bundle-free method was the relation \((\nabla \mathcal {M}_{\epsilon }(0),\delta z) < -q(\delta z)\). To see how the choice of 𝜖k influences this, see Table 6. There, we observe that far from the solution, a larger value of 𝜖k seems to yield a good approximation. However, the choice becomes critical once we close in on the solution.
Clockwise from upper left: characteristic functions \(\chi _{\varOmega ^{b}_{\star }}\) (red) and \(\chi _{\varOmega ^{a}_{\star }} \) (blue) (set of all indices with \(z^{\star }_i \ge b_i-\)1e−6 and \(z^{\star }_i \le a_i+\)1e−6), optimal control z⋆, state u⋆, multiplier λ⋆, adjoint p⋆, and multiplier ξ⋆ for Example 4
6 Conclusion
Despite being a topic of interest for several decades, the optimal control of variational inequalities continues to be an active field of research. The rapidly growing interest in the past decade appears to be a result of the many theoretical, algorithmic, and computational advances in PDE-constrained optimization to date. We have seen here that both reduced space and full-space approaches are possible; however, the difficulties due to either a non-smooth control-to-state mapping or degenerate complementarity constraints persist. The various techniques for deriving optimality conditions in the presence of non-smoothness or degeneracy have led both in finite and infinite dimensions to a hierarchy of first-order optimality conditions. Some of these conditions are directly related to function-space-based numerical methods (C-stationarity) whereas other conditions (e.g., those of Mignot and Puel) are derived using concepts of generalized differentiation and a fine analysis of the regularity properties of the underlying functions and multipliers. These facts should therefore always be taken into account when developing numerical optimization algorithms.
In our numerical studies, we considered two main types of solution methods: smooth and non-smooth. Using approximation techniques for variational inequalities as in [30, 31], the smooth methods are almost always available and allow us to immediately take advantage of existing solvers for (smooth) PDE-constrained optimization problems. For the smoothed/regularized problems, we are only limited by our knowledge of the corresponding parameter-dependent PDE-constrained optimization problem. In our study, we make use of a smooth continuation approach and solve the first-order conditions directly using a semismooth Newton method. For small penalty parameters 𝜖, the solution of the linear system (24) needed to calculate the updates is relatively well-behaved. However, the lower off-diagonal block becomes increasingly problematic as we attempt to approach the limiting problem for 𝜖 ↓ 0. Thus, we eventually pay a major price for smoothing the original problem.
As mentioned in the introduction, we present here several possible non-smooth methods that mirror related approaches in smooth PDE-constrained optimization. The first method is inspired by the classical projected subgradient methods in [54, 76]. Just as in these classical methods, the relative cost of each iteration is roughly as cheap as a standard projected-gradient approach sans line search: solve the VI, then a linear elliptic PDE, and compute a pointwise projection. As with all subgradient gradient methods, the strong convergence statements are essentially limited to convex problems. Nevertheless, the method presented here behaves quite well in practice and thus, warrants a deeper study in future research.
The active-set method has been taken from [36] and adapted to the setting of the canonical example. At every iteration, the cost of solving the nonlinear system is slightly more than in the smooth continuation approach due to the feasibility restoration step, which requires the solution of a mixed complementarity problem. However, the conditioning issues are now absent as the potentially problematic perturbation in the lower off-diagonal blocks has been removed. Just as in [36], this method performs exceptionally well, even on a problem with persistent biactivity throughout the iterations. However, as mentioned in the text, proving convergence of this method is rather difficult. One possibility would be to make regularity and monotonicity arguments on the data and active sets throughout the iterations (as was done in [42] for a related problem).
Finally, we considered the bundle-free implicit programming approach, which can be thought of as a globalization of the active-set strategy since we typically choose a step size of τ = 1 at the beginning of every line search. Though the theory does contain several strong assumptions to guarantee unconditional global convergence to a stationary point, there appear to be no other genuinely non-smooth function-space-based algorithms for non-smooth non-convex problems currently in the literature. As noted in [46], if one can prove a kind of semismooth property of the reduced objective, then the convergence theory is greatly simplified. In comparison to the other non-smooth methods, it is clearly more costly due to the usage of the line search. The caveats for this method are the need to monitor the step sizes (essentially restarting if they get too small) and a meaningful heuristic for the convergence criteria. Nevertheless, the theory stands in contrast to non-convex bundle methods as outlined in, e.g., [75]. There, in the ideal non-convex setting, the algorithm terminates at a point at which 0 lies up to some tolerance ε > 0 in a convex hull of certain subgradients corresponding to points yi that are not “far away” from the current iterate xk. The connection to the various MPEC stationarity concepts is therefore unclear.
References
R. A. Adams and J. J. F. Fournier. Sobolev spaces, volume 140 of Pure and Applied Mathematics (Amsterdam). Elsevier/Academic Press, Amsterdam, second edition, 2003.
S. Albrecht and M. Ulbrich. Mathematical programs with complementarity constraints in the context of inverse optimal control for locomotion. Optimization Methods and Software, pages 1–29, 2017.
M. Anitescu, P. Tseng, and S.J. Wright. Elastic-mode algorithms for mathematical programs with equilibrium constraints: global convergence and stationarity properties. Math. Program, 110:337–371, 2005.
H. Antil, M. Hintermüller, R. H. Nochetto, T. M. Surowiec, and D. Wegner. Finite horizon model predictive control of electrowetting on dielectric with pinning. Interfaces Free Bound., 19(1):1–30, 2017.
H. Attouch. Variational Convergence for Functions and Operators. Pitman Advanced Publishing Program, Boston, London, Melbourne, 1984.
H. Attouch, G. Buttazzo, and G. Michaille. Variational analysis in Sobolev and BV spaces, volume 6 of MPS/SIAM Series on Optimization. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, 2006. Applications to PDEs and optimization.
V. Barbu. Optimal control of variational inequalities, volume 100 of Research Notes in Mathematics. Pitman (Advanced Publishing Program), Boston, MA, 1984.
M. P. Bendsøe and O. Sigmund. Topology Optimization. Theory, methods and Applications. Springer Verlag, Berlin, Heidelberg, New York, 2003.
M. Bergounioux. Optimal control of variational inequalities: a mathematical programming approach. In Modelling and optimization of distributed parameter systems (Warsaw, 1995), pages 123–130. Chapman & Hall, New York, 1996.
M. Bergounioux. Optimal control of an obstacle problem. Appl. Math. Optim., 36(2):147–172, 1997.
M. Bergounioux. Use of augmented Lagrangian methods for the optimal control of obstacle problems. J. Optim. Theory Appl., 95(1):101–126, 1997.
A. Bermúdez and C. Saguez. Optimal control of a Signorini problem. SIAM J. Control Optim., 25(3):576–582, 1987.
D. P. Bertsekas. On the Goldstein-Levitin-Polyak gradient projection method. IEEE Transactions on Automatic Control, pages 174–184, 1976.
J. Bezanson, A. Edelman, S. Karpinski, and V. B. Shah. Julia: A Fresh Approach to Numerical Computing. SIAM Rev., 59(1):65–98, 2017.
J. F. Bonnans and A. Shapiro. Perturbation Analysis of Optimization Problems. Springer Verlag, Berlin, Heidelberg, New York, 2000.
M. Boukrouche and D. A. Tarzia. Convergence of distributed optimal control problems governed by elliptic variational inequalities. Comput. Optim. Appl., 53(2):375–393, 2012.
C. Brett, C. M. Elliott, M. Hintermüller, and C. Löbhard. Mesh adaptivity in optimal control of elliptic variational inequalities with point-tracking of the state. Interfaces Free Bound., 17(1):21–53, 2015.
H. R. Brezis and G. Stampacchia. Sur la régularité de la solution d’inéquations elliptiques. Bull. Soc. Math. France, 96:153–180, 1968.
X. Chen, Z. Nashed, and L. Qi. Smoothing methods and semismooth methods for nondifferentiable operator equations. SIAM J. Numer. Anal., 38(4):1200–1216 (electronic), 2000.
P. Colli, M. H. Farshbaf-Shaker, G. Gilardi, and J. Sprekels. Optimal boundary control of a viscous Cahn–Hilliard system with dynamic boundary condition and double obstacle potentials. SIAM Journal on Control and Optimization, 53(4):2696–2721, 2015.
J. C. De Los Reyes. Optimal control of a class of variational inequalities of the second kind. SIAM J. Control Optim., 49(4):1629–1658, 2011.
J. C. De los Reyes, R. Herzog, and C. Meyer. Optimal control of static elastoplasticity in primal formulation. SIAM J. Control Optim., 54(6):3016–3039, 2016.
J. C. De los Reyes and C. Meyer. Strong stationarity conditions for a class of optimization problems governed by variational inequalities of the second kind. J. Optim. Theory Appl., 168(2):375–409, 2016.
A. K. Dond, T. Gudi, and N. Nataraj. A nonconforming finite element approximation for optimal control of an obstacle problem. Comput. Methods Appl. Math., 16(4):653–666, 2016.
I. Ekeland and R. Témam. Convex analysis and variational problems, volume 28 of Classics in Applied Mathematics. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, English edition, 1999. Translated from the French.
L. C. Evans and R. F. Gariepy. Measure theory and fine properties of functions. Studies in advanced mathematics. CRC Press, Boca Raton (Fla.), 1992.
M. H. Farshbaf-Shaker. A penalty approach to optimal control of Allen-Cahn variational inequalities: MPEC-view. Numerical Functional Analysis and Optimization, 33(11):1321–1349, 2012.
M. H. Farshbaf-Shaker and C. Hecht. Optimal control of elastic vector-valued Allen–Cahn variational inequalities. SIAM Journal on Control and Optimization, 54(1):129–152, 2016.
G. Fichera. Problemi elastostatici con vincoli unilaterali: Il problema di Signorini con ambigue condizioni al contorno. Atti Accad. Naz. Lincei Mem. Cl. Sci. Fis. Mat. Natur. Sez. I (8), 7:91–140, 1963.
R. Glowinski. Numerical methods for nonlinear variational problems. Springer Series in Computational Physics. Springer-Verlag, New York, 1984.
R. Glowinski, J. L. Lions, and R. Trémolières. Numerical analysis of variational inequalities, volume 8 of Studies in Mathematics and its Applications. North-Holland Publishing Co., Amsterdam, 1981.
W. Han and B. D. Reddy. Plasticity, volume 9 of Interdisciplinary Applied Mathematics. Springer, New York, second edition, 2013. Mathematical theory and numerical analysis.
A. Haraux. How to differentiate the projection on a convex set in Hilbert space. some applications to variational inequalities. J. Math. Soc. Japan, 29(4):615–631, 1977.
R. Herzog, C. Meyer, and G. Wachsmuth. C-stationarity for optimal control of static plasticity with linear kinematic hardening. SIAM J. Control Optim., 50(5):3052–3082, 2012.
R. Herzog, C. Meyer, and G. Wachsmuth. B- and strong stationarity for optimal control of static plasticity with hardening. SIAM J. Optim., 23(1):321–352, 2013.
M. Hintermüller. An active-set equality constrained Newton solver with feasibility restoration for inverse coefficient problems in elliptic variational inequalities. Inverse Problems, 24(3):23pp., 2008.
M. Hintermüller, R. H. W. Hoppe, and C. Löbhard. Dual-weighted goal-oriented adaptive finite elements for optimal control of elliptic variational inequalities. ESAIM Control Optim. Calc. Var., 20(2):524–546, 2014.
M. Hintermüller, K. Ito, and K. Kunisch. The primal-dual active set strategy as a semismooth newton method. SIAM Journal on Optimization, 13(3):865–888, 2002.
M. Hintermüller and I. Kopacka. Mathematical programs with complementarity constraints in function space: C- and strong stationarity and a path-following algorithm. SIAM J. Optim., 20(2):868–902, 2009.
M. Hintermüller and I. Kopacka. A smooth penalty approach and a nonlinear multigrid algorithm for elliptic MPECs. Comput. Optim. Appl., 50(1):111–145, 2011.
M. Hintermüller and K. Kunisch. Path-following methods for a class of constrained minimization problems in function space. SIAM Journal on Optimization, 17(1):159–187, 2006.
M. Hintermüller and A. Laurain. Optimal shape design subject to elliptic variational inequalities. SIAM Journal on Control and Optimization, 49(3):1015–1047, 2011.
M. Hintermüller, C. Löbhard, and M. H. Tber. An ℓ1-penalty scheme for the optimal control of elliptic variational inequalities. In Mehiddin Al-Baali, Lucio Grandinetti, and Anton Purnama, editors, Numerical Analysis and Optimization, volume 134 of Springer Proceedings in Mathematics & Statistics, pages 151–190. Springer International Publishing, 2015.
M. Hintermüller, B. S. Mordukhovich, and T. M. Surowiec. Several approaches for the derivation of stationarity conditions for elliptic MPECs with upper-level control constraints. Math. Program., 146(1):555–582, 2014.
M. Hintermüller and T. Surowiec. First-order optimality conditions for elliptic mathematical programs with equilibrium constraints via variational analysis. SIAM J. Optim., 21(4):1561–1593, 2011.
M. Hintermüller and T. Surowiec. A bundle-free implicit programming approach for a class of elliptic MPECs in function space. Math. Program., 160(1):271–305, 2016.
M. Hintermüller and D. Wegner. Optimal control of a semidiscrete Cahn–Hilliard–Navier–Stokes system. SIAM Journal on Control and Optimization, 52(1):747–772, 2014.
M. Hinze, R. Pinnau, M. Ulbrich, and S. Ulbrich. Optimization with PDE constraints, volume 23 of Mathematical Modelling: Theory and Applications. Springer, New York, 2009.
B. Horn and S. Ulbrich. Shape optimization for contact problems based on isogeometric analysis. Journal of Physics: Conference Series, 734(3):032008, 2016.
K. Ito and K. Kunisch. Optimal control of elliptic variational inequalities. Applied Mathematics and Optimization, 41(3):343–364, 2000.
P. Jaillet, D. Lamberton, and B. Lapeyre. Variational inequalities and the pricing of American options. Acta Appl. Math., 21(3):263–289, 1990.
N. Kikuchi and J. T. Oden. Contact problems in elasticity: a study of variational inequalities and finite element methods, volume 8 of SIAM Studies in Applied Mathematics. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, 1988.
D. Kinderlehrer and G. Stampacchia. An introduction to variational inequalities and their applications, volume 88 of Pure and Applied Mathematics. Academic Press Inc. [Harcourt Brace Jovanovich Publishers], New York, 1980.
Krzysztof C. Kiwiel. Methods of descent for nondifferentiable optimization. Lecture Notes in Mathematics. 1133. Berlin etc.: Springer-Verlag, 1985.
R. Kornhuber. Monotone multigrid methods for elliptic variational inequalities. I. Numer. Math., 69(2):167–184, 1994.
K. Kunisch and T. Pock. A bilevel optimization approach for parameter learning in variational models. SIAM J. Imaging Sci., 6(2):938–983, 2013.
J. L. Lions. Contrôle optimal de systèmes gouvernés par des équations aux dérivées partielles. Dunod, Paris, 1968.
J.-L. Lions. Various topics in the theory of optimal control of distributed systems. In Optimal control theory and its applications (Proc. Fourteenth Biennial Sem. Canad. Math. Congr., Univ. Western Ontario, London, Ont., 1973), Part I, pages 116–309. Lecture Notes in Econom. and Math. Systems, Vol. 105. Springer, Berlin, 1974.
J.-L. Lions. Contrôle des systèmes distribués singuliers, volume 13 of Méthodes Mathématiques de l’Informatique [Mathematical Methods of Information Science]. Gauthier-Villars, Montrouge, 1983.
J.-L. Lions and G. Stampacchia. Variational inequalities. Comm. Pure Appl. Math., 20:493–519, 1967.
Z.-Q. Luo, J.-S. Pang, and D. Ralph. Mathematical Programs with Equilibrium Constraints. Cambridge University Press, Cambridge, 1996.
C. Meyer and O. Thoma. A priori finite element error analysis for optimal control of the obstacle problem. SIAM J. Numer. Anal., 51(1):605–628, 2013.
F. Mignot. Contrôle dans les inéquations variationelles elliptiques. J. Functional Analysis, 22(2):130–185, 1976.
F. Mignot and J.-P. Puel. Optimal control in some variational inequalities. SIAM J. Control and Optimization, 22(3):466–476, 1984.
K. Mombaur, A. Truong, and J.-P. Laumond. From human to humanoid locomotion–an inverse optimal control approach. Autonomous Robots, 28(3):369–383, 2010.
B. S. Mordukhovich. Variational analysis and generalized differentiation. I: Basic Theory, volume 330 of Grundlehren der Mathematischen Wissenschaften. Springer-Verlag, Berlin, 2006.
D. Mumford and J. Shah. Optimal approximations by piecewise smooth functions and associated variational problems. Comm. Pure Appl. Math., 42(5):577–685, 1989.
P. Neittaanmäki, J. Sprekels, and D. Tiba. Optimization of Elliptic Systems. Springer Monographs in Mathematics. Springer, New York, 2006.
J. V. Outrata, M. Kočvara, and J. Zowe. Nonsmooth Approach to Optimization Problems with Equilibrium Constraints, volume 28 of Nonconvex Optimization and its Applications. Kluwer Academic Publishers, Dordrecht, 1998.
P. Perona and J. Malik. Scale-space and edge detection using anisotropic diffusion. IEEE transactions on pattern analysis and machine intelligence, 12(7):174–184, 1990.
J.-F. Rodrigues. Obstacle Problems in Mathematical Physics. Number 134 in North-Holland Mathematics Studies. North-Holland Publishing Co., Amsterdam, 1984.
L. I. Rudin, S. Osher, and E. Fatemi. Nonlinear total variation based noise removal algorithms. Phys. D, 60(1–4):259–268, 1992. Experimental mathematics: computational issues in nonlinear science (Los Alamos, NM, 1991).
C. Saguez. Optimal control of free boundary problems. In System modelling and optimization (Budapest, 1985), volume 84 of Lecture Notes in Control and Inform. Sci., pages 776–788. Springer, Berlin, 1986.
H. Scheel and S. Scholtes. Mathematical programs with complementarity constraints: Stationarity, optimality, and sensitivity. Mathematics of Operations Research, 25(1):1–22, 2000.
H. Schramm and J. Zowe. A version of the bundle idea for minimizing a nonsmooth function: Conceptual idea, convergence analysis, numerical results. SIAM Journal on Optimization, 2(1):121–152, 1992.
N. Z. Shor. Minimization Methods for Non-differentiable Functions. Springer-Verlag, New York, 1985.
F. Tröltzsch. Optimal control of partial differential equations, volume 112 of Graduate Studies in Mathematics. American Mathematical Society, Providence, RI, 2010. Theory, methods and applications, Translated from the 2005 German original by Jürgen Sprekels.
J. N. Tsitsiklis, D. P. Bertsekas, and M. Athans. Distributed asynchronous deterministic and stochastic gradient optimization algorithms. IEEE Trans. Automat. Control, 31(9):803–812, 1986.
M. Ulbrich. Semismooth Newton methods for operator equations in function spaces. SIAM J. Optim., 13(3):805–842 (2003), 2002.
G. Wachsmuth. Strong stationarity for optimal control of the obstacle problem with control constraints. SIAM J. Optim., 24(4):1914–1932, 2014.
G. Wachsmuth. Mathematical programs with complementarity constraints in Banach spaces. J. Optim. Theory Appl., 166(2):480–507, 2015.
G. Wachsmuth. A guided tour of polyhedric sets: Basic properties, new results on intersections and applications. Technical report, TU Chemnitz, 2016.
G. Wachsmuth. Towards M-stationarity for optimal control of the obstacle problem with control constraints. SIAM J. Control Optim., 54(2):964–986, 2016.
S. W. Walker, A. Bonito, and R. H. Nochetto. Mixed finite element method for electrowetting on dielectric with contact line pinning. Interfaces Free Bound., 12(1):85–119, 2010.
Y-S. Wu, K. Pruess, and P. A. Witherspoon. Flow and displacement of Bingham non-Newtonian fluids in porous media. SPE Reservoir Engineering, 7(3), 1992.
J.-P. Yvon. Etude de quelques problèmes de contrôle pour des systèmes distribués. PhD thesis, Paris VI, 1973.
J.-P. Yvon. Optimal control of systems governed by variational inequalities. In Fifth Conference on Optimization Techniques (Rome, 1973), Part I, pages 265–275. Lecture Notes in Comput. Sci., Vol. 3. Springer, Berlin, 1973.
J. Zowe and S. Kurcyusz. Regularity and stability for the mathematical programming problem in Banach spaces. Appl. Math. Optim., 5(1):49–62, 1979.
Acknowledgements
This paper is an extension of a short course given by the author at the “Frontiers in PDE-constrained Optimization” workshop on June 6–10, 2016 at the Institute for Mathematics and its Applications at the University of Minnesota, Minneapolis, which was sponsored by ExxonMobil. The author would therefore like to express his gratitude for the financial support and the opportunity to write this article. In addition, the author would like to thank Harbir Antil, Patrick Farrell, and the two anonymous reviewers for their helpful comments and thought-provoking questions on the text.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer Science+Business Media, LLC, part of Springer Nature
About this chapter
Cite this chapter
Surowiec, T.M. (2018). Numerical Optimization Methods for the Optimal Control of Elliptic Variational Inequalities. In: Antil, H., Kouri, D.P., Lacasse, MD., Ridzal, D. (eds) Frontiers in PDE-Constrained Optimization. The IMA Volumes in Mathematics and its Applications, vol 163. Springer, New York, NY. https://doi.org/10.1007/978-1-4939-8636-1_4
Download citation
DOI: https://doi.org/10.1007/978-1-4939-8636-1_4
Publisher Name: Springer, New York, NY
Print ISBN: 978-1-4939-8635-4
Online ISBN: 978-1-4939-8636-1
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)