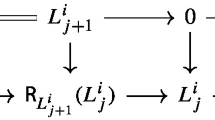Equations and Tropicalization of Enriques Surfaces

Abstract

In this article, we explicitly compute equations of an Enriques surface via the involution on a K3 surface. We also discuss its tropicalization and compute the tropical homology, thus recovering a special case of the result of [18], and establish a connection between the dimension of the tropical homology groups and the Hodge numbers of the corresponding algebraic Enriques surface.

1 Introduction

In the classification of algebraic surfaces, Enriques surfaces comprise one of four types of minimal surfaces of Kodaira dimension 0. There are a number of surveys on Enriques surfaces. For those new to the theory, we recommend the excellent exposition found in [2] and [3], and for a more thorough treatment, the book [10]. Another recommended source is Dolgachev’s brief introduction to Enriques surfaces [11] .

The first Enriques surface was constructed in 1896 by Enriques himself [12] to answer negatively a question posed by Castelnuovo (1895): Is every surface with p _g = q = 0 rational?; see Sect. 2 for the meaning of p _q and q. Enriques’ original surface has a beautiful geometric construction: the normalization of a degree 6 surface in $\mathbb{P}^{3}$ with double lines given by the edges of a tetrahedron. Another construction, the Reye congruence , defined a few years earlier by Reye [25], was later proved by Fano [13] to be an Enriques surface. Since these first constructions, there have been many examples of Enriques surfaces, most often as quotients of K3 surfaces by a fixed-point-free involution. In [9], Cossec describes all birational models of Enriques surfaces given by complete linear systems.

As we recall in Sect. 2, every Enriques surface has an unramified double cover given by a K3 surface . Often exploiting this double cover, topics of particular interest relate to lattice theory, moduli spaces and their compactifications, automorphism groups of Enriques surfaces, and Enriques surfaces in characteristic 2. While there are many constructions of Enriques surfaces, none give explicit equations for an Enriques surface embedded in a projective space. In this paper, by interpreting the work of Cossec–Verra, we give explicit ideals for all Enriques surfaces.

Theorem 1.1

Let Y be the toric fivefold of degree 16 in $\mathbb{P}^{11}$ that is obtained by taking the join of the Veronese surface in $\mathbb{P}^{5}$ with itself. The intersection of Y with a general linear subspace of codimension 3 is an Enriques surface, and every Enriques surface arises in this way.

By construction, the Enriques surface in Theorem 1.1 is arithmetically Cohen–Macaulay. Its homogeneous prime ideal in the polynomial ring with 12 variables is generated by the twelve binomial quadrics that define Y and three additional linear forms. Code for producing this Enriques surface in Macaulay2 appears in Sect. 3.

Fig. 1

A tropical K3 surface in $\mathbb{P}^{1} \times \mathbb{P}^{1} \times \mathbb{P}^{1}$ that is fixed under the involution

After having constructed Enriques surfaces explicitly, we focus on their tropicalizations, with the purpose of studying their combinatorial properties. For this we choose a different K3 surface , namely a hypersurface $S \subset (\mathbb{P}^{1})^{3}$ with an involution σ, see Example 4.3. We get a fairly complete picture for its tropicalization (Fig. 1). In particular, we recover its Hodge numbers and, conjecturally, the Hodge numbers of S∕σ, which was [28, Problem 10 on Surfaces]; this was the starting point of this work.

Proposition 1.2 (Example 4.3, Propositions 5.7–5.8)

The dimensions of tropical homology groups of the tropicalization of the K3 surface S agree with the Hodge numbers of S. The dimensions of the σ-invariant parts of tropical homology groups agree with the Hodge numbers of the Enriques surface S∕σ.

Finally, we discuss an analogue of Castelnuovo’s question on the tropical and analytic level. Since the analytifications of rational varieties are contractible by Corollary 1.1.4 in [6], we ask: are the analytifications of K3 or Enriques surfaces contractible? We give a negative answer to this question, the counterexample being the analytification of S from Example 4.3.

Theorem 1.3

The analytification S ^an of the K3 surface S is homotopy equivalent to a two-dimensional sphere. The surface S has a fixed-point-free involution σ and the analytification of the Enriques surface S∕σ retracts onto the real projective plane  $\mathbb{R}\mathbb{P}^{2}$ . In particular, neither S ^an nor (S∕σ)^an is contractible.

The contents of the paper are as follows. In Sect. 2, we give some background about Enriques surfaces. Next, in Sect. 3, we exploit a classical construction to obtain an Enriques ideal in a codimension 3 linear space in $\mathbb{P}^{11}$ and prove Theorem 1.1. In Sect. 4, we discuss the basics of tropical geometry and analytic spaces in the sense of Berkovich. Example 4.3 provides an Enriques surface S∕σ arising from a K3 surface $S \subset \mathbb{P}^{1} \times \mathbb{P}^{1} \times \mathbb{P}^{1}$ with an involution σ. The surface S is suitable from the tropical point of view (its tropical variety is schön and multiplicity one everywhere) and is used throughout the paper. In Sect. 5, we compute the tropical homology groups of $\mathop{\mathrm{trop}}\nolimits (S)$ and, conjecturally, of $\mathop{\mathrm{trop}}\nolimits (S/\sigma )$. We also prove Proposition 1.2. In Sect. 6, we discuss the topology of analytifications of S and S∕σ and prove Theorem 1.3.

2 Background

Apart from the code snippets, we work over an algebraically closed field of characteristic zero. An Enriques surface X is a smooth projective surface such that $q(X):= h^{1}(X,\mathcal{O}_{X}) = 0$, $\omega _{X}^{\otimes 2} \simeq \mathcal{ O}_{X}$ and $\omega _{X}\not\simeq \mathcal{O}_{X}$, where $\omega _{X} =\bigwedge ^{2}\varOmega _{X}^{1}$ is the canonical bundle of X. It follows that X is minimal, see [3], and its geometric genus is $p_{g}(X):= h^{2}(X,\mathcal{O}_{X}) = 0$. Enriques surfaces are defined the same way over any field of characteristic other than 2. By Lemma 15.1 in [2], the Hodge diamond of an Enriques surface X appears in Fig. 2. An Enriques surface admits an unramified double cover f: Y → X, where Y is a K3 surface , see [2, Lemma 15.1] or [3, Proposition VIII.17]. The Hodge diamond of Y appears in Fig. 3. Since Y is simply connected, the fundamental group of an Enriques surface is $\mathbb{Z}/2\mathbb{Z}$; see [2, Sect. 15]. The cover Y → X is a quotient of Y by an involution σ that exchanges the two points of each fibre. Conversely, for a K3 surface Y with a fixed-point-free involution σ, the quotient Y∕σ is an Enriques surface.

Fig. 2

Hodge diamond of an Enriques surface

Fig. 3

Hodge diamond of a K3 surface

3 Enriques Surfaces via K3 Complete Intersections in $\mathbb{P}^{5}$

In this section, we construct Enriques surfaces via K3 surfaces in $\mathbb{P}^{5}$. One cannot hope for especially simple equations—for instance, an Enriques surface cannot be a hypersurface in $\mathbb{P}^{3}$.

Proposition 3.1

If $X \subset \mathbb{P}_{\mathbb{C}}^{N}$ is a smooth toric threefold and S = X ∩ H is a smooth hyperplane section, then S is simply connected, and is not an Enriques surface .

Proof

Since X is a smooth projective toric variety, it is simply connected; see [14, Sect. 3.2]. A homotopical version of Lefschetz’ theorem asserts that the fundamental groups of X ∩ H and X are isomorphic via the natural map; see [1] and [4, 2.3.10]. Thus, S is simply connected. Since an Enriques surface admits a non-trivial étale double cover, it is never simply connected. □

Remark 3.2

This proof generalizes to other complete intersections inside smooth toric varieties, provided that intermediate complete intersections are smooth.

Following [3, Example VIII.18], we construct an Enriques surface from a K3 surface that is an intersection of quadrics in $\mathbb{P}^{5}$. Fix $\mathbb{P}^{5}:=\mathop{ \mathrm{Proj}}\nolimits (\mathbb{C}[x_{0},x_{1},x_{2},y_{0},y_{1},y_{2}])$. The fixed point set of the involution $\sigma: \mathbb{P}^{5} \rightarrow \mathbb{P}^{5}$ given by σ(x _i ) = x _i and σ(y _i ) = −y _i , for all 0 ≤ i ≤ 2, is equal to the union of $\mathbb{P}^{2} =\mathop{ \mathrm{V}}\nolimits (y_{0},y_{1},y_{2})$ and $\mathbb{P}^{2} =\mathop{ \mathrm{V}}\nolimits (x_{0},x_{1},x_{2})$. Fix quadrics $F_{i} \in \mathbb{C}[x_{0},x_{1},x_{2}]$ and $G_{i} \in \mathbb{C}[y_{0},y_{1},y_{2}]$, where 0 ≤ i ≤ 2 and set Q _i : = F _i + G _i . By construction, these quadrics are fixed by σ. Choose Q ₀, Q ₁, Q ₂ so that they form a complete intersection. For the surface $S = S_{\mathbf{Q}}:=\mathop{ \mathrm{V}}\nolimits (Q_{0},Q_{1},Q_{2})$, the Adjunction Formula gives $K_{S} = \mathcal{O}_{S}(-6 + 2 + 2 + 2) = \mathcal{O}_{S}$. Since the surface S is a complete intersection of quadrics in $\mathbb{P}^{5}$, it follows that $h^{1}(\mathcal{O}_{S}) = 0$; see [3, Lemma VIII.9]. Thus, if S is smooth, then it is a K3 surface fixed under the involution σ. We now formalize exactly which assumptions must be satisfied by the three quadrics to obtain a smooth Enriques surface .

Definition 3.3

Let Q: = (Q ₀, Q ₁, Q ₂) be a triple of quadrics where Q _i : = F _i + G _i for some $F_{i} \in \mathbb{C}[x_{0},x_{1},x_{2}]$ and $G_{i} \in \mathbb{C}[y_{0},y_{1},y_{2}]$. We say that the quadrics Q are enriquogeneous if the following conditions are satisfied:

• 1. the forms Q = (Q ₀, Q ₁, Q ₂) are a complete intersection,

• 2. the surface $S =\mathop{ \mathrm{V}}\nolimits (Q_{0},Q_{1},Q_{2})$ is smooth,

• 3. the surface $S =\mathop{ \mathrm{V}}\nolimits (Q_{0},Q_{1},Q_{2})$ does not intersect the fixed-point set of σ.

The third condition is equivalent to F ₀, F ₁, F ₂ having no common zeros in $\mathbb{C}[x_{0},x_{1},x_{2}]$ and G ₀, G ₁, G ₂ having no common zeros in $\mathbb{C}[y_{0},y_{1},y_{2}]$, so it is an open condition. For a choice of enriquogeneous quadrics Q, we obtain an Enriques surface as S _Q ∕σ. The set of enriquogeneous quadrics is open inside $(\mathbb{A}^{6+6})^{3}$, so that a general choice of forms gives an Enriques surface. In [9], Cossec shows that every complex Enriques surface may be obtained in this way if one allows Q not satisfying the smoothness condition; see also [30]. Notably, Lietdke proves that the same is true for Enriques surfaces over any characteristic [21]. To develop our intuition, we demonstrate that, over $\mathbb{C}$, these surfaces give at most a ten-dimensional space of Enriques surfaces .

Each Q _i is chosen from the same 12-dimensional affine space and S _Q depends only on their span, which is an element of the 27-dimensional variety $\mathop{\mathrm{Gr}}\nolimits \left (3, \mathbb{C}^{12}\right )$. Since we have fixed σ, the quadrics Q _i yield an isomorphic K3 surface (with an isomorphic involution) if we act on $\mathbb{P}^{5}$ by an automorphism that commutes with σ. Such automorphisms are given by block matrices in PGL(6) of the form

$$\displaystyle\begin{array}{rcl} \begin{array}{rclrclrcl} C & =&\left [\begin{array}{*{10}c} A&0\\ 0 &B \end{array} \right ]&&\text{or}&C & =&\left [\begin{array}{*{10}c} 0&A\\ B &0 \end{array} \right ]\end{array}& & {}\\ \end{array}$$

where A and B are matrices in $\mathop{\mathrm{GL}}\nolimits (3, \mathbb{C})$, up to scaling. Thus, the space of automorphisms preserving the σ-invariant quadrics has dimension (2)(9) − 1 = 17. Modulo these automorphisms, we obtain a ten-dimensional projective space of K3 surfaces with an involution. The condition that Q be enriquogeneous is an open condition, so the space of Enriques surfaces is also ten-dimensional.

We now aim to make the Enriques surfaces constructed as S _Q ∕σ explicit. In other words, we want to present them as embedded into a projective space. The first step is to identify the quotient of $\mathbb{P}^{5}$ by the involution σ. Let $S = \mathbb{C}[x_{0},x_{1},x_{2},y_{0},y_{1},y_{2}]$ be the homogeneous coordinate ring, so the quotient is $\mathop{\mathrm{Proj}}\nolimits \left (S^{\sigma }\right ) =\mathop{ \mathrm{Proj}}\nolimits \left (\mathbb{C}[x_{i},y_{i}y_{j}]\right )$. The Enriques surface S _Q is cut out of $\mathop{\mathrm{Proj}}\nolimits \left (\mathbb{C}[x_{i},y_{i}y_{j}]\right )$ by the quadrics Q such that $S_{\mathbf{Q}} =\mathop{ \mathrm{Proj}}\nolimits \left (\mathbb{C}[x_{i},y_{i}y_{j}]/\mathbf{Q}\right )$. This does not give us an embedding into $\mathbb{P}^{8}$, because the variables x _i and y _i y _j have different degrees. Rather we obtain an embedding into a weighted projective space $\mathbb{P}(1^{3},2^{6})$. Therefore, we replace $\mathbb{C}[x_{i},y_{i}y_{j}]$ by the Veronese subalgebra $\mathbb{C}[x_{i}x_{j},y_{i}y_{j}]/\mathbf{Q}$. This algebra is generated by the 12 elements x _i x _j , y _i y _j , where 0 ≤ i, j ≤ 2, which implies that S _Q is embedded into a $\mathbb{P}^{11}$. The relations Q are linear in the variables x _i x _j and y _i y _j , so S _Q is embedded into a $\mathbb{P}^{8}$.

Let us rephrase this geometrically. Consider the second Veronese embedding $v: \mathbb{P}^{5} \rightarrow \mathbb{P}^{20}$. The coordinates of $\mathbb{P}^{20}$ are forms of degree two in x _i and y _i . The involution σ extends to an involution on $\mathbb{P}^{20}$ and the invariant coordinate ring is generated by the linear forms corresponding to the products x _i x _j and y _i y _j . Thus, the quotient is embedded into $\mathbb{P}^{11}$; we have

where π denotes the quotient by the involution σ. The image $\pi (\mathbb{P}^{5})$ is cut out by 12 binomial quadrics: the six usual equations between x _i x _j and the six corresponding equations for y _i y _j . It is the join of two Veronese surfaces which constitute its singular locus. Quadrics in $\mathbb{C}[x_{i},y_{i}]$ of the form F _i + G _i for $F_{i} \in \mathbb{C}[x_{i}]$ and $G_{i} \in \mathbb{C}[y_{i}]$ correspond bijectively to linear forms on the above $\mathbb{P}^{11}$. A choice of enriquogeneous quadrics Q corresponds to a general choice of three linear forms on $\mathbb{P}^{11}$. We obtain the corresponding Enriques surface S _Q as a linear section of $\pi (\mathbb{P}^{5})$. Summing up, we have the chain of inclusions $V \cap \pi (\mathbb{P}^{5}) \subset \pi (\mathbb{P}^{5}) \subset \mathbb{P}(1^{3},2^{6}) \subset \mathbb{P}^{11}$, where V is a codimension three linear section. Although $V \cap \pi (\mathbb{P}^{5})$ is a complete intersection in $\pi (\mathbb{P}^{5})$, this does not contradict (the natural generalisation of) Proposition 3.1, because $\pi (\mathbb{P}^{5})$ is singular. Since sufficiently ample embeddings of varieties are always cut out by quadrics, see [23, 27], this suggests that our embedding is sufficiently good.

Proof of Theorem 1.1

The surfaces obtained from enriquogeneous quadrics are arithmetically Cohen–Macaulay of degree 16 as they are linear sections of $\pi (\mathbb{P}^{5})$ possessing those properties. Every Enriques surface can be obtained by this procedure if one allows Q not satisfying the smoothness condition by [9]. □

We provide Macaulay2 [15] code for finding the equations of S _Q . To simplify the computation, we work over a finite field.

kk = ZZ/1009; P5 = kk[x0,x1,x2,y0,y1,y2]; P11 = kk[z0,z1,z2,z3,z4,z5,z6,z7,z8,z9,z10,z11]; pii = map(P5, P11, {x0^2, x0*x1, x0*x2, x1^2,                     x1*x2, x2^2, y0^2, y0*y1,                     y0*y2, y1^2, y1*y2, y2^2});

The kernel of pii is generated by 12 binomial quadrics and has degree 16.

assert(kernel pii == ideal(       z10^2-z9*z11, z8*z10-z7*z11, z8*z9-z7*z10,       z8^2-z6*z11,  z7*z8-z6*z10,  z7^2-z6*z9,       z4^2-z3*z5,   z2*z4-z1*z5,   z2*z3-z1*z4,       z2^2-z0*z5,   z1*z2-z0*z4,   z1^2-z0*z3)) assert(degree kernel pii == 16)

We next generate an Enriques surface from a random set of linear forms named linForms. To see the quadrics in $\mathbb{P}^{5}$, compute pii(linForms).

linForms = random(P11^3, P11^{-1})

randomEnriques = (kernel pii) + ideal linForms

We now verify that this is in fact an Enriques surface. Computationally, it is much easier to check this for the associated K3 surface , because we need only check that K3 is a smooth surface (first two assertions below) and that the involution is fixed-point-free on K3 (last two assertions).

K3 = ideal pii(linForms) assert (dim K3 == 3) assert (dim saturate ideal singularLocus K3 == -1) assert (dim saturate (K3 + ideal(y0,y1,y2)) == -1) assert (dim saturate (K3 + ideal(x0,x1,x2)) == -1)

If the K3 passes all the assertions, then randomEnriques is an Enriques surface . Its ideal is given by 12 binomial quadrics listed above and three linear forms in P11.

Example 3.4

Over $\mathbb{k} = \mathbb{F}_{1009}$, the choice of

linForms = matrix{{2*z2+z6+5*z7+8*z11,                    2*z0+8*z4+z9,                    5*z1+4*z3+4*z5+6*z8}}

in the above algorithm gives an Enriques surface .

Finally, we check that $\pi (\mathbb{P}^{5})$ is arithmetically Cohen-Macaulay . Using betti res kernel pii, we obtain its Betti table.

$$\displaystyle{\begin{array}{*{10}c} 1&. &. &. &. &. &.\\.&12&16&6&.&.&. \\. &. &36&96&100&48&9\\ \end{array} }$$

The projective dimension of $\pi (\mathbb{P}^{5})$ (the number of columns) is equal to the codimension, thus $\pi (\mathbb{P}^{5}) \subset \mathbb{P}^{11}$ is arithmetically Cohen-Macaulay ; see [26, Sect. 10.2]. Therefore, all its linear sections are also arithmetically Cohen-Macaulay .

4 Analytified and Tropical Enriques Surfaces

This section discusses the basics of tropical and analytic geometry and constructs a K3 surface whose tropicalization is nice enough for computations of tropical homology . In Example 4.3, we present a K3 surface with an involution, which on the tropical side is the antipodal map. As an excellent reference for tropical varieties , we recommend [22], especially Sect. 6.2. For analytic spaces in the sense of Berkovich, we recommend [5, 17].

Let $\mathbb{k}$ be a field extension of $\mathbb{C}$ with a nontrivial valuation $\mathop{\mathrm{val}}\nolimits: \mathbb{k}^{{\ast}}\rightarrow \mathbb{R}$ such that $\mathop{\mathrm{val}}\nolimits (\mathbb{C}^{{\ast}}) =\{ 0\}$. We assume that $\mathbb{k}$ is algebraically closed, so the image $\mathop{\mathrm{val}}\nolimits (\mathbb{k}^{{\ast}})$ is dense in $\mathbb{R}$. Without much loss of generality, one could simply consider the field $\mathbb{k} = \mathbb{C}\{\!\{z\}\!\} =\bigcup _{n\in \mathbb{N}}\mathbb{C}(\!(z^{1/n})\!)$ of Puiseux series , with valuation yielding the lowest exponent of z appearing in the series. For every point $p = (p_{1},p_{2},\mathop{\ldots },p_{n}) \in (\mathbb{k}^{{\ast}})^{n}$, its valuation is $\mathop{\mathrm{val}}\nolimits (p) =\big (\mathop{\mathrm{val}}\nolimits (p_{1}),\mathop{\mathrm{val}}\nolimits (p_{2}),\mathop{\ldots },\mathop{\mathrm{val}}\nolimits (p_{n})\big)$.

Definition 4.1

Let X be a toric variety with torus $(\mathbb{k}^{{\ast}})^{n}$ and Y ⊂ X be a closed subvariety. The tropical variety of Y, denoted by $\mathop{\mathrm{trop}}\nolimits (Y \subset X)$ or briefly $\mathop{\mathrm{trop}}\nolimits (Y )$, is the closure of the set $\{\mathop{\mathrm{val}}\nolimits (p): p \in (\mathbb{k}^{{\ast}})^{n} \cap Y \} \subset \mathbb{R}^{n}$.

The tropical variety $\mathop{\mathrm{trop}}\nolimits (Y \subset X)$ is a polyhedral complex of dimension dimY with rich combinatorial structure; see [22, Chapter 3].

A morphism of tori $\varphi: (\mathbb{k}^{{\ast}})^{n} \rightarrow (\mathbb{k}^{{\ast}})^{m}$ is given by φ = (φ ₁, φ ₂, … , φ _m ) where $\varphi _{i}(t) = b_{i} \cdot t^{a_{i}}$ for 1 ≤ i ≤ m. For each such φ, there is a tropicalized map $\mathop{\mathrm{trop}}\nolimits (\varphi ): \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}$ given by $\mathop{\mathrm{trop}}\nolimits (\varphi )_{i}(v) =\mathop{ \mathrm{val}}\nolimits (b_{i}) + (a_{i} \cdot v)$ for 1 ≤ i ≤ m. One verifies that the following diagram commutes:

This naive tropicalization is not a functor—it is known how to tropicalize a map only when it is monomial. This problem is solved by passing to Berkovich spaces . We will not discuss Berkovich spaces in detail: we invite the reader to see [5, 17] or [24] for a slightly more elementary introduction.

For every finite-type scheme X over a valued field $\mathbb{k}$, its Berkovich analytification X ^an is the analytic space which best approximates X; see [5, Chap. 3]. The space X ^an is locally ringed (in the usual sense, see [29, 4.3.6]) and there is a morphism π: X ^an → X such that every other map from an analytic space factors through π. If $X =\mathop{ \mathrm{Spec}}\nolimits A$ is affine, then the points of X ^an are in bijection with the multiplicative semi-norms on A which extend the norm on $\mathbb{k}$. Most importantly, the analytification is functorial: for every map f: X → Y, we get an induced map f ^an: X ^an → Y ^an. If $X =\mathop{ \mathrm{Spec}}\nolimits A$ and $Y =\mathop{ \mathrm{Spec}}\nolimits B$ are affine, then f induces f ^#: B → A and the map f ^an takes a seminorm | ⋅ | on A to the seminorm b → | f ^#(b) | on B.

The analytification of an affine variety X is the limit of its tropicalizations by [24]. To be more precise, let X be an affine variety. For two embeddings $i: X \rightarrow \mathbb{A}^{n}$ and $j: X \rightarrow \mathbb{A}^{m}$, and a toric morphism $\varphi: \mathbb{A}^{n} \rightarrow \mathbb{A}^{m}$ satisfying j = φ ∘ i, we obtain a tropicalized map $\mathop{\mathrm{trop}}\nolimits (X \subset \mathbb{A}^{n}) \rightarrow \mathop{\mathrm{trop}}\nolimits (X \subset \mathbb{A}^{m})$. For every embedding $X \subset \mathbb{A}^{n}$, there is an associated map $X^{\text{an}} \rightarrow \mathop{\mathrm{trop}}\nolimits (X \subset \mathbb{A}^{n})$, sending a multiplicative seminorm | ⋅ | to the valuation − log | ⋅ |, see [24, p. 544]. The main result in [24] is that the inverse limit is homeomorphic to the Berkovich analytification . Hence, one has $X^{\text{an}} = \mathop{\lim }\limits_\longleftarrow \mathop{\mathrm{trop}}\nolimits (X \subset \mathbb{A}^{n})$.

We now return to the case of Enriques surfaces . We are interested in finding an Enriques surface S∕σ with a K3 cover S suitable for tropicalization. Specifically, we would like σ to be an involution acting without fixed points on the tropical side. In this sense, the examples obtained as in Sect. 3 are not suitable.

Example 4.2

Consider the K3 surface S _Q defined via the enriquogeneous quadrics in Sect. 3 with σ(x ₀, x ₁, x ₂, y ₀, y ₁, y ₂) = (x ₀, x ₁, x ₂, −y ₀, −y ₁, −y ₂). Since we have $\mathop{\mathrm{val}}\nolimits (-1) = 0$, the tropicalized involution $\mathop{\mathrm{trop}}\nolimits (\sigma )$ is the identity map on $\mathbb{R}^{6}$.

To obtain a K3 surface with an involution σ tropicalizing to a fixed-point-free involution, we consider embeddings into products of $\mathbb{P}^{1}$. Consider the involution $\tau: \mathbb{P}^{1} \rightarrow \mathbb{P}^{1}$ given by τ([x: y]) = [y: x] and the involution $\sigma: (\mathbb{P}^{1})^{3} \rightarrow (\mathbb{P}^{1})^{3}$ given by applying τ to every coordinate. The map τ restricts to the torus $\mathbb{C}^{{\ast}}$ and is given by $\mathbb{C}^{{\ast}}\ni t \rightarrow t^{-1} \in \mathbb{C}^{{\ast}}$. Therefore, we have $\mathop{\mathrm{trop}}\nolimits (\tau )(v) = -v$. Consequently, the tropicalization $\mathop{\mathrm{trop}}\nolimits (\sigma ): \mathbb{R}^{3} \rightarrow \mathbb{R}^{3}$ is given by $\mathop{\mathrm{trop}}\nolimits (\sigma )(v) = -v$. This map is non-trivial and has only one fixed point.

Example 4.3 (A K3 Surface with a Fixed-Point-Free Involution)

Let $S \subset \mathbb{P}^{1} \times \mathbb{P}^{1} \times \mathbb{P}^{1}$ be a smooth surface given by a section of the anticanonical divisor of $(\mathbb{P}^{1})^{3}$, namely a triquadratic polynomial. The Newton polytope of S is the three-dimensional cube [0, 2]³. We introduce the following assumptions on S:

• 1. S is smooth;

• 2. S is invariant under the involution σ; and

• 3. the subdivision induced by S on its Newton polytope [0, 2]³ is a unimodular triangulation, that is, the polytopes in the triangulation are tetrahedra of volume equal to 1∕6; see [22, p. 13].

Each such S is a K3 surface . Under our assumptions, the point (0, 0, 0) is not in the tropical variety of S. Indeed, if it were in $\mathop{\mathrm{trop}}\nolimits (S)$, that variety would not be locally linear at (0, 0, 0). But $\mathop{\mathrm{trop}}\nolimits (S)$ is coming from a unimodular triangulation, so it is locally linear everywhere. Hence, the point (0, 0, 0) is outside and $\mathop{\mathrm{trop}}\nolimits (\sigma )$ is a fixed-point-free involution on $\mathop{\mathrm{trop}}\nolimits (S)$. The map σ: S → S induces also an involution σ ^an: S ^an → S ^an which is compatible with $\mathop{\mathrm{trop}}\nolimits (\sigma )$ under the projection π; the following diagram commutes.

Fig. 4

The bounded part of a tropical K3 surface in $\mathbb{P}^{1} \times \mathbb{P}^{1} \times \mathbb{P}^{1}$

5 The Tropical Homology

In this section, we explicitly calculate the tropical homology of a tropical K3 surface and a tropical Enriques surface. We use the construction in Example 4.3 in order to obtain tropicalizations which are locally linear (locally look like tropicalizations of linear spaces), and then compute their tropical cohomology groups. In accordance with the results in [18], the dimensions of such homology groups coincide with the Hodge numbers of the surfaces themselves. We carry out the calculation by hand for some curves, a tropical K3 surface and also for an object, which we believe to be the associated tropical Enriques surface ; see [20] for computation of tropical homology using polymake .

Theorem 5.1 ([18, Special Case of Theorem 2])

If $X \subset \mathbb{P}^{N}$ , and its tropicalization $\mathop{\mathrm{trop}}\nolimits (X) \subset \mathop{\mathrm{trop}}\nolimits (\mathbb{P}^{N})$ has multiplicities all equal to 1 and is locally linear, then the tropical Hodge numbers agree with Hodge numbers of X: $\dim H_{p,q}(\mathop{\mathrm{trop}}\nolimits (X)) =\dim H^{p,q}(X, \mathbb{R})$ .

For the definition of multiplicities, we refer to [22, Chap. 3]. A tropical variety is locally linear if a Euclidean neighbourhood of each point is isomorphic to a Euclidean open subset of the tropicalization of a linear subspace $\mathbb{P}^{n} \subset \mathbb{P}^{m}$; see [31]. A hypersurface in $\mathbb{P}^{N}$ is locally linear if and only if the subdivision of its Newton polygon is a triangulation. It has multiplicities one if and only if this triangulation is unimodular.

In Theorem 5.1, we do not assume that X intersects the torus of $\mathbb{P}^{N}$. Therefore, this theorem applies to $X\,\subset \,(\mathbb{P}^{1})^{3}\,\subset \,\mathbb{P}^{7}$ or more generally to X in any projective toric variety with fixed embedding. Moreover, one might wonder whether Theorem 5.1 identifies not only dimensions but homology classes. This is possible when the appropriate spectral sequence degenerates at the E ₂ page. This E ₂ page is $H^{q}(X,\mathcal{F}^{p})$, where $\mathcal{F}^{p} =\mathop{ \mathrm{Hom}}\nolimits (\mathcal{F}_{p}, \mathbb{R})$; see the discussion after Corollary 2 in [18] or [8].

We provide generalities about tropical homology and compute some examples of interest; for a more detailed introduction see [7, 18]. We compute the dimensions of the tropical homology groups and show how Theorem 5.1 holds. The last part of the paper is dedicated to showing a particular instance of this theorem for a special tropical K3 surface with involution and for its quotient.

Tropical projective space $\mathop{\mathrm{trop}}\nolimits (\mathbb{P}^{n}) = \mathbb{T}\mathbb{P}^{n}$ is homeomorphic to an n-simplex; see [22, Chap. 6.2]. It is covered by n + 1 copies of $\mathbb{T}^{n} =\mathop{ \mathrm{trop}}\nolimits (\mathbb{A}^{n}) = (\{-\infty \}\cup \mathbb{R})^{n}$, that are complements of torus invariant divisors. Let X be a tropical subvariety of $\mathbb{T}\mathbb{P}^{n}$. The definitions of sheaves $\mathcal{F}_{p}$ and groups C _p, q computing the homology are all local, so we assume that $X \subset \mathop{\mathrm{trop}}\nolimits (\mathbb{A}^{n})$ is contained in one of the distinguished open subsets. We denote by $\mathbb{T}^{J} =\{ x \in \mathbb{T}^{n}: x_{i} = -\infty \text{ for all }i\not\in J\}$, for J ⊆ {1, 2, … , n}, the tropicalization of smaller torus orbits. Let $X \in \mathbb{T}^{n}$ be a polyhedral complex. The sedentarity I(x) of a point x ∈ X is the set of coordinates of x which are equal to −∞, and we set J(x): = {1, …, n}∖I(x). We denote by $\mathbb{R}^{J(x)} = \mathbb{R}^{n}/\mathbb{R}^{I(x)}$ the interior of $\mathbb{T}^{J(x)}$. For a face $E \subset X \cap \mathbb{R}^{J(x)}$ adjacent to x, we let $T_{x}(E) \subset T_{x}(\mathbb{R}^{J(x)})$ be the cone spanned by the tangent vectors to E starting at x and directed towards E. Fix the following terminology:

• 1. The tropical tangent space $\mathcal{F}_{1}(x) \subset T_{x}(\mathbb{R}^{J(x)})$ is the vector space generated by all T _x (E) for all E adjacent faces to x;

• 2. The tropical multitangent space $\mathcal{F}_{p}(x) \subset \bigwedge ^{p}T_{x}(\mathbb{R}^{J(x)})$ is the vector space generated by all vectors of the form v ₁ ∧ v ₂ ∧⋯ ∧ v _p where v ₁, v ₂, … , v _p ∈ T _x (E) for all E adjacent faces to x (this implies $\mathcal{F}_{0}(x)\cong \mathbb{R}$)

The multitangent vector space $\mathcal{F}_{p}(x)$ for x ∈ X only depends on the minimal face Δ ⊂ X containing x. Hence, we can write $\mathcal{F}_{p}(\varDelta ):=\mathcal{ F}_{p}(x)$ for each x ∈ Δ. We have the following group of (p, q)-chains

$$\displaystyle{C_{p,q}(X):=\bigoplus _{\varDelta \ q-\text{dim face of }X}\mathcal{F}_{p}(\varDelta )}$$

giving rise to the chain complex

$$\displaystyle{C_{p,\bullet } = \cdots \longrightarrow C_{p,q+1}(X)\mathop{\longrightarrow }\limits^{\partial }C_{p,q}(X)\mathop{\longrightarrow }\limits^{\partial }C_{p,q-1}(X)\longrightarrow \cdots }$$

where the differential ∂ is the usual simplicial differential (we choose orientation for each face) composed with inclusion maps given by $\iota: \mathcal{F}_{p}(\varDelta ) \rightarrow \mathcal{ F}_{p}(\varDelta ^{{\prime}})$ for Δ ^′ ≺ Δ. Even when Δ ^′ and Δ have different sedentarities, we have I(Δ ^′) ⊃ I(Δ) so we get a natural map $\mathbb{R}^{J(x)} = \mathbb{R}^{n}/\mathbb{R}^{I(x)} \twoheadrightarrow \mathbb{R}^{n}/\mathbb{R}^{I(x^{{\prime}}) } = \mathbb{R}^{J(x^{{\prime}}) }$ inducing the map $\iota: \mathcal{F}_{p}(\varDelta ) \rightarrow \mathcal{ F}_{p}(\varDelta ^{{\prime}})$.

Definition 5.2

The (p, q)th tropical homology group H _p, q (X) of X is the qth homology group of the complex C _p, •.

In the light of Theorem 5.1, if $X =\mathop{ \mathrm{trop}}\nolimits (X^{{\prime}})$ is a tropicalization of suitable variety X ^′, then dimH _p, q (X) are the Hodge numbers of X ^′. For all X, the tropical Poincaré duality holds: dimH _{d−p, d−q} (X) = dimH _p, q (X), see [19].

Example 5.3

Let’s compute the tropical homology of a tropical line L; see Fig. 5.

p = 0: :

From the discussion above, we see that $C_{0,0}(L) = \mathbb{R}^{4}$ and $C_{0,1} = \mathbb{R}^{3}$ injects into C _0,0. Thus, we have dimH _0,0(X) = 1 and H _0,1(X) = 0.

p = 1: :

The chain complex is 0 → C _1,1(X) → C _1,0(X) → 0. As in the previous case, we see that $C_{1,0}(X) =\mathcal{ F}_{1}(v_{1}) = \mathbb{R}\langle e_{1},e_{2}\rangle$, where e ₁ = (−1, 0) and e ₂ = (0, −1) are the standard basis vectors of $\mathbb{R}^{2}$ up to a sign. Moreover, we have

$$\displaystyle{C_{1,1}(X) =\mathcal{ F}_{1}(p) \oplus \mathcal{ F}_{1}(q) \oplus \mathcal{ F}_{1}(r) = \mathbb{R}\langle e_{1}\rangle \oplus \mathbb{R}\langle e_{2}\rangle \oplus \mathbb{R}\langle - e_{1} - e_{2}\rangle \,.}$$

The differential $\mathbb{R}\langle e_{1}\rangle \oplus \mathbb{R}\langle e_{2}\rangle \oplus \mathbb{R}\langle - e_{1} - e_{2}\rangle \mathop{\longrightarrow }\limits^{\partial }\mathbb{R}\langle e_{1},e_{2}\rangle$ is given by the natural inclusion e ₁ ↦ e ₁, e ₂ ↦ e ₂, and − e ₁ − e ₂ ↦ − e ₁ − e ₂. Hence, the kernel of the differential is one-dimensional, generated by the sum 〈e ₁〉 + 〈e ₂〉 + 〈 − e ₁ − e ₂〉, so we conclude that dimH _1,0(X) = 0 and dimH _1,1(X) = 1.

Fig. 5

A tropical line

Remark 5.4

By definition, we have $\mathcal{F}_{0}(x) = \mathbb{R}$, so the complex C _0,• is the singular homology complex for the subdivision of X by polyhedra. Thus, the tropical homology group H _0,q (X) is identified with the singular homology group $H_{q}(X, \mathbb{R})$.

Example 5.5 (Elliptic Curve)

We next compute the tropical homology of an elliptic curve in $\mathbb{P}^{1} \times \mathbb{P}^{1}$. Its tropicalization is shown in Fig. 6. From the isomorphism $H_{0,q}(X)\cong H_{q}(X, \mathbb{R})$, it follows that $H_{0,0}(X)\cong \mathbb{R}$ and $H_{0,1}(X)\cong \mathbb{R}$. We can compute H _1,1(X) directly from the complex C _1,1(X) → C _1,0(X). It follows that $C_{1,1}(X)\cong \mathbb{R}^{E}$ and $C_{1,0}(X)\cong \mathbb{R}^{2V }$, where E = 16 (respectively, V = 8) denotes the number of edges (respectively, of interior vertices). The kernel of the map C _1,1(X) → C _1,0(X) is generated by the boundary of the square, hence $H_{1,1}(X)\cong \mathbb{R}$.

Fig. 6

A tropical elliptic curve in $\mathbb{P}^{1} \times \mathbb{P}^{1}$

del Pezzo in $(\mathbb{P}^{1})^{3}$

Consider a surface S in $\mathbb{P}^{1} \times \mathbb{P}^{1} \times \mathbb{P}^{1}$ given by a section of $\mathcal{O}(1,1,1):= \mathcal{O}(1) \boxtimes \mathcal{O}(1) \boxtimes \mathcal{O}(1)$; this is a del Pezzo surface, its anticanonical divisor is, by adjunction, the restriction of $\mathcal{O}(1,1,1)$, so the anticanonical degree is 6. The equation for S can be written as F = ∑ _{0 ≤ i, j, k ≤ 1} a _i, j, k x ⁱ y ^j z ^k, where x, y, z are local coordinates on the three projective lines. Suppose that we are over a valued field and that a _i, j, k = a _{1−i, 1−j, 1−k} for all indices and that a _1,0,0 > max(a _0,1,0, a _0,0,1). Hence, the induced subdivision of a cube is regular, as seen in Fig. 8. From the picture, we see that there are 6 points, 18 edges, and 19 faces in the non-sedentary part of $\mathop{\mathrm{trop}}\nolimits (S)$. The tropical variety $\mathop{\mathrm{trop}}\nolimits \big((\mathbb{P}^{1})^{3}\big) \simeq (\mathbb{R} \cup \left \{\pm \infty \right \})^{3}$ is homeomorphic to the cube, see Fig. 7. Its faces correspond to torus-invariant divisors in $(\mathbb{P}^{1})^{3}$. The boundary $\mathop{\mathrm{trop}}\nolimits (S)\setminus \mathbb{R}^{3}$ decomposes into six components, the intersections of $\mathop{\mathrm{trop}}\nolimits (S)$ with those faces. To understand the sedentary points, we use the following result.

Fig. 7

A tropicalization of $\mathbb{P}^{1} \times \mathbb{P}^{1} \times \mathbb{P}^{1}$ with the sedentarities of the faces at infinity

Fig. 8

Regular subdivision of the cube and tropical del Pezzo

Theorem 5.6 ([22, Theorem 6.2.18])

If Y ⊂ T and $\overline{Y }$ is the closure of Y in a toric variety X, then the tropical variety $\mathop{\mathrm{trop}}\nolimits (\overline{Y })$ is the closure of $\mathop{\mathrm{trop}}\nolimits (Y )$ in $\mathop{\mathrm{trop}}\nolimits (X)$ .

Applying Theorem 5.6 to $Y =\bar{ S}$, we see that the boundary of the tropicalization is the tropicalization of the boundary, so we have $\mathop{\mathrm{trop}}\nolimits (S) \cap \mathop{\mathrm{trop}}\nolimits (D) =\mathop{ \mathrm{trop}}\nolimits (S \cap D)$ for each torus-invariant divisor. The torus-invariant divisors are defined by x ^±1, y ^±1, z ^±1. Without loss of generality, assume $D =\mathop{ \mathrm{V}}\nolimits (x)$. By restricting the element F to D, we obtain the quadric ∑ _{0 ≤ j, k ≤ 1} a _0,j, k y ^j z ^k whose tropicalization is given in Fig. 9. In particular, it has five edges, two mobile points, and four sedentary points. Table 1 summarizes the strata.

This information enables us to compute the C _p, q without analyzing the maps, because our del Pezzo is locally linear: near each vertex the tropical structure looks like the tropicalization of $\mathbb{P}^{2} \subset \mathbb{P}^{3}$, as shown in Fig. 4. The complexes are

$$\displaystyle\begin{array}{llll} \begin{array}{lllllll} & C_{0,2} = \mathbb{R}^{19} & & \rightarrow C_{0,1} = \mathbb{R}^{18} \oplus \mathbb{R}^{30} & & \rightarrow C_{0,0} = \mathbb{R}^{30} \\ & C_{1,2} = \mathbb{R}^{2\cdot 19} & & \rightarrow C_{1,1} = \mathbb{R}^{3\cdot 18} \oplus \mathbb{R}^{30} & & \rightarrow C_{1,0} = \mathbb{R}^{3\cdot 6} \oplus \mathbb{R}^{2\cdot 12} \\ & C_{2,2} = \mathbb{R}^{19} & & \rightarrow C_{2,1} = \mathbb{R}^{2\cdot 18} & & \rightarrow C_{2,0} = \mathbb{R}^{3\cdot 6}.\end{array} & & {}\\ \end{array}$$

Fig. 9

A tropical quadric in $\mathbb{P}^{1} \times \mathbb{P}^{1}$

Table 1 Strata in tropical del Pezzo

By comparing H _0,• with singular homology and using Poincaré duality, we obtain $H_{0,0} \simeq H_{2,2} \simeq \mathbb{R}\quad H_{0,1} = H_{0,2} = H_{2,0} = H_{2,1} = 0$, so the interesting part is the homology of C _1,•. It is not impossible to compute this homology by hand. However, to save space, we only outline a series of reductions. Each of these reductions involves to finding an exact subcomplex D ⊂ C _1,• and reducing to computing homology of C _1,•∕D. Consider a sedentary point p on the face of a cube. This point has two edges e ₁, e ₂ going towards the boundary of this face (and a third edge, which is irrelevant here). In C _1,•, these polyhedra give an exact subcomplex $\mathbb{R}[e_{1}] \oplus \mathbb{R}[e_{2}] \rightarrow \mathbb{R}^{2}[p]$, so the homology of C _1,• is the homology of the quotient C ^′ by all these subcomplexes for 12 choices of p. The quotient is $\mathbb{R}^{(2)(19)} \rightarrow \mathbb{R}^{(3)(18)} \oplus \mathbb{R}^{6} \rightarrow \mathbb{R}^{(3)(6)}$. Next, consider one of the two corner vertices in Fig. 8 and all its adjacent faces (three edges, three faces, one simplex). In the tropical variety , those correspond to one point p, three edges e _i , and three faces f _i that glue together to form on tropical $\mathbb{A}^{2}$. Such an $\mathbb{A}^{2}$ has no higher homology, so the sequence $\bigoplus \mathbb{R}^{2}[f_{i}] \rightarrow \bigoplus \mathbb{R}^{3}[e_{i}] \rightarrow \bigoplus \mathbb{R}^{3}[p]$ is an exact subcomplex of C ^′. Dividing C ^′ by the subcomplexes given by two corner vertices, we see that C ^″ equal to $\mathbb{R}^{(2)(13)} \rightarrow \mathbb{R}^{(3)(12)} \oplus \mathbb{R}^{6} \rightarrow \mathbb{R}^{(3)(4)}$. The module $\mathbb{R}^{(3)(4)}$ corresponds to four multitangent spaces at four vertices of the square in the interior; see Fig. 8. Since none of the edges adjacent to them was modified in the process, the right map is surjective. Hence, we have H _1,0 = 0. By Poincaré duality, we deduce that H _1,2 = 0 and dimH _1,1 = 36 + 6 − 26 − 12 = 4, as expected from the Hodge diamond of a del Pezzo of anticanonical degree 6.

A K3 Surface in $(\mathbb{P}^{1})^{3}$

Let $S \subset \mathbb{P}^{1} \times \mathbb{P}^{1} \times \mathbb{P}^{1}$ be a K3 surface over a valued field $\mathbb{k}$ as in Example 4.3. This subsection discusses its tropical homology and relations to its Hodge classes; using tropical homology , we recover the expected Hodge numbers and an anti-symplectic involution.

As explained in [22, Definition 2.3.8, Fig. 1.3.3], the polyhedral decomposition of the tropicalization is dual to the subdivision induced on the 2 × 2 × 2 cube by the coefficients of S; see Fig. 4. Restrict to the torus and consider polyhedra with empty sedentarity . The tropical variety $\mathop{\mathrm{trop}}\nolimits (S)$ comes from a regular subdivision into 48 simplices, so it has 48 distinguished points. Each face of the subdivision (or edge in the tropicalization) is either “inner”, shared by two tetrahedra, or “outer”, adjacent to only one of them. There are 48 outer faces and each tetrahedron has four faces, so there is a total of $\big((48)(4) + 48\big)/2 = 120$ faces. As seen in the del Pezzo case, there are 19 edges in a subdivision of a unit cube. In the 2 × 2 × 2 cube, we have (8)(19) of those segments; 36 of them are adjacent to exactly two cubes, six of them are adjacent to four cubes, and the others stick to one cube. Therefore, there are (8)(19) − 36 − (3)(6) = 98 segments. The boundary of $\mathop{\mathrm{trop}}\nolimits (S)$ is the intersection of $\mathop{\mathrm{trop}}\nolimits (S)$ with the boundary of this cube. Pick a face $\mathcal{F}$ of the cube. It is the tropicalization of one of the six toric divisors x _i ^±1 for 1 ≤ i ≤ 3, say to x ₁. Theorem 5.6 implies that $\mathop{\mathrm{trop}}\nolimits (S) \cap \mathcal{ F} =\mathop{ \mathrm{trop}}\nolimits \big(S \cap \mathop{\mathrm{V}}\nolimits (x_{1})\big)$. But $S \cap \mathop{\mathrm{V}}\nolimits (x_{1})$ is an elliptic curve in $\mathbb{P}^{1} \times \mathbb{P}^{1}$ and Sect. 5.5 shows that its tropicalization has 16 edges, 8 mobile points, and 8 sedentary points; see Fig. 6. Table 2 enumerates the strata.

Table 2 Strata in tropical K3

Fig. 10

Tropicalization of $\mathbb{P}^{2}$

Once again, this information enables us to compute the C _p, q without analyzing the maps. Near each vertex the tropical structure looks like the tropicalization of $\mathbb{P}^{2} \subset \mathbb{P}^{3}$ see Fig. 10 and compare with Fig. 4. The complexes are

$$\displaystyle\begin{array}{rcl} \begin{array}{llllll} &C_{0,2} = \mathbb{R}^{98} & & \rightarrow C_{0,1} = \mathbb{R}^{120} \oplus \mathbb{R}^{96} & & \rightarrow C_{0,0} = \mathbb{R}^{120} \\ & C_{1,2} = \mathbb{R}^{2\cdot 98} & & \rightarrow C_{1,1} = \mathbb{R}^{3\cdot 120} \oplus \mathbb{R}^{96} & & \rightarrow C_{1,0} = \mathbb{R}^{3\cdot 48} \oplus \mathbb{R}^{2\cdot 48} \\ & C_{2,2} = \mathbb{R}^{98} & & \rightarrow C_{2,1} = \mathbb{R}^{2\cdot 120} & & \rightarrow C_{2,0} = \mathbb{R}^{3\cdot 48}.\end{array} & & {}\\ \end{array}$$

In particular, we see that χ(C _1,•) = 2 ⋅ 98 − 3 ⋅ 120 − 96 + 3 ⋅ 48 + 2⋅ = −20 as expected. Moreover, one can show that H _1,0 = 0, roughly because the classes of sedentary edges surject to classes of sedentary points and other points can be analyzed directly by Fig. 4. By Poincaré duality, we have H _1,2 = 0, so we obtain

$$\displaystyle{-20 =\chi (C_{1,\bullet }) =\dim H_{1,0} -\dim H_{1,1} +\dim H_{1,2} = -\dim H_{1,1}\,.}$$

We now consider (0, q)-classes. The homology of C _0,• is just the singular homology of the tropical variety by Remark 5.4. The tropical variety is contractible to the boundary of the cube. Thus, C _0,• is exact in the middle and its homology groups are the homology groups of the sphere: $H_{0,0} \simeq \mathbb{R}$, H _0,1 = 0, and $H_{0,2} = \mathbb{R}$. In other words, this gives an explicit proof for our special case of Theorem 5.1.

Proposition 5.7

The tropical Hodge numbers of tropical variety $\mathop{\mathrm{trop}}\nolimits (S)$ agree with the Hodge numbers of the surface S. □

We expose an explicit generator of H _0,2 and analyze the action of σ on this space. Briefly speaking, this class is obtained as the boundary of the interior of the cube. To expand this, consider the boundary of the cube and the complex C ₂ ^′ → C ₁ ^′ → C ₀ ^′ computing its singular homology. This boundary can be embedded into a full cube and the complex C ^′ becomes part of the complex C ^″ computing the homology of the cube 0 → C ₃ ^″ → C ₂ ^″ → C ₁ ^″ → C ₀ ^″. Since the cube is contractible, the complex C ^″ is exact. Hence, the unique class ω in H ²(C ^′) is the boundary of the class Ω in C ₃ ^″. Consider the action of σ on the $\mathbb{R}^{3}$ containing the tropical variety. We have σ(x) = −x in $\mathbb{R}^{3}$, so σ changes orientation and σ(Ω) = −Ω. It follow that σ(ω) = σ(∂Ω) = −ω.

Finally, we investigate the σ-invariant part C _p, • ^σ of the complexes C _p, •. Since we work over characteristic different from two, the functor (−)^σ is exact and the homology of C _p, • ^σ is the invariant part of the homology of C _p, •. Since $\mathop{\mathrm{trop}}\nolimits (S)/\sigma$ is a tropical manifold, C _•,• ^σ computes its tropical homology; see [7, Chap. 7]. In particular, the homology groups H _p, q ^σ = H ^q(C _p, • ^σ) satisfy H _p, q ^σ = H _{2−p, 2−q} ^σ. We believe, although we have not proved it formally, that the manifold $\mathop{\mathrm{trop}}\nolimits (S)/\sigma$ is a tropicalization of the Enriques surface S∕σ. If this is the case, the homology classes of C _•,• ^σ compute the tropical homology of Enriques surface S∕σ. It is straightforward to compute the dimensions of C _p, q ^σ, because $\mathop{\mathrm{trop}}\nolimits (S)$ does not contain the origin. As a consequence, every face F of $\mathop{\mathrm{trop}}\nolimits (S)$ is mapped by σ to a unique face F ^′ so that the action of σ on the space spanned by [F] and [F ^′] always decomposes into an invariant subspace [F] + [F ^′] and an anti-invariant space [F] − [F ^′]. Therefore, we have $\dim C_{p,q}^{\sigma } = \frac{1} {2} \cdot \dim C_{p,q}$, for all p, q, and the sequences are

$$\displaystyle\begin{array}{rcl} \begin{array}{lllllll} &C_{0,2}^{\sigma } = \mathbb{R}^{49} & & \rightarrow C_{0,1}^{\sigma } = \mathbb{R}^{60} \oplus \mathbb{R}^{48} & & \rightarrow C_{0,0}^{\sigma } = \mathbb{R}^{60} \\ & C_{1,2}^{\sigma } = \mathbb{R}^{2\cdot 49} & & \rightarrow C_{1,1}^{\sigma } = \mathbb{R}^{3\cdot 60} \oplus \mathbb{R}^{48} & & \rightarrow C_{1,0}^{\sigma } = \mathbb{R}^{3\cdot 24} \oplus \mathbb{R}^{2\cdot 24} \\ & C_{2,2}^{\sigma } = \mathbb{R}^{49} & & \rightarrow C_{2,1}^{\sigma } = \mathbb{R}^{2\cdot 60} & & \rightarrow C_{2,0}^{\sigma } = \mathbb{R}^{3\cdot 24}.\end{array} & & {}\\ \end{array}$$

The generator ω of H _0,2 does not lie in H _0,2 ^σ. Thus, we have H _0,2 ^σ = H _0,1 ^σ = 0 and $H_{0,0}^{\sigma } \simeq \mathbb{R}$. By symmetry, we also have H _2,0 ^σ = H _2,1 ^σ = 0 and $H_{2,2}^{\sigma } \simeq \mathbb{R}$, which yields

$$\displaystyle{-\dim H_{1,1} =\dim H_{1,0} -\dim H_{1,1} +\dim H_{1,2} = -\chi \left (C_{1,\bullet }^{\sigma }\right ) = -\tfrac{1} {2}\chi (C_{1,\bullet }) = -10\,.}$$

Summarizing these calculations, we obtain the following counterpart of Proposition 5.7.

Proposition 5.8

The dimensions of the σ-invariant parts of tropical homology groups of S agree with the Hodge numbers of S∕σ. □

6 Topology of Analytifications of Enriques Surfaces

In this section, we analyze the analytification of an Enriques surface that is the quotient of the K3 surface from Example 4.3. Fix a valued field $\mathbb{k}$ and a K3 surface $S \subset (\mathbb{P}^{1})^{3}$ over $\mathbb{k}$ together with an involution σ: S → S, as in Example 4.3. We first analyze the topology of S ^an itself.

Proposition 6.1

The topological space S ^an has a strong deformation retraction onto a two-dimensional sphere C. More precisely, there exist continuous maps s: C → S ^an and e: S ^an → C, so that $e \circ s =\mathop{ \mathrm{id}}\nolimits _{C}$ and s ∘ e is homotopic to $\mathop{\mathrm{id}}\nolimits _{S^{\mathit{\text{an}}}}$ . The maps s and e may be chosen to be σ-equivariant, where σ acts on C antipodally.

Proof

We consider the tropicalization $\mathop{\mathrm{trop}}\nolimits (S) \subset (\mathbb{R} \cup \{\pm \infty \})^{3}$ with the antipodal involution $\mathop{\mathrm{trop}}\nolimits (\sigma )$. We abbreviate $\mathop{\mathrm{trop}}\nolimits (\sigma )$ as σ. There is a cube $C \subset \mathop{\mathrm{trop}}\nolimits (S)$ fixed under the involution, see Fig. 4. This cube is a strong deformation retract of $\mathop{\mathrm{trop}}\nolimits (S)$ and the retraction can be chosen to be σ-equivariant. In the following we identify C with a two-dimensional sphere.

It remains to prove that the tropical variety $\mathop{\mathrm{trop}}\nolimits (S)$ is a strong deformation retract of S ^an under the map $\pi: S^{\text{an}} \rightarrow \mathop{\mathrm{trop}}\nolimits (S)$. The tropical variety $\mathop{\mathrm{trop}}\nolimits (S)$ is schön; its intersection with every torus orbit is smooth; see [22, Definition 6.4.19]. Moreover, all multiplicities of top degree polyhedra are equal to one, so the multiplicity at each point is equal to one by semicontinuity; see [22, Lemma 3.3.6]. Therefore, π has a section $\mathop{\mathrm{trop}}\nolimits (S) \rightarrow S^{\text{an}}$ whose image is equal to a skeleton $S(\mathcal{S},H)$ of a suitable semistable model $(\mathcal{S},H)$ of S; see [16, Remark 9.12]. The skeleton $S(\mathcal{S},H)$ is a proper strong deformation retract of S ^an by [17, Sect. 4.9]. The retraction map $S^{\text{an}} \rightarrow \mathop{\mathrm{trop}}\nolimits (S)$ is equal to π, so σ-equivariant as discussed in Example 4.3. The retraction s in the claim of the theorem is the composition of retractions from S ^an to $\mathop{\mathrm{trop}}\nolimits (S)$ and from $\mathop{\mathrm{trop}}\nolimits (S)$ to the cube constructed above. □

Corollary 6.2

The analytified K3 surface S ^an is homotopy equivalent to a two-dimensional sphere. □

Remark 6.3

From Proposition 6.1, it does not follow that the homotopy between s ∘ e and $\mathop{\mathrm{id}}\nolimits _{S^{\text{an}}}$ can be chosen σ-equivariantly. This is most likely true, but presently there seems to be no reference for this fact.

We now analyze the topology of the analytification of the Enriques surface S∕σ using our knowledge about S ^an. The quotient map q: S → S∕σ analytifies to q ^an: S ^an → (S∕σ)^an. For any X, we denote π: X ^an → X the natural map. Summarizing, we consider the following diagram.

It is crucial that q ^an is a quotient by σ ^an, as we now prove.

Proposition 6.4

We have (S∕σ)^an = S ^an∕σ ^an as topological spaces.

Proof

First, we prove the equality of sets (S∕σ)^an = S ^an∕σ ^an. Consider x ∈ (S∕σ)^an and its image π(x) ∈ S∕σ. If $U =\mathop{ \mathrm{Spec}}\nolimits (A)$ is an affine neighbourhood of the point π(x), then the point x corresponds to a semi-norm | ⋅ | _x on A and π(x) corresponds to the prime ideal $\mathfrak{p}_{x} =\{ f \in A: \vert f\vert _{x} = 0\}$; see [5, Remark 1.2.2]. We denote by $\mathcal{H}(x)$ the completion of the fraction field of $A/\mathfrak{p}_{x} =\kappa (\pi (x))$. We have the equality of fibres $S_{x}^{\text{an}} =\big (S_{x} \times _{\kappa (\pi (x))}\mathcal{H}(x)\big)^{\text{an}}$; see [5, p. 65]. In down-to-earth terms, the set S _x ^an consists of multiplicative seminorms on the $\mathcal{H}(x)$-algebra $R = H^{0}(S_{x},\mathcal{O}_{S_{x}}) \otimes _{\kappa (\pi (x))}\mathcal{H}(x)$ which extend the norm | ⋅ | _x on $\mathcal{H}(x)$. Using Proposition 1.3.5 in [5], we may assume $\mathcal{H}(x)$ is algebraically closed. Since $H^{0}(S_{x},\mathcal{O}_{S_{x}})^{\sigma } =\kappa (\pi (x))$, we have $R^{\sigma } =\mathcal{ H}(x)$. Similarly, the ring R is a free $\mathcal{H}(x)$-module of rank 2. It follows that R is isomorphic to either $\mathcal{H}(x)^{\times 2}$ with σ permuting the coordinates or to $\mathcal{H}(x)[\varepsilon ]/\varepsilon ^{2}$. Given a multiplicative seminorm | ⋅ | _y on R, its kernel $\mathfrak{q} =\{ f \in R: \vert f\vert _{y} = 0\}$ is a prime ideal in R. In both cases, we have $R/\mathfrak{q} =\mathcal{ H}(x)$. Since | ⋅ | _y agrees with | ⋅ | _x on $\mathcal{H}(x)$, we see that | ⋅ | _y is determined uniquely by its kernel. The involution σ acts transitively on those, hence σ ^an acts transitively on the set S _x ^an and the equality is proven.

Second, we prove that (S∕σ)^an = S ^an∕σ ^an as topological spaces; in other words, the topology on (S∕σ)^an is induced from this of S ^an. Take an open subset U ⊂ S ^an. We want to show that q ^an(U) is open. Clearly, the union U ∪σ ^an(U) ⊂ S ^an is open and a union of fibres, so its complement Z ⊂ S ^an is closed and a union of fibres. The map q ^an is finite, so it proper and hence closed; see [5, 3.4.7 and 3.3.6]. In particular, the image q ^an(Z) ⊂ (S∕σ)^an is closed, so its complement π(U) = (S∕σ)^an ∖q ^an(Z) is open. This proves that (S∕σ)^an = S ^an∕σ ^an as topological spaces. □

Corollary 6.5

There exists a retraction from (S∕σ)^an onto $\mathbb{R}\mathbb{P}^{2}$ . In particular (S∕σ)^an is not contractible.

Proof

The argument follows formally from Proposition 6.1 and Proposition 6.4. If C is a two dimensional sphere with an antipodal involution σ and $C/\sigma \simeq \mathbb{R}\mathbb{P}^{2}$, then Proposition 6.1 provides the σ-invariant map e: S ^an → C and its section s: C → S ^an. We now produce equivalents of s and e on the level of S ^an∕σ ^an ≃ (S∕σ)^an.

The map $q \circ e: S^{\text{an}} \rightarrow s(C)/\sigma = \mathbb{R}\mathbb{P}^{2}$ satisfies q ∘ e ∘σ ^an = q ∘ e so, by Proposition 6.4, it induces a unique map $e: S^{\text{an}}/\sigma ^{\text{an}} = (S/\sigma )^{\text{an}} \rightarrow \mathbb{R}\mathbb{P}^{2}$. Similarly, the map q ^an ∘ s satisfies $q^{\text{an}} \circ s \circ \mathop{\mathrm{trop}}\nolimits (\sigma ) = q^{\text{an}} \circ s$, so induces a unique map $s: \mathbb{R}\mathbb{P}^{2} \rightarrow (S/\sigma )^{\text{an}}$. It follows that $e \circ s: \mathbb{R}\mathbb{P}^{2} \rightarrow \mathbb{R}\mathbb{P}^{2}$ is the unique map induced σ-invariant map q ∘ e ∘ s = q. Therefore, we have $e \circ s =\mathop{ \mathrm{id}}\nolimits _{\mathbb{R}\mathbb{P}^{2}}$ and s ∘ e is a retraction of (S∕σ)^an onto s(ℝℙ ²) ≃ ℝℙ ². □

Remark 6.6

If the difficulty presented in Remark 6.3 was removed, a similar argument would show that (S∕σ)^an strongly deformation retracts onto $\mathbb{R}\mathbb{P}^{2}$.

Proof of Theorem 1.3

Follows from Proposition 6.1 and Corollary 6.5. □