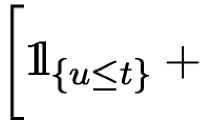On Some Problems Concerning Log-Concave Random Vectors

Abstract

A Radon measure μ on a locally convex linear space F is called logarithmically concave (log-concave in short) if for any compact nonempty sets K, L ⊂ F and λ ∈ [0, 1], μ(λ K + (1 −λ)L) ≥ μ(K)^λ μ(L)^1−λ. A random vector with values in F is called log-concave if its distribution is logarithmically concave.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

A Radon measure μ on a locally convex linear space F is called logarithmically concave (log-concave in short) if for any compact nonempty sets K, L ⊂ F and λ ∈ [0, 1], μ(λ K + (1 −λ)L) ≥ μ(K)^λ μ(L)^1−λ. A random vector with values in F is called log-concave if its distribution is logarithmically concave.

The class of log-concave measures is closed under affine transformations, convolutions, and weak limits. By the result of Borell [4] an n-dimensional vector with a full dimensional support is log-concave iff it has a log-concave density, i.e. a density of the form e ^−h, where h is a convex function with values in (−∞, ∞]. A typical example of a log-concave vector is a vector uniformly distributed over a convex body. It may be shown that the class of log-concave distributions on $\mathbb{R}^{n}$ is the smallest class that contains uniform distributions on convex bodies and is closed under affine transformations and weak limits.

Every full-dimensional logarithmically concave probability measure on $\mathbb{R}^{n}$ may be affinely transformed into an isotropic distribution, i.e. a distribution with mean zero and identity covariance matrix.

In recent years the study of log-concave vectors attracted attention of many researchers, cf. monographs [2] and [5]. There are reasons to believe that logarithmically concave isotropic distributions have similar properties as product distributions. The most important results confirming this belief are the central limit theorem of Klartag [9] and Paouris’ large deviation for Euclidean norms [21]. However, many important questions concerning log-concave measures are still open – in this note we present and discuss some of them.

Notation. By 〈⋅ , ⋅ 〉 we denote the standard scalar product on $\mathbb{R}^{n}$. For $x \in \mathbb{R}^{n}$ we put ∥ x ∥  _p  = (∑ _i = 1 ⁿ | x _i  | ^p)^1∕p for 1 ≤ p < ∞ and ∥ x ∥  _∞  = max _i  | x _i  | , we also use | x | for ∥ x ∥ ₂. We set B _p ⁿ for a unit ball in l _p ⁿ, i.e.. $B_{p}^{n} =\{ x \in \mathbb{R}^{n}: \|x\|_{p} \leq 1\}$. $\mathcal{B}(\mathbb{R}^{n})$ stands for the family of Borel sets on $\mathbb{R}^{n}$.

By a letter C we denote absolute constants, value of C may differ at each occurence. Whenever we want to fix a value of an absolute constant we use letters C ₁, C ₂, ….

2 Optimal Concentration

Let ν be a symmetric exponential measure with parameter 1, i.e. the measure on the real line with the density $\frac{1} {2}e^{-\vert x\vert }$. Talagrand [23] (see also [17] for a simpler proof based on a functional inequality) showed that the product measure ν ⁿ satisfies the following two-sided concentration inequality

$$\displaystyle{\forall _{A\in \mathcal{B}(\mathbb{R}^{n})}\ \forall _{t>0}\ \nu ^{n}(A) \geq \frac{1} {2}\ \Rightarrow \ 1 -\nu ^{n}(A + C\sqrt{t}B_{ 2}^{d} + CtB_{ 1}^{d}) \leq e^{-t}(1 -\nu ^{n}(A)).}$$

This is a very strong result – a simple transportation of measure argument shows that it yields the Gaussian concentration inequality

$$\displaystyle{\forall _{A\in \mathcal{B}(\mathbb{R}^{n})}\ \forall _{t>0}\ \gamma _{n}(A) \geq \frac{1} {2}\ \Rightarrow \ 1 -\gamma _{n}(A + C\sqrt{t}B_{2}^{n}) \leq e^{-t}(1 -\gamma _{ n}(A)),}$$

where γ _n is the canonical Gaussian measure on $\mathbb{R}^{n}$, i.e. the measure with the density (2π)^−d∕2exp(− | x | ²∕2).

It is natural to ask if similar inequalities may be derived for other measures. To answer this question we should first find a right way to enlarge sets.

Definition 1

Let μ be a probability measure on $\mathbb{R}^{n}$, for p ≥ 1 we define the following sets

$$\displaystyle{\mathcal{M}_{p}(\mu ):=\Big\{ v \in \mathbb{R}^{n}: \int \vert \langle v,x\rangle \vert ^{p}d\mu (x) \leq 1\Big\},}$$

and

$$\displaystyle{\mathcal{Z}_{p}(\mu ):= (\mathcal{M}_{p}(\mu ))^{\circ } =\Big\{ x \in \mathbb{R}^{n}: \vert \langle v,x\rangle \vert ^{p} \leq \int \vert \langle v,y\rangle \vert ^{p}d\mu (y)\mbox{ for all }v \in \mathbb{R}^{n}\Big\}.}$$

Sets $\mathcal{Z}_{p}(\mu _{K})$ for p ≥ 1, when μ _K is the uniform distribution on the convex body K are called L _p -centroid bodies of K. They were introduced (under a different normalization) in [16], their properties were also investigated in [21]. Observe that for isotropic measures $\mathcal{M}_{2}(\mu ) = \mathcal{Z}_{2}(\mu ) = B_{2}^{n}$.

Obviously $\mathcal{M}_{p}(\mu ) \subset \mathcal{M}_{q}(\mu )$ and $\mathcal{Z}_{p}(\mu ) \supset \mathcal{Z}_{q}(\mu )$ for p ≥ q. Next definition allows to reverse these inclusions.

Definition 2

We say that moments of a probability measure μ on $\mathbb{R}^{n}$ grow α-regularly for some α ∈ [1, ∞) if for any p ≥ q ≥ 2 and $v \in \mathbb{R}^{n}$,

$$\displaystyle{\left (\int \vert \langle v,x\rangle \vert ^{p}d\mu (x)\right )^{1/p} \leq \alpha \frac{p} {q}\left (\int \vert \langle v,x\rangle \vert ^{q}d\mu (x)\right )^{1/q}.}$$

It is easy to see that for measures with α-regular growth of moments and p ≥ q ≥ 2 we have $\alpha \frac{p} {q}\mathcal{M}_{p}(\mu ) \supset \mathcal{M}_{q}(\mu )$ and $\mathcal{Z}_{p}(\mu ) \subset \alpha \frac{p} {q}\mathcal{Z}_{q}(\mu )$.

Moments of log-concave measures grow 3-regularly (1-regularly for symmetric measures and 2-regularly for centered measures). The following easy observation was noted in [15].

Proposition 3

Suppose that μ is a symmetric probability measure on $\mathbb{R}^{n}$ with α-regular growth of moments. Let K be a convex set such that for any halfspace A,

$$\displaystyle{\mu (A) \geq \frac{1} {2}\ \Rightarrow \ 1 -\mu (A + K) \leq \frac{1} {2}e^{-p}.}$$

Then $K \supset c(\alpha )\mathcal{Z}_{p}$ if p ≥ p(α), where c(α) and p(α) depend only on α.

The above motivates the following definition.

Definition 4

We say that a measure μ satisfies the optimal concentration inequality with constant β (​ CI(β) in short) if

$$\displaystyle{\forall _{p\geq 2}\ \forall _{A\in \mathcal{B}(\mathbb{R}^{n})}\ \mu (A) \geq \frac{1} {2}\ \Rightarrow \ 1 -\mu (A +\beta \mathcal{Z}_{p}(\mu )) \leq e^{-p}(1 -\mu (A)).}$$

By the result of Gluskin and Kwapien [6], $\mathcal{M}_{p}(\nu ^{n}) \sim p^{-1}B_{\infty }^{n} \cap p^{-1/2}B_{2}^{n}$, so $\mathcal{Z}_{p}(\nu ^{n}) \sim pB_{1}^{n} + p^{1/2}B_{2}^{n}$. Therefore Talagrand’s two-sided concentration inequality states that ν ⁿ satisfy CI(β) with β ≤ C.

Remark 5

By Proposition  2.7 in [15] CI(β) may be equivalently stated as

$$\displaystyle{ \forall _{p\geq 2}\ \forall _{A\in \mathcal{B}(\mathbb{R}^{n})}\ \mu (A +\beta \mathcal{Z}_{p}(\mu )) \geq \min \left \{\frac{1} {2},e^{p}\mu (A)\right \}. }$$

(1)

In [15] a very strong conjecture was posed that every symmetric log-concave measure on $\mathbb{R}^{n}$ satisfy CI(β) with a uniform constant β. Unfortunately there are very few examples supporting this conjecture.

Theorem 6

The following probability measures satisfy the optimal concentration inequality with an absolute constant β:

• i) symmetric product log-concave measures;

• ii) uniform distributions on B _p ⁿ -balls, 1 ≤ p ≤∞;

• iii) rotationally invariant logconcave measures.

Parts i) ii) were showed in [15], iii) may be showed using a radial transportation and the Gaussian concentration inequality.

Property CI(β) is invariant under linear transformations, so it is enough to study it for isotropic measures. For isotropic log-concave measures and p ≥ 2 we have $\mathcal{Z}_{p}(\mu ) \subset p\mathcal{Z}_{2}(\mu ) = pB_{2}^{n}$, so CI(β) implies the exponential concentration:

$$\displaystyle{\forall _{A\in \mathcal{B}(\mathbb{R}^{n})}\ \mu (A) \geq \frac{1} {2}\ \Rightarrow \ 1 -\mu (A +\beta pB_{2}^{n}) \leq e^{-p}\mbox{ for }p \geq 2.}$$

By the result of E. Milman [20] the exponential concentration for log-concave measures is equivalent to Cheeger’s inequality:

$$\displaystyle{\forall _{A\in \mathcal{B}(\mathbb{R}^{n})}\ \mu ^{+}(A):=\lim _{ t\rightarrow 0+}\frac{\mu (A + tB_{2}^{n}) -\mu (A)} {t} \geq \frac{1} {\beta '} \min \{\mu (A),1 -\mu (A)\},}$$

and constants β, β′ are comparable up to universal multiplicative factors. The long-standing open conjecture of Kannan, Lovasz, and Simonovits [8] states that isotropic log-concave probability measures satisfy Cheeger’s inequality with a uniform constant.

The best known bound for the exponential concentration constant for isotropic log-concave measures $\beta \leq Cn^{1/3}\sqrt{\log n}$ is due to Eldan [7]. We will show a weaker estimate for the CI constant.

Proposition 7

Every centered log-concave probability measure on $\mathbb{R}^{n}$ satisfies the optimal concentration inequality with constant $\beta \leq C\sqrt{n}$.

Our proof is based on the following two simple lemmas.

Lemma 8

Let μ be a probabilistic measure on $\mathbb{R}^{n}$ . Then

$$\displaystyle{\mu (10\lambda \mathcal{Z}_{p}(\mu )) \geq 1 -\lambda ^{-p}\quad \mbox{ for }p \geq n,\ \lambda \geq 1.}$$

Proof

Let T = { u ₁, …, u _N } be a 1∕2-net in $\mathcal{M}_{p}(\mu )$ of cardinality N ≤ 5ⁿ, i.e. such set $T \subset \mathcal{M}_{p}(\mu )$ that $\mathcal{M}_{p}(\mu ) \subset T + \frac{1} {2}\mathcal{M}_{p}(\mu )$. Then the condition $x\notin \mathcal{Z}_{p}(\mu )$ implies 〈u _j , x〉 > 1∕2 for some j ≤ N. Hence

$$\displaystyle\begin{array}{rcl} 1 -\mu (10\lambda \mathcal{Z}_{p}(\mu )) =\mu (\mathbb{R}^{n}\setminus 10\lambda \mathcal{Z}_{ p}(\mu ))& \leq & \sum _{j=1}^{N}\mu \{x \in \mathbb{R}^{n}: \ \langle u_{ j},x\rangle > 5\lambda \} {}\\ & \leq & N(5\lambda )^{-p} \leq \lambda ^{-p}, {}\\ \end{array}$$

where the second inequality follows by Chebyshev’s inequality. □ 

Lemma 9

Let μ be a log-concave probability measure on $\mathbb{R}^{n}$ and K be a symmetric convex set such that μ(K) ≥ 1 − e ^−p for some p ≥ 2. Then for any Borel set A in  $\mathbb{R}^{n}$,

$$\displaystyle{\mu (A + 9K) \geq \min \left \{\frac{1} {2},e^{p}\mu (A)\right \}.}$$

Proof

By Borell’s lemma [4] we have for t ≥ 1,

$$\displaystyle{1 -\mu (tK) \leq \mu (K)\left (\frac{1 -\mu (K)} {\mu (K)} \right )^{\frac{t+1} {2} } \leq e^{-\frac{t+1} {3} p}.}$$

Let μ(A) = e ^−u for some u ≥ 0. Set

$$\displaystyle{\tilde{u}:=\max \{ u,2p\}\quad \mbox{ and }\quad \tilde{A}:= A \cap 4\frac{\tilde{u}} {p}K.}$$

We have

$$\displaystyle{\mu (\tilde{A}) \geq \mu (A) -\left (1 -\mu \left (4\frac{\tilde{u}} {p}K\right )\right ) \geq e^{-u} - e^{-\frac{p} {3} }e^{-\frac{4\tilde{u}} {3} } \geq \frac{1} {2}e^{-\tilde{u}}.}$$

Observe that if $x \in \tilde{ A}$ then $\frac{2p} {\tilde{u}} x \in 8K$, therefore $(1 -\frac{2p} {\tilde{u}} )\tilde{A} \subset \tilde{ A} + 8K$ and

$$\displaystyle\begin{array}{rcl} \mu (A + 9K)& \geq & \mu (\tilde{A} + 8K + K) \geq \mu \left (\left (1 -\frac{2p} {\tilde{u}} \right )\tilde{A} + \frac{2p} {\tilde{u}} K\right ) \geq \mu (\tilde{A})^{1-\frac{2p} {\tilde{u}} }\mu (K)^{\frac{2p} {\tilde{u}} } {}\\ & \geq & \left (\frac{1} {2}e^{-\tilde{u}}\right )^{1-\frac{2p} {\tilde{u}} }\left (\frac{1} {2}\right )^{\frac{2p} {\tilde{u}} } = \frac{1} {2}e^{2p-\tilde{u}} \geq \min \left \{\frac{1} {2},e^{p}\mu (A)\right \}. {}\\ \end{array}$$

 □ 

Proof of Proposition 7.

By the linear invariance we may and will assume that μ is isotropic.

Applying Lemma 8 with λ = e and Lemma 9 with $K = 10e\mathcal{Z}_{p}(\mu )$ we see that (1) holds with β = 90e for p ≥ n. For $p \geq \sqrt{n}$ we have $2\sqrt{n}\mathcal{Z}_{p}(\mu ) \supset \mathcal{Z}_{p\sqrt{n}}(\mu )$ and we get (1) with $\beta = 180e\sqrt{n}$ in this case.

The Paouris inequality (4) gives

$$\displaystyle{1 -\mu (C_{1}t\sqrt{n}B_{2}^{n}) \leq e^{-t\sqrt{n}}\quad \mbox{ for }t \geq 1.}$$

Together with Lemma 9 this yields for any Borel set A and t ≥ 1,

$$\displaystyle{\mu (A + 9C_{1}t\sqrt{n}B_{2}^{n}) \geq \min \left \{\frac{1} {2},e^{t\sqrt{n}}\mu (A)\right \}.}$$

Using the above bound for t = 1 and the inclusion $\mathcal{Z}_{p}(\mu ) \supset \mathcal{Z}_{2}(\mu ) = B_{2}^{n}$ we obtain (1) with $\beta = 9C_{1}\sqrt{n}$ for $2 \leq p \leq \sqrt{n}$. □ 

It would be of interest to improve the estimate from Proposition 7 to β ≤ Cn ^1∕2−ɛ for some ɛ > 0. Suppose that we are able to show that

$$\displaystyle{ \mu \left (C_{2}\sqrt{\frac{n} {p}}\mathcal{Z}_{p}(\mu )\right ) \geq 1 - e^{-p}\quad \mbox{ for }2 \leq p \leq n. }$$

(2)

Then (assuming again that μ is isotropic)i) if p ≤ p ₀: = n ^1∕9(logn)^−1∕3, we obtain by the Eldan’s bound on Cheeger’s constant

$$\displaystyle\begin{array}{rcl} \mu (A + Cn^{4/9}(\log n)^{1/6}\mathcal{Z}_{ p}(\mu ))& \geq & \mu (A + Cp_{0}n^{1/3}\sqrt{\log n}B_{ 2}^{n}) \geq \min \left \{\frac{1} {2},e^{p_{0} }\mu (A)\right \} {}\\ & \geq & \min \left \{\frac{1} {2},e^{p}\mu (A)\right \}. {}\\ \end{array}$$

ii) if p ₀ ≤ p ≤ n, then by (2) and Lemma 9,

$$\displaystyle{\mu (A + 9C_{2}n^{4/9}(\log n)^{1/6}\mathcal{Z}_{ p}(\mu )) \geq \mu \left (A + 9C_{2}\sqrt{\frac{n} {p}}\mathcal{Z}_{p}(\mu )\right ) \geq \min \left \{\frac{1} {2},e^{p}\mu (A)\right \}.}$$

So (2) would yield CI(β) for μ with β ≤ Cn ^4∕9(logn)^1∕3. Unfortunately we do not know whether (2) holds for symmetric log-concave measures (we are able to show it in the unconditional case).

A measure μ on $\mathbb{R}^{n}$ is called unconditional if it is invariant under symmetries with respect to coordinate axes. If μ is a log-concave, isotropic, and unconditional measure on $\mathbb{R}^{n}$, then the result of Bobkov and Nazarov [3] yields $\mathcal{Z}_{p}(\mu ) \subset C\mathcal{Z}_{p}(\nu ^{n})$. Therefore property CI(β) yields two-level concentration inequality for such measures

$$\displaystyle{ \forall _{A\in \mathcal{B}(\mathbb{R}^{n})}\ \forall _{t>0}\ \mu (A) \geq \frac{1} {2}\ \Rightarrow \ 1 -\mu (A + C\beta (\sqrt{t}B_{2}^{d} + tB_{ 1}^{d})) \leq e^{-t}(1 -\mu (A)). }$$

(3)

Klartag [10] showed that unconditional isotropic log-concave measures satisfy exponential concentration inequality with a constant β ≤ Clogn. We do not know if similar bound for β holds for the optimal concentration inequality or its weaker form (3).

3 Weak and Strong Moments

One of the fundamental properties of log-concave vectors is the Paouris inequality [21] (see also [1] for a shorter proof).

Theorem 10

For any log-concave vector X in $\mathbb{R}^{n}$,

$$\displaystyle{(\mathbb{E}\vert X\vert ^{p})^{1/p} \leq C(\mathbb{E}\vert X\vert +\sigma _{ X}(p))\quad \mbox{ for }p \geq 1,}$$

where

$$\displaystyle{\sigma _{X}(p):=\sup _{\vert v\vert \leq 1}\left (\mathbb{E}\vert \langle v,X\rangle \vert ^{p}\right )^{1/p}.}$$

Equivalently, in terms of tails we have

$$\displaystyle{\mathbb{P}(\vert X\vert \geq Ct\mathbb{E}\vert X\vert ) \leq \exp \left (-\sigma _{X}^{-1}(t\mathbb{E}\vert X\vert )\right )\quad \mbox{ for }t \geq 1.}$$

Observe that if X is additionally isotropic then σ _X (p) ≤ p σ _X (2) = p for p ≥ 2 and $\mathbb{E}\vert X\vert \leq (\mathbb{E}\vert X\vert ^{2})^{1/2} = \sqrt{n}$, so we get

$$\displaystyle{ \mathbb{P}(\vert X\vert \geq Ct\sqrt{n}) \leq e^{-t\sqrt{n}}\quad \mbox{ for }t > 1\mbox{ and isotropic log-concave vector }X. }$$

(4)

It would be very valuable to have a reasonable characterization of random vectors which satisfy the Paouris inequality. The following example shows that the regular growth of moments is not enough.

Example 11

Let $Y = \sqrt{n}gU$, where U has a uniform distribution on S ⁿ⁻¹ and g is the standard normal $\mathcal{N}(0,1)$ r.v., independent of U. Then it is easy to see that Y is isotropic, rotationally invariant and for any seminorm on $\mathbb{R}^{n}$

$$\displaystyle{(\mathbb{E}\|Y \|^{p})^{1/p} = \sqrt{n}(\mathbb{E}\vert g\vert ^{p})^{1/p}(\mathbb{E}\|U\|^{p})^{1/p} \sim \sqrt{pn}(\mathbb{E}\|U\|^{p})^{1/p}\quad \mbox{ for }p \geq 1.}$$

In particular this implies that for any $v \in \mathbb{R}^{n}$,

$$\displaystyle{\left (\mathbb{E}\vert \langle v,Y \rangle \vert ^{p}\right )^{1/p} \leq C\frac{p} {q}\left (\mathbb{E}\vert \langle v,Y \rangle \vert ^{q}\right )^{1/q}\quad \mbox{ for }p \geq q \geq 2.}$$

So moments of Y grow C-regularly. Moreover

$$\displaystyle{(\mathbb{E}\vert Y \vert ^{p})^{1/p} \sim \sqrt{pn},\quad (\mathbb{E}\vert Y \vert ^{2})^{1/2} = \sqrt{n},\quad \sigma _{ Y }(p) \leq Cp,}$$

thus for 1 ≪ p ≪ n, $(\mathbb{E}\vert Y \vert ^{p})^{1/p} \gg (\mathbb{E}\vert Y \vert ^{2})^{1/2} +\sigma _{Y }(p)$.

It is natural to ask whether Theorem 10 may be generalized to non-Euclidean norms. In [11] the following conjecture was formulated and discussed.

Conjecture 12

There exists a universal constant C such that for any n-dimensional log-concave vector X and any norm ∥ ∥ on $\mathbb{R}^{n}$,

$$\displaystyle{(\mathbb{E}\|X\|^{p})^{1/p} \leq C\left (\mathbb{E}\|X\| +\sup _{\| v\|_{{\ast}}\leq 1}\left (\mathbb{E}\vert \langle v,X\rangle \vert ^{p}\right )^{1/p}\right )\quad \mbox{ for }p \geq 1,}$$

where ∥v∥ _∗ = sup {|〈 v,x〉 |: ∥x∥≤ 1} denotes the dual norm on $\mathbb{R}^{n}$.

Note that obviously for any random vector X and p ≥ 1,

$$\displaystyle{(\mathbb{E}\|X\|^{p})^{1/p} \geq \max \left \{\mathbb{E}\|X\|,\sup _{\| v\|_{{\ast}}\leq 1}\left (\mathbb{E}\vert \langle v,X\rangle \vert ^{p}\right )^{1/p}\right \}.}$$

The following simple observation from [15] shows that the optimal concentration yields comparison of weak and strong moments.

Proposition 13

Suppose that the law of an n-dimensional random vector X is α-regular and satisfies the optimal concentration inequality with constant β. Then for any norm ∥ ∥ on $\mathbb{R}^{n}$,

$$\displaystyle{(\mathbb{E}\vert \|X\| - \mathbb{E}\|X\|\vert ^{p})^{1/p} \leq C\alpha \beta \sup _{\| v\|_{{\ast}}\leq 1}(\mathbb{E}\vert \langle v,X\rangle \vert ^{p})^{1/p}\quad \mbox{ for }p \geq 1.}$$

Recall that log-concave measures are 3-regular. Therefore if the law of X is of one of three types listed in Theorem 6 then for any norm ∥   ∥ ,

$$\displaystyle{(\mathbb{E}\|X\|^{p})^{1/p} \leq \mathbb{E}\|X\| + C\sup _{\| v\|_{{\ast}}\leq 1}(\mathbb{E}\vert \langle v,X\rangle \vert ^{p})^{1/p}\quad \mbox{ for }p \geq 1.}$$

We do not know if such inequality is satisfied for Euclidean norms and arbitrary log-concave vectors, i.e. whether Paouris inequality holds with the constant 1 in front of $\mathbb{E}\vert X\vert$. This question is related to the so-called variance conjecture, discussed in [2].

The following extension of the Paouris inequality was shown in [13].

Theorem 14

Let X be a log-concave vector with values in a normed space (F,∥ ∥) which may be isometrically embedded in ℓ _r for some r ∈ [1,∞). Then for p ≥ 1,

$$\displaystyle{(\mathbb{E}\|X\|^{p})^{1/p} \leq Cr\left (\mathbb{E}\|X\| +\sup _{\varphi \in F^{{\ast}},\|\varphi \|_{{\ast}}\leq 1}(\mathbb{E}\vert \varphi (X)\vert ^{p})^{1/p}\right ).}$$

Remark 15

Let X and F be as above. Then by Chebyshev’s inequality we obtain large deviation estimate for ∥ X ∥ :

$$\displaystyle{\mathbb{P}(\|X\| \geq Crt\mathbb{E}\|X\|) \leq \exp \left (-\sigma _{X,F}^{-1}(t\mathbb{E}\|X\|)\right )\quad \mbox{ for }t \geq 1,}$$

where

$$\displaystyle{\sigma _{X,F}(p):=\sup _{\varphi \in F^{{\ast}},\|\varphi \|_{{\ast}}\leq 1}(\mathbb{E}\varphi (X)^{p})^{1/p}\quad \mbox{ for }p \geq 1}$$

denotes the weak p-th moment of ∥ X ∥ .

Remark 16

If i: F → ℓ _r is a nonisometric embedding and $\lambda =\| i\|_{F\rightarrow \ell_{r}}\|i^{-1}\|_{i(F)\rightarrow F}$, then we may define another norm on F by $\|x\|':=\| i(x)\|/\|i\|_{F\rightarrow \ell_{r}}$. Obviously (F, ∥   ∥ ′) isometrically embeds in ℓ _r , moreover ∥ x ∥ ′ ≤ ∥ x ∥ ≤ λ ∥ x ∥ ′ for x ∈ F. Hence Theorem 14 gives

$$\displaystyle\begin{array}{rcl} (\mathbb{E}\|X\|^{p})^{1/p}& \leq & \lambda (\mathbb{E}(\|X\|')^{p})^{1/p} \leq C_{ 2}r\lambda \left (\mathbb{E}\|X\|' +\sup _{\varphi \in F^{{\ast}},\|\varphi \|_{{\ast}}^{'}\leq 1}(\mathbb{E}\vert \varphi (X)\vert ^{p})^{1/p}\right ) {}\\ & \leq & C_{2}r\lambda \left (\mathbb{E}\|X\| +\sup _{\varphi \in F^{{\ast}},\|\varphi \|_{{\ast}}\leq 1}(\mathbb{E}\vert \varphi (X)\vert ^{p})^{1/p}\right ). {}\\ \end{array}$$

Since log-concavity is preserved under linear transformations and, by the Hahn-Banach theorem, any linear functional on a subspace of l _r is a restriction of a functional on the whole l _r with the same norm, it is enough to prove Theorem 14 for F = l _r . An easy approximation argument shows that we may consider finite dimensional spaces l _r ⁿ. This way Theorem 14 reduces to the following finite dimensional statement.

Theorem 17

Let X be a log-concave vector in $\mathbb{R}^{n}$ and r ∈ [1,∞). Then

$$\displaystyle{(\mathbb{E}\|X\|_{r}^{p})^{1/p} \leq Cr\left (\mathbb{E}\|X\|_{ r} +\sigma _{r,X}(p)\right )\quad \mbox{ for }p \geq 1,}$$

where

$$\displaystyle{\sigma _{r,X}(p):=\sigma _{X,l_{r}^{n}}(p) =\sup _{\|v\|_{r'}\leq 1}\left (\mathbb{E}\vert \langle v,X\rangle \vert ^{p}\right )^{1/p}}$$

and r′ denotes the Hölder’s dual of r, i.e. $r' = \frac{r} {r-1}$ for r > 1 and r′ = ∞ for r = 1.

Any finite dimensional space embeds isometrically in ℓ _∞ , so to show Conjecture 12 it is enough to establish Theorem 17 (with a universal constant in place of Cr) for r = ∞. Such a result was shown for isotropic log-concave vectors.

Theorem 18 ([12])

Let X be an isotropic log-concave vector in $\mathbb{R}^{n}$ . Then for any a ₁ ,…,a _n and p ≥ 1,

$$\displaystyle{(\mathbb{E}\max _{i}\vert a_{i}X_{i}\vert ^{p})^{1/p} \leq C\left (\mathbb{E}\max _{ i}\vert a_{i}X_{i}\vert +\max _{i}(\mathbb{E}\vert a_{i}X_{i}\vert ^{p})^{1/p}\right )\quad \mbox{ for }p \geq 1.}$$

However a linear image of an isotropic vector does not have to be isotropic, so to establish the conjecture we need to consider either isotropic vectors and an arbitrary norm or vectors with a general covariance structure and the standard ℓ _∞ -norm.

In the case of unconditional vectors slightly more is known.

Theorem 19 ([11])

Let X be an n-dimensional isotropic, unconditional, log-concave vector and Y = (Y ₁ ,…,Y _n ), where Y _i are independent symmetric exponential r.v’s with variance 1 (i.e., with the density $2^{-1/2}\exp (-\sqrt{2}\vert x\vert )$ ). Then for any norm ∥ ∥ on $\mathbb{R}^{n}$ and p ≥ 1,

$$\displaystyle{(\mathbb{E}\|X\|^{p})^{1/p} \leq C\left (\mathbb{E}\|Y \| +\sup _{\| v\|_{{\ast}}\leq 1}(\mathbb{E}\vert \langle v,X\rangle \vert ^{p})^{1/p}\right ).}$$

Proof is based on the Talagrand generic-chaining type two-sided estimate of $\mathbb{E}\|Y \|$ [24] and the Bobkov-Nazarov [3] bound for the joint d.f. of X, which implies $(\mathbb{E}\vert \langle v,X\rangle \vert ^{p})^{1/p} \leq C(\mathbb{E}\vert \langle v,Y \rangle \vert ^{p})^{1/p}$ for p ≥ 1 and $v \in \mathbb{R}^{n}$.

Using the easy estimate $\mathbb{E}\|Y \| \leq C\log n\ \mathbb{E}\|X\|$ we get the following.

Corollary 20

For any n-dimensional unconditional, log-concave vector X, any norm ∥ ∥ on $\mathbb{R}^{n}$ and p ≥ 1 one has

$$\displaystyle{(\mathbb{E}\|X\|^{p})^{1/p} \leq C\left (\log n\ \mathbb{E}\|X\| +\sup _{\| v\|_{{\ast}}\leq 1}(\mathbb{E}\vert \langle v,X\rangle \vert ^{p})^{1/p}\right ).}$$

The Maurey-Pisier result [18] implies $\mathbb{E}\|Y \| \leq C\mathbb{E}\|X\|$ in spaces with nontrivial cotype.

Corollary 21

Let 2 ≤ q < ∞ and $F = (\mathbb{R}^{n},\|\ \|)$ has a q-cotype constant bounded by β < ∞. Then for any n-dimensional unconditional, log-concave vector X and p ≥ 1,

$$\displaystyle{(\mathbb{E}\|X\|^{p})^{1/p} \leq C(q,\beta )\left (\mathbb{E}\|X\| +\sup _{\| v\|_{{\ast}}\leq 1}(\mathbb{E}\vert \langle v,X\rangle \vert ^{p})^{1/p}\right ).}$$

where C(q,β) is a constant that depends only on q and β.

For a class of invariant measures Conjecture 12 was established in [12].

Proposition 22

Let X be an n-dimensional random vector with the density of the form $e^{-\varphi (\|x\|_{r})}$ , where 1 ≤ r ≤∞ and φ: [0,∞) → (−∞,∞] is nondecreasing and convex. Then for any norm ∥ ∥ on $\mathbb{R}^{n}$ and any p ≥ 1,

$$\displaystyle{\left (\mathbb{E}\|X\|^{p}\right )^{1/p} \leq C(r)\mathbb{E}\|X\| + C\sup _{\| v\|_{{\ast}}\leq 1}\left (\mathbb{E}\vert \langle v,X\rangle \vert ^{p}\right )^{1/p}.}$$

4 Sudakov Minoration

For any norm ∥   ∥ on $\mathbb{R}^{n}$ we have

$$\displaystyle{\|x\| =\sup _{\|v\|_{{\ast}}\leq 1}\langle v,x\rangle = \frac{1} {2}\sup _{\|v\|_{{\ast}},\|w\|_{{\ast}}\leq 1}\langle v - w,x\rangle \quad \mbox{ for }x \in \mathbb{R}^{n}.}$$

Thus to estimate the mean of a norm of a random vector X one needs to investigate $\mathbb{E}\sup _{v,w\in V }\langle v - w,X\rangle$ for bounded subsets V in $\mathbb{R}^{n}$.

There are numerous powerful methods to estimate suprema of stochastic processes (cf. the monograph [25]), let us however present only a very easy upper bound. Namely for any p ≥ 1,

$$\displaystyle\begin{array}{rcl} \mathbb{E}\sup _{v,w\in V }\langle v - w,X\rangle & \leq & \left (\mathbb{E}\sup _{v,w\in V }\vert \langle v - w,X\rangle \vert ^{p}\right )^{1/p} \leq \left (\mathbb{E}\sum _{ v,w\in V }\vert \langle v - w,X\rangle \vert ^{p}\right )^{1/p} {}\\ & \leq & \vert V \vert ^{2/p}\sup _{ v,w\in V }\left (\mathbb{E}\vert \langle v - w,X\rangle \vert ^{p}\right )^{1/p}. {}\\ \end{array}$$

In particular,

$$\displaystyle{\mathbb{E}\sup _{v,w\in V }\langle v - w,X\rangle \leq e^{2}\sup _{ v,w\in V }\left (\mathbb{E}\vert \langle v - w,X\rangle \vert ^{p}\right )^{1/p}\quad \mbox{ if }\vert V \vert \leq e^{p}.}$$

It is natural to ask when the above estimate may be reversed. Namely, when is it true that if the set $V \subset \mathbb{R}^{n}$ has large cardinality (say at least e ^p) and variables (〈v, X〉) _v ∈ V are A-separated with respect to the L _p -distance then $\mathbb{E}\sup _{v,w\in V }\langle v - w,X\rangle$ is at least of the order of A? The following definition gives a more precise formulation of such property.

Definition 23

Let X be a random n-dimensional vector. We say that X satisfies the L _p -Sudakov minoration principle with a constant κ > 0 (SMP _p (κ) in short) if for any nonempty set $V \subset \mathbb{R}^{n}$ with | V | ≥ e ^p such that

$$\displaystyle{ d_{X,p}(v,w):= \left (\mathbb{E}\vert \langle v - w,X\rangle \vert ^{p}\right )^{1/p} \geq A\quad \mbox{ for all }v,w \in V,\ v\neq w, }$$

(6)

we have

$$\displaystyle{ \mathbb{E}\sup _{v,w\in V }\langle v - w,X\rangle \geq \kappa A. }$$

(7)

A random vector X satisfies the Sudakov minoration principle with a constant κ (SMP(κ) in short) if it satisfies SMP _p (κ) for any p ≥ 1.

Example 24

If X has the canonical n-dimensional Gaussian distribution $\mathcal{N}(0,I_{n})$ then $(\mathbb{E}\vert \langle v,X\rangle \vert ^{p})^{1/p} =\gamma _{p}\vert v\vert$, where $\gamma _{p} = (\mathbb{E}\vert \mathcal{N}(0,1)\vert ^{p})^{1/p} \sim \sqrt{p}$ for p ≥ 1. Hence condition (6) is equivalent to | v − w | ≥ A∕γ _p for distinct vectors v, w ∈ V and the classical Sudakov minoration principle for Gaussian processes [22] then yields

$$\displaystyle{\mathbb{E}\sup _{v,w\in V }\langle v - w,X\rangle = 2\mathbb{E}\sup _{v\in V }\langle v,X\rangle \geq \frac{A} {C\gamma _{p}}\sqrt{\log \vert V \vert }\geq \frac{A} {C}}$$

provided that | V | ≥ e ^p. Therefore X satisfies the Sudakov minoration principle with a universal constant. In fact it is not hard to see that for centered Gaussian vectors the Sudakov minoration principle in the sense of Definition 23 is formally equivalent to the minoration property established by Sudakov.

The Sudakov minoration principle for vectors X with independent coordinates was investigated in detail in [14]. It was shown there that for SMP in such a case the sufficient (and necessary if coordinates of X have identical distribution) condition is the regular growth of moments of coordinates of X, i.e. the existence of α < ∞ such that $(\mathbb{E}\vert X_{i}\vert ^{p})^{1/p} \leq \alpha \frac{p} {q}(\mathbb{E}\vert X_{i}\vert ^{q})^{1/q}$ for all i and p ≥ q ≥ 1. In particular log-concave vectors X with independent coordinates satisfy SMP with a universal constant κ.

In the sequel we will discuss the following conjecture.

Conjecture 25

Every n-dimensional log-concave random vector satisfies the Sudakov-minoration principle with a universal constant.

Remark 26

Suppose that X is log-concave and (6) is satisfied, but | V |  = e ^q with 1 ≤ q ≤ p. Since $d_{X,q}(v,w) \geq \frac{q} {3p}d_{X,p}(v,w)$, the Sudakov minoration principle for a log-concave vector X implies the following formally stronger statement – for any nonempty $V \subset \mathbb{R}^{n}$ and A > 0,

$$\displaystyle{\mathbb{E}\sup _{v,w\in V }\langle v - w,X\rangle \geq \frac{\kappa } {C}\sup _{p\geq 1}\min \left \{\frac{A} {p} \log N(V,d_{X,p},A),A\right \},}$$

where N(V, d, ɛ) denotes the minimal number of balls in metric d of radius ɛ that cover V.

The Sudakov minoration principle and Conjecture 25 were posed independently by Shahar Mendelson, Emanuel Milman, and Grigoris Paouris (unpublished) and by the author in [12]. In [19] there is discussed approach to the Sudakov minoration and its dual version based on variants of the Johnson-Lindenstrauss dimension reduction lemma. The results presented below were proven in [12].

It is easy to see that the Sudakov minoration property is affinely invariant, so it is enough to investigate it only for isotropic random vectors. Using the fact that isotropic log-concave vectors satisfy exponential concentration with constant Cn ^γ with γ < 1∕2 one may show that the lower bound (6) holds for special classes of sets.

Proposition 27

Suppose that X is an n-dimensional log-concave random vector, p ≥ 2, $V \subset \mathbb{R}^{n}$ satisfies (6) and Cov (〈 v,X〉 ,〈 w,X〉 ) = 0 for v,w ∈ V with v ≠ w. Then (7) holds with a universal constant κ provided that |V |≥ e ^p.

In the case of general sets we know at the moment only the following much weaker form of the Sudakov minoration principle.

Theorem 28

Let X be a log-concave vector, p ≥ 1 and $V \subset \mathbb{R}^{n}$ be such that $\vert V \vert \geq e^{e^{p} }$ and (6) holds. Then

$$\displaystyle{\mathbb{E}\sup _{v,w\in V }\langle v - w,X\rangle \geq \frac{1} {C}A.}$$

Stronger bounds may be derived in the unconditional case. Comparing unconditional log-concave vectors with vectors with independent symmetric exponential coordinates one gets the following bound on κ.

Proposition 29

Suppose that X is an n-dimensional log-concave unconditional vector. Then X satisfies SMP (1∕Clog (n + 1)).

The next result presents a bound on κ independent of dimension but under a stronger assumptions on the cardinality of V than in the definition of SMP.

Theorem 30

Let X be a log-concave unconditional vector in $\mathbb{R}^{n}$ , p ≥ 1 and $V \subset \mathbb{R}^{n}$ be such that $\vert V \vert \geq e^{p^{2} }$ and (6) holds. Then

$$\displaystyle{\mathbb{E}\sup _{v,w\in V }\langle v - w,X\rangle = 2\mathbb{E}\sup _{v\in V }\langle v,X\rangle \geq \frac{1} {C}A.}$$

Remark 31

Theorems 28 and 30 may be rephrased in terms of entropy numbers as in Remark 26. Namely, for any nonempty set $V \subset \mathbb{R}^{n}$ and log-concave vector X,

$$\displaystyle{\mathbb{E}\sup _{v,w\in V }\langle v - w,X\rangle \geq \frac{1} {C}\sup _{p\geq 1,A>0}\min \left \{\frac{A} {p} \log \log N(V,d_{X,p},A),A\right \}.}$$

If X is unconditional and log-concave, then

$$\displaystyle{\mathbb{E}\sup _{v,w\in V }\langle v - w,X\rangle \geq \frac{1} {C}\sup _{p\geq 1,A>0}\min \left \{\frac{A} {p} \sqrt{\log N(V, d_{X,p }, A)},A\right \}.}$$

We know that a class of invariant log-concave vectors satisfy SMP(κ) with uniform κ.

Theorem 32

All n-dimensional random vectors with densities of the form exp (−φ(∥x∥ _p )), where 1 ≤ p ≤∞ and φ: [0,∞) → (−∞,∞] is nondecreasing and convex satisfy the Sudakov minoration principle with a universal constant. In particular all rotationally invariant log-concave random vectors satisfy the Sudakov minoration principle with a universal constant.

One of the important consequences of the SMP-property is the following comparison-type result for random vectors.

Proposition 33

Suppose that a random vector X in $\mathbb{R}^{n}$ satisfies SMP (κ). Let Y be a random n-dimensional vector such that $\mathbb{E}\vert \langle v,Y \rangle \vert ^{p} \leq \mathbb{E}\vert \langle v,X\rangle \vert ^{p}$ for all p ≥ 1, $v \in \mathbb{R}^{n}$ . Then for any norm ∥ ∥ on $\mathbb{R}^{n}$ and p ≥ 1,

$$\displaystyle\begin{array}{rcl} (\mathbb{E}\|Y \|^{p})^{1/p}& \leq & C\Big(\frac{1} {\kappa } \log _{+}\Big(\frac{en} {p} \Big)\mathbb{E}\|X\| +\sup _{\|v\|_{{\ast}}\leq 1}(\mathbb{E}\vert \langle v,Y \rangle \vert ^{p})^{1/p}\Big) \\ & \leq & C\Big(\frac{1} {\kappa } \log _{+}\Big(\frac{en} {p} \Big) + 1\Big)(\mathbb{E}\|X\|^{p})^{1/p}. {}\end{array}$$

(8)

As a consequence we know that for random vectors which satisfy Sudakov minoration principle weak and strong moments are comparable up to a logarithmic factor.

Corollary 34

Suppose that X is an n-dimensional random vector, which satisfies SMP (κ). Then for any norm ∥ ∥ on $\mathbb{R}^{n}$ and any p ≥ 1,

$$\displaystyle{\big(\mathbb{E}\|X\|^{p}\big)^{1/p} \leq C\Big(\frac{1} {\kappa } \log _{+}\Big(\frac{en} {p} \Big)\mathbb{E}\|X\| +\sup _{\|v\|_{{\ast}}\leq 1}\big(\mathbb{E}\vert \langle v,X\rangle \vert ^{p}\big)^{1/p}\Big).}$$