Recent Developments in Spectral Element Simulations of Moving-Domain Problems

Abstract

Presented here are recent developments in spectral element methods for simulations of incompressible and low-Mach-number flows in domains with moving boundaries. Features include PDE-based mesh motion, implicit treatment of fluid–structure interaction based on a Green’s function decomposition, and an arbitrary Lagrangian-Eulerian formulation for low-Mach-number flows that includes an evolution equation for the background thermodynamic pressure. Several examples illustrate the basic principles introduced in the text.

1 Introduction

With advances in high-performance parallel computers, scalable iterative solvers, and high-order discretizations, much progress has been made toward direct numerical simulation (DNS) and large eddy simulation (LES) of transitional and turbulent flows in complex domains. Indeed, researchers now can consider spectral-element-based DNS for flow past wing sections at chord-Reynolds number Re _c = 400, 000 [1]. DNS of the flow in internal combustion (IC) engines is close at hand, with significant advances recently presented in [2–4].

Since its introduction by Patera [5], several developments have made the spectral element method (SEM) a powerful tool for simulation of turbulent flows in complex geometries. Key advances include high-order operator splitting strategies that lead to decoupled linear symmetric positive definite subproblems at each timestep [6–10]; fast multilevel preconditioners [11–13] coupled with scalable parallel coarse grid solvers [14–16]; stable formulations for the convective operator [17–19]; and high-performance implementations [20]. Here, we present recent developments in the SEM for simulations of incompressible and low-Mach number flows in domains with moving boundaries. Our interests are in turbulent flows having prescribed boundary motion, such as piston and valve motion in IC engines, and in fluid-structure interactions where the motion of the domain boundary is part of the solution that derives from dynamical constraints coupled with the Navier-Stokes equations.

The standard approach to efficient simulation of turbulent flow is to treat the nonlinear terms explicitly in time, which leaves a linear symmetric unsteady-Stokes operator to be solved, implicitly, at every timestep. (As discussed below, the Stokes problem is typically solved by using an additional time-splitting in order to decouple the pressure and velocity solves.) The justification for this semi-implicit approach to temporal discretization derives from the following. First, the viscous and incompressibility constraints are associated with fast time scales (infinite, in the case of incompressibility, as it derives from letting the speed of sound go to infinity), which warrant implicit treatment. Second, these terms are linear and symmetric, which make them amenable to robust iterative solution strategies such as preconditioned conjugate gradients. Third, explicit treatment of the convection operator avoids solution of a nonlinear nonsymmetric system and requires a mild timestep restriction of Δt = O( | U | Δx) to ensure stability, where U and Δx are respectively characteristic sizes of the velocity and grid-spacing. Moreover, this timestep restriction is typically comparable to that required from an accuracy standpoint because the principal dynamics of turbulent flow are governed by first-order derivatives in space and time. The stability requirement Δt = O(Δx) is thus generally not overly constraining.

Moving domains introduce new sources of nonlinearity and stiffness. In closed systems such as internal combustion engines, one must address the changes in thermodynamic pressure and, in the presence of combustion, changes in geometry on short timescales associated with the chemistry. Fluid-structure interaction (FSI) problems, where the solid part of the domain constitutes an additional unknown, introduce additional sources of stiffness associated with disparate timescales between the fluid and solid response. Here, we describe recent developments that address several of these moving-domain issues while retaining the computational efficiency demanded for turbulent flow simulations. The work describes novel developments in time-accurate low-Mach combustion for closed domains and in stable decoupled FSI solution strategies that are particularly appropriate for the response of rigid bodies subjected to forces generated by incompressible flows.

The article is organized as follows. Section 2 provides a review of the arbitrary Lagrangian-Eulerian (ALE) formulation based on the $\mathbb{P}_{N} - \mathbb{P}_{N-2}$ spectral element method for the incompressible Navier-Stokes equations, as developed by Ho and collaborators [21–23]. Section 3 describes an ALE formulation for low-Mach-number flows that allow compression and expansion of the domain volume. Specifics of the SEM are provided in Sect. 4, and several schemes for efficient mesh-velocity updates are described in Sect. 5. Section 6 presents a decoupled-implicit formulation for fluid-structure systems with a few degrees of freedom. We give examples in Sect. 7 and a short conclusion in Sect. 8.

2 $\mathbb{P}_{N} - \mathbb{P}_{N-2}$ Navier-Stokes Formulation

We consider unsteady incompressible flow in a given computational domain Ω(t) governed by the Navier-Stokes equations,

$$\displaystyle\begin{array}{rcl} \begin{array}{rccccccl} \frac{\partial \mathbf{u}} {\partial t} & =& -\nabla p&+& \frac{1} {Re}\nabla \cdot (\nabla + \nabla ^{T})\mathbf{u}&-&\mathbf{u} \cdot \nabla \mathbf{u},&\qquad \nabla \cdot \mathbf{u} = 0, \end{array} & &{}\end{array}$$

(1)

subject to prescribed velocity conditions on the domain boundary, ∂Ω(t). Here, u(x, t) = (u ₁, u ₂ u ₃) represents the fluid velocity components as a function of space, x = (x ₁, x ₂, x ₃), and time, t; p is the pressure field; and Re = L ₀ U ₀∕ν ₀ is the Reynolds number based on a characteristic length scale, L ₀, velocity scale, U ₀, and kinematic viscosity of the fluid, ν ₀. We are interested in moving-geometry simulations where the motion of the domain boundary, ∂Ω(t), may be either prescribed or unknown, as is the case for fluid–structure interaction problems. Our moving-domain formulation is based on the ALE formulation for the spectral element method developed by Ho and collaborators [21–23]. We review those developments here to set the stage for subsequent sections.

To highlight the key aspects of the ALE formulation, we introduce the weighted residual formulation of (1): Find (u, p) ∈ X _b ^N(Ω(t)) × Y ^N(Ω(t)) such that

$$\displaystyle\begin{array}{rcl} \frac{d} {dt}(\mathbf{v},\mathbf{u}) = (\nabla \cdot \mathbf{v},p) - \frac{1} {Re}(\nabla \mathbf{v},\mathbf{s}) - (\mathbf{v},\mathbf{u} \cdot \nabla \mathbf{u}) + c(\mathbf{v},\mathbf{w},\mathbf{u}),\;\;\;(\nabla \cdot \mathbf{u},q) = 0,\;\;& &{}\end{array}$$

(2)

for all test functions (v, q) ∈ X ₀ ^N(Ω(t)) × Y ^N(Ω(t)). Here, we use the compatible velocity-pressure spaces introduced by Maday and Patera [24]: X ^N(Ω(t)) ⊂ H ¹(Ω(t)) is the set of continuous Nth-order spectral element (SE) basis functions described in Sect. 4; X _b ^N is the subset of X ^N satisfying the Dirichlet conditions on ∂Ω(t); X ₀ ^N is the subset of X ^N satisfying homogeneous Dirichlet conditions on ∂Ω(t); Y ^N is the space of discontinuous SE basis functions of degree N-2; and H ¹ is the usual Sobolev space of functions that are square integrable on Ω(t), whose derivatives are also square integrable. Furthermore, in (2), we have introduced the $\mathcal{L}^{2}$ inner product, (f, g): = ∫ _Ω(t) f ⋅ g dV and the stress tensor s having components $s_{ij}:= (\frac{\partial u_{i}} {\partial x_{j}} + \frac{\partial u_{j}} {\partial x_{i}} )$. A new term in (2) is the trilinear form involving the mesh velocity, w,

$$\displaystyle\begin{array}{rcl} c(\mathbf{v},\mathbf{w},\mathbf{u}):=\int _{\varOmega (t)}\sum _{i=1}^{3}\sum _{ j=1}^{3}v_{ i}\frac{\partial w_{j}u_{i}} {\partial x_{j}} \,dV,& &{}\end{array}$$

(3)

which derives from the Reynolds transport theorem when the time derivative is moved outside the bilinear form, (v, u _t ).

The advantage of (2) is that it greatly simplifies time differencing and avoids grid-to-grid interpolation as the domain evolves in time. With the time derivative outside the integral, each bilinear or trilinear form involves functions at a specific time, t ^n−j, integrated over Ω(t ^n−j). Geometric deformation within elements is specified by a mesh velocity, w: = x _t , that is essentially arbitrary provided that w is smooth and satisfies the kinematic condition

$$\displaystyle\begin{array}{rcl} \mathbf{w} \cdot \hat{\mathbf{n}}\vert _{\partial \varOmega }& =& \mathbf{u} \cdot \hat{\mathbf{n}}\vert _{\partial \varOmega },{}\end{array}$$

(4)

where $\hat{\mathbf{n}}$ is the unit normal at the domain surface, ∂Ω(t).

Our temporal discretization is based on a semi-implicit formulation in which the time derivative at t ⁿ is approximated with a kth-order backward difference formula (BDFk). Terms on the right-hand side of (2) are evaluated either implicitly at t ⁿ or via kth-order extrapolation (EXTk). Specifically, we write

$$\displaystyle\begin{array}{rcl} \sum _{j=0}^{k}\frac{\beta _{j}} {\varDelta t}\,(\mathbf{v}^{n-j},\mathbf{u}^{n-j})_{ n-j}& \,=\,& (\nabla \cdot \mathbf{v}^{n},p^{n})_{ n}\! -\! \frac{1} {Re}(\nabla \mathbf{v}^{n},\mathbf{s}^{n})_{ n}\! +\!\sum _{ j=1}^{k}\alpha _{ j}\,\widetilde{N}^{n-j}\! +\! O(\varDelta t^{k})\;\;{}\end{array}$$

(5)

$$\displaystyle\begin{array}{rcl} (q^{n},\nabla \cdot \mathbf{u}^{n})_{ n}& =& 0.{}\end{array}$$

(6)

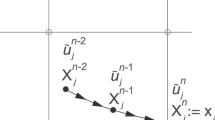
The subscript on the inner products (. , . ) _n−j indicates integration over Ω(t ^n−j). The coefficients β _j and α _j are standard BDFk/EXTk coefficients (e.g., as in Table 1), and the approximations are accurate to O(Δt ^k), which is the global truncation error for this timestepping scheme. The term $\widetilde{N}^{n-j}$ accounts for all nonlinear contributions at time level t ^n−j, including the mesh motion term (3). For any time level t ^m we define

$$\displaystyle\begin{array}{rcl} \widetilde{N}^{m}&:=& c(\mathbf{v}^{m},\mathbf{w}^{m},\mathbf{u}^{m})_{ m} - (\mathbf{v}^{m},\mathbf{u}^{m} \cdot \nabla \mathbf{u}^{m})_{ m} \\ & \,=& \sum _{i=1}^{3}\sum _{ j=1}^{3}\,\int _{ \varOmega (t)}\,v_{i}^{m}\left [\,\frac{\partial w_{j}^{m}u_{ i}^{m}} {\partial x_{j}^{m}} - u_{j}^{m} \frac{\partial u_{i}^{m}} {\partial x_{j}^{m}}\right ]\,dV.{}\end{array}$$

(7)

Table 1 BDFk/EXTk coefficients for uniform Δt

Moving to the left all terms in (5)–(6) that involve unknowns at t ⁿ and neglecting the O(Δt ^k) terms, we obtain the update step for (2): Find (u ⁿ, p ⁿ) ∈ X ₀ ^N(Ω) × Y ^N(Ω) such that, for all (v ⁿ, q ⁿ) ∈ X ₀ ^N(Ω ⁿ) × Y ^N(Ω ⁿ),

$$\displaystyle\begin{array}{rcl} \frac{\beta _{0}} {\varDelta t}\,(\mathbf{v}^{n},\mathbf{u}^{n})_{ n}\, +\, \frac{1} {Re}(\nabla \mathbf{v}^{n},\mathbf{s}^{n})_{ n} - (\nabla \cdot \mathbf{v}^{n},p^{n})_{ n}& =& r^{n},\;\;\;\;\;\;(q^{n},\nabla \cdot \mathbf{u}^{n})_{ n}\, =\, 0.{}\end{array}$$

(8)

Here, the right-hand side is

$$\displaystyle\begin{array}{rcl} r^{n}& =& \sum _{ j=1}^{k}\left [\,\alpha _{ j}\,\widetilde{N}^{n-j} -\frac{\beta _{j}} {\varDelta t}\,(\mathbf{v}^{n-j},\mathbf{u}^{n-j})_{ n-j}\,\right ].{}\end{array}$$

(9)

We note that the test functions v and q are functions of time as a result of the motion of Ω(t). In practice, however, all integrals are evaluated in a fixed reference frame and they are stationary basis functions in this frame, integrated against the time-evolving functions with the appropriate Jacobian. Specifically, for the spectral element method, $\varOmega (t) =\bigcup _{e}\varOmega ^{e}(t)$, where each element is represented by a map x ^e(r, t), where $\mathbf{r} \in \hat{\varOmega }:= [-1,1]^{d}$ and d is the number of space dimensions. Such a decomposition is illustrated in Fig. 1 for d = 2. The test functions and the underlying bases for the unknowns are taken as tensor product Lagrange interpolating polynomials in $\hat{\varOmega }$. Thus, an inner product I: = (v, u) = ∫ _Ω v u dV in the two-dimensional case takes the form

$$\displaystyle\begin{array}{rcl} \mathbf{I}& =& \int _{\varOmega (t)}\,v\,u\,dV \; =\;\sum _{ e=1}^{E}\,\int _{ \varOmega ^{e}(t)}\,v\,u\,dV \\ & =& \sum _{e=1}^{E}\,\int _{ -1}^{1}\int _{ -1}^{1}\,v^{e}(r,s)\,u^{e}(r,s,t)\,\mathcal{J}^{e}(r,s,t)\,dr\,ds,{}\end{array}$$

(10)

where the Jacobian $\mathcal{J}^{e}(r,s,t) = \left \vert \frac{\partial x_{i}^{e}} {\partial r_{j}} \right \vert$ is the determinant of the d × d matrix of the metric terms associated with the transformation x ^e(r, t) that maps $\hat{\varOmega }$ to Ω ^e(t). (Here, superscript e refers to element number and should not be confused with the temporal index m or n in (5)–(9).) Because the test functions are stationary in $\hat{\varOmega }$ their time derivative following the material points is zero,

$$\displaystyle\begin{array}{rcl} \frac{dv_{i}} {dt} & =& \frac{\partial v_{i}} {\partial t} + \mathbf{w} \cdot \nabla v_{i}\; =\; 0,{}\end{array}$$

(11)

which is a critical component in the derivation of (2)–(3) because it allows one to substitute − w ⋅ ∇v _i for $\frac{\partial v_{i}} {\partial t}$ [21]. Spectral element bases are discussed further in Sect. 4 and in [25].

Fig. 1

Two-dimensional illustration of a spectral element domain decomposition

The timestepping strategy (8) has the advantage that all terms associated with the fast time scales (i.e., the pressure and second-order viscous diffusion terms) are linear, which makes an implicit treatment straightforward. Explicit treatment of the nonlinear terms results in a stability constraint on the step size that scales as Δt = O(Δx∕U), corresponding to the standard Courant condition. (The stability regions for BDFk/EXTk are shown in Fig. 2.) The ALE time advancement from step t ⁿ⁻¹ to t ⁿ is outlined in Algorithm 1.

Fig. 2

Stability regions for BDFk/EXTk

Algorithm 1

In Step 4, one can solve the full Stokes problem using an Uzawa algorithm (e.g, [24, 26]). For large timesteps and highly viscous flows, Uzawa iteration is a reasonable choice. For high Reynolds-number flows, however, an approximate solution strategy via high-order algebraic splitting of the Stokes operator is more effective [7, 9–11, 27]. This splitting can be viewed as a single step in an iterative process. With kth-order extrapolation of the pressure prior to splitting, however, one can realize kth-order accuracy in time without the need for iteration. We refer to [11] for further details and to Sect. 7.1 for temporal convergence results for both stationary and moving domain examples.

Save for the inertial terms associated with advection, (8) implicitly captures all the dynamics of the system including, most importantly, the unsteady components of the fluid inertia. The key point is that (8) is linear and thus admits superposition when satisfying dynamical constraints, such as addressed in Sect. 6, with no need for nonlinear iteration.

3 $\mathbb{P}_{N} - \mathbb{P}_{N}$ Low-Mach-Number Formulation

Many engineering systems feature flows where compressibility is not negligible. In internal combustion engines, for example, thermal dilation and especially compression from the piston motion result in significant density variations. In this section we address recent developments extending the SE-based low-Mach-number formulation of [28, 29] to support moving domains and in particular closed systems of variable volume.

For the numerical simulation of low-speed compressible reacting flows, the existence of acoustic pressure waves severely restricts explicit-integration timestep sizes because of the large discrepancy between the flow velocity and the speed of sound. When acoustic waves are not of interest, regular perturbation techniques can be used to decouple the waves from the governing equations [30–32]. This analysis leads to a decomposition of the pressure as

$$\displaystyle{ p(x,t) = p_{0}(t) +\epsilon p_{1}(x,t), }$$

(12)

where the hydrodynamic pressure (p ₁) is decoupled from the thermodynamic pressure (p ₀), and ε is defined as γMa ², where γ is the ratio of specific heat capacities and Ma is the Mach number. The resulting low-Mach-number governing equations for N _g -component reactive gaseous mixtures are the following.

Continuity

$$\displaystyle{ \frac{\partial \rho } {\partial t} + \nabla \cdot (\rho \mathbf{u}) = 0 }$$

(13)

Momentum

$$\displaystyle{ \rho \left (\frac{\partial \mathbf{u}} {\partial t} + \mathbf{u} \cdot \nabla \mathbf{u}\right ) = -\nabla p_{1} + \nabla \cdot (\mu \mathbf{s}) }$$

(14)

$$\displaystyle{ \mathbf{s} = \nabla \mathbf{u} + \left (\nabla \mathbf{u}\right )^{T} -\frac{2} {3}\left (\nabla \cdot \mathbf{u}\right )\mathbf{\mathsf{}}I }$$

(15)

Energy

$$\displaystyle{ \rho c_{p}\left (\frac{\partial T} {\partial t} + \mathbf{u} \cdot \nabla T\right ) = \nabla \cdot \left (\lambda \nabla T\right ) -\sum _{i=1}^{N_{g} }h_{i}\dot{\omega _{i}} + \frac{\gamma -1} {\gamma } \frac{dp_{0}} {dt} }$$

(16)

$$\displaystyle{ c_{p} =\sum _{ i=1}^{N_{g} }c_{p,i}Y _{i} }$$

(17)

Species

$$\displaystyle{ \rho \left (\frac{\partial Y _{i}} {\partial t} + \mathbf{u} \cdot \nabla Y _{i}\right ) = -\nabla \cdot \left (\rho Y _{i}\mathbf{V}_{i}\right ) +\dot{\omega _{i}}\;\;\;i = 1,\ldots,N_{g} }$$

(18)

Ideal gas law

$$\displaystyle{ p_{0} =\rho T/W }$$

(19)

In (13)–(19), $h_{i},\dot{\omega }_{i},Y _{i},$ and V _i , W _i , c _p, i are the enthalpy, chemical production term, mass fraction, diffusion velocity, molecular weight, and heat capacity of species i, respectively; λ is the thermal conductivity; p ₁ and p ₀ are the so-called hydrodynamic and thermodynamic pressures, respectively; $W = \left (\sum _{i=1}^{N_{g}}Y _{i}/W_{i}\right )^{-1}$ is the mean molecular weight; c _p is the mixture heat capacity; and I is the identity matrix. The species diffusion velocities V _i are given by Fick’s law

$$\displaystyle\begin{array}{rcl} \mathbf{V}_{i} = -\left (D_{i}/X_{i}\right )\nabla X_{i},& &{}\end{array}$$

(20)

D _i and X _i = Y _i W _i ∕W being the ith species mixture-averaged diffusivity and mole fraction, respectively. All quantities appearing in the equations above are already nondimensionalized by using reference values for L ₀, U ₀, ρ ₀, W ₀, c _p0 and T ₀; in particular p ₁ is nondimensionalized by using ρ ₀ U ₀ ² and p ₀ by using $\rho _{0}\mathcal{R}T_{0}/W_{0}$, where $\mathcal{R}$ is the universal gas constant. The reaction rate constants for the calculation of the chemical source terms $\dot{\omega _{i}}$ in Eqs. (16) and (18) are assumed to follow an extended Arrhenius expression.

In the low-Mach-number formulation, Eq. (13) is replaced by Eq. (21), which is obtained by combining the continuity (13), energy (16), species (18), and state (19) equations. When the domain volume changes in time, the temporal variation of the thermodynamic pressure, p ₀, is nonzero. The governing system for this background pressure is derived below, starting with the low-Mach relationship for the divergence,

$$\displaystyle\begin{array}{rcl} \nabla \cdot \mathbf{u} = -\frac{1} {\rho } \frac{D\rho } {Dt}& =& \frac{1} {T} \frac{DT} {Dt} +\sum _{ i=1}^{N_{g} } \frac{W} {W_{i}} \frac{DY _{i}} {Dt} - \frac{1} {p_{0}} \frac{dp_{0}} {dt} \\ & =& Q_{T} + \left ( \frac{1} {c_{p}W} \frac{\gamma -1} {\gamma } - 1\right ) \frac{1} {p_{0}} \frac{dp_{0}} {dt}. {}\end{array}$$

(21)

Here, Q _T is the thermal divergence, which couples the flow field with the temperature and species,

$$\displaystyle{ Q_{T} = \frac{1} {\rho } \sum _{i=1}^{N_{g} } \frac{W} {W_{i}}\left (-\nabla \cdot \rho Y _{i}\mathbf{V}_{i} +\dot{\omega } _{i}\right )\ + \frac{1} {\rho c_{p}T}\left (\nabla \cdot \left (\lambda \nabla T\right ) -\sum _{i=1}^{N_{g} }h_{i}\dot{\omega }_{i}\right ). }$$

(22)

In (21), density is determined only by the thermodynamic state T, Y _i , and p ₀ and not by the velocity, since acoustic waves are neglected. By contrast, incompressible formulations do not consider the effect of density variations because ∇⋅ u ≡ 0.

The background thermodynamic pressure, p ₀, is obtained by integrating over the domain as follows:

$$\displaystyle\begin{array}{rcl} \int _{\varOmega }\, \frac{1} {p_{0}} \frac{dp_{0}} {dt} \,dv& =& \left (1 - \frac{1} {c_{p}W} \frac{\gamma -1} {\gamma } \right )^{-1}\left (\int _{\varOmega }Q_{ T}\,dv -\int _{\partial \varOmega }\mathbf{u} \cdot \mathbf{n}\,ds\right ).{}\end{array}$$

(23)

Because p ₀ is a function of time only, the integral on the left corresponds to multiplying the integrand by the domain volume.

Numerical Methodology

Spatial discretization of (13)–(21) is based on the weighted residual formulation of the preceding section, save that pressure in this case is continuous and of the same order as the velocity. We consequently refer to this scheme as the $\mathbb{P}_{N} - \mathbb{P}_{N}$ method. The resultant system of ordinary differential equations (ODEs) is integrated in time with a high-order splitting scheme for low-Mach-number reactive flows [28]. The low-Mach-number formulation allows the thermochemistry subsystem to be decoupled from the hydrodynamic subsystem, which has the advantage that an appropriate stiff ODE solver can be used to integrate the fully coupled discretized energy and species equations, thus avoiding additional splitting errors.

For the thermochemistry subsystem, the spatially discretized energy, species, and thermodynamic pressure equations, (16)–(18) and (23), are integrated in time with a variable-step kth-order (k = 1, …, 5) integrator, CVODE [33]. The density is removed from the equations by using the equation of state. The equations are solved implicitly with the exception of the convecting velocity fields, which are approximated by using high-order explicit extrapolation. The links between thermo- and hydrodynamic subsystems are the density and the divergence constraint (21), which account for the influence of density variations on the velocity field.

The solution of the hydrodynamic subsystem is based on a projection-type velocity correction scheme introduced by Orszag et al. [34]. As a first step, the velocities are updated with the nonlinear terms and a pressure Poisson equation is solved by using boundary conditions based on a third-order extrapolation of viscous contribution of the velocity. Once the hydrodynamic pressure, p ₁, is known, the velocity is corrected in a second implicit viscous correction step based on standard Helmholtz equations (36). The low-Mach-number formulation yields kth-order accuracy in time (typ., k = 3) for all hydrodynamic variables in combination with minimal splitting errors as shown in [29] and [34]. As is the case for the $\mathbb{P}_{N} - \mathbb{P}_{N-2}$ formulation (8), this projection scheme amounts to solving, approximately, a linear Stokes problem at each timestep, with boundary conditions being applied at time t ⁿ.

Arbitrary Lagrangian-Eulerian Formulation Extension of the $\mathbb{P}_{N} - \mathbb{P}_{N}$ formulation to the ALE framework follows essentially the same steps as for the incompressible $\mathbb{P}_{N} - \mathbb{P}_{N-2}$ method of Sect. 2. A detailed derivation of the ALE equations can be found in [35]. Sections 7.2 and 7.3 discuss validation of the code modifications for constant and variable thermodynamic pressures.

In addition to solving the ALE momentum equations (13)–(15) and the pressure Poisson equation, the ALE/low-Mach formulation requires the energy and species equations to be integrated together with the single ODE for the thermodynamic pressure (23). Similar to the momentum equation, the ALE form of temperature (energy) and species equations is derived by introducing the mesh velocity, w, in the convective operator. The resulting weighted residual statement reads as follows: Find T, Y _i  ∈ X _b ^N such that

$$\displaystyle\begin{array}{rcl} \frac{d} {dt}\left (\psi,T\right )& -& \left (\psi,\nabla \cdot (\mathbf{w}T) -\mathbf{u} \cdot \nabla T\right ) = \\ & -& \left (\nabla \psi,\lambda \nabla T\right ) -\left (\psi,\sum _{i=1}^{N_{g} }h_{i}\dot{\omega _{i}}\right ) + \frac{\gamma -1} {\gamma } \left (\psi, \frac{dp_{0}} {dt} \right ){}\end{array}$$

(24)

$$\displaystyle\begin{array}{rcl} \frac{d} {dt}\left (\psi,Y _{i}\right )& -& \left (\psi,\nabla \cdot (\mathbf{w}Y _{i}) -\mathbf{u} \cdot \nabla Y _{i}\right ) = \\ & -& \left (\nabla \psi,\rho D_{i}\nabla Y _{i}\right ) + \left (\psi,\dot{\omega _{i}}\right )\;\;\forall \,\psi \, \in X_{0}^{N},{}\end{array}$$

(25)

where the ψs are interpreted to be a different set of test functions for each of the thermal/species equations. Here, the surface integrals have been omitted under the assumption that only homogeneous boundary conditions are considered.

In the absence of chemical reactions (i.e., of numerical stiffness) and when the thermodynamic pressure is constant, the ALE energy and species equations are integrated by using the same semi-implicit formulation as with the momentum. In this case, the semi-discrete form of the equations becomes

$$\displaystyle\begin{array}{rcl} \frac{\beta _{0}} {\varDelta t}& & \left (\psi,T^{n}\right )_{ n} + \left (\nabla \psi,\lambda \nabla T^{n}\right )_{ n} = \\ & & -\sum _{j=1}^{k}\frac{\beta _{j}} {\varDelta t}\left (\psi,T^{n-j}\right )_{ n-j} +\sum _{ j=1}^{k}\alpha _{ j}\tilde{N}_{T}^{n-j}{}\end{array}$$

(26)

$$\displaystyle\begin{array}{rcl} \frac{\beta _{0}} {\varDelta t}& & \left (\psi,Y _{i}^{n}\right )_{ n} + \left (\nabla \psi,\rho D_{i}\nabla Y _{i}^{n}\right )_{ n} = \\ & & -\sum _{j=1}^{k}\frac{\beta _{j}} {\varDelta t}\left (\psi,Y _{i}^{n-j}\right )_{ n-j} +\sum _{ j=1}^{k}\alpha _{ j}\tilde{N}_{Y _{i}}^{n-j},{}\end{array}$$

(27)

where

$$\displaystyle{\tilde{N}_{T}^{n-j} = \left (\psi,[\nabla \cdot \mathbf{w}T -\mathbf{u} \cdot \nabla T]^{n-j}\right )_{ n-j}}$$

and

$$\displaystyle{\tilde{N}_{Y _{i}}^{n-j} = \left (\psi,[\nabla \cdot \mathbf{w}Y _{ i} -\mathbf{u} \cdot \nabla Y _{i}]^{n-j}\right )_{ n-j}.}$$

In the presence of chemical reactions and thermodynamic pressure variation, the ALE energy and species equations are integrated implicitly by using CVODE as follows.

$$\displaystyle\begin{array}{rcl} \left (\psi, \frac{dT} {dt} \right )_{n}& =& \left (\psi,[\tilde{\mathbf{w}} -\tilde{\mathbf{u}}] \cdot \nabla T^{n}\right )_{ n} \\ & -& \left (\nabla \psi,\lambda \nabla T^{n},\right )_{ n} -\sum _{i=1}^{N_{g} }\left (\psi,h_{i}\dot{\omega _{i}^{n}}\right )_{ n} + \frac{\gamma -1} {\gamma } \left (\psi, \frac{dp_{0}} {dt} \right )_{n}{}\end{array}$$

(28)

$$\displaystyle\begin{array}{rcl} \left (\psi, \frac{dY _{i}} {dt} \right )_{n}& =& \left (\psi,[\tilde{\mathbf{w}} -\tilde{\mathbf{u}}] \cdot \nabla Y _{i}^{n}\right )_{ n} \\ & -& \left (\nabla \psi,\lambda \nabla Y _{i}^{n}\right )_{ n} + \left (\psi,\dot{\omega _{i}^{n}}\right )_{ n}{}\end{array}$$

(29)

and

$$\displaystyle{\tilde{\mathbf{w}} -\tilde{\mathbf{u}} =\sum _{ j=1}^{k}\alpha _{ j}\mathbf{w}^{n-j} -\sum _{ j=1}^{k}\alpha _{ j}\mathbf{u}^{n-j}}$$

The ALE formulation is thus implemented in the energy and species equations by replacing the fluid velocity u in the convective term with (u − w) and by updating the geometry Ω(t). We note that because CVODE uses adaptive timestepping, the mass matrix must be updated and inverted at intermediate time points in the interval [t ⁿ⁻¹, t ⁿ]. Fortunately, as shown in the next section, the high-order quadrature of the spectral element method yields a diagonal mass matrix that allows this system to be advanced at low cost. We summarize the low-Mach ALE formulation in Algorithm 2.

Algorithm 2

4 Spectral Element Method

Here, we describe the spectral element bases, operator evaluation, and implementation of inhomogeneous boundary conditions that are central to our moving-domain simulations. A critical aspect of the SEM is that neither the global nor the local stiffness matrices are ever formed. Elliptic problems are solved iteratively and thus require only the action of matrix-vector multiplication. Preconditioning is based on either diagonal scaling or hybrid multigrid-Schwarz methods with local smoothing effected through the use of separable operators [11–13, 36]. Exclusive reliance on matrix-free forms is particularly attractive in an ALE context because the overhead to update the operators as the mesh evolves is effectively nil.

We illustrate the basic components by considering the scalar elliptic problem,

$$\displaystyle\begin{array}{rcl} -\nabla \cdot \mu \nabla u\; +\;\gamma u& =& f,\;\;u = g\;\mbox{ on}\,\partial \varOmega _{D},\;\;\nabla u \cdot \mathbf{\hat{n}}\, =\, 0\;\mbox{ on}\,\partial \varOmega \setminus \partial \varOmega _{D},{}\end{array}$$

(30)

with Dirichlet conditions imposed on ∂Ω _D and Neumann conditions on the remainder of the boundary, ∂Ω∖∂Ω _D . The coefficients and data satisfy μ > 0, γ ≥ 0, $f \in \mathcal{ L}^{2}(\varOmega )$, and g ∈ C ⁰(∂Ω _D ). This boundary value problem arises in many contexts in our Navier-Stokes solution process. With γ = β ₀∕Δt and ν a constant, it is representative of the implicit subproblem for the velocity components in (5). With γ = 0 we have a variable-coefficient Poisson problem that arises in the pressure substep for the low-Mach formulation and in the lifting operators for the mesh velocity that will be introduced at the end of this section.

The discrete variational formulation of (30) is as follows: Find u(x) in X _b ^N such that

$$\displaystyle\begin{array}{rcl} (\nabla v,\,\mu \nabla u)\; +\; (v,\,\gamma u)& =& (v,f)\qquad \forall \;v\; \in \; X_{0}^{N},{}\end{array}$$

(31)

where, as in the Navier-Stokes case, X _b ^N (X ₀ ^N) denotes the space of functions in X ^N that satisfy u = g (u = 0) on ∂Ω _D . We symmetrize (31) by moving the boundary data to the right-hand side. If u _b is any known function in X _b ^N, the reformulated system is as follows: Find u ₀(x) in X ₀ ^N such that

$$\displaystyle\begin{array}{rcl} (\nabla v,\,\mu \nabla u_{0})\; +\; (v,\,\gamma u_{0})& =& (v,f)\; -\; (\nabla v,\,\mu \nabla u_{b})\; -\; (v,\,\gamma u_{b}) \\ & & \forall \;v\; \in \; X_{0}^{N}, {}\end{array}$$

(32)

with u : = u ₀ + u _b .

We formally introduce a global representation of u(x), which is never used in practice but which affords compact representation of the global system matrices. Let any u ∈ X ^N be represented in terms of a Lagrange (nodal) interpolating basis,

$$\displaystyle\begin{array}{rcl} u(\mathbf{x})& =& \sum _{{\hat\jmath}=1}^{\bar{n}}\,u_{{\hat\jmath}}\phi _{{\hat\jmath}}(\mathbf{x}),{}\end{array}$$

(33)

with basis functions $\phi _{{\hat\jmath}}(\mathbf{x})$ that are continuous on Ω. The number of coefficients, $\bar{n}$, corresponds to all basis functions in X ^N. Ordering the coefficients with boundary nodes numbered last yields n interior nodes such that X ₀ ^N = span$\{\phi _{{\hat\jmath}}\}_{1}^{n}$. Let I _n be the n × n identity matrix and R = [I _n   O] be an $n \times \bar{n}$ restriction matrix whose last $(\bar{n} - n)$ columns are empty. For any function u(x) ∈ X ^N we will denote the set of $\bar{n}$ basis coefficients by $\bar{\underline{u}}$ and the set of n interior coefficients by u. Note that $\underline{u} = R\bar{\underline{u}}$ always holds, whereas $\bar{\underline{u}}_{0} = R^{T}\underline{u}_{0}$ holds only for functions u ₀ ∈ X ₀ ^N.

We define the stiffness $\bar{A}$ and mass $\bar{B}$ matrices having entries

$$\displaystyle\begin{array}{rcl} \bar{A}_{ij}&:=& (\nabla \phi _{i},\,\mu \nabla \phi _{j}),\quad \bar{B}_{ij}\;:=\; (\phi _{i},\,\phi _{j}),\quad i,\,j \in \{ 1,\ldots,\bar{n}\}^{2}.{}\end{array}$$

(34)

The systems governing the interior coefficients of u ₀ are the n × n restricted stiffness and mass matrices, $A\,=\,R\bar{A}R^{T}$ and $B\,=\,R\bar{B}R^{T}$, respectively. A is invertible if $n\,<\,\bar{n}$. We refer to $\bar{A}$ as the Neumann operator because it is the stiffness matrix that would result if there were no Dirichlet boundary conditions. It has a null space of dimension one, corresponding to the constant function.¹

With the preceding definitions, the discrete equivalent of (32) is

$$\displaystyle\begin{array}{rcl} \underline{v}^{T}\,A\,\underline{u}_{ 0}\, +\,\gamma \underline{v}^{T}\,B\,\underline{u}_{ 0}& =& \underline{v}^{T}R\left [\,\bar{B}\,\bar{\underline{f}}\, -\,\bar{A}\,\bar{\underline{u}}_{ b}\, -\,\gamma \bar{B}\,\bar{\underline{u}}_{b}\right ].{}\end{array}$$

(35)

Here, we have exploited the fact that u ₀ and v are in X ₀ ^N, and for illustration we have made the simplifying assumptions that γ is constant and that f ∈ X ^N. Neither of these assumptions is binding. Full variability, including jumps in μ, γ, and f across element boundaries, can be handled in the SEM.

Because (35) holds for all v ∈ lRⁿ, the linear system for the unknown interior basis coefficients is

$$\displaystyle\begin{array}{rcl} H\,\underline{u}_{0}& =& R\left [\,\bar{B}\,\bar{\underline{f}}\, -\,\bar{H}\,\bar{\underline{u}}_{b}\right ],{}\end{array}$$

(36)

with $\bar{H}\,:=\, \bar{A}\, +\,\gamma \bar{B}$ and $H\,:=\, R\bar{H}R^{T}$. The full solution to (30) then is given by (33) plus

$$\displaystyle\begin{array}{rcl} \bar{\underline{u}}& =& R^{T}\underline{u}_{ 0}\; +\; \bar{\underline{u}}_{b}.{}\end{array}$$

(37)

For the case f = 0, we recognize in (36)–(37) the energy-minimizing projection,

$$\displaystyle\begin{array}{rcl} \bar{\underline{u}}& =& \bar{\underline{u}}_{b}\, -\, R^{T}\left (R\bar{H}R^{T}\right )^{-1}R\,\bar{H}\,\bar{\underline{u}}_{ b},{}\end{array}$$

(38)

which extends the trace of u _b into the interior of Ω in a smooth way provided that γ is also smooth.

Spectral Element Bases In the SEM, the global bases ϕ _j are never formed. Rather, all operations are evaluated locally within each of E nonoverlapping hexahedral (curvilinear brick) elements whose union forms the domain $\varOmega =\bigcup _{ e=1}^{E}\varOmega ^{e}$. Functions in X ^N are represented as tensor-product polynomials in the reference element, $\hat{\varOmega }:= [-1,1]^{d}$, whose image is mapped isoparametrically to each of the elements, as illustrated for the case d = 2 in Fig. 1. As an example, a scalar field u(r) on Ω ^e in three dimensions would be represented in terms of local basis coefficients u _ijk ^e as

$$\displaystyle\begin{array}{rcl} u^{e}(\mathbf{r})& =& \sum _{ k=0}^{N}\sum _{ j=0}^{N}\sum _{ i=0}^{N}\,h_{ i}(r)\,h_{j}(s)\,h_{k}(t)\,u_{ijk}^{e}.{}\end{array}$$

(39)

Here, $\mathbf{r} = [r,s,t] = [r_{1},r_{2},r_{3}]\, \in \,\hat{\varOmega }$ are the computational coordinates,² and h _i (ξ) are Nth-order Lagrange polynomials having nodes at the Gauss-Lobatto-Legendre (GLL) quadrature points, ξ _j  ∈ [−1, 1]. This choice of nodes provides a stable basis and allows the use of pointwise quadrature, resulting in significant savings in operator evaluation. Typical discretizations involve E = 10²–10⁷ elements of order N = 8 − 16 (corresponding to 512-4,096 points per element). Vectorization and cache efficiency derive from the local lexicographical ordering within each element and from the fact that the action of discrete operators, which nominally have O(EN ⁶) nonzeros, can be evaluated in only O(EN ⁴) work and O(EN ³) storage through the use of tensor-product-sum factorization [25, 37].

The geometry, x ^e(r), takes exactly the same form as (39), and derivatives are evaluated by using the chain rule. For example, the pth component of the gradient of u at the GLL node $\boldsymbol{\xi }_{ijk}:= (\xi _{i},\xi _{j},\xi _{k})$ is computed as

$$\displaystyle\begin{array}{rcl} \left. \frac{\partial u} {\partial x_{p}}\right \vert _{\boldsymbol{\xi }_{ijk}}& =& \left.\frac{\partial r_{1}} {\partial x_{p}}\right \vert _{\boldsymbol{\xi }_{ijk}}\sum _{i'=0}^{N}\hat{D}_{ ii'}u_{i'jk}\, +\, \left.\frac{\partial r_{2}} {\partial x_{p}}\right \vert _{\boldsymbol{\xi }_{ijk}}\sum _{j'=0}^{N}\hat{D}_{ jj'}u_{ij'k}\, +\, \left.\frac{\partial r_{3}} {\partial x_{p}}\right \vert _{\boldsymbol{\xi }_{ijk}}\sum _{k'=0}^{N}\hat{D}_{ kk'}u_{ijk'},{}\\ \end{array}$$

where $\hat{D}$ is the one-dimensional derivative matrix on [−1, 1]. $\hat{D}_{ij} = \left.\frac{dh_{j}} {dr} \right \vert _{\xi _{i}}.$ We note that if the metric terms $\frac{\partial r_{q}} {\partial x_{p}}$ are precomputed, then the work to evaluate all components of the gradient, $\frac{\partial u} {\partial x_{p}}$, is $(6N + 15)EN^{3} \approx (6N + 15)\bar{n}$, and the number of memory accesses is $O(\bar{n})$. The work to compute the metrics $\frac{\partial r_{q}} {\partial x_{p}^{e}}$ is similarly $O(N\bar{n})$. Using $\hat{D}$, one evaluates the 3 × 3 matrix $\frac{\partial x_{q}^{e}} {\partial r_{p}}$, then inverts this matrix pointwise in O(N ³) operations to obtain $(F_{pq}^{e})_{\xi _{ijk}}:= \left. \frac{\partial r_{q}} {\partial x_{p}^{e}}\right \vert _{\xi _{ijk}}$. If u ^e is the lexicographically ordered set of basis coefficients on element Ω ^e, its gradient can be compactly expressed as

$$\displaystyle\begin{array}{rcl} \underline{w}_{p}^{e}& =& \sum _{ q=1}^{3}F_{ pq}^{e}D_{ q}\underline{u}^{e},\;\;\;p = 1,\,2,\,\mbox{ or}\,3,{}\end{array}$$

(40)

where $D_{1} = I \otimes I \otimes \hat{D}$, $D_{2} = I \otimes \hat{D} \otimes I$, $D_{3} = \hat{D} \otimes I \otimes I$, and, for each p, q and e, F _pq ^e is a diagonal matrix.

The high order of the SEM coupled with the use of GLL-based Lagrangian interpolants allows the integrals in (34) to be accurately approximated by using pointwise quadrature. In particular, the mass matrix becomes diagonal. For a single element one has

$$\displaystyle\begin{array}{rcl} B_{{\hat\imath}{\hat\imath}'}^{e}&:=& \!\!\int _{\varOmega ^{e }}\phi _{{\hat\imath}}\,\phi _{{\hat\imath}'}\,d\mathbf{x} =\!\int _{ -1}^{1}\int _{ -1}^{1}\int _{ -1}^{1}\!\left [\,h_{ i}(r)h_{j}(s)h_{k}(t)\right ]\,\left [\,h_{i'}(r)h_{j'}(s)h_{k'}(t)\right ]\!\mathcal{J}^{e}\,dr\,ds\,dt \\ & \approx & \!\!\sum _{i''\,j''\,k''}\rho _{i''}\rho _{j''}\rho _{k''}\left [\,h_{i}(\xi _{i''})h_{j}(\xi _{j''})h_{k}(\xi _{k''})\right ]\,\left [\,h_{i'}(\xi _{i''})h_{j'}(\xi _{j''})h_{k'}(\xi _{k''})\right ]\,\mathcal{J}_{i''\,j''\,k''}^{e} \\ & =& \rho _{i}\rho _{j}\rho _{k}\mathcal{J}_{ijk}^{e}\;\delta _{ ii'}\delta _{jj'}\delta _{kk'}, {}\end{array}$$

(41)

where $\mathcal{J}^{e} = \left \vert \frac{\partial x_{p}^{e}} {\partial r_{q}} \right \vert$ is the pointwise Jacobian associated with the mapping x ^e(r), ρ _j is the quadrature weight corresponding to the GLL point ξ _j , and δ _ii′ is the Kronecker delta. For compactness, we have also introduced the lexicographical ordering ${\hat\imath}\,:=\,i + (N + 1)(j - 1) + (N + 1)^{2}(k - 1)$. The same map takes the trial function (i′, j′, k′) to ${\hat\imath}'$. The tensor-product form of the local mass matrix is $B^{e} = J^{e}(\hat{B} \otimes \hat{B} \otimes \hat{B})$, where $\hat{B} =$ diag(ρ _k ) is the 1D mass matrix containing the GLL quadrature weights and J ^e is the diagonal matrix of Jacobian values at the quadrature points.

Combining the mass matrix with the gradient operator yields the local stiffness matrix as typically applied in the SEM, namely,

$$\displaystyle\begin{array}{rcl} A^{e}& =& \sum _{ p=1}^{3}\sum _{ q=1}^{3}D_{ p}^{T}\,\left (\mu \,G_{ pq}^{e}\right )\,D_{ q},\;\;\;\;\;G_{pq}^{e}\;:=\; B^{e}\,\sum _{ q'=1}^{3}F_{ q'\!p}^{e}\,F_{ q'q}^{e}.{}\end{array}$$

(42)

We note that G _pq ^e = G _qp ^e is a symmetric tensor field that amounts to six diagonal matrice of size (N + 1)³ for each element Ω ^e. Likewise, the variable diffusivity μ is understood to be a diagonal matrix evaluated at each gridpoint, ξ _ijk ^e. We emphasize that for the general curvilinear element case A ^e is completely full, with (N + 1)⁶ nonzeros, which makes it prohibitive to form for N > 3. However, the factored form (42) is sparse, with only 6(N + 1)³ nonzeros for all the geometric factors G _pq ^e plus O(N ²) for derivative matrices (and an additional (N + 1)³ if μ is variable). The total storage for the general factored stiffness matrix is ∼ 7n _l , where n _l  = E(N + 1)³ is the total number of gridpoints in the domain. Moreover, the total work per matrix-vector product is only ∼ 12Nn _l , and this work is effectively cast as highly vectorizable matrix-matrix products [20, 25, 38].

To complete the problem statement, we need to assemble the local stiffness and mass matrices, B ^e and A ^e, and apply the boundary conditions, both of which imply restrictions on the nodal values u _ijk ^e and v _ijk ^e. For any u(x) ∈ X ^N we can associate a single nodal value u _g for each unique x _g  ∈ Ω. where $g\, \in \{ 1,\ldots,\bar{n}\}$ is a global index. Let g = g _ijk ^e be an integer that maps any x _ijk ^e to x _g ; let l = i + (N + 1)(j − 1) + (N + 1)²(k − 1) + (N + 1)³(e − 1) represent a lexicographical ordering of the local nodal values; and let m = E(N + 1)³ be the total number of local nodes. We define Q ^T as the $\bar{n} \times m$ Boolean gather-scatter matrix whose lth column is $\hat{\underline{e}}_{g(l)}$, where g(l) is the local-to-global pointer and $\hat{\underline{e}}_{g}$ is the gth column of the $\bar{n} \times \bar{n}$ identity matrix. For any u ∈ X ^N we have the global-to-local map u _L = Qu, where u _L = {u ^e} _{e = 1} ^E is the collection of local basis coefficients. With these definitions, the discrete bilinear form for the Laplacian becomes

$$\displaystyle\begin{array}{rcl} (\nabla v,\mu \nabla u)& =& \sum _{e=1}^{E}\,(\underline{v}^{e})^{T}A^{e}\underline{u}^{e}\ =\ \underline{v}_{ L}^{T}A_{ L}\,\underline{u}_{L}\ =\ (Q\underline{v})^{T}A_{ L}\,Q\underline{u}\ =\ \underline{v}^{T}Q^{T}A_{ L}\,Q\underline{u},\ =\ \underline{v}^{T}\bar{A}\underline{u}.{}\\ \end{array}$$

Here A _L = block-diag{A ^e} is termed the unassembled stiffness matrix, and $\bar{A}\,=\,Q^{T}$ A _L Q is the assembled stiffness matrix. To obtain the mass matrix, we consider the inner product,

$$\displaystyle\begin{array}{rcl} (v,u)& =& \sum _{e=1}^{E}\,(\underline{v}^{e})^{T}B^{e}\underline{u}^{e}\; =\; \underline{v}_{ L}^{T}B_{ L}\,\underline{u}_{L}\; =\; (Q\underline{v})^{T}B_{ L}\,Q\underline{u}\; =\; \underline{v}^{T}Q^{T}B_{ L}\,Q\underline{u},\;=\; \underline{v}^{T}\bar{B}\underline{u}.{}\\ \end{array}$$

Here, B _L = block-diag{B ^e} and $\bar{B} = Q^{T}B_{L}Q$ are, respectively, the diagonal unassembled and assembled mass matrices comprising local mass matrices, B ^e.

We close this section on basis functions by defining elements of the pressure space. For the $\mathbb{P}_{N} - \mathbb{P}_{N}$ (low-Mach) formulation described in Sect. 3, we take Y ^N = X ^N. That is, the pressure is continuous and represented by basis functions having the form (39). For the $\mathbb{P}_{N} - \mathbb{P}_{N-2}$ formulation of Maday and Patera [24], the elements of Y ^N have the tensor-product form of (39) except that the index ranges from 0 to N-2 and the nodal points are chosen to be the Gauss-Legendre quadrature points rather than the GLL points. Furthermore, interelement continuity is not enforced on either the pressure, p, or the corresponding test function, q. Element-to-element interaction for the pressure derives from the fact that the velocity u and test functions v are in X ^N ⊂ H ¹. We refer to [11, 24, 25] for additional detail concerning the SEM bases and implementation of the $\mathbb{P}_{N} - \mathbb{P}_{N-2}$ formulation.

5 Mesh Motion

Mesh displacement is computed by integrating the ODE $\mathbf{w} = \mathbf{\dot{x}}$ in time, where the mesh velocity w is subject to the kinematic constraint (4). The main idea is to smoothly blend the boundary data into the domain interior. The original SEM-ALE formulation of Ho [21] used an elasticity solver in order to lift the mesh-velocity boundary data to the domain interior. This approach has proven robust for many complex motions, including free-surface applications. It is expensive, however, with the mesh solve costing as much as or more than the velocity/pressure solve.

We have found in several instances that simpler strategies offer significant cost savings and can generate adequate blending functions. For example, for a tensor-product domain with a free surface located at height z = H(x, y) and no motion on the floor at z = 0, one can define the vertical mesh velocity satisfying (4),

$$\displaystyle\begin{array}{rcl} w_{z}(x,y,z)& =& \frac{z} {H(x,y)}\,\frac{\mathbf{u}(x,y,H) \cdot \mathbf{\hat{n}}} {\mathbf{\hat{z}}} \cdot \mathbf{\hat{n}},{}\end{array}$$

(43)

where u is the fluid velocity, $\mathbf{\hat{n}}$ is the unit normal at the surface, and z is the unit vector in the z direction. This approach has been used in free-surface Orr-Sommerfeld examples [39].

For more complex domains, we typically solve Laplace’s equation (i.e., (30) with γ = f = 0) in order to blend the surface velocities to the interior, relying on the maximum principle to give a bounded interpolant. Fluid dynamics applications often require high-resolution meshes near walls in order to resolve boundary-layer turbulence. If unconstrained, mesh deformation can compromise the quality of these critical boundary-layer elements. The deformation can be mitigated, however, by increasing the diffusivity near the walls so that the mesh velocity tends to match that of the nearby object. The bulk of the mesh deformation is effectively pushed into the far field, where elements are larger and thus better able to absorb significant deformation. We usually set $\mu (\mathbf{x}) = 1 +\alpha e^{-\delta ^{2} }$ with α = 9 and δ: = d∕Δ the distance to the wall normalized by a chosen length scale, Δ. In the absence of any other scale information, we set Δ equal to the average thickness of the first layer of spectral elements in contact with the given object. To compute d, we use a Euclidian graph-based approximation to the true distance function. A naïve computation of the distance function begins by initializing d to a large number at each gridpoint, setting d = 0 on boundary nodes, and then iterating, with each point i assigning d _i to be min(d _i , d _j + d _ij ) for all points j connected to i, where d _ij is the Euclidian distance between i and j. The iteration proceeds until no distances are updated. The idea of using variable diffusivity has been explored by other authors in finite-element contexts where the coefficient is based on local element volumes (e.g., [40, 41]) and can also be applied to the elasticity equations.

Figure 3 shows a close-up of an ALE spectral element mesh for a pair of unit-diameter cylinders moving toward each other until the gap is.03. Here, Δ = 0. 1; and a new diffusivity function, μ _new, is computed every 100 timesteps based on an updated distance function. In order to make the function smooth in time, the diffusivity is blended with preceding values by using a weighted update, μ ⁿ = 0. 95μ ⁿ⁻¹ +. 05μ _new. (With a more efficient distance function, one could simply update the diffusivity at every step instead of using a weighted update.) Jacobi-preconditioned conjugate gradient (CG) iteration is used to solve for the mesh velocity. When coupled with projection in time [42], only a few iterations per step are required in order to reduce the CG residual to 10⁻⁵. Figure 3 shows clearly that this procedure preserves element shapes near the cylinders except in the gap region where the near-wall elements must yield to the cylinder motion. By tuning the parameters one can ensure that compression in the gap is evenly distributed so that the centermost elements are not squeezed to zero thickness before the near-wall elements yield. We note that because the diffusivity is based on the geometry, there is little hysteresis in the mesh deformation, which is not necessarily true if the mesh diffusivity is based on element sizes.

Fig. 3

Two-cylinder mesh deformation resulting from variable-diffusivity solver for mesh velocity

We remark that if the geometric motion is prescribed, one can solve for the mesh position at a few time points, optimize the mesh at these points (while retaining the base topology), and then use a spline to generate the mesh velocity at all instances in time. Such a strategy would yield optimal meshes that vary smoothly in time and that incur low overhead for mesh motion. The base solutions can be generated in a separate off-line calculation, for example, with the PDE-based approach just described.

6 Fluid–Structure Interaction

Here, we consider systems in which the boundary motion is determined dynamically through interactions with the external flow field, rather than prescribed. A critical feature of these problems is that the resulting system can be extremely stiff. Indeed, because of incompressibility, the pressure responds instantaneously to acceleration of boundaries, with the net effect that the system has added apparent mass arising from the Navier-Stokes equations.

The stiffness associated with fluid-structure interaction (FSI) problems is well known and has been the topic of much recent activity. Several strategies have been pursued to develop robust and fast methods. A particularly robust approach is to use a monolithic scheme with nonlinear iteration to solve for all fluid and solid variables at each step. A comprehensive overview of this strategy is provided by Hron and Turek [43]. Another strategy is to couple independent fluid and structural codes, which offers the potential for using the state of the art from each of the disciplines (e.g., using a structural code with support for contact problems, nonlinear material response, and anisotropic materials). Decoupled methods generally either are explicit or rely on subiterations at each step to improve stability. Gerbeau et al. [44] analyze the stability of several coupling strategies, including subiteration approaches, and identify added mass as one of the principal sources of instability. In a subsequent paper [45], Gerbeau and coworkers identify that the added-mass effect constitutes a linear phenomenon and suggest a coupled, but linear, FSI solution strategy to keep the work low while retaining good stability properties. Farhat et al. [46] demonstrate that a fully explicit subiteration-free strategy using staggered fluid/structure updates can be robust even in the presence of strong added-mass effects for examples having catastrophic (i.e., rapid) structural response.

Recently, a set of schemes with implicit treatment of the added-mass effect have been developed by Banks and coworkers that allow for a decoupled approach without subiteration [47–49]. The authors consider incompressible flows interacting with elastic solids [48] and structural shells [49], as well as FSI for light rigid bodies in compressible flow [47]. The key idea of these papers is to identify the added-mass tensor from a characteristic analysis of the fluid-structure interaction. For the incompressible flow cases, they further introduce a new set of mixed (Robin) boundary conditions for the velocity and pressure, as has been considered by other authors (see, e.g., [50] for an extensive review).

We consider an extension of these ideas to the case of light rigid bodies for incompressible flow. The scheme is fully implicit and exploits the linearity of the unsteady Stokes problem (8). The approach of [47] for rigid-body responses is based on a characteristics analysis associated with compressible flow. The authors identify the interface stress with the difference in velocity between the fluid and the structure. Consideration of such a difference is sensible in the compressible case because it is a measure of the temporal response of the fluid to the motion of the structure. In the case of a rigid solid and an incompressible fluid, however, there is no compliance, and the response is instantaneous. Nonetheless, the added-mass effect is a linear phenomena associated with the acceleration of the object that ultimately manifests as a linear function of the unknown velocity at time t ⁿ. Here, we introduce a Green’s function approach to identifying the added mass in the incompressible case and incorporating its effect into the implicit Stokes update step (8) through superposition.³

We illustrate the procedure with the example of flow past a cylinder of mass m that is allowed to oscillate in the y direction, subject to a restoring force F _κ = −κ η, where the positive spring coefficient κ may be a function of the displacement η. In addition to providing a relatively simple model, this problem is of interest in its own right and continues to be a topic of analysis [51, 52]. From Newton’s third law, the cylinder motion is governed by

$$\displaystyle\begin{array}{rcl} m\ddot{\eta }& =& F_{\mbox{ net}}\; =\; F_{f}\; +\; F_{\kappa }.{}\end{array}$$

(44)

The challenge of (44) is that the fluid forces F _f are strongly dependent on the acceleration of the object, $\ddot{\eta }$, particularly as the mass, m, tends toward zero. In this limit we must have F _f   ≡  −F _κ or suffer unbounded acceleration. For this reason, we seek an implicit coupling between (44) and the ALE formulation (8).

We begin with a BDFk/EXTk temporal discretization of (44),

$$\displaystyle\begin{array}{rcl} \frac{m} {\varDelta t} \sum _{j=0}^{k}\,\beta _{ j}\,\dot{\eta }^{n-j}& =& F_{ f}^{n}\; +\; \tilde{F}_{\kappa }^{n},{}\end{array}$$

(45)

where kth-order extrapolation is used to compute the restoring force,

$$\displaystyle\begin{array}{rcl} \tilde{F}_{\kappa }^{n}& =& \sum _{ j=1}^{k}\alpha _{ j}F_{\kappa }^{n-j}\; =\; F_{\kappa }^{n}\; +\; O(\varDelta t^{k}){}\end{array}$$

(46)

Note that $\dot{\eta }^{n}\,\mathbf{\hat{y}}$, the product of the unknown cylinder velocity at t ⁿ with the unit normal in the y direction, corresponds to the boundary condition on the cylinder surface for u ⁿ in (8).

We next break F _f ⁿ into two contributions: F _f ⁿ = F _s + αF _g , where F _s is the standard fluid lift force that would result from advancing (8) with a given cylinder velocity, $\dot{\eta }_{s}$, whose value is at our discretion and whose choice is discussed shortly. We denote the solution of this system as (u _s , p _s ).

The second part of the force, F _g , is the lift that results from the Green’s function pair (u _g , p _g ) satisfying the following: Find (u _g , p _g ) ∈ X ₁ ^N × Y ^N such that

$$\displaystyle\begin{array}{rcl} \frac{\beta _{0}} {\varDelta t}\,(\mathbf{v},\mathbf{u}_{g})_{n}\, +\, \frac{1} {Re}(\nabla \mathbf{v},\mathbf{s}_{g})_{n} - (\nabla \cdot \mathbf{v},p_{g})_{n}& =& 0\;\;\;\;\;\;(q,\nabla \cdot \mathbf{u}_{g})_{n}\, =\, 0{}\end{array}$$

(47)

for all (v, q) ∈ X ₀ ^N × Y ^N, where X ₁ ^N is the subset of X ^N that vanishes on ∂Ω _D save for the cylinder surface, where u _g = (0, 1, 0). From the velocity pressure pair (u _g , p _g ) we compute the lift F _g . Note that we do not actually solve the unsteady Stokes problem (47), but rather its time-split surrogate consistent with that used to advance (8).

For either of the formulations described in the preceding sections the implicit substep used to update (u ⁿ, p ⁿ) is linear, and superposition may be used to satisfy any number of constraints. The key idea is thus to set

$$\displaystyle\begin{array}{rcl} \mathbf{u}^{n}& =& \mathbf{u}_{ s}\, +\,\alpha \mathbf{u}_{g},\;\;\;p^{n}\, =\, p_{ s}\, +\,\alpha p_{g},\;\;\;F^{n}\, =\, F_{ s}\, +\,\alpha F_{g},\;\;\;\dot{\eta }^{n}\, =\,\dot{\eta } _{ s}+\alpha,\;\;\;{}\end{array}$$

(48)

where α is chosen to satisfy (45) exactly. Because both sides of (45) are linear in α, one has directly

$$\displaystyle\begin{array}{rcl} \alpha & =& \frac{F_{s}\; +\; \tilde{F}_{\kappa }^{n}\; -\;\frac{m} {\varDelta t} \left (\beta _{0}\dot{\eta }_{s}\, +\,\sum _{ j=1}^{n}\beta _{ j}\dot{\eta }^{n-j}\right )} {\frac{m} {\varDelta t} \beta _{0}\; -\; F_{g}}.{}\end{array}$$

(49)

We make several remarks concerning this procedure. First, the case m = 0 presents no difficulty because F _g is never zero. In fact, F _g is negative (the restoring force is opposite the applied velocity perturbation), so (49) can never suffer from a vanishing denominator. Second, (u _s , p _s , F _s ) results from the standard Navier-Stokes update. Most of the expense is in iterative solution of the pressure, which can be minimized if the apparent acceleration of the cylinder is zero, that is, if $\dot{\eta }_{s}:= -(\sum _{j=1}^{k}\,\beta _{j}\eta ^{n-j})/\beta _{0}$. The variation in $\dot{\eta }^{n}$ is made up by the contribution from the Green’s function, whose cost is independent of α. For computation of both the s and g variables, significant cost savings are realized by using initial guesses that are projections onto the space of prior solutions [42]. We remark further that F _g represents the influence of the added mass. From the denominator of (49) we see that the effective added mass is

$$\displaystyle\begin{array}{rcl} m_{a} = -\varDelta tF_{g}/\beta _{0}.& & {}\\ \end{array}$$

The only time dependence for (u _g , p _g ) arises from the fact that the domain is time varying. Otherwise, one could compute (u _g , p _g ) once in a preprocessing step and reuse it for all time provided that β ₀ and Δt are invariant. We use such an approach for rotating cylinder cases where the geometry is indeed invariant.

We note that explicit computation of $\tilde{F}_{\kappa }^{n}$, which readily admits incorporation of fully nonlinear responses (e.g., [52]), is a potential source of instability. Under standard conditions, however, the Courant restriction on the fluid velocity update will suffice to ensure that explicit treatment of the mass-spring system will be stable. Consider the case where the spring is sufficiently stiff such that stability is a concern. The dominant eigenvalue in this case is $\lambda _{\kappa }:= \pm i\sqrt{\kappa /m_{v}}$, where m _v = m + m _a is the nonzero virtual mass that includes the added mass. Figure 2 shows that the BDFk/EXTk stability region for k = 3 includes a portion of the imaginary axis and that this system will be stable when | λ _κ Δt | < 0. 6. For the same timestepper, explicit treatment of advection imposes a stability constraint of the form Δtλ _CFL ≤ 0. 6, where, for the SEM,

$$\displaystyle\begin{array}{rcl} \lambda _{CFL}& \approx & 1.5\max _{i}\left \vert \frac{u_{i}} {\varDelta x_{i}}\right \vert,{}\end{array}$$

(50)

with u _i and Δx _i representing characteristic velocities and grid spacing at gridpoint x _i . (See Fig. 3.5.2 in [25].) If the cylinder is oscillating in the stiff-spring limit with amplitude η ₀, then the velocity scale is $\vert u_{i}\vert \approx \eta _{0}\sqrt{\kappa /m_{v}}$, and we have

$$\displaystyle\begin{array}{rcl} \varDelta t& \leq & \frac{0.6} {\max (1,1.5 \frac{\eta _{0}} {\varDelta x_{i}})}\sqrt{ \frac{m_{v}} {\kappa }}.{}\end{array}$$

(51)

The Courant condition will hold under the assumption that the displacement is larger than the characteristic grid spacing (i.e., η ₀∕Δx _i > 1). However, if the spring is so stiff that translational motion is suppressed (η ₀ < Δx _i ), then the Courant condition due to spring motion will not come into play, and the stiffness associated with a large spring constant could restrict Δt.

Extension of the Green’s function approach to more structural degrees of freedom is straightforward. For each DoF, one generates a solution pair (u _g , p _g ), g = 1, …, N _DoF , each of which leads to a nontrivial force or torque on each and every object. One obtains an N _DoF × N _DoF matrix corresponding to (49) whose solution results in an implicit solution to all the dynamical constraints. For a few DoFs, solution of this system is not a challenge. However, the cost of solving N _DoF systems for the independent Green’s functions can become prohibitive if N _DoF becomes too large. Another extension is to use the Green’s function approach to remove the stiffest contributions to an otherwise explicitly coupled strategy. In particular, for compressible solids the mean compression mode (i.e., the volumetric change) induces long-range accelerations in the fluid. It is straightforward to compute the associated added mass by solving for the Greens function associated with the mean compression mode and to add a multiple of this solution to obtain the requisite force balance, as done in (48)–(49). We are currently investigating this idea, to be discussed in a future article, in the context of coupling Nek5000 with a large nonlinear structures code.

7 Results

Here, we consider several examples that illustrate the techniques introduced in the preceding sections. These methods have been implemented Nek5000, which is an open source spectral element code for fluid, thermal, and combustion simulations that scales to over a million processors [53].

7.1 Temporal-Spatial Accuracy

We illustrate the spatial and temporal convergence of the baseline $\mathbb{P}_{N} - \mathbb{P}_{N}$ and $\mathbb{P}_{N} - \mathbb{P}_{N-2}$ discretizations using the BDFk/EXTk schemes outlined in the text.

We consider the family of exact eigenfunctions for the incompressible Stokes and Navier-Stokes equations derived by Walsh [54], which are generalizations of Taylor-Green vortices in the periodic domain Ω = [0, 2π]². For all integer pairs (m, n) satisfying λ = −(m ² + n ²), families of eigenfunctions can be formed by defining streamfunctions that are linear combinations of the functions

$$\displaystyle\begin{array}{rcl} \cos (mx)\cos (ny),\;\sin (mx)\cos (ny),\;\cos (mx)\sin (ny),\;\sin (mx)\sin (ny).& & {}\\ \end{array}$$

With the eigenfunction u ⁰: = (−ψ _y , ψ _x ) as an initial condition, a solution to the Navier-Stokes equations is u = e ^νλt u ⁰(x). Figure 4 shows the vorticity for a case proposed by Walsh, with ψ = (1∕4)cos(3x)sin(4y) − (1∕5)cos(5y) − (1∕5)sin(5x). The analytical solution is stable only for modest Reynolds numbers. Interesting long-time solutions can be realized, however, by adding a relatively high-speed mean flow $\mathbf{\bar{u}}$, in which case the exact solution is

$$\displaystyle\begin{array}{rcl} \mathbf{\tilde{u}}(\mathbf{x},t)& =& \mathbf{\bar{u}} + e^{\nu \lambda t}\mathbf{u}^{0}[\mathbf{x} -\mathbf{\bar{u}}t],{}\end{array}$$

(52)

where the brackets imply that the argument is modulo 2π in x and y. By varying $\mathbf{\bar{u}}$, one can advect the solution a significant number of characteristic lengths before the eigensolution decays.

Fig. 4

Eddy solution results at Re = 100: (left) vorticity at t = 0 for the initial condition (52), (center) maximum pointwise error at time t = 2π as a function Δt for $\mathbb{P}_{N} - \mathbb{P}_{N}$ with N = 6–10 and (right) for $\mathbb{P}_{N} - \mathbb{P}_{N-2}$ with N = 8–10. The dashed curve is 500Δt ³

We typically run this case with periodic boundary conditions, but that is not as strong of a test as having Dirichlet conditions, which are a well known source of difficulty in time advancement of the incompressible Navier-Stokes equations [27, 34]. In the present case, since we have an exact solution as a function of space and time we can run the Dirichlet case with the solution prescribed on all four sides of the domain. Starting with the initial condition of Fig. 4 (left), we take ν =. 01 and $\mathbf{\bar{u}} = (1,.3)$ and evolve the solution to a final time T = 2π. In that time, the peak amplitude of the perturbation velocity, $\mathbf{u} -\mathbf{\bar{u}}$, decays from 2.0 to 0.46. The mesh consists of a 16×16 array of square spectral elements.

The right two panels in Fig. 4 show the maximum pointwise error in the x-component of the velocity for $\mathbb{P}_{N} - \mathbb{P}_{N}$ (center) and $\mathbb{P}_{N} - \mathbb{P}_{N-2}$ (right) as a function of Δt for several values of N. The general trend is that the error is dominated by spatial error for sufficiently small values of Δt and becomes dominated by temporal error as Δt is increased until the CFL condition is violated, at which point the solution is unstable. Both discretizations demonstrate O(Δt ³) accuracy for the velocity and both show exponential convergence in space. For small Δt, increasing the polynomial order by just 1 yields more than an order-of-magnitude reduction in error until the curve hits the temporal-error threshold. Notice that the relatively poor performance of $\mathbb{P}_{N} - \mathbb{P}_{N-2}$ may be explained by lack of resolution for the pressure. Based on this argument, one would expect the N = 10 error for $\mathbb{P}_{N} - \mathbb{P}_{N-2}$ to be about the same as N = 8 for $\mathbb{P}_{N} - \mathbb{P}_{N}$. Indeed, the N = 10 $\mathbb{P}_{N} - \mathbb{P}_{N-2}$ result is bracketed by N = 8 and 9 for $\mathbb{P}_{N} - \mathbb{P}_{N}$. We note that for this case the resolution of the pressure is a gating issue because its maximum wavenumber is essentially twice that of the velocity, as must be the case given that the pressure is the only term that can cancel the quadratic product involving the velocity eigenfunctions.

We next use the Walsh example to test our ALE formulations. Once again we have inhomogeneous Dirichlet conditions on all of ∂Ω corresponding to $\mathbf{\tilde{u}}$ (52). We prescribe the mesh velocity, and for these tests we also lift the kinematic constraint (4) since there is no need for the boundary to be a material surface. We take an initial configuration (x ⁰, y ⁰) ∈ Ω ⁰ = [0, 7]² and evolve this with the prescribed mesh velocity

$$\displaystyle\begin{array}{rcl} \dot{x}& =& \omega \cos (\omega t)\;\sin (\pi y^{0}/7),{}\end{array}$$

(53)

$$\displaystyle\begin{array}{rcl} \dot{y}& =& \omega \cos (\omega t/2)\;\sin (\pi x^{0}/7)(2y - 1),{}\end{array}$$

(54)

with ω = 5. Configurations of the domain at two time points are shown in Fig. 5, from which one can see that this is not a volume-preserving transformation. Of course it does not need to be because the known boundary data corresponds to a divergence-free field at each point in space and time. The rightmost panel in Fig. 5 shows that third-order accuracy is once again attained, albeit with a larger error than for the nonmoving case of Fig. 4. Somewhat surprisingly, the mesh motion leads to a greater increase in temporal error than the increase in spatial error that one might expect from the deformation of the elements. This increased temporal error results from the rapid mesh motion combined with the relatively high spatial wavenumber of the solution, which gives rise to rapid fluctuations in u _t .

Fig. 5

Eddy solution results at Re = 100 for moving domain case: (left and center) vorticity and domain configurations at two timepoints, (right) maximum pointwise error vs. Δt at time t = 7 for $\mathbb{P}_{N} - \mathbb{P}_{N}$ and $\mathbb{P}_{N} - \mathbb{P}_{N-2}$ with N = 10. The dashed curve is 50000Δt ³

7.2 Constant Pressure Example

The discretization of the convective term including the mesh velocity used in the newly implemented ALE method in the $\mathbb{P}_{N} - \mathbb{P}_{N}$ formulation is identical to the one used in the $\mathbb{P}_{N} - \mathbb{P}_{N-2}$ approach by Ho and Patera, which was extensively validated in [21] and [23]. The accuracy of this scheme was also assessed in [55] using an analytic solution in an expanding mesh setup.

For the 3D case, verification of the $\mathbb{P}_{N} - \mathbb{P}_{N}$ implementation begins with tube setup of Fig. 6. The moving mesh in this case generates a peristaltic pumping that strongly influences the temporal and spatial evolution of the velocity field. The pipe has a base radius R = 1∕2 and length L = 16. The prescribed mesh velocity is

$$\displaystyle\begin{array}{rcl} w_{x}& =& -W\, \frac{x} {R}\cos (kz -\omega t),\;\;\;w_{y}\; =\; -W\, \frac{y} {R}\cos (kz -\omega t),\;\;\;w_{z}\; =\; 0,{}\end{array}$$

(55)

where W: = A∕ω is the velocity amplitude and A : = 0. 1 tanh(0. 2z) tanh(0. 2t) is the amplitude of the displacement. The prescribed wavenumber is k = π∕3, and the frequency is ω = 1. The Reynolds-number is always below 200 so that the flow remains laminar. At the inflow a steady parabolic velocity profile with a maximum axial velocity u _z = 1 at the cylinder center is imposed while at the outflow zero-Neumann boundary conditions are used. At the pipe walls the velocity is set equal to the mesh velocity in order to prevent a flow across the walls. The numerical setup including the mesh is given in the example peris of the Nek5000 package.

Fig. 6

Distribution of velocity magnitude for the $\mathbb{P}_{N} - \mathbb{P}_{N}$ approach on a vertical slice at t = 50

Figure 6 shows the velocity magnitude | u | distribution on an axial slice through the pipe. The highest flow velocities can be observed in regions with larger pipe diameters. The velocity magnitude of the $\mathbb{P}_{N} - \mathbb{P}_{N}$ ALE formulation compared with the $\mathbb{P}_{N} - \mathbb{P}_{N-2}$ results at t = 50 in Fig. 7. The dashed line and the circle markers represent the averaged axial velocity magnitude versus the channel length, while the solid line and the square markers indicate the velocity magnitude along the centerline (marked by the dashed line in Fig. 6). The mean and the instantaneous velocity magnitudes show excellent agreement between the two formulations.

Fig. 7

Instantaneous and averaged axial velocity for $\mathbb{P}_{N} - \mathbb{P}_{N}$ and $\mathbb{P}_{N} - \mathbb{P}_{N-2}$ at t = 50

The implementation of the ALE approach in the temperature equation is verified by simulating in the same setup using non-isothermal conditions at the inflow. Initial and boundary conditions for the velocity field and mesh movement are identical to the preceding flow case. The temperature at the walls is fixed to T/Tref = 1, where Tref = 300 K. At the inflow a parabolic temperature profile is imposed with a maximum temperature of T/Tref = 1.125 in the pipe center, while zero-Neumann boundary conditions are used at the outflow boundary. A homogeneous N ₂∕O ₂ mixture ($Y _{O_{2}} = 0.21$, $Y _{N_{2}} = 0.79$) flows into the channel at a constant pressure of 1 atm. The temperature difference between pipe wall and inflow is chosen low enough to limit its influence on the flow field, because in the $\mathbb{P}_{N} - \mathbb{P}_{N-2}$ formulation the incompressible Navier-Stokes equations are solved, whereas the $\mathbb{P}_{N} - \mathbb{P}_{N}$ approach is based on the low-Mach-number formulation.

The computed temperature fields are shown at t = 8 in Fig. 8 (left). The decreasing temperatures in the flow direction are due to the cooler pipe walls. The local temperature peaks in the thicker pipe segments are due to the larger distance from the cylinder wall. The temperature distributions show excellent agreement using the two formulations, as also seen in the instantaneous centerline profiles of Fig. 8 (right).

Fig. 8

Comparison of temperature for the $\mathbb{P}_{N} - \mathbb{P}_{N-2}$ and $\mathbb{P}_{N} - \mathbb{P}_{N}$ ALE formulations at t = 8: (left) centerplane distribution at t = 8 and (right) instantaneous centerline temperatures

7.3 Varying Pressure Examples

The implementation of the variable thermodynamic pressure is validated by comparison with a zero-dimensional CHEMKIN [56] simulation of isentropic compression. A two-dimensional setup with a constant width of 75 mm and an initial height of 90 mm is compressed until a height of 15 mm is reached, resulting in a compression ratio of 6. The piston speed is 200 rpm. Homogeneous conditions for temperature (T = 819.45 K), pressure (p = 1 atm), and composition (YN2 = 0.7288, YO2 = 0.1937 and YCH4 = 0.0775) are used at BDC. Zero-velocity boundary conditions are employed at the liner and the cylinder head, and the piston velocity is imposed at the piston. Zero-flux conditions are imposed for the temperature and species boundaries at all walls. For the homogeneous adiabatic CHEMKIN calculation the same geometry and initial conditions are considered. In both cases, the chemical reactions are calculated based on a reduced mechanism for CH4 combustion with 21 species and 87 reactions.

In Fig. 9, the computed temperature and pressure time-histories are compared with the 0-D CHEMKIN calculation. At time t = 0 the piston is at BDC and at t = 4 at TDC. The continuously increasing temperature during compression results in autoignition at a nondimensional time t = 3. At TDC the temperature and pressure are 2731 K and 20 atm, respectively. The plots show nearly identical evolutions of the temperature and pressure profiles. The minimal offset in the autoignition timing lies within the uncertainty of numerical settings such as the chosen timesteps or imposed tolerances.

Fig. 9

Comparison of the temperature (left) and pressure (right) evolution during compression between CHEMKIN and Nek5000

We next consider an example of fully turbulent compression from the direct numerical simulations (DNS) presented in [2, 4]. The initial condition at bottom dead center (BDC) (180^o CA) were derived by a precursor DNS of the intake stroke simulating the mixing of a unburnt λ = 2 H2/air mixture at 500 K in the intake channel with a burnt λ = 2 H2/air mixture at 900 K in the cylinder. During compression the wall temperature is fixed to 500 K, and the Reynolds number based on cylinder diameter and maximum piston velocity is Re = 2, 927.The temperature rise resulting from compression is evident in Fig. 10, which shows the temperature distributions at 180^o, 225^o, and 270^oCA. The relatively cool region at the bottom of the cylinder results from the piston scouring cold fluid from the walls and the relatively hot regions in the upper part of the cylinder at 180^oCA are related to hot EGR gases entrained into the core of the ring vortex generated during the intake stroke. As demonstrated in [2, 4], the final temperature distribution is not strongly dependent on the initial thermal distribution; one obtains essentially the same distribution at 270^oCA even when the initial distribution at 180^oCA is uniform. A detailed analysis of the flow and temperature field evolutions during compression can be found in [3].

Fig. 10

Centerplane temperature distributions during a compression stroke for an engine-like flow configuration at 180^o, 225^o, and 270^oCA

7.4 Dynamic Response

We illustrate the implicit fluid–structure interaction formulation by considering the case of flow past a cylinder of radius R ₀ and mass m = ρ _c πR ₀ ² that is allowed to oscillate in the y-direction subject to a spring constant κ = (2πf _b )². Here, the density of the cylinder is ρ _c ; the characteristic length scale is the cylinder diameter D ₀ = 2R ₀; and the time scale is the convective time, τ: = D ₀∕U ₀, where U ₀ is the inflow velocity. We assume the fluid density ρ = 1 and define the Reynolds number Re = U ₀ D ₀∕ν ₀. We consider Re = 100, f _b = 0. 167, and ρ _c = 0 and 10. Several authors have studied the ρ _c = 10 case under these conditions and found the displacement amplitude to be η _max in interval 0.49 to 0.503 [52, 57, 58].

The cylinder is centered at (x, y) = (0, 0), and the domain consists of 218 spectral elements of order N = 14 with inflow conditions (u, v) = (1, 0) at x = −13. 75, homogeneous Neumann (outflow) conditions at x = 38. 75, and periodic boundary conditions at y = ±25. The timestep is Δt =. 005. A close-up of the mesh and the vorticity at the peak vertical displacement is shown in Fig. 11a. Time traces of the displacement for ρ _c = 0 and 10 are shown in Fig. 11b. These cases were started with an initial condition corresponding to a fully developed von Karman street at Re = 100. The asymptotic amplitude and frequencies were found by a nonlinear least-squares fit (over a longer time than shown in the figure) to be A =. 0242 and ω = 1. 075 for ρ _c = 0 and A =. 505 and ω = 1. 040 for ρ _c = 10. For these cases, the added mass from (50) is m _a ≈ 1. 234 times the displaced mass, which is slightly greater than the unit value predicted by potential theory for flow past a cylinder. This increase is explained by the fact that the unsteady Stokes subproblem, which includes the Δt time constant, entrains additional mass due to viscous effects. With a reduction in Δt and viscosity, (47) with (50) predicts the potential flow result to within five significant digits.

Fig. 11

Sprung cylinder example: (a) vorticity and part of the domain showing the spectral element boundaries at peak displacement; (b) amplitude and frequency as a function of cylinder mass

8 Conclusions

We have described recent advances in the SEM that target efficient simulation of turbulent flows in moving domains. A new ALE-based low-Mach formulation has been introduced that allows simulation of turbulence in closed domains such as IC engine cylinders. Several examples attest to the fidelity of this approach when compared with the baseline $\mathbb{P}_{N} - \mathbb{P}_{N-2}$ formulation [21, 23, 24], with analytical solutions in two dimensions, and with the zero-dimensional results of CHEMKIN [56]. Strategies for efficient mesh motion have been described, including the use of variable-coefficient Laplace solvers with projection in time to yield low-cost extension of boundary data into the domain interiors with controlled mesh quality. A decoupled, iteration-free, implicit solution strategy for fluid–structure systems with a few degrees of freedom has also been presented that exploits the underlying linearity of the governing processes to allow superpositions of solutions. These developments set the stage for several forthcoming turbulence simulations of relevance to the transportation and energy sectors and for future FSI simulations in which the structural code is essentially a black-box routine.