Using Mathematical Modeling and Prior Knowledge for QbD in Freeze-Drying Processes

Abstract

This chapter deals with the use of mathematical modeling to get quality-by-design in a freeze-drying process. The target is to identify the design space of the process, i.e., the values of the operating conditions that allow maintaining product temperature below the limit value during primary and secondary drying stages, with a sublimation rate compatible with the capacity of the condenser, avoiding choking flow in the duct connecting the chamber to the condenser, minimizing drying duration, and getting the target value of residual moisture in the final product. Mathematical models of product evolution in the vials during the whole process, and of the freeze-drying equipment, are presented, and the experimental investigation required to get the values of model parameters is discussed, pointing out that model accuracy and level of parameters uncertainty influence the quality of the results. Then, the use of mathematical models to calculate the design space for primary and secondary drying stages is presented, pointing out how the design space can be used to optimize the cycle and to analyze the effect of any deviation of process variables from their set-point values.

CFD:

Computational fluid dynamics

DMSC:

Direct Simulation Monte Carlo

PRT:

Pressure rise test

A _v :

Cross section area of the vial, m²

a :

Specific surface of the dried product, m² $\text{kg}_{\text{dried product}}^{-\text{1}}$

C _s :

Residual moisture, kg_water $\text{kg}_{\text{dried product}}^{-\text{1}}$

C _s,0 :

Residual moisture at the beginning of secondary drying, kg_water $\text{kg}_{\text{dried product}}^{-\text{1}}$

C _s,eq :

Weight fraction of sorbed water in the solid that would be in local equilibrium with the partial pressure of water in the drying chamber, kg_water $\text{kg}_{\text{dried product}}^{-\text{1}}$

C _s,t :

Target value of the residual moisture in the product, kg_water $\text{kg}_{\text{dried product}}^{-\text{1}}$

C ₁ :

Parameter used in Eq. (23.8), W K⁻¹ m⁻²

C ₂ :

Parameter used in Eq. (23.8), W K⁻¹m⁻² Pa⁻¹

C ₃ :

Parameter used in Eq. (23.8), Pa⁻¹

c _p,liquid :

Specific heat of the liquid, J kg⁻¹ K⁻¹

c _p,p :

Specific heat of the product, J kg⁻¹ K⁻¹

D :

Duct diameter, m

E _a,d :

Activation energy of the desorption reaction, J mol⁻¹

ΔH _d :

Heat of desorption, J $\text{kg}_{\text{water}}^{-\text{1}}$

ΔH _s :

Heat of sublimation, J $\text{kg}_{\text{water}}^{-\text{1}}$

J _q :

Heat flux to the product, W m⁻²

J _w :

Mass flux, kg s⁻¹ m⁻²

K :

Parameter used in Eq. (23.19)

K _v :

Overall heat transfer coefficient between the heating fluid and the product at the vial bottom, W m⁻² K⁻¹

k _d :

Kinetic constant of the desorption rate, $\text{kg}_{\text{dried product}}^{-\text{1}}$ s⁻¹ m⁻²

k _d,0 :

Pre-exponential factor of the kinetic constant of the desorption rate, $\text{kg}_{\text{dried product}}^{-\text{1}}$ s⁻¹ m⁻²

L :

Duct length, m

L ₀ :

Product thickness after freezing, m

L _dried :

Thickness of the dried product, m

L _frozen :

Thickness of the frozen product, m

M _w :

Water molar mass, kg mol⁻¹

m :

Mass, kg

m _dried :

Mass of dried product, kg

P _c :

Chamber pressure, Pa

P ₁ :

Parameter used in Eq. (23.10), s⁻¹

P ₂ :

Parameter used in Eq. (23.10), m⁻¹

p _w,c :

Water vapor partial pressure in the drying chamber, Pa

p _w,i :

Water vapor partial pressure at the interface of sublimation, Pa

R _p :

Resistance of the dried product to vapor flow, m s⁻¹

R _p,0 :

Parameter used in Eq. (23.10), m s⁻¹

R :

Ideal gas constant, J K⁻¹ mol⁻¹

r _d :

Water desorption rate, kg_water $\text{kg}_{\text{dried product}}^{-\text{1}}$ s⁻¹

r _d,PRT :

Water desorption rate measured through the test of pressure rise,kg_water $\text{kg}_{\text{dried product}}^{-\text{1}}$ s⁻¹

T :

Temperature, K

T _B :

Product temperature at the vial bottom, K

T _c :

Temperature of the vapor in the drying chamber, K

T _fluid :

Heating fluid temperature, K

T _g :

Glass transition temperature, K

T _g,s :

Sucrose glass transition temperature, K

T _g,w :

Ice glass transition temperature, K

T _i :

Product temperature at the interface of sublimation, K

T _p :

Product temperature, K

t :

Time, s

t _0,PRT :

Initial time of the PRT, s

t _d :

Duration of secondary drying, h

V _c :

Free volume of the chamber, m³

V _p :

Volume of the product, m³

λ _frozen :

Heat conductivity of frozen product, W m⁻¹ K⁻¹

λ _liquid :

Heat conductivity of liquid product, W m⁻¹ K⁻¹

ρ _dried :

Apparent density of the dried product, kg m⁻³

ρ _frozen :

Density of the frozen product, kg m⁻³

ρ _liquid :

Density of the liquid product, kg m⁻³

23.1 Introduction

Freeze-drying is widely used in pharmaceuticals manufacturing to provide long-term stability to formulations containing an active pharmaceutical ingredient. At first, the aqueous solution containing the drug and the excipients is put in vials, loaded onto the shelves of the drying chamber of the freeze-dryer. Then, product temperature is decreased by means of a cold fluid flowing through the shelves: part of the water (“free water”) crystallizes, and part (“bound water”) remains unfrozen. Ice sublimation (primary drying) is then obtained by decreasing the chamber pressure: during this step the temperature of the fluid flowing through the shelves is increased, and the fluid is used to supply heat to the product as the sublimation is an endothermic process. As a result of ice sublimation, a porous cake is obtained: water vapor flows through this cake, moving from the interface of sublimation (the boundary between the frozen product and the cake) to the drying chamber, and then to a condenser, where it sublimates over cold surfaces. Finally, the target value of residual moisture in the product is obtained by further increasing product temperature in order to desorb the bound water (secondary drying).

The values of the operating conditions of the freeze-drying process, i.e., the temperature of the heating fluid (T _fluid) and the pressure in the drying chamber (P _c ) during primary and secondary drying , as well as the duration of both drying steps, can significantly affect final product quality. In particular, the following issues have to be taken into account:

• i. Product temperature has to remain below a limit value that is a characteristic of the formulation being processed, during both primary and secondary drying stages. This is required to avoid product denaturation, melting (in case of crystalline products), or collapse of the dried cake (in case of amorphous products). Cake collapse can be responsible for blockage of cake pores, thus increasing cake resistance to vapor flow, and retarding the end of primary drying due to the lower sublimation rate. Moreover, a collapsed cake can retain a higher amount of water in the final product, the reconstitution time can increase, and the physical appearance is unattractive (Bellows and King 1972; Tsourouflis et al. 1976; Adams and Irons 1993; Pikal 1994; Franks 1998; Wang et al. 2004).

• ii. The sublimation rate has to be compatible with the condenser capacity, and choking flow has to be avoided in the duct connecting the chamber to the condenser (Searles 2004; Nail and Searles 2008; Patel et al. 2010).

• iii. A target value of residual moisture has to be obtained in the final product in order to maximize product stability.

• iv. The duration of the whole process has to be minimized in order to maximize plant productivity.

Finally, it must be evidenced that the final quality of the product may be also related to the design of the equipment: the chamber design (and in particular shelf size and interdistance, shelf-wall clearance, duct size, and location) may affect the intrabatch variability. Moreover, duct and valve type and size and condenser design may affect pressure drop and, thus, they determine the minimum controllable pressure in the chamber and the quality of pressure control and, in the worst case, they are responsible for choked flow and lose of pressure control.

According to the “Guidance for Industry PAT—A Framework for Innovative Pharmaceutical Development, Manufacturing, and Quality Assurance” issued by FDA in September 2004, a true quality by design manufacturing principle, rather than the classical quality-by-testing approach, should be implemented to have safe, effective, and affordable medicines. By this way product quality is built-in, or is by design, and it is no longer tested in final products.

This chapter is focused on obtaining quality-by-design in a pharmaceuticals freeze-drying process. To this purpose, it is necessary to determine the design space of the process. According to “ICH Q8 Pharmaceutical Development Guideline” (2009), a design space is the multidimensional combination of input variables and process parameters that have been demonstrated to provide assurance of quality. Generally, the empirical approach is used to determine the design space: various tests are carried out using different values of T _fluid and P _c , and final product properties are measured experimentally (Chang and Fisher 1995; Nail and Searles 2008; Hardwick et al. 2008). Obviously, this approach is expensive and time consuming, even if the number of tests can be reduced by using the experimental design technique (Box et al. 1981) and the multi-criteria decision making method (De Boer et al. 1988, 1991; Baldi et al. 1994). Moreover, the experimental approach does not guarantee to obtain the optimal cycle, and in case the cycle is determined in the lab-scale freeze-dryer, the scale-up to the industrial-scale freeze-dryer is required, and this is a challenging and complex task.

Mathematical modeling can be effectively used to determine the design space for a pharmaceuticals freeze-drying process as it allows studying in silico the evolution of the product (i.e., how the temperature, the residual amount of ice, and the sublimation flux change during time) as a function of the operating conditions. Clearly, a suitable model has to be used to perform the calculations. Primarily, the mathematical model has to be accurate, i.e., it has to account for all the heat and mass transfer phenomena occurring in the product, and a deep mechanistic understanding is required for this purpose. Secondly, the mathematical model has to involve few parameters, whose values can be easily and accurately determined by means of theoretical calculations or (few) experimental investigations: the accuracy of complex and very detailed models can be impaired by the uncertainty on the value of the parameters. Finally, the time required by the calculations can be an important concern.

The structure of the chapter is the following: at first, mathematical modeling of product evolution in the vial (during freezing , primary and secondary drying) and of freeze-drying equipment is addressed; second, the use of mathematical models to calculate the design space for primary and secondary drying is discussed, pointing out how the design space can be used to optimize the cycle, as well as to analyze the effect of any deviation of process variables from their set-point values.

23.2 Mathematical Modeling

23.2.1 Freezing

The ice crystals morphology (mean size, shape, and size distribution) obtained in the freezing step can significantly influence both primary and secondary drying stages. In fact, in case small-size ice crystals are obtained, then the resistance of the cake to vapor flow will be increased (as small cake pores are obtained from ice sublimation), thus decreasing the sublimation rate , and increasing the duration of primary drying . The larger cake-specific surface obtained in this case can be beneficial in the secondary drying stage, when water desorption takes place. As a general trend, large ice crystals are obtained from slow cooling rates, while faster cooling results into smaller and more numerous ice crystals (Kochs et al. 1991). Kochs et al. (1993) mentioned that nucleation temperature has no great impact on a macroscopic sample freezing, which was controlled mainly by cooling conditions. In case of small scale frozen systems, like pharmaceutical freeze-drying in vials, many authors consider the nucleation temperature as a key factor: the undercooling degree of the solution determines the number of nuclei and, thus significantly influences the ice crystals size distribution (Searles et al. 2001a, b). Nakagawa et al. (2007) proposed a simple model for the freezing process to calculate the temperature profile in the vial during the freezing stage. They used a commercial finite element code in two-dimensional axial-symmetric space to take into account the actual vial geometry. In the cooling step, the well-known conductive heat equation is solved:

$${{\rho }_{\text{liquid}}}{{c}_{p,\text{liquid}}}\frac{\partial T}{\partial t}=\nabla \left( {{\lambda }_{\text{liquid}}}\nabla T \right).$$

(23.1)

Nakagawa et al. (2007) assume that nucleation starts at the vial bottom at a given temperature (which is a parameter of the model); the freezing model is based on Eq. (23.1), where c _p,liquid is replaced by an apparent heat capacity (Lunardini 1981) that takes into account the coexistence of liquid and ice, and the heat generation due to ice nucleation and ice crystallization is added on the right-hand side. From calculated experimental temperatures profiles, a semi-empirical model was set up to estimate the mean ice crystal size and, consequently, the water vapor dried layer permeability (using standard diffusion theory). It is assumed that the ice crystals mean size is proportional to the freezing rate and to the temperature gradient in the frozen layer (Bomben and King 1982; Reid 1984; Kochs et al. 1991; Kurz and Fisher 1992; Woinet et al. 1998). The model was validated against experiments carried out using mannitol and BSA-based formulations. The results obtained by means of a numerical simulation confirmed that nucleation temperature is the key parameter that determines the ice morphology, and that an increase of the cooling rate leads to smaller ice crystal sizes (Nakagawa et al. 2007).

23.2.2 Primary Drying

During the primary drying stage ice sublimation occurs: water vapor flows from the interface of sublimation to the drying chamber, going through the dried layer. As primary drying goes on, the interface of sublimation moves from the top surface of the product to the bottom of the vial.

Detailed multidimensional model were proposed in the past to study in silico the process. A bidimensional axial-symmetric model was first proposed by Tang et al. (1986) to investigate the freeze-drying of pharmaceutical aqueous solutions in vials, but no results were shown. This model was also proposed by Liapis and Bruttini (1995) to demonstrate that radial gradients of temperature exist when the radiative flux at the vial side is taken into account, and that the sublimation interface is always curved downward at the edges of the vial. A finite-element formulation was used by Mascarenhas et al. (1997) and by Lombraña et al. (1997) to solve the bidimensional model: an arbitrary Lagrangian–Eulerian description is proposed, treating the finite-element mesh as a reference frame that may be moving with an arbitrary velocity. According to Sheehan and Liapis (1998), this formulation has major problems related to the way the problem is treated from a numerical point of view. In fact, it fails to describe the dynamic behavior of the primary drying stage in a vial when the moving interface does not extend along the whole length of the diameter of the vial; moreover, it cannot describe properly the dynamic behavior of the geometric shape and position of the sublimation interface because the water vapor mass flux is considered to be time invariant when the position of the moving interface is located between mesh points of the grid. Thus, a different numerical method, based on the orthogonal collocations, was proposed by Sheehan and Liapis (1998): they evidenced that when there is no heat input from the vial sides, as in the majority of the vials of the batch, the geometry of the moving interface is flat. Only in case vials are heated by radiation from chamber walls (i.e., for vials at the edges of the shelf), a curvilinear shape is obtained for the sublimation interface, but, in any case, the difference between the position of the interface at the center and at the side of the vial is less than 1 % of the total thickness of the product. These results were confirmed also by Velardi and Barresi (2011), who evidenced that even in case of radiation from chamber walls, radial gradients of temperature are very small. This is in agreement with the results given by Pikal (1985), where it was found with a series of experiments that the temperature at the bottom center of the vial was equal to the temperature of the bottom edge, within the uncertainty of the temperature measurement (0.5 °C). Thus, taking also into account that the numerical solution of a multidimensional model can be highly time consuming, and that they involve many parameters whose values are very often unknown, and/or could be estimated only with high uncertainty, various monodimensional models were proposed in the literature (see, among the others, Pikal 1985; Millman et al. 1985; Sadikoglu and Liapis 1997): they are based on the heat and mass balance equations for the frozen and the dried product, neglecting radial gradients of temperature and composition, as well as the effect of heat transfer in the sidewall of the vial, although it has been argued that this could play an important role as energy can be transferred to the product from the vial wall as a consequence of conduction through the glass (Ybema et al. 1995; Brülls and Rasmuson 2002). Recently, a monodimensional model including the energy balance for the vial glass has been proposed by Velardi and Barresi (2008). Also in case of monodimensional models, it is possible to vary the complexity of the model itself by neglecting some heat and mass transfer phenomena (that not significantly affect the dynamics of the process), thus obtaining simplified models that can be really useful as they involve few parameters that can be measured experimentally.

The product in a vial is heated from the fluid flowing through the shelf, and the heat flux is proportional to a driving force given by the difference between the temperature of the fluid and that of the product at the vial bottom:

$${{J}_{q}}={{K}_{v}}\left( {{T}_{\text{fluid}}}-{{T}_{B}} \right).$$

(23.2)

The sublimation flux from the sublimation interface is assumed to be proportional to a driving force given by the difference between the water vapor partial pressure at the interface and in the drying chamber:

$${{J}_{w}}=\frac{1}{{{R}_{p}}}\left( {{p}_{w,i}}-{{p}_{w,c}} \right),$$

(23.3)

where the water vapor partial pressure at the sublimation interface is a well-known function of product temperature at that position (Goff and Gratch 1946), while water vapor partial pressure in the drying chamber can be assumed to be equal to total chamber pressure . Thus, a simple model of the process (Velardi and Barresi 2008) consists of the heat balance at the interface of sublimation and the mass balance for the frozen layer:

$${{J}_{q}}=\Delta {{H}_{s}}{{J}_{w}}$$

(23.4)

$$\frac{d{{L}_{\text{frozen}}}}{dt}=-\frac{1}{{{\rho }_{\text{frozen}}}-{{\rho }_{\text{dried}}}}{{J}_{w}}.$$

(23.5)

Heat accumulation in the frozen layer is assumed to be negligible and, thus, heat flux is constant in the frozen layer. This allows to determine the relationship between T _i (and, thus, p _w,i ) and T _B :

$${{T}_{B}}={{T}_{\text{fluid}}}-\frac{1}{{{K}_{v}}}{{\left( \frac{1}{{{K}_{v}}}+\frac{{{L}_{\text{frozen}}}}{{{\lambda }_{\text{frozen}}}} \right)}^{-1}}\left( {{T}_{\text{fluid}}}-{{T}_{i}} \right).$$

(23.6)

In order to calculate the evolution of product temperature and frozen layer thickness vs. time, it is required to know the values of the operating conditions (T _fluid and P _c ), of some physical parameters (ρ _frozen, ρ _dried, λ _frozen, ΔH _s ), and of the two parameters of the model, namely, the overall heat transfer coefficient between the heating fluid and the product at the vial bottom (K _v ), and the total resistance (including the contribution of dried layer, stopper, and chamber) to the vapor flow (R _p ).

A simple experiment can be carried out to determine the value of K _v for the various vials of the batch (Pikal et al. 1984; Pikal 2000; Pisano et al. 2011a). It is required to fill the vials with water, and to measure the weight loss Δm after ice sublimation for a time interval Δt:

$$K_{v}^{{}}=\frac{\Delta m\Delta H_{s}^{{}}}{{{A}_{v}}\int\limits_{0}^{\Delta t}{\left( T_{\text{fluid}}^{{}}-T_{B}^{{}} \right)dt}}.$$

(23.7)

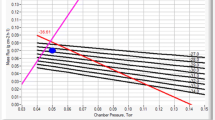
In order to use Eq. (23.7), ice temperature at the vial bottom has to be measured: wired thermocouples can be used in lab-scale and pilot-scale freeze-dryers, while wireless sensors are much more suitable in industrial-scale units (Vallan et al. 2005; Corbellini et al. 2010). An example of the results that can be obtained is shown in Fig. 23.1: it appears that the value of the heat transfer coefficient K _v is not the same for all the vials of the batch. This is due to the fact that Eq. (23.2) assumes that the product in the vial is heated only by the fluid flowing through the shelf, but, actually, it can be heated also by radiation from the chamber walls and the upper shelf, and by conduction from metal frames, in case they are used to load/unload the batch. As a consequence, the value of K _v for the vials of the first raw is higher than that obtained for vials in the central part of the shelf due to the contribution of radiation from chamber walls. Thus, it is possible to classify the vials of a batch in various groups, depending on their position over the shelf (Table 23.1). The gravimetric test has to be repeated at least at three different values of chamber pressure, as for a given vial-freeze-dryer system P _c significantly affects the value of K _v :

Table 23.1 Characteristics of the various groups of vials considered in the case study

Fig. 23.1

Values of the heat transfer coefficient K _v for the vials of the batch (tubing vials, internal diameter = 14.25 mm, T _fluid = − 15 °C, P _c  = 10 Pa). Values obtained for half of the batch are shown

$${{K}_{v}}={{C}_{1}}+\frac{{{C}_{2}}{{P}_{c}}}{1+{{C}_{3}}{{P}_{c}}}.$$

(23.8)

Figure 23.2 shows an example of results obtained by measuring experimentally K _v for the various group of vials identified in Table 23.1 at different values of P _c .

Fig. 23.2

Effect of chamber pressure on the values of K _v for the various groups of vials (tubing vials, internal diameter = 14.25 mm). Symbols refer to the experimentally measured values; lines correspond to the values calculated using Eq. (23.8)

The heat transfer coefficient K _v can also be determined using the measurement of the sublimation flux J _w obtained with the Tunable Diode Laser Absorption Spectroscopy (TDLAS) (Kessler et al. 2006; Gieseler et al. 2007; Kuu et al. 2009):

$$K_{v}^{{}}=\frac{J_{w}^{{}}\Delta t\Delta H_{s}^{{}}}{{{A}_{v}}\int\limits_{0}^{\Delta t}{\left( T_{\text{fluid}}^{{}}-T_{B}^{{}} \right)dt}}.$$

(23.9)

In this case a “mean” value of K _v is obtained, as it is assumed that the value of this parameter is the same for all the vials of the batch (this value is an approximation of the heat transfer coefficient of central vials, as they represent the majority of the batch). Similarly, a “mean” value of K _v is obtained also when using one of the algorithms proposed to monitor the process using the pressure rise test (PRT): the valve in the duct connecting the drying chamber to the condenser is closed for a short time interval (e.g., 30 s), and various variables (temperature and residual ice content of the product, and model parameters K _v and R _p ) are determined looking for the best fit between the measured and the calculated values of pressure rise (Milton et al. 1997; Liapis and Sadikoglu 1998; Chouvenc et al. 2004; Velardi et al. 2008; Fissore et al. 2011a).

The parameter R _p depends on the freezing protocol, on the type of product and of freeze-dryer, and on the thickness of the cake according to the following equation:

$${{R}_{p}}={{R}_{p,0}}+\frac{{{P}_{1}}{{L}_{\text{dried}}}}{1+{{P}_{2}}{{L}_{\text{dried}}}}.$$

(23.10)

The parameters R _p,0, P ₁, and P ₂ have to be determined by means of experiments, looking for the best-fit between the reference curve and the measured values of R _p vs. L _dried. The PRT can be used for this purpose, as well as the TDLAS sensor using the following equation:

$${{R}_{p}}=\frac{{{p}_{w,i}}-{{p}_{w,c}}}{{{J}_{w}}}.$$

(23.11)

A weighing device placed in the drying chamber can be used to measure the sublimation flux and, in case also, product temperature is measured to estimate R _p through Eq. (23.11). The Lyobalance (Vallan 2007; Barresi and Fissore 2011; Fissore et al. 2012) can be effectively used for this purpose as the weighed vials are frozen with all the other vials of the batch, they remain almost always in contact with the shelf (they are lifted just during the measurement), and the geometrical characteristics of the weighed vials are the same as the rest of the batch. Figure 23.3 shows the values of R _p vs. L _dried in case of the freeze-drying of a 5 % by weight mannitol aqueous solution: a good agreement is obtained when comparing the values obtained using Lyobalance and the PRT.

Fig. 23.3

Comparison between the value of R _p vs. L _dried measured by Lyobalance (solid line), estimated by the pressure rise test technique (symbol), and the value calculated using Eq. (23.10) (dashed line) in case of the freeze-drying of a 5 % by weight mannitol solution (T _fluid = − 22 °C, P _c  = 10 Pa) processed into ISO 8362-1 2R tubing vials (internal diameter = 14.25 mm), filled with 1.5 mL of solution. The internal structure of the solid is also shown (Scanning Electron Microscope images)

23.2.3 Secondary Drying

The secondary drying stage involves the removal of the bound (unfrozen) water. For an amorphous solid, the water removal rate per unit of mass can be dependent on:

• Water molecular diffusion in the glassy solid from the interior of the solid to the surface;

• Evaporation at the solid–vapor interface;

• Water vapor transport through the porous dried cake;

• Water vapor transport from the headspace in the vial to the condenser.

Generally, water desorption from the solid is assumed to be the rate-determining step, as it has been evidenced by extensive investigations carried out with crystalline (mannitol) and amorphous (moxalactam di-sodium and povidone) products (Pikal et al. 1980), and various equations were proposed to model the dependence of r _d on C _s , assuming that the desorption rate is proportional either to residual moisture :

$${{r}_{d}}=a{{k}_{d}}{{C}_{s}}$$

(23.12)

or to the difference between residual moisture and the equilibrium value:

$${{r}_{d}}=a{{k}_{d}}\left( {{C}_{s}}-{{C}_{s,eq}} \right).$$

(23.13)

Equation (23.12) has been demonstrated to be able to describe the process adequately (Sadikoglu and Liapis 1997): this has a very important practical advantage when compared with Eq. (23.13), because its expression does not require detailed information about the structure of the porous matrix of the dried layer of the material being freeze-dried. In fact, in order to use Eq. (23.13) one would have to construct an expression for the equilibrium concentration C _s,eq , and this requires tedious and time consuming adsorption–desorption equilibrium experiments (Millman et al. 1985; Liapis and Bruttini 1994; Liapis et al. 1996)

A detailed multidimensional model of the secondary drying was proposed by Liapis and Bruttini (1995): results evidenced that radial gradients of temperature and concentration are very small, even in those vials placed at the edges of the shelf where lateral heating, due to radiation from the chamber walls, is significant (Gan et al. 2004, 2005). A detailed monodimensional model was proposed by Sadikoglu and Liapis (1997), even if also axial gradients of temperature and concentration were shown to be small (Gan et al. 2004, 2005). Thus, a lumped model can be effective to describe the evolution of product temperature and of the amount of residual moisture during secondary drying. The energy and mass balances for the product in the vial are given by the following equations:

$${{\rho }_{p}}{{c}_{p,p}}{{V}_{p}}\frac{d{{T}_{p}}}{dt}={{K}_{v}}{{A}_{v}}\left( {{T}_{\text{fluid}}}-{{T}_{p}} \right)+{{V}_{p}}{{\rho }_{p}}{{r}_{d}}\Delta {{H}_{d}}$$

(23.14)

$$\frac{d{{C}_{s}}}{dt}=-{{r}_{d}}$$

(23.15)

where r _d is given by Eq. (23.12). The kinetic constant k _d is dependent on product temperature, e.g., according to an Arrhenius-type equation (Pisano et al. 2012):

$${{k}_{d}}={{k}_{d,0}}\exp \left( -\frac{{{E}_{a,d}}}{\text{R}{{T}_{p}}} \right).$$

(23.16)

The effect of chamber pressure on desorption rate is assumed to be negligible, at least in case P _c is lower than 20 Pa as reported by Pikal et al. (1980) and Pikal (2006).

In order to use Eqs. (23.14) and (23.15) to calculate the evolution of the product during secondary drying, it is required to determine the value of the kinetic constant k _d , or better the Arrhenius parameters k _d,0 and E _a,d , and to check how r _d depends on C _s . A soft sensor, recently proposed to monitor secondary drying (Fissore et al. 2011b, c), can be effectively used to this purpose. It is based on the measurement of the desorption rate obtained from the pressure rise curve measured during the PRT:

$${{r}_{d,PRT}}=100\cdot \frac{\frac{{{M}_{w}}{{V}_{c}}}{R{{T}_{c}}}{{\left. \frac{d{{P}_{c}}}{dt} \right|}_{t={{t}_{0,PRT}}}}}{{{m}_{\text{dried}}}}$$

(23.17)

and on a mathematical model describing the water desorption from the product (Eqs. (23.12)–(23.15)). The value of the residual moisture in the product at the beginning of secondary drying (C _s,0) and of the kinetic constant k _d are obtained looking for the best fit between the measured and the calculated values of desorption rate. In case the test is repeated during secondary drying, it is possible to determine the evolution of C _s vs. time. By this way it is possible to determine also how r _d depends on C _s . Finally, in case the test is repeated using different values of T _fluid, it is possible to calculate the Arrhenius parameters (looking for the best fit between the measured values of k _d and values calculated using Eq. (23.16)).

Figure 23.4 (graph a) shows the dependence of r _d on C _s for different set-points of the heating fluid temperature in case of drying of 5 % w/w aqueous solutions of mannitol, thus proving that a linear equation like Eq. (23.12) is suitable to model this dependence. The desorption rate is measured using the PRT, and the soft-sensor designed by Fissore et al. (2010, 2011b) to monitor secondary drying is used to determine k _d . The Arrhenius plot (not shown) points out that Eq. (23.16) is able to model the dependence of k _d on T _p . In this case k _d,0 is equal to 54720 s⁻¹, while the activation energy (E _a,d ) is equal to 5920 J mol⁻¹. Figure 23.4 (graphs b and c) compares the values of residual moisture in the product with the values obtained extracting vials from the chamber and using Karl Fisher titration, as well as the calculated product temperature with the values obtained through a T-type thermocouple inserted in some vials: the agreement between measured and calculated values is particularly good and satisfactory.

Fig. 23.4

Graph A: Desorption rate vs. residual moisture for different temperatures of the heating fluid (solid line, black circles: T _fluid luid circdashed line, black squares: T _fluid luid squaP _c  luid sq. Graphs B and C: Comparison between calculated (lines) and measured (symbols) values of residual moisture (graph B), and product temperature (graph C) when T _fluid luidn producP _c  luidn p Data refer to a 5 % by weight mannitol aqueous solution processed into ISO 8362-1 2R tubing vials (internal diameter = 14.25 mm), filled with 1.5 mL of solution; primary drying was carried out at T _fluid luid solution;P _c  lui Pa

23.2.4 Freeze-Dryer Equipment Modeling

As anticipated in the introduction, the final product quality may be related to the design of the equipment and, in any case, the selection of the operating conditions required to obtain the desired product characteristics may be significantly influenced by the equipment design (chamber, duct and valve, condenser), and thus the drying time may be affected. In this section, the state-of-the-art in modeling the different parts of the freeze-dryer, or the dynamic behavior of the whole equipment, will be summarized.

Recently, Computational Fluid Dynamics (CFD) started to be applied to model either single parts or the whole equipment in steady-state conditions (Barresi et al. 2010b): with this approach, continuity and Navier–Stokes equations, along with other relevant governing equations (e.g., enthalpy balance), are solved through a finite-volume numerical scheme. The transport properties appearing in these equations (e.g., gas viscosity and thermal conductivity) are calculated with the standard kinetic theory (often resorting to simple molecular potentials), as explained in the book of Chapman and Cowling (1939).

The main limitation of this technique stands in its description of the sublimating gas as a continuum (Batchelor 1965); to establish whether or not a fluid is in the continuous regime, it is sufficient to compute the Knudsen number (Kn), usually calculated as the ratio of the molecular free path length to a certain representative macroscopic length-scale of the flow (Knudsen 1909): if Kn < 10⁻³ the medium can be considered as a continuum (when Kn < 10⁻⁴ the Euler equations can be used instead of the Navier–Stokes equations).

If the mean free path of the gas molecules is neither very large nor very small as compared to the macroscopic length-scale of the flow, a more complicated law applies, in particular with respect to the gas flow near solid surfaces. It is generally accepted that the range of applicability of the continuum approach can be extended into the rarefied regime (10⁻³ < Kn < 10⁻¹) if special boundary conditions, taken into account the possibility of having a velocity slip or a temperature jump at the walls, are adopted. This is called the slip regime (Maxwell 1879).

When Kn assumes very high values (larger than 1) the flow is in the molecular regime. Under this regime collisions between molecules are not very frequent and the molecule velocity distribution is not Maxwellian; the Boltzmann equation has to be solved. In these cases, it is necessary to resort to alternative simulation frameworks, such as the Lattice–Boltzmann scheme. For the transition regime (10⁻¹ < Kn < 1), no reliable model exists.

In the drying chamber, as the characteristics size is relatively large and the gas pressure not so low, the CFD approach is generally feasible, even if in case of small clearance between the shelves, the slip boundary conditions must be adopted. In the past, the role played by water vapor fluid dynamics was assumed to be negligible, also because of the difficulty to identify and isolate its effects from the experimental results. Rasetto et al. (2008, 2010) and Rasetto (2009) studied the effect of some geometrical parameters of a drying chamber (clearances between the shelves and position of the duct leading the vapor to the condenser) on the fluid dynamics of the water vapor as a function of the sublimation rate, both in a small-scale and in an industrial-scale apparatus. Their results evidenced the presence of significant pressure gradients along the shelves, in particular in the large-scale units (Barresi et al. 2010a).

Also, the addition of inert to control the pressure may have a significant influence not only on the fluid dynamics in the chamber but also on the local composition of the atmosphere, and thus on the local partial pressure of water; this can be an additional source of variability in the batch. This aspect is very important especially for the laboratory-scale apparatus, where the inert is typically introduced in the drying chamber only by one inlet, as shown by Barresi et al. (2010a). Furthermore, these concentration gradients can worsen the performance of all those sensors that use a local measurement of water vapor concentration to monitor the process. These sensors are usually confined to peripheral positions to allow the shelves movements for vials stoppering, or are connected to the chamber by short pipes. Rasetto et al. (2009) showed that these phenomena can be more or less marked depending on freeze-dryer geometry and size.

The evolution of product temperature and of residual ice content in the various vials of a batch during a freeze-drying process in some cases may be significantly affected by local conditions around each vial. In fact, vapor fluid dynamics in the drying chamber determines the local pressure that, taking into account the heat flow from the shelf and, eventually, radiation from chamber surfaces, is responsible for the sublimation rate and product temperature. It is very important to be able to predict the expected variability in certain conditions, and to evaluate the effect of a change in the design of the apparatus (for example, in the distance between shelves, and thus in the maximum loading) in product temperature and in the drying time of the vials of the batch.

To this purpose, a dual-scale model which couples a three-dimensional model, describing the fluid dynamics in the chamber, and a second mathematical model, either mono- or bidimensional, describing the drying of the product in the vials, can significantly improve the understanding of a pharmaceutical freeze-drying process. A two-scales model can be useful to simulate the dynamics in single vials placed in particular positions (e.g., where the radiation effects are more important or where the pressure is higher), as well as that of the whole batch, thus calculating the mean value of the product temperature and of the residual water content, as well as the standard deviation around this mean value. An example of the results obtainable with this approach, suitable for process transfer and scale up has been already presented (Rasetto et al. 2010; Barresi and Fissore 2011): in this case, the dependence of local pressure on geometry and operating condition has been given by empirical correlations obtained by CFD preliminary simulations. This approach is valid in case of “one-way coupling,” that is in case the general hydrodynamics is not significantly affected by the distributions of the local sources.

When different sublimation fluxes in different vials affect the fluid dynamics in the chamber, resulting in what is usually known as “two-way coupling,” a simplified model describing the evolution of each single vial could be directly implemented in the CFD code, e.g., by means of user-defined functions. Only simple models can be implemented in a CFD code and, therefore, this approach is preferable only when a certain degree of uncertainty on the results about the time evolution of the product is acceptable, and the focus is on the equipment design (Barresi et al. 2010b).

As already discussed, great care must be paid to the possibility of choked flow in the duct connecting chamber and condenser. In fact, due to the very low pressure values (and therefore very high water vapor velocities) critical sonic flow conditions may be encountered (Searles 2004; Nail and Searles 2008). The diameter and length of the duct, as well as the geometry of the isolating valve, must be properly designed in order to guarantee under a wide range of operating conditions that the desired sublimation rate is evacuated.

Recently Alexeenko et al. (2009) investigated fluid flow in the duct connecting the drying chamber of a freeze-drying apparatus to the condenser both in an industrial scale and in a lab-scale unit. The flows under continuum gas conditions were analyzed using the Navier–Stokes equations, whereas the rarefied flow solutions were obtained by the Direct Simulation Monte Carlo (DSMC) method for the Boltzmann equation. The comparison of the results showed that under extreme operating conditions the continuum approach (used by CFD) can be no longer valid.

Recent unpublished work carried out by the authors and by other researchers (Patel et al. 2010; Barresi et al. 2010b) has confirmed that in many cases the CFD approach is still suitable, even if discrepancies (not completely explained) have been evidenced between experimental results and predictions.

Figure 23.5 reports an example of the mass flow rate as a function of condenser and chamber pressures . As it is possible to see, when the pressure difference increases, critical flow conditions are reached, resulting in a maximum flow rate, known as “critical flow rate,” which increases with the pressure in the chamber, because this affects the static density of the fluid. This critical flow rate depends on the chemical composition of the vapor (it is modified by the presence of inert) and is strongly influenced by the length-to-diameter ratio of the duct and the geometry of the isolating valve. To this purpose, it must be evidenced that even if it has been suggested that the conductance of a duct is independent on the duct diameter, if the results are plotted in term of mass flow (Oetjen 1999; Oetjen and Haseley 2004) the duct size actually affects the conductance. Another aspect that must be carefully considered is that the conductance of an empty duct is strongly affected by the inlet conditions, as the largest part of the pressure drop takes place just in the inlet, then accurate simulations must include also the inlet of the chamber and the exit. Finally, the real conductance may be much larger than that estimated according to the procedure proposed by Oetjen (1997, 1999).

Fig. 23.5

Graph A: Mass flow rate as a function of the chamber pressure for different condenser pressures. Straight duct, DN 350, L/D  Mass flodashed line with empty symbols corresponds to sonic flow and represents the asymptote. Graph B: Dependence of critical mass flow rate on chamber pressure and duct geometry. (Data published by permission of Telstar Technologies S. L.)

In case of the valves, the type (mushroom or butterfly) and even more the shape of the disk strongly affect the conductance. Thus, in case of scale up or process transfer from a freeze-dryer to another, significantly different limitation to maximum sublimation rate may occur. Figure 23.6 shows an example of the critical flows that can be estimated by CFD for two different valves: the case of an empty duct is also shown for comparison, to show that the concept of duct equivalent length, often adopted to handle the case of valves, must be used with great care. As the slope of the curves is different, the correct equivalent length would change with chamber pressure.

Fig. 23.6

Examples of critical flow conditions, estimated using CFD, with empty duct and different valve geometries. The filled symbols refer to two different valve shapes, the opens symbols to a straight duct with L/D = 10. (Data published by permission of Telstar Technologies S. L.)

The performance of the condenser may have a significant effect on the drying cycle and on the final product quality. If its efficiency is low, it may be difficult to reach the minimum pressure required in the chamber, and in case, it is not able to condense all the vapor sublimated, in fact, the pressure in the chamber will increase up to when the pressure control is lost (and a pressure increase is always related to a fast increase in the product temperature). The factors that influence the condenser efficiency are condenser geometry, fluid dynamics of sublimated vapor, chamber design, duct size, location and type of closing valve used, and the dynamics of ice deposition, but little work has been done to investigate in detail the influence of the condenser geometry on its efficiency (Kobayashi 1984).

The design of the condenser can largely benefit from the knowledge of the real fluid dynamics inside the condenser itself and from the evaluation of the ice deposition rate on coils and surfaces, but very little work has been done on modeling of the condenser up to now: due to the very low pressure, depending on the geometry considered, the continuum approach may be valid or not. Ganguly et al. (2010) focused on the simulation of ice deposition in a laboratory-scale condenser by means of DSMC, comparing the efficiencies of two different geometries, but without investigating the role played by the inert gas. Computational fluid dynamics was instead used by Petitti et al. (2013) to model both a whole lab-scale apparatus (including drying chamber, duct, valve, and condenser) and an industrial condenser, with the purpose to achieve a better comprehension of the flow dynamics and of the process of ice condensation and deposition in the condenser, in order to evaluate condenser efficiency. Computations can become extremely heavy in this case, especially in the complex geometry of an industrial apparatus, due to the necessity of modeling the vapor disappearance (and the ice formation) with a realistic mechanism that takes into account the proper kinetics.

Finally, a multiscale model of the process, which couples a lumped model of the dryer and of the condenser, with a detailed model of the vial, can be used for better understanding the dependence of process/product dynamics upon processing conditions, or to predict the product quality in presence of unexpected variations in the fluid temperature and/or in the chamber pressure due, for example, to a plant malfunctioning (Sane and Hsu 2007, 2008).

23.3 Design Space Calculation for the Primary Drying Stage

The design space for the primary drying stage can be defined as the set of operating conditions (temperature of the heating fluid and pressure in the drying chamber) that allows to maintain product temperature below the limit value, beside avoiding choking flow in the duct connecting the drying chamber to the condenser. Process simulation allows calculating quickly the design space: the accuracy of the results is affected by model accuracy and by parameters uncertainty. As a consequence, the mathematical model used for the calculations has to be accurate, and it should involve few parameters that could be easily measured (or estimated) with few experimental runs. To this purpose, the simplified model previously described (Eqs. (23.2)–(23.6)) can be effectively used.

When calculating the design space for the primary drying stage two different approaches can be used. In fact, it is possible to look for the values of T _fluid and P _c that maintain product temperature below the limit value throughout the primary drying stage, or it is possible to take into account that the design space changes as drying goes on due to the increase of the cake thickness. In fact, Eqs. (23.4) and (23.6) can be written as:

$${{\left( \frac{1}{{{K}_{v}}}+\frac{{{L}_{\text{frozen}}}}{{{\lambda }_{\text{frozen}}}} \right)}^{-1}}\left( {{T}_{\text{fluid}}}-{{T}_{i}} \right)=\Delta {{H}_{s}}\frac{1}{{{R}_{p}}}\left( {{p}_{w,i}}-{{p}_{w,c}} \right)$$

(23.18)

evidencing that the same couple of operating conditions (T _fluid and P _c ) can determine different values of product temperature (and of sublimation flux) depending on the value of L _dried and, thus, of R _p . This means that a couple of values of T _fluid and P _c can be inside the design space at a certain time instant during primary drying, and they can be outside in a different time instant.

In case T _fluid and P _c are kept constant throughout the primary drying stage, the following calculations can be done to investigate if their values are inside the design space (Giordano et al. 2011):

• 1. Selection of the range of values of T _fluid and P _c of interest.

• 2. Selection of a couple of values of operating conditions T _fluid,k and P _c,j .

• 3. Calculation of the evolution of product temperature and sublimation flux until the end of primary drying.

• 4. The operating conditions T _fluid,k and P _c,j belong to the design space in case maximum product temperature is lower than the limit value, and the maximum sublimation flux is lower than the limit value.

• 5. Repetitions of steps 3–4 for all the values of T _fluid,k and P _c,j of interest.

The approach proposed by Giordano et al. (2011) can be effectively used to account for model parameters uncertainty in the calculation of the design space. It has to be remarked that as the batch is nonuniform, mainly due to the different heat transfer mechanisms to the product, the previously described procedure has to be repeated for each group of vials, characterized by a specific value of the heat transfer coefficient.

Figure 23.7 shows the design spaces calculated for the vials of group a (center of the shelf) and of group d (first external raw) in case of freeze-drying of a 5 % mannitol aqueous solution. Various iso-flux curves are shown, and they can help in identifying the operating conditions that minimize the duration of primary drying. It is evident that the design space of vials of group a is larger than that of vials of group d: this is due to the fact that for a given couple of values of T _fluid and P _c product temperature is lower, due to the lower value of K _v . As a consequence, for a value of chamber pressure of 5 Pa it could be possible to set T _fluid = − 15 °C without breaking the constraint on maximum product temperature in vials of group a, but vials of group d would be overheated. Thus, if the goal is to maintain product temperature below the limit value in the whole batch, it is required to set a lower value of T _fluid, e.g., − 20 °C, even if this will result in a higher drying time. In fact, primary drying is completed first in the vials of group d, and then in vials of group a, where the sublimation flux is lower than that obtained in case T _fluid = − 15 °C, as product temperature is lower.

Fig. 23.7

Design space for the freeze-drying of a 5 % by weight mannitol solution for vials of group A (on the left) and of group D (on the right). Isoflux curves (in kg h^−gm^−g) are also shown (dashed lines)

Figure 23.8 shows the results obtained when the operating conditions (shown in graph A) are selected in such a way that product temperature remains below the limit value throughout the primary drying stage in the whole batch as shown by the thermocouple measurement in vials of groups a and d (shown in graph c), as well as by the temperature estimated using the PRT (that can be assumed to be equal to that of vials in the central position of the shelf, as they are the most numerous). In this case, the duration of the primary drying is equal to about 31 h, as determined by the ratio between the pressure signal of a capacitive and of a thermal conductivity gauge (shown in graph b).

Fig. 23.8

Example of freeze-drying cycle carried out using a 5 % by weight mannitol solution. Evolution of: (graph A) T _fluid and P _c ; (graph B) Pirani-Baratron pressure ratio (solid line) and J _w as estimated by the PRT technique (symbols); (graph C) T _B as measured by thermocouples (solid line: vial of group A, dashed line: vial of group D) or estimated by PRT technique (symbols). The vertical line evidences the completion of ice sublimation as detected by the pressure ratio

The choice of the container type is an important aspect to be considered during the design process. This decision is dictated by the filling volume used in manufacturing, and by the volume of liquid required for the product reconstitution. With this regard, various solutions are feasible, as the same solid content per vial can be obtained varying both the solution concentration and the filling volume. However, these various combinations are not equivalent in terms of drying length, as they entail a different value of the product resistance to vapor flow and of the total amount of water to be removed. To better clarify this aspect, let us consider an example, that is, the freeze-drying of a mannitol-based formulation. Let us imagine that the objective is to get 50 mg of dried product per vial, and that the same type of vials used above for carrying out the experimental study is considered here. To achieve this objective, two different configurations are investigated: (1) 1.5 mL of a 5 % by weight mannitol solution per vial, thus L ₀ = 10.6 mm; and (2) 0.38 mL of a 20 % by weight mannitol solution, thus L ₀ = 2.65 mm. The product resistance to vapor flow measured for the two formulations is displayed in Fig. 23.9 (graph a): as expected, the value of R _p of the second formulation increases faster with L _dried. These values have been then used to build the design space, and hence to design an appropriate cycle for the drying of the two formulations, see Fig. 23.9 (graphs b). Figure 23.9 (graph c) shows how the drying time varies with the solid content, and for two different values of chamber pressure . As expected from the design spaces displayed in Fig. 23.9 (graph b) for 5 and 20 % by weight mannitol solutions, the value of chamber pressure does not significantly modifies the drying time. On the contrary, the duration of the sublimation step significantly reduces as the solid content increases and the filling volume decreases. In order to optimize the drying duration, these results suggest to use, when possible, a high solid content and a low filling volume. Of course, in a similar way it is possible to evaluate the influence of a change in the vial geometry and size.

Fig. 23.9

Graph A: Comparison between the value of R _p vs. L _dried in case of the freeze-drying of a 5 % (solid line) and of a 20 % (dashed line) by weight mannitol solution. Graph B: Design space for the freeze-drying of a 5 % (solid line) and of a 20 % (dashed line) by weight mannitol solution for vials of group A. Graph C: Duration of the primary drying stage for mannitol solutions having a different solid content and processed at (dashed line) P _c   shed lineofsolid line) P _c   lid lineeof the primary drying stage for mannitol solutions having a different solulation. The filling volume is fixed to get 50 mg of dried product per vial

In case the variation of the design space vs. time is taken into account, the approach proposed by Fissore et al. (2011d) can be effectively used. It is based on the use of L _dried (or L _frozen) as third coordinate of the diagram instead of time. In fact, at the same time instant, the value of L _dried can be different due to the past history of the product and, thus, it would be impossible to get a unique diagram using time as coordinate of the diagram. On the contrary, the use of L _dried, beside T _shelf and P _c , allows obtaining a unique diagram. The following calculations are required:

• 1. Selection of the range of values of T _fluid and P _c of interest.

• 2. Selection of the range of values of L _dried of interest.

• 3. Selection of a couple of values of operating conditions T _fluid,k and P _c,j .

• 4. Calculation of product temperature and sublimation flux for the ith value of L _dried.

• 5. The operating conditions T _fluid,k and P _c,j belong to the design space for the selected value of L _dried in case product temperature is lower than the limit value, and the sublimation flux is lower than the limit value.

• 6. Repetitions of steps 4–5 for all the values of T _fluid,k and P _c,j of interest, thus obtaining the design space for the selected value of L _dried.

• 7. Repetitions of steps 4–6 for all the values of L _dried of interest.

Figure 23.10 shows the results of the calculations for the vials of group A of the previous case study: each curve identifies the highest value of T _fluid that keep product temperature below the limit value for the values of L _dried and P _c considered. As far as the primary drying goes on, i.e., L _dried increases, the design space shrinks because of the variation of R _p with time. Figure 23.11 shows an example of results obtained when using a cycle selected using the design space shown in Fig. 23.10. It appears evident that it is possible to carry out the first part of primary drying using higher values of T _fluid and P _c with respect to the values required for the second part, and this could be useful to further optimize the process (in this case primary drying is completed in 25 h, 6 h less than in case the operating conditions are kept constant throughout primary drying).

Fig. 23.10

Design space for 5 % by weight mannitol solution calculated at various values of L _dried/L ₀

Fig. 23.11

Example of freeze-drying process carried out using a 5 % by weight mannitol solution. Evolution of: (graph A) T _fluid and P _c ; (graph B) Pirani–Baratron pressure ratio (solid line) and J _w as estimated by the PRT technique (symbols); (graph C) T _B as measured by thermocouples (solid line: vial of group A, dashed line: vial of group D) or estimated by PRT technique (symbols). The vertical line evidences the completion of ice sublimation as detected by the pressure ratio

Beside cycle design and optimization, the design space can be effectively used for process failure analysis, i.e., to evaluate if the product remains inside the design space after an unexpected variation of T _fluid and/or P _c due to some kind of failure or disturbances. In this case, misleading results can be obtained if the design space calculated without taking into account the variation of L _dried during primary drying is used. As an example it is possible to consider the following case study. Let us consider the case of T _fluid = − 20 °C and P _c  = 5 Pa and that at about one-half of primary drying, the temperature of the heating fluid increases to − 10 °C. According to the design spaces shown in Fig. 23.7, the new values of the operating conditions are outside the design space and, thus, the cycle can be stopped and the product discarded. According to the design space shown in Fig. 23.10, the product is still in the design space, at least until L _dried/L ₀ is lower than 55 %.

A final remark concerns the scale-up of the design space. Actually, as the design space is calculated using the model of the process, and the results depends on the values of the parameters K _v and R _p and also on the limit curve to avoid the occurrence of choked flow in the duct. As the heat transfer coefficient K _v takes into account all the heat transfer mechanisms to the product, and some of these can vary in different freeze-dryers (e.g., radiation from chamber walls, radiation from upper shelf,…), then this parameter has to be experimentally measured also in the industrial-scale freeze-dryer. Actually, in case the coefficients C ₁, C ₂, and C ₃ of Eq. (23.8) have been determined in the lab-scale freeze-dryer, only one gravimetric test might be necessary for a different equipment (to determine the value of the coefficients C ₁), as the parameters C ₂ and C ₃ gives the dependence of K _v on P _c , and their dependence on the type of equipment can be neglected. Once also the parameter R _p has been determined in the industrial-scale freeze-dryer, then previous algorithms can be used to determine the new design space.

As concerns the choked flow conditions, it must be evidenced that these are generally reached more easily in an industrial apparatus than at laboratory and pilot scale; and as shown in Fig. 23.6, changes in the geometry of the duct, and in the characteristics of the valves installed, may modify significantly the conductance.

23.4 Design Space Calculation for the Secondary Drying Stage

The design space for the secondary drying stage can be defined as the set of operating conditions (temperature of the heating fluid and duration of the secondary drying) that allows to get the target value of residual moisture in the product, beside maintaining product temperature below the limit value. This requires to know how the glass transition temperature changes as a function of the residual moisture content in the product. In case of sucrose solutions, the equation proposed by Hancock and Zografi (1994) can be used:

$${{T}_{g}}=\frac{{{C}_{s}}{{T}_{g,w}}+K\left( 1-{{C}_{s}} \right){{T}_{g,s}}}{{{C}_{s}}+K\left( 1-{{C}_{s}} \right)}$$

(23.19)

with K = 0.2721, T _g,w  = 135 K, and T _g,s  = 347 K.

The design space for the secondary drying stage can be calculated using the lumped model previously described (Eqs. (23.14)–(23.15)) according to the following procedure (Pisano et al. 2012):

• 1. Selection of the range of values of T _fluid of interest.

• 2. Determination of the maximum allowed value of product temperature as a function of the residual moisture content.

• 3. Selection of the value of C _s,0.

• 4. Calculation of the evolution of T _p and C _s , using the model of the process, for the ith value of fluid temperature T _fluid,i .

• 5. Determination of the time (t _d,i ) required to get the target value of residual moisture (C _s,t ) for the selected value of heating fluid temperature.

• 6. The point corresponding to the couple of values (t _d,i , T _fluid,i ) belongs to the design space in case product temperature remains below the limit value throughout the drying phase.

• 7. Repetition of steps 4–6 for all the values of T _fluid,i of interest.

• 8. Repetition of steps 4–7 for different values of C _s,0, as this variable can be hardly known and it can be not the same for the various vials of the batch.

When the design space has been calculated, it is possible to optimize the secondary drying stage by selecting the value of T _fluid that minimizes the drying time.

Figure 23.12 shows the design space obtained for the secondary drying of a 5 % w/w aqueous solutions of mannitol (the maximum temperature of the heating fluid is assumed to be 40 °C). For a target value of residual moisture (e.g., 1 or 2 %), the design space is coincident with the area of the diagram below the solid line. In case the target value of residual moisture must be comprised between two values, e.g., 1 and 2 %, then the design space corresponds to the area comprised between the two curves.

Fig. 23.12

Design space calculated for the secondary drying of a 5 % by weight mannitol solution in case C _s,0 0sign space calculated for the secondary drying of a 5 %solid line) or 2 % (dashed line)

23.5 Conclusions

Mathematical modeling can be really effective in obtaining quality-by-design in a freeze-drying process. In fact, mathematical simulation of the freezing stage, as well as of the primary and secondary drying stages can allow determining the effect of the operating conditions of the process and, thus, to preserve product quality , beside optimizing the process. Evidently, this approach requires a preliminary investigation to determine the values of the parameters of the model: model accuracy and level of parameters uncertainty influence the quality of the results. As an alternative, it could be possible to design the freeze-drying cycle inline, using a suitable monitoring system (e.g., the PRT) and a control algorithm (Pisano et al. 2010, 2011b). Obviously, in this case, only the best cycle (according to the target specified in the control algorithm) is obtained, and the additional information supplied by the design space, concerning the robustness and the effect of eventual deviations, are not available. In addition, the feasibility of the approach based on the use of control algorithms is limited by the availability of a suitable monitoring system, in particular in industrial-scale freeze-dryers.