Stochasticity and Determinism in Models of Hematopoiesis

Kimmel, Marek

doi:10.1007/978-1-4939-2095-2_7

Marek Kimmel⁸

Part of the book series: Advances in Experimental Medicine and Biology ((AEMB,volume 844))

3247 Accesses
10 Citations
3 Altmetric

Abstract

This chapter represents a novel view of modeling in hematopoiesis, synthesizing both deterministic and stochastic approaches. Whereas the stochastic models work in situations where chance dominates, for example when the number of cells is small, or under random mutations, the deterministic models are more important for large-scale, normal hematopoiesis. New types of models are on the horizon. These models attempt to account for distributed environments such as hematopoietic niches and their impact on dynamics. Mixed effects of such structures and chance events are largely unknown and constitute both a challenge and promise for modeling. Our discussion is presented under the separate headings of deterministic and stochastic modeling; however, the connections between both are frequently mentioned. Four case studies are included to elucidate important examples. We also include a primer of deterministic and stochastic dynamics for the reader’s use.

Access provided by Autonomous University of Puebla. Download chapter PDF

Large fluctuations in multi-scale modeling for rest hematopoiesis

Article 11 May 2021

Statistical and Mathematical Modeling of Spatiotemporal Dynamics of Stem Cells

Counting generations in birth and death processes with competing Erlang and exponential waiting times

Article Open access 04 July 2022

Keywords

Introduction

The role of stochastic events in hematopoiesis has been discussed for the past 60 years since the beginnings of experimental hematology by Till and McCulloch [1]. The two opposing paradigms, deterministic hematopoiesis based on the firm regulation of peripheral blood cell populations, and stochastic hematopoiesis based on variability observed in seeded bone marrow cells, are still awaiting a grand synthesis. This is in spite of the existence of substantial experimental findings, particularly those in the recent decade, using techniques of single-cell measurements. Disease-accompanying dynamics have been over the years variously modeled as deterministic or stochastic. Examples of stochastic phenomena observed in hematopoiesis include, but are not limited to:

Stochastic fluctuations in the number of hematopoietic stem cell (HSC) making self-renewal versus commitment decisions result in high variability in the magnitude of the response to infection.
The same stochastic fluctuations may lead to depletion of the HSC compartment when facing massive infections such as neonatal sepsis.
Presence of variant proteins in molecular switches responding to hematopoietic growth factors such as granulocyte colony-stimulating factor (GCSF) leads to aberrant proliferation and leukemia, again with an important chance component.
Molecular switches under stochastic fluctuations in molecular pathways and receptor noise may become reversible, which results in reversibility and plasticity at the level of the HSC and early committed cell level.

Recently, a third approach is emerging, which may be termed the molecular determinism (term coined based on ideas in [2, 3]). According to molecular determinism, stochastic variability of the proliferating bone marrow cells can be reduced to complicated series of deterministic events including molecular switches, which are multistable by nature and which trigger proliferation and/or maturation decisions. This is distinct from older proposals involving chaotic dynamics [4, 5].

Mathematical, and in particular stochastic, principles have been used to explain the balance of factors contributing to behavior of a cell population as a whole. However, new techniques for gathering data and probing biological processes at a molecule and cell level continuously provide unprecedented amounts of new information, which leads to reexamination of these models. This has led to a renewed skepticism concerning stochastic modeling as a paradigm. As argued by Snijder and Pelkmans [2], deterministic approach (or, what was called “molecular determinism” earlier in the current chapter) can resolve apparently stochastic phenomena with deterministic variability. They argue that cell-state parameters, such as cell size, growth rate, and cell cycle state, can be used to explain cell-to-cell variability, similarly as spatial cell population context parameters such as local cell density and location on cell colony edges. Tracing back cell-to-cell variability in time over multiple cell cycles may identify inherited, predetermining factors in cells of the same lineage. Snijder and Pelkmans [2] also advocate repeated stimulation of the same cells to help identify the presence of deterministic factors in seemingly stochastic cell-to-cell variability. Complicated dynamics leading to chaotic (and sometimes indistinguishable from stochastic) behavior has been appreciated for some time. For example, existing mathematical models of cell cycle regulation (cf. e.g., [6] and references therein) rely on nonlinear regulatory functions to control cell population distribution. However, these models also include a very real phenomenon of uneven allocation of constituents to progeny cells, which arguably is either truly stochastic or is indistinguishable from stochastic. Moreover, the idea of “backtracking” complicated (chaotic) trajectories seems to be doubtful from mathematical viewpoint. Schroeder [7] discussed the need for long-term continuous follow-up on individual cells in order to understand the specific rules of proliferation and differentiation. This chapter also touches upon issues such as influence of imaging techniques on cell behavior and difficulty in cell tracking using existing software.

Returning to molecular determinism, a very good example of this approach seems to be the paper by Takizawa et al. [8], concerning a purely deterministic and demand-driven integrated model of regulation of early hematopoiesis. This models is very complex and it involves “view of how cytokines, chemokines, as well as conserved pathogen structures, are sensed, leading to divisional activation, proliferation, differentiation, and migration of HSCs and progenitor cells, all aimed at efficient contribution to immune responses and rapid reestablishment of hematopoietic homeostasis.” Takizava et al. [8] paper is too involved physiologically to be discussed at length here. Let us notice that it contrasts with the simpler (and stochastic) models of Ogawa [9] and Abkowitz et al. [10]. In these models, the branching process (bp) paradigm is used at its simplest, with cells depicted as independent individuals, splitting at random and possibly interacting with a limited number of smaller entities.

Another current concept is that of nongenetic variability as a substrate for natural section, as espoused by Huang’s group [11]. For example, slow fluctuations in mammalian cells are the expression of heritability (memory) of protein abundance in successive generations of normal or cancer cells [12, 13]. One example is the noninherited form of drug resistance in cancer. Theoreticians have been suggesting this for several decades because of similar experimental evidence. The memories of protein abundance and dynamic homeostasis, which implied slow fluctuations in individual cells, were important constituents of many of the cell cycle regulation and unequal division models [14–16]. Development of resistance to chemotherapy by gene amplification (genetic, but nonmutation driven) has been pondered by theorists equally long ago [17, 18].

Questions about the dynamics of hematopoiesis are resurfacing due to new experimental studies concerning lineage-specific growth factors, morphogens, the microenvironment, and the plasticity of stem cells. These new findings allow a reexamination of two long-standing questions: whether hematopoiesis is stochastic or deterministic, and whether it is discrete or continuous. These issues exist for other non-HSC systems; however, hematopoiesis serves as the most informative and accessible mammalian tissue system to look for answers [1]. Since quantitative systems analysis based on multi-scale modeling is needed to understand the complexity and dynamics of hematopoiesis, determining the correct approach to this modeling is of more than academic interest. Much work has been recently published on this topic and some of it will be reviewed in the current chapter. We will first pose three key questions and then use a simple “toy” model to explain basic ideas and problems.

Question 1. Is Hematopoiesis Deterministic or Stochastic?

Experimental data suggest stochastic factors play a role in determining fate of daughter cells of a stem cell [19, 20]. However, it is not clear at which critical junction stochasticity operates in lineage-specific regulation (principal examples being erythropoietin (Epo)-driven erythropoiesis and GCSF-driven granulopoiesis. Recent systemic and modeling studies of dynamics of signaling pathways in cells at various stages of hematopoiesis, underscore the role of bistable (or multistable) switches, which can direct the cell towards “fates” such as differentiation in various directions, proliferation, or apoptosis [21]. These switches, as described and modeled, are essentially deterministic circuits, displaying a series of stable and unstable steady states [22]. The stable steady states correspond to distinct patterns of expression of target genes, characteristic of a given cell “fate.” Small change in initial conditions at individual cell’s level or in type or strength of receptor activation results in switching from one stable work regime to another [23]. Although this paradigm explains the interplay of positive and negative feedbacks in cells, it does not explain the intrinsic stochasticity, implied by both classical and more recent experiments on hematopoietic cells [9, 10]. Independently, there exists a sizeable body of evidence that eukaryotic cells may make individual decisions based on nondeterministic rules [24, 25]. The sources of intrinsic stochasticity in eukaryotic cells are related to processes in which a small number of interacting molecules may trigger a large-scale effect [26]. Stochastic effects may provide robust evolutionarily adaptive mechanisms [27]. A critical property of hematopoiesis is the ability to protect against environmental insults (e.g., infection), which may require a design incorporating stochastic dynamics.

Question 2. Do HSCs and Their Progeny Constitute Discrete Subsets or a Continuum?

The general question of stem cell plasticity and, in particular, the reversibility of the HSC has gained much interest due to stem cell engineering and induced pluripotent stem cells. A related question is to what extent the succession and timing and commitment and differentiation (maturation) processes in hematopoiesis can be altered or “stretched” within the bounds of normality. On an operational level, is it sufficient to model hematopoiesis in the terms of discrete stages or is it necessary to include continuous maturation?

Question 3. What Role Is Played in Hematopoiesis by Spatial Effects?

The usual approach has been to treat the process as spatially uniform in both the bone marrow and peripheral circulation. However, recent research on niches and environments in the bone marrow and the interaction of HSC and mesenchymal stem cells (see [28]), has led to a realization that spatial effects and interaction between spatial and stochastic effects cannot be ignored. Such interactions in mathematical models result in qualitatively new dynamics (as in Roeder’s 2006 model [29]). The reason is that spatial separation provides opportunity for small colonies of cells to fix stochastic fluctuations despite the fact the total size of the population is large.

Primer in Deterministic and Stochastic Dynamics

This primer is intended for the wide audience who study systems biology, and depending on your expertise can be skipped or used as a loose reference.

Deterministic Dynamical Systems

To understand deterministic models of hematopoiesis, we will need definitions and theorems from the mathematical theory of dynamical systems. In general, these are objects that evolve in time and, when “stopped” as a result of either a physical or a “thought” intervention, can be restarted and continued “as if nothing happened.” This is known as the “continuation principle.” Mathematically, let us denote by $x(t;{{t}_{0}},{{x}_{0}})$ the state of the system at time t, if at time ${{t}_{0}}$ the state was ${{x}_{0}}$, i.e., $x({{t}_{0}};{{t}_{0}},{{x}_{0}})={{x}_{0}}$. In these terms, the continuation principle can be stated as $x(t+s;{{t}_{0}},{{x}_{0}})=x(t;{{t}_{0}}+s;x(s;{{t}_{0}},{{x}_{0}}))$.

The most commonly employed dynamical systems have the form of differential equations (DEs; including multidimensional or infinitely dimensional DEs). In this setup, $x(t;{{t}_{0}},{{x}_{0}})$ is the solution of the DE of the form $\text{d}x/\text{d}t=f(x)$, with solution $x(t)$ satisfying the $x({{t}_{0}})={{x}_{0}}$. Such solution can be denoted by $x(t;{{t}_{0}},{{x}_{0}})$, and it can be proved that it satisfies the continuation principle. Solutions of DEs have been extensively studied and therefore constitute a convenient tool.

Solution $x(t;{{t}_{0}},{{x}_{0}})$ of a DE $\text{d}x/\text{d}t=f(x)$ is stable if there can be found a disc of radius δ in the space of initial conditions, such that the solution stays forever in a “pipe” of a desired radius ε. In mathematical terms, for each ε there exists a δ such that if $\left| {{x}_{0}}'-{{x}_{0}}\right|<\delta $, then $\left| x(t;{{t}_{0}},{{x}_{0}}')-x(t;{{t}_{0}},{{x}_{0}}) \right|<\varepsilon $, for all $t\ge {{t}_{0}}$. Solution $x(t;{{t}_{0}},{{x}_{0}})$ is asymptotically stable if it is stable and moreover $\left| x(t;{{t}_{0}},{{x}_{0}}')-x(t;{{t}_{0}},{{x}_{0}}) \right|$ converges to 0 with t converging to infinity. In many cases, it is interesting to investigate stability of the equilibrium solution, i.e., the solution along which the time derivative $\text{d}x/\text{d}t=0$. This solution is a constant function solving the equation $0=f(x)$. Useful mathematical tools for investigating stability include the Lyapunov functions and characteristic equations.

Bifurcation

Most commonly applied to the mathematical study of dynamical systems, a bifurcation occurs when a small smooth change made to the parameter values of a system causes a sudden qualitative or topological change in its behavior. The name “bifurcation” was first introduced by the mathematician Henri Poincaré in 1885. The two best-known types of bifurcation are exchange of stability and Hopf bifurcation. In exchange of stability, change of parameter causes a new equilibrium to appear, which becomes stable, while the old one remains but becomes unstable. In Hopf bifurcation, a stable equilibrium becomes unstable, with oscillations around it appearing at the same time.

Chaos theory is a field of study in mathematics, with applications in disciplines including physics and biology. In a chaotic system, small differences in initial conditions (even those due to rounding errors) yield widely diverging trajectories, rendering long-term prediction impossible in general. Chaotic systems are deterministic, so their trajectories are mathematically determined by their initial conditions, with no random elements involved. However, the deterministic nature of these systems does not make them predictable. In many ways, chaos can mimic randomness (stochasticity).

Stochastic Processes

Proliferation of cells is frequently stochastic. Therefore, it is useful to introduce definitions and theorems from the theory of probabilities and the theory of stochastic processes. The following account is a brief intuitive introduction. The definitions will be highlighted by italics.

Random variable (rv) X is, intuitively, a numerical result of observation, which displays random variation. The notation $X(\omega)$ highlights the dependence of the rv on the “chance” element $\omega $ of the sample space $\Omega $ (wherever it is superfluous, the $\omega $ is omitted. Stochastic process (or random function) $X(t;\omega)$ is, intuitively, a function of time t with a random component. Mathematically, it is a family of rv’s parameterized by time. Function of time $X(t;\omega)$, with $\omega $ fixed is called the realization or the sample path of the process. Self-recurrence is an important property of the stochastic process $X(t;\omega)$. Suppose that a process such that at $X(0;\omega)={{x}_{0}}$ is stopped at some time ${{t}_{0}}$. Then, if also $X({{t}_{0}};\omega)={{x}_{0}}$, the continuation process restarted from time ${{t}_{0}}$ is identical (it has the same distributions) as the original process, except that it is shifted by ${{t}_{0}}$. A process with such property is called self-recurrent. Self-recurrence may be considered a rephrasing of a causality principle. It leads to recurrent relationships for a wide class of stochastic processes, including Markov processes and bp’s.

Markov process is a process with a limited memory (the Markov property). Intuitively, given the state of the process at time s, the future of the process (at some t such that s < t) depends only on this state and not on its states at times before s. Mathematically, $\Pr [X(t)\in A|X(u),u\le s<t]=\Pr [X(t)\in A|X(s),s<t]$, where A is a subset of the state space of the process (space of values assumed by the process). The probability listed above is the transition probability from state $x=X(s)$ to the set of states A, in time t s. If the states of the process form a finite or denumerable set, then the process is called a Markov chain. In this case, it is possible to define a matrix (finite or infinite) of transition probabilities between states $P(t)=[{{P}_{ij}}(t)],$ where ${{P}_{ij}}(t)=\Pr [X(s+t)=j|X(s)=i]$.

Branching process (bp) is a random collection of individuals (such as particles, objects, or cells), proliferating according to rules involving various degrees of randomness of the individual’s life length and the number of progeny of an individual. The unifying principle is the so-called branching property, which states that the longevity and type of progeny of a newborn particle, conditional on the current state of the process, are independent of any characteristics of other particles present at this time or in the future. The branching property is a form of self-recurrence, as defined earlier on. Galton–Watson bp (G–W bp) is the simplest bp. It evolves in discrete time measured by nonnegative integers. At time 0, an ancestor individual (a particle, cell, or object) is born. At time 1, the ancestor dies, producing a random number of progeny. Each of these becomes an ancestor of an independent subprocess, distributed identically as the whole process. This definition implies that the numbers of progeny produced by each particle ever existing in the process are independent identically distributed rv’s and that all particles live for one time unit. Discrete time moments coincide with generations of particles. The number of particles existing in the G–W bp, as a function of time, constitutes a time-discrete Markov chain.

Bp’s occur frequently in biological systems. They serve as models for proliferating cells, amplified genes, and shortening telomeres. Bp is critical if the expected (mean) count of progeny of a particle is equal to 1. It is supercritical, if the mean count of progeny of a particle is greater than 1 and subcritical if it is less than 1. This classification leads to profound differences in asymptotic properties (properties after sufficiently long time) of the process. In particular, critical bp’s behave in a paradoxic way since they become extinct (i.e., all particles die out) with probability 1, while the expected number of particles stays constant. Asymptotic properties of subcritical bp’s are summarized by the Yaglom’s theorem, which states that for a subcritical bp, which also becomes extinct with probability 1, there exists a quasi-stationary distribution, conditional on nonextinction. This means that the sample paths that do not become extinct will be, for times sufficiently long, distributed according to a law (distribution) that does not vary with time (i.e., stationary). All bp’s share the property of instability, which means that, as time tends to infinity, the bp becomes either extinct or indefinitely large. Instability is due to the independent assumptions inherent in the definition of a bp (see earlier on).

Supercritical bp’s have the property called the exponential steady state, which characterizes populations growing without spatial or selective constraints, the condition in which the number of individuals increases or decreases exponentially, while the proportions of individuals in distinct age classes and any other identifiable categories remain constant. Related notion is that of the Malthusian parameter, i.e., a parameter α such that the number $Z(t)$ of particles present in the process, normalized by dividing it by $\exp (\alpha t)$, converges to a limit rv, as time tends to infinity.

Markov bp is a type of time-continuous bp. At time 0, an ancestor individual (a particle, cell, or object) is born. The ancestor lives for time $\tau,$ which is an exponentially distributed rv, and then the ancestor dies, producing a random number of progeny. Each of these becomes an ancestor of an independent subprocess, distributed identically as the whole process. The number of particles existing in the Markov bp, as a function of time, is a Markov chain.

Type space is a collection of possible particle (cell) types existing in a bp. If there is more than one but finitely many types, the process is called multitype. Multitype G–W bp is a generalization of the usual (single-type) G–W bp. In the multitype process, each individual belongs to one of a finite number of types. At time 0, an ancestor individual (a particle, cell, or object), of some type, is born. Processes started by individuals of different types are generally different. At time 1, the ancestor dies, producing a random number of progeny of various types. The distribution of progeny counts depends on the type of parent. Each of the first-generation progeny becomes an ancestor of an independent subprocess, distributed identically as the whole process (modulo ancestor’s type). In the multitype process, asymptotic behavior depends on the matrix of expected progeny count. Rows of this matrix correspond to the parental types, and columns to the progeny types. The largest positive eigenvalue of this matrix (the Perron–Frobenius eigenvalue), is the Malthusian parameter (see earlier on) of the process, provided the process is supercritical (the Perron–Frobenius eigenvalue larger than 1) and positive regular. The latter means that parent of any given type will have among its (not necessarily direct) descendants individuals of all possible types, with nonzero probability.

Probability generating function (pgf) is a function ${{f}_{X}}(s)$ of a symbolic argument s, which is an equivalent of the distribution of a nonnegative integer-valued rv X. If numbers ${{p}_{0}},{{p}_{1}},{{p}_{2}},\ldots $ constitute the distribution of rv X, i.e., $\Pr [X=k]={{p}_{k}}$, then the pgf of rv X is defined as ${{f}_{X}}(s)=E({{s}^{X}})=\sum\nolimits_{i=0}^{\infty }{{{p}_{i}}}$, for $s\in [0,1]$. Use of the pgf simplifies mathematical derivations involving nonnegative integer rv’s and processes, among them the bp’s.

Poisson process is one of the most important stochastic processes, since it is frequently used as a model for mutation dynamics. It can be intuitively defined as a random collection of time points having the properties of complete randomness (the counts of events in any two disjoint time intervals are independent), and stationarity (the probability of an event occurring in a short time interval (t, t + Δt) is equal to λ Δt + o(Δt), where a small o(Δt) with respect to Δt has the property it converges to 0 faster than Δt itself, i.e., $o(\Delta t)/\Delta t\to 0$, as $\Delta t\to 0$. Constant λ is called the intensity of the process. The number N of epochs of the Poisson process in an interval of length t has Poisson distribution of the form ${{p}_{n}}=\Pr [N=n]=\exp (-{}\lambda{}t){{{}\lambda{}}^{n}}/n!$, for $n=0,1,2,\ldots $, and the time intervals T between any two epochs have exponential distribution with the same parameter $\lambda $, i.e., the density of distribution of T is equal to ${{f}_{T}}(t)={}\lambda{}\exp (-{}\lambda{}t)$.

The Wright–Fisher (W–F) model is a stochastic construct that is frequently used in genetics to explain loss of variants in a finite population. In brief, it is assumed that there exist N individuals, which produce progeny from one synchronous generation to another. Individuals in generation $n+1$ are copies of individuals randomly and independently chosen from generation n, so that the probability that individuals $1,2,\ldots,i,\ldots,N$ are represented respectively ${{k}_{1}},{{k}_{2}},\ldots,{{k}_{i}},\ldots,{{k}_{N}}$ times in the succeeding generation is equal to ${{p}_{{{k}_{1}},{{k}_{2}},\ldots,{{k}_{i}},\ldots,{{k}_{N}}}}={{(1/N)}^{{{k}_{1}}+{{k}_{2}}+\ldots +{{k}_{i}}+\ldots +{{k}_{N}}}}N!/({{k}_{1}}!{{k}_{2}}!\ldots,{{k}_{i}}!\ldots {{k}_{N}}!)$, where ${{k}_{1}}+{{k}_{2}}+\ldots +{{k}_{i}}+\ldots +{{k}_{N}}=N$, i.e., the rv’s ${{k}_{1}},{{k}_{2}},\ldots,{{k}_{i}},\ldots,{{k}_{N}}$ are multinomially distributed. One consequence is that in each generation there exists a nonzero probability of one (or more) individuals leaving no progeny. This leads eventually (after a finite number of generations) to loss of copies of all the individuals except one. This individual (or genetic variant) is called fixed. The W–F model differs from the G–W bp, in that the former has a fixed total number of individuals, while in the latter the number of individuals is fluctuating from one generation to another. The W–F model applies in situations in which the environment pressure makes population size change unlikely.

Turing pattern formation

One of the most interesting mathematical phenomena arising in models structured by spatial coordinates is pattern formation via diffusion-driven instability (DDI). Discovered by Alan Turing, this effect has been used to explain emergence of biological, physical, and chemical patterns, such as patterns in colonies of microorganisms, embryo segmentation, or dynamics of the Belousov–Zhabotinsky reactions. The usual mathematical framework is that of the system of at least two reaction-diffusion equations, i.e., partial differential equations (PDEs) of the form

$$ \begin{aligned}& \partial u/\partial t={{D}_{1}}{{\Delta }_{x}}u+f(u,v), \\& \partial v/\partial t={{D}_{2}}{{\Delta }_{x}}v+g(u,v), \end{aligned} $$

where $u(x,t)$and $v(x,t)$ are defined as functions of spatial coordinates $x$ and time $t,$ $\partial (\cdot)/\partial t$ id partial differentiation with respect to time, ${{\Delta }_{x}}(\cdot)$ is the second order partial differentiation operator with respect to the spatial coordinates $x$ (diffusion operator or Laplacian), and nonlinear functions $f(u,v)$ and $g(u,v)$ are reaction terms. Spatial pattern is a stable spatially heterogeneous equilibrium solution (DDI or Turing pattern), which arises in the reaction-diffusion system, but which does not exist for the corresponding pure reaction system

$$ \begin{aligned}& \partial u/\partial t=f(u,v), \\& \partial v/\partial t=g(u,v), \end{aligned} $$

for which only spatially homogeneous (constant in $x$) solution exist.

Deterministic Models of Hematopoiesis

Deterministic Models of Regulatory Feedbacks

Simplest Model of Hematopoiesis

Case study: Simple Hierarchical Model

Some basic concepts on which hematopoiesis models are based can be explained using a simplified deterministic model of granulopoiesis. Let us consider a sequence of populations of bone marrow cells, where:

Population $i=0$ consists of the HSC
Populations $\,i=1,\ldots,J$ include several stages of cells committed to granulopoiesis
Populations $\,i=J+1,\ldots,I$ include differentiated granulopoietic precursors
Population $\,i=I+1$ includes the mature blood granulocytes

Let us denote by ${{N}_{i}}(t),\ i=0,\ldots,I+1,\ t=0,\Delta t,\ldots,k\Delta t$ the respective numbers of cells in population $\,i$ (or, in other words, of type i) at times $k\Delta t$ being the integer multiples of the duration of the cell cycle, this latter for this example assumed equal for all cell populations. Let us further assume that cells of type $\,i=1,\ldots,I$ proliferate without losses, i.e., each produces two viable progeny cells upon division. Mature granulocytes do not proliferate but at each time point $k\Delta t$ they die with probability $\alpha \Delta t$. As a result, the expected lifetime of a granulocyte is equal to $1/(\alpha \Delta t)$.

The rules of maturation and differentiation are described as follows:

Each of the HSC (type $i=0$) progeny remains a HSC with probability $1-d$ and differentiates into a cell committed to the granulocyte lineage with probability ${{d}_{0}}<d$ such that $d-{{d}_{0}}$ is the probability of commitment to the remaining lineages.
Each of the progeny of the committed and progenitor type i cells may either remain type i (with probability $1-{{d}_{i}}$) or become type $\,i+1$ (with probability ${{d}_{i}}$).

These rules lead to the following system of difference equations for the expected numbers of cells of all types:

$$ {{N}_{0}}(t+\Delta t)=q{{N}_{0}}(t) $$

(7.1)

$$ {{N}_{i}}(t+\Delta t)={{q}_{i}}{{N}_{i}}(t)+{{p}_{i-1}}{{N}_{i-1}}(t),\ i=0,\ldots,I $$

(7.2)

$$ {{N}_{I+1}}(t+\Delta t)={{N}_{I+1}}(t)+{{p}_{I}}{{N}_{I}}(t)-(\alpha \Delta t){{N}_{I+1}}(t), $$

(7.3)

where for brevity we denote $p=2d$, ${{p}_{i}}=2{{d}_{i}}$, and ${{q}_{i}}=2(1-{{d}_{i}})$, so that $p+{{q}_{0}}<2$ and ${{p}_{i}}+{{q}_{i}}=2$.

Equations (7.1)–(7.3) can be solved recursively. In particular, we are able to compute steady-state (equilibrium) values assuming ${{N}_{i}}(t)={{N}_{i}}=\text{const}$. This results in the following expressions:

$$ {{N}_{i}}={{N}_{0}}\left(\prod\nolimits_{j=0}^{i-1}{{{p}_{j}}}\right)\left(\prod\nolimits_{j=1}^{i}{(1-{{q}_{j}})} \right),\ i=1,\ldots,I $$

(7.4)

$$ {{N}_{I+1}}={{N}_{0}}\left(\prod\nolimits_{j=0}^{I}{{{p}_{j}}}\right)\left(\prod\nolimits_{j=1}^{I}{(1-{{q}_{j}})} \right){{(\alpha \Delta t)}^{-1}}. $$

(7.5)

Let us note that biologically feasible steady state exists if ${{d}_{i}}\ge 1/2$. Further, for simplicity, we will assume that the probabilities of commitment to the subsequent stage are all equal to ${{d}_{i}}=\delta $ for $i=1,\ldots,J$, hence all ${{p}_{i}}=2\delta =\pi $ and ${{q}_{i}}=2(1-\delta)=\psi $ for $i=1,\ldots,J$. We may also assume that all differentiated precursors differentiate further at the subsequent division, i.e., ${{d}_{i}}=1$ for $i=J+1,\ldots,I$, hence ${{p}_{i}}=2$ and ${{q}_{i}}=0$ for $i=J+1,\ldots,I$. This yields

$$ {{N}_{I+1}}={{N}_{0}}{{p}_{0}}{{[\pi (1-\psi)]}^{J}}{{2}^{I-J}}{{(\alpha \Delta t)}^{-1}}={{N}_{0}}{{p}_{0}}{{[2\delta (2\delta -1)]}^{J}}{{2}^{I-J}}{{(\alpha \Delta t)}^{-1}}. $$

(7.6)

Nonlinear (polynomial) action of GCSF feedback

Equation (7.6) demonstrates that the number of peripheral granulocytes at equilibrium depends polynomially on the commitment probability $\delta $. Therefore, if at the normal equilibrium the value of $\delta $ is below 1 (i.e., not all committed cells commit further), then if GCSF action increases $\delta $ so that in each of the $J$ stages of committed cells more cells commit further upon each division, this causes the equilibrium number of peripheral granulocytes to increase (neglecting transients) with the $J$th power of $\delta $, i.e., nonlinearly. Therefore, small deviations of $\delta $ may cause large changes of the equilibrium number of ${{N}_{I+1}}(t),$ the number of mature cells.

Need for a negative internal feedback of HSC

If the commitment probability ${{p}_{0}}$ of HSC is kept unchanged and probability $d$ is equal to ½, then (see Eq. (8.1)) the steady state ${{N}_{0}}(t)={{N}_{0}}=\text{const}$ is maintained. However, if the GCSF feedback causes d to exceed ½, then Equation (7.1) shows that the HSC will be geometrically (exponentially) depleted with time. To prevent this from happening in long term, a protective mechanism is needed. Interplay between the GCSF feedback and the internal negative feedback was first considered by Arino and Kimmel [15]. It has been showed there that some forms of the feedback may not be sufficient for a complete return to equilibrium, a possibility observed in some disease states such as neonatal sepsis [30].

What Does the Simplified Model Fail to Explain?

I.
Interindividual and temporal fluctuations in the number of granulocytes. The simplified model is a mean value model, so it does not account for fluctuations caused by stochastic events at the level of HSC and further amplified in the commitment/differentiation cascade.
II.
Feedbacks. The model is also missing the explicit form of the GCSF and internal feedbacks, although it helps realizing these are needed.
III.
Differentiation arrest and dedifferentiation. The model does not involve the chance state of molecular circuitry guiding the cell to commitment/differentiation, instead it uses aggregate coefficients ${{d}_{i}}$ the simplification it shares with many published models [9, 10].

Deterministic Feedbacks in Hematopoiesis

Deterministic mathematical theory of cell production systems primarily relies on systems of nonlinear DEs. These models perform differently depending on the configuration of regulation feedbacks. Cell production systems are self-renewing cell populations which maintain the continuous supply of differentiated functional cells to various parts of a living organism. The dynamics of cell production systems attracted the attention of biologists and mathematicians a long time ago in the context of blood cell production [31]. Despite differences depending on the type of cells considered, certain common elements can be found in all the cell production systems and their models. First, there exists a self-renewing subpopulation of stem cells. Stem cell divisions can produce both stem cells and cells of greater lineage commitment, called the precursor cells. The precursor cells, in turn, produce cells with an even greater degree of maturity. After a certain number of maturation (differentiation) stages, the mature (differentiated) cells are produced. They usually do not have the ability to divide, and after fulfilling their specific tasks, are removed from the organism.

In normal conditions, the cell production system maintains a constant supply of differentiated mature cells. In the emergency cases, when for some reasons the organism suffers from the loss of certain mature cells (such as loss of erythrocytes in a hemorrhage) the system reacts, providing an increased supply of cells. These two postulates imply that the system is regulated through a long-range feedback mechanism detecting the perturbations in the number of mature cells and accordingly adjusting the production rate of the stem and precursor cells.

It seems logical to suppose at least one more regulation feedback exists. Indeed, the long-range feedback would have a tendency towards “draining” the stem cell population to compensate for the loss. Then, if all the stem cells were committed towards maturation, the whole system might collapse, since only the stem cells are truly self-renewing. Therefore, another feedback should “cut off” the supply of precursor cells if the number of stem cells decreases, preventing the system from extinction. This will be called a short-range feedback.

Based on ideas similar to those presented above, mathematical models of cell production systems were constructed, mainly for various lines of the blood-forming system in man and in experimental animals. For example, Mackey’s periodic neutropenia model (as cited in Haurie et al. [32]) described the effects of a short-range feedback of the stem cell cycle, while the Wazewska and Lasota model included the long-range feedback only [33]. Recently, various possible configurations of short-, mid-, and long-range feedbacks have been discussed and analyzed mathematically [34].

Case study: Configuration of Feedbacks in a Deterministic Model of Hematopoiesis

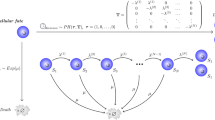
We will use as a case study the series of models devised by Arino and Kimmel [35]. Considering these models will explain the modeling paradigm, which has been later on perfected in various ways. The models are based on the following assumptions (Fig. 7.1):

1.
Stem cell proliferation dynamics is represented by a cell cycle model consisting of two phases: active and passive. A stem cell leaving mitosis enters the passive phase and then it may either transform into a more mature precursor cell or enter the active phase (and then divide and enter the passive phase again). It is assumed that the cell residence time in the resting phase has the exponential distribution with parameter $\alpha (t)$ (the reciprocal of the mean residence time in this phase). Such a hypothesis is consistent with the Smith–Martin model of the cell cycle. The probability of stem cell differentiation (transformation) is denoted by $d(t)$. The residence time in the active phase is equal to T. We understand that our “active phase” is S + G1 + M, where S stands for the deoxyribonucleic acid (DNA) synthesis. G2 denotes the premitotic phase and M the cell division (mitosis). Our “passive phase” is assumed to be G0 + G1, where G0 is the resting (quiescent or “storage”) phase, while G1 is the initial growth phase.
2.
Regulated factors are $d(t)$ probability of stem cell differentiation and/or $\alpha (t)$ reciprocal of the mean residence time in the passive phase.
3.
Each stem cell, once differentiated, produces after time H an average number of A mature (completely differentiated) cells. Quantities A and H represent all the stages of the precursor cells maturation, division, and so forth.
4.
Mature cell life length is a rv with exponential distribution with expected value $1/\beta $.

Model structure implied by the assumptions (1)–(4) is depicted in Fig. 7.1. The equation for the stem cell number $N(t)$ in G0 + G1, takes the following form:

$$ \dot{N}(t)=-\alpha (t)N(t)+2(1-d(t))\alpha (t)N(t). $$

The equation for the number $R(t)$ of mature cells is:

$$ \dot{R}(t)=-\beta R(t)+r(t), $$

where $r(t)$ is the rate of cell flow into the mature cell compartment. Assumption (3) implies

that:

$$ r(t)=Ad(t-H) \alpha (t-H)N(t-H), $$

so that

$$ \dot{R}(t)=-\beta R(t)+r(t)Ad(t-H) \alpha (t-H)N(t-H). $$

We may also compute the number $P(t)$ of cells present at time t in the active phase of the stem cell cycle:

$$ P(t)=\int_{t-T}^{t}{(1-d(\tau))\alpha (\tau)N(\tau)d\tau }. $$

Equations above provide a complete description of the cell production system dynamics, if the regulated factors $\alpha (t)$ and $d(t)$ are specified.

Depletion and Nonunique Equilibria

We will make the case for the possibility of depletion of HSC and nonunique equilibria, by considering the deterministic model of erythropoietic regulation [35].

Model 1: The fraction $d(t)$ of differentiating stem cells is an increasing function of the number of dormant stem cells: $d(t)=g[N(t)]$ . The rate $\alpha (t)$ of the outflow from the dormant stem cell compartment is a decreasing function of the number of mature cells: $\alpha (t)=h[R(t)]$. Intuitively, the mature cell number is influencing the production rate of stem cells, while the contents of the “storage” dormant compartment controls the proportion of differentiating stem cells.
Model 2: In this variant, both $\alpha (t)$ and $d(t)$ depend on the mature cell number: $d(t)=g[R(t)]$, $\alpha (t)=h[R(t)]$ with $g(\cdot)$ and $h(\cdot)$ being decreasing functions. The assumption that both feedbacks here are designed to “exploit” the stem cell population causes system instability.
Model 3: This is, in a sense, a reversal of model 1. The long-range feedback controls the differentiating stem cell fraction, while the “defensive” one, the exit rate from the dormant compartment: $d(t)=g[R(t)]$, $\alpha (t)=h[N(t)]$, where $g(\cdot)$ and $h(\cdot)$ are decreasing.
Model 4: This is a special case of model 1, with $d(t)=1/2$. In this case, model equations assume the form, $\dot{N}(t)=-h[R(t)]N(t)+h[R(t-T)]N(t-T)$ and $\overset{.}{\mathop{R}}\,(t)=-\beta R(t)+(A/2)h[R(t-H)]N(t-H)$.

Importance of the Internal Feedback

Models 1, 2, and 3 have (under additional hypotheses; see the exhaustive discussion in Arino and Kimmel [35]), two equilibria, the trivial one $(N,R)=(0,0)$ and the nontrivial one $(N,R)=(\tilde{N},\tilde{R})$, which is a solution of nonlinear algebraic equations involving functions $g(\cdot)$ and $h(\cdot)$. Without getting into mathematical details, we can state, that in models 1 and 3, which involve autonomic internal feedbacks of the dormant HSC, the trivial equilibrium usually (i.e., for a region of parameter values) repels solutions, while the nontrivial one attracts them. Hence, the system is resistant to shocks. In model 2, which does not include an internal feedback, the situation is reversed, given a deviation from the nontrivial equilibrium, the system decays to the trivial one. This supports the assertion that without an internal feedback, the hematopoietic system may be unstable.

Nonunique equilibria of model 4 display an unusual behavior. Function $V(t)=N(t)+2P(t)$ equal to the number of stem cells in the dormant phase plus twice the number of stem cells in the proliferative phase (“potential” number of HSC) stays constant along the trajectories of the system. Therefore, also at the equilibrium it will be the same value it had at time 0. Simple calculations show that in model 4, initial conditions dictate the equilibrium value: If the system undergoes a shock such as depletion of bone marrow HSC, it will forever linger near that low value. This situation only concerns an impaired internal feedback, but it may correspond to a specific biological defect such as one caused by a defective cytokine receptor (see further on).

Topics concerning configuration and functional forms of deterministic models of feedbacks have been further developed in more recent works of other authors. As an example, Marciniak-Czochra, Stiehl, and coworkers consider a range of general issues related to the question of hierarchy in the cell production systems, such as the granulopoietic system, using rigorous mathematical approaches [36]. HSCs are characterized by their ability of self-renewal to replenish the stem cell pool and differentiation to more mature cells. The subsequent stages of progenitor cells also share some of this dual ability. It is yet unknown whether external signals modulate proliferation rate or rather the fraction of self-renewal. They propose three multicompartment models, which rely on a single external feedback mechanism. In model 1, the signal enhances proliferation, whereas the self-renewal rates in all compartments are fixed. In model 2, the signal regulates the rate of self-renewal, whereas the proliferation rate is unchanged. In model 3, the signal regulates both proliferation and self-renewal rates. The study demonstrates that a unique strictly positive stable steady state can only be achieved by regulation of the rate of self-renewal. Furthermore, it requires a lower number of effective cell doublings. To maintain the stem cell pool, the self-renewal ratio of the HSC has to be greater than or equal to 50 % and it has to be higher than the self-renewal ratios of all downstream compartments. Interestingly, the equilibrium level of mature cells depends only on the parameters of self-renewal of HSC and it is independent of the parameters of dynamics of all upstream compartments. The model is compatible with the increase of leukocyte numbers following HSC transplantation. A more theoretical analysis of feedbacks has been published in ref. [37, 38]. In another paper, Marciniak-Czochra and Stiehl [39] find that that certain conditions have to be met for proliferative parameters of stem cells relative to those of the committed cells. Otherwise, the stem cells die out and their function is fulfilled by cells of one of the committed stages, the one that satisfies these conditions. Their other contributions concern replicative senescence of HSCs [40]. Logic of control, in a more intuitive framework, but considering competing feedbacks, has been considered in the works of Lander and coworkers [41].

Much of classical deterministic analysis has been developed over past 35 years by the school of Mackey and his coworkers. Initially he collaborated with Lasota and Wazewska, who had developed the first mathematical model of erythroid production [33]. They suggested that decreasing the rate of erythroid precursor maturation increases the steady-state level of nonproliferating erythroid cells. A patient would quickly recover red blood cell levels following treatment-induced anemia. Since erythroid precursor maturation rate increases with Epo levels, which are negatively correlated with blood oxygen content, the model suggests that by increasing a patient’s blood oxygen level one can accelerate the rate of erythrocyte recovery following chemotherapeutic insult or radiation therapy. This conclusion was successfully validated in patients, showing the insight mathematical modeling can provide into disease. Another major topic was cytopenias and leukemias. Some neutropenias and anemias are characterized by periodic oscillations in blood cell counts [42]. The dynamics of these disorders has attracted model making, with the goal that the model will illuminate their pathophysiology as well as normal hematopoiesis. The oscillatory behavior seen in these diseases is thought by some to be due to irregular feedback control [42]. Other, more sophisticated models suggest that the abnormality lies not in the feedback loop but in an elevated neutrophil apoptotic rate that perturbs the normal regulation of stem cell dynamics [43].

There exists a category of recent deterministic models, which account for variability among disease cases or different types of disease. For example, Stiehl et al. [44] consider heterogeneity of responses to bone marrow transplants; they developed a model-based methodology for using averaged clinical trial data to estimate responses of individual patients. Other papers address the role of multiple cell lineages, including evolution of leukemia, competition between healthy and leukemic cells and dynamics of multiclonal structure of acute myeloid leukemia (AML) [45, 46]. One implication is that enhanced self-renewal may be a key mechanism in the clonal selection process. Simulations suggest that fast proliferating and highly self-renewing cells dominate at primary diagnosis, while relapse following therapy-induced remission is triggered mostly by highly self-renewing but slowly proliferating cells. A similar framework was applied to myelodysplastic syndrome (MDS) which is an important example of a malignant disease with a hypothetical stem cell origin [47]. The results stress the importance of self-renewal in cancer dynamics and allow concluding that invoking slowly proliferating cancer cells helps explain clinical dynamics and observations such as treatment resistance.

Models with Structure

Case Study: Structured Roeder Model and Competing Feedback

In Roeder’s model, HSCs are assumed to exist in two growth compartments: quiescent (denoted by A) and proliferating (denoted by Ω). At the beginning of every time step (representing 1 h), a stem cell may transfer from A to Ω with probability ω or from Ω to A with probability α. Each stem cell has a time-dependent affinity, denoted by $a(t)$, and the affinity ranges between ${{a}_{\min }}$ and ${{a}_{\max }}$ (which are estimated to be 0.002 and 1.0, respectively [29]). A cell with a high affinity has a high chance of remaining in the A environment or transferring to it. Likewise, a cell with a low affinity is more likely to remain in the Ω environment or transfer to it, where it starts proliferating. The transition probabilities can be variously defined.

Proliferating cells in the Ω compartment progress through various stages of the cell cycle: G1, S, G2, and M. The G1 phase is the longest period of growth during which the cell generates new organelles. The S phase is the period when DNA synthesis and replication occurs. The G2 phase is the short period of growth when the cell prepares for mitosis, and the M phase, or mitosis, is when the cell divides into two daughter cells. Only Ω cells in the G1 phase of the cell cycle can transfer to A. The Ω cells spend about two thirds of their time in the G1 phase. For each cell that remains in the A compartment, its affinity increases by a factor of r (estimated as 1.1). Similarly, cells that remain in Ω, decrease their affinity by a factor of d (estimated as 1.05). The affinity of a cell stops increasing once it reaches the maximal value, ${{a}_{\max }}$. Stem cells whose affinity reaches the minimum affinity, ${{a}_{\min }}$, differentiate into a proliferating precursor and then into a nonproliferating mature cell. Each cell in Ω has an internal time counter, $c(t)$, that indicates its position in the cell cycle (measured in hours). Each time step is equivalent to 1 h. Consequently, at each time step, $c(t)$ increases by 1. After $c(t)$ reaches its maximal value of 48, it recycles back to 0 at the next time step, resulting in a 49-h cell cycle. Cells entering Ω start with a counter that is set at $c(t)$ = 32 corresponding to the beginning of the S phase. For the first 17 h, the cell progresses through the S, G2, and M phases and divides into two cells once $c(t)$ = 48. Then for the next 32 h, ($c(t)$ = 0, …, 31), the cell remains in the G1 phase. If at the end of this period the cell has not transferred to A, it reenters the S, G2, and M phases and the cycle repeats.

In the original work of Roeder et al. [29], an agent-based model has been used to follow the dynamics of stem cell counts in the bone marrow. In a subsequent work by Kim et al. [48], a quasi-stochastic (operating on mean values) model has been derived, for the purpose of elucidating the progression of chronic myelogenous leukemia (CML). As it can be noticed, the mechanism of A↔Ω transitions amounts to an elaborate protective system for the dormant HSC (the “internal feedback” of Arino and Kimmel [35]). This is one of the places in the model, where stochastic effects are likely to play a major role, since HSC may be organized in relatively small clonal colonies [28].

Continuous Maturation

Cell differentiation is a process by which dividing hematopoietic precursor cells become specialized, less proliferative, and equipped to perform specific functions. More generally, differentiation occurs many times during the development of a multicellular organism as the organism changes from a single zygote to a complex system with cells of different types. During tissue repair and normal cell turnover, a steady supply of somatic cells is ensured by proliferation of corresponding adult stem cells (such as the hemopoietic stem cells), which retain the capability for self-renewal. Nonhematologic cancers are likely to originate from a population of cancer stem cells that have properties comparable to those of stem cells [49]. Stem cell state and fate depend on the environment, which ensures that the critical stem cell character and activity in homeostasis is conserved, and that repair and development are accomplished [50]. While different genetic and epigenetic processes are involved in formation and maintenance of different tissues, the dynamics of population depends on the relative importance of symmetric and asymmetric cell divisions, cell differentiation, and death. One established view of the differentiation process is that of a series of discrete compartments, which can be modeled by a system of ordinary DEs describing dynamics of cells at different maturation stages and transition between the stages. This corresponds to the assumption [51, 52] that in each lineage of cell precursors there exists a discrete chain of maturation stages, which are sequentially traversed. However, differentiated precursors form such a clear sequence only under homeostatic (steady-state) conditions. Committed cells generally form a continuous sequence, which may involve incremental stages, part of which may be reversible. These observations invoke not only the fundamental biological questions of whether cell differentiation is a discrete or a continuous process and what the measure of cell differentiation is but also the question of how to choose an appropriate modeling approach. Is the pace of maturation (commitment) dictated by successive divisions, or is maturation a continuous process decoupled from proliferation? Early continuous maturation models have been conceived by Mackey group [43], but the question of correspondence of the discrete compartment and continuous maturation models is still open.

A recent paper that mathematically compares these two types of models is Doumic et al. [53]. The continuous maturation model has the form of a partial DE of transport type—a structured population equation with a nonlinear feedback loop. This models the signaling process due to cytokines, which regulate the differentiation and proliferation process. The dynamics of the model is compared to that of its discrete counterpart. Without an attempt to describe the details, let us note that the continuous and discrete maturation model (which assume the same mode of regulation) differ with respect to dynamics. One of the manifestations is that the discrete model has a richer set of stable equilibria including some with the upper stages of the hierarchy depleted, but the lower ones still capable of maintaining proliferation. Another mathematical approach is to unify the continuous and discrete maturation in a single model [54]. An earlier attempt includes mathematical proof of equivalence between a transport type approach and a bp [55]).

Stochastic Models of Hematopoiesis

Stochastic processes (in particular the bp’s) can be used to model biological phenomena of some complexity, at cellular or subcellular levels [56]. Probabilistic population dynamics arise from the interplay of the population growth pattern with probability. Thus, the classical G–W bp defines the pattern of population growth using sums of independent and identically distributed (iid) rv’s; the population evolves from generation to generation by the individuals getting iid numbers of children. This mode of proliferation is frequently referred to as “free growth” or “free reproduction.” The “simple deterministic model of hematopoiesis” considered earlier on is in fact describing the expected (mean) trajectories of a multitype G–W process.

The formalism of the G–W process provides insight into one of the fundamental problems of cell populations, the extinction problem and its complement, the question of size stabilization: If a freely reproducing population does not die out, can it stabilize, or does it have to grow beyond bounds? The answer is that there are no freely reproducing populations with stable sizes. Population size stability, if it exists in the real world, is the result of forces other than individual reproduction, of the interplay between populations, and their environment. This is true for processes much more general than the G–W process. A fusion between branching and environment pressure constitutes a challenge for stochastic models (if one does not wish to resort to simulation only); the same way, selection constitutes a challenge to population genetics models.

If unlimited growth models make more sense in the context of proliferation of cancer cells, then what the rate of the unlimited growth is? It can be answered not only within the generation counting framework of G–W type processes but also in more general branching models. In all these frameworks, in the supercritical case, when the average number of progeny of an individual is greater than 1, the growth pattern is asymptotically exponential. The parameter of this exponential growth is the famous Malthusian parameter. In the supercritical case, we can answer not only questions about the rate of growth but also questions about the asymptotic composition of nonextinct populations. What will the age distribution tend to be? What is the probability of being firstborn? What is the average number of second cousins? Importantly for biological applications, many of these questions do not have natural counterparts in deterministic models of unlimited growth.

Case Study: Model of SNC → MDS → AML Transition [57]

Severe congenital neutropenia (SCN) is a life-threatening infection in children which can be avoided through the use of recombinant GCSF. However, SCN often transforms into secondary MDS (sMDS) and then into secondary AML (sAML). A great unresolved clinical question is whether chronic, pharmacological doses of GCSF contribute to this transformation [58]. A number of epidemiological clinical trials have demonstrated a strong association between exposure to GCSF and sMDS/sAML [59–62] Mutations in the distal domain of the GCSF receptor (GCSFR) have been isolated from patients with SCN who developed sMDS/sAML or patients with de novo MDS [63]. Recently, clonal evolution over approximately 20 years was documented in a patient with SCN who developed sMDS/sAML [64]. Clonal evolution of a sick hematopoietic progenitor cell in SCN involves perturbations in proximal and distal signaling networks triggered by a mutant GCSFR. A summary of signaling pathways taking part in the response to GCSF in normal and mutant cells is presented in Fig. 7.2. Transition from SCN → sMDS → sAML involves chance mechanisms, such as mutations, drift, and transcription and receptor noise, which require that stochastic models to be used [1].

The model of this process in Kimmel and Corey [57] assumes that a limited mutation load at the SCN phase causes neutropenia and fluctuations of cell population size. With time, accumulation of driver mutations causes expansion of mutant clones, which however are not yet expanding at a dramatic rate. At some point in time, mutations accumulate sufficiently to cause a major change in the proliferation law and the now malignant cell population starts rapidly expanding. In summary: (i) At the time of diagnosis of SCN, GCSF therapy is initiated, which induces an initial series of X driver mutations, occurring at random times. (ii) The X-th mutation causes transition to the MDS, during which further Y mutations occur. (iii) After X + Y mutations, the AML stage begins, during which the subsequent mutant clones grow at increasing rate, which in turn shortens the times at which still new mutations appear. In the model, the increasing proliferation rate of successive mutant clones causes acceleration of growth of the malignant bone marrow stem cell population, which shortens the time interval to appearance of new clones, which in turn increases proliferation rate, and so forth; this results in a positive feedback (Fig. 7.3). Stochastic nature of the process (the times to appearance of each next mutant are random) causes a spread of the timing of the subsequent mutations, particularly the first X mutations during the SCN phase. This may result in the transition to MDS not manifesting itself for a very long time in a fraction of cases.

Stochastic dynamics plays a major role in the model. For a new subclone, stochastic theory is used to estimate extinction probability, with extinction after more than a few cell generations being negligible in view of the growth advantage of the new clone. However, the time at which the next mutation occurs in a cell clone is also stochastic and it is as a rule more dispersed for the slower-growing clones. Therefore, the time to reach the threshold number of bone marrow stem cells (which in our model defines the time at sAML diagnosis) is an rv. One of the questions asked is whether dispersion of this time matches the wide distribution of the times at diagnosis [65].

Mathematically, the population-genetic effect of population size-dependent accumulation of mutations occurs as a natural consequence of the proliferation law in the form of a multitype G–W bp [66]. (i) Consecutively arising surviving mutant clones are numbered with the index k, ranging from 1 to k; time interval between the appearance of the k-th and k + 1-st surviving mutant clones is denoted by ${{\tau }_{k}}.$ k-th mutant cells have accumulated k driver mutations. (ii) All clones expand as G–W bp’s. Cell life length is constant and equal to T, and at that time the cell either produces two progeny with probability ${{b}_{k}}$ (cell type k) or dies (or becomes quiescent or differentiated, which does not make a difference for disease dynamics) with probability $1-{{b}_{k}}$. (iii) A cell of type k can mutate upon its birth (for definiteness) to type k + 1 with probability u. These three rules allow one to derive the probability distributions of time intervals ${{\tau }_{k}},$ probabilities of survival of each clone, and expected growth laws of each clone. Fig. 7.4 depicts the impact of successive driver mutations on the natural course of the SCN → sMDS → sAML transition. Fig. 7.4a depicts counts ${{N}_{i}}(t)$ of cells in successive mutant clones as a function of time. Straight lines with increasing slopes are counts of cells in successive mutant clones. We observe that the time intervals separating the origins of successive clones are decreasing with each mutation event. Thick dashed line represents the total mutant cell count. Fig. 7.4b depicts relative proportions ${{n}_{i}}(t)={{N}_{i}}(t)/\sum\nolimits_{j}{{{N}_{j}}(t)}$ of cells belonging to successive mutant clones. It is interesting to observe that clones with increasing numbers of mutations dominate transiently, until they are replaced by other clones with higher proliferative capacity (selective value).

It is somewhat surprising that under any combination of coefficients of the model, the range of simulated times at which sAML arises is rather narrow [57]. This outcome is in contrast to the wide spread of times at diagnosis summarized in Rosenberg et al. [65]. The observed distributions of times (and ages) at diagnosis can be matched if a large interindividual variability is assumed. This illustrates how important it is to take into account potential different sources of stochasticity when modeling human disease.

Underlying stochastic effects

Most likely mechanisms creating stochastic behavior in hematopoiesis are: (i) asymmetric division of progeny cells, with resulting difference in their fates, and (ii) on–off switching of differentiation status of cells accomplished by hormonal controls such as GCSF or Epo.

Asymmetric division is a possible mechanism by which randomness is inserted into stem cells’ decision making. In the past, a prevailing hypothesis concerning stem cell decisions was that at each stem cell division, one of the progeny becomes a committed cell whereas the other remains a stem cell, in this manner providing a perfect balance between commitment and self-renewal. There exist at least two problems with this simple paradigm: first, that this does not seem satisfactory when the demand for committed cells is greater than average, and second, that it has been observed that stem cells can divide both asymmetrically and symmetrically. Observations are consistent with stochastic decisions as to which mode of division to choose. Consequences for population dynamics are different for different stochastic scenarios of asymmetric division, even if on the average these scenarios produce 50–50 committed and stem cells.

An interesting discussion of symmetry and asymmetry in stem cell division has been proposed by Schroeder [67]. Discussing findings in an experimental paper by Wu et al. [68], Schroeder [67] considers a catalogue of versions of symmetric and asymmetric divisions. Symmetric division: undifferentiated hemopoietic precursor cells (HPCs) produce two undifferentiated progeny, whose later fate decisions are not linked to the parent’s mitosis. Hypothetical mechanisms of asymmetric divisions in HPCs include: (i) orientation of the division plane that leads to positioning of only one of the progeny close enough to localized extrinsic signals provided by a self-renewal or differentiation niche, (ii) generation of two identical undifferentiated progeny, which being in close spatial contact immediately after mitosis engage in reciprocal feedback signaling, leading to differentiation of only one of them, and (iii) intrinsic cell fate determinants segregate asymmetrically between daughter cells, instructing either self-renewal or differentiation of the receiving daughter. Let us notice that these distinct scenarios do not produce distinctions in deterministic models, where only averages matter, but they lead to possibly widely divergent scenarios in stochastic dynamics. As an example of mechanism (iii), Wu [68] found that Numb, a negative modulator of Notch signaling, which is known to asymmetrically segregate to one progeny during asymmetric division is indeed frequently enriched in one of the two emerging progeny cells. This has been accomplished by analyzing Numb localization in HPCs that had been fixed during mitosis and visualized.

Switches have been proposed to effectively translate the hormonal signals into decision about commitment or further progression. An archetypical molecular bistable switch (Gardner, Collins, and Cantor genetic toggle switch [69]) is deterministic and involves a system of two genes, the products of which are mutual cross-repressors. The system also involves two activators, which momentarily annul the action of the repressors and allow the system to switch. From mathematical point of view, the switch is a dynamical system with two stable equilibria separated by an unstable one. A more sophisticated switch, which moreover is based on confirmed molecular mechanism, is the Laslo switch [21].

However, a molecular switch may involve stochastic mechanisms, which make its action less predictable. This may mean that, if the level of fluctuations is sufficiently high, the switch is oscillating between the two stable equilibria, before or instead of being absorbed by one of them. Such behavior has been observed. In disease state, we may have to do with an aberrant switch with dynamics altered by mutation in one of the important molecular circuits.

Several transcription factors play key roles in regulating myelopoiesis and granulopoiesis. These include the ETS protein PU.1 and the cytosine-cytosine-adenosine-adenosine-thymidine (CCAAT)-enhancer-binding protein-α (CEBP-α), and are often referred to as the “master regulators” of myeloid development [21]. Although PU.1 is sometimes considered to induce myeloid versus lymphoid and monocyte versus granulocyte differentiation, the data suggest that the effects of PU.1 are more complex than this. Similarly, CEBP-α has been considered to direct granulocyte versus monocyte differentiation. PU.1 and CEBP-α constitute a gene regulatory network with bistable properties. Gene regulatory networks may be modified by protein abundance and posttranslational modification, both of which were shown to be induced by activation of cytokine receptors such as GCSFR via kinases. First, PU.1 and CEBP-α undergo serine/threonine phosphorylated triggered by GCSFR activation. Second, GCSFR activation modulates CEBP-α expression, which influences PU.1 function via unidentified mechanisms. Third, GCSFR also influences Gfi-1 expression and activity.

For the granulocyte lineage, the most essential growth factor is GCSF. Its cognate receptor, GCSFR is a member of the hematopoietin cytokine receptor superfamily, which includes receptors for many of the interleukins, colony-stimulating factors (e.g., Epo), cytokines (e.g., leptin), and hormones (e.g., prolactin). As a drug, recombinant human GCSF is used widely to reduce the duration of chemotherapy-induced neutropenia and mobilize into the periphery hematopoietic progenitor cells for transplant [70]. A number of clinical disorders demonstrate importance of GCSF/GCSFR (see below). Mutations in the GCSFR have been found in patients with SCN, MDS, and AML [59, 71].

Laslo et al. [21] describe a regulatory network demonstrating bistability based on a feedback loop between two transcriptional repressors (Egr/Nab-2 and Gfi-1) of PU.1 and GATA-1 genes that drive a common myeloid progenitor cell toward either granulocyte or macrophage fate. As mentioned above, deterministic toggle, or bistable, switch is a circuit which has two stable equilibria, usually separated by an unstable one [69]. Stochastic toggle switches have much richer behavior [72]. Instead of a monotonous approach to the stable equilibrium, the absorbing state is reached via a “saw-like” trajectory. If the time before absorption extends over more than a single cell cycle, the cell remains uncommitted, or in one of the the “intermediate” states, as for example in the paper by Laslo et al. [73] where existence of graded states of cells was experimentally observed and theoretically predicted (albeit using a deterministic switch). On the theoretical side, state space methods have been used by Michaels et al. [74] to find the range of dynamical behaviors exhibited by Laslo-type switch.

Jaruszewicz et al. [75] demonstrate that in a system of bistable genetic switch, the randomness characteristics control in which of the two epigenetic attractors the cell population will settle. They focus on two types of randomness: the one related to gene switching and the one related to protein dimerization. Change of relative magnitudes of these random components for one of the two competing genes introduces a large asymmetry of the protein stationary probability distribution and changes the relative probability of individual gene activation. Increase of randomness associated with a given gene can both promote and suppress activation of the gene. Each gene is repressed by an increase of gene switching randomness and activated by an increase of protein dimerization randomness. In summary, the authors demonstrated that randomness may determine the relative strength of the epigenetic attractors, which may provide a unique mode of control of cell fate decisions.

Traulsen et al. [76] concentrate on the role of hierarchy of the hematopoietic system, discussing the influence of mutations in the hematopoietic system. Although mutations can occur in any cell within hematopoiesis, both the size of the circulating clone and its lifetime depend on the location of the cell of origin in the hematopoietic hierarchy. Mutations in more primitive cells give rise to larger clones that survive for longer, taking also a longer time to appear in the circulation. On the contrary, the smaller clones caused by mutations of more differentiated precursors appear in the circulation much more rapidly after the causal mutation, but they are smaller and survive shorter. Three disease-causing mutations serve as illustrations: the breakpoint cluster region gene–V-abl Abelson murine leukemia viral oncogene homolog 1 gene (BCR–ABL) associated with chronic myeloid leukemia; mutations of the PIG-A gene associated with paroxysmal nocturnal hemoglobinuria; and the V617 F mutation in the JAK2 gene associated with myeloproliferative diseases. Among other, evidence is presented of existence of these mutations in asymptomatic individuals, speculatively, these are mutations in more differentiated precursors. Citing from Traulsen et al. [76]: “In general, we can expect that only a mutation in a hematopoietic stem cell will give long-term disease; the same mutation taking place in a cell located more downstream may produce just a ripple in the hematopoietic ocean.”

Wilson et al. [77] argue based on a combination of flow cytometry with label-retaining assays (BrdU and histone H2B-GFP) that there exists a population of dormant mouse HSCs (d-HSCs) within the lin− Sca1+ cKit+ CD150+ CD48− CD34− population. Computational modeling suggests that d-HSCs divide about every 145 days, or five times per lifetime. d-HSCs harbor the vast majority of multilineage long-term self-renewal activity. They form a reservoir of the most potent HSCs during homeostasis, and are efficiently activated to self-renew in response to bone marrow injury or GCSF stimulation. After reestablishment of homeostasis, activated HSCs return to dormancy, suggesting that HSCs are not stochastically entering the cell cycle but they reversibly switch from dormancy to self-renewal under conditions of hematopoietic stress.

Becker et al. [78] show that Epo receptors have the ability to cope with steady-state and acute demand in the hematopoietic system. By mathematical modeling of quantitative data and experimental validation, these authors showed that rapid ligand depletion and replenishment of the cell surface receptor are characteristic features of the Epo receptor (EpoR). The amount of Epo–EpoR complexes and EpoR activation integrated over time corresponds linearly to ligand input.

Models of Mutations and Evolution of Disease

Carcinogenesis Models

Carcinogenesis modeling has had an established history of using stochastic models, beginning with the Knudson two-hit model. Successor models include the multi-hit model and eventually to the two-stage clonal expansion model of Moolgavkar [79]. With almost 1000 citations, this paper might be called one of the most influential ever mathematical models in cancer research. Concerning its application in leukemias, see, e.g., Radivoyevich et al. [80].

We will focus mostly on models of leukemogenesis, conceived in the genome-sequencing era. These models have the following features, which are a novelty due to both evolution of thinking in inflow of a large number of new variant data:

1.
Mutations are identified as variants in studies in which whole exomes or even genomes are sequenced for each individual in the study.
2.
Functionality of mutations is determined in two stages: first by bioinformatics algorithms (usually based on evolutionary comparisons) and then by wet-laboratory studies of pathways influenced by these mutations.
3.
Progression of leukemogenesis is based on the concept of driver and passenger mutations. Driver mutations are selected for most advantageous phenotype of cancer cells, whereas the passenger mutations are neutral byproducts of carcinogenesis and serve as molecular clocks of the process.

A number of interesting models of mutations leading to cancer have recently been published (see references further on). They all explore models of proliferation, frequently using bp’s, combining them with models of driver and passenger mutations. Driver mutations are those that, although they might have arisen spontaneously, provide selective advantage for the emerging cancer proliferation, particularly against the background of already existing inherited or acquired mutations. Passenger mutations are generally neutral and their accumulation may provide a molecular “clock” indicating how long it has been since the cancer cells deviated from normal cells. Tumors are initiated by the first genetic alteration that provides a relative fitness advantage. In the case of leukemias, this might represent the first alteration of an oncogene, such as a translocation between BCR and ABL.

Recent paper by Ley et al. [81] addressed the issue of driver mutations contributing to the pathogenesis of AML, using analysis of the genomes of 200 adult cases of de novo AML, either whole-genome sequencing (50 cases) or whole-exome sequencing (150 cases), along with ribonucleic acid (RNA) and microRNA sequencing and DNA-methylation analysis. The conclusion was that AML genomes have fewer mutations than most other adult cancers, with an average of only 13 mutations found in genes. Of these, an average of five was in genes that are recurrently mutated in AML. A total of 23 genes were significantly mutated, and another 237 were mutated in two or more samples. Further analysis suggested strong biologic relationships among several of the genes and categories. Further studies of this kind are likely to lead to insights into the nature of these relationships, although with very few exceptions (such as Beekman et al. [64]) only a single time point in patient lifetime is usually available.

One of the important recent papers with this focus is the mathematical model of the relationship between accumulation of driver and passenger mutation in tumors published by Nowak and Vogelstein groups [82]. In most previous models of tumor evolution, mutations accumulate in cell populations of constant size or of variable size, but the models take into account only one or two mutations. Such models typically address certain aspects of cancer evolution, but not the whole process. In the model presented in Bozic et al. [82], it has been assumed that each new driver mutation leads to a slightly faster tumor growth rate. This model is as simple as possible, because the analytical results depend on only three parameters: the average driver mutation rate u, the average selective advantage associated with driver mutations s, and the average cell division time T. The model is based on G–W bp.

The hypotheses are as follows: At each time step, a cell can either divide or differentiate, senesce, or die. In the context of tumor expansion, there is no difference between differentiation, death, and senescence, because none of these processes will result in a greater number of tumor cells than present prior to that time step. It is assumed that driver mutations reduce the probability that the cell will become “stagnate,” i.e., it will differentiate, die, or senesce, although the stagnant cells are not removed from the tumor. A cell with k driver mutations has a stagnation probability ${{d}_{k}}={{(1-s)}^{k}}/2$. The division probability is ${{b}_{k}}=1-{{d}_{k}}$. The parameter s is the selective advantage provided by a driver mutation. When a cell divides, one of the daughter cells can acquire an additional driver mutation with probability u. The theory can accommodate any realistic mutation rate and the major numerical results are only weakly affected by varying the mutation rate.

We can calculate the average time between the appearances of successful cell lineages. Not all new mutants are successful, because stochastic fluctuations may lead to the extinction of a lineage. The lineage of a cell with k driver mutations survives only with a probability of approximately $1-{{d}_{k}}/{{b}_{k}}\cong 2sk$. Assuming that u ≪ ks ≪ 1, the average time between the first successful cell with k and the first successful cell with k + 1 driver mutations is given by

$$ {{\tau }_{k}}=\frac{T}{ks}\log \frac{2ks}{u}. $$

This result is obtainable from the theory of the G–W process (by elementary means) and the derivation is found in the supplement to Bozic et al. [82]. The cumulative time to accumulate k mutations grows logarithmically with k. On the other hand, the average number of passenger mutations, $n(t)$, present in a tumor cell after t days is proportional to t, that is $n(t)=\nu t/T$, where $\nu $ is the rate of acquisition of neutral mutations. Combining the results for driver and passenger mutations, results in a formula for the number of passenger mutations that are expected in a tumor that has accumulated k driver mutations

$$ n=\frac{\nu }{2s}\log \frac{4k{{s}^{2}}}{{{u}^{2}}}\log k. $$

Here, n is the number of passengers that were present in the last cell that clonally expanded. Bozic et al. [82] demonstrate that this dependence fits empirical data on several human cancers.

Distribution of Mutational Events in Various Phases of Tumor Growth

This question has been recently addressed by Tomasetti et al. [83]. The framework is not very different from that of Bozic et al. [82]. However, the paper describes mathematically the different phases in which somatic mutations occur in a tissue giving rise to a cancer. Starting from a single fertilized egg, all tissues are created via clonal expansion (development phase). The tissue is then subjected to periodic self-renewals. During development and tissue renewal, passenger mutations occur randomly, undergo clonal expansions and either become extinct or expand as successive passenger mutations accumulate. A driver gene mutation may initiate a tumor cell clone, which then can expand through subsequent driver mutations, eventually yielding a clinically detectable tumor mass (cancerous phase). Passenger mutations occur during this phase as well. The model makes the novel prediction, validated by empirical findings, that the number of somatic mutations in tumors of self-renewing tissues is positively correlated with the age of the patient at diagnosis. Importantly, the analysis indicates that half or more of the somatic (i.e., acquired, non-germline) mutations in tumors of self-renewing tissues occur prior to the onset of neoplasia. This is the case, among others for the chronic lymphocytic leukemia (CLL). The model also provides a novel way to estimate the in vivo tissue-specific somatic mutation rates in normal tissues directly from the sequencing data of tumors.

Stochastic models also allow modeling of eradication of leukemic stem cells while saving healthy stem cells. The paper by Sehl et al. [84] uses an impressive array of analytical and computational tools to analyze a pair of stochastic processes describing proliferation and death of healthy and cancer stem cells under chemotherapy. The question asked concerns the birth and death rates differential between these two cell types, required to eradicate the latter and preserve the former. Mutations, emergence of drug resistance, interactions of cancer and healthy cells, and other complicating factors are disregarded. Because the biological setup is simplified to the extreme, it allows effective mathematical analysis.

A review of gene copy number and loss of heterozygosity and gene mutation profiles demonstrated that relapsed AML invariably represented reemergence or evolution of a founder clone Parkin et al. [85]. Analysis of informative paired persistent AML disease samples uncovered cases with two coexisting dominant clones of which at least one was chemotherapy sensitive and one resistant, respectively. These data support the conclusion that incomplete eradication of AML founder clones rather than stochastic emergence of fully unrelated novel clones underlies AML relapse and persistence.

As a side note, it seems surprising that quite few papers offer estimates of absolute numbers of HSCs and committed cells. Against this background, the paper by Peixoto et al. [86] discusses the mathematics of hematopoiesis based on stochastic hypotheses. Mathematical model that describes normal hematopoiesis across mammals as a stable steady state of a hierarchical stochastic process is also used to understand the detailed dynamics of a range of blood disorders both in humans and in animal models. The paper includes comparative numerical estimates of the numbers of cells in different compartments.

Models of Spatial Effects and Structure

Niches

One of the most important realizations of recent years has been that there existed spatial organization in normal and malignant HSCs in bone marrow. This finding allowed correlating such states as proliferative activity, dormancy, and differentiation, not only with the locations in the bone marrow but also with proximity to some other cells type such as mesenchymal stem cells or osteoblasts. Such organization has been previously postulated in the papers by Roeder and coauthors; however, now it is based on biologically verifiable findings. The locations are referred to as stem cell niches. A recent review by Tieu et al. [28] states that the HSC niche is an important regulator of stem cell fate. Complex signaling pathways, such as those involving Notch, Wnt, and Hedgehog, regulate stem cell renewal, differentiation, and quiescence [87 – 89]. Mathematical models can be useful in studying the dynamics of stem cell maintenance and, specifically, spatial considerations related to the structural relationships between stem cells and their progeny with cells of the microenvironment. This paradigm will trigger development of a new generation of deterministic and stochastic models, in which the interaction of spatial and stochastic effects poses new mathematical problems.

Huang [90] discusses in qualitative terms three perspectives outside the realm of their familiar linear deterministic view: (i) state space, (ii) high dimensionality, and (iii) heterogeneity. These concepts jointly offer a new vista on stem cell regulation that naturally explains many novel, counterintuitive observations and their inherent inevitability, obviating the need for ad hoc explanations of their existence based on natural selection.

Bertolusso and Kimmel [91] considered the early carcinogenesis model originally proposed as a deterministic reaction-diffusion system of the following form:

$$ \begin{aligned}& \partial c/\partial t=(a(b,c)-{{d}_{c}})c+\mu\\& \partial b/\partial t=\alpha (c)g-{{d}_{b}}b-db \\& \partial g/\partial t={{\gamma }^{-1}}({{\partial }^{2}}g/\partial {{x}^{2}})-\alpha (c)g-{{d}_{g}}g+\kappa (c)+db, \end{aligned} $$

where c, g, and b are the spatial densities of cells, free-diffusing growth factor, and bound growth factor, respectively. The model explores the spatial effects stemming from growth regulation of precancerous cells by diffusing growth factor molecules. The model has been originally devised [92] for solid tumors spreading along linear or tubular structures such as in lung or breast cancer, but it might apply to systems of similar geometry, which are found in bone marrow. The original deterministic model exhibits Turing instability, producing transient spatial density spikes in cells which are model counterparts of emerging foci of malignant cells. However, the process of diffusion of growth factor molecules is by its nature a stochastic random walk. An interesting question emerges to what extent the dynamics of the deterministic diffusion model approximates the stochastic process generated by the model. Bertolusso and Kimmel [91] addressed this question using simulations with a new software tool called sbioPN (spatial biological Petri Nets). The conclusion is that whereas single-realization dynamics of the stochastic process is very different from the behavior of the reaction diffusion system, it is becoming more similar when averaged over a large number of realizations. The degree of similarity depends on model parameters. Interestingly, despite the differences, typical realizations of the stochastic process include spikes of cell density, which however are spread more uniformly and are less dependent of initial conditions than those produced by the reaction-diffusion system.

References

Whichard ZL, Sarkar CA, Kimmel M, Corey SJ. Hematopoiesis and its disorders: a systems biology approach. Blood. 2010;115(12):2339–47.
Article CAS PubMed Central PubMed Google Scholar
Snijder B, Pelkmans L. Origins of regulated cell-to-cell variability. Nat Rev Mol Cell Biol. 2011;12(2):119–25.
Article CAS PubMed Google Scholar
Pelkmans L. Using cell-to-cell variability-a new era in molecular biology. Science. 2012;336(6080):425–6.
Article CAS PubMed Google Scholar
Raue A, Becker V, Klingmüller U, Timmer J. Identifiability and observability analysis for experimental design in nonlinear dynamical models. Chaos. 2010;20(4):045105.
Article CAS PubMed Google Scholar
Laurent M, Deschatrette J, Wolfrom Claire M. Unmasking chaotic attributes in time series of living cell populations. PLoS ONE. 2010;5(2):e9346.
Article PubMed Central PubMed Google Scholar
Kimmel M, Darzynkiewicz Z, Arino O, Traganos F. Analysis of a cell cycle model based on unequal division of metabolic constituents to daughter cells during cytokinesis. J Theor Biol. 1984;110(4):637–64.
Article CAS PubMed Google Scholar
Schroeder T. Long-term single-cell imaging of mammalian stem cells. Nat Methods. 2011;8(4):S30–5.
Article CAS PubMed Google Scholar
Takizawa H, Boettcher S, Manz MG. Demand-adapted regulation of early hematopoiesis in infection and inflammation. Blood. 2012;119(13):2991–3002.
Article CAS PubMed Google Scholar
Ogawa M. Stochastic model revisited. Int J Hematol. 1999;69(1):2.
CAS PubMed Google Scholar
Abkowitz JL, Catlin SN, Guttorp P. Evidence that hematopoiesis may be a stochastic process in vivo. Nat Med. 1996;2(2):190–7.
Article CAS PubMed Google Scholar
Brock A, Chang H, Huang S. Non-genetic heterogeneity—a mutation-independent driving force for the somatic evolution of tumours. Nat Rev Genet. 2009;10(5):336–42.
Article CAS PubMed Google Scholar
Cohen Ariel A, et al. Dynamic proteomics of individual cancer cells in response to a drug. Science. 2008;322(5907):1511–6.
Article Google Scholar
Sigal A, et al. Variability and memory of protein levels in human cells. Nature. 2006;444(7119):643–6.
Article CAS PubMed Google Scholar
Webb GF. Random transitions, size control, and inheritance in cell population dynamics. Math Biosci. 1987;85(1):71–91.
Article Google Scholar
Arino O, Kimmel M. Asymptotic analysis of a cell cycle model based on unequal division. SIAM J Appl Math. 1987;47(1):128–45.
Article Google Scholar
Tyson JJ, Hannsgen KB. Cell growth and division: a deterministic/probabilistic model of the cell cycle. J Math Biol. 1986;23(2):231–46.
Article CAS PubMed Google Scholar
Harnevo LE, Agur Z. Drug resistance as a dynamic process in a model for multistep gene amplification under various levels of selection stringency. Cancer Chemother Pharmacol. 1992;30(6):469–76.
Article CAS PubMed Google Scholar
Kimmel M, Axelrod DE. Mathematical models of gene amplification with applications to cellular drug resistance and tumorigenicity. Genetics. 1990;125(3):633–44.
CAS PubMed Central PubMed Google Scholar
Gupta PB, Fillmore CM, Jiang G, Shapira SD, Tao K, Kuperwasser C, Lander ES. Stochastic state transitions give rise to phenotypic equilibrium in populations of cancer cells. Cell. 2011;146(4):633–44.
Article CAS PubMed Google Scholar
Chang HH, Hemberg M, Barahona M, Ingber DE, Huang S. Transcriptome-wide noise controls lineage choice in mammalian progenitor cells. Nature. 2008;453(7194):544–7.
Article CAS PubMed Google Scholar
Laslo P, Spooner CJ, Warmflash A, Lancki DW, Lee H-J, Sciammas R, Gantner BN, Dinner AR, Singh H. Multilineage transcriptional priming and determination of alternate hematopoietic cell fates. Cell. 2006;126(4):755–66.
Article CAS PubMed Google Scholar
Muzzey D, van Oudenaarden A. When it comes to decisions, myeloid progenitors crave positive feedback. Cell. 2006;126(4):650–2.
Article CAS PubMed Google Scholar
Loose M, Swiers G, Patient R. Transcriptional networks regulating hematopoietic cell fate decisions. Curr Opin Hematol. 2007;14(4):307–14.
Article CAS PubMed Google Scholar
Raser JM, O’Shea EK. Noise in gene expression: origins, consequences, and control. Science. 2005;309(5743):2010–13.
Article CAS PubMed Central PubMed Google Scholar
Elowitz MB, Levine AJ, Siggia ED, Swain PS. Stochastic gene expression in a single cell. Sci Sig. 2002;297(5584):1183.
CAS Google Scholar
Lipniacki T, Paszek P, Marciniak-Czochra A, Brasier AR, Kimmel M. Transcriptional stochasticity in gene expression. J Theor Biol. 2006;238(2):348–67.
Article CAS PubMed Google Scholar
Samoilov MS, Price G, Arkin AP. From fluctuations to phnotypes: the physiology of noise. Sci Signal. 2006;2006(366):re17.
Google Scholar
Tieu KS, Tieu RS, Martinez-Agosto JA, Sehl ME. Stem cell niche dynamics: from homeostasis to carcinogenesis. Stem Cells Int. 2012;2012:9.
Article Google Scholar
Roeder I, Horn M, Glauche I, Hochhaus A, Mueller Martin C, Loeffler M. Dynamic modeling of imatinib-treated chronic myeloid leukemia: functional insights and clinical implications. Nat Med. 2006;12(10):1181–4.
Article CAS PubMed Google Scholar
Uguz A, Coskun M, Yuzbey S, Kizilors A, Karadogan I, Gura A, Yoldas B, Oygur N, Yegin O. Apoptosis of cord blood neutrophils and their response to colony-stimulating factors. Am J Perinatol. 2003;19(08):427–34.
Article Google Scholar
Lajtha LG, Pozzi LV, Schofield R, Fox M. Kinetic properties of haemopoietic stem cells. Cell Prolif. 1969;2(1):39–49.
Article Google Scholar
Haurie C, Dale DC, Mackey MC. Cyclical neutropenia and other periodic hematological disorders: a review of mechanisms and mathematical models. Blood. 1998;92(8):2629–40.
CAS PubMed Google Scholar
Wazewska-Czyzewska M, Lasota A. Mathematical models of the red cell system. Mat Stos. 1976;6:25–40.
Google Scholar
Lo W-C, Chou C-S, Gokoffski KK, Wan FY-M, Lander AD, Calof AL, Nie Q. Feedback regulation in multistage cell lineages. Math Biosci Eng. 2009;6(1):59.
Article PubMed Central PubMed Google Scholar
Arino, Ovide, and Marek Kimmel. “Stability analysis of models of cell production systems.” Mathematical Modelling 1986;7(9):1269-1300.
Google Scholar
Marciniak-Czochra A, Stiehl T, Ho AD, Jäger W, Wagner W. Modeling of asymmetric cell division in hematopoietic stem cells-regulation of self-renewal is essential for efficient repopulation. Stem Cells Dev. 2009;18(3):377–86.
Article CAS PubMed Google Scholar
Nakata Y, Getto P, Marciniak-Czochra A, Alarcón T. Stability analysis of multi-compartment models for cell production systems. J Biol Dyn. 2012;6(Supp. 1):2–18.
Article PubMed Google Scholar
Getto P, Marciniak-Czochra A, Nakata Y, Vivanco M. dM. Global dynamics of two-compartment models for cell production systems with regulatory mechanisms. Math Biosci. 2013;245:258–68.
Article PubMed Google Scholar
Stiehl T, Marciniak-Czochra A. Characterization of stem cells using mathematical models of multistage cell lineages. Math Comput Model. 2011;53(7):1505–17.
Article Google Scholar
Marciniak-Czochra A, Stiehl T, Wagner W. Modeling of replicative senescence in hematopoietic development. Aging. 2009;1(8):723.
CAS PubMed Central PubMed Google Scholar
Lander AD, Gokoffski KK, Wan FYM, Nie Q, Calof AL. Cell lineages and the logic of proliferative control. PLoS Biol. 2009;7(1):e1000015.
Article PubMed Central Google Scholar
Foley C, Mackey MC. Dynamic hematological disease: a review. J Math Biol. 2009;58(1-2):285–322.
Article PubMed Google Scholar
Bernard S, Bélair J, Mackey MC. Oscillations in cyclical neutropenia: new evidence based on mathematical modeling. J Theor Biol. 2003;223(3):283–98.
Article PubMed Google Scholar
Stiehl T, Ho AD, Marciniak-Czochra A. The impact of CD34 + cell dose on engraftment after stem cell transplantations: personalized estimates based on mathematical modeling. Bone Marrow Transp. 2014;49:30–7.
Article CAS Google Scholar
Stiehl T, Marciniak-Czochra A. Mathematical modelling of leukemogenesis and cancer stem cell dynamics. Math Mod Natural Phenomena. 2012;7:166–202.
Article Google Scholar
Stiehl T, Baran N, Ho AD, Marciniak-Czochra A. Clonal selection and therapy resistance in acute leukemias: mathematical modelling explains different proliferation patterns at diagnosis and relapse. J R Soc Interface. 2014;11:20140079. http://dx.doi.org/10.1098/rsif.2014.0079.
Walenda T, Stiehl T, Braun H, Froebel J, Ho AD, Schroeder T, Goecke T, Germing U, Marciniak-Czochra A, Wagner W. Feedback signals in myelodysplastic syndromes: increased self-renewal of the malignant clone suppresses normal hematopoiesis. PLoS Comput Biol. 2014;10(4):e1003599.
Google Scholar
Kim PS, Lee PP. Levy Doron. A PDE model for imatinib-treated chronic myelogenous leukemia. Bull Math Biol. 2008;70(7):1994–2016.
Article PubMed Google Scholar
Al-Hajj M, Clarke MF. Self-renewal and solid tumor stem cells. Oncogene. 2004;23(43):7274–82.
Article CAS PubMed Google Scholar
Moore KA, Lemischka IR. Stem cells and their niches. Science. 2006;311(5769):1880–5.
Article CAS PubMed Google Scholar
Lord BI. Biology of the haemopoietic stem cell. In: Stem cells. 1997. pp. 401–22.
Google Scholar
Uchida N, Fleming WH, Alpern EJ, Weissman IL. Heterogeneity of hematopoietic stem cells. Curr Opin Immunol. 1993;5(2):177–84.
Article CAS PubMed Google Scholar
Doumic M, Marciniak-Czochra A, Perthame B, Zubelli JP. A structured population model of cell differentiation. SIAM J Appl Math. 2011;71(6):1918–40.
Article Google Scholar
Gwiazda P, Jamróz G, Marciniak-Czochra A. Models of discrete and continuous cell differentiation in the framework of transport equation. SIAM J Math Anal. 2012;44(2):1103–33.
Article Google Scholar
Arino O, Kimmel M. Comparison of approaches to modeling of cell population dynamics. SIAM J Appl Math. 1993;53(5):1480–504.
Article Google Scholar
Haccou P, Jagers P, Vatutin VA. Branching processes: variation, growth, and extinction of populations. Vol. 5. Cambridge: Cambridge University Press; 2005.
Google Scholar
Kimmel M, Corey S. Stochastic hypothesis of transition from inborn neutropenia to AML: interactions of cell population dynamics and population genetics. Front Oncol. 2013;3:89.
Article PubMed Central PubMed Google Scholar
Glaubach T, Corey SJ. From famine to feast: sending out the clones. Blood. 2012;119(22):5063–4.
Article CAS PubMed Google Scholar
Dong F, Van Paassen M, Van Buitenen C, Hoefsloot LH, Lowenberg B, Touw IP. A point mutation in the granulocyte colony-stimulating factor receptor (G-CSF-R) gene in a case of acute myeloid leukemia results in the overexpression of a novel G-CSF-R isoform. Blood. 1995;85(4):902–11.
CAS PubMed Google Scholar
Donadieu J, Leblanc T, Bader Meunier B, Barkaoui M, Fenneteau O, Bertrand Y, Maier-Redelsperger M, et al. Analysis of risk factors for myelodysplasias, leukemias and death from infection among patients with congenital neutropenia. Experience of the French Severe Chronic Neutropenia Study Group. Haematologica. 2005;90(1):45–53.
PubMed Google Scholar
Rosenberg PS, Alter BP, Bolyard AA, Bonilla MA, Boxer LA, Cham B, Fier C, et al. The incidence of leukemia and mortality from sepsis in patients with severe congenital neutropenia receiving long-term G-CSF therapy. Blood. 2006;107(12):4628–35.
Article CAS PubMed Central PubMed Google Scholar
Germeshausen M, Skokowa J, Ballmaier M, Zeidler C, Welte K. G-CSF receptor mutations in patients with congenital neutropenia. Curr Opin Hematol. 2008;15(4):332–7.
Article CAS PubMed Google Scholar
Beekman R, Touw IP. G-CSF and its receptor in myeloid malignancy. Blood. 2010;115(25):5131–6.
Article CAS PubMed Google Scholar
Beekman R, Valkhof MG, Sanders MA, van Strien PMH, Haanstra JR, Broeders L, Geertsma-Kleinekoort WM, et al. Sequential gain of mutations in severe congenital neutropenia progressing to acute myeloid leukemia. Blood. 2012;119(22):5071–7.
Article CAS PubMed Google Scholar
Rosenberg PS, Zeidler C, Bolyard AA, Alter BP, Bonilla MA, Boxer LA, Dror Y, et al. Stable long‐term risk of leukaemia in patients with severe congenital neutropenia maintained on G-CSF therapy. Br J Haematol. 2010;150(2):196–9.
CAS PubMed Central PubMed Google Scholar
Kimmel M, Axelrod DE. Branching processes in biology. Springer New York;2002.
Google Scholar
Schroeder T. Asymmetric cell division in normal and malignant hematopoietic precursor cells. Cell Stem Cell. 2007;1(5):479–81.
Article CAS PubMed Google Scholar
Wu M, Kwon HY, Rattis F, Blum J, Zhao C, Ashkenazi R, Jackson TL, Gaiano N, Oliver T, Reya T. Imaging hematopoietic precursor division in real time. Cell Stem Cell. 2007;1(5):541–54.
Article CAS PubMed Central PubMed Google Scholar
Gardner TS, Cantor CR, Collins JJ. Construction of a genetic toggle switch in Escherichia coli. Nature. 2000;403(6767):339–42.
Article CAS PubMed Google Scholar
Vose JM, Armitage JO. Clinical applications of hematopoietic growth factors. J Clin Oncol. 1995;13(4):1023–35.
CAS PubMed Google Scholar
Awaya N, Uchida H, Miyakawa Y, Kinjo K, Matsushita H, Nakajima H, Ikeda Y, Kizaki M. Novel variant isoform of G-CSF receptor involved in induction of proliferation of FDCP‐2 cells: relevance to the pathogenesis of myelodysplastic syndrome. J Cell Physiol. 2002;191(3):327–35.
Article CAS PubMed Google Scholar
Loinger A, Lipshtat A, Balaban NQ, Biham O. Stochastic simulations of genetic switch systems. Phys Rev E. 2007;75(2):021904.
Article Google Scholar
Laslo P, Pongubala JMR, Lancki DW, Singh H. Gene regulatory networks directing myeloid and lymphoid cell fates within the immune system. Semin Immunol. 2008;20(4):228–35.
Article CAS PubMed Google Scholar
Michaels JL, Naudot V, Liebovitch LS. Dynamic stabilization in the PU1-GATA1 circuit using a model with time-dependent kinetic change. Bull Math Biol. 2011;73(9):2132–51.
Article PubMed Google Scholar
Jaruszewicz J, Zuk PJ, Lipniacki T. Type of noise defines global attractors in bistable molecular regulatory systems. J Theor Biol. 2013;317:140–51.
Article PubMed Central PubMed Google Scholar
Traulsen A, Pacheco JM, Luzzatto L, Dingli D. Somatic mutations and the hierarchy of hematopoiesis. Bioessays. 2010;32(11):1003–8.
Article CAS PubMed Google Scholar
Wilson A, Laurenti E, Oser G, van der Wath RC, Blanco-Bose W, Jaworski M, Offner S, et al. Hematopoietic stem cells reversibly switch from dormancy to self-renewal during homeostasis and repair. Cell. 2008;135(6):1118–29.
Article CAS PubMed Google Scholar
Becker V, Schilling M, Bachmann J, Baumann U, Raue A, Maiwald T, Timmer J, Klingmuller U. Covering a broad dynamic range: information processing at the erythropoietin receptor. Sci Signal. 2010;328(5984):1404.
CAS Google Scholar
Moolgavkar SH, Knudson AG. Mutation and cancer: a model for human carcinogenesis. J Natl Cancer Inst. 1981;66(6):1037–52.
CAS PubMed Google Scholar
Radivoyevitch T, et al. Quantitative modeling of chronic myeloid leukemia: insights from radiobiology. Blood. 2012;119(19):4363–71.
Article CAS PubMed Central PubMed Google Scholar
Ley TJ, et al. Genomic and epigenomic landscapes of adult de novo acute myeloid leukemia. N Engl J Med. 2013;368(22):2059–74.
Article Google Scholar
Bozic I, Antal T, Ohtsuki H, Carter H, Kim D, Chen S, Karchin R, Kinzler KW, Vogelstein B, Nowak MA. Accumulation of driver and passenger mutations during tumor progression. Proc Natl Acad Sci U S A. 2010;107(43):18545–50.
Article CAS PubMed Central PubMed Google Scholar
Tomasetti C, Vogelstein B, Parmigiani G. Half or more of the somatic mutations in cancers of self-renewing tissues originate prior to tumor initiation. Proc Natl Acad Sci U S A. 2013;110(6):1999–2004.
Article CAS PubMed Central PubMed Google Scholar
Sehl M, Zhou H, Sinsheimer JS, Lange KL. Extinction models for cancer stem cell therapy. Math Biosci. 2011;234(2):132–46.
Article PubMed Central PubMed Google Scholar
Parkin B, Ouillette P, Li Y, Keller J, Lam C, Roulston D, Li C, Shedden K, Malek SN. Clonal evolution and devolution after chemotherapy in adult acute myelogenous leukemia. Blood. 2013;121(2):369–77.
Article CAS PubMed Central PubMed Google Scholar
Peixoto D, Dingli D, Pacheco JM. Modelling hematopoiesis in health and disease. Math Comput Model. 2011;53(7):1546–57.
Article Google Scholar
Morrison SJ, Kimble J. Asymmetric and symmetric stem-cell divisions in development and cancer. Nature. 2006;441(7097):1068–74.
Article CAS PubMed Google Scholar
Molofsky AV, Pardal R, Morrison SJ. Diverse mechanisms regulate stem cell self-renewal. Curr Opin Cell Biol. 2004;16(6):700–7.
Article CAS PubMed Google Scholar
Shenghui H, Nakada D, Morrison SJ. Mechanisms of stem cell self-renewal. Annu Rev Cell Dev. 2009;25:377–406.
Article Google Scholar
Huang S. Systems biology of stem cells: three useful perspectives to help overcome the paradigm of linear pathways. Philos Trans R Soc Lond B Biol Sci. 2011;366(1575):2247–59.
Article CAS PubMed Central PubMed Google Scholar
Bertolusso R, Kimmel M. Modeling spatial effects in early carcinogenesis: stochastic versus deterministic reaction-diffusion systems. Math Model Nat Phenom. 2012;7(1):245–60.
Article Google Scholar
Marciniak-Czochra A, Kimmel M. Reaction-difusion model of early carcinogenesis: the effects of influx of mutated cells. Math Model Nat Phenom. 2008;3(7):90–114.
Article Google Scholar

Download references

Author information

Authors and Affiliations

Department of Statistics and Bioengineering, Rice University, 2102 Duncan Hall, 6100 Main St., 77005, Houston, TX, USA
Marek Kimmel

Authors

Marek Kimmel
View author publications
You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Marek Kimmel .

Editor information

Editors and Affiliations

Departments of Pediatrics and Cell & Molecular Biology, Northwestern University Feinberg School of Medicine and Lurie Children’s Hospital of Chicago, Chicago, Illinois, USA
Seth Joel Corey
Department of Statistics, Rice University, Houston, Texas, USA
Marek Kimmel
Northwestern University Comprehensive Cancer Center, Evanston, Illinois, USA
Joshua N. Leonard

Rights and permissions

Reprints and permissions

Copyright information

About this chapter

Cite this chapter

Kimmel, M. (2014). Stochasticity and Determinism in Models of Hematopoiesis. In: Corey, S., Kimmel, M., Leonard, J. (eds) A Systems Biology Approach to Blood. Advances in Experimental Medicine and Biology, vol 844. Springer, New York, NY. https://doi.org/10.1007/978-1-4939-2095-2_7

Download citation

DOI: https://doi.org/10.1007/978-1-4939-2095-2_7
Published: 06 December 2014
Publisher Name: Springer, New York, NY
Print ISBN: 978-1-4939-2094-5
Online ISBN: 978-1-4939-2095-2
eBook Packages: Biomedical and Life SciencesBiomedical and Life Sciences (R0)

Publish with us

Policies and ethics