Keywords

Mathematics Subject Classification

1 Introduction

This paper is based on a lecture I gave at a conference in San Diego in honor of the achievements of Nolan Wallach.

Suppose Δ to be a finite set. In this paper a Cartan matrix indexed by Δ will be an arbitrary integral matrix C = (c α, β ) (α, β ∈ Δ) satisfying these conditions:

(C1):

c α, α  = 2;

(C2):

for α ≠ β, c α, β  ≤ 0;

(C3):

c α, β  = 0 if and only if c β, α  = 0.

More commonly such a matrix is called a generalized Cartan matrix, whereas a Cartan matrix is taken to be one with the additional requirement that

(CD):

there exist a diagonal matrix D such that CD is positive definite.

But times change, and “generalized” is now closer to “usual”. In this paper, if condition (CD) is satisfied I will call C positive definite. For purely technical reasons I will assume further that

(C4):

C is irreducible;

(C5):

C is invertible.

The first condition means that Δ cannot be expressed as \(\varDelta _{1} \cup \varDelta _{2}\) with c α, β  = 0 for α ∈ Δ 1, β ∈ Δ 2. This condition is no significant restriction on results, since one can work with the summands of the root systems corresponding to the Δ i . The second condition excludes the affine Cartan matrices. This will restrict results, but the missing cases can be easily dealt with separately.

Let

$$\displaystyle{L = \mathbb{Z}^{\varDelta },\quad L^{\vee } =\mathop{ \mathrm{Hom}}(L, \mathbb{Z})\,.}$$

Thus Δ embeds into L as a basis. For every subset Θ of Δ let L Θ be the span of Θ in L, so that in particular L Δ  = L. Since C is integral and invertible, there exists a unique maximal linearly independent subset Δ ∨ of L ∨ and a bijection α ↦ α ∨ with

$$\displaystyle{\langle \alpha,\beta ^{\vee }\rangle = c_{\alpha,\beta }\,.}$$

Let \(L_{\varDelta ^{\vee }}^{\vee }\) be the submodule of L ∨ spanned by Δ ∨. The linear transformation

$$\displaystyle{s_{\alpha }: \;\lambda \mapsto \lambda -\langle \lambda,\alpha ^{\vee }\rangle \alpha }$$

is a (possibly skew) reflection, taking L to itself. Its contragredient \(s_{\alpha ^{\vee }}\) takes L ∨ and \(L_{\varDelta ^{\vee }}^{\vee }\) to themselves. These reflections generate the Weyl group W associated to the Cartan matrix. The W-orbit of Δ is the set of real roots Σ ℝ . It is the disjoint union of two halves, positive and negative. The positive (resp. negative) roots Σ ℝ + (resp. Σ ℝ −) are integral linear combinations of elements in Δ with non-negative (resp. non-positive) coefficients.

Let \(\mathcal{D}\) be the region of all v in L ⊗ ℝ such that \(\langle v,\alpha ^{\vee }\rangle \geq 0\) for all α ∈ Δ, and define the closed Tits cone \(\overline{\mathcal{C}}\) to be the closure of \(W(\mathcal{D})\). It is convex, and has a non-empty interior, on which the group W acts discretely with fundamental domain \(\mathcal{D}\). I define \(\Sigma_{\mathbb{I}}\), the set of imaginary roots, to be the union of

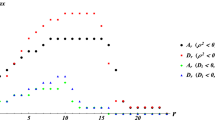
$$\displaystyle{\varSigma _{\mathbb{I}}^{+} =\big (L_{\varDelta } \cap \;\overline{\mathcal{C}}\big) -\{ 0\}}$$

and its opposite \(\Sigma_{\mathbb{I}}\). It, too, is W-stable, as is each half \(\Sigma^{\pm}_{\mathbb{I}}\) and the set Σ of all roots, the union of real and imaginary ones. (For all this, refer to Proposition 5.2, Theorem 5.4,Lemma 5.8, and Exercise 5.12 in Chapter 5 of [Kac85]. Figure 1 shows how things look in a simple case.) The terminology is perhaps motivated by the fact that many root systems possess a natural quadratic form with respect to which real roots have real lengths and imaginary ones have imaginary ones.

Figure 1
figure 1

Real and imaginary roots for a system of rank 2

Full size image

Let

$$\displaystyle{\mathfrak{h} = L^{\vee }\otimes \mathbb{C}\,,}$$

which may be identified with an Abelian Lie algebra, and let

$$\displaystyle{\mathfrak{h}^{\vee } = L \otimes \mathbb{C}}$$

be its complex linear dual. For each α in Δ let h α be the image of α ∨ in \(\mathfrak{h}\). In other words, α ∨ may be identified with a linear injection of \(\mathbb{C}\) into \(\mathfrak{h}\) taking x to xh α . Let \(\mathfrak{g}\) be the Kac–Moody Lie algebra associated to these data. One is given in the construction of \(\mathfrak{g}\) an embedding of \(\mathfrak{h}\) into it. The adjoint action of \(\mathfrak{h}\) on \(\mathfrak{g}\) is semi-simple and locally finite, breaking it up into the sum of \(\mathfrak{h}\) and a number of root spaces \(\mathfrak{g}_{\lambda }\), with \(\lambda: \mathfrak{h} \rightarrow \mathbb{C}\) lying inside the image of L in \(\mathfrak{h}^{\vee }\). The fundamental fact about these data is that \(\mathfrak{g}_{\lambda }\neq 0\) if and only if λ is a root in the sense spoken of earlier. This is complemented by the assertion that for each α in Δ, \(\mathfrak{g}_{\alpha }\) has dimension one. It is also true that \(\mathfrak{g}_{\lambda }\) has dimension one for every real root λ.

The validity of these assertions depends on assumption (C5). Without it, there still exists a Kac–Moody algebra defined by C, but its description is a bit more subtle, as explained in the opening chapter of [Kac85], and elaborated on in Chapter 6 The corresponding Lie algebras turn out to be extensions of \(\mathfrak{g} \otimes \mathbb{C}[t^{\pm 1}]\), with \(\mathfrak{g}\) finite-dimensional, and computations in it reduce easily to computations in \(\mathfrak{g}\) itself. This is why (C5) is not very restrictive.

There are two basic problems this paper will deal with:

Problem 1. To specify a good choice of basis elements \(e_{\lambda }\) of \(\mathfrak{g}_{\lambda }\) for all real roots λ;

Problem 2. To find, for every pair of real roots λ, μ such that λ + μ is also a real root, the structure constant N λ,μ such that [e λ ,e μ ] = N λ,μ e λ+μ .

The method I will use to solve these problems originates in [Tits66a], which sketches what happens when \(\mathfrak{g}\) has finite dimension. The extension to Kac–Moody algebras is not quite trivial, but neither is it particularly tricky. I hope that it will be useful in exploring what happens for bracket computations involving imaginary roots, which is one of the great mysteries of Kac–Moody algebras, although I say nothing about this problem here.

When \(\mathfrak{g}\) is finite-dimensional, there are already in the literature two practical approaches to constructing the e λ and computing the N λ, μ . One can be found in [Car72] and is explained in more detail in [CMT04]. The construction uses induction on roots, going from λ to λ +α (α ∈ Δ) according to a certain rule. Calculation of the structure constants amounts to transliterations of the Jacobi identity. The other method, introduced in [FK80], exhibits an interesting extension of groups to interpret the constants as related to cohomology. This technique was applied originally only to simply laced systems, but it has since been extended to the rest of the finite-dimensional \(\mathfrak{g}\) in [Ryl00] by ‘folding’. As far as I can tell these methods cease to be valid for arbitrary Kac–Moody algebras. In any event, in the cases for which they do work they do not seem to be a great deal faster than a program based on the method to be explained here. To the extent to which they are faster, they are ‘hard-wired’, incorporating for each system special short-cuts that do not apply in general.

Acknowledgments. I thank the organizers of the conference in honor of Nolan Wallach for inviting me to contribute to it. I also wish to thank my colleague Julia Gordon, who—rather casually—started me off on this project. I am extremely happy to have had this opportunity to try to understand and elaborate on Jacques Tits’ work on structure constants. I first saw that volume of the Publications de l’IHES for sale in Schoenhof’s when I was a very ignorant graduate student, and the memory of my puzzled thought, “What exactly is a structure constant?” has remained with me ever since. And finally I wish to thank the referee, who complained much about lacunae in an earlier draft but nonetheless continued to read and criticize carefully.

2 Chevalley bases

In this section I will start looking at Problem 1, that of constructing a good basis of \(\mathfrak{g}\). The beginning is straightforward—for each α in Δ choose an arbitrary e α ≠ 0 in \(\mathfrak{g}_{\alpha }\). It doesn’t make any difference what choice you make, because all choices will be conjugate with respect to an automorphism of the Lie algebra \(\mathfrak{g}\). For each α in Δ, \([\mathfrak{g}_{\alpha },\mathfrak{g}_{-\alpha }]\) will be the one-dimensional subspace spanned by h α . Following [Tits66a], then choose e −α so

$$\displaystyle{[e_{\alpha },e_{-\alpha }] = -h_{\alpha }\,.}$$

The usual convention imposes a plus sign on the right hand side of this equation, but Tits’ change of sign is extraordinarily convenient, in fact obligatory if the symmetries exploited later on in this paper are to remain comprehensible. In my opinion, Tits’ choice should have become the conventional one long ago.

For example, if \(\mathfrak{g} = \mathfrak{s}l_{2}\), we get

$$\displaystyle{e_{+} = \left [\begin{array}{cc} \ 0\ & \ 1\ \\ 0 & 0\\ \end{array} \right ],\quad e_{-} = \left [\begin{array}{cc} \, 0\, & \ 0\ \\ \, - 1\, & \ 0\ \\ \end{array} \right ],\quad h = \left [\begin{array}{cc} \,1\, & \, 0\,\\ 0 & \, - 1\,\\ \end{array} \right ]\;.}$$

The data of \(\mathfrak{h}\) together with the e α make up what I will call a frame for \(\mathfrak{g}\). (It is called in French an épinglage, frequently translated awkwardly into English as pinning. The reference in French is to the way butterflies are mounted. To those of us who have been parents of young children, the proposed English term has other, less fortunate, connotations.)

—————

From now on, assume a frame to have been fixed. With this assumption, we are given also for each α in Δ a well-defined embedding

$$\displaystyle{\varphi _{\alpha }: \;\mathfrak{s}l_{2}\longrightarrow \mathfrak{g}\quad \vert \quad e_{+}\longmapsto e_{\alpha },\quad h\longmapsto h_{\alpha },\quad e_{-}\longmapsto e_{-\alpha }\,.}$$

Let \(\mathfrak{s}l_{2}^{[\alpha ]}\) be its image.

—————

The map taking each e ±α to e ∓α , h ↦ − h for h in \(\mathfrak{h}\) extends to an involutory automorphism θ of all of \(\mathfrak{g}\) called the canonical involution.

For x in \(\mathfrak{g}_{\lambda }\) and y in \(\mathfrak{g}_{\mu }\), the bracket [x, y] lies in \(\mathfrak{g}_{\lambda +\mu }\) (which may be 0). If μ = −λ, this means it will lie in \(\mathfrak{h}\). For each real root λ the subspace \([\mathfrak{g}_{\lambda },\mathfrak{g}_{-\lambda }]\) has dimension one in \(\mathfrak{h}\), and is not contained in the kernel of λ. Hence there exists a unique h λ in it with \(\langle \lambda,h_{\lambda }\rangle = 2\).

Lemma 2.1.

For each real root λ there exists up to sign a unique e λ in \(\mathfrak{g}_{\lambda }\) such that

$$\displaystyle{[e_{\lambda },\theta (e_{\lambda })] = -h_{\lambda }\;.}$$

Proof.

Given e ≠ 0 in \(\mathfrak{g}_{\lambda }\), we know that θ(e) lies in \(\mathfrak{g}_{-\lambda }\) and hence

$$\displaystyle{[e,\theta (e)] = ah_{\lambda }}$$

for some constant a ≠ 0. But then

$$\displaystyle{[ce,\theta (ce)] = c^{2}ah_{\lambda }}$$

so we choose ce with c 2 a = −1. □ 

We may thus assemble a basis of \(\mathfrak{g}\) by choosing for each root λ one of the two choices this gives us. This is called a Chevalley basis. Part of the solution to Problem 1 above is to choose a Chevalley basis. It is unique only up to signs, and there is apparently no canonical choice.

Suppose we are given a Chevalley basis. Suppose further we are given real roots λ, μ such that λ +μ is also a real root. We have

$$\displaystyle{[e_{\lambda },e_{\mu }] = N_{\lambda,\mu }e_{\lambda +\mu }}$$

in which the absolute value | N λ, μ  | is now uniquely determined. It is known never to be 0. We should not be too surprised to learn that it has a relatively simple expression. I will next explain the formula for it.

If λ and μ are roots with λ real, the λ-string through μ is the intersection of \(\mu +\mathbb{Z}\lambda\) with Σ. It is always finite. Define p λ, μ to be the maximum p such that μ − p λ is in the string, and q λ, μ to be the maximum q such that μ + q λ lies in it. The string is the full segment [μ − p λ, μ + q λ]. The following identities are easy to verify:

$$\displaystyle{\begin{array}{rl} p_{\mu,\lambda }& = p_{-\mu,-\lambda } \\ p_{\mu +\lambda,\lambda }& = p_{\mu,\lambda } + 1 \\ p_{\mu,-\lambda }& = n - p_{\mu,\lambda }\;\mbox{ if $n$ is the length of the string.}\\ \end{array} }$$

The following was first proved by Chevalley for finite-dimensional Lie algebras, probably by Tits more generally. See also [Mor87]. Following [Tits66a], I shall in effect reprove it later on.

Theorem 2.2 (Chevalley’s Theorem).

If λ, μ, and λ + μ are all real roots, then

$$\displaystyle{\vert N_{\lambda,\mu }\vert = p_{\lambda,\mu } + 1\,.}$$

The constants p λ, μ are simple to evaluate, so the whole problem of computing structure constants comes down to computing a sign.

This result makes it possible to assign a ℤ-structure to \(\mathfrak{g}\), and was classically the basis for Chevalley’s construction of split group schemes defined over \(\mathbb{Z}\). Incidentally, the usual proof of Chevalley’s theorem is a case-by-case examination. This is somewhat unsatisfactory, and moreover it will not be possible when working with arbitrary Kac–Moody algebras. One is forced to come up with a proof that is illuminating even in the finite-dimensional cases.

3 The root graph

The algorithm we shall eventually see will require that we be able to list as many roots as we want. In fact, in principle we can construct even an infinite number all at the same time, as I will explain later.

Every real root is w α for some w in W, α in Δ. The natural way to construct real roots is therefore to start with all the α in Δ and apply the elements of W to them. How does this go? Keep in mind that the group W is generated by the elementary reflections s α . We maintain two lists of positive roots, one the current list to be processed—the waiting list—and the other that of roots that have been processed—serviced customers. Processing a root means (a) removing it from the waiting list and (b) applying all elementary reflections to it to see whether we get new roots or roots we have already seen. When we see a new one, we put it on the waiting list, if the new root has height below some bound we have initially set. (I recall that the height of λ = ∑ λ α α is ∑ | λ α  | .) Of course one may as well restrict oneself to the task of finding only positive roots.

It is not hard to use a look-up table to follow this method. It is guaranteed to give us eventually as many roots as we need, but it is not at all clear how long it will take. The problem that comes to mind is that when we apply elementary reflections we might expect a priori to go down in height to get a new root, and then down in height again, and so on. This is reminiscent of solving the word problem in group theory. In this case it ought not to be necessary—we would like to know that we can proceed by adding to the waiting list only reflections of greater height. This is easy to carry out, since s α λ has height more than λ if and only if \(\langle \lambda,\alpha ^{\vee }\rangle < 0\). But seeing why this procedure will work is not quite trivial.

Define the depth of a positive root λ to be ℓ(w) for the w of least length such that w −1 λ < 0. Equivalently this is ℓ(w) + 1 where w is of least length such that λ = w α with α ∈ Δ. For example, the depth of every α in Δ is 1. The fundamental fact about depth is Proposition 2.3 of [BH93], which is simple to state but not quite so simple to prove:

Proposition 3.1 (Brink and Howlett).

The depth of s α λ is greater than that of λ if and only if \(\langle \lambda,\alpha ^{\vee }\rangle < 0\) .

This is also part of Lemma 3.3 in [Cas06].

One consequence is that the height of a root is greater than or equal to its depth, so if we have found all roots of depth ≤ n we have also found all roots of height  ≤ n. Another consequence is one we’ll need in a later section:

Corollary 3.2.

If λ is a positive real root not in Δ, then there exists α in Δ with \(\langle \lambda,\alpha ^{\vee }\rangle > 0\) .

Here is another natural consequence:

Corollary 3.3.

If Θ ⊆Δ, then the real roots in L Θ are in the W Θ -orbit of Θ.

Here W Θ is the subgroup of W generated by the s α with α in Θ.

Proof.

Arguing by induction on depth, it has to be shown that if λ is a positive real root in the linear span of Θ, there exists α ∈ Θ such that \(\langle \lambda,\alpha ^{\vee }\rangle > 0\). But since λ is positive and in L Θ , \(\langle \lambda,\beta ^{\vee }\rangle \leq 0\) for all β not in Θ, so that the claim follows from the previous Corollary. □ 

In finding positive roots, we are in effect building what I call the root graph, from the bottom up. It is an important structure. With one exception the nodes of this graph are the positive roots. The exception is that for technical convenience I add a ‘dummy’ node at the bottom (Figures 2 and 3).

Figure 2
figure 2

The roots and root graph of G 2

Full size image
Figure 3
figure 3

A different version of the root graph of G 2

Full size image

What about edges? They are oriented. There is an edge labeled s α from the dummy node to α, for each α in Δ. There is an edge from a root λ to another μ if μ = s α λ and the height of μ is greater than the height of λ. It is labeled by s α . Since

$$\displaystyle{s_{\alpha }\lambda =\lambda -\langle \lambda,\alpha ^{\vee }\rangle \alpha }$$

this will happen if and only if \(\langle \lambda,\alpha ^{\vee }\rangle < 0\).

In drawing the root graph, the loops are redundant, since the total number of edges coming in or out is a constant. (This is the reason for adding the ‘dummy’.) Furthermore, in the diagrams that follow the arrows can be replaced by simple lines, because the orientation is always upward (Figs. 4 and 5).

Figure 4
figure 4

The root graphs for A 3 and C 3

Full size image
Figure 5
figure 5

The bottom of an infinite root graph

Full size image

Each root can be reached by one or more paths in the root graph, starting at the dummy node. But if we are to construct roots by traversing paths, we want to specify a unique path to every node. I choose the ISL (Inverse Short Lex) path, which is defined recursively (Figure 6). Assign an order to Δ. A path

$$\displaystyle{\gamma =\lambda _{0}\stackrel{\alpha _{1}}{\longrightarrow }\,\cdots \,\stackrel{\alpha _{n}}{\longrightarrow }\lambda _{n}}$$

is ISL if α n is the least label on the edges leading up to λ n , and similarly for all its initial segments.

Figure 6
figure 6

The ISL root graph for A 3

Full size image

4 Rank two systems

Chevalley’s formula for | N λ, μ  | indicates that the geometry of root configurations will likely be important in this business. In this section and the next I prove a few crucial properties.

I begin by recalling the original way of thinking about bases of roots. Suppose V to any real vector space, given a coordinate system (x i ). Impose on V the associated lexicographic order: x < y if x i  = y i for i < m but x m  < y m . This is a linear order, invariant under translation, and [Sat51] points out that any translation-invariant linear order that is continuous in some sense has to be one of these. In any free \(\mathbb{Z}\)-module contained in V there exists a least non-zero positive vector.

Suppose Δ to be a basis of a set Σ of roots, and take \(V\) to be \(L_{\varDelta } \otimes \mathbb{R}\). If we assign an order to Δ, we get a corresponding lexicographic order on V. The positive roots in Σ are those > 0 with respect to the lexicographic order. This should motivate the following discussion.

Lemma 4.1.

Suppose we are given an ordered set of real and linearly independent roots λ i , and let Λ k be the subset of the first k. There exists a subset of roots α i in Δ and w in W such that wλ 1 = α 1 , and each wΛ k is contained in the non-negative integral span of the α i for i ≤ k.

Proof.

Extending the set of λ i if necessary, we may assume they form a basis of V. Assign V the associated lexicographic order. Let V k be the real span of Λ k .

Define β 1 to be λ 1, and define β k to be the least positive root in V k that is not in V k−1 (look at the linear order induced on the quotient to see that this exists). Let B be the set of all β i , B k the subset of the first k. The real span of B k is V k .

I claim that every real root λ in the real span of B k positive with respect to this linear order (including the λ i themselves) is in the non-negative integral span of B k . For k = 1, there is nothing to prove. Proceed by induction on the smallest k such that λ is in the real span of Λ k . Applying induction, we may assume λ is in V k − V k−1. If λ = β k , no problem. Otherwise λ > β k . According to Corollary 3.2 of § 3 there exists i ≤ k such that \(\langle \lambda,\beta _{i}^{\vee }\rangle > 0\). Then λ −β i will again be a root, of smaller height. Repeat as required.

Now apply Theorem 2 of §5.9 in [MP95] to see that there exists w in W with wB = Δ. □ 

Proposition 4.2.

If λ, μ are real roots, there exists w in W, α and β in Δ such that wλ = α, wμ is a non-negative integral combination of α and β. The real root wμ is in W α,β {α,β}.

Proof.

The last assertion follows from Corollary 3.3. □ 

The map from Δ to Δ ∨ has a natural extension to a map λ ↦ λ ∨ from \(\varSigma _{\mathbb{R}}\) to \(\varSigma _{\mathbb{R}}^{\vee } \subset L^{\vee }\). It is characterized by the formula \((w\lambda )^{\vee } = w\lambda ^{\vee }\) for all real roots λ. If λ = w(α), then the reflection corresponding to λ is s λ  = ws α w −1:

$$\displaystyle{s_{\lambda }u = u -\langle u,\lambda ^{\vee }\rangle \lambda \,.}$$

For any pair of distinct real roots λ, μ let L λ, μ be their integral span.

Proposition 4.3.

If λ and μ are any two distinct real roots with \(\langle \lambda,\mu ^{\vee }\rangle \neq 0\) , there exists on L λ,μ an inner product with respect to which s λ and s μ are orthogonal reflections, and λ ⋅λ > 0. It is unique up to a positive scalar, and κ ⋅κ > 0 for all real roots κ in L λ,μ .

Proof.

The reflection s κ is orthogonal if and only if

$$\displaystyle{2\left ({u\cdot \kappa \over \kappa \cdot \kappa } \right ) =\langle u,\kappa ^{\vee }\rangle }$$

for all u in L λ, μ . This requires that

$$\displaystyle{\begin{array}{rl} \langle \lambda,\mu ^{\vee }\rangle & = 2\left (\frac{\lambda \cdot \mu }{\mu \cdot \mu }\right ) \\ \langle \mu,\lambda ^{\vee }\rangle & = 2\left (\frac{\lambda \cdot \mu }{\lambda \cdot \lambda }\right ). \\ \end{array} }$$

These equations tell us that λ ⋅ μ and μ ⋅ μ are both determined by λ ⋅ λ, so certainly there is a unique inner product defined uniquely on L λ, μ by λ ⋅ λ and the requirement that reflections be orthogonal. Why are the norms of real roots then all positive?

According to Proposition 4.2, we may assume that λ = α, μ = p α + q β with α, β in Δ. In these circumstances \(\langle \alpha,\beta ^{\vee }\rangle \neq 0\), so there exists on L α, β an essentially unique inner product with α ⋅ α > 0. By the definition of a Cartan matrix, we also have β ⋅ β > 0. The given inner product on L λ, μ must be some scalar multiple of this one. But both λ and μ are Weyl transforms of α or β, so both also have positive norms. □ 

Corollary 4.4.

Given two real roots λ, μ we have

$$\displaystyle{\langle \lambda,\mu ^{\vee }\rangle \langle \mu,\lambda ^{\vee }\rangle \geq 0}$$

and one factor is 0 if and only if both are.

Proof.

Since

$$\displaystyle{\langle \lambda,\mu ^{\vee }\rangle \langle \mu,\lambda ^{\vee }\rangle = 4{(\lambda \cdot \mu )^{2} \over \Vert \lambda \Vert ^{2}\Vert \mu \Vert ^{2}} \,.}$$

 □ 

Since the transpose of a Cartan matrix is also a Cartan matrix, the previous result implies that there exists an essentially unique metric on Σ ∨ as well.

Corollary 4.5.

In an irreducible root system of rank two, the product \(\Vert \lambda \Vert \,\Vert \lambda ^{\vee }\Vert\) is constant.

Proof.

It is immediate from the defining formulas that

$$\displaystyle{ \Vert \alpha \Vert \,\Vert \alpha ^{\vee }\Vert =\Vert \beta \Vert \,\Vert \beta ^{\vee }\Vert \,.({\ast}) }$$

Any other real root λ is of the form w α or w β, from which the claim follows. □ 

Corollary 4.6.

The map

$$\displaystyle{\nu \longmapsto \frac{\nu ^{\vee }} {\Vert \nu ^{\vee }\Vert ^{2}}}$$

is linear on \(\varSigma _{\mathbb{R}} \cap L_{\lambda,\mu }\) .

5 Tits triples

In this section, suppose λ, μ, and ν to be what I call a Tits triple—a trio of real roots with λ +μ +ν = 0. In these circumstances, either \(\langle \mu,\lambda ^{\vee }\rangle\) or \(\langle \nu,\lambda ^{\vee }\rangle\) does not vanish, so by Corollary 4.3 there exists a well-defined inner product on L λ, μ  = L λ, ν , with respect to which all real roots have positive norm.

In particular, the λ-string through μ contains at least the two real roots μ and −ν. It is stable under s λ , which reflects in the point where \(\langle \mu,\varLambda ^{\vee }\rangle = 0\). By assumption, both μ and −ν are in this string.

Lemma 5.1.

Let \(n =\langle \mu,\lambda ^{\vee }\rangle\) .

  1. (a)

    n < −1 if and only if \(\Vert \mu \Vert >\Vert \nu \Vert\) ;

  2. (b)

    n = −1 if and only if \(\Vert \mu \Vert =\Vert \nu \Vert\) ;

  3. (c)

    n > −1 if and only if \(\Vert \mu \Vert <\Vert \nu \Vert\) .

Proof.

If n = −1, then s λ μ = −ν. If n ≥ 0, then evaluate (μ +λ) ⋅ (μ +λ) to see that \(\Vert \nu \Vert ^{2} >\Vert \mu \Vert ^{2}\). In the remaining case, with n ≤ −2, consider instead s λ λ = −λ, s λ ν, s λ μ. □ 

There are a limited number of configurations of the λ-string through μ. If κ is a positive (resp. negative) imaginary root in the string, then s λ κ is also one, since the positive (resp. negative) imaginary roots are stable under W. Since the positive (resp. negative) imaginary roots are the intersection of a convex set with the roots, all intervening roots must also be positive (resp. negative) and imaginary. Therefore any real roots in the string must be at its ends. Since s λ reflects in the hyperplane \(\langle \mu,\lambda ^{\vee }\rangle = 0\) and the real roots in the string can have at most two lengths, the previous result implies:

Lemma 5.2.

There do not exist three real roots \(\kappa\) in a \(\lambda\) -string with \(\langle \kappa,\lambda ^{\vee }\rangle \leq 0\) .

In other words, the following figures, with real roots dark, show all possibilities for strings containing a real root. The lengths in the string decrease until at most the half-way point, then increase (Figure 7).

Figure 7
figure 7

Possible root strings containing a real root

Full size image

All these are in fact possible, as you can see by perusing classical root diagrams or Figure 1.

Lemma 5.3.

The following are equivalent:

  1. (a)

    \(s_{\lambda }\mu = -\nu\) ;

  2. (b)

    \(\langle \mu,\lambda ^{\vee }\rangle = -1\) ;

  3. (c)

    \(\Vert \lambda \Vert \geq \Vert \mu \Vert\) , \(\Vert \nu \Vert\) .

The point of this result is that whenever λ +μ +ν = 0 we can cycle to obtain s λ μ = −ν, since we can certainly cycle to get the third condition by taking λ of maximum length.

Proof.

The equivalence of (a) and (b) is immediate.

Assume (b). Then s λ μ = −ν, so \(\Vert \mu \Vert =\Vert \nu \Vert\). But also \(\langle \lambda,\mu ^{\vee }\rangle \leq -1\), so by Lemma 5.1 we have \(\Vert \lambda \Vert \geq \Vert \mu \Vert\). Thus (b) implies (c).

Assume (c). First of all, Lemma 5.1 implies that \(\langle \lambda,\mu ^{\vee }\rangle < 0\), for if not then \(\Vert \nu \Vert ^{2} =\Vert \lambda +\mu \Vert ^{2} >\Vert \lambda \Vert ^{2}\), a contradiction. This implies that \(n =\langle \mu,\lambda ^{\vee }\rangle < 0\) as well.

If n = −1 then s λ μ = −ν and \(\Vert \mu \Vert =\Vert \nu \Vert\). If n < −1. But then by Lemma 5.1 we have \(\Vert \mu \Vert \geq \Vert \mu +\lambda \Vert =\Vert \nu \Vert\). By symmetry, we also have \(\Vert \nu \Vert \geq \Vert \mu \Vert\). But then \(\Vert \mu \Vert =\Vert \nu \Vert\) and by Lemma 5.1 s λ μ = −ν. □ 

One consequence is that we cannot have a trio of real roots with λ +μ +ν = 0, \(\Vert \lambda \Vert\), \(\Vert \mu \Vert >\Vert \nu \Vert\). The diagram of Figure 8 is impossible.

Figure 8
figure 8

An impossible real root configuration

Full size image

I shall now examine what happens when \(\Vert \lambda \Vert \geq \Vert \mu \Vert =\Vert \nu \Vert\). There are two different cases.

—————

Suppose first that \(\Vert \lambda \Vert =\Vert \mu \Vert =\Vert \nu \Vert\). Then by Lemma 5.1

$$\displaystyle{\begin{array}{rl} s_{\lambda }:&\lambda \longmapsto -\lambda \\ &\mu \longmapsto -\nu \\ &\nu \longmapsto -\mu \\ s_{\mu }:&\lambda \longmapsto -\nu \\ &\mu \longmapsto -\mu \\ &\nu \longmapsto -\lambda \\ \end{array} }$$

so s λ s μ rotates (λ, μ, ν) to (μ, ν, λ). Following this by s μ maps

$$\displaystyle{\begin{array}{rl} \lambda &\longmapsto -\mu \\ \mu &\longmapsto -\lambda \\ \nu &\longmapsto -\nu \,.\\ \end{array} }$$

Thus

$$\displaystyle{p_{\lambda,\mu } = p_{\mu,\nu }\;\mbox{ etc.},\quad p_{\lambda,\mu } = p_{\mu,-\lambda } = p_{\mu,\lambda }\,.}$$

—————

Suppose next that \(\Vert \lambda \Vert >\Vert \mu \Vert =\Vert \nu \Vert\). We may set these last to 1, \(\Vert \lambda \Vert ^{2} = n > 1\). By Lemma 5.1 we must have \(\langle \mu,\lambda ^{\vee }\rangle = -1\). Since

$$\displaystyle{\langle \lambda,\mu ^{\vee }\rangle \Vert \mu \Vert ^{2} =\langle \mu,\lambda ^{\vee }\rangle \Vert \lambda \Vert ^{2}}$$

we must also have \(\langle \lambda,\mu ^{\vee }\rangle = -n < -1\).

But then λ and −ν = λ +μ must also lie in the initial half of the μ-string through λ, and therefore by Lemma 5.2 λ must be its beginning. Similarly, λ is at the beginning of its ν-string. Therefore

$$\displaystyle{p_{\lambda,\mu } = p_{\lambda,\nu } = 0\,.}$$

If ν were not at the beginning of its λ-string, there would exist a root ν −λ of squared-length

$$\displaystyle{\Vert \nu -\lambda \Vert ^{2} =\Vert \nu \Vert ^{2} - 2\nu \dot{\lambda } +\Vert \lambda \Vert ^{2}}$$

greater than that of λ. Again by Lemma 5.2, this cannot happen. So ν is at the beginning of its λ-string. The same holds for μ. So

$$\displaystyle{p_{\nu,\lambda } = p_{\mu,\lambda } = 0\,.}$$

Since λ is at the beginning of its ν-string, s ν λ = λ + n ν is the end of that string, which is of length n. But λ +ν = −μ, so

$$\displaystyle{p_{\mu,\nu } = p_{-\mu,-\nu } = n - 1}$$

and also

$$\displaystyle{p_{\nu,\mu } = p_{-\nu,-\mu } = n - 1\,.}$$

—————

These computations now imply:

Lemma 5.4 (Geometric Lemma).

We have

$$\displaystyle{{p_{\lambda,\mu } + 1 \over \Vert \nu \Vert ^{2}} ={ p_{\mu,\nu } + 1 \over \Vert \lambda \Vert ^{2}} ={ p_{\nu,\lambda } + 1 \over \Vert \mu \Vert ^{2}} \,.}$$

Lemma 5.5.

We have p μ,λ = p λ,μ .

Proposition 5.6.

We have

$$\displaystyle{(p_{\lambda,\mu } + 1)\nu ^{\vee } + (p_{\mu,\nu } + 1)\lambda ^{\vee } + (p_{\nu,\lambda } + 1)\mu ^{\vee } = 0\,.}$$

Proof.

Identify λ with \(2\lambda ^{\vee }/\Vert \lambda ^{\vee }\Vert ^{2}\), etc. Since λ +μ +ν = 0 we also have by Corollary 4.6

$$\displaystyle{ \frac{\lambda ^{\vee }} {\Vert \lambda ^{\vee }\Vert ^{2}} + \frac{\mu ^{\vee }} {\Vert \mu ^{\vee }\Vert ^{2}} + \frac{\nu ^{\vee }} {\Vert \nu ^{\vee }\Vert ^{2}} = 0}$$

But the product \(\Vert \kappa \Vert \,\Vert \kappa ^{\vee }\Vert\) does not depend on κ, so

$$\displaystyle{\Vert \lambda \Vert ^{2}\lambda ^{\vee } +\Vert \mu \Vert ^{2}\mu ^{\vee } +\Vert \nu \Vert ^{2}\nu ^{\vee } = 0\,.}$$

Lemma 5.4 now implies that

$$\displaystyle{(p_{\lambda,\mu } + 1)\nu ^{\vee } + (p_{\mu,\nu } + 1)\lambda ^{\vee } + (p_{\nu,\lambda } + 1)\mu ^{\vee } = 0\,.}$$

 □ 

6 Representations of SL(2)

Representations of SL2 play an important role in both Carter’s and Tits’ approaches to structure constants. In this section I recall briefly what is needed. Of course this is well-known material, but perhaps not in quite the form I wish to refer to.

Let

$$\displaystyle{u = \left [\begin{array}{c} 1\\ 0\\ \end{array} \right ],\quad v = \left [\begin{array}{c} 0\\ 1\\ \end{array} \right ]}$$

be the standard basis of \(\mathbb{C}^{2}\), on which \(\mathop{\mathrm{SL}}\nolimits _{2}(\mathbb{C})\) and \(\mathfrak{s}l_{2}\) act. They also act on the symmetric space \(S^{n}(\mathbb{C})\), with basis u k v n−k for 0 ≤ k ≤ n. Let π n be this representation, which is of dimension n + 1.

$$\displaystyle{\begin{array}{rl} \pi _{n}\left (\left [\begin{array}{cc} e^{x} & \;0 \\ 0 & \;e^{-x}\\ \end{array} \right ]\right )&: \;u^{k}v^{n-k}\longmapsto e^{(2k-n)x}u^{k}v^{n-k} \\ \pi _{n}\left (\left [\begin{array}{cc} 1\; & \;x\\ 0\; & \;1\\ \end{array} \right ]\right )&: \;u^{k}v^{n-k}\longmapsto u^{k}(v + xu)^{n-k} \\ \pi _{n}\left (\left [\begin{array}{cc} 1\; & \;0\\ - x\; & \;1 \end{array} \right ]\right )&: \;u^{k}v^{n-k}\longmapsto (u - xv)^{k}v^{n-k}\,.\\ \end{array} }$$

Now to translate these formulas into those for the action of \(\mathfrak{g}\). Let w k  = u k v n−k.

$$\displaystyle{\begin{array}{rl} \pi _{n}(h)&: \;w_{k}\longmapsto (2k - n)\,w_{k} \\ \pi _{n}(e_{+})&: \;w_{k}\longmapsto (n - k)w_{k+1} \\ \pi _{n}(e_{-})&: \;w_{k}\longmapsto - kw_{k-1}\,.\\ \end{array} }$$

For many reasons, it is a good idea to use a different basis of the representation. Define divided powers

$$\displaystyle{u^{[k]} ={ u^{k} \over k!} \,,}$$

and set w [k] = u [k] v [n−k] (Figure 9). Then

$$\displaystyle{\begin{array}{rl} \pi _{n}(h)&: \;w_{[k]}\longmapsto (2k - n)\,w_{[k]} \\ \pi _{n}(e_{+})&: \;w_{[k]}\longmapsto (k + 1)w_{[k+1]} \\ \pi _{n}(e_{-})&: \;w_{[k]}\longmapsto - (n - k + 1)w_{[k-1]}\,.\\ \end{array} }$$
Figure 9
figure 9

The representation π 3

Full size image

If

$$\displaystyle{\sigma = \left [\begin{array}{cc} 0 &\;1\\ - 1 &\;0\\ \end{array} \right ],}$$

then we also have

$$\displaystyle{\pi _{n}(\sigma ): \;w_{[k]}\longmapsto (-1)^{k}w_{ [n-k]}\,.}$$

The π n exhaust the irreducible finite-dimensional representations of both \(\mathop{\mathrm{SL}}\nolimits _{2}(\mathbb{C})\) and \(\mathfrak{s}l_{2}\), and every finite-dimensional representation of either is a direct sum of them.

Let d = n + 1, the dimension of π n , assumed even. The weights of this with respect to h are

$$\displaystyle{-d,\ldots,-1,1,\ldots,d\,,}$$

The formulas above imply immediately:

Proposition 6.1.

Suppose v to be a vector of weight − 1 in this representation. Then π(e + )v and π(σ)v are both of weight 1, and

$$\displaystyle{\pi (e_{+})v = -(-1)^{d/2}\left ({d \over 2}\right )\pi (\sigma )v\,.}$$

The sum of weight spaces \(\mathfrak{g}_{\mu }\) for μ in a given λ-string is a representation of \(\mathfrak{s}l_{2}\). The formulas laid out in this section relate closely to the numbers p λ, μ and q λ, μ . For one thing, as the picture above suggests and is easy to verify, they tell us that we can choose basis elements e μ for each μ in the chain so that

$$\displaystyle{\begin{array}{rl} [e_{\lambda },e_{\mu }]& = (p_{\lambda,\mu } + 1)e_{\mu +\lambda } \\{} [e_{-\lambda },e_{\mu }]& = (-1)^{p_{\lambda,\mu }}(q_{\lambda,\mu } + 1)e_{\mu -\lambda }.\\ \end{array} }$$

The choice of basis for one chain unfortunately affects other chains as well, so this observation doesn’t make the problem of structure constants trivial. But it is our first hint of a connection between structure constants and chains.

7 The extended Weyl group …

Tits’ beautiful idea is to reduce the computation of structure constants to computation in a certain extension of the Weyl group, the extended Weyl group, fitting into a short exact sequence

$$\displaystyle{1 \rightarrow \{\pm 1\}^{\varDelta } \rightarrow W_{\mathrm{ext}} \rightarrow W \rightarrow 1\,.}$$

If \(\mathfrak{g}\) has finite dimension, the group W ext can be described succinctly as the normalizer of a maximal torus in the integral form of the simply connected split group with Lie algebra \(\mathfrak{g}\). For arbitrary \(\mathfrak{g}\) it is a subgroup of a group G constructed in [KP85], a simply connected analogue for general Kac–Moody algebras.

I cannot resist remarking here about the literature in this field. That on Kac–Moody algebras is adequate. The primary reference is still [Kac85], but it needs updating and its exposition is dense. A useful supplement is [MP95]. For that matter, it is puzzling that there are a number of extremely basic questions about the algebras that have not yet been answered, such as whether or not they can be defined by Serre relations. This makes it very difficult to do explicit calculations with them. But the literature on the associated groups is far less satisfactory. The original paper [MT72] is very readable, but doesn’t tell enough for practical purposes. There are a number of valuable expositions by Jacques Tits, such as [Tits87] and [Tits88], but many of these are difficult to obtain, and are in any event inconclusive. The paper [KP85] is exceptionally clear, but for full proofs one must refer back to earlier papers by the same authors that are not so clear. There is the book [Kum02], but it doesn’t contain everything one wants. There are a number of expositions by Olivier Mathieu, but I have the impression that he stopped writing on this subject before he was through.

The good news is that we do not need to know a great deal about the Kac–Peterson group G.

  1. (G1)

    There exists for each α in Δ a unique embedding

    $$\displaystyle{\varphi _{\alpha }: \;\mathop{\mathrm{SL}}\nolimits _{2}(\mathbb{C})\hookrightarrow G}$$

    compatible with the map \(\varphi _{\alpha }\) of Lie algebras. The images \(\mathop{\mathrm{SL}}\nolimits _{2}^{[\alpha ]}(\mathbb{C})\) generate G.

  2. (G2)

    If π is any representation of \(\mathfrak{g}\) whose restriction to \(\mathfrak{s}l_{2}^{[\alpha ]}\) is a direct sum of irreducible representations of finite dimension, it lifts to a representation I will call π α of \(SL_{2}(\mathbb{C})\). There exists a unique representation of G that I will also call π such that \(\pi \,\circ \varphi _{\alpha }=\pi _{\alpha }\) . This is true in particular if π = ad.

  3. (G3)

    Let ι be the embedding of \(\mathbb{C}^{\times }\) into \(\mathop{\mathrm{SL}}\nolimits _{2}(\mathbb{C})\):

    $$\displaystyle{\iota: \;x\longmapsto \left [\begin{array}{cc} x& 0\\ 0 &1/x\\ \end{array} \right ]\,.}$$

    Abusing terminology slightly, for every α in Δ let \(\alpha ^{\vee } =\varphi _{\alpha }\circ \iota\). These give us a homomorphism

    $$\displaystyle{\varphi =\prod \alpha ^{\vee }: \;(\mathbb{C}^{\times })^{\varDelta }\longrightarrow G\,.}$$

    It is an embedding, say with image H, which is its own centralizer in G. Let \(H_{\mathbb{Z}}\) be the image of { ± 1}Δ. (The notation is suggested by what happens for \(\mathfrak{g}\) finite-dimensional, in which case \(H_{\mathbb{Z}}\) is the group of integral points in a maximal torus.)

  4. (G4)

    Let

    $$\displaystyle{\omega (x) = \left [\begin{array}{cc} 0 &\;x\\ - 1/x & \;0\\ \end{array} \right ]\,}$$

    The normalizer N G (H) is generated by H and the elements \(\omega _{\alpha }(x) =\varphi _{\alpha }\big(\omega (x)\big)\). The adjoint action of ω α (x) on \(\mathfrak{h}\) is the same as that of the Weyl reflection s α . Let

    $$\displaystyle{\sigma _{\alpha } =\omega _{\alpha }(1)\,.}$$
  5. (G5)

    The group W ext is defined to be the subgroup of G generated by the σ α . It fits into a short exact sequence:

    $$\displaystyle{1 \rightarrow H_{\mathbb{Z}} \rightarrow W_{\mathrm{ext}} \rightarrow W \rightarrow 1\,.}$$
  6. (G6)

    There exists a useful cross-section \(w\mapsto \widehat{w}\) of the projection from W ext to W. Define \(\hat{s}_{\alpha }\) to be σ α . If \(w = s_{1}\ldots s_{n}\) is an expression for w as a product of elementary reflections, the product

    $$\displaystyle{\widehat{w} =\hat{ s}_{1}\ldots \hat{s}_{n}}$$

    depends only on w. Multiplication in W ext is determined by the formulas

    $$\displaystyle{\widehat{s_{\alpha }w} = \left \{\begin{array}{rl} \widehat{s_{\alpha }}\widehat{w}&\mbox{ if }\ell(s_{\alpha }w) = 1 +\ell (w)\\ \alpha ^{\vee } (-I)\,\hat{s}_{\alpha }\widehat{w} &\mbox{ otherwise.} \\ \end{array} \right.}$$

    and

    $$\displaystyle{\widehat{w}\hat{s}_{\alpha } = \left \{\begin{array}{rl} \widehat{ws_{\alpha }}&\mbox{ if $ws_{\alpha } > w$ }\\{} [w\alpha ^{\vee } ](-1)\widehat{ws_{\alpha }} &\mbox{ otherwise.}\\ \end{array} \right.}$$

The properties of the cross section were first found by Tits and proved in [Tits66b] in the case of finite-dimensional \(\mathfrak{g}\). Curiously, the explicit cocycle of the extension of W by \(H_{\mathbb{Z}}\) was first exhibited in [LS87].

The generalization to arbitrary Kac–Moody algebras is by Kac and Peterson.

Why is W ext relevant to structure constants? The connection between N G (H) and nilpotent elements of the Lie algebra can be seen already in \(\mathop{\mathrm{SL}}\nolimits _{2}\). In this group, the normalizer breaks up into two parts, the diagonal matrices and the inverse image M of the non-trivial element of the Weyl group, made up of the matrices ω(x) for x ≠ 0. The matrix ω = ω(x) satisfies

$$\displaystyle{\omega ^{2} = \left [\begin{array}{cc} 0 &\;x \\ - 1/x&\;0\\ \end{array} \right ]^{2} = \left [\begin{array}{cc} - 1& \; 0 \\ 0 &\; - 1\\ \end{array} \right ],\quad \mbox{ hence }\quad \sigma _{\alpha }^{-1} =\alpha ^{\vee }(-1)\sigma _{\alpha }\,.}$$

According to the Bruhat decomposition, every element of \(\mathop{\mathrm{SL}}\nolimits _{2}\) is either upper triangular or can be factored as n 1 w(x)n 2 with the n i unipotent and upper triangular. Making this explicit:

$$\displaystyle{\begin{array}{rl} \left [\begin{array}{cc} 1&\;\,0\\ x &\;\,1\\ \end{array} \right ]& = \left [\begin{array}{cc} 1&\;\,1/x\\ 0 & \;\,1\\ \end{array} \right ]\left [\begin{array}{cc} 0&\;\, - 1/x\\ x & \;\, 0\\ \end{array} \right ]\left [\begin{array}{cc} 1&\;1/x\\ 0 & \;1\\ \end{array} \right ] \\ \left [\begin{array}{cc} 0 &\;\,x\\ - 1/x &\;\,0\\ \end{array} \right ]& = \left [\begin{array}{cc} 1&\;\,x\\ 0 &\;\,1\\ \end{array} \right ]\left [\begin{array}{cc} 1 &\;\,0\\ - 1/x &\;\,1\\ \end{array} \right ]\left [\begin{array}{cc} 1&\;\,x\\ 0 &\;\,1\\ \end{array} \right ]\,.\\ \end{array}}$$

Some easy calculating will verify further the following observation of Tits:

Lemma 7.1.

For any σ in the non-trivial coset of H in N G (H) in \(\mathop{\mathrm{SL}}\nolimits _{2}\) there exist unique upper-triangular nilpotent e + and lower-triangular nilpotent e − such that

$$\displaystyle{\sigma =\exp (e_{+})\exp (e_{-})\exp (e_{+})\,.}$$

In this equation, any one of the three determines the other two.

Applying the involution θ we see that the roles of e + and e − may be reversed. In other words, specifying an upper triangular nilpotent e + or a lower triangular nilpotent e − is equivalent to specifying an element of M.

Suppose λ = w α to be a root of \(\mathfrak{g}\). If ω in W ext maps to w, define \(\mathop{\mathrm{SL}}\nolimits _{2}^{[\lambda ]}\) to be \(\omega \mathop{\mathrm{SL}}\nolimits _{2}^{[\alpha ]}\omega ^{-1}\). This group is independent of the choice of ω, although its identification with \(\mathop{\mathrm{SL}}\nolimits _{2}\) is not. Let \(H_{\mathbb{Z}}^{[\lambda ]}\) be the image of the diagonal matrices in \(\mathop{\mathrm{SL}}\nolimits _{2}^{[\lambda ]}(\mathbb{Z})\), and let \(M_{\mathbb{Z}}^{[\lambda ]}\) be the image of the matrices

$$\displaystyle{\left [\begin{array}{cc} 0 &\; \pm 1\\ \mp 1 & \; 0\\ \end{array} \right ]}$$

in N G (H). Each \(M_{\mathbb{Z}}^{[\lambda ]}\) has exactly two elements in it, corresponding to the possible choices of e ±λ . In other words, there is a well-defined map taking \(\sigma \in M_{\mathbb{Z}}^{[\lambda ]}\) to e λ, σ such that

$$\displaystyle{\sigma =\exp (e_{\lambda,\sigma })\exp (e_{-\lambda,\sigma })\exp (e_{\lambda,\sigma })\,.}$$

Here is the whole point:

—————

A choice of e λ or e −λ is equivalent to a choice of σ in \(M_{\mathbb{Z}}^{[\lambda ]}\) .

—————

So now we can at last see the connection between structure constants and the extended Weyl group.

Lemma 7.2.

For ω in W ext with image w in W we have

$$\displaystyle{\omega M_{\mathbb{Z}}^{[\lambda ]}\omega ^{-1} = M_{ \mathbb{Z}}^{[w\lambda ]}\,.}$$

and furthermore for σ in \(M_{\mathbb{Z}}^{[\lambda ]}\)

$$\displaystyle{\mathop{\mathrm{Ad}}(\omega )e_{\lambda,\sigma } = e_{w\lambda,\omega \sigma \omega ^{-1}}\,.}$$

Let me now solve Problem 1. We must choose for each real root λ > 0 an element σ λ n in \(M_{\mathbb{Z}}^{[\lambda ]}\). We have already chosen σ α for α in Δ. Now follow the ISL root graph to set

$$\displaystyle{\sigma _{\mu } =\sigma _{\alpha }\sigma _{\lambda }\sigma _{\alpha }^{-1}}$$

when

$$\displaystyle{\lambda \stackrel {\alpha} {\longrightarrow} \mu}$$

is an edge in it. This technique, of defining objects associated to nodes of a graph by finding a spanning tree in it, is common in computer algorithms.

8 … and structure constants

How will this new scheme relate to structure constants? Suppose we are given choices of the elements σ λ . These determine nilpotent elements \(e_{\pm \lambda,\sigma _{\lambda }}\) etc. in \(\mathfrak{s}l_{2}^{[\lambda ]}\). Suppose λ +μ +ν = 0. According to our definitions,

$$\displaystyle{[e_{\lambda,\sigma _{\lambda }},e_{\mu,\sigma _{\mu }}] =\varepsilon (\lambda,\mu,\nu,\sigma _{\lambda },\sigma _{\mu },\sigma _{\nu })(p_{\lambda,\mu } + 1)e_{-\nu,\sigma _{\nu }}\,,}$$

for some \(\varepsilon\) factor. According to the generalization of Chevalley’s theorem this factor is ± 1, but I won’t assume that.

The dependence on the roots λ, μ, ν is manifest but weak, in that σ λ determines both e λ and e −λ . In fact we don’t need to take it into account at all. If λ +μ +ν = 0 then the only other linear combination ±λ ±μ ±ν that vanishes is −λ −μ −ν. Since θ(e +) = e − we know that \(\varepsilon (-\lambda,-\mu,-\nu,\ldots \ ) =\varepsilon (\lambda,\mu,\nu,\ldots \ )\), so we can just write \(\varepsilon (\sigma _{\lambda },\sigma _{\mu },\sigma _{\nu })\):

Proposition 8.1.

For real roots λ, μ, ν with λ + μ + ν = 0 we have

$$\displaystyle{[e_{\lambda,\sigma _{\lambda }},e_{\mu,\sigma _{\mu }}] =\varepsilon (\sigma _{\lambda },\sigma _{\mu },\sigma _{\nu })(p_{\lambda,\mu } + 1)e_{-\nu,\sigma _{\nu }}\,.}$$

where \(\varepsilon\) depends only on σ λ , σ μ , σ ν .

How do we compute \(\varepsilon (\sigma _{\lambda },\sigma _{\mu },\sigma _{\nu })\) ? Following §2.9 of [Tits66a], we get four basic rules.

Theorem 8.2.

Suppose that λ, μ, ν are real roots with λ + μ + ν = 0. Then

  1. (a)

    \(\varepsilon (\sigma _{\mu },\sigma _{\lambda },\sigma _{\nu }) = -\varepsilon (\sigma _{\lambda },\sigma _{\mu },\sigma _{\nu })\) .

  2. (b)

    \(\varepsilon (\sigma _{\lambda },\sigma _{\mu },\sigma _{\nu }^{-1}) = -\varepsilon (\sigma _{\lambda },\sigma _{\mu },\sigma _{\nu })\) .

  3. (c)

    Suppose \(\Vert \lambda \Vert \geq \Vert \mu \Vert\) , \(\Vert \nu \Vert\) . In this case s λ μ = −ν and s ν = s λ s μ s λ , so σ λ σ μ σ λ −1 lies in \(M_{\mathbb{Z}}^{[\nu ]}\) and satisfies

    $$\displaystyle{\varepsilon (\sigma _{\lambda },\sigma _{\mu },\sigma _{\lambda }\sigma _{\mu }\sigma _{\lambda }^{-1}) = (-1)^{p_{\lambda,\mu } }\,.}$$
  4. (d)

    The function \(\varepsilon\) is invariant under cyclic permutations:

    $$\displaystyle{\varepsilon (\sigma _{\lambda },\sigma _{\mu },\sigma _{\nu }) =\varepsilon (\sigma _{\mu },\sigma _{\nu },\sigma _{\lambda })\,.}$$

Proof.

(a) follows from Lemma 5.5, since [x, y] = −[y, x]. (b) is elementary, since \(e_{\nu,\sigma _{\nu }^{-1}} = -e_{\nu,\sigma _{\nu }}\).

It is the last two results that are significant. The first tells us that there is one case in which we can calculate the constant explicitly, and the second tells us that we can manipulate any case so as to fall in this one.

For (c): Proposition 6.1 tells that in this case

$$\displaystyle{\begin{array}{rl} [e_{\lambda,\sigma _{\lambda }},e_{\mu,\sigma _{\mu }}]& = (-1)^{p_{\lambda,\mu }}(p_{\lambda,\mu } + 1)\mathop{\mathrm{Ad}}(\sigma _{\lambda })e_{\mu,\sigma _{ \mu }} \\ & = (-1)^{p_{\lambda,\mu }}(p_{\lambda,\mu } + 1)e_{s_{ \lambda }\mu,\sigma _{\lambda }\sigma _{\mu }\sigma _{\lambda }^{-1}}\,.\\ \end{array} }$$

For (d): This reduces to the fact that the Jacobi identity has cyclic symmetry. For e λ , e μ , and e ν it tells us that

$$\displaystyle{\begin{array}{rl} 0& = [[e_{\lambda },e_{\mu }],e_{\nu }] + [[e_{\mu },e_{\nu }],e_{\lambda }] + [[e_{\nu },e_{\lambda }],e_{\mu }] \\ & =\varepsilon (\sigma _{\lambda },\sigma _{\mu },\sigma _{\nu })(p_{\lambda,\mu } + 1)[e_{-\nu },e_{\nu }] \\ &\quad +\;\varepsilon (\sigma _{\mu },\sigma _{\nu },\sigma _{\lambda })(p_{\mu,\nu } + 1)[e_{-\lambda },e_{\lambda }] \\ &\qquad \quad +\;\varepsilon (\sigma _{\nu },\sigma _{\lambda },\sigma _{\mu })(p_{\nu,\lambda } + 1)[e_{-\mu },e_{\mu }] \\ & =\varepsilon (\sigma _{\lambda },\sigma _{\mu },\sigma _{\nu })(p_{\lambda,\mu } + 1)h_{\nu } \\ &\quad +\;\varepsilon (\sigma _{\mu },\sigma _{\nu },\sigma _{\lambda })(p_{\mu,\nu } + 1)h_{\lambda } \\ &\qquad \quad +\;\varepsilon (\sigma _{\nu },\sigma _{\lambda },\sigma _{\mu })(p_{\nu,\lambda } + 1)h_{\mu }\,.\\ \end{array} }$$

But according to Proposition 5.6,

$$\displaystyle{(p_{\lambda,\mu } + 1)h_{\nu } + (p_{\mu,\nu } + 1)h_{\lambda } + (p_{\nu,\lambda } + 1)h_{\mu } = 0\,.}$$

The vectors h λ and h μ are linearly independent, so the conclusion may be deduced from the following trivial observation: if u, v, w are vectors, two of them linearly independent, and

$$\displaystyle{\begin{array}{rl} au + bv + cw& = 0\\ u + v + w & = 0,\\ \end{array} }$$

then a = b = c. □ 

The relevance to computation should be evident. If λ +μ +ν = 0, then one of the three roots will at least weakly dominate in length, and by Theorem 8.2(d) we can cycle to get the condition assumed in Lemma 5.3.

Incidentally, from these rules follows Chevalley’s theorem:

Proposition 8.3.

The function \(\varepsilon\) always takes values ± 1.

At any rate, we are now faced with the algorithmic problem: Suppose λ + μ + ν = 0 with \(\Vert \lambda \Vert \geq \Vert \mu \Vert =\Vert \nu \Vert\) . Then −ν = s λ μ and \(\sigma _{\lambda }\sigma _{\mu }\sigma _{\lambda }^{-1}\) lies in \(M_{\mathbb{Z}}^{[\nu ]}\) . Is it equal to σ ν or \(\sigma _{\nu }^{-1} =\nu ^{\vee }(-1)\sigma _{\nu }\) ? If \(\sigma _{\lambda }\sigma _{\mu }\sigma _{\lambda }^{-1} =\nu ^{\vee }(\pm 1)\sigma _{\nu }\) we can deduce now:

$$\displaystyle{[e_{\lambda,\sigma _{\lambda }},e_{\mu,\sigma _{\mu }}] = \pm (-1)^{p_{\lambda,\mu } }(p_{\lambda,\mu } + 1)e_{\nu,\sigma _{\nu }}\,.}$$

9 The extended root graph

To each real root λ are associated two elements σ λ ±1 in \(M_{\mathbb{Z}}^{[\lambda ]}\). These are the nodes of the extended root graph, which is a two-fold covering of the root graph itself. Make edges from each node σ to σ α σ σ α −1, and from σ to \(\sigma _{\alpha }^{-1}\sigma \sigma _{\alpha }\) (for α ∈ Δ). Compute these as we assign the σ λ . This can all be calculated by using the formulas for multiplication in W ext (Figure 10).

This is what we need in order to compute the edges in the extended root graph, which we use to compute all \(\sigma _{\lambda }\sigma _{\mu }\sigma _{\lambda }^{-1}/\sigma _{\nu }\) for Tits triples (λ, μ, ν).

Let’s look at an example, the Lie algebra \(\mathfrak{s}l_{3}\).

Figure 10
figure 10

The root system A 2

Full size image

Set

$$\displaystyle{\sigma _{\gamma } =\sigma _{\alpha }\sigma _{\beta }\sigma _{\alpha }^{-1} = s_{\alpha }s_{\beta }\alpha ^{\vee }(-1)\hat{s}_{\alpha }\hat{s}_{\beta }\hat{s}_{\alpha } =\beta ^{\vee }(-1)\hat{s}_{\gamma }\,.}$$

Thus by definition [e α , e β ] = e γ .

We can also use Tits’ trick to calculate [e β , e α ]. We know

$$\displaystyle{[e_{\beta },e_{\alpha }] = e_{\gamma,\sigma _{\beta }\sigma _{\alpha }\sigma _{\beta }^{-1}}\,.}$$

But

$$\displaystyle{\sigma _{\beta }\sigma _{\alpha }\sigma _{\beta }^{-1} = s_{\beta }s_{\alpha }\beta ^{\vee }(-1)\hat{s}_{\beta }\hat{s}_{\alpha }\hat{s}_{\beta } =\alpha ^{\vee }(-1)\hat{s}_{\gamma } =\gamma ^{\vee }(-1)\sigma _{\gamma },}$$

so [e β , e α ] = −e γ . Of course this just confirms what we already knew.

10 Admissible triples

At this point I have explained how to construct the σ λ and computed as much as we want of the extended root graph.

According to Proposition 8.2, we can reduce the computation of the factors \(\varepsilon\) to the case in which the arguments come from a Tits triple (λ, μ, ν), and in this case it reduces more precisely to a calculation of a comparison of \(\sigma _{\lambda }\sigma _{\mu }\sigma _{\lambda }^{-1}/\sigma _{\nu }\).

We therefore start by making a list of Tits triples, and the ISL tree can be used to do this. We start by dealing directly with all cases in which λ = α lies in Δ and μ > 0, following from λ up the ISL tree. The cases where μ < 0 can be dealt with at the same time, since if α +μ = ν, then −ν +α = −μ. Then we add the ones where λ is not in Δ. If (λ, μ, ν) is a Tits triple with s α λ > 0, then so is

$$\displaystyle{s_{\alpha }(\lambda,\mu,\nu ) = (s_{\alpha }\lambda,s_{\alpha }\mu,s_{\alpha }\nu )\,.}$$

Thus we can compile a complete list of Tits triples by going up the ISL tree.

We must then compare \(\sigma _{\lambda }\sigma _{\mu }\sigma _{\lambda }^{-1}\) to σ ν for all Tits triples (λ, μ, ν). This computation may also be done inductively in the ISL tree, since

$$\displaystyle{\sigma _{\alpha }\sigma _{\lambda }\sigma _{\alpha }^{-1} \cdot \sigma _{\alpha }\sigma _{\mu }\sigma _{\alpha }^{-1} \cdot \sigma _{\alpha }\sigma _{\lambda }^{-1}\sigma _{ \alpha }^{-1} =\sigma _{\alpha } \cdot \sigma _{\lambda }\sigma _{\mu }\sigma _{\lambda }^{-1} \cdot \sigma _{\alpha }^{-1}\,.}$$

To see exactly how this goes, fix for the moment assignments λ ↦ σ λ . For every triple (λ, μ, ν) with s λ μ = ν (not just Tits triples) define the factor τ λ, μ, ν ∨ by the formula

$$\displaystyle{\begin{array}{rl} \sigma _{\lambda }\sigma _{\mu }\sigma _{\lambda }^{-1} & =\tau _{ \lambda,\mu,\nu }^{\vee }\cdot \sigma _{\nu }\,.\\ \end{array} }$$

The factor \(\tau _{\lambda,\mu,\nu }^{\vee }\) will lie in \(H_{\nu }(\mathbb{Z})\), hence will be either 1 or ν ∨(−1). I will show in the next section how to compute these factors when λ lies in Δ. This will depend on something we haven’t seen yet. But for the moment assume that the τ α, μ, ν ∨ have been calculated for all α in Δ and μ an arbitrary positive root. We can then proceed to calculate the τ-factors for all Tits triples by induction. Let

$$\displaystyle{(\lambda _{\bullet },\mu _{\bullet },\nu _{\bullet }) = (s_{\alpha }\lambda,s_{\alpha }\mu,s_{\alpha }\nu )\,.}$$

Then

$$\displaystyle{\begin{array}{rl} \sigma _{\lambda }\sigma _{\mu }\sigma _{\lambda }^{-1} & =\tau _{ \lambda,\mu,\nu }^{\vee }\cdot \sigma _{\nu } \\ \sigma _{\alpha }\sigma _{\lambda }\sigma _{\alpha }^{-1} \cdot \sigma _{\alpha }\sigma _{\mu }\sigma _{\alpha }^{-1}\! \cdot \!\sigma _{\alpha }\sigma _{\lambda }^{-1}\sigma _{\alpha }^{-1} & =\sigma _{\alpha } \cdot \sigma _{\lambda }\sigma _{\mu }\sigma _{\lambda }^{-1}\! \cdot \!\sigma _{\alpha }^{-1} \\ (\tau _{\alpha,\lambda,\lambda _{\bullet }}^{\vee }\cdot \sigma _{\lambda _{\bullet }})(\tau _{\alpha,\mu,\mu _{\bullet }}^{\vee }\cdot \sigma _{\mu _{\bullet }})(\tau _{\alpha,\lambda,\lambda _{\bullet }}^{\vee }\cdot \sigma _{\lambda _{\bullet }})^{-1} & =\sigma _{\alpha } \cdot \tau _{\lambda,\mu,\nu }^{\vee }\sigma _{\nu }\!\cdot \!\sigma _{\alpha }^{-1} \\ (\tau _{\alpha,\lambda,\lambda _{\bullet }}^{\vee }\!\! +\! s_{\lambda _{\bullet }}\tau _{\alpha,\mu,\mu _{\bullet }}^{\vee }\!\! +\! s_{\lambda _{\bullet }}s_{\mu _{\bullet }}s_{\lambda _{\bullet }}\tau _{\alpha,\lambda,\lambda _{\bullet }}^{\vee })\! \cdot \!\sigma _{\lambda _{\bullet }}\sigma _{\mu _{\bullet }}\sigma _{\lambda _{\bullet }}^{-1} & = s_{\alpha }\tau _{\lambda,\mu,\nu }^{\vee }\cdot \sigma _{\alpha }\sigma _{\nu }\sigma _{\alpha }^{-1} \\ (\tau _{\alpha,\lambda,\lambda _{\bullet }}^{\vee } + s_{\lambda _{\bullet }}\tau _{\alpha,\mu,\mu _{\bullet }}^{\vee }\! +\! s_{\nu _{\bullet }}\tau _{\alpha,\lambda,\lambda _{\bullet }}^{\vee })\! \cdot \!\sigma _{\lambda _{\bullet }}\sigma _{\mu _{\bullet }}\sigma _{\lambda _{\bullet }}^{-1} & = (s_{\alpha }\tau _{\lambda,\mu,\nu }^{\vee }\! +\!\tau _{ \alpha,\nu,\nu _{\bullet }}^{\vee })\! \cdot \!\sigma _{\nu _{\bullet }}\\ \end{array} }$$

leading to:

Lemma 10.1.

If (λ,μ,ν) is a Tits triple and λ ≠ α ∈Δ, then so is

$$\displaystyle{(\lambda _{\bullet },\mu _{\bullet },\nu _{\bullet }) = (s_{\alpha }\lambda,s_{\alpha }\mu,s_{\alpha }\nu )\,,}$$

and

$$\displaystyle{\tau _{\lambda _{\bullet },\mu _{\bullet },\nu _{\bullet }}^{\vee } = s_{\alpha }\tau _{\lambda,\mu,\nu }^{\vee } +\tau _{ \alpha,\lambda,\lambda _{\bullet }}^{\vee } + s_{\lambda _{\bullet }}\tau _{\alpha,\mu,\mu _{\bullet }}^{\vee } + s_{\nu _{\bullet }}\tau _{\alpha,\lambda,\lambda _{\bullet }}^{\vee } +\tau _{ \alpha,\nu,\nu _{\bullet }}^{\vee }\,.}$$

I wish this formula were more enlightening. One must conclude that the relationship between the groups \(\mathop{\mathrm{SL}}\nolimits _{2}^{[\lambda ]}\) and Tits’ cross section is complicated.

The principal conclusion of these preliminary formulas is that for both the specification of the σ λ and the calculation of the σ λ σ μ σ λ −1 we are reduced to the single calculation: for α in Δ and λ > 0, given σ λ how do we calculate \(\sigma _{\alpha }\sigma _{\lambda }\sigma _{\alpha }^{-1}\) ? I must explain in detail not only how calculations are made, but also how elements of \(N_{H}(\mathbb{Z})\) are interpreted in a computer program. I have already explained the basis of calculation in the extended Weyl group.

In understanding how efficient the computation of structure constants will be, we have to know roughly how many admissible triples there are. Following [Car72] and [CMT04], I assume the positive roots to be ordered, and I define a trio of roots λ, μ, ν to be special if 0 < λ < μ and λ +μ = −ν is again a root. If λ, μ, ν is any triple of roots with λ +μ +ν = 0, then (as Carter points out) exactly one of the following twelve triples is special:

$$\displaystyle{\begin{array}{*{10}c} (\lambda,\mu,\nu ),&(-\lambda,-\mu,-\nu ),&(\mu,\lambda,\nu ),&(-\mu,-\lambda,-\nu ) \\ (\nu,\lambda,\mu ),&(-\nu,-\lambda,-\mu ),&(\lambda,\nu,\mu ),&(-\lambda,-\nu,-\mu ) \\ (\mu,\nu,\lambda ),&(-\mu,-\nu,-\lambda ),&(\nu,\mu,\lambda ),&(-\nu,-\mu,-\lambda ).\\ \end{array} }$$

Hence there are at most 12 times as many Tits triples as special triples. How many special triples are there? This is independent of the ordering of Σ +, since it is one-half the number of pairs of positive roots λ, μ with λ +μ also a root. In [CMT04] it is asserted that for all classical systems the number is O(n 3), where n is the rank of the system. Don Taylor has given me the following more precise table:

$$\displaystyle{\begin{array}{cccc} &\mbox{ System}&\mbox{ Number of special triples}& \\ & A_{n} & n(n^{2} - 1)/6 & \\ & B_{n} & n(n - 1)(2n - 1)/3 & \\ & C_{n} & n(n - 1)(2n - 1)/3 & \\ & D_{n} & 2n(n - 1)(n - 2)/3 & \\ & E_{6} & 120 & \\ & E_{7} & 336 & \\ & E_{8} & 1120 & \\ & F_{4} & 68 & \\ & G_{2} & 5 & \\ \end{array} }$$

11 Some details of computation

For this section I am going to simplify notation. Every element of the extended Weyl group may be represented uniquely as \(t^{\vee }(-1) \cdot \widehat{ w}\), where t ∨ is in \(X_{{\ast}}(H) = L_{\varDelta ^{\vee }}\) and w is in W. I will express it as just \(t^{\vee }\cdot \widehat{ w}\), and of course it is only t ∨ modulo 2X ∗(H) that counts. Also, I will refer to the group operation in \(L_{\varDelta ^{\vee }}\) additively.

Proposition 11.1.

Suppose α to be in Δ, λ ≠ α > 0. Then

$$\displaystyle{\hat{s}_{\alpha }\hat{s}_{\lambda }\hat{s}_{\alpha } = \left \{\begin{array}{@{}l@{\quad }l@{}} \widehat{s_{s_{\alpha }\lambda }} \quad &\mbox{ if $\langle \alpha,\lambda ^{\vee }\rangle < 0$} \\ \alpha ^{\vee }\cdot \hat{ s}_{\lambda } \quad &\mbox{ $\langle \alpha,\lambda ^{\vee }\rangle = 0$} \\ (\alpha ^{\vee } + s_{\alpha }s_{\lambda }\alpha ^{\vee }) \cdot \widehat{ s_{s_{\alpha }\lambda }}\quad &\mbox{ $\langle \alpha,\lambda ^{\vee }\rangle > 0$}.\\ \quad \end{array} \right.}$$

Proof.

A preliminary calculation:

$$\displaystyle{\begin{array}{rl} s_{\lambda }\alpha & =\alpha -\langle \alpha,\lambda ^{\vee }\rangle \lambda \\ s_{\alpha }s_{\lambda }\alpha & = -\alpha -\langle \alpha,\lambda ^{\vee }\rangle s_{\alpha }\lambda \\ & = -\alpha -\langle \alpha,\lambda ^{\vee }\rangle (\lambda -\langle \lambda,\alpha ^{\vee }\rangle \alpha ) \\ & = -\alpha -\langle \alpha,\lambda ^{\vee }\rangle \lambda +\langle \alpha,\lambda ^{\vee }\rangle \langle \lambda,\alpha ^{\vee }\rangle \alpha \\ & = -\langle \alpha,\lambda ^{\vee }\rangle \lambda +\big (\langle \alpha,\lambda ^{\vee }\rangle \langle \lambda,\alpha ^{\vee }\rangle - 1\big)\alpha.\\ \end{array} }$$

Recall that by Corollary 4.4 the product \(\langle \alpha,\lambda ^{\vee }\rangle \langle \lambda,\alpha ^{\vee }\rangle \geq 0\). Recall also that ws α  > w if and only if w α > 0.

  1. (a)

    \(\langle \alpha,\lambda ^{\vee }\rangle < 0\). Here s λ α > 0 and s α s λ α > 0 so \(s_{\lambda } < s_{\alpha }s_{\lambda } < s_{\alpha }s_{\lambda }s_{\alpha }\), and \(\ell(s_{\alpha }s_{\lambda }s_{\alpha }) =\ell (s_{\lambda }) + 2\), and

    $$\displaystyle{\hat{s}_{\alpha }\hat{s}_{\lambda }\hat{s}_{\alpha } =\widehat{ s_{\alpha }s_{\lambda }s_{\alpha }} =\widehat{ s_{s_{\alpha }\lambda }}\,.}$$
  2. (b)

    \(\langle \alpha,\lambda ^{\vee }\rangle = 0\). Here s α λ = λ, and \(\hat{s}_{\lambda }\hat{s}_{\alpha } =\widehat{ s_{\lambda }s_{\alpha }}\), but s α (s λ s α ) = s λ so

    $$\displaystyle{\hat{s}_{\alpha }\hat{s}_{\lambda }\hat{s}_{\alpha } =\hat{ s}_{\alpha }\widehat{s_{\lambda }s_{\alpha }} =\alpha ^{\vee }\cdot \hat{ s}_{\lambda }\,.}$$
  3. (c)

    \(\langle \alpha,\lambda ^{\vee }\rangle > 0\). Here one sees easily that s λ α < 0. But since λ ≠ α we also have s α s λ α < 0 also. So \(\ell(s_{s_{\alpha }\lambda }) =\ell (s_{\lambda }) - 2\).

    $$\displaystyle{\begin{array}{rl} \hat{s}_{\alpha }\hat{s}_{\lambda }& =\alpha ^{\vee }\cdot \widehat{ s_{\alpha }s_{\lambda }} \\ \hat{s}_{\alpha }\hat{s}_{\lambda }\hat{s}_{\alpha }& =\alpha ^{\vee }\cdot \widehat{ s_{\alpha }s_{\lambda }}\hat{s}_{\alpha } \\ & =\alpha ^{\vee }\cdot \widehat{ s_{s_{\alpha }\lambda }} \cdot \alpha ^{\vee }\cdot 1 \\ & = (\alpha ^{\vee } + s_{\alpha }s_{\lambda }\alpha ^{\vee }) \cdot \widehat{ s_{s_{\alpha }\lambda }}\,.\\ \end{array} }$$

 □ 

Corollary 11.2.

Suppose \(\sigma _{\lambda } = t_{\lambda }^{\vee }\cdot \hat{ s}_{\lambda }\) . Then for α ≠ λ

$$\displaystyle{\sigma _{\alpha }\sigma _{\lambda }\sigma _{\alpha }^{-1} = \left \{\begin{array}{@{}l@{\quad }l@{}} (s_{\alpha }t_{\lambda }^{\vee } + s_{\alpha }s_{\lambda }\alpha ^{\vee }) \cdot \widehat{ s_{s_{\alpha }\lambda }}\quad &\mbox{ $\langle \alpha,\lambda ^{\vee }\rangle < 0$} \\ (s_{\alpha }t_{\lambda }^{\vee }) \cdot \widehat{ s_{s_{\alpha }\lambda }} \quad &\mbox{ $\langle \alpha,\lambda ^{\vee }\rangle = 0$} \\ (s_{\alpha }t_{\lambda }^{\vee } +\alpha ^{\vee })\widehat{s_{s_{\alpha }\lambda }} \quad &\mbox{ $\langle \alpha,\lambda ^{\vee }\rangle > 0$}.\\ \quad \end{array} \right.}$$

Keep in mind that the reflection associated to s α λ is s α s λ s α .

Proof.

We start with

$$\displaystyle{\sigma _{\alpha }\sigma _{\lambda }\sigma _{\alpha }^{-1} =\hat{ s}_{\alpha }t_{\lambda }^{\vee }\hat{s}_{\lambda }\alpha ^{\vee }\hat{s}_{\alpha } = (s_{\alpha }t_{\lambda }^{\vee } + s_{\alpha }s_{\lambda }\alpha ^{\vee }) \cdot \hat{ s}_{\alpha }\hat{s}_{\lambda }\hat{s}_{\alpha }\,.}$$

Apply the Proposition. □ 

There are three cases, according to whether \(\langle \alpha,\lambda ^{\vee }\rangle\) is < , = , or > 0. These correspond to how the length ℓ(s α s λ s α ) relates to ℓ(s λ ). So now finally we can compute the factors \(\tau _{\alpha,\mu,s_{\alpha }\mu }^{\vee }\), comparing σ α σ μ σ α −1 to \(\sigma _{s_{\alpha }\mu }\).

Lemma 11.3.

Suppose s α μ = ν. If \(\sigma _{\alpha }\sigma _{\mu }\sigma _{\alpha }^{-1} = t^{\vee }\hat{s}_{\nu }\) and \(\sigma _{\nu } = t_{\nu }^{\vee }\hat{s}_{\nu }\) , then

$$\displaystyle{\tau _{\alpha,\mu,\nu }^{\vee } = t^{\vee } + t_{\nu }^{\vee }\,.}$$

12 Patterns in the computation

As a consequence of the main theorem of [BH93], Bob Howlett proved that the root graph of an arbitrary Coxeter group is described by a finite automaton. What this means is that paths in the root graph are the same as paths in a certain finite state machine. The machine, although finite, can be quite large. As Figure 11 indicates, there are 31 states in the machine producing paths in the root graph of the root system we have seen earlier in Figure 1. (In this diagram, nodes give rise to equivalent states if and only if the subsequent paths out of them are equivalent. Each state is noted by a unique shaded box. An unshaded one with the same label signifies another occurrence. The labeled boxes are all one needs to specify the finite state machine.)

Figure 11
figure 11

The finite state machine for the root graph of an infinite root system

Full size image

One thing evident in this picture is the repetition of the weak Bruhat order of the finite groups W Θ . Lemma 5.2 of [Cas06] explains this.) This as well as regularity should have some significance for the extended root graph as well, but I don’t yet completely understand what is going on, and I will not discuss this topic here.