Acoustic Holography

Abstract

One of the subtle problems that make noise control difficult for engineers is the invisibility of noise or sound. A visual image of noise often helps to determine an appropriate means for noise control. There have been many attempts to fulfill this rather challenging objective. Theoretical (or numerical) means for visualizing the sound field have been attempted, and as a result, a great deal of progress has been made. However, most of these numerical methods are not quite ready for practical applications to noise control problems. In the meantime, rapid progress with instrumentation has made it possible to use multiple microphones and fast signal-processing systems. Although these systems are not perfect, they are useful. A state-of-the-art system has recently become available, but it still has many problematic issues; for example, how can one implement the visualized noise field. The constructed noise or sound picture always consists of bias and random errors, and consequently, it is often difficult to determine the origin of the noise and the spatial distribution of the noise field. Section 26.2 of this chapter introduces a brief history, which is associated with sound visualization, acoustic source identification methods and what has been accomplished with a line or surface array. Section 26.2.3 introduces difficulties and recent studies, including de-Dopplerization and de-re verberation methods, both essential for visualizing a moving noise source, such as occurs for cars or trains. This section also addresses what produces ambiguity in realizing real sound sources in a room or closed space. Another major issue associated with sound/noise visualization is whether or not we can distinguish between mutual dependencies of noise in space (Sect. 26.2.4); for example, we are asked to answer the question, Can we see two birds singing or one bird with two beaks?

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

The Methodology of Acoustic Source Identification

The famous article written by Kac [1], Can one hear the shape of the drum? clearly addresses the essence of the inverse problem. It can be regarded as an attempt to obtain what is not available, using what is available, using the example of the relationship between sound generation by membrane vibration and its reception in space. One can find many other examples of inverse problems [2,3,4,5,6,7,8]. Often, in the inverse problem, it is hard to predict or describe data that are not measured because the available data are insufficient. This circumstance is commonly referred to as an ill-posed problem in the literature [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]. Figure 26.1 demonstrates what might happen in practice; the prediction depends on how well the basis function (the elephants or dogs in Fig. 26.1) mimics what happens in reality. When we try to see the shape of noise/sound sources, how well we see the shape of a noise source completely depends on this basis function, because we predict what is not available by using this selected basis function.

Fig. 26.1

The inverse problem and basis function. Are the measured data the parts of elephants or dogs?

One of the common methods of classifying methods used in noise/sound source identification, is by the type of basis function. According to this classification, one approach is the nonparametric method, which uses basis functions that do not model the signal. In other words, the basis functions do not map the unmeasured sound field; all orthogonal functions fall into this category. One of the typical methods of this kind uses Fourier transforms. Acoustic holography uses this type of basis function, mapping the sound field of interest with regard to every measured frequency; it therefore sees the sound field in the frequency domain. In fact, the ideas of acoustic holography originated from optics [20,21,22,23,24,25,26,27,28,29,30]. Acoustic holography was simply extended or modified from the basic idea of optical holography. Near-field acoustic holography [31,32] has been recognized as a very useful means of predicting the true appearance of the source Fig. 26.2. (The near-field effect on resolution was first introduced in the field of microwaves [33].) The basis of this method is to include or measure exponentially decaying waves as they propagate from the sound source so that the sources can be completely reconstructed.

Fig. 26.2

Illustration of acoustic holography. Near-field acoustic holography measures evanescent waves on the measurement plane. The measurement plane is always finite, i.e. there is always a finite aperture. Therefore, we only get limited data

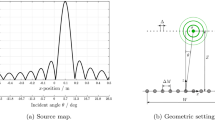
Another class of approaches are based on the parametric method, which derives its name from the fact that the signal is modeled using certain parameters. In other words, the basis function is chosen depending upon the prediction of the sound source. A typical method of this kind is the so-called beam-forming method. Different types of basis functions can be chosen for this method, entirely depending on the sound field that the basis function is trying to map [34,35]. In Fig. 26.1, we can select either the elephants or dogs (or another choice), depending on what we want to predict. This type of mapping gives information about the source location. As illustrated in Fig. 26.1, the basis function maps the signal by changing its parameter; in the case of forming a plane-wave beam, the incident angle of the plane wave can be regarded as a parameter. The main issues that have been discussed for this kind of mapping method are directly related to the structure of the correlation matrix that comes from the measured acoustic pressure vector and its complex conjugate (see Fig. 26.3 for the details). In this method, each scan vector has a multiplicative parameter; for the plane wave in Fig. 26.3 it is the angle of arrival. The correlation matrix is given as illustrated in Fig. 26.3. The scan vector is a basis function in this case. As one can see immediately, this problem is directly related to the structure of the correlation matrix and the basis function used. The signal-to-noise (S/N) ratio of the measured correlation matrix determines the effectiveness of the estimation. There have been many attempts to improve the estimatorʼs performance with regard to the signal-to-noise ratio [35,36]. These methods have mainly been developed for applications in the radar and underwater communities [37]. This technique has also been applied to a noise source location finding problem; high-speed-train noise source estimation [38,39,40] is one such example. Various shapes of arrays have been tried to improve the spatial resolution [41,42,43]. However, it is obvious that these methods cannot sense the shape of the sound or noise source; they only provide its location. Therefore, we will not discuss the beam-forming method in this chapter. In the next section, the problems that we have discussed will be defined.

Fig. 26.3

The beam-forming method

Acoustic Holography: Measurement, Prediction and Analysis

Introduction and Problem Definitions

Acoustic holography consists of three components: measurement, which consists of measuring the sound pressure on the hologram plane, prediction of the acoustic variables, including the velocity distribution, on the plane of interest, and analysis of the holographic reconstruction. This last component was not recognized as important as the others in the past. However, it yields the real meaning of the sound picture: visualization.

The issues associated with measurement are all related to the hologram measurement configuration; we measure the sound pressure at discrete measurement points over a finite measurement area (finite aperture), as illustrated in Fig. 26.2. References [44,45,46,47,48,49,50,51,52] explain the necessary steps to avoid spatial aliasing, wrap-around errors, and the effect of including evanescent waves on the resolution (near-field acoustic holography). If sensors are incorrectly located on the hologram surface, errors result in the prediction results. Similar errors can be produced when there is a magnitude and phase mismatch between sensors. This is well summarized in [53]. There have been many attempts to reduce the aperture effect. One method is to extrapolate the pressure data based on the measurements taken [50,52]. Another method allows the measurement of sound pressure in a sequence and interprets the measured sound pressures with respect to reference signals, assuming that the measured sound pressure field is stationary during the measurement and the number of independent sources is smaller than the number of reference microphones [54,55,56,57,58,59,60,61]. Another method allows scanning or moving of the microphone array, thereby extending the aperture size as much as possible [62,63,64,65]. This also allows one to measure the sound pressure generated by moving sound sources, such as a vehicleʼs exterior noise.

The prediction problem is rather well defined and relatively straightforward. Basically, the solution of the acoustic wave equation usually results in the sound pressure distribution on the measurement plane. Prediction can be attempted using a Greenʼs function, an example of which may be found in the Kirchhoff–Helmholtz integral equation. It is noteworthy, however, that the prediction depends on the shape of the measurement and prediction surfaces, and also on the presence of sound reflections [54,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87].

The acoustic holography analysis problem was introduced rather recently. As mentioned earlier in this section, this is one of the essential issues connected to the general inverse problem. One basic question is whether what we see and imagine is related to what happens in reality. There are two different sound/noise sources, one of which is really radiating the sound, and the another that is reflecting the sound. The former is often called active sound/noise, while the latter is called passive sound/noise. This is an important practical concept for establishing noise control strategies; we want to eliminate the active noise source. Another concern is whether the sources are independently or dependently correlated (Fig. 26.23). The concept of an independent and dependent source has to be addressed properly to understand the issues.

Fig. 26.23

Spatially independent or dependent sources

Prediction Process

The prediction process is related to how we predict the unmeasured sound pressure or other acoustic variables based on the measured sound pressure information. The following equation relates the unmeasured and measured pressure

$${\displaystyle \begin{array}{cc}\hfill P(x;f)& ={\int }_{S_{\text{h}}}[G(x|x_{\text{h}};f){\frac{\partial P}{\partial n}|}_{(x=x_{\text{h}};f)}\hfill \\ -P(x_{\text{h}};f)\frac{\partial G(x|x_{\text{h}};f)}{\partial n}]d{S}_{\text{h}}.\hfill \end{array}}$$

(26.1)

Equation (26.1) is the well-known Kirchhoff–Helmholtz integral equation, where G(x | x _h;f) is the free-space Greenʼs function. This equation essentially says that we can predict the sound pressure anywhere if we know the sound pressures and velocities on the boundary Fig. 26.4. However, it is noteworthy that measuring the velocity on the boundary is more difficult than measuring the sound pressure. This rather practical difficulty can be solved by introducing a Greenʼs function that satisfies the Dirichlet boundary condition: G _D(x | x _h;f). Then, (26.1) becomes

$${\displaystyle P(x;f)={\int }_{S_{\text{h}}}[-P(x_{\text{h}};f)\frac{\partial G_{\text{D}}(x|x_{\text{h}};f)}{\partial n}]d{S}_{\text{h}}.}$$

(26.2)

This equation allows us to predict the sound pressure on any surface of interest. It is noteworthy that we can choose a Greenʼs function as long as it satisfies the linear inhomogeneous wave equation, or the inhomogeneous Helmholtz equation in the frequency domain. That is,

$${\displaystyle \begin{array}{cc}\hfill {\nabla }^2& G(x|x_{\text{h}};f)+k^{2}G(x|x_{\text{h}};f)=-\delta (x-x_{\text{h}}).\hfill \end{array}}$$

(26.3)

Therefore, we can select a Greenʼs function in such a way that we can eliminate one of the terms on the right-hand side of (26.1); (26.2) is one such case.

Fig. 26.4

The geometry and nomenclature for the Kirchhoff–Helmholtz integral (26.1)

To see what essentially happens in the prediction process, let us consider (26.2) when the measurement and prediction plane are both planar. Planar acoustic holography assumes that the sound field is free from reflection (Fig. 26.5); then we can write (26.2) as

$${\displaystyle \begin{array}{cc}\hfill P(x,y,z;f)& ={\int }_{S_{\text{h}}}P(x_{\text{h}},y_{\text{h}},z_{\text{h}};f)\hfill \\ \times K_{\text{PP}}(x-x_{\text{h}},y-y_{\text{h}},z-z_{\text{h}};f)d{S}_{\text{h}},\hfill \end{array}}$$

(26.4)

$${\displaystyle \begin{array}{cc}\hfill K_{\text{PP}}(x,y,z;f)& =\frac{1}{2\pi }\frac{z}{r^3}(1-i\mathrm{kr})\exp (i\mathrm{kr}),\hfill \end{array}}$$

(26.5)

$${\displaystyle \begin{array}{cc}\hfill \text{where}r& =\sqrt{x^2+y^2+z^2},\hfill \\ \hfill k& =\frac{2\pi f}{c},\hfill \\ \hfill x& =(x,y,z),\hfill \\ \hfill x_{\text{h}}& =(x_{\text{h}},y_{\text{h}},z_{\text{h}}).\hfill \end{array}}$$

K _PP can be readily obtained by using two free-field Greenʼs functions that are located at z _h and − z _h, so that it satisfies the Dirichlet boundary condition.

Fig. 26.5

Illustration of the planar acoustic holography

This is a convolution integral, and therefore we can write this in the wave-number domain as

$${\displaystyle \begin{array}{cc}\hfill & \hat{\hat{P}}(k_x,k_y,z;f)\hfill \\ =\hat{\hat{P}}(k_x,k_y,z_{\text{h}};f)\exp [\text{i}{k}_z(z-z_{\text{h}})],\hfill \end{array}}$$

(26.6)

where

$${\displaystyle \begin{array}{cc}\hfill & \hat{\hat{P}}(k_x,k_y,z;f)\hfill \\ ={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }P(x,y,z;f)e^{-i(k_{x}x+k_{y}y)}dxdy,\hfill \end{array}}$$

(26.7)

$${\displaystyle \begin{array}{cc}\hfill k_z& =\sqrt{k^2-k_x^2-k_y^2}.\hfill \end{array}}$$

This equation essentially predicts the sound pressure with respect to the wave number (k _x , k _y ). If k ² ≥ k _x ² + k _y ², the wave in z-direction (k _z ) is propagating in space. Otherwise, the z-direction wave decays exponentially, i.e. it is an evanescent wave (Fig. 26.6).

Fig. 26.6

Propagating and exponentially waves in acoustic holography

We have derived the formulas that can predict what we did not measure based on what we measured, by using a Greenʼs function. It is noteworthy that we can get the same results if we use the characteristic solutions of the Helmholtz equation; the Appendix describes the details. The Appendix also includes discrete expressions for the formula, which are normally used in the computation.

Equation (26.6) also allows us to predict the sound pressure on the source plane, when z = z _s. This is an inverse problem because it predicts the pressure distribution on the source plane based on the hologram pressure (Figs. 26.3 and 26.6).

Figure 26.7 essentially illustrates how we can process the data for predicting what we did not measure based on what we measure. There are four major areas that cause errors in acoustic holography prediction. One is related to the integration of (26.4). Equation (26.4) has to be implemented on the discretized surface Fig. 26.8. This surface, therefore, has to be spatially sampled according to the selected surface. This spatial sampling can produce spatial aliasing, depending on the spatial distribution of the sound source: the sampling wave number must be larger than twice the maximum wave number of interest. It is noteworthy that, as illustrated in Fig. 26.8, the distance between the hologram and source planes is usually related to the sampling distance d. The closer one is to the source, the smaller the sampling distance needs to be. We must also note that the size of the aperture determines the wave-number resolution of acoustic holography. The finite aperture inevitably produces very sharp data truncation, as illustrated in Fig. 26.9. This produces unrealistic high-wave-number noise (see without window in Fig. 26.9). Therefore, it is often required that we use a window, which can result in a smoother data transition from what is on the measurement plane to what is not measured (Fig. 26.9).

Fig. 26.7

The data-processing procedure for acoustic holography

Fig. 26.8

The error due to discrete measurement: the spatial aliasing problem. The microphone spacing determines the Nyquist wave number. This wave number has to be smaller than the maximum wave number of the acoustic pressure distribution on the hologram plane. The microphone spacing, therefore, has to get smaller as the distance between the hologram (the measurement plane) and source decrease. The rule of thumb is δ< d ◂

Fig. 26.9

The effect of a finite aperture: the rapid change at the aperture edges produces high-wave-number noise ◂

The spatial Fourier transform that has to be done in the prediction process (26.6) has to be carried out in the domain for which data is available, i.e. a finite Fourier transform. It therefore produces a ghost hologram, as illustrated in Fig. 26.10 [46,50]. This effect can be effectively removed by adding zeros to the hologram data (Fig. 26.11). The last thing to note is what can happen when we do backward propagation. As we can see in (26.6), when we predict the sound pressure distribution on a plane close to the sound source (z < z _h (Fig. 26.5)) and k _z has an imaginary value (evanescent wave), then the sound pressure distribution of the exponentially decaying part will be unrealistically magnified (Fig. 26.11) [47]. Figure 26.12 graphically summarizes the entire processing steps of acoustic holography.

Fig. 26.10

The effect of the finite spatial Fourier transform on acoustic holography: the ghost image is due to the finite Fourier transform; circular convolution can be eliminated by adding zeros

Fig. 26.11

Wave-number filtering in backward prediction. Evanescent wave components are magnified without filtering (after [47])

Fig. 26.12

Summary of the acoustic holography prediction process

The issues related with the evanescent wave and its measurement are well addressed in the literature [88]. The measurement of evanescent waves essentially allows us to achieve higher resolution than conventional acoustic holography [89,90,91,92,93,94]. However, it is noteworthy that the evanescent-wave component is substantially smaller than the other propagating components. Therefore, it is easy to produce errors that are associated with sensor or position mismatch [53]; in other words, it is very sensitive to the signal-to-noise ratio. Errors due to position and sensor mismatch are bias errors and random errors, respectively. It has been shown [53] that the bias error due to the mismatches is negligible, but the random error is significant in backward prediction. This is related to the measurement spacing on the hologram plane (Δ_h), prediction plane (Δ _z ), and the distance between the hologram plane and the prediction plane (d). It is approximately proportional to 24.9(d/Δ _z ) + 20 log ₁₀(Δ_h/Δ _z ) in a dB scale. The signal-to-noise ratio can be amplified when we try to reconstruct the source field: a typical ill-posed phenomena. There have been many attempts to reduce this effect by using a spatial filter [47,95,96,97,98,99], which is often called the regularization of acoustic holography [100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115].

Depending on the separable coordinates that we use for acoustic holography, we can construct cylindrical or spherical coordinates [54,67,69] (Figs. 26.13 and 26.14). These methods predict the sound field in exactly the same manner as in planar holography but with respect to different coordinates. As expected, however, these methods have some advantages. For example, the wrap-around error is negligible – in fact, there is no such error in spherical acoustic holography – and there is no aperture-related error [54]. Recently, the advantage of using spherical functions has also been noted [79,81,86,87,113].

Fig. 26.13

Cylindrical holography

Fig. 26.14

Spherical holography

Measurement

To construct a hologram, we commonly measure the sound pressure at discrete positions, as illustrated in Fig. 26.2. However, if the sound generated by the source, and therefore the sound field, can be assumed to be stationary, then we do not have to measure them at the same time.

Figure 26.15 illustrates one way to accomplish this measurement. This method normally measures the sound pressure field using a stepped line array (Fig. 26.15a). To understand the issues associated with this measurement system for the sake of its simplicity, let us see how we process a signal of frequency f when there is a single source. The relationship between the sound source and sound pressure in the field, or measurement position (x _h), can be written as

$${\displaystyle P(x_{\text{h}};f)=H(x_{\text{h}};f)Q(f),}$$

(26.8)

where Q(f) is the source input signal and H(x _h;f) is the transfer function between the source input and the measured pressure. This means that, if we know the transfer function and the input, we can find the magnitude and phase between the measured positions. Because it is usually not practical to measure the input, we normally use reference signals (Fig. 26.15a). By using a reference signal, the pressure can be written as

$${\displaystyle P(x_{\text{h}};f)=H\prime (x_{\text{h}};f)R(f),}$$

(26.9)

where R(f) is the reference signal. We can obtain H′(x _h;f) by

$${\displaystyle H\prime (x_{\text{h}};f)=\frac{P(x_{\text{h}};f)}{R(f)}.}$$

(26.10)

The input and reference are related through

$${\displaystyle R(f)=H_{\text{R}}(f)Q(f),}$$

(26.11)

where H _R(f) is the transfer function between the input and the reference. As a result, we can see that (26.9) has the same form as (26.8).

Fig. 26.15

Two measurement methods for the pressure on the hologram plane: (a) step-by-step scanning (b) continuous scanning

It is noteworthy that (26.8) holds for the case that we have only one sound source and the sound field is stationary and random. However, if there are two sound sources, then (26.8) becomes

$${\displaystyle P(x_{\text{h}};f)=H_1(x_{\text{h}};f)Q_1(f)+H_2(x_{\text{h}};f)Q_2(f),}$$

(26.12)

where Q _i (f) is the i-th input and H _i (x _h;f) is its transfer function. There are now two independent sound fields. This requires, of course, two independent reference signals. It has been well accepted that the number of reference microphones has to be greater than the number of independent sources [57]. However, if this is strictly true, then it means that we have to somehow know the number of sources, and this, in some degree, contradicts the the acoustic holography approach.

A recent study [61] demonstrated that the measured information, the location of the sources, and the number of independent sources converge to their true values as the number of reference microphones increases. This study also showed that high-power sources are likely to be identified even if the number of reference microphones is less than the number of sources. Figure 26.16 shows an example of this method when there are many independent sound fields. On the other hand, one study showed that we can even continuously scan the sound field by using a line array of microphones (Fig. 26.15b) [62,63,64,65]. This method essentially allows us to extend the aperture size without any limit as long as the sound field is stationary. In fact, [65] also showed that this method can be used for a slowly varying (quasi-stationary) sound field.

Fig. 26.16

Application result of the step-by-step scanning method to the wind noise of a car. This figure is the pressure distribution at 710∼900  Hz in a source plane when the flow velocity is 110 km/h. In this experiment, 17 reference microphones are randomly located in the car, to see the coherence between interior noise and what are measured by the array microphone system. The array microphone system was initially located at 3 m forward from the middle point of a car, and moved 6 cm in step until it reached at 3 m backward from the middle point ◂

This method has to deal with the Doppler shift. For example, let us consider a plane wave in the $(k_{x_0},k_{y_0},k_{z_0})$ direction and a pure tone of frequency $f_{{\text{h}}_0}$. Then the pressure on the hologram plane can be written as

$${\displaystyle \begin{array}{cc}\hfill & p(x_{\text{h}},y_{\text{h}},z_{\text{h}};t)\hfill \\ =P_0\exp [\text{i}(k_{x_0}{x}_{\text{h}}+k_{y_0}{y}_{\text{h}}+k_{z_0}{z}_{\text{h}})]\exp (-\text{i},f_{{\text{h}}_0}t),\hfill \end{array}}$$

(26.13)

where P ₀ denotes the complex magnitude of the plane wave. Spatial information about the plane wave with respect to the x-direction can be represented by a wave-number spectrum, and can be described as

$${\displaystyle \begin{array}{cc}\hfill \hat{P}(k_x,y_{\text{h}},z_{\text{h}};t)& ={\int }_{-\infty }^{\infty }p(x_{\text{h}},y_{\text{h}},z_{\text{h}};t)e^{-\text{i}{k}_x{x}_{\text{h}}}d{x}_{\text{h}}\hfill \\ =P_0\exp [\text{i}(k_{y_0}{y}_{\text{h}}+k_{z_0}{z}_{\text{h}})]\hfill \\ \times \delta (k_x-k_{x_0})\exp (-\text{i}2\pi f_{{\text{h}}_0}t)\hfill \\ =P(k_{x_0},y_{\text{h}},z_{\text{h}})\delta (k_x-k_{x_0})\hfill \\ \times \exp (-\text{i}2\pi f_{{\text{h}}_0}t),\hfill \end{array}}$$

(26.14)

where $P(k_{x_0},y_{\text{h}},z_{\text{h}})=P_0\exp [\text{i}(k_{y_0}{y}_{\text{h}}+k_{z_0}{z}_{\text{h}})]$ is the wave-number spectrum of the plane wave at $k_x=k_{x_0}$.

If a microphone is moving at an x-velocity u _m, the measured signal p _m(x _h, y _h, z _h;t) is

$${\displaystyle p_{\text{m}}(x_{\text{h}},y_{\text{h}},z_{\text{h}};t)=p(u_{\text{m}}t,y_{\text{h}},z_{\text{h}};t).}$$

(26.15)

The Fourier transform of (26.15) with respect to time F _T, using (26.13), can be expressed as

$${\displaystyle \begin{array}{cc}\hfill & F_{\text{T}}[p_{\text{m}}(u_{\text{m}}t,y_{\text{h}},z_{\text{h}};t)]\hfill \\ ={\int }_{-\infty }^{\infty }{p}_{\text{m}}(u_{\text{m}}t,y_{\text{m}},z_{\text{h}};t)e^{i2\pi \mathrm{ft}}dt\hfill \\ =P_0\exp [i(k_{y_0}{y}_{\text{h}}+k_{z_0}{z}_{\text{h}})]\hfill \\ \times \delta (\frac{u_{\text{m}}}{2\pi }{k}_{x_0}-f_{{\text{h}}_0}+f)\hfill \\ =P(k_{x_0},y_{\text{h}},z_{\text{h}})\delta (\frac{u_{\text{m}}}{2\pi }{k}_{x_0}-f_{{\text{h}}_0}+f).\hfill \end{array}}$$

(26.16)

Equation (26.16) means that the complex amplitude of the plane wave is located at the shifted frequency $f_{{\text{h}}_0}-u_{\text{m}}{k}_{x_0}/2\pi$, as shown in Fig. 26.17. In general, the relation between the shifted frequency f and x-direction wave number k _x is expressed as Fig. 26.18

$${\displaystyle k_x=\frac{2\pi (f_{{\text{h}}_0}-f)}{u_{\text{m}}}.}$$

(26.17)

We can measure the original frequency $f_{{\text{h}}_0}$ by a fixed reference microphone. Using the Doppler shift, we can therefore obtain the wave-number components from the frequency components of the moving microphone signal. Figure 26.19 illustrates how we obtain the wave-number spectrum.

Fig. 26.17

The continuous scanning method for a plane wave and a pure tone (one-dimensional illustration). $f_{{\text{h}}_0}$ is the source frequency, f is the measured frequency, u _m is the microphone velocity, c is the wave speed, $k_{x_0}$ is the x-direction wave number, and P ₀ is the complex amplitude of a plane wave ◂

Fig. 26.18

De-Dopplerization procedure for a line spectrum

Fig. 26.19

The continuous scanning method for a more general case (one-dimensional illustration)

This method essentially uses the relative coordinate between the hologram and microphone. Therefore, it can be used for measuring a hologram of moving noise sources (Fig. 26.20), which is one of the major contributions of this method [62,63,64,65].

Fig. 26.20

Experimental configuration and result of the continuous scanning method to vehicle pass-by noise. The tire pattern noise distribution (pressure) on the source plane is shown when the car passed the microphone array with constant speed of 50 km/h

Analysis of Acoustic Holography

Once we have a picture of the sound (acoustic holography), the questions about its meaning are the next topic of interest. What we have is usually a contour plot of the sound pressure distribution or a vector plot of the sound intensity on a plane of interest. This plot may help us to imagine where the sound source is and how it radiates into space with respect to a frequency of interest. However, in the strict sense, the only thing we can do from the two-dimensional expression of sound pressure or intensity distribution is to guess what was really there. We do not know, precisely, where the sound sources are (Fig. 26.21).

Fig. 26.21

Illustration of analysis problem in acoustic holography

As mentioned earlier, there are two types of sound sources: active and passive sound source. The former is the source that radiates sound itself, while the latter only radiates reflected sound. These two different types of sound sources can be distinguished by eliminating reflected sound [116]. This is directly related to the way boundary conditions are treated in the analysis.

The boundary condition for a locally reacting surface can be written as [116,117,118]

$${\displaystyle V(x_s;f)=A(x_s;f)P(x_s;f)+S(x_s;f),}$$

(26.18)

where V(x _s ;f) and P(x _s ;f) are the velocity and pressure on the wall. A(x _s ;f) is the wall admittance and S(x _s ;f) is the source strength on the wall. The active sound source is located at a position such that the source strength is not zero. This equation says that we can estimate the source strength if we measure the wall admittance. To do this, it is necessary to first turn off the source or sources, and then measure the wall admittance by putting a known source in the desired position (Fig. 26.22a). The next step is to turn on the sources and obtain the sound pressure and velocity distribution on the wall, using the admittance information (Fig. 26.22b). This provides us with the location and strength of the source (i.e. the source power; for example, see Fig. 26.24).

Fig. 26.22

Two steps to separate the active and passive source: (a) Admittance measurement, (b) source strength measurement

Fig. 26.24

Experiment results that separate the active and passive sources. The top surface is made by the sound absorption material. The speaker on the bottom surface, which is reflecting sound, is eliminated by this separation

Another very important problem is whether or not we can distinguish between independent or dependent sources, i.e. two birds singing versus one bird with two beaks (Fig. 26.23). This has a rather significant practical application. For example, to control noise sources effectively, we only need to control independent noise sources. This can be achieved by using the statistical differences between signals that are induced by independent and dependent sound sources.

For example, let us consider a two-input single-output system (Fig. 26.25). If the two inputs are independent, the spectrum S _PP(f) of the output P(f) can be expressed as

$${\displaystyle S_{\text{PP}}(f)=|H_1(f){|}^2{S}_{{\text{Q}}_1{\text{Q}}_1}(f)+|H_2(f){|}^2{S}_{{\text{Q}}_2{\text{Q}}_2}(f),}$$

(26.19)

where $S_{{\text{Q}}_i{\text{Q}}_i}(f)$ is the spectrum of the i-th input Q _i (f), and H _i (f) is its transfer function. The first and second terms represent the contributions of the first and second input to the output spectrum, respectively. If we can obtain a signal as

$${\displaystyle W_1(f)=C(f)Q_1(f),}$$

(26.20)

then we can estimate the contribution of the first source as [119]

$${\displaystyle S_{{\text{P}}_1{\text{P}}_1}(f)=|H_1(f){|}^2{S}_{{\text{Q}}_1{\text{Q}}_1}(f)={\gamma }_{W_{1}P}^2(f)S_{\text{PP}}(f),}$$

(26.21)

where ${\gamma }_{W_{1}P}^2(f)$ is the coherence function between W ₁(f) and Q ₁(f) (Fig. 26.26).

Fig. 26.25

A two-input single-output system and its partial field

Fig. 26.26

The conventional method to obtain the partial field

We can simply extend (26.21) to the case of multiple outputs, as in the case of acoustic holography (Fig. 26.27). The main problem is how to obtain a signal that satisfies (26.20). We can generally say that, by putting sensors closer to the source or sources [57,58,120,121,122,123], we may have a better signal that can be used to distinguish between independent or dependent sources. However, this is neither well proven nor practical, as it is not always easy to put the sensors close to the sources. Very recently, a method that does not require this [124,125] was developed. Figure 26.28 explains the methodʼs procedures. The first and second steps are the same as in acoustic holography: measurement and prediction. The third step is to search for the maximum pressure on the source plane. This method assumes that the maximum pressure satisfies (26.20). The fourth step is to estimate the contribution of the first source by using the coherence functions between the maximum pressure and other points, as in (26.21). The fifth step is to calculate the remaining spectrum by subtracting the first contribution from the output spectrum. These steps are repeated until the contributions of the other sources are estimated (Fig. 26.29).

Fig. 26.27

Acoustic holography and partial field decomposition

Fig. 26.28

The procedure to separate the independent and dependent sources

Fig. 26.29

The separation method applied to a vortex experiment

Summary

As expected, it is not simple to answer the question of whether we can see the sound field. However, it is now understood that the analysis of what we obtained, acoustic holography, needs to be properly addressed, although little attention was given to this problem in the past. We now understand better how to obtain information from the sound picture. Making a picture is the job of acoustic holography, but the interpretation of this picture is the responsibility of the observer. This paper has reviewed some useful guidelines for better interpretation of the sound field to deduce the right impression or information from the picture.

Mathematical Derivations of Three Acoustic Holography Methods and Their Discrete Forms

We often use the Kirchhoff–Helmholtz integral equation to explain how we predict what we do not measure based on what we do measure. It is noteworthy, however, that the same result can be obtained by using the characteristic solutions of the Helmholtz equation. The following sections address how these can be obtained. Planar, cylindrical, and spherical acoustic holography are derived using characteristic equations in terms of a corresponding coordinate system. The equations for holography are also expressed in a discrete form.

Planar Acoustic Holography

If we see solutions of the Helmholtz equation

$${\displaystyle {\nabla }^{2}P+k^{2}P=0,}$$

(26.22)

in terms of Cartesian coordinate, then we can write them as

$${\displaystyle P(x,y,z;f)=X(x)Y(y)Z(z),}$$

(26.23)

where $k=\frac{\omega }{c}=\frac{2\pi f}{c}$. We assume then P is separable with respect to X, Y and Z. Equations (26.A1) and (26.A2) yield the characteristic equation

$${\displaystyle \begin{array}{cc}\hfill & \psi (x,y,z;k_x,k_y,k_z)\hfill \\ =\left(\begin{array}{c}\hfill e^{i{k}_{x}x}\hfill \\ \hfill e^{-i{k}_{x}x}\hfill \end{array}\right)\left(\begin{array}{c}\hfill e^{i{k}_{y}y}\hfill \\ \hfill e^{-i{k}_{y}y}\hfill \end{array}\right)\left(\begin{array}{c}\hfill e^{i{k}_{z}z}\hfill \\ \hfill e^{-i{k}_{z}z}\hfill \end{array}\right),\hfill \end{array}}$$

(26.24)

where

$${\displaystyle k^2=k_x^2+k_y^2+k_z^2.}$$

(26.25)

Now we can write

$${\displaystyle P(x,y,z;f)=\int \hat{P}(k)\psi (x,y,z;k_x,k_y,k_z)dk,}$$

(26.26)

where

$${\displaystyle k=(k_x,k_y,k_z).}$$

(26.27)

Let us assume that the sound sources are all located at z < z _s and we measure at z = z _h > z _s. Then we can write (26.A5) as

$${\displaystyle \begin{array}{cc}\hfill & P(x,y,z;f)\hfill \\ ={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }\hat{\hat{P}}(k_x,k_y)e^{i(k_{x}x+k_{y}y+k_{z}z)}d{k}_{x}d{k}_y.\hfill \end{array}}$$

(26.28)

It is noteworthy that we selected only + ik _z z. This is because of the assumptions we made (z < z _s and z = z _h > z _s). The k _x and k _y can be either positive or negative. Therefore it is not necessary to include − ik _x x or − ik _y y in (26.A3).

In (26.7),

$${\displaystyle k_z=\{\begin{array}{c}\hfill \sqrt{k^2-k_x^2-k_y^2},\text{when}{k}^2>k_x^2+k_y^2\hfill \\ \hfill i\sqrt{k_x^2+k_y^2-k^2},\text{when}{k}^2<k_x^2+k_y^2.\hfill \end{array}}$$

(26.29)

Figure 26.6 illustrates what these two different k _z values essentially mean. We measure P(x, y, z = z _h;f), therefore we have data of the sound pressure data on z = z _h. A Fourier transform of (26.A7) leads to

$${\displaystyle \begin{array}{cc}\hfill & \hat{\hat{P}}(k_x,k_y)\hfill \\ ={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }P(x,y,z;f)e^{-i(k_{x}x+k_{y}y+k_{z}z)}dxdy.\hfill \end{array}}$$

(26.30)

Using (26.A9) and (26.A7), we can always estimate the sound pressure on z, which is away from the source.

It is noteworthy that (26.A9) has to be preformed in the discrete domain. In other words, we have to use a finite rectangular aperture, which is spatially sampled (26.8 and 26.30a). If the number of measurement points along the x-and y-directions are M and N, respectively, and the corresponding sampling distances are Δx and Δy, then (26.A9) can be rewritten as

$${\displaystyle \begin{array}{cc}\hfill & \hat{\hat{P}}(k_x,k_y)=\frac{1}{(2\pi {)}^2}{e}^{-i{k}_z{z}_{\text{h}}}\Delta x\Delta y\hfill \\ \sum _{m=0}^{M-1}\sum _{n=0}^{N-1}P(x_m,y_n,z_{\text{h}})e^{-i{k}_x{x}_m}{e}^{-i{k}_y{y}_n}.\hfill \end{array}}$$

(26.31)

where

$${\displaystyle \begin{array}{cc}\hfill x_m& =(m+\frac{1-M}{2})\Delta x,\hfill \\ \hfill y_n& =(n+\frac{1-N}{2})\Delta y.\hfill \end{array}}$$

(26.32)

M and N are the number of data points in the x- and y-directions, respectively.

Fig. 26.30

Coordinates system for acoustic holography: (a) planar acoustic holography (b) cylindrical acoustic holography (c) spherical acoustic holography

Cylindrical Acoustic Holography

A solution can also found in cylindrical coordinate, that is

$${\displaystyle P(r,\varphi ,z)=R(r)\Phi (\varphi )Z(z).}$$

(26.33)

Figure 26.1 shows the coordinate systems. Then, its characteristic solutions are

$${\displaystyle \begin{array}{cc}\hfill & \psi (r,\varphi ,z;k_r,k_z)\hfill \\ \hfill =& \left(\begin{array}{c}\hfill H_m^{(1)}(k_{r}r)\hfill \\ \hfill H_m^{(2)}(k_{r}r)\hfill \end{array}\right)\left[\begin{array}{c}\hfill e^{im\varphi }\hfill \\ \hfill e^{-im\varphi }\hfill \end{array}\right]\left[\begin{array}{c}\hfill e^{i{k}_{z}z}\hfill \\ \hfill e^{-i{k}_{z}z}\hfill \end{array}\right],\hfill \end{array}}$$

(26.34)

where

$${\displaystyle k^2=k_r^2+k_z^2.}$$

(26.35)

It is noteworthy that m is a nonnegative integer. H _m ⁽¹⁾ and H _m ⁽²⁾ are first and second cylindrical Hankel functions, respectively. e^imϕ and e^−imϕ express the mode shapes in the ϕ-direction.

Using the characteristic function (26.A6), we can write a solution of the Helmholtz equation with respect to cylindrical coordinate as

$${\displaystyle P(r,\varphi ,z;f)=\int {\hat{P}}_m(k){\psi }_m(r,\varphi ,z;k_r,k_z)dk,}$$

(26.36)

where

$${\displaystyle k=(k_r,k_z).}$$

(26.37)

Assuming that the sound sources are all located at r < r _s and that the hologram surface is situated on the surface r = r _h, and that r _h > r _s, then no waves propagate into the negative r-direction, in other words, toward the sources. Then (26.A15) can be rewritten as

$${\displaystyle \begin{array}{cc}\hfill & P(r,\varphi ,z;f)\hfill \\ =\sum _{m=-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\hat{P}}_m(k_z)e^{im\varphi }{e}^{i{k}_{z}z}{H}_m^{(1)}(k_{r}r)d{k}_z,\hfill \end{array}}$$

(26.38)

and k _r has to be

$${\displaystyle k_r=\{\begin{array}{c}\hfill \sqrt{k^2-k_z^2},\text{when}{k}^2>k_z^2\hfill \\ \hfill i\sqrt{k_z^2-k^2},\text{when}{k}^2<k_z^2.\hfill \end{array}}$$

(26.39)

We measure the acoustic pressure at r = r _h, therefore P(r _h, ϕ, z) is available. ${\hat{P}}_m(k_z)$ can then be readily obtained.

That is

$${\displaystyle \begin{array}{cc}\hfill {\hat{P}}_m(k_z)& =\frac{1}{(2\pi {)}^2}{\int }_0^{2\pi }{\int }_{-\infty }^{\infty }P(r_{\text{h}},\varphi ,z)e^{-m\varphi }{e}^{-i{k}_{z}z}\hfill \\ \times {\{H_m^{(1)}(k_r{r}_{\text{h}})\}}^{-1}dzd\varphi .\hfill \end{array}}$$

(26.40)

Inserting (26.A19) into (26.A17) provides us with the acoustic pressure at the unmeasured surface at r.

Discretization of (26.A19) leads to a formula that can be used in practical calculations

$${\displaystyle \begin{array}{cc}\hfill {\hat{P}}_m(k_z)& =\frac{1}{(2\pi {)}^2{H}_m^{(1)}(k_r{r}_{\text{h}})}\frac{2\pi }{L}\Delta z\hfill \\ \times \sum _{l=0}^{L-1}\sum _{n=0}^{N-1}P(r_{\text{h}},{\varphi }_l,z_n)e^{-im{\varphi }_l}{e}^{-i{k}_z{z}_n},\hfill \end{array}}$$

(26.41)

where

$${\displaystyle \begin{array}{cc}\hfill {\varphi }_l& =\frac{(2l+1)\pi }{L},\hfill \\ \hfill z_n& =(n+\frac{1-N}{2})\Delta z.\hfill \end{array}}$$

(26.42)

L and N are the number of data points in the ϕ- and z-directions, respectively.

Spherical Acoustic Holography

The Helmholtz equation can also be expressed in spherical coordinate (Fig. 26.30c). Assuming again that the separation of variable also holds in this case, we can write

$${\displaystyle P(r,\theta ,\varphi )=R(r)\Theta (\theta )\Phi (\varphi ).}$$

(26.43)

Substituting this into (26.A1) gives the characteristic equation

$${\displaystyle \begin{array}{cc}\hfill & {\psi }_{\mathrm{mn}}(r,\theta ,\varphi ;k)=\hfill \\ \left(\begin{array}{c}\hfill h_m^{(1)}(\mathrm{kr})\hfill \\ \hfill h_m^{(2)}(\mathrm{kr})\hfill \end{array}\right)\left(\begin{array}{c}\hfill P_m^n\cos \theta \hfill \\ \hfill Q_m^n\cos \theta \hfill \end{array}\right)\left(\begin{array}{c}\hfill e^{in\varphi }\hfill \\ \hfill e^{-in\varphi }\hfill \end{array}\right).\hfill \end{array}}$$

(26.44)

m is a nonnegative integer and n can be any integer between 0 and m. h _m ⁽¹⁾ and h _m ⁽²⁾ are first and second spherical Hankel functions. It is also noteworthy that P _m ⁿ and Q _m ⁿ are first and second Legendre polynomials.

Then we can write the solution of the Helmholtz equation as

$${\displaystyle P(r,\theta ,\varphi )=\sum _{m=0}^{\infty }\sum _{n=-m}^m{\hat{P}}_{\mathrm{mn}}{\psi }_{\mathrm{mn}}(r,\theta ,\varphi ;k).}$$

(26.45)

Suppose that we have sound sources at r < r _s and the hologram is on the surface r = r _h > r _s; then (26.A24) can be simplified to

$${\displaystyle P(r,\theta ,\varphi )=\sum _{m=0}^{\infty }\sum _{n=-m}^m{\hat{P}}_{\mathrm{mn}}{Y}_{\mathrm{mn}}(\theta ,\varphi )h_m^{(1)}(\mathrm{kr}),}$$

(26.46)

where

$${\displaystyle Y_{\mathrm{mn}}(\theta ,\varphi )=P_m^{|n|}(\cos \theta )e^{in\varphi }.}$$

(26.47)

This is a spherical harmonic function. It is noteworthy that we only have first spherical harmonic functions because all waves propagate away from the sources. The second Legendre function was discarded because it would have finite acoustic pressure at θ = 0 or π.

Similarly, as previously stated, the sound pressure data on the hologram is available, therefore we can obtain P _mn in (26.A25) by

$${\displaystyle \begin{array}{cc}\hfill {\hat{P}}_{\mathrm{mn}}& =\frac{2m+1}{4\pi h_m^{(1)}({\mathrm{kr}}_{\text{h}})}\frac{(m-|n|)!}{(m+|n|)!}\hfill \\ \times {\int }_0^{\pi }{\int }_0^{2\pi }P(r_{\text{h}},\theta ,\varphi )Y_{\mathrm{mn}}^{*}(\theta ,\varphi )\sin \theta d\varphi d\theta ,\hfill \end{array}}$$

(26.48)

where we have used the orthogonality property of Y _mn . The * represents the complex conjugate. Using (26.A27) and (26.A25), we can estimate the acoustic pressure anywhere away from the sources.

The discrete form of (26.A27) can be written as

$${\displaystyle \begin{array}{cc}\hfill {\hat{P}}_{\mathrm{mn}}& =A_{\mathrm{mn}}\frac{2{\pi }^2}{\mathrm{LQ}}\sum _{l=0}^{L-1}\sum _{q=0}^{Q-1}P(r_{\text{h}},{\theta }_l,{\varphi }_q)\hfill \\ \times P_m^{|n|}(\cos {\theta }_l)(\sin {\theta }_l)e^{-in{\varphi }_q},\hfill \end{array}}$$

(26.49)

where

$${\displaystyle \begin{array}{cc}\hfill {\theta }_l& =\frac{(2l+1)\pi }{2L},\hfill \\ \hfill {\varphi }_q& =\frac{(2q+1)\pi }{Q}.\hfill \end{array}}$$

(26.50)

where L is the number of data points in θ and Q is what is in ϕ-direction.