Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

During cutting, high temperatures are generated in the region of the tool cutting edge as a form of cutting energy dissipation. These temperatures have a controlling influence on the rate of wear of the cutting tool and on the friction between the chip and tool, and they can significantly affect the functional performance of a machined part due to residual stress or thermal distortion. Therefore, considerable attention has been paid to the measurement and prediction of the temperatures in the tool, chip, and workpiece in metal cutting.

For example, experiments have shown that when copper is turned with a carbide tool under 0.3 mm radial depth of cut, 0.2 mm/rev feed, and 100 m/min feed rate, the cutting temperature is around 300 °C. For a copper workpiece with a diameter of 30 mm and a linear coefficient of thermal expansion (CTE) at 20 °C of 17 × 10−6/°C, the diameter variation due to thermal effect would be 30 × 17 × 10−6 × 300 = 0.153 mm. Therefore, the size of workpiece measured after it is cooled would be smaller than it is during machining by about 50 % of the depth of cut. Of course, this estimate involves many unjustified assumptions including the uniformity of cutting temperature distribution and the constant CTE. However, it gives us a rough sense of the possible effect of cutting temperature on the process performance.

9.1 The Measurement of Cutting Temperatures

A number of methods have been developed for the temperature measurements in metal cutting. Some of these only measure the average cutting temperature, although methods for determining temperature distribution in the cutting zone under carefully controlled laboratory conditions are possible.

9.1.1 Thermocouple Method

The method most widely used to determine cutting temperature is the thermocouple technique. It can be applied either in a work-tool thermocouple configuration or embedded thermocouple configuration. Figure 9.1 shows a work-tool thermocouple arrangement on a lathe. The thermocouple circuit is insulated from the machine, and the same circuit is used to calibrate the thermocouple. This arrangement is limited to the measurement of mean temperature along the chip–tool interface without indication of the distribution of temperature. Figure 9.2 shows the setup of an embedded thermocouple and typical temperature–time traces. It offers the temperature reading at a localized point close to the cutting tool surface. Both work-tool and embedded methods have been used extensively to investigate the effects of changes in cutting conditions on cutting temperatures and to obtain empirical relationships between temperature and cutting tool wear rate.

Fig. 9.1
figure 1

Work-tool thermocouple device for cutting temperature measurement

Full size image
Fig. 9.2
figure 2

a Typical embedded thermocouple set-up and b tool tip temperature in turning of Al6061-T6 with a carbide insert

Full size image

9.1.2 Radiation Method

Cameras and films sensitive to infrared radiation can be used to determine the temperature distribution in the cutting zone. A furnace of known temperature is usually photographed simultaneously with the cutting operation to allow calibration. Although the current improvements in infrared-sensitive films and developments of thermal imaging video cameras now make it possible to determine temperature of workpiece from room temperature to well over 1000 °C, the technique is applicable only to cutting processes with visually observable tool-workpiece area. This factor limits the technique to no more than laboratory testing purposes. Figure 9.3 shows a typical digital image obtained with an infrared camera during a tube-facing operation.

Fig. 9.3
figure 3

a Infrared thermal image and b processed image with 10 °F isotherms for dry cut of Al6061-T6 with HSS at 28 m/min, 0.058 mm/rev

Full size image

9.1.3 Hardness and Microstructure Method

The room-temperature hardness of hardened steel decreases after reheating and the loss in hardness is related to the temperature and time of heating. The hardness decrease is the result of changes in the microstructure of the steel. These structural changes can be observed using optical and electron microscopes. These changes provide an effective means of determining temperature distributions in the tool during cutting. Microhardness measurements on tools after cutting can be used to determine constant-temperature contours in the tool, but the technique is time-consuming, requiring very accurate hardness measurements, and relying upon experienced interpretation of the observed structural changes. For steels, the commonly achievable accuracy is on the order of ± 25 °C at the current state of the art.

9.2 Heat Generation in Machining

When a material is deformed elastically, the energy required is stored in the material as strain energy, and no heat is generated. However, when a material is deformed plastically, most of the energy used is converted into heat. In metal cutting, the material is subject to extremely high strains. Since the elastic deformation forms only a very small portion of the total deformation, it may be assumed that all the energy required in cutting is converted into heat. It is recalled that the rate of energy consumption during machining, P, is given by

$$ P={{F}_{P}}v, $$
(9.1)

where F P is the cutting component of the resultant tool force and ν is the cutting speed.

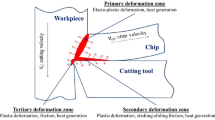
In cutting, there are two major regions of plastic deformation responsible for the conversion of energy into heat: shearor primary deformation zone and secondary deformation zone as seen in Fig. 9.4. If the tool is not severely worn, the workpiece deformation at the contact with the tool flank can be considered negligible. Thus,

Fig. 9.4
figure 4

Heat sources in orthogonal cutting

Full size image
$$ P={{P}_{S}}+{{P}_{F}}, $$
(9.2)

where P S is the rate of heat generation in the primary deformation zone (shear-zone heat rate) and P F is the rate of heat generation in the secondary deformation zone (frictional heat rate). P F is given by F C ν c , where F C is the frictional force on the tool face and ν c is the velocity of chip flow, which is given by rν.

To understand how heat is removed from these zones by the workpiece, chip, and tool motions, it is necessary to consider the transfer of heat in a material moving relative to a heat source. Figure 9.5 shows four stationary points located in a Cartesian coordinate. There is a material flowing through these points in the X direction. The material at point A is assumed to have an instantaneous temperature T. Coordinates and temperatures at points A, B, C, and D are shown in the figure.

Fig. 9.5
figure 5

Flow of heated material through an element b

Full size image

Heat is transferred across the boundaries AB and CD by the combination of conduction due to the temperature gradients in the X direction and by convection because of the flow of heated material across these boundaries. Across BC and AD, heat can only be transferred by conduction since there is no material flowing across these boundaries. If there is a heat source with intensity of P (time rate of heat generation) within the element defined by ABCD, the balance of energy requires that

$$ \frac{{{\partial }^{2}}T}{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}T}{\partial {{y}^{2}}}+\left(\frac{R}{b}\text{ }\frac{\partial T}{\partial \text{x}}\right)=P, $$
(9.3)

where R is a dimensionless number given by ρcνb/k and is known as the thermal number with ρ being the density (kg/m3), k the thermal conductivity (W/m-K), c the specific heat capacity (J/(kgK)), ν the velocity of the material (m/s), and b the linear dimension along the lateral (Z) direction (width of cut). The first term in the equation is attributed to the conduction across AB and CD, the second term to the conduction across BC and AD, and the third term to the convection through AB and CD. Note that b should be equivalent to δy in Fig. 9.5. For single-point turning, b is typically the width of cut (in the radial direction).

The solution of Eq. (9.3) is possible with simple boundary conditions. Figure 9.6 shows its solution for a 1-D case, in which a point in the material approaching the heat source is heated rapidly, reaches its maximum temperature at the heat source, and then remains at constant temperature.

Fig. 9.6
figure 6

Temperature distribution in a fast-moving material for a 1-D case, in which T s  = P/ρcνtb. Note that the P is in the unit of W (J/s)

Full size image

9.3 Temperature Distribution in Machining

Figure 9.7 shows the experimentally determined temperature distribution in the workpiece and the chip during orthogonal metal cutting. As a point X in the material, moving toward the cutting tool, approaches and passes through the primary deformation zone, it is heated until it leaves the zone. Point Y, however, passes through both deformation zones and is heated until it leaves the region of secondary deformation. Thus the maximum temperature occurs along the tool face with some distance from the cutting edge. Point Z, which remains in the workpiece, is heated by the conduction of heat from the primary deformation zone. Some heat is conducted from the secondary deformation into the body of the tool as well. In summary,

Fig. 9.7
figure 7

Temperature distribution (obtained from an infrared photograph) for machining of free-cutting mild steel at a speed of 75 ft/min, width of cut of 0.25 in., by a tool rake of 30°. The workpiece temperature is 611°C

Full size image
$$ P=\Phi {}_{c}+{{\Phi }_{w}}+{{\Phi }_{t}}, $$
(9.4)

where P = total rate of heat generation, Ф c  = rate of heat transportation by the chip, Ф w  = rate of heat conduction into the workpiece, and Ф t  = rate of heat conduction into the tool. The chip material at the tool face usually flows rather fast, thus Ф t forms a very small proportion of P and may be neglected except at a very low-cutting speed.

9.3.1 Temperatures in the Primary Deformation Zone

The rate of heat generation in the primary deformation (shear) zone is P S . A fraction, Γ, of this heat is conducted into the workpiece, and the remainder is transported with the chip. Thus, the average temperature rise, T S , of the material passing through the primary deformation zone is given by

$$ {{T}_{S}}=\frac{(1-\Gamma){{P}_{S}}}{\rho cvtb}, $$
(9.5)

in which t is the uncut chip thickness and b is the width of cut. Figure 9.8 shows an idealized model of cutting process employed by Rapier in 1954. This model assumed that the primary deformation zone could be regarded as a uniform plane heat source that no heat was lost from the free surfaces of the workpiece and chip, and that the thermal properties of the work material were constant and independent of temperature. To solve for Eq. (9.3), Weiner in 1955 further suggested that no heat was conducted into the material in the direction of its motion, since the transfer of heat in this direction of motion is mainly due to convection at high speeds. Equation (9.3) then simplifies to

Fig. 9.8
figure 8

Idealized cutting model in theoretical study on cutting temperature

Full size image
$$ \frac{{{\partial }^{2}}T}{\partial {{y}^{2}}}+\frac{R}{b}\text{ }\frac{\partial T}{\partial x}=P. $$
(9.6)

The solution to Eq. (9.6) with the stipulated boundary conditions as seen in Fig. 9.8 is provided in Fig. 9.9. Compared with experimental data, it is seen that the theory provides slightly underestimated results at high values of Rtanφ (i.e., at high speeds and feeds). In the theory where a plane heat source was assumed, heat can only flow into the workpiece by conduction. In reality, heat is generated over a wide zone, part of which extends into the workpiece. The effect of this wide heat generation zone becomes increasingly important at high speeds and feeds, and therefore the deviation between theoretical and experimental data could be explained.

Fig. 9.9
figure 9

Effect of R tan φ on division of shear-zone heat between chip and work, where Γ = the proportion of shear zone conducted into the work, R = thermal number and φ = shear angle

Full size image

9.3.2 Temperatures in the Secondary Deformation Zone

The maximum temperature in the chip takes place at the exit from the secondary deformation zone, point C in Fig. 9.8. It is given by

$$ {{T}_{\max }}={{T}_{o}}+{{T}_{s}}+{{T}_{m}}, $$
(9.7)

where T o  = initial workpiece temperature, T s  = temperature increase as material passes through the primary deformation zone, and T m  = temperature increase as material passes through the secondary deformation zone. Also, Fig. 9.8 shows the idealization by Rapier that the heat source resulting from the friction between the chip and the tool face was a plane heat source of uniform strength over the length of l f . The following solution was obtained:

$$ {{T}_{m}}=1.13{{T}_{f}}\sqrt{\frac{R}{{{l}_{o}}}}, $$
(9.8)

where l o is the ratio of the heat source length to the chip thickness (l f /t c ) and T f is the average temperature increase of the chip, resulting from the secondary deformation as given by

$$ {{T}_{f}}=\frac{{{P}_{F}}}{\rho cvtb}. $$
(9.9)

A comparison of Eq. (9.9) with experimental data by Rapier showed that his theory considerably overestimated T m . This could be explained again by the fact that the friction-deformation zone, instead of being planar, has a finite width. The boundary conditions that more closely approximate reality is shown in Fig. 9.10, and an analysis based on this revised model by Boothroyd in 1963 yielded better agreement with experimental data. Figure 9.11 gives these results in terms of the effect of the zone width (w o t c ) on temperature increase. When these curves are used, l o can be estimated from the wear marks on the tool face, and the zone width can be estimated from a photomicrograph of the chip cross section as shown in Fig. 9.12.

Fig. 9.10
figure 10

Revised boundary condition for chip

Full size image
Fig. 9.11
figure 11

Effect of secondary deformation zone width on chip temperatures, where R = thermal number, l o t c  = chip–tool contact length, w o t c  = width of secondary deformation zone, T m  = maximum temperature rise in chip, and T f  = mean temperature rise in chip

Full size image
Fig. 9.12
figure 12

Grain deformation in chip cross section

Full size image

Example

The maximum temperature along the tool face and the temperature on the newly machined surface are to be estimated for the following condition during the turning of mild steel at a room temperature of 22 °C:

Rake angle α = 0

Cutting force F P  = 890 N

Thrust force F Q  = 667 N

Cutting speed v = 2 m/s

Undeformed chip thickness t = 0.25 mm = feed

Width of cut b = 2.5 mm

Cutting ratio r = 0.3

Length of contact between chip and tool face l f  = 0.75 mm

Width of secondary deformation zone under unlubricated condition w o  = 0.2

Mild steel density ρ = 7200 kg/m3

Mild steel thermal conductivity k = 436 W/m-K

Mild steel specific heat capacity c = 502 J/kgK

Solution:

The total heat generation rate is \(P={{F}_{P}}v=\text{890}(\text{2} )=\text{1780}~\text{J/s}\).

In this example, α = 0, therefore \({{F}_{C}}\,=\,-\,{{F}_{P}}\sin{}\alpha \,-\,{{F}_{Q}}\cos{}\alpha \,=\,-\,{{F}_{Q}}\). Thus, the rate of heat generated by friction between the chip and the tool is given by

$$ {{P}_{F}}={{F}_{C}}{{v}_{c}}={{F}_{C}}vr=667(2 )(0.3 )=400\text{ J/s}. $$

From Eq. (9.2), the rate of heat generation from shearing in the primary deformation zone is \({{P}_{S}}=P-{{P}_{F}}=\text{1380 J/s}\).

To estimate the temperature increase T s , Fig. 9.9 is first used to find Γ for a given Rtanφ value. The thermal number is \(R=\frac{\text{7200}(\text{502} )(\text{2} )(\text{0}\text{.0025} )}{\text{436}}\text{= 41}\text{.5}\).

As the rake angle equals 0, tanφ = rcosα/(1 − rsinα), thus

$$ R\tan \varphi =41.5(0.3 )=12.45. $$

From Fig. 9.9, Γ is found to be 0.1, and it implies that the majority of the heat is transported with the chip instead of being conducted into the workpiece. The temperature increase through the primary deformation zone is

$$ {{T}_{S}}=\frac{(1-\Gamma){{P}_{S}}}{\rho cvtb}=\frac{(1-0.1 )1380}{7200(502 )2(0.00025 )0.0025}=\frac{(1-0.1 )1380}{4.518}=275{}^\circ \text{C}. $$

To have a reasonable estimate of the temperature increase across the friction deformation zone, Fig. 9.11 instead of Eq. (9.8) is used here. Noting that w o  = 0.2 and

$$ \frac{R}{{{l}_{o}}}=\frac{R}{{{l}_{f}}(r/t )}=\frac{(41.5 )}{0.75(0.3/0.25 )}=46.1, $$

the ratio T m /T f can be looked up from the figure to be 4.2 and

$$ {{T}_{f}}=\frac{400}{4.518}=88.5{}^\circ \text{C,} $$

therefore \({{T}_{m}}\,=\,\text{4}\text{.2}(\text{88}\text{.5} )\,=\,\text{372}\,{}{}^\circ\text{C}\). From Eq. (9.7), the maximum temperature at the tool rake face is

$$ {{T}_{\max }}={{T}_{o}}+{{T}_{s}}+{{T}_{m}}=22+275+372=669{}^\circ \text{C}. $$

Temperature on the newly machined surface T w is

$$ 22+{{T}_{w}}=22+\frac{\Gamma {{P}_{S}}}{\rho cvtb}=22+\frac{\Gamma }{1-\it\Gamma }{{T}_{S}}=22+\frac{0.1}{0.9}(275 )=52.5{}^\circ \text{C}. $$

It should be noted that these calculations assume that the thermal properties of the material are constant and independent of temperature. In reality, with many engineering materials, the specific heat capacity and thermal conductivity do vary with changes in temperature. If more accurate predictions of cutting temperatures are required, the relationships between the thermal properties of the material and temperature must be known and taken into account.

Suppose the tool forces and the cutting ratio do not vary with cutting speed, for the conditions used in the case study the relationships between temperature and cutting speed as shown in Fig. 9.13 is obtained. Here, it is seen that the main shear-zone temperature increases slightly with cutting speed and then tends to constant out, whereas the maximum tool face temperature increases rapidly with cutting speed. It can be generally concluded that the cutting speed is the main operating variable that affects temperature. This is why the empirical relationship referred to as the Taylor’s tool life equation depends mostly on speed.

Fig. 9.13
figure 13

Cutting speed and temperature

Full size image

Homework

  1. 1.

    In a cutting process, the temperatures of the exposed chip surface and the newly machined workpiece surface are relatively easy to measure, while to obtain the temperature at the inside surface of the chip facing the tool rake is not trivial. With the use of the infrared technique in a shaping operation, the exposed chip surface showed 275 °C and the machined workpiece surface showed 87.5 °C. You are asked to estimate the maximum temperature at the inside surface of the chip in contact with the tool rake. The cutting conditions were known to be: tangential cutting force = 2500 N, cutting surface velocity = 1 m/s, chip thickness = 1.2 mm, undeformed chip thickness = 1 mm, width of chip = 2 mm, initial work temperature = 25 °C, length of contact between chip and tool face = 1.8 mm, workpiece density = 5000 kg/m3, thermal conductivity = 62 W/m-K, and workpiece heat capacity = 600 J/kg-°C.

  2. 2.

    The specific cutting energy of a material is mostly a property-dependent quantity, and it can be identified in cutting based on the temperature distribution. For example, in the turning of a certain material, the temperature distribution is found to be 342 °C on the exposed chip surface, 602 °C at the chip–tool interface, and 74 °C on the machined surface. While the initial temperature of the workpiece is 22 °C, could you estimate its specific cutting energy (in the unit of N/mm2)? Given that: thermal conductivity = 82 W/m-K, density = 6900 kg/m3, specific heat capacity = 480 J/(kg)(°C), cutting velocity = 4.5 m/s, feed = 0.2 mm/rev, major cutting edge angle = 90°, radial depth of cut = 1 mm, chip thickness = 0.25 mm, contact length between chip and tool rake = 8 mm.

  3. 3.

    A magnesium alloy (density of 5800 kg/m3, specific heat capacity of 105 J/kg(°C), and thermal conductivity of 75 W/m-K) is turned by a carbide tool of 10° rake angle and 90° major cutting edge angle. At a surface cutting velocity of 8 m/s, feed of 0.15 mm, depth of cut of 0.15 mm, and a chip thickness of 0.45 mm, the temperature at the exposed chip surface is measured to be 320 °C and the maximum temperature at the chip–tool interface is 650 °C. If the cutting velocity is increased to 25 m/s, what will be the maximum temperature at the chip–tool interface? Note that the Weiner’s solution for heat partition (as show in Fig. 9.9) can be approximated by Γ = 0.47 − 0.385log(R tan φ). You can also assume that the secondary shear zone has zero width, that is, w o = 0.