Keywords

53.1 Introduction

Internet stocks obtained huge gains in the late 1990s, followed by huge losses from early 2000. In just 2 years from 1998 to early March 2000, prices of Internet stocks rose by sixfold and outperformed the S&P 500 by 482 %. Technology stocks generally showed a similar trend based on the fact that NASDAQ 100 index quadrupled in value over the same period and outperformed the S&P 500 index by 268 %. On the other hand, NASDAQ 100 index dropped by 64.28 % in value during the Internet bubble crash and underperformed the S&P 500 index by 173.87 %.

The spectacular rise and fall of Internet stocks in the late 1990s has stimulated research into the causes of the Internet stock bubble. Theories had been developed to explain the Internet bubble. For example, Baker and Stein (2004) develop a model of market sentiment with irrationally overconfident investors and short-sale constraints. Ofek and Richardson (2003) provide circumstantial evidence that Internet stocks attract mostly retail investors who are more prone to be overconfident about their ability to predict future stock prices than institutional investors. Perkins and Perkins (1999) suggest that during the Internet boom, investors were confidently betting on the continued rise of Internet stocks because they knew that high demand and limited equity float implies substantial upside returns. Moreover, Ofek and Richardson (2003) provide indirect evidence that Internet stock prices were supported by a combination of factors such as limited float, short-sale constraints, and aggressive trend chased by retail investors, whereas Statman (2002) shows that this asymmetric payoff must have made Internet stocks appear to be an extremely attractive gamble for risk seekers. On the other hand, Fong et al. (2008) use stochastic dominance methodology (Fong et al. 2005; Broll et al. 2006; Chan et al. 2012; Lean et al. 2012) to identify dominant types of risk preferences in the Internet bull and bear markets. They conclude that investor risk preferences (Wong and Li 1999; Wong and Chan 2008) have changed over this cycle, and the change is related to utility theory (Wong 2007; Sriboonchitta et al. 2009) and behavioral finance (Lam et al. 2010, 2012).

In this paper, we apply both the mean-variance ratio (MVR) test and the Sharpe ratio (SR) test to examine the performance of the NASDAQ 100 index and the S&P 500 index during the bursting of the Internet bubble in the 2000s. The tests are relied on the theory of the mean-variance (MV) portfolio optimization (Markowitz 1952; Bai et al. 2009a, b). The Markowitz efficient frontier also provides the basis for many important financial economics advances, including the Sharpe-Lintner capital asset pricing model (CAPM, Sharpe 1964; Lintner 1965) and the well-known optimal one-fund theorem (Tobin 1958). Originally motivated by the MV analysis, the optimal one-fund theorem, and the CAPM model, the Sharpe ratio, the ratio of the excess expected return to its volatility or standard deviation, is one of the most commonly used statistics in the MV framework. The SR is now widely used in many different areas in Finance and Economics, from the evaluation of portfolio performance to market efficiency tests (see, e.g., Ofek and Richardson 2003).

Jobson and Korkie (1981) develop a SR statistic to test for the equality of two SRs. The test statistic has been modified and improved by Cadsby (1986) and Memmel (2003). Lo (2002) carries out a more thorough study of the statistical property of the SR estimator. Using standard econometric methods with several different sets of assumptions imposed on the statistical behavior of the returns series, Lo derives the asymptotic statistical distribution for the SR estimator and shows that confidence intervals, standard errors, and hypothesis tests can be computed for the estimated SRs in much the same way as regression coefficients such as portfolio alphas and betas are computed.

The SR test statistic developed by Jobson and Korkie (1981) and others provides a formal statistical comparison of performance among portfolios. One deficiency of the SR statistic is that it has only an asymptotic distribution. Hence, the SR test has its statistical properties only for large samples, but not for small samples. Nevertheless, the performance of assets is often compared by using small samples, especially when markets undergo substantial changes resulting from changes in short-term factors and momentum. Under these circumstances, it is more meaningful to use limited data to predict the assets’ future performance. In addition, it is not meaningful to measure SRs for extended periods when the means and standard deviations of the underlying assets are found empirically to be nonstationary and/or to possess structural breaks. For small samples, the main difficulty in developing the SR test is that it is impossible to obtain a uniformly most powerful unbiased (UMPU) test to check for the equality of SRs. To circumvent this problem, Bai et al. (2011d) propose to use an alternative statistic, the MVR tests to compare performance of assets. They also discuss the evaluation of the performance of assets for small samples by providing a theoretical framework and then invoking both one-sided and two-sided UMPU MVR tests. Moreover, Bai et al. (2012) further extend the MVR statistics to compare the performance of prospects after the effect of the background risk has been mitigated.

Applying the traditional SR test, we fail to reject the possibility of having any significant difference between the performance of the S&P 500 index and the NASDAQ 100 index during the bursting of the Internet bubble in the 2000s. This finding implies that the two indices being analyzed could be indistinguishable in their performance during the period under the study. However, we conjecture that this conclusion is most likely to be inaccurate as the lack of sensitivity of the SR test in analyzing small samples. Thus, we propose to use the MVR test in the analysis. As expected, the MVR test shows that the MVR of the weekly return on S&P 500 index is different from that on the NASDAQ 100 index. We conclude that the NASDAQ 100 index underperformed the S&P 500 index during the period under the study. The proposed MVR test can discern the performance of the two indices and hence is more informative than tests using the SR statistics for investors to decide on their investments.

The rest of the paper is organized as follows: Section 53.2 discusses the data while Sect. 53.3 provides the theoretical framework and discusses the theory for both one-sided and two-sided MVR tests. In Sect. 53.4, we demonstrate the superiority of the MVR tests over the traditional SR tests by applying both tests to analyze the performance of the S&P 500 index and the NASDAQ 100 index during the bursting of the Internet bubble in the 2000s. This is followed by Sect. 53.4 which summarizes our conclusions and shares our insights.

53.2 Data

The data used in this study consists of weekly returns on two stock indices: the S&P 500 and the NASDAQ 100 index. We use the S&P 500 index to represent non-technology or “old economy” firms. Our proxy for the Internet and technology sectors is the NASDAQ 100 index. Firms represented in the NASDAQ 100 include those in the computer hardware and software, telecommunications, and biotechnology sectors. The NASDAQ 100 index is value weighted.

Our sample period is from January 1, 2000 to December 31, 2002, to study the effect of the crash in the Internet bubble. Before 2000, there is a clear upward trend in technology stock prices emerging from around that period and this period spans a period of intense IPO and secondary market activities for Internet stocks. Schultz and Zaman (2001) report that 321 Internet firms went public between January 1999 and March 2000, accounting for 76 % of all new Internet issues since the first wave of Internet IPOs began in 1996. Ofek and Richardson (2003) find that the extraordinary high valuations of Internet stocks between the early 1998 and February 2000 were accompanied by very high trading volume and liquidity. The unusually high volatility of technology stocks is only partially explained by the rise in the overall market volatility. Our interest centers on the bear market from January 1, 2000 to December 31, 2002. All data for this study are from datastream.

53.3 Methodology

Let X i and Y i (i = 1, 2,⋯ċ, n) be independent excess returns drawn from the corresponding normal distributions N(μ, σ 2) and N(η,τ 2) with joint density p(x, y) such that

$$ p\left(x,y\right)=k\times \exp \left(\frac{\mu }{\sigma^2}{\displaystyle \sum {x}_i-\frac{1}{2{\sigma}^2}}{\displaystyle \sum {x}_i^2+\frac{\eta }{\tau^2}}{\displaystyle \sum {y}_i-\frac{1}{2{\tau}^2}}{\displaystyle \sum {y}_i^2}\right) $$
(53.1)

Where \( k={\left(2\pi {\sigma}^2\right)}^{-n/2}{\left(2\pi {\tau}^2\right)}^{-n/2} \exp \left(-\frac{n{\mu}^2}{2{\sigma}^2}\right) \exp \left(-\frac{n{\eta}^2}{2{\tau}^2}\right) \)

To evaluate the performance of the prospects X and Y, financial professionals are interested in testing the hypotheses

$$ {H}_0^{*}:\frac{\mu }{\sigma}\le \frac{\eta }{\tau}\kern0.5em \mathrm{versus}\kern0.5em {H}_1^{*}:\frac{\mu }{\sigma }>\frac{\eta }{\tau } $$
(53.2)

to compare the performance of their corresponding SRs, \( \frac{\mu }{\sigma } \) and \( \frac{\eta }{\tau } \), the ratios of the excess expected returns to their standard deviations.

If the hypothesis H *0 is rejected, it infers that X is the better investment prospect with larger SR because X has either larger excess mean return or smaller standard deviation or both. Jobson and Korkie (1981) and Memmel (2003) develop test statistics to test the hypotheses in Eq. 53.2 for large samples but their tests would not be appropriate for testing small samples as the distribution of their test statistics is only valid asymptotically but not valid for small samples. However, it is especially relevant in investment decisions to test the hypotheses in Eq. 53.2 for small samples to provide useful investment information to investors. Furthermore, as it is impossible to obtain any UMPU test statistic to test the inequality of the SRs in Eq. 53.2 for small samples, Bai et al. (2011d) propose to use the following hypothesis to test for the inequality of the MVRs:

$$ {H}_{01}:\frac{\mu }{\sigma^2}\le \frac{\eta }{\tau^2}\kern1em \mathrm{versus}\kern1em {H}_{11}:\frac{\mu }{\sigma^2}>\frac{\eta }{\tau^2}. $$
(53.3)

In addition, they develop the UMPU test statistic to test the above hypotheses. Rejecting the hypothesis H 0 infers that X will have either smaller variance or larger excess mean return or both leading to the conclusion that X is the better investment. As sometimes investors conduct the two-sided test to compare the MVRs, the following hypotheses are included in our study:

$$ {H}_{02}:\frac{\mu }{\sigma^2}=\frac{\eta }{\tau^2}\kern0.5em \mathrm{versus}\kern1em {H}_{12}:\frac{\mu }{\sigma^2}\ne \frac{\eta }{\tau^2}. $$
(53.4)

One may argue that the MVR test is that SR test is scale invariant, whereas the MV ratio test is not. To support the MVR test to be an acceptable alternative test statistic, Bai et al. (2011d) show the theoretical justification for the use of the MVR test statistic in the following remark:

Remark 53.1

One may think that the MVR can be less favorable than the SR as the former is not scale invariant while the latter is. However, in some financial processes, the mean change in a short period of time is proportional to its variance change. For example, many financial processes can be characterized by the following diffusion process for stock prices formulated as

$$ d{Y}_t={\mu}^P\left({Y}_t\right) dt+\sigma \left({Y}_t\right)d{W}_t^P, $$

where μ P is an N-dimensional function, σ is an N × N matrix and W P t is an N-dimensional standard Brownian motion under the objective probability measure P. Under this model, the conditional mean of the increment dY t given Y t is μ P(Y t )dt and the covariance matrix is σ(Y t )σ T(Y t )dt. When N = 1, the SR will be close to 0 while the MVR will be independent of dt. Thus, when the time period dt is small, the MVR will be advantageous over the SR.

To further support for the use of MVR, Bai et al. (2011d) document the MVR in the context of Markowitz MV optimization theory as follows: suppose that there is p-branch of assets S = (s 1,⋯ċ, s p )T whose returns are denoted by r = (r 1,⋯∙, r p )T with mean μ = (μ 1,⋯ċ, μ p )T and covariance matrix Σ = (σ ij ). In addition, we suppose that investors will invest capital C on the p-branch of securities S such that they solve for their optimal investment plans c = (c 1,⋯∙, c p )T to allocate their investable wealth on the p-branch of securities to obtain maximize return subject at a given level of risk.

The above maximization problem can be formulated as the following optimization problem:

$$ \max\ R={\mathrm{c}}^T\boldsymbol{\mu}, \kern0.5em \mathrm{subject}\kern0.5em \mathrm{to}\kern0.5em {\mathrm{c}}^T\Sigma \mathrm{c}\le {\sigma}_0^2 $$
(53.5)

where σ 20 is a given risk level. We call R satisfying Eq. 53.5 the optimal return and c be its corresponding allocation plan. One could easily extend the separation theorem and the mutual fund theorem to obtain the solution of Eq. 53.5 Footnote 1 from the following lemma:

Lemma 53.1

For the optimization setting displayed inEq. 53.5, the optimal return, R, and its corresponding investment plan, c, are obtained as follows:

$$ R={\sigma}_0\sqrt{{\boldsymbol{\mu}}^T{\Sigma}^{-1}\boldsymbol{\mu}} $$

and

$$ c=\frac{\sigma_0}{\sqrt{{\boldsymbol{\mu}}^T{\Sigma}^{-1}\boldsymbol{\mu}}}{\Sigma}^{-1}\boldsymbol{\mu}. $$
(53.6)

From Lemma 53.1, the investment plan, c, is proportional to the MVR when Σ is a diagonal matrix. Hence, when the asset is concluded as superior in performance utilizing the MVR test, its corresponding weight could then be computed based on the corresponding MVR test value. Thus, another advantage of using the MVR test over the SR test is that it not only allows investors to compare the performance of different assets, but it also provides investors with information of the assets weight. The MVR test enables investors to compute the corresponding allocation for the assets. On the other hand, as the SR is not proportional to the weight of the corresponding asset, an asset with the highest SR would not infer that one should put highest weight on this asset as compared with our MVR. In this sense, the test proposed by Bai et al. (2011d) is superior to the SR test.

Bai et al. (2011d) have also developed both one-sided UMPU test and two-sided UMPU test of equality of the MVRs in comparing the performances of different prospects with hypotheses stated in Eqs. 53.3 and 53.4, respectively. We first state the one-sided UMPU test for the MVRs as follows:

Theorem 53.1

Let X i and Y i (i = 1, 2,⋯ċ, n) be independent random variables with joint distribution function defined inEq. 53.1. For the hypotheses setup inEq. 53.3, there exists a UMPU level-α test with the critical function ϕ(u, t) such that

$$ \phi \left(u,t\right)\left\{\begin{array}{cc}\hfill 1,\hfill & \hfill when\kern0.24em u\ge {C}_0(t)\hfill \\ {}\hfill 0,\hfill & \hfill when\kern0.24em u<{C}_0(t)\hfill \end{array}\right. $$
(53.7)

where C 0 is determined by

$$ {\displaystyle {\int}_{C_0}^{\infty }{f}_{n,t}^{*}}(u)\kern0.5em du={K}_1; $$
(53.8)

with

$$ \begin{array}{l}{f}_{n,t}^{*}(u)={\left({t}_2-\frac{u^2}{n}\right)}^{\frac{n-1}{2}-1}{\left({t}_3-\frac{{\left({t}_1-u\right)}^2}{n}\right)}^{\frac{n-1}{2}-1},\\ {}{K}_1=\alpha {\displaystyle {\int}_{\Omega}{f}_{n,t}^{*}}(u)\kern0.24em du;\end{array} $$

in which

$$ U={\displaystyle \sum_{i=1}^n{X}_i},\kern1em {T}_1={\displaystyle \sum_{i=1}^n{X}_i+}{\displaystyle \sum_{i=1}^n{Y}_i,\kern1em }{T}_2={\displaystyle \sum_{i=1}^n{X}_i^2,\kern1em {T}_3=}{\displaystyle \sum_{i=1}^n{Y}_i^2,\kern1em T=\left({T}_1,{T}_2,{T}_3\right);} $$

with \( \Omega =\left\{u\Big| \max \left(-\sqrt{n{t}_2},{t}_1-\sqrt{n{t}_3}\right)\le u\le \min \left(\sqrt{n{t}_2},{t}_1+\sqrt{n{t}_3}\right)\right\} \) to be the support of the joint density function of (U, T).

We call the statistic U in Theorem 53.1 the one-sided MVR test statistic or simply the MVR test statistic for the hypotheses setup in Eq. 53.3 if no confusion arises. In addition, Bai et al. (2011d) have introduced the two-sided UMPU test statistic as stated in the following theorem to test for the equality of the MVRs listed in Eq. 53.4:

Theorem 53.2

Let X i and Y i (i = 1, 2,⋯ċ, n) be independent random variables with joint distribution function defined inEq. 53.1. Then, for the hypotheses setup inEq. 53.4, there exists a UMPU level-α test with critical function

$$ \phi \left(u,t\right)=\left\{\begin{array}{cc}\hfill 1,\hfill & \hfill when\kern0.24em u\le {C}_1(t)\kern0.24em or\ge {C}_2(t)\hfill \\ {}\hfill 0,\hfill & \hfill when\kern0.36em {C}_1(t)<u<{C}_2(t)\hfill \end{array}\right. $$
(53.9)

in which C 1 and C 2 satisfy

$$ \left\{\begin{array}{c}\hfill {\displaystyle {\int}_{C_1}^{C_2}{f}_{n,t}^{*}(u)\kern0.24em du={K}_2}\hfill \\ {}\hfill {\displaystyle {\int}_{C_1}^{C_2}u{f}_{n,t}^{*}(u)\kern0.24em du={K}_3}\hfill \end{array}\right., $$
(53.10)

where

$$ \begin{array}{l}{K}_2=\left(1-\alpha \right){\displaystyle {\int}_{\Omega}{f}_{n,t}^{*}(u)\kern0.24em du,}\\ {}{K}_3=\left(1-\alpha \right){\displaystyle {\int}_{\Omega}u\;{f}_{n,t}^{*}(u)\kern0.24em du.}\end{array} $$

The terms f * n,t (u), T i (i = 1, 2, 3) and T are defined inTheorem 53.1.

We call the statistic U in Theorem 53.2 the two-sided MVR test statistic or simply the MVR test statistic for the hypotheses setup in Eq. 53.4 if no confusion arises. To obtain the critical values C 1 and C 2 for the test, readers may refer to Bai et al. (2011d, 2012).

53.4 Illustration

In this section, we demonstrate the superiority of the MVR tests over the traditional SR tests by illustrating the applicability of the MVR tests to examine the Internet bubble during January 2000 and December 2002. For simplicity, we only demonstrate the two-sided UMPU test.Footnote 2 The data for this study consists of weekly returns on two stock indices: the S&P 500 and the NASDAQ 100 index. The sample period covers from January 2000 to December 2002 in which the data from the first week of November 2000 to the last week of January 2001 (3 months) are used to compute the MVR in January 2001, while the data from the first week of December 2000 to the last week of February 2001 are used to compute the MVR in February 2001, and so on. However, if the period used to compute the SRs is too short, the result would not be meaningful as discussed in our previous sections. Thus, we utilize a longer period from the first week of February 2000 to the last week of January 2001 (12 months) to compute the SR ratio in January 2001, from the first week of March 2000 to the last week of February 2001 to compute the SR ratio in February 2001, and so on.

Let X with mean μ X and variance σ 2 X be the weekly return on S&P 500 while Y with mean μ Y and variance σ 2 Y be the weekly return on the NASDAQ 100 index. We test the following hypotheses:

$$ {H}_0:\frac{\mu_X}{\sigma_X^2}=\frac{\mu_Y}{\sigma_Y^2}\kern1em \mathrm{versus}\kern1em {H}_1:\frac{\mu_X}{\sigma_X^2}\ne \frac{\mu_Y}{\sigma_Y^2}. $$
(53.11)

To test the hypotheses in Eq. 53.11, we first compute the values of the test function U for the MVR statistic shown in Eq. 53.9, then compute the critical values C 1 and C 2 under the test level of 5 % for the pair of indices and display the values in Table 53.1.

Table 53.1 The results of the mean-variance ratio test and Sharpe ratio test for NASDAQ and S&P 500, from January 2001 to December 2002
Full size table

For comparison, we also compute the corresponding SR statistic developed by Jobson and Korkie (1981) and Memmel (2003) such that

$$ z=\frac{{\widehat{\sigma}}_Y\;{\widehat{\mu}}_X-{\widehat{\sigma}}_X\;{\widehat{\mu}}_Y}{\sqrt{\widehat{\theta}}}, $$
(53.12)

which follows standard normal distribution asymptotically with

$$ \theta =\frac{1}{T}\left(2{\sigma}_X^2{\sigma}_Y^2-2{\sigma}_X{\sigma}_Y{\sigma}_{X,Y}+\frac{1}{2}{\mu}_X^2{\sigma}_{{}^Y}^2+\frac{1}{2}{\mu}_Y^2{\sigma}_X^2-\frac{\mu_X{\mu}_Y}{\sigma_X{\sigma}_Y}{\sigma}_{X,Y}^2\right) $$

to test for the equality of the SRs for the funds by setting the following hypotheses such that

$$ {H}_0^{*}:\frac{\mu_X}{\sigma_X}=\frac{\mu_Y}{\sigma_Y}\kern1em \mathrm{versus}\kern1em {H}_1^{*}:\frac{\mu_X}{\sigma_X}\ne \frac{\mu_Y}{\sigma_Y}. $$
(53.13)

Instead of using a 2-month data to compute the values of our proposed statistic, we use the overlapping 12-month data to compute the SR statistic. The results are also reported in Table 53.1.

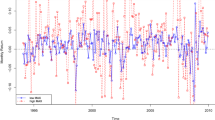
The limitation of applying the SR test is that it would usually conclude indistinguishable performances between the indices, which may not be the situation in reality. In this aspect, looking for a statistic to evaluate the difference between indices for short periods is essential. The situation in reality is that the Internet stocks registered large gains in the late 1990s, followed by large losses from 2000. As we mentioned before, the NASDAQ 100 index comprises 100 of the largest domestic and international technology firms including those in the computer hardware and software, telecommunications, and biotechnology sectors, while the S&P 500 index represents non-technology or “old economy” firms. After the bursting of the Internet bubble in the 2000s, as shown in Fig. 53.1, the NASDAQ 100 declined much more and underperformed the S&P 500. From Table 53.1, we find that the MVR test statistic does not disappoint us in that it does pick up significant differences in performances between the S&P 500 and the NASDAQ 100 index in September 2001, July 2002, August 2002, and September 2002, but SR test does not conclude any distinguishable performances between the indices. Further to say, from Table 53.1, we observe that \( {\widehat{\mu}}_X>{\widehat{\mu}}_Y \) in September 2001, July 2002, August 2002, and September 2002. This infers that the MVR test statistics can detect the real situation that the NASDAQ 100 index underperformed the S&P 500 index, but the traditional SR test cannot detect any difference. Thus, we conclude that investors could be able to profiteer from the Internet bubble if they apply the MVR test.

Fig. 53.1
figure 1

Weekly indices of NASDAQ and S&P 500 from January 3, 2000 to December 31, 2003

Full size image

53.5 Concluding Remarks

In this paper, we employ the MVR test statistics developed by Bai et al. (2011d) to examine the performances between the S&P 500 index and the NASDAQ 100 index during Internet bubble from January 2000 to December 2002. We illustrate the superiority of the MVR test over the traditional SR test by applying both tests to analyze the performance of the S&P 500 index and the NASDAQ 100 index after the bursting of the Internet bubble in the 2000s. Our findings show that while the traditional SR test concludes the two indices being analyzed to be indistinguishable in their performance, the MVR test statistic shows that the NASDAQ 100 index underperformed the S&P 500 index, which is the real situation after the bursting of the Internet bubble in the 2000s. This shows the superiority of the MVR test statistic in revealing short-term performance and, in turn, enables the investors to make better decisions about their investments.

There are two basic approaches to the problem of portfolio selection under uncertainty. One approach is based on the concept of utility theory (Gasbarro et al. 2007; Wong et al. 2006, 2008). Several stochastic dominance (SD) test statistics have been developed; see, for example, Bai et al. (2011a) and the references therein for more information. This approach offers a mathematically rigorous treatment for portfolio selection, but it is not popular among investors since investors would have to specify their utility functions and choose a distributional assumption for the returns before making their investment decisions.

The other approach is the mean-risk (MR) analysis that has been discussed in this paper. In this approach, the portfolio choice is made with respect to two measures – the expected portfolio mean return and portfolio risk. A portfolio is preferred if it has higher expected return and smaller risk. These are convenient computational recipes and they provide geometric interpretations for the trade-off between the two measures. A disadvantage of the latter approach is that it is derived by assuming the Von Neumann-Morgenstern quadratic utility function and that returns are normally distributed (Hanoch and Levy 1969). Thus, it cannot capture the richness of the former approach. Among the MR analyses, the most popular measure is the SR introduced by Sharpe (1966). As the SR requires strong assumptions that the returns of assets being analyzed have to be iid, various measures for MR analysis have been developed to improve the SR, including the Sortino ratio (Sortino and van der Meer 1991), the conditional SR (Agarwal and Naik 2004), the modified SR (Gregoriou and Gueyie 2003), value at risk (Ma and Wong 2010), expected shortfall (Chen 2008), and the mixed Sharpe ratio (Wong et al. 2012). However, most of the empirical studies, see, for example, Eling and Schuhmacher (2007), find that the conclusions drawn by using these ratios are basically the same as that drawn by the SR. Nonetheless, Leung and Wong (2008) have developed a multiple SR statistic and find that the results drawn from the multiple Sharpe ratio statistic can be different from its counterpart pair-wise SR statistic comparison, indicating that there are some relationships among the assets that have not being revealed using the pair-wise SR statistics. The MVR test could be the right candidate to reveal these relationships.

One may claim that the limitation of the MVR test statistic is that it can only draw conclusion for investors with quadratic utility functions and for normal-distributed assets. Wong (2006), Wong and Ma (2008), and others have shown that the conclusion drawn from the MR comparison is equivalent to the comparison of expected utility maximization for any risk-averse investor, not necessarily with only quadratic utility function, and for assets with any distribution, not necessarily normal distribution, if the assets being examined belong to the same location-scale family. In addition, one can also apply the results from Li and Wong (1999) and Egozcue and Wong (2010) to generalize the result so that it will be valid for any risk-averse investor and for portfolios with any distribution if the portfolios being examined belong to the same convex combinations of (same or different) location-scale families. The location-scale family can be very large, containing normal distributions as well as t-distributions, gamma distributions, etc. The stock returns could be expressed as convex combinations of normal distributions, t-distributions, and other location-scale families; see, for example, Wong and Bian (2000) and the references therein for more information. Thus, the conclusions drawn from the MVR test statistics are valid for most of the stationary data including most, if not all, of the returns of different portfolios.

Last, we note that to improve the effectiveness of applying the MVR test in evaluating financial assets performance, one may incorporate other techniques/approaches/models, for example, fundamental analysis (Wong and Chan 2004), technical analysis (Wong et al. 2001, 2003), behavioral finance (Matsumura et al. 1990), prospect theory (Broll et al. 2010; Egozcue et al. 2011), and advanced econometrics (Wong and Miller 1990; Bai et al. 2010, 2011b), to measure the performance of different financial assets and assist investors to make wiser decisions.