Surrogate Models for Aerodynamic Shape Optimisation

Abstract

The main challenges in full-scale aerospace systems development are related to the level of our understanding with respect to the systems behaviour. Computational modelling, through high-fidelity simulations, provides a viable approach towards efficient implementation of the design specifications and enhancing our understanding of the system’s response. Although high-fidelity modelling provides valuable information the associated computational cost restricts its applicability to full-scaled systems. This chapter presents a Computational Fluid Dynamics optimisation strategy based on surrogate modelling for obtaining high-fidelity predictions of aerodynamic forces and aerodynamic efficiency. An Aerodynamic Shape Optimisation problem is formulated and solved using Genetic Algorithm with surrogate models in the place of actual computational fluid dynamics algorithms. Ordinary Kriging approach and Hammersley Sequence Sampling plan are used to construct the surrogate models.

1 Introduction

The computational cost involved in performing numerical simulations for designing and optimising various engineering systems, such as aircraft wings, has been continuously increasing. From an engineering perspective, the design process is crucial for achieving maximum efficiency with the minimum possible cost and within the manufacturing restrictions. In the context of aircraft wings, aerodynamic shape optimisation (ASO) techniques are of great importance for designing a lifting surface with maximum aerodynamic efficiency. In ASO, aerodynamic constraints such as flow properties, Mach number (M), etc. alone are taken into account, in contrast to multidisciplinary design optimisation (MDO) where constraints from various (financial, structural, manufacturing, etc.) disciplines are considered. As the number of influencing disciplines increases, the complexity of the optimisation problem increases.

The constraints of the optimisation problem define the spectrum of the design variables and strongly influence the search space where the optimal solution lies. Parameterisation parameters, which will parameterise the geometry of the engineering system to be optimised, serve as a part of the design variables of the optimisation problem. Since the number of design variables directly influences the complexity of the problem, various parameterisation approaches such as the discrete point approach, partial differential equation approach and polynomial approach have been developed with the intention of simplifying the parameter space without compromising the accurate description of the geometry [1].

Once the geometry is generated, the flow-governing equations can be solved on a suitable mesh using a high- (computationally very intensive) or low-fidelity (computationally less intensive) solver based on the availability of computational resources and time. The solution algorithm is the most time-consuming part of an optimisation approach, since the entire simulation process must be repeated several times within the optimiser until an optimum solution is obtained or the entire search space is explored.

The optimisation schemes can be broadly classified into two different categories: gradient-based optimisation schemes and evolutionary optimisation schemes. The choice of the starting point becomes increasingly important in gradient-based optimisation schemes, as they are more likely to be converged or stuck into local optima [2, 3]. The non-derivative methods are more powerful in finding the global optimum within the given search space; however they are lacking in terms of finding the exact global optimum [2, 3]. These characteristics are given by the concepts of exploration (ability to find the location of the global optimum without getting trapped in a local extremum) and exploitation (ability to exploit the exact optimum solution).

The cost of the ASO process increases by several orders of magnitude when the actual, computationally expensive solution algorithms are employed for resolving the fluid flow [4]. Consequently, the computational cost becomes prohibitively expensive, and a need arises to use well-tuned optimisation methods in order to efficiently identify the optimum configurations within the design space. The computational limitations become more apparent when numerically demanding solution methods, such as computational fluid dynamics (CFD), are coupled with the optimiser. As a consequence, the fidelity of the analysis at the early stages of the design process is sacrificed with the aim of reducing the overall computational burden. In order to circumvent this problem, the use of approximation models has become more popular in recent years in imitating complex solution algorithms due to their quick response and reduced computing requirements. Within this framework, approximation models are constructed for computationally demanding solution algorithms and, further, are used in the place of actual solution algorithms during the optimisation [5, 6].

The process of constructing an approximation model usually involves the following steps: (a) generation of computational data, (b) learning from the collected computational data, and (c) constructing a surrogate model based on the learning. Various approaches such as polynomial regression, response surfaces, neural networks and kriging are used to construct the approximation models [4, 7].

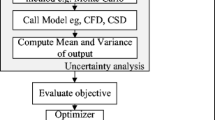
In this chapter, in order to show the advantage of surrogate-assisted optimisation, an ASO problem is formulated to identify the best possible airfoil geometry which will have an improved aerodynamic efficiency for the given flow, structural and aerodynamic conditions. The aerodynamic efficiency (E) is defined as the ratio of lift to drag. Lift and drag are the vertical and horizontal forces, respectively, which act on an airfoil when it is introduced into the airflow. These forces are primarily responsible for the aerodynamic efficiency of an airfoil. The example problem formulated in this chapter considers the NACA 2411 airfoil geometry as the baseline shape to be optimised. The airfoil is assumed to be introduced into a viscous, compressible and low turbulence airflow with M varying between 0.1 and 0.6 at a fixed angle of attack of 5.0^∘. The formulated problem is solved to optimise the baseline airfoil in the assumed airflow conditions. Figure 1 depicts the work flow involved in solving the formulated optimisation problem.

Fig. 1

Work flow of the problem

2 Methodology

This section provides an overview of the methodology used in this chapter and is structured as follows. Section 2.1 describes the parameterisation method employed, called PARSEC, Sect. 2.2 describes the sampling algorithm used, Sect. 2.3 describes the construction of approximation models using the OK approach, and finally Sect. 2.4 provides the overall optimisation procedure.

2.1 Parameterisation

PARSEC is a parameterisation scheme which describes the lower and the upper surface of an airfoil independently using a sixth order polynomial [8]. In this approach, the shape of the airfoil is controlled by the following 11 parameters [9, 10]: leading edge radius (R _le), upper crest point (y _up), lower crest point (y _lo), position of upper crest (x _up), position of lower crest (x _lo), upper crest curvature $(y_{xx_{\mathrm{up}}})$, lower crest curvature $(y_{xx_{\mathrm{lo}}})$, trailing edge thickness (T _te), trailing edge offset (T _off), trailing edge wedge angle (β _te), trailing edge direction angle (α _te). These parameters are shown in Fig. 2 [8].

Fig. 2

PARSEC control parameters

R _le is divided into lower leading edge radius (R _leu) and upper leading edge radius (R _lel) in order to increase the accuracy of the method near the leading edge. Hence, 12 design parameters are used instead of the typical 11 parameters [11].

The mathematical formulation of the approach is given by Eqs. (1) and (2) for the upper and lower surfaces of the airfoil, respectively [1, 11, 12].

$$\begin{aligned} & y_u = \sum_{i=1}^6a_ix^{i-(1/2)}, \end{aligned}$$

(1)

$$\begin{aligned} & y_l = \sum_{i=1}^6b_ix^{i-(1/2)}, \end{aligned}$$

(2)

where, y _u is the required y co-ordinate for the upper surface, y _l is the required y co-ordinate for the lower surface, x is the non-dimensional chord-wise location (chord (c) is assumed to be 1) and a _i and b _i are the coefficients to be solved. The surface of the airfoil is obtained from the solution of the above two equations subject to the following geometrical conditions: (1) at x=maximum, y=maximum, (2) at x=maximum, $\genfrac{}{}{0.2pt}{}{dy}{dx} = 0$, (3) at x=maximum, $\genfrac {}{}{0.2pt}{}{d^{2}y}{dx^{2}} = \mathrm{maximum}$, (4) at x _up=1, $y_{\mathrm{up}} = T_{\mathrm{off}} + \genfrac{}{}{0.2pt}{}{T_{\mathrm{TE}}}{2}$, (5) at x _lo=1, $y_{\mathrm{lo}} = T_{\mathrm{off}} - \genfrac{}{}{0.2pt}{}{T_{\mathrm{TE}}}{2}$, (6) at x _up=1, $\genfrac{}{}{0.2pt}{}{dy_{\mathrm{up}}}{dx} = \tan(\alpha_{\mathrm{TE}}-\genfrac {}{}{0.2pt}{}{\beta_{\mathrm{TE}}}{2})$, (7) at x _lo=1, $\genfrac {}{}{0.2pt}{}{dy_{\mathrm{lo}}}{dx} = \tan(\alpha_{\mathrm{TE}} + \genfrac {}{}{0.2pt}{}{\beta_{\mathrm{TE}}}{2})$.

2.2 Sample Generation

The Hammersley sequence sampling (HSS) technique is a low-discrepancy sampling approach that generates N sample points in a k-dimensional hypercube [13]. Each sample point that falls within the design space constitutes a design point by defining the design variables. For measuring the deviation of the generated sample points from a uniform distribution a quantitative criterion is employed, called the discrepancy [14]. It is always desired to have a more uniform distribution of the sample points within the design space, since it increases the efficiency of the learning from the collected data during the construction of surrogate models. An extensive description regarding the HSS technique can be found in Kalagnanam and Diwekar [15].

In this approach, an integer n is represented by the radix-R notation as shown below [15]:

$$\begin{aligned} & n \equiv n_{m}n_{m-1}\cdots n_{2}n_{1}n_{0}, \end{aligned}$$

(3)

$$\begin{aligned} & n = n_{0}+n_{1}R+n_{2}R^{2}+ \cdots+ n_{m}R^{m}, \end{aligned}$$

(4)

where m=[log _R n] = $[\genfrac{}{}{0.1pt}{}{\ln n}{\ln R}]$ is the integer portion of log _R n. For example, the integer 1,256 has p ₀=6, p ₁=5, p ₂=2, p ₃=1, R=10 and m=3 in the radix-10 notation [14]. The inverse radix number, which is defined as a unique fractional value located between 0 and 1, is obtained by reversing the order of the digits of the integer around the decimal point [14]:

$$\begin{aligned} & \phi_{R}(n) = .n_{0}n_{1}n_{2} \cdots n_{m}, \end{aligned}$$

(5)

$$\begin{aligned} & \phi_{R}(n) = n_{0}R^{-1}+n_{1}R^{-2}+ \cdots+n_{m}R^{-m-1}. \end{aligned}$$

(6)

The HSS algorithm generates N sample points in a k-dimensional hypercube using the following relation [14]:

$$\begin{aligned} & x_{k}(n) = \biggl( \frac{n}{N},\phi R_{1}(n), \phi R_{2}(n), \ldots,\phi_{R_{k-1}}(n) \biggr), \\&\quad n = 0,1,2,\ldots,N-1, \end{aligned}$$

(7)

where R ₁,R ₂,…,R _k−1 represent the first k−1 prime numbers. For the opted problem, ten PARSEC parameters (T _te and T _off are fixed due to structural and aerodynamic constraints) together with M serve as the design variables.

2.3 Surrogate Model Construction

Kriging techniques are employed for interpolations of random responses and are based on stochastic processes. In the case of ordinary kriging (OK), the mathematical expression for the function is defined as

$$ \hat{f}(x_{p}) = \sum_{i=1}^{N} \gamma_{i}(x_{p})f(x_{i}) \quad \forall x_{p} \in S, $$

(8)

where $\hat{f}$ is the linear estimator function for f, γ _i (x _p ) is the weighting function and x _p is a vector of sample points in the design space, which in our case is defined through the range of values of ten PARSEC parameters along with M and is denoted by $S \subset\mathbb{R}^{11}$.

Since the OK model is an isotropic stationary model [16], it is implied that the covariance of f between two sample points is described by a function which is solely based on the distance between the two sample points rather than their exact locations. It can be expressed as

$$ C \bigl[f(x_{a}),f(x_{b}) \bigr] = C\bigl(|x_{a}-x_{b}|\bigr). $$

(9)

C[f(x _a ),f(x _b )] is often expressed by the covariance matrix as [16]

$$ \underline{C}= \begin{Bmatrix} \sigma^{2}=C(0) & C( \Arrowvert x_{1}-x_{2}\Arrowvert) & \dots& C( \Arrowvert x_{1}-x_{N}\Arrowvert) \\C(\Arrowvert x_{2}-x_{1}\Arrowvert) & \sigma^{2} & \dots& C(\Arrowvert x_{2}-x_{N}\Arrowvert) \\\vdots& \vdots& \ddots& \vdots \\C(\Arrowvert x_{N}-x_{1}\Arrowvert) & C(\Arrowvert x_{N}-x_{2}\Arrowvert ) & \dots& \sigma^{2} \end{Bmatrix} , $$

(10)

where σ ² is the variance of the sample points. For the unknown sample point x _p ∈S, the covariance vector ($\overrightarrow{c}$) and the weighting functions vector can be expressed as [16]

$$ \overrightarrow{c}({x_p}) = \begin{Bmatrix} C(\Arrowvert x_{p} - x_{1}\Arrowvert) \\ C(\Arrowvert x_{p} - x_{2}\Arrowvert) \\ \vdots \\ C(\Arrowvert x_{p} - x_{N}\Arrowvert) \end{Bmatrix} ; \qquad \gamma_{i}(x_{p})= \begin{Bmatrix} \gamma_{1}(x_{p}) \\ \gamma_{2}(x_{p}) \\ \vdots \\ \gamma_{N}(x_{p}) \end{Bmatrix} . $$

(11)

Since it is an isotropic stationary model, the sum of all the weighting functions should be equal to 1, as given in Eq. (12). Hence the covariance matrix and covariance vector are then expressed as Eqs. (13) and (14), respectively.

$$\begin{aligned} \displaystyle \sum_{i=1}^{N} \gamma_{i}(x_{p}) = 1 \quad \forall x_{p} \in S, \end{aligned}$$

(12)

$$\begin{aligned} \displaystyle \underline{C}= \begin{Bmatrix} \sigma^{2}=C(0) & C(\Arrowvert x_{1}-x_{2} \Arrowvert) & \dots& C(\Arrowvert x_{1}-x_{N}\Arrowvert) & 1 \\C(\Arrowvert x_{2}-x_{1}\Arrowvert) & \sigma^{2} & \dots& C(\Arrowvert x_{2}-x_{N}\Arrowvert) & 1 \\\vdots& \vdots& \ddots& \vdots& \vdots \\C(\Arrowvert x_{N}-x_{1}\Arrowvert) & C(\Arrowvert x_{N}-x_{2}\Arrowvert ) & \dots& \sigma^{2} & 1 \\1 & 1 & \dots& 1 & 0 \end{Bmatrix} , \end{aligned}$$

(13)

$$\begin{aligned} \displaystyle \mathbf {c}(x_{p}) = \begin{Bmatrix} C(\Arrowvert x_{p}-x_{1}\Arrowvert) \\C(\Arrowvert x_{p}-x_{2}\Arrowvert) \\\vdots \\C(\Arrowvert x_{p}-x_{n}\Arrowvert) \\1 \end{Bmatrix} . \end{aligned}$$

(14)

A Lagrange multiplier ($\lambda_{x_{p}}$) is introduced in the weighting functions vector in order to enforce the unbiasedness constraint of the OK model. Hence the weighting functions vector becomes:

$$ \gamma_{i}(x_{p})= \begin{Bmatrix} \gamma_{1}(x_{p}) \\ \gamma_{2}(x_{p}) \\ \vdots \\ \gamma_{N}(x_{p}) \\ \lambda_{x_{p}} \end{Bmatrix} . $$

(15)

The weighting functions are calculated using the covariance matrix and covariance vector as given by the following relation:

$$ \gamma_{i}(x_{p}) = \underline{C}^{-1} \mathbf {c}(x_{p}). $$

(16)

Since the predicted value of the response at an unknown sample point is always different from the actual value at that sample point, an error measure is introduced to measure the prediction capability of the OK model. This measure of error is known as the estimation error (e _p ) and is defined as follows:

$$ e_{p}=\hat{f}(x_{p}) - f(x_{p}), $$

(17)

where f(x _p ) is the actual value at an unknown point x _p ∈S. If the weighting functions are obtained in such a way that they will reduce the variance of the estimation error, then a function predictor with optimal prediction capability can be obtained. The error variance can be computed using the following expression:

$$ V(e_{p}) = \sum_{i=1}^{N} \bigl(\mathbf {c}(x_{p}) \gamma_{i}(x_{p}) \bigr). $$

(18)

Since the covariogram function is arbitrarily computed from the observed data, a suitable theoretical variogram model should be used to fit the experimental variogram model, so that the kriging equations become solvable. Generally, the selection of a suitable theoretical variogram model is carried out using maximum likelihood estimation (MLE) or cross-validation (CV) approaches. For the current problem, the following theoretical variogram models are employed and the most suitable one is selected based on the MLE approach.

• Gaussian model with actual range:

  $$ C(h) = \mathit{sill} \biggl(1-\exp \biggl(\frac{-h^{2}}{\mathit{range}^{2}} \biggr) \biggr) $$

  (19)

• Gaussian model with practical range:

  $$ C(h) = \mathit{sill} \biggl(1-\exp \biggl(\frac{-3h^{2}}{\mathit{prange}^{2}} \biggr) \biggr) $$

  (20)

• Spherical model with actual range:

  $$ C(h) = \mathit{sill} \biggl( \biggl(\frac{3.0}{2.0} \biggr) \biggl( \frac{h}{\mathit{range}} \biggr) - 0.5 \biggl(\frac{h}{\mathit{range}} \biggr)^{3} \biggr) $$

  (21)

• Exponential model with actual range:

  $$ C(h) = \mathit{sill} \biggl(1-\exp \biggl(\frac{-h}{\mathit{range}} \biggr) \biggr) $$

  (22)

• Exponential model with practical range:

  $$ C(h) = \mathit{sill} \biggl(1-\exp \biggl(\frac{-3h}{\mathit{prange}} \biggr) \biggr), $$

  (23)

where h is the isotropic lag defined as the distance between two sample points in S. In the semivariogram, the lag value at which the semivariance becomes constant is called the range, and the corresponding semivariance value is called the sill. The practical range is the value of the lag at which 0.94 % of the sill is achieved.

2.4 Aerodynamic Shape Optimisation

A genetic algorithm (GA), which is one of a class of evolutionary algorithms where the evolution is based on the theory of the mechanics of natural selection and the evolution process, is used to carry out the optimisation problem. Here the optimisation parameters are described by a group of genes called chromosomes [17–20]; each chromosome is a binary string which describes an individual (i.e. a sample point). In the current problem, the PARSEC parameters T _te and T _off are fixed during the optimisation along with the flow parameter α. This is done to avoid the evolution of airfoils with trailing edge thickness and trailing edge offset during the optimisation. The parameter α is fixed because the optimisation procedure is carried out for a fixed value of (α=5.0^∘) angle of attack. These two fixed parameters will also ensure the satisfaction of the structural and aerodynamic constraints of the current problem. Hence, the remaining ten PARSEC parameters along with the flow parameter, M, serve as the optimisation parameters in the current problem. The typical work flow of the GA is depicted in Fig. 3 and is discussed further below.

Fig. 3

Genetic algorithm approach

2.4.1 Search Space

The search space for the current problem is defined by the range of values of the ten PARSEC parameters and M and their required decimal accuracy. For each optimisation parameter, the required accuracy of the decimal place (d) can be specified.

Once d is specified, the domain length for a particular optimisation parameter can be expressed as follows [21]:

$$ \mathit{Domain~length} = 10^{d}(X_{u} - X_{l}), $$

(24)

where X _u and X _l are the upper and lower bound values of the optimisation parameter, respectively. The binary string corresponding to the parameter X is expressed as b _m−1,b _m−2,…,b ₁,b ₀, which will be equal to $X' = \sum_{i=1}^{m}(b_{i}2^{i})$. The value of m, which is defined to specify the number of possibilities for a given ‘d’, can be chosen as [21]

$$ 2^{m-1} < 10^{d} (X_{u}-X_{l} ) < 2^{m}. $$

(25)

All the optimisation parameters are represented as binary strings of length (L _i ) and combined as a single binary string. The length of the single binary string (L _k ) can be calculated as follows:

$$ L_{k} = \sum_{i=1}^{k}L_{i}, $$

(26)

where k is the number of optimisation parameters, which is equal to n in the current problem. The first L ₁ binary strings of the single binary string (L _k ) correspond to the first optimisation parameter, the second L ₂ binary strings correspond to the second optimisation parameter and so on.

2.4.2 Initial Population

The random number approach is employed to generate the initial pool of optimisation parameters. In this approach, a random number is generated between 0 and 1. If the random number is between 0 and 0.5, then the bit is considered as 0, whereas if it lies between 0.5 and 1, then the bit is set to 1. The size of the initial population can be controlled by a parameter called popsize.

2.4.3 Selection of Parents

Individuals (containing the optimisation parameters) are selected from the pool of the initial population and placed into the mating pool. These individuals are further used for mating and generating new offspring. Since the characters of these individuals are passed to the next generation, only the individuals who have desirable properties are selected. This is accomplished by the tournament wheel selection technique. In this approach, a tournament is defined among the individuals by specifying a selection pressure. The individuals with higher fitness are considered as winners of the tournament and will be placed in the mating pool [22]. The fitness function (P(i)) is evaluated by calculating the total objective function (F) as follows:

$$\begin{aligned} & f(i) = \mathit{obj}(V_{i}), \quad i=1, \mathit{popsize}, \end{aligned}$$

(27)

$$\begin{aligned} & F = \sum_{i=1}^{\mathit{popsize}} \bigl(f(i) \bigr);\qquad P(i) = \frac{f(i)}{F}, \end{aligned}$$

(28)

where f(i) (different from the f(x) defined in the OK section) is the objective function to be optimised and V is the set of optimisation parameters. The process of selection holds some important properties: (a) Best individuals are preferred but not always selected. (b) Worst individuals are not always excluded in order to maintain the variability in each generation.

2.4.4 Crossover

Crossover is performed to combine the desirable characters of two different parents who are selected for mating. The method of crossover depends on the kind of problem to be solved and the method of encoding. For the current problem, the uniform crossover approach is employed. In this approach, a crossover probability (p _c ) is defined and a probability test is performed for each bit in the bit string. If passed, then the bits are randomly exchanged between the two parents selected for mating [23].

2.4.5 Mutation

Mutation is performed in order to refine the process of mating. Here a mutation probability (p _m ) is defined and the probability test is performed on each bit in the bit stream. If passed, the bit is flipped directly. If not passed, the bit is generated randomly and compared with the current one. If the randomly generated bit is different from the original bit, then the original bit is flipped [23].

2.4.6 Fitness Evaluation

Fitness evaluation is the process of evaluating the objective function for each set of optimisation parameters. Based on the fitness of the new offspring, they are considered as new parents and selected for further mating. This process is repeated until the convergence is achieved. The following fitness criterion is used in the current problem to select the best possible airfoil geometries:

$$ \mathit{Fitness} (f) = \mathit{obj}(E) = \mathit{obj} \biggl(\frac{(C_{l})_{\mathrm{High}{\scriptstyle\mbox{-}}\mathrm{fidelity}}}{ (C_{d})_{\mathrm{High}{\scriptstyle\mbox{-}}\mathrm{fidelity}}} \biggr), $$

(29)

where $(C_{l})_{\mathrm{High}{\scriptstyle\mbox{-}}\mathrm{fidelity}}$ and $(C_{d})_{\mathrm{High}{\scriptstyle\mbox{-}}\mathrm{fidelity}}$ are the high-fidelity coefficient of lift and the high-fidelity coefficient of drag, respectively. The method of estimating their values is described in the following section.

3 Results and Analysis

Computer-based simulations must be performed at the optimal sample points generated by the HSS algorithm to obtain data. The collected data are used to initiate the learning process during the construction of surrogate models. As discussed earlier, the dimension (n) and the design space of the current problem are 11 and $S \subset\mathbb {R}^{11}$, respectively. Table 1 gives the design variables and their ranges of values for the current problem.

Table 1 Design variables and their ranges of values

A sample point has ten PARSEC parameters and M. 50 (N) such sample points are generated where the simulations need to be performed. The HSS technique generates uniform sample points in an unstructured way. Figures 4 and 5 show the uniformity and space-filling properties of the Hammersley sequence (HS) sample points. These sample points are generated for a two-dimensional problem defined in the design space of [0,1]². It can be seen from these figures that the HSS technique retains its uniformity and space-filling properties irrespective of the number of sample points. Observe also that the sample points are spread over the interior of the design space for the given number of “N” sample points in contrast to the classical design of experiments (DOE) techniques, where the sample points are generated mainly near the boundaries of the design space [14].

Fig. 4

Number of HS sample points: 20

Fig. 5

Number of HS sample points: 50

Computer-based simulations, both panel (low-fidelity) and CFD (high-fidelity), are performed at these 50 sample points. A Linear Vorticity Surface Panel method code developed by Ilan Kroo [24] is used for the low-fidelity simulations. Panel methods are more effective in giving reasonably accurate results without being computationally expensive. The flow around the NACA 2411 airfoil is solved using the panel code for different angles of attack with N _p =1,000 (number of panels). The results (C _l ) (which are theoretically valid at M=0.0) are compared with the Xfoil viscous simulation results obtained at M=0.1, as shown in Fig. 6. The influence of N _p on the low-fidelity results is shown in Fig. 7. It can be seen that the panel method slightly over-predicts the C _l , and the accuracy of the solution increases as the number of panels increases.

Fig. 6

C _l as a function of α

Fig. 7

Influence of number of panels on C _l

High-fidelity, CFD simulations are performed by solving two-dimensional, steady and compressible Navier–Stokes equations using the FLUENT software [25]. The turbulence phenomena have been modelled using the Spalart–Allmaras turbulence model, which is a one-equation model for solving the turbulent viscosity transport equation [26, 27] and has been widely used for aerospace applications. The computational grid is generated with the ICEM CFD package. The C-grid topology is used since it is quite good at capturing the flow physics in the wake region of the airfoil [28, 29]. Figure 8 shows the topology of the grid and the dimensions involved with the grid generation. The grid extends to a dimension of 14c in the downstream direction (L), 9c in the upstream direction (A) and 10c in the cross-stream direction (H). In order to capture the flow physics within the boundary layer region, y ⁺=1 has been used [30].

Fig. 8

Grid topology

The density-based implicit solver in FLUENT is used to solve the flow around the airfoil geometry with an ideal gas as a working fluid. The viscosity is calculated from the three-coefficient Sutherland law, and the basic flow properties are given in Table 2. Turbulence is specified in terms of turbulent intensity (I) and turbulent length scale (l), and a least squares cell-based discretisation scheme is used for the gradient together with the Roe-FDS flux type. Third order Monotone Upstream-centred Schemes for Conservation Laws (MUSCL), which can provide more accurate numerical results even when the solutions exhibit shock, are employed for the spatial discretisation of the flow [31, 32]. The solution converges down to an accuracy of 10⁻⁵ and 10⁻⁶ in about 3,000 iterations.

Table 2 Fluid flow properties

In order to validate the mesh generation and solution techniques, the flow over the NACA 2411 and NACA 0012 airfoils is solved using the above-described mesh generation and solution methods. The flow properties for the current validation case are the same as tabulated above except for α and M. The validation is carried out for various α at M=0.1. The fine grid, which is obtained after a grid convergence study, has 1,000 points on the surface of the airfoil in the circumferential direction and has about 80,000 cells in total. A two-stage boundary layer is used in the grid generation to have more cells around the geometry of the airfoil (see Fig. 9). Figures 10 and 11 show the error (variation of CFD results from the actual results) of C _l and C _d for the NACA 2411 and NACA 0012 airfoils, respectively. One can see that the error increases when the number of cells (N _c ) goes above 8,000. Figure 12 shows the variation of C _l from the results published by Klimas and Sheldahl in Ref. [33] for NACA 2411 with fine mesh (N _c =8,000). Figure 13 shows the variation of C _d from the Xfoil viscous simulation results for NACA 0012 with fine mesh.

Fig. 9

Two-stage boundary layer

Fig. 10

Grid convergence [C _l ] error estimation

Fig. 11

Grid convergence [C _d ] error estimation

Fig. 12

C _l as a function of α for NACA 2411

Fig. 13

C _d as a function of α for NACA 0012

The grid generation process for the remaining 50 sample points is automated, so that the same grid generation technique can be applied for all the airfoil geometries.

It is also ensured that the applied grid generation technique results in a fine mesh for all the airfoil geometries. The flow around the 50 airfoil geometries is solved using both the low-fidelity panel simulations and high-fidelity CFD simulations. Once the aerodynamic forces ($(C_{l})_{\mathrm{Low}{\scriptstyle\mbox{-}}\mathrm{fidelity}}$, $(C_{l})_{\mathrm{High}{\scriptstyle\mbox{-}}\mathrm{fidelity}}$ and $(C_{d})_{\mathrm{High}{\scriptstyle\mbox{-}}\mathrm{fidelity}}$) are obtained for the generated 50 airfoil geometries, they can then be used for the learning process.

Three surrogate models are constructed using the in-house OK code. The first surrogate model is constructed using the low-fidelity panel data and can predict the low-fidelity C _l for any airfoil geometry placed within the design space S. The second surrogate model is constructed using the high-fidelity C _d data and can predict the high-fidelity C _d for any airfoil geometry placed within S. The third one is constructed using the difference in C _l between the low- and high-fidelity data (ΔC _l ) and can be used to estimate the difference in C _l between the low- and high-fidelity analysis for any airfoil geometry placed within S.

Figures 14, 15 and 16 show the capability of different theoretical semivariogram models in fitting the experimental semivariogram model for the first, second and third black surrogate models respectively. It can be clearly observed that the Gaussian model with practical range fits the experimental semivariogram model more accurately than any other theoretical models for all the three surrogate models. The second most accurate one is the spherical model with actual range. These conclusions are confirmed by carrying out the prediction at various unknown sample points. Figures 17, 18 and 19 show the comparison at some of these unknown sample points for all three surrogate models with N=50. For all the predictions, the e _p is on the order of 10⁻² and 10⁻³.

Fig. 14

Theoretical semivariogram models [low-fidelity C _l ]

Fig. 15

Theoretical semivariogram models [high-fidelity C _d ]

Fig. 16

Theoretical semivariogram models [ΔC _l ]

Fig. 17

Estimation error of the predictions [low-fidelity C _l ]

Fig. 18

Estimation error of the predictions [high-fidelity C _d ]

Fig. 19

Estimation error of the predictions [ΔC _l ]

The number of sample points (N) (and so the amount of data) which is used to construct the surrogate models has a huge influence on the prediction capability of the constructed surrogate models. As “N” increases, the capability of the surrogate model to predict the right solution increases until a saturation level is reached for “N”. This behaviour is further depicted in Figs. 20, 21 and 22 for the first, second and third surrogate models, respectively. It can be observed that e _p is reduced as “N” increases for all three surrogate models.

Fig. 20

Influence of “N” on the predictions [low-fidelity C _l ]

Fig. 21

Influence of “N” on the predictions [high-fidelity C _d ]

Fig. 22

Influence of “N” on the predictions [ΔC _l ]

The aerodynamic efficiency (E) of an airfoil geometry which is placed within ‘S’ can be calculated using the constructed surrogate models. Once an unknown sample point (airfoil geometry and M) is generated, it can be supplied to the three surrogate models. As discussed earlier, the first surrogate model can predict the low-fidelity C _l , while the second one can predict the high-fidelity C _d . The ΔC _l can be predicted by the third surrogate model. Now the E of the airfoil at α=5.0^∘ for the above discussed flow conditions can be calculated from the following relations. Since the airfoil is placed within ‘S’, the M will have a value between 0.1 and 0.6.

$$\begin{aligned} \displaystyle (C_{l})_{\mathrm{High}{\scriptstyle\mbox{-}}\mathrm{fidelity}} = (C_{l})_{\mathrm{Low}{\scriptstyle\mbox{-}}\mathrm{fidelity}} - \varDelta C_{l}, \end{aligned}$$

(30)

$$\begin{aligned} \displaystyle E = \frac{L}{D} = \frac{(C_{l})_{\mathrm{High}{\scriptstyle\mbox{-}}\mathrm{fidelity}}q_{\infty }S}{(C_{d})_{\mathrm{High}{\scriptstyle\mbox{-}}\mathrm{fidelity}}q_{\infty}S}, \end{aligned}$$

(31)

where L is the lift force of the airfoil, D is the drag force of the airfoil, $q = (\frac{\rho V^{2}}{2} )$ is the dynamic pressure of the flow, ρ is the density of the flow, V is the velocity of the flow and S is the surface area of the airfoil. Since S and q are constant for a given airfoil and flow conditions (M, ρ, temperature) respectively, the above relation can be written as follows:

$$ E = \frac{L}{D} = \frac{(C_{l})_{\mathrm{High}{\scriptstyle\mbox{-}}\mathrm{fidelity}}}{(C_{d})_{\mathrm{High}{\scriptstyle\mbox{-}}\mathrm{fidelity}}}. $$

(32)

E is estimated at various sample points (i.e. airfoil geometries) placed within the design space ‘S’ using the constructed surrogate models. The estimated values are compared with the actual values of E which are calculated from separate CFD simulations. The comparison is shown in Fig. 23.

Fig. 23

% of error of E prediction

Figure 23 shows that the prediction of the constructed surrogate models leads to having E within low error bounds with the maximum % of error being smaller than 4.8 %. The deviation can be further reduced by increasing the accuracy of the predictions by increasing the number of training sample points.

The constructed surrogate models have been coupled with the GA [34]. The parameters for controlling the ASO are summarised in Table 3. Each generation of the GA has 5 different individuals (i.e. airfoil geometries) and the ASO process is carried out in 500 generations. In total, 2,500 different airfoil geometries with different M are obtained and tested for maximum E. An optimised solution, which has an aerodynamic efficiency of E=80.326, is obtained and converges around the 495th generation of the GA. The flow around the optimised airfoil geometry is solved in FLUENT using the corresponding flow properties as shown in Table 4. The CFD calculations show that the optimised airfoil geometry has E=77.106, corresponding to a 4.1 % error. As already discussed, this value is less than the maximum expected error of 4.8 %. Despite the small prediction error, the obtained airfoil geometry is still better than the baseline shape, which has 67.015 for the flow conditions tabulated in Table 4, and other explored airfoil geometries. It can then be confirmed that the optimised geometry has 15.04 % improvement in E over the actual NACA 2411 at the specified flow conditions. The variation in the geometry, pressure and velocity distribution between the baseline airfoil and optimised airfoil are depicted in Figs. 24–29. It can be observed from these figures that the higher airflow acceleration at the suction side and higher positive C _p at the pressure side are the primary reasons for the optimised airfoil to have more E than its counterpart.

Fig. 24

Optimised geometry

Fig. 25

C _p distribution

Fig. 26

Pressure distribution around the NACA 2411 airfoil

Fig. 27

Velocity distribution around the NACA 2411 airfoil

Fig. 28

Pressure distribution around the optimised airfoil

Fig. 29

Velocity distribution around the optimised airfoil

Table 3 GA parameters to control the evolution (ASO)

Table 4 Flow properties to solve the optimised geometry

The whole ASO problem is carried out in 0.341399E+03 sec (5.6 min) with a computer system which has 1.5 GB of DDR 2 RAM, 2.6 GHz of processor speed and 2 MB of L2 cache memory. If the actual CFD algorithm were to be employed for solving the flow during the optimisation, 156 days would have been required for the same computer system to obtain the optimised solution. This is calculated based on the time taken for a single CFD simulation (90 min approximately) during the data mining process. Clearly, applying the surrogate models in the place of actual CFD algorithms has drastically reduced the required computational time and resources to carry out an ASO problem.

The method of the parameterisation scheme is crucial for both surrogate model construction and optimiser, since its variables are used as the design and optimisation variables. The PARSEC parameterisation scheme is effective, since it offers flexibility in controlling the aerodynamic characteristics of the airfoil geometry with a minimum number of parameters. The distribution of sample points within the design space strongly influences the performance of the surrogate models. Hence, it is important to use a sampling plan that is able to explore the design space uniformly rather than just distributing the sample points in an arbitrary fashion. The Hammersley sequence sampling (HSS) technique has more uniformity and stratification properties for the given “N” irrespective of “n” of the problem. These properties make this algorithm suitable for problems where the evaluation of objective functions at one sample point is computationally more expensive. The statistically unbiased characteristics of the ordinary kriging (OK) approach enhance the ability and accuracy of the surrogate models in predicting response values at an unexplored space. The GA is observed to be more effective in exploring the search space. Since variability exists in all the generations of the GA, a huge number of desirable solutions to the defined problem are generated. Hence, this process can also be considered as a data mining process and can be further used for airfoil design and analysis.

4 Conclusions

This chapter may be summarised as follows. The chapter begins with a review of the basic activities involved in an aerodynamic shape optimisation problem. Next, it gives more information about the construction of the surrogate models for various aerodynamic functions and their application to the aerodynamic shape optimisation problems. The chapter is concluded with a discussion on the practical challenges involved in employing the surrogate models to aerodynamic shape optimisation problems.