Multiscale Coarsening for Linear Elasticity by Energy Minimization

Abstract

In this work, we construct energy-minimizing coarse spaces for the finite element discretization of mixed boundary value problems for displacements in compressible linear elasticity. Motivated from the multiscale analysis of highly heterogeneous composite materials, basis functions on a triangular coarse mesh are constructed, obeying a minimal energy property subject to global pointwise constraints. These constraints allow that the coarse space exactly contains the rigid body translations, while rigid body rotations are preserved approximately. The application is twofold. Resolving the heterogeneities on the finest scale, we utilize the energy-minimizing coarse space for the construction of robust two-level overlapping domain decomposition preconditioners. Thereby, we do not assume that coefficient jumps are resolved by the coarse grid, nor do we impose assumptions on the alignment of material jumps and the coarse triangulation. Weonly assume that the size of the inclusions is small compared to the coarse mesh diameter. Ournumerical tests show uniform convergence rates independent of the contrast in the Young’s modulus within the heterogeneous material. Furthermore, we numerically observe the properties of the energy-minimizing coarse space in an upscaling framework. Therefore, we present numerical results showing the approximation errors of the energy-minimizing coarse space w.r.t. the fine-scale solution.

Mathematics Subject Classification (2010): 35R05, 65F10, 65F10, 65N22, 65N55, 74B05, 74S05

1 Introduction

Constantly rising demands on the range of application of today’s industrial products require the development of innovative, highly effective composite materials, specifically adapted to their field of application. Virtual material design provides essential support in the development process of new materials as it substantially reduces costs and time for the construction of prototypes and performing measurements on their properties. Of special interest is the multiscale analysis of particle-reinforced composites. They combine positive features of their components such as light weight and high stiffness.

Due to large variations in the material parameters, the linear system arising from the finite element discretization of the linear elasticity PDE on such heterogeneous materials is in general very ill-conditioned. Our goal is to develop two-level domain decomposition preconditioners which are robust w.r.t. the jumps in the material coefficients of the PDE. Two-level overlapping domain decomposition preconditioners for the equations of linear elasticity are presented in several papers [9, 19, 22]. Under certain conditions on the alignment of the material jumps with the coarse grid, the aggregation-based method in [19] (see also [26] in the context of AMG) promises mesh and coefficient independent condition number bounds. These methods might not be fully robust when variations in the coefficients appear on a very small scale where the coefficients cannot be resolved by a coarse mesh. A more recent approach in [23] guarantees robustness w.r.t. arbitrary coefficient variations by solving generalized eigenvalue problems in the overlapping regions of the coarse basis functions. The dimension of the resulting coarse space strongly depends on the coefficient distribution. This approach is a variation of the method in [7, 30], where it is applied to abstract symmetric positive definite operators in a multiscale framework.

Further robust methods for solving linear elasticity problems include multilevel methods studied in [14] and further developed in [11] and [12]. A purely algebraic multigrid method for linear elasticity problems is constructed, based on computational molecules, a new variant of AMGe [3]. Such an approach has been studied earlier for scalar elliptic PDEs in [15]. Classical AMG methods for linear elasticity problems are presented in [1, 5] and the references therein.

In this paper, we construct coarse basis functions with a minimal energy property subject to the constraints that the coarse space exactly contains the rigid body translations, while the rigid body rotations are preserved approximately. Energy-minimizing methods have been proposed in [29] and [16] and were further studied in [25, 31]. In [17], such an approach is generalized and applied to non-Hermitian matrices. The approach was motivated in [29] from experimental results of one-dimensional problems. It is based on improving the approximation properties of the coarse space by reducing its dependence on the PDE coefficients. In [25], energy-minimizing coarse spaces were motivated from developments in the convergence theory for two-level Schwarz methods of scalar elliptic PDEs in [8]. In [16], energy-minimizing coarse spaces are presented also for isotropic linear elasticity, in the context of smoothed aggregation. The novel part in the paper at hand is the application to the multiscale framework. The construction on a coarse tetrahedral mesh allows large overlaps in the supports of the basis functions and the coarse space promises good upscaling properties.

An interesting method proposed in [20] constructs basis functions by minimizing their energy subject to a set of functional rather than pointwise constraints. This approach is applied to scalar elliptic PDEs. Similar to the method in [7], the objective is to prove the approximation property in a weighted Poincaré inequality. By a proper choice of the functional constraints, mesh and coefficient independent convergence rates can be obtained. Further variants of coarse spaces with a minimal energy property, including local variants, can be found in [6, 10, 13, 28].

The outline of the paper is as follows. We proceed with the continuous formulation of the governing PDE system and the discretization on the fine grid in Sect. 2. In Sect. 3 we shortly recapitulate the two-level additive Schwarz method, followed by introducing the precise structure of the underlying fine and coarse grid in three spatial dimensions. In Sect. 4, we present a detailed construction of the energy-minimizing basis. Section 5 is devoted to numerical results, a short discussion follows in Sect. 6.

2 Governing Equations and Their Discretization

2.1 The Equations of Linear Elasticity

For the sake of simplicity, let $\Omega \subset {\mathbb{R}}^{3}$ be a Lipschitz domain. We shall assume that Γ = ∂ Ω admits the decomposition into two disjoint subsets $\Gamma _{D_{i}}$ and $\Gamma _{N_{i}}$, $\Gamma = \overline{\Gamma _{D_{i}} \cup \Gamma }_{N_{i}}$ and $\mathrm{meas}(\Gamma _{D_{i}}) > 0$ for i ∈ { 1, 2, 3}. We consider a solid body in Ω, deformed under the influence of volume forces $\boldsymbol{f}$ and traction forces $\boldsymbol{t}$. Assuming a linear elastic material behavior, the displacement field $\boldsymbol{u}$ of the body is governed by the mixed b.v.p. [2]

$$\displaystyle{ -\text{div}\,\boldsymbol{\sigma }(\boldsymbol{u}) = \boldsymbol{f}\;\text{ in }\Omega, }$$

(1)

$$\displaystyle{ \boldsymbol{\sigma }(\boldsymbol{u}) = \boldsymbol{C} : \boldsymbol{\varepsilon }(\boldsymbol{u})\;\text{ in }\Omega, }$$

(2)

$$\displaystyle\begin{array}{rcl} u_{i}& =& g_{i}\:\text{ on }\Gamma _{D_{i}},\quad i = 1,2,3, {}\\ \sigma _{ij}n_{j}& =& t_{i}\;\;\text{ on }\Gamma _{N_{i}},\quad i = 1,2,3, {}\\ \end{array}$$

where $\boldsymbol{\sigma }$ is the stress tensor, the strain tensor $\boldsymbol{\varepsilon }$ is given by the symmetric part of the deformation gradient,

$$\displaystyle{ \boldsymbol{\varepsilon }(\boldsymbol{u}) = \frac{1} {2}\left (\nabla \boldsymbol{u} + \nabla \boldsymbol{{u}}^{T}\right ) }$$

and $\boldsymbol{n}$ is the unit outer normal vector on Γ and $\sigma _{ij}n_{j} = (\boldsymbol{\sigma }\cdot \boldsymbol{n})_{i}$. The fourth-order elasticity tensor $\boldsymbol{C} =\boldsymbol{ C}(x),x \in \Omega$ describes the elastic stiffness of the material under mechanical load. The coefficients c _{i j k l} , 1 ≤ i, j, k, l ≤ 3 may contain large jumps within the domain Ω. They depend on the parameters of the particular materials which are enclosed in the composite. The boundary conditions are imposed separately for each component u _i , i = 1, 2, 3 of the vector-field $\boldsymbol{u} = {(u_{1},u_{2},u_{3})}^{T} :\bar{ \Omega } \rightarrow {\mathbb{R}}^{3}$.

Equation (1) is the general form of the PDE system for anisotropic linear elasticity, which simplifies when the solid body consists of one or more isotropic materials. In this case, (2) can be expressed in terms of the Lamé coefficients $\lambda \in \mathbb{R}$ and μ > 0, which are characteristic constants of the specific material. The stiffness tensor of an isotropic material is given by $c_{ijkl} =\lambda \delta _{ij}\delta _{kl} +\mu (\delta _{ik}\delta _{jl} +\delta _{il}\delta _{jk})$, and the stress is $\boldsymbol{\sigma }(\boldsymbol{u}) =\lambda \text{tr}(\boldsymbol{\varepsilon }(\boldsymbol{u}))\boldsymbol{I} + 2\mu \boldsymbol{\varepsilon }(\boldsymbol{u})$.

2.2 Weak Formulation

Consider the Sobolev space $\mathcal{V} := {[{H}^{1}(\Omega )]}^{3}$ of vector-valued functions whose components are square-integrable with weak first-order partial derivatives in the Lebesgue space L ²(Ω). We define the subspace $\mathcal{V}_{0} \subset \mathcal{V}$,

$$\displaystyle\begin{array}{rcl} \mathcal{V}_{0} := \left \{\boldsymbol{v} \in {[{H}^{1}(\Omega )]}^{3} : v_{ i} = 0\text{ on }\,\Gamma _{D_{i}},\,i = 1,2,3\right \}.& &{}\end{array}$$

(3)

Additionally, we define the manifold

$$\displaystyle\begin{array}{rcl} \mathcal{V}_{g} := \left \{\boldsymbol{v} \in {[{H}^{1}(\Omega )]}^{3} : v_{ i} = g_{i}\text{ on }\,\Gamma _{D_{i}},\,i = 1,2,3\right \}.& &{}\end{array}$$

(4)

The Sobolev space $\mathcal{V}$ inherits its scalar product from H ¹(Ω); it is given by

$$\displaystyle{ (\boldsymbol{u},\boldsymbol{v})_{{[{H}^{1}(\Omega )]}^{3}} :=\sum _{ i=1}^{3}(u_{ i},v_{i})_{{H}^{1}(\Omega )}. }$$

We assume $\boldsymbol{f} \in \mathcal{V}_{0}^{{\prime}}$ to be in the dual space of $\mathcal{V}_{0}$, $\boldsymbol{t}\, \in \, {[{H}^{-\frac{1} {2} }(\Gamma _{N})]}^{3}$ is in the trace space, and c _{i j k l}   ∈ L ^∞(Ω) to be uniformly bounded. Additionally, we require the stiffness tensor $\boldsymbol{C}$ to be positive definite, i.e., it holds $\left (\boldsymbol{C} : \boldsymbol{\varepsilon }(\boldsymbol{v})\right ) :\boldsymbol{\varepsilon } (\boldsymbol{v}) \geq C_{0}\,\boldsymbol{\varepsilon }(\boldsymbol{v}) :\boldsymbol{\varepsilon } (\boldsymbol{v})$ for a constant C ₀ > 0. Note that for an isotropic material with the parameters λ and μ, this condition holds when C ₀ ∕ 2 < μ < ∞ and C ₀ ≤ 2μ + 3λ < ∞. We define the bilinear form $a : \mathcal{V}\times \mathcal{V}\rightarrow \mathbb{R}$,

$$\displaystyle{ a(\boldsymbol{u},\boldsymbol{v}) :=\int _{\Omega }\left (\boldsymbol{C} : \boldsymbol{\varepsilon }(\boldsymbol{u})\right ) :\boldsymbol{\varepsilon } (\boldsymbol{v})\,dx. }$$

(5)

This form is symmetric, continuous, and coercive. The coercivity, i.e.,

$$\displaystyle{ \exists \:c_{0} > 0\; :\; a(\boldsymbol{v},\boldsymbol{v}) \geq c_{0}\,\Vert \boldsymbol{v}\Vert _{{[{H}^{1}(\Omega )]}^{3}}\;\;\forall \boldsymbol{v} \in \mathcal{V}_{0}, }$$

can be shown by using Korn’s inequality (cf. [2]). Furthermore, we define the continuous linear form $F : \mathcal{V}\rightarrow \mathbb{R}$,

$$\displaystyle{ F(\boldsymbol{v}) :=\int _{\Omega }\boldsymbol{f} \cdot \boldsymbol{ v}\,dx +\int _{\Gamma _{N}}\boldsymbol{t} \cdot \boldsymbol{ v}\,ds. }$$

The weak solution of (1) is then given in terms of a( ⋅,  ⋅) and F( ⋅) by $\boldsymbol{u} \in \mathcal{V}_{g}$, such that

$$\displaystyle{ a(\boldsymbol{u},\boldsymbol{v}) = F(\boldsymbol{v})\;\forall \boldsymbol{v} \in \mathcal{V}_{0}. }$$

(6)

Under the assumptions above, a unique solution of the weak formulation in (6) is guaranteed by the Lax–Milgram lemma [2].

2.3 Finite Element Discretization

We want to approximate the solution of (6) in a finite dimensional subspace ${\mathcal{V}}^{h} \subset \mathcal{V}$. Therefore, let $\mathcal{T}_{h}$ be a quasi-uniform triangulation of $\Omega \subset {\mathbb{R}}^{3}$ into tetrahedral finite elements with mesh parameter h, and let $\bar{\Sigma }_{h}$ be the set of vertices of $\mathcal{T}_{h}$ contained in $\bar{\Omega }$. Furthermore, let $\bar{\mathcal{N}}_{h}$ denote the corresponding index set of nodes in $\bar{\Sigma }_{h}$. We denote the number of grid points in $\bar{\Sigma }_{h}$ by n _p . In Sect. 3, the regular grid and its triangulation are introduced in more detail. Let

$$\displaystyle{ {\mathcal{V}}^{h} := \text{span}\big\{\varphi _{ k}^{j,\mathrm{h}} :\ \bar{ \Omega } \rightarrow {\mathbb{R}}^{3},\,j \in \bar{\mathcal{N}}_{ h},\,k = 1,2,3\big\} }$$

be the space of continuous piecewise linear vector-valued functions on $\mathcal{T}_{h}$. Each such basis function is of the form

$$\displaystyle{ \varphi _{k}^{j,\mathrm{h}} = {(\varphi _{ k1}^{j,\mathrm{h}},\varphi _{ k2}^{j,\mathrm{h}},\varphi _{ k3}^{j,\mathrm{h}})}^{T},\quad \;\varphi _{ kl}^{j,\mathrm{h}}({x}^{i}) =\delta _{ ij}\delta _{kl},\;\;{x}^{i} \in \bar{ \Sigma }_{ h},\;l \in \{ 1,2,3\}, }$$

where δ _{i j} denotes the Kronecker delta. For the sake of simplifying the notation, we assume a fixed numbering of the basis functions to be given. To be more specific, we assume that there exists a suitable surjective mapping $\{\varphi _{k}^{j,\mathrm{h}}\} \rightarrow \{ 1,\ldots,n_{d}\}$, $\varphi _{k}^{j,\mathrm{h}}\mapsto (j,k)$. Here, n _d  = 3n _p denotes the total number of degrees of freedom (DOFs) of ${\mathcal{V}}^{h}$. Note that this mapping automatically introduces a renumbering from $\{1,\ldots,n_{p}\} \times \{ 1,2,3\} \rightarrow \{ 1,\ldots,n_{d}\}$. We introduce the discrete analogies to the space in (3) and the manifold in (4) by

$$\displaystyle\begin{array}{rcl} \mathcal{V}_{0}^{h} :& =& \left \{\boldsymbol{{v}}^{h} \in {\mathcal{V}}^{h} : v_{ i}^{h} = 0\text{ on }\,\Gamma _{ D_{i}},\,i = 1,2,3\right \},{}\end{array}$$

(7)

$$\displaystyle\begin{array}{rcl} \mathcal{V}_{g}^{h} :& =& \left \{\boldsymbol{{v}}^{h} \in {\mathcal{V}}^{h} : v_{ i}^{h} = g_{ i}\text{ on }\,\Gamma _{D_{i}},\,i = 1,2,3\right \}.{}\end{array}$$

(8)

We want to find $\boldsymbol{{u}}^{h} \in \mathcal{V}_{g}^{h}$, where $\boldsymbol{{u}}^{h} =\boldsymbol{ {w}}^{h} +\boldsymbol{ {g}}^{h}$, with $\boldsymbol{{w}}^{h} \in \mathcal{V}_{0}^{h}$ and $\boldsymbol{{g}}^{h} \in \mathcal{V}_{g}^{h}$. More precisely, we seek $\boldsymbol{{u}}^{h} = {(u_{1}^{h},u_{2}^{h},u_{3}^{h})}^{T}$ with

$$\displaystyle{ u_{k}^{h} =\sum \limits _{ j=1}^{n_{p} }\text{u}_{(j,k)}\varphi _{k}^{j,h},\;k = 1,2,3, }$$

such that

$$\displaystyle{ a(\boldsymbol{{w}}^{h},\boldsymbol{{v}}^{h}) = F(\boldsymbol{{v}}^{h}) - a(\boldsymbol{{g}}^{h},\boldsymbol{{v}}^{h})\;\;\forall \boldsymbol{{v}}^{h} \in \mathcal{V}_{ 0}^{h}. }$$

We define the index set of DOFs of ${\mathcal{V}}^{h}$ by ${\mathcal{D}}^{h} =\{ 1,\ldots,n_{d}\}$ and introduce the subset

$$\displaystyle\begin{array}{rcl} \mathcal{D}_{0}^{h} :& =& \left \{(i,k) \in \mathbb{N} : i \in \bar{\mathcal{N}}_{ h},\,{x}^{i}\not\in \Gamma _{ D_{k}}\right \}. {}\\ \end{array}$$

Furthermore, we may introduce $\mathcal{D}_{\Gamma _{D}}^{h} := {\mathcal{D}}^{h}\setminus \mathcal{D}_{0}^{h}\neq \varnothing$. The bilinear form in (5) applied to the basis functions of ${\mathcal{V}}^{h}$ reads

$$\displaystyle\begin{array}{rcl} a(\varphi _{m}^{i,h},\varphi _{ k}^{j,h})& =& \int _{ \Omega }\boldsymbol{\varepsilon }(\varphi _{m}^{i,h}) :\boldsymbol{ C} :\boldsymbol{\varepsilon } (\varphi _{ k}^{j,h})\,\mathrm{d}x.{}\end{array}$$

(9)

We define $A \in {\mathbb{R}}^{n_{d}\times n_{d}}$, $f \in {\mathbb{R}}^{n_{d}}$ by

$$\displaystyle\begin{array}{rcl} A_{(i,m)(j,k)} = \left \{\begin{array}{@{}l@{\quad }l@{}} a(\varphi _{m}^{i,h},\varphi _{k}^{j,h})\quad &\text{ if }(i,m) \in \mathcal{D}_{0}^{h},(j,k) \in \mathcal{D}_{0}^{h}, \\ a(\varphi _{m}^{i,h},\varphi _{k}^{j,h})\quad &\text{ if }(i,m) = (j,k) \in \mathcal{D}_{\Gamma _{D}}^{h}, \\ 0 \quad &\text{otherwise } \end{array} \right.& & {}\\ \end{array}$$

and

$$\displaystyle\begin{array}{rcl} f_{(j,k)} = \left \{\begin{array}{@{}l@{\quad }l@{}} F(\varphi _{k}^{j,h}) -\sum \limits _{(i,m)\in \mathcal{D}_{\Gamma _{ D}}^{h}}a(\varphi _{m}^{i,h},\varphi _{ k}^{j,h})g_{ m}({x}^{i})\quad &\text{ if }(j,k) \in \mathcal{D}_{ 0}^{h}, \\ F(\varphi _{k}^{j,h}) = a(\varphi _{k}^{j,h},\varphi _{k}^{j,h})g_{k}({x}^{j}) \quad &\text{ if }(j,k) \in \mathcal{D}_{\Gamma _{D}}^{h}. \end{array} \right.& & {}\\ \end{array}$$

Observe that common supports of basis functions $\varphi _{m}^{i,h}$ and $\varphi _{k}^{j,h}$ with $(i,m) \in \mathcal{D}_{0}^{h}$, $(j,k) \in \mathcal{D}_{\Gamma _{D}}^{h}$ do not have a contribution to the entries in A. They only contribute to the loadvector f. This leads to the sparse linear system

$$\displaystyle{ A\mathbf{u} = \mathbf{f} }$$

(10)

with the symmetric positive definite (spd) stiffness matrix A. The symmetry of A is inherited from the symmetry of a( ⋅,  ⋅), while the positive definiteness is a direct consequence of the coercivity of the bilinear form. Note that in the construction above, the essential DOFs in $\mathcal{D}_{\Gamma _{D}}^{h}$ are not eliminated from the linear system. Degrees of freedom related to Dirichlet boundary values are contained in A by strictly imposing $u_{i}^{h} = g_{i}^{h}$ on $\Gamma _{D_{i}},i \in \{ 1,2,3\}$, i.e., any row in A related to a Dirichlet DOFs contains only a nonzero entry on the diagonal. The remaining Dirichlet DOFs in the columns of A vanish as they are transferred to the right-hand side in (10).

3 The Two-Level Method

We are interested in solving the linear system (10) iteratively and the construction of preconditioners for A which remove the ill-conditioning due to (i) mesh parameters and (ii) variations in the PDE coefficients. Such preconditioners involve corrections on local subdomains as well as a global solve on a coarse grid. Specifically, we apply the two-level additive Schwarz preconditioner, which we shortly recapitulate in this section. Furthermore, we precisely introduce the fine and coarse triangulation on a structured grid. The structure is such that the coarse elements can be formed by an agglomeration of fine elements.

3.1 Two-Level Additive Schwarz

Let {Ω _i , i = 1, …, N} be an overlapping covering of $\bar{\Omega }$, such that Ω _i  ∖ ∂ Ω is open for i ∈ { 1, …, N}. Ω _i  ∖ ∂ Ω is assumed to consist of the interior of a union of fine elements $\tau \in \mathcal{T}_{h}$. The part of Ω _i which is overlapped with its neighbors should be of uniform width δ _i  > 0. We define the local submatrices of A corresponding to the subdomains $\Omega _{i} \subset \bar{ \Omega }$ by $A_{i} = R_{i}AR_{i}^{T}$. Roughly speaking, R _i is the restriction matrix of a vector defined in Ω to Ω _i (more details can be found in [24]).

Additionally to the local subdomains, we need a coarse triangulation $\mathcal{T}_{H}$ of $\bar{\Omega }$ into coarse elements. Here, we assume again that each coarse element T consists of a union of fine elements $\tau \in \mathcal{T}_{h}$ of the fine triangulation. We will construct a coarse basis whose values are determined on the coarse grid points in $\bar{\Omega }$ (excluding coarse DOFs on the Dirichlet boundaries), given by the vertices of the coarse elements in $\mathcal{T}_{H}$. The coarse space $\mathcal{V}_{0}^{H} \subset \mathcal{V}_{0}^{h}$ is constructed such that it is a subspace of the vector-field of piecewise linear basis functions on the fine grid. That is, each function ${\phi }^{H} \in \mathcal{V}_{0}^{H}$ omits a complete representation w.r.t. the fine-scale basis. The restriction matrix R _H describes a mapping from the coarse to the fine space and contains the corresponding coefficient vectors of the coarse basis functions by row. The coarse grid stiffness matrix is then defined as the Galerkin product $A_{H} := R_{H}AR_{H}^{T}$. With these tools in hand, the action of the two-level additive Schwarz preconditioner M _AS ^− 1 is defined implicitly by

$$\displaystyle\begin{array}{rcl} M_{\mathrm{AS}}^{-1} = R_{ H}^{T}A_{ H}^{-1}R_{ H} +\sum _{ i=1}^{N}R_{ i}^{T}A_{ i}^{-1}R_{ i}.& & {}\\ \end{array}$$

In the following, we write A ₀ and R ₀ instead of A _H and R _H . The following two theorems are basic results in domain decomposition theory. Proofs can be found in [24]. Theorem 1 also states a reasonable assumption on the choice of the overlapping subdomains.

Theorem 1 (Finite Covering). 

The set of overlapping subspaces {Ω _i ,i = 1,…,N} can be colored by N _C ≤ N different colors such that if two subspaces Ω _i and Ω _j have the same color, it holds Ω _i ∩ Ω _j = ∅. For the smallest possible number N _C , the largest eigenvalue of the two-level preconditioned Schwarz linear system is bounded by

$$\displaystyle{ \lambda _{\mathrm{max}}(M_{\mathrm{AS}}^{-1}A) \leq N_{ C} + 1 }$$

Theorem 2 (Stable Decomposition). 

Suppose there exists a number C ₁ ≥ 1, such that for every $\boldsymbol{{u}}^{h} \in \mathcal{V}_{0}^{h}$ , there exists a decomposition $\boldsymbol{{u}}^{h} =\sum _{ i=0}^{N}\boldsymbol{{u}}^{i}$ with $\boldsymbol{{u}}^{0} \in \mathcal{V}_{0}^{H}$ and $\boldsymbol{{u}}^{i} \in {\mathcal{V}}^{h}(\Omega _{i})$ , i = 1,…,N such that

$$\displaystyle{ \sum _{i=0}^{N}a(\boldsymbol{{u}}^{i},\boldsymbol{{u}}^{i}) \leq C_{ 1}^{2}\,a(\boldsymbol{{u}}^{h},\boldsymbol{{u}}^{h}). }$$

Then, it holds

$$\displaystyle{ \lambda _{\mathrm{min}}(M_{\mathrm{AS}}^{-1}A) \geq C_{ 1}^{-2}. }$$

As we can see, the choice of the coarse space has no influence on the estimate of the largest eigenvalue of the preconditioned system. However, it is crucial for obtaining a small constant C ₁ in the estimate of the smallest eigenvalue in Theorem 2. We continue with introducing the structured fine and coarse grid.

3.2 Fine and Coarse Triangulation

3.2.1 The Fine Grid

Let the domain Ω be a 3D cube, i.e., $\bar{\Omega } = [0,L_{x}] \times [0,L_{y}] \times [0,L_{z}] \subset {\mathbb{R}}^{3}$ for given $L_{x},L_{y},L_{z} > 0$. The fine grid is constructed from an initial voxel structure which is further decomposed into tetrahedral finite elements [21]. More precisely, the set of grid points in $\bar{\Omega }$ is given by

$$\displaystyle\begin{array}{rcl} & & \bar{\Sigma }_{h} :=\big\{ {(x_{i},y_{j},z_{k})}^{T}\: :\: x_{ i} = ih_{x},\,y_{j} = jh_{y},\,z_{k} = kh_{z}, \\ & & \qquad \quad i = 0,\ldots,n_{x},\,j = 0,\ldots,n_{y},\,k = 0,\ldots,n_{z}\big\} {}\end{array}$$

(11)

where $n_{x} = L_{x}/h_{x},$, $n_{y} = L_{y}/h_{y},$ $n_{z} = L_{z}/h_{z}$. For simplicity, we may assume that $L := L_{x} = L_{y} = L_{z}$ and $h := h_{x} = h_{y} = h_{z}$, and thus $n_{h} := n_{x} = n_{y} = n_{z}$. That is, the fine grid can be decomposed into $n_{h} \times n_{h} \times n_{h}$ grid blocks of size h ×h ×h. We denote such a fine grid block by $\square _{h}^{ijk},$ 1 ≤ i, j, k ≤ n _h . The triple (i, j, k) uniquely determines the position of the corresponding block in $\bar{\Omega }$. Each block is further decomposed into 5 tetrahedral elements. The decomposition depends on the position of the specific grid block. To identify them, we introduce the notation ${s}^{ijk} := s(\square _{h}^{ijk}) = i + j + k$. We distinguish between two different decompositions, depending on the value of s ^{i j k}18mu { mod}. We follow the numbering of the 8 vertices of a block as given in Fig. 1. If s ^{i j k} is even (see Fig. 1a), block $\square _{h}^{ijk}$ is decomposed into 5 tetrahedra which are defined by the set of their four vertices within each block,

$$\displaystyle\begin{array}{rcl} \big\{\{1,2,4,6\},\{1,3,4,7\},\{1,5,6,7\},\{4,6,7,8\},\{1,4,6,7\}\big\}.& & {}\\ \end{array}$$

If s ^{i j k} is odd (see Fig. 1b), the decomposition of block $\square _{h}^{ijk}$ into the tetrahedra is done such that their vertices are given by

$$\displaystyle\begin{array}{rcl} \big\{\{1,2,3,5\},\{2,3,4,8\},\{2,5,6,8\},\{3,5,7,8\},\{2,3,5,8\}\big\}.& & {}\\ \end{array}$$

With the given decomposition, a conformal triangulation of Ω into tetrahedral elements is uniquely defined, we denote this partition by $\mathcal{T}_{h}$. $\mathcal{T}_{h}$ is referred to as the fine grid triangulation, whereas the coarse grid triangulation, introduced in the following, is denoted by $\mathcal{T}_{H}$.

Fig. 1

Decomposition of grid block into 5 tetrahedral elements

3.2.2 Forming Coarse Elements by Agglomeration

The coarse elements $T \in \mathcal{T}_{H}$ are constructed by an agglomeration of the fine elements. We construct a set of agglomerated elements $\{T\} = \mathcal{T}_{H}$ such that each $T =\bigcup _{ i=1}^{n_{T}}\tau _{i}$, $\tau _{i} \in \mathcal{T}_{h}$ is a simply connected union of fine grid elements. Thus, for any two $\tau _{i},\tau _{j} \in \mathcal{T}_{h}$, there exists a connecting path of elements $\{\tau _{k}\}_{k} \subset T$ beginning in τ _i and ending in τ _j . Each fine grid element τ should belong to exactly one agglomerated element T. Due to the regular structure of the underlying grid, the agglomeration is done such that the coarse elements have the same tetrahedral form as the fine elements, and automatically form a coarser grid of equal structure. The table AE_element (cf. [27]) is used to store the fine elements which belong to an agglomerated (coarse) element. Given the fine triangulation $\mathcal{T}_{h}$ of Ω, the agglomeration process proceeds as follows:

• 1. Given a fixed coarsening-factor c _f , compute the position of the coarse nodes to decompose the domain Ω into imaginary coarse blocks $\square _{H}^{ijk}$ of size H ×H ×H, where $1 \leq i,j,k \leq n_{H} \in \mathbb{N}$, $n_{H} = n_{h}/c_{f}$, and H = c _f h.

• 2. Build the CB_element table: For each $\tau \in \mathcal{T}_{h}$, obtain the position of τ in Ω and assign it to the belonging coarse block _H ^{i j k}.

• 3. Build the AE_element table: For each coarse block $\square _{H}^{ijk} \subset \bar{ \Omega }$ and each τ ⊂ _H ^{i j k} (CB_element), measure the position of τ in _H ^{i j k} and assign it to the belonging coarse tetrahedron.

In step 3 of the agglomeration process, we use again the mapping ${s}^{ijk} := s(\square _{H}^{ijk}) = i + j + k$ to identify the coarse tetrahedra into which a given block is decomposed. This partition automatically defines a set of coarse grid points, given by the vertices of the coarse elements. It remains to show that a straightforward decomposition of a coarse block into coarse tetrahedral elements leads to the same result as forming the coarse tetrahedra by agglomerating fine elements. The proof of this concept is given in Lemma 1.

Lemma 1 (Mesh Alignment). 

The meshes $\mathcal{T}_{h}$ and $\mathcal{T}_{H}$ are aligned.

Proof.

Let $\square _{h}^{ijk} \subset \bar{ \Omega }$ be a fine grid block. We introduce the four vectors ${n}^{1} = {(-1,1,1)}^{T},\,{n}^{2} = {(1,-1,1)}^{T},\,{n}^{3} = {(1,1,-1)}^{T}$, and ${n}^{4} = {(-1,-1,-1)}^{T}$. If s _h ^{i j k} is odd (see Fig. 1a), they form the inner normal vectors on the four faces of the tetrahedron which is centered in the interior of the block _h ^{i j k}; if s _h ^{i j k} is even (see Fig. 1b), they form the outer normal vectors on the faces of the tetrahedron in the center of _h ^{i j k}. The given normal vectors n ^ℓ, ℓ = 1, …, 4, characterize the four families of planes $\Xi _{\ell}^{h} :=\big\{ {n}^{\ell} \cdot x = 2zh,\,x \in \bar{ \Omega },\,z \in \mathbb{Z}\big\}$. We want to show that these families induce the splitting of any fine voxel $\square _{h}^{ijk} \subset \bar{ \Omega }$ into the five tetrahedra by their intersection with _h ^{i j k}. To see this, let us first assume that s _h ^{i j k} is odd, that is, the fine voxel is decomposed according to the splitting in Fig. 1a. We denote by $\mathcal{F}_{\ell}(\square _{h}^{ijk})$ the face of the tetrahedra in _h ^{i j k} which is normal to n ^ℓ, ℓ ∈ { 1, …, 4}. Moreover, let x ^{i ′ j ′ k ′} = (i ′ h, j ′ h, k ′ h)^T be the vertex of _h ^{i j k} which is closest to the origin (node 1 in Fig. 1a), that is, $(i^{\prime},j^{\prime},k^{\prime}) = (i - 1,j - 1,k - 1)$. Then it holds indeed that $({n}^{\ell} \cdot x)/h {\rm mod}\,\,2 = (i^{\prime} + j^{\prime} + k^{\prime}) {\rm mod}\,\,2$ for all $x \in \mathcal{F}_{\ell}(\square _{h}^{ijk})$, ℓ = 1, …, 4. Since $i + j + k$ is odd by assumption, we have that $(i^{\prime} + j^{\prime} + k^{\prime}) {\rm mod}\,\,2 = 0$. Hence, it holds $\mathcal{F}_{\ell}(\square _{h}^{ijk}) = \Xi _{\ell}^{h} \cap \square _{h}^{ijk}$, and the decomposition of _h ^{i j k} into tetrahedra is induced by the families ${\Xi }^{\ell}$, ℓ = 1, …, 4. Assuming now that s _h ^{i j k} is even, the fine voxel is decomposed according to the splitting in Fig. 1b. For ℓ = 1, …, 4, let $\mathcal{F}_{\ell}(\square _{h}^{ijk})$ denote the angular face of the tetrahedra in _h ^{i j k} to which n ^ℓ is normal. We denote by x ^{i j k} = (i h, j h, k h)^T the vertex of _h ^{i j k} which is most distant form the origin (node 8 in Fig. 1b). It holds for all $x \in \mathcal{F}_{\ell}(\square _{h}^{ijk})$, ℓ ∈ { 1, …, 4}, that $({n}^{\ell} \cdot x)/h {\rm mod}\,\,2 = (i + j + k) {\rm mod}\,\,2$. Since $i + j + k$ is even by assumption, we conclude again that $\Xi _{\ell}^{h} \cap \square _{h}^{ijk}$ defines the decomposition of _h ^{i j k} into tetrahedra. The same arguments can be applied to show that for ℓ ∈ { 1, …, 4}, the sets $\Xi _{\ell}^{H} :=\big\{ {n}^{\ell} \cdot x = 2zH,\,x \in \bar{ \Omega },\,z \in \mathbb{Z}\big\}$ form the family of planes which induce the decomposition of the coarse blocks into tetrahedra. Since the families $\Xi _{\ell}^{h}$ and $\Xi _{\ell}^{H}$, ℓ = 1, …, 4, intersect in the origin and due to H = c _f h for some $c_{f} \in \mathbb{N}$, the coarse grid family of planes is a subset of the fine ones which shows that fine and coarse meshes are aligned.

3.3 Abstract Multiscale Coarse Space

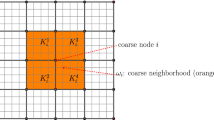
In Sect. 3.2, we introduced the structured fine and coarse mesh which will be used in our numerical tests. For the construction of the basis functions, the assumptions on $\mathcal{T}_{H}$ can be slightly weakened. In general, we require that $\mathcal{T}_{H}$ is a conforming tetrahedral coarse mesh, such that each $T \in \mathcal{T}_{H}$ consists of a union of fine elements $\tau \in \mathcal{T}_{h}$ with $\mathcal{T}_{H}$ being shape-regular w.r.t. $H :=\max _{T\in \mathcal{T}_{H}}H_{T}$, H _T  = diam(T). Let $\bar{\Sigma }_{H}$ be the set of coarse nodes of $\mathcal{T}_{H}$ in $\bar{\Omega }$. We denote the index set of coarse nodes of $\mathcal{T}_{H}$ on $\bar{\Omega }$ by $\bar{\mathcal{N}}_{H}$. For each coarse grid point ${x}^{p} \in \bar{ \Sigma }_{H}$, we introduce the set

$$\displaystyle{ \omega _{p} := \text{interior}\left (\bigcup _{\{T\in \mathcal{T}_{H}:{x}^{p}\in T\}}T\right ), }$$

(12)

given by the interior of the union of coarse elements which are attached to node x ^p. We will construct a coarse vector-valued basis whose values are determined on the coarse grid points in $\bar{\Omega }$, given by the vertices of the coarse elements in $\mathcal{T}_{H}$. The coarse basis functions are constructed such that they can be represented w.r.t. the vector-field of piecewise linear basis functions ${\mathcal{V}}^{h}$ on the fine grid. Given the coarse basis functions, we introduce the coarse space in abstract form by

$$\displaystyle{ {\mathcal{V}}^{H} := \text{span}\big\{\phi _{ m}^{p,\mathrm{H}},p \in \bar{\mathcal{N}}_{ H},\,m = 1,2,3\big\}. }$$

(13)

This space can be viewed as a generalization of the space of piecewise linear vector-fields on $\mathcal{T}_{H}$. The coarse basis functions are constructed to have the following form.

Assumption 3.1 (Abstract Coarse Space). 

(C1) $\quad \phi _{m}^{p,\mathrm{H}} = {(\phi _{m1}^{p,\mathrm{H}},\phi _{m2}^{p,\mathrm{H}},\phi _{m3}^{p,\mathrm{H}})}^{T}$, $\phi _{mk}^{p,\mathrm{H}}({x}^{q}) =\delta _{pq}\,\delta _{mk},\;p \in \bar{\mathcal{N}}_{H},\,k \in \{ 1,2,3\}$,

(C2) $\quad \mathrm{supp}\:\phi _{m}^{p,\mathrm{H}} \subset \bar{\omega }_{p}$,

(C3) $\quad \|\phi _{mk}^{p,\mathrm{H}}\|_{{L}^{\infty }(\Omega )} \leq C,\:k \in \{ 1,2,3\}$,

(C4) $\quad \sum _{p\in \bar{\mathcal{N}}_{H}}\phi _{mk}^{p,\mathrm{H}}(x) =\delta _{mk},\;x \in \bar{ \Omega },\:k \in \{ 1,2,3\}$,

Assumption (C4) implies that the rigid body translations are globally contained in the coarse space. Additionally, we might require that the coarse space also contains the rigid body rotations, and thus,

• (C5) $\mathcal{R}\mathcal{B}\mathcal{M}\subset \mathrm{ span}\big\{\phi _{m}^{p,\mathrm{H}}\, :\, p \in \bar{\mathcal{N}}_{H},\:k \in \{ 1,2,3\}\big\}$,

where the space $\mathcal{R}\mathcal{B}\mathcal{M}$ of rigid body modes in $\bar{\Omega }$ is defined by

$$\displaystyle{ \mathcal{R}\mathcal{B}\mathcal{M} =\{ \mathbf{\textit{v}} \in {[{L}^{2}(\bar{\Omega })]}^{3}\, :\, \mathbf{\textit{v}} = \mathbf{\textit{a}} + \mathbf{\textit{b}} \times x,\,\mathbf{\textit{a}},\mathbf{\textit{b}} \in {\mathbb{R}}^{3},x \in \bar{ \Omega }\}. }$$

It is shown in [4] that multiscale finite element coarse spaces for linear elasticity with vector-valued linear boundary conditions contain the rigid body modes globally. Although the construction of the energy-minimizing coarse space which we present in Sect. 4 does not guarantee that the three rigid body rotations are globally contained in the coarse space, the numerical tests in Sect. 5 validate the robustness of the method for problems where the boundary conditions prohibit global rotations, i.e., $\mathrm{meas}(\Gamma _{D_{i}}) > c_{0}$, i = 1, 2, 3, with c ₀ > 0.

4 Energy Minimization for the Elasticity System

In this section we present the construction of the energy-minimizing coarse space for the 3D system of linear elasticity. We start with the definition of the basis and the corresponding coarse space ${\mathcal{V}}^{H} = {\mathcal{V}}^{\mathrm{EMin}}$, followed by some details of its properties. Furthermore, we provide a precise definition of the interpolation operators which are determined by the coarse basis and show how these basis functions can be computed efficiently.

4.1 The Energy-Minimizing Coarse Space

We construct the energy-minimizing coarse space ${\mathcal{V}}^{H}$ on $\mathcal{T}_{H}$ according to assumption 3.1. We denote by $\vert \,\cdot \,\vert _{a,\Omega } := a{(\cdot,\cdot )}^{1/2}$ the semi-norm on [H ¹(Ω)]³, induced by the bilinear form in (5). For m = 1, 2, 3 and each $p \in \bar{\mathcal{N}}_{H}$, we construct a basis function

$$\displaystyle\begin{array}{rcl} \phi _{m}^{p,\mathrm{EMin}} :\omega _{ p} \rightarrow {\mathbb{R}}^{3}.& & {}\\ \end{array}$$

Ensuring that the three translations are exactly contained in the coarse space, the construction is done separately for m ∈ { 1, 2, 3}, such that

$$\displaystyle\begin{array}{rcl} \sum _{p\in \bar{\mathcal{N}}_{H}}& & \vert \phi _{m}^{p,\mathrm{EMin}}\vert _{ a,\Omega }^{2}\; \rightarrow \;\min {}\end{array}$$

(14)

$$\displaystyle\begin{array}{rcl} \mbox{ subject to}\quad \sum _{p\in \bar{\mathcal{N}}_{H}}& & \phi _{mk}^{p,\mathrm{EMin}} =\delta _{ mk}\quad k = 1,2,3,\;\mbox{ in }\Omega.{}\end{array}$$

(15)

Thus, the basis is constructed such that the coarse basis preserves the three translations exactly. The rigid body rotations are contained only approximately. The basis satisfies Assumption 3.1 (C1)–(C4). Hence, the given functions are linearly independent and the energy-minimizing coarse space is defined as in (13). Note that we define the subspace $\mathcal{V}_{0}^{\mathrm{EMin}} \subset {\mathcal{V}}^{\mathrm{EMin}}$ as the subspace which contains only basis functions which correspond to coarse nodes ${x}^{p} \in \bar{ \Sigma }_{H}$ which do not touch the global Dirichlet boundary. Furthermore, we exclude any fine grid DOFs on the boundary $\Gamma _{D_{i}},i = 1,2,3$ when constructing the interpolation operator. More details are given in Sect. 4.3. In the following, we give a constructive proof for the existence and uniqueness of the solution of the minimization problem in (14) and (15). Therefore, we denote by $\bar{A} \in {\mathbb{R}}^{n_{d}\times n_{d}}$ the global stiffness matrix where no essential boundary conditions are applied. The entries of $\bar{A}$ are determined by (9). Furthermore, we denote by R _p the matrix describing the restriction to ω _p of a vector which corresponds to DOFs on ${\mathcal{V}}^{h}$ in $\bar{\Omega }$. The principal submatrix of $\bar{A}$ is then given by $\bar{A}_{p} = R_{p}\bar{A}R_{p}^{T}$. Note that $\bar{A}_{p}$ is non-singular for any suitable R _p . Furthermore, let ${\mathbf{1}}^{m} \in {\mathbb{R}}^{n_{d}}$ be the coefficient vector which represents a rigid body translation in the component m ∈ { 1, 2, 3} in terms of the fine-scale basis of ${\mathcal{V}}^{h}$.

Theorem 3.

The solution of the minimization problem in (14) and (15) on the space ${\mathcal{V}}^{h}$ is given by

$$\displaystyle\begin{array}{rcl} \Phi _{m}^{p,\mathrm{EMin}} = R_{ p}^{T}\bar{A}_{ p}^{-1}R_{ p}\Lambda _{m},& &{}\end{array}$$

(16)

where $\Lambda _{m} \in {\mathbb{R}}^{n_{d}}$ is the vector of Lagrange multipliers, which satisfies

$$\displaystyle\begin{array}{rcl} \sum _{p\in \bar{\mathcal{N}}_{H}}R_{p}^{T}\bar{A}_{ p}^{-1}R_{ p}\Lambda _{m} ={ \mathbf{1}}^{m}.& & {}\\ \end{array}$$

Proof.

The minimization problem couples the quadratic objective function in (14) with linear constraints, given in (15). Introducing the Lagrange multiplier Λ _m , a solution can be found by the extrema of the quadratic Lagrange functional

$$\displaystyle\begin{array}{rcl} \mathcal{L}_{m}\Big(\big\{\Phi _{m}^{p,\mathrm{EMin}}\big\},\Lambda _{ m}\Big) = \frac{1} {2}\sum _{p\in \bar{\mathcal{N}}_{H}}{\Phi _{m}^{p,\mathrm{EMin}}}^{T}\,\bar{A}\,\Phi _{ m}^{p,\mathrm{EMin}}\;-\;{\Lambda _{ m}}^{T}\bigg(\sum _{ p\in \bar{\mathcal{N}}_{H}}\Phi _{m}^{p,\mathrm{EMin}}-{\mathbf{1}}^{m}\bigg).& & {}\\ \end{array}$$

We enforce an additional constraint on the support of the basis functions by substituting $\Phi _{m}^{p,\mathrm{EMin}} = R_{p}^{T}\hat{\Phi }_{m}^{p,\mathrm{EMin}}$. The vector $\hat{\Phi }_{m}^{p,\mathrm{EMin}}$ can be considered as the local representation of Φ _m ^p, EMin on its support ω _p w.r.t. the basis of ${\mathcal{V}}^{h}(\omega _{p})$. To find the critical point of this functional, we impose $\nabla _{\Lambda _{m}}\mathcal{L}_{m} = 0$ and $\nabla _{\hat{\Phi }_{m}^{p,\mathrm{EMin}}}\mathcal{L}_{m} = 0$, which results in the saddle point problem

$$\displaystyle\begin{array}{rcl} \bar{A}_{p}\hat{\Phi }_{m}^{p,\mathrm{EMin}} - R_{ p}\Lambda _{m}& =& 0\quad \forall \:p \in \bar{\mathcal{N}}_{H},{}\end{array}$$

(17)

$$\displaystyle\begin{array}{rcl} \sum _{p\in \bar{\mathcal{N}}_{H}}R_{p}^{T}\hat{\Phi }_{ m}^{p,\mathrm{EMin}} -{\mathbf{1}}^{m}& =& 0.{}\end{array}$$

(18)

From (17), we conclude

$$\displaystyle\begin{array}{rcl} \hat{\Phi }_{m}^{p,\mathrm{EMin}} =\bar{ A}_{ p}^{-1}R_{ p}\Lambda _{m}\quad \forall \:p \in \bar{\mathcal{N}}_{H}.& &{}\end{array}$$

(19)

Substituting (19) into (18) yields

$$\displaystyle\begin{array}{rcl}{ \mathbf{1}}^{m} =\sum _{ p\in \bar{\mathcal{N}}_{H}}R_{p}^{T}\bar{A}_{ p}^{-1}R_{ p}\Lambda _{m}.& & {}\\ \end{array}$$

We introduce $L :=\sum _{p\in \bar{\mathcal{N}}_{H}}R_{p}^{T}\bar{A}_{p}^{-1}R_{p}$ and obtain for m ∈ { 1, 2, 3},

$$\displaystyle\begin{array}{rcl} \Lambda _{m} = {L}^{-1}{\mathbf{1}}^{m}.& &{}\end{array}$$

(20)

Thus, to compute the basis, we have to solve the global Lagrange multiplier system in (20) for each m ∈ { 1, 2, 3} and solve local subproblems in (19) to compute the particular basis functions.

4.2 Properties of the Energy-Minimizing Coarse Space

As we can conclude from the construction, the coarse space contains the three rigid body translations globally in $\bar{\Omega }$. However, it is not clear how well this coarse space approximates the set of rigid body rotations. The rotations are, in general, not exactly contained in ${\mathcal{V}}^{H}$. The energy-minimizing construction of the basis functions allows quite general supports, and the method is easily applicable to unstructured meshes. If we denote by $\omega _{p}^{\mathrm{int}} :=\{ x \in \omega _{p} : x\not\in \omega _{q}$ for any q≠p} the subset of ω _p which is not overlapped with the support of any other basis function, it is clear that rigid body rotations cannot be globally contained in the coarse space as long as meas(ω _p ^int) > 0. Thus, to ensure that the presented construction of the coarse space allows an adequate approximation of the rigid body rotations, a necessary requirement needs to be stated on the supports of the basis functions. Defining the coarse basis functions on the coarse mesh $\mathcal{T}_{H}$ as introduced before yields large overlaps in the supports of neighboring basis functions. It holds $\omega _{p}^{\mathrm{int}} =\{ {x}^{p}\}$, and thus, we obtain meas(ω _p ^int) = 0. However, this requirement is not sufficient to ensure that all the rigid body rotations are preserved exactly by the coarse space.

An important property, showing the multiscale character of the presented energy-minimizing coarse space, is summarized in the following. We show that the Lagrange multipliers Λ _m , m = 1, 2, 3, are supported on the coarse element boundaries, and thus, the energy-minimizing basis functions are given by a discrete PDE-harmonic extension of local boundary data. Before proving this statement, we introduce the following notation. For $T \in \mathcal{T}_{H}$, let

$$\displaystyle\begin{array}{rcl} \text{range}(T) := \bigcap _{p\in \bar{\mathcal{N}}_{H}(T)}\text{range}(R_{p}^{T})& & {}\\ \end{array}$$

be the set of vectors in ${\mathbb{R}}^{n_{d}}$ which correspond to functions in ${\mathcal{V}}^{h}$ which are supported in the interior of T. We show that the Lagrange multiplier Λ _m , m = 1, 2, 3, has nonzero values only in a set which is complementary to $\{\text{range}(T) : T \in \mathcal{T}_{H}\}$. The nonzero entries correspond to fine basis functions which are supported on the boundaries of the coarse elements $T \in \mathcal{T}_{H}$.

Lemma 2.

Let m ∈{ 1,2,3} be fixed and let $\Lambda _{m} = {L}^{-1}{\mathbf{1}}^{m}$ . Then for each $T \in \mathcal{T}_{H}$ , we have

$$ \displaystyle\begin{array}{rcl} {\xi }^{T}\,\Lambda _{ m} = 0\quad \forall \xi \in \mathrm{ range}(T).& & {}\\ \end{array}$$

Proof.

Let $n_{T} = \#\{p \in \bar{\mathcal{N}}_{H}(T)\}$ be the number of vertices of T. For m ∈ { 1, 2, 3}, it holds

$$\displaystyle\begin{array}{rcl} \sum _{p\in \bar{\mathcal{N}}_{H}(T)}\Phi _{m}^{p,\mathrm{EMin}} ={ \mathbf{1}}^{m}\;\;\,\text{on }T.& & {}\\ \end{array}$$

For each ξ ∈ range(T), let $\hat{\xi }_{p} := R_{p}\xi$, $p \in \bar{\mathcal{N}}_{H}(T)$ be the local representation of ξ in ω _p  ⊂ Ω. Note that it also holds $R_{p}^{T}\hat{\xi }_{p} =\xi$ since ξ _p is supported in range(R _p ^T) by assumption. We have by (17),

$$\displaystyle\begin{array}{rcl} n{_{T}\:\xi }^{T}\,\Lambda _{ m} =\sum _{p\in \bar{\mathcal{N}}_{H}(T)}\hat{\xi }_{p}^{T}R_{ p}\Lambda _{m} =\sum _{p\in \bar{\mathcal{N}}_{H}(T)}\hat{\xi }_{p}^{T}\bar{A}_{ p}\hat{\Phi }_{m}^{p,\mathrm{EMin}} {=\xi }^{T}\bar{A}{\mathbf{1}}^{m} = 0,& & {}\\ \end{array}$$

where we used ξ ∈ range(T) twice. The last equality follows since ${\mathbf{1}}^{m} \in \text{Ker}(\bar{A})$.

This shows that the basis functions are locally PDE-harmonic, a well-known property (cf. [31]) of the energy-minimizing basis. From the solution of the Lagrange multiplier system, optimal boundary conditions for the local basis functions are extracted on $\{\partial T,T \in \mathcal{T}_{H}\}$. It is obvious that the energy-minimizing basis functions are continuous along the boundaries of the coarse elements and lead to a conforming coarse space.

4.3 The Interpolation Operator

In the following, we construct the interpolation operator which is given by the energy-minimizing coarse space. Let us first summarize some notations. The number of grid points in $\bar{\Omega }$ on the fine grid is denoted by n _p ; the number of grid points on the coarse grid is denoted by N _p . To each grid point, fine or coarse, we associate a vector-field $u = {(u_{1},u_{2},u_{3})}^{T} :\bar{ \Omega } \rightarrow {\mathbb{R}}^{3}$ of displacements. We denote the corresponding components u _i , i = 1, 2, 3 of the vector-field by unknowns. The number of fine and coarse DOFs on the fine and coarse triangulation (in $\bar{\Omega }$) is given by n _d  = 3n _p , N _d  = 3N _p , respectively. Furthermore, for β ∈ { h, H}, the set ${\mathcal{D}}^{\beta } = {\mathcal{D}}^{\beta }(\bar{\Omega })$ denotes the index set of fine (β = h), respectively, coarse (β = H) DOFs of ${\mathcal{V}}^{\beta }$. For any subset $W \subset \bar{ \Omega }$, let ${\mathcal{D}}^{\beta }(W) \subset {\mathcal{D}}^{\beta }(\bar{\Omega })$ be the restriction of ${\mathcal{D}}^{\beta }$ to the local set of DOFs in W, given in a local numbering. To keep the notation with indices more intuitive for the reader, we use the following convention. To indicate DOFs in ${\mathcal{D}}^{h}$, we use (i, k) or (j, l) to indicate DOFs, while the index (p, m) or (q, r) are used for the indication of a coarse degree of freedom in ${\mathcal{D}}^{H}$. We use the fine-scale representation of a coarse basis function ϕ _m ^p, EMin to define the interpolation operator, respectively, the restriction operator. Each energy-minimizing basis function omits the representation

$$\displaystyle\begin{array}{rcl} \phi _{m}^{p,\mathrm{EMin}} =\sum _{ k=1}^{3}\sum _{ i=1}^{n_{p} }\bar{r}_{(p,m),(i,k)}\varphi _{k}^{i,h}.& &{}\end{array}$$

(21)

This representation defines a matrix $\bar{R} \in {\mathbb{R}}^{N_{d}\times n_{d}}$ which contains the coefficient vectors, representing a coarse basis function in terms of the fine-scale basis, by rows. Note that $\bar{R}$ does not define the final restriction operator used in the additive Schwarz setting. The restriction operator R _H , which we use in the additive Schwarz algorithm is then constructed as a submatrix of $\bar{R}$, which contains only the rows corresponding to coarse basis functions of $\mathcal{V}_{0}^{H}$. Thus, it contains the rows related to coarse basis functions which vanish on the global Dirichlet boundaries $\Gamma _{D_{i}},\,i = 1,2,3$ and do not contain any fine DOFs on the global Dirichlet boundary. Denoting the entries of R _H by (r _{p ′, j ′} ) _{p ′, j ′} , we define

$$\displaystyle\begin{array}{rcl} r_{p^{\prime},j^{\prime}} = \left \{\begin{array}{@{}l@{\quad }l@{}} \bar{R}_{p^{\prime},j^{\prime}}\quad &\text{ if }p^{\prime} \in {\mathcal{D}}^{H}({\Omega }^{{\ast}}),\;\;j^{\prime} \in \mathcal{D}_{ 0}^{h}(\bar{\Omega }), \\ 0 \quad &\text{ if }p^{\prime} \in {\mathcal{D}}^{H}({\Omega }^{{\ast}}),\;\;j^{\prime} \in \mathcal{D}_{\Gamma _{D}}^{h}(\bar{\Omega }), \end{array} \right.& & {}\\ \end{array}$$

where ${\mathcal{D}}^{H}({\Omega }^{{\ast}})$, ${\Omega }^{{\ast}} :=\bar{ \Omega }\setminus ({\cup }^{i}\Gamma _{D_{i}})$ denotes the coarse interior DOFs in Ω ^∗. The matrix representing the interpolation from the coarse space $\mathcal{V}_{0}^{H}$ to the fine space $\mathcal{V}_{0}^{h}$ is simply given by the transposed, R _H ^T. The coarse stiffness matrix can be computed by the Galerkin product ${A}^{H} = R_{H}AR_{H}^{T}$.

5 Numerical Experiments

In this section, we give a series of examples involving binary media, showing the performance of the energy-minimizing preconditioner under variations of the mesh parameters as well as the material coefficients. In addition to that, we measure the approximation error of the energy-minimizing coarse space to a fine-scale solution. In each numerical test, we compare the energy-minimizing coarse space with a standard linear coarse space. We perform our simulations on the domain $\bar{\Omega } = [0,1] \times [0,1] \times [0,L],L > 0$, with fine and coarse mesh as introduced in Sect. 3.2. Dirichlet conditions in the first unknown are given on $\Gamma _{1} =\{ {(x,y,z)}^{T} \in \partial \Omega : x = 0,x = 1\}$, in the second unknown on $\Gamma _{2} =\{ {(x,y,z)}^{T} \in \partial \Omega : y = 0,y = 1\}$, and in the third unknown on $\Gamma _{3} =\{ {(x,y,z)}^{T} \in \partial \Omega : z = 0,z = L\}$. For the numerical tests, we consider different heterogeneous media. First, we assume that the discontinuities are isolated, that is, the material jumps occur only in the interior of coarse elements. Figure 2 shows such a binary medium with one inclusion inside each coarse tetrahedral element.

Fig. 2

Medium 1: binary composite; matrix material and 1 ×1 ×1 inclusions; discretization in 12 ×12 ×12 voxels; each voxel is decomposed in 5 tetrahedra; inclusions lie in the interior of a coarse tetrahedral element; 3D view (left) and 2D projection with fine mesh, showing the position of the inclusions (right)

For a second medium, we do not impose any restriction on the position of the small inclusions. More precisely, we generate a binary medium whose inclusions are identically distributed. An example of such a medium is given in Fig. 3.

Fig. 3

Medium 2: binary composite: discretization in 240 ×240 ×12 voxels; matrix material and 1 ×1 ×1 inclusions identically distributed; 3D view (left) and 2D projection (right)

In the following, we refer to the binary medium where inclusions are isolated in the interior of coarse elements as medium 1, while the medium with identically distributed inclusions is referred to as medium 2. For each medium, the Young’s modulus E as well as Poisson ratio ν for matrix material and inclusions are given in Table 1. The contrast $\Delta _{E} := E_{inc}/E_{mat}$ may vary over several orders of magnitude.

Table 1 Young’s modulus and Poisson ratio of matrix material and inclusions

5.1 Coarse Space Robustness

We choose the overlapping subdomains such that they coincide with the supports $\bar{\omega }_{p}$, $p \in \bar{\mathcal{N}}_{H}$ of the coarse basis functions. Then, $\{\Omega _{i},\,i = 1,\ldots,N\} =\{\omega _{p},\,p \in \bar{\mathcal{N}}_{H}\}$ defines an overlapping covering of $\bar{\Omega }$ with overlap width δ = O(H), often referred to as a generous overlap. We perform tests observing the performance of the two-level additive Schwarz preconditioner using linear and energy-minimizing coarsening. We show condition numbers as well as iteration numbers of the preconditioned conjugate gradient (PCG) algorithm. The stopping criterion is to reduce the preconditioned initial residual by six orders of magnitude, i.e., $\|r\|_{M_{AS}^{-1}} \leq 1{0}^{-6}\|r_{0}\|_{M_{AS}^{-1}}$. For the construction of the energy-minimizing basis functions, the Lagrange multiplier systems are solved using the CG algorithm; the initial residual is reduced by three orders of magnitude. The estimated condition numbers of κ(M _{A S} ^− 1 A) are computed based on the three-term recurrence which is implicitly formed by the coefficients within the PCG algorithm (cf. [18]).

In a first experiment (1), we test the robustness of the method on medium 1 for fixed mesh parameters under the variation of the contrast Δ _E . Tables 2 and 3 show the corresponding condition numbers and iteration numbers having stiff (Δ _E  > 1) and soft (Δ _E  < 1) inclusions. In the former case, robustness is achieved only for the energy-minimizing coarse space, while linear coarsening leads to nonuniform convergence results.

Table 2 Iteration numbers n _{i t} and condition numbers κ(M _{A S} ^− 1 A) for experiment 1; geometry: $1/h \times 1/h \times H/h$, $h = 1/240$, H = 12h; linear and energy-minimizing coarsening for different contrasts Δ _E  ≥ 1

Table 3 Iteration numbers n _{i t} and condition numbers κ(M _{A S} ^− 1 A) for experiment 1; geometry: $1/h \times 1/h \times H/h$, $h = 1/240$, H = 12h; linear and energy-minimizing coarsening for different contrasts Δ _E  ≤ 1

In experiment 2, performed on medium 1, we measure the condition numbers and iteration numbers under variation of the mesh parameters, while the PDE coefficients remain fixed. We observe similar results as in experiment 1.

Table 4 Iteration numbers n _{i t} and condition numbers κ(M _{A S} ^− 1 A) for experiment 2; geometry: $1/h \times 1/h \times H/h$; H = 12h; linear and energy-minimizing coarsening for different h; contrast: Δ _E  = 10⁶

Table 4 shows the condition numbers for linear and energy-minimizing coarsening. For the linear coarse space, the condition number shows a linear dependence on the number of subdomains, while the condition number for energy-minimizing coarsening is uniformly bounded.

In the experiment above, we obtained coefficient independent convergence rates of the energy-minimizing coarse space on medium 1. In a second part, we test the performance of the method on medium 2, where the small inclusions are identically distributed. This is what we see in Tables 5 and 6 for experiment 1 on medium 2: For fixed mesh parameters under the variation of the contrast Δ _E , they show the corresponding condition numbers and iteration numbers having stiff (Δ _E  > 1) and soft (Δ _E  < 1) inclusions. Robustness for the linear coarse space is only achieved in the later case where soft inclusions are considered. For stiff inclusions, the linear coarsening strategy leads to iteration numbers and condition numbers which strongly depend on the contrast in the medium. The energy-minimizing coarse space is fully robust w.r.t. coefficient variations.

Table 5 Iteration numbers n _{i t} and condition numbers κ(M _{A S} ^− 1 A) for experiment 1 on medium 2; geometry: $1/h \times 1/h \times H/h$, $h = 1/240$, H = 12h; linear and energy-minimizing coarsening for different contrasts Δ _E  ≥ 1

Table 6 Iteration numbers n _{i t} and condition numbers κ(M _{A S} ^− 1 A) for experiment 1 on medium 2; geometry: $1/h \times 1/h \times H/h$, $h = 1/240$, H = 12h; linear and energy-minimizing coarsening for different contrasts Δ _E  ≤ 1

Now, we perform experiment 2 on medium 2 and measure the condition numbers and iteration numbers under variation of the mesh parameters and fixed PDE coefficients. Table 7 shows iteration and condition numbers for linear and energy-minimizing coarsening. Mesh independent bounds are achieved for the energy-minimizing coarse space, while for the linear coarse space, iteration numbers as well as condition numbers grow with the number of subdomains.

Table 7 Iteration numbers n _{i t} and condition numbers κ(M _{A S} ^− 1 A) for experiment 2 on medium 2; geometry: $1/h\times 1/h\times H/h$; H = 12h; linear and energy-minimizing coarsening for different h; contrast: Δ _E  = 10⁶

5.2 Coarse Space Approximation

In a second set of experiments, we test the approximation properties of the energy-minimizing coarse space. The domain $\bar{\Omega } = [0,1] \times [0,1] \times [0,L]$ contains a binary medium with small inclusions. Again, we distinguish between medium 1 (Fig. 2: inclusions in the interior of each coarse element) and medium 2 (Fig. 3: identically distributed inclusions). We solve the linear system $-\text{div}\boldsymbol{\sigma }(\boldsymbol{u}) =\boldsymbol{ f}$ in $\bar{\Omega } \setminus \Gamma _{D}$ with a constant volume force $\boldsymbol{f} = {(1,1,0)}^{T}$ in the x- and y-component. Homogeneous Dirichlet and Neumann boundary conditions are applied on the boundary ∂ Ω.

Let $\boldsymbol{{u}}^{h}$ denote the approximate solution on a fine mesh $\mathcal{T}_{h}$. With the bilinear form defined in (6) and the space $\mathcal{V}_{0}^{h}$ of piecewise linear vector-valued basis functions as defined in (7), it holds $a(\boldsymbol{{u}}^{h},\boldsymbol{{v}}^{h}) = F(\boldsymbol{{v}}^{h})$ $\forall \boldsymbol{{v}}^{h} \in \mathcal{V}_{0}^{h}$. This formulation leads to the linear system A u ^h = f ^h. Let $\mathcal{V}_{0}^{H}$ be the space of energy-minimizing basis functions on the coarse triangulation $\mathcal{T}_{H}$ which vanish on the Dirichlet boundary Γ _i , i = 1, 2, 3 (see Sect. 4.3). The energy-minimizing solution is given by $\boldsymbol{{u}}^{\mathrm{EMin}} \in \mathcal{V}_{0}^{H}$, such that $a(\boldsymbol{{u}}^{\mathrm{EMin}},\boldsymbol{{v}}^{H}) = F(\boldsymbol{{v}}^{H})$ $\forall \boldsymbol{{v}}^{H} \in \mathcal{V}_{0}^{H}$. Using the fine-scale representation of an energy-minimizing basis function as defined in (21), the equivalent linear system reads A _H u ^H = f ^H. Here, $A_{H} = R_{H}AR_{H}^{T}$ is the coarse stiffness matrix, ${\mathbf{f}}^{H} = R_{H}{\mathbf{f}}^{h}$, and ${\mathbf{u}}^{\mathrm{EMin}} = R_{H}^{T}{\mathbf{u}}^{H}$ is the vector whose entries define the fine-scale representation of $\boldsymbol{{u}}^{\mathrm{EMin}}$ in terms of the basis of $\mathcal{V}_{0}^{h}$.

For fixed mesh parameters h and H, under the variation of the contrast Δ _E , Tables 8 and 9 show the relative approximation errors $\|{\mathbf{u}}^{h} -{\mathbf{u}}^{c}\|$ in l ₂ and in the “energy”-norm for linear (c=Lin) and energy-minimizing (c=EMin) coarse space for medium 1 and medium 2, respectively.

Table 8 Approximation of fine-scale solution by linear and energy-minimizing coarse space for medium 1; geometry: $1/h \times 1/h \times H/h$, $h = 1/120$, H = 12h

The fine solution u ^h is computed approximately within the PCG algorithm by reducing the initial preconditioned residual by 12 orders of magnitude. The coarse solution u ^H is computed exactly by a sparse direct solve of the coarse linear system. For both media, the energy-minimizing coarse space gives stable approximation errors, only slightly varying with the contrast. The linear coarse space only shows a poor approximation of the fine-scale solution for high contrasts Δ _E  ≫ 1. The explanation is that for Δ _E  ≫ 1, the fine-scale solution is contained in a space which is nearly A-orthogonal to the space spanned by the linear coarse basis functions. Note that this is in agreement with the results presented in Table 4, where the condition number grows almost linearly with the number of subdomains.

Table 9 Approximation of fine-scale solution by linear and energy-minimizing coarse space for medium 2; geometry: $1/h \times 1/h \times H/h$, $h = 1/120$, H = 12h

We also observe from Tables 8 and 9 that for soft inclusions (Δ _E  ≤ 1), the approximation error is smaller by the linear coarse space than by the energy-minimizing coarse space. The latter is due to the circumstance that the vector-valued energy-minimizing basis is, even for homogeneous coefficients, not piecewise linear on the coarse triangulation. It is known that the shape of the energy-minimizing basis functions is in general mesh dependent, e.g., for the discretization of the scalar Poisson problem on a regular mesh in 2D, an energy-minimizing basis is observed to be piecewise linear in [29] (see also [25]). However, for the vector-valued problem considered here with the mesh as in Sect. 3.2, the vector-valued energy-minimizing basis is not piecewise linear on the coarse mesh for reasonable mesh sizes H > h > 0. The latter also implies that the rigid body rotations are only approximated globally.

We can summarize the numerical results obtained in this section as follows. The energy-minimizing construction allows a low-energy approximation of the basis functions, independently of the Young’s modulus of the inclusions. We considered different media where the discontinuities are either isolated in the interior of coarse elements or randomly distributed. Using an energy-minimizing coarse space, our experiments show uniform condition number bounds w.r.t. both, coefficient variations in the Young’s modulus and the mesh size. In contrast, robustness is not achieved with the linear coarse space. The linear basis function cannot capture the smallest eigenvalues associated to the discontinuities in the material parameters. The energy of the basis function strongly depends on the Young’s modulus of the inclusion. As the experiments show, no uniform iteration number or condition number bounds are achieved. This observation holds for all considered media.

6 Discussion

We constructed energy-minimizing coarse spaces for microstructural problems in 3D linear elasticity. The coarse basis is such that it contains the rigid body translations exactly, while the rigid body rotations are preserved approximately. We used the coarse basis for the construction of two-level overlapping domain decomposition preconditioners in the additive version and performed experiments on binary media. For the class of problems which excludes pure traction boundary values, the results show uniform condition number bounds w.r.t. both, coefficient variations in the Young’s modulus and the mesh size. Furthermore, we tested the fine-scale approximation of the energy-minimizing coarse space and observed uniform results, independent of the contrast in the composite material.