Keywords

1 Introduction

Anisotropy arises in many applications such as heat transfer, electrostatics, magnetostatics, flow in porous media (see, e.g., [12]), and many other areas in science and engineering. For instance, in porous media a strong anisotropy of conductivity can be due to fractures, where the direction of dominating anisotropy is determined by the orientation of the fractures. The presence of fracture corridors can form long and tiny highly anisotropic channels. The network of channels is resolved at the finest mesh. The ratio of anisotropy in the channels can be of 5–6 orders of magnitude. Such kind of high-contrast and high-frequency anisotropic problems are still beyond the limits of robust algebraic multilevel preconditioning. At the end of the paper we experimentally study the robustness of algebraic multilevel iteration (AMLI) methods on model problems with channels.

In this paper we consider the elliptic boundary value problem

$$\displaystyle{ \begin{array}{rcll} Lu \equiv -\nabla \cdot \left (\mathbf{a}(x)\nabla u(x)\right )& =&f(x)&\mathrm{in}\quad \Omega, \\ u& =&0 &\mathrm{on}\quad \Gamma _{D}, \\ (\mathbf{a}(x)\nabla u(x)) \cdot \mathbf{n}& =&0 &\mathrm{on}\quad \Gamma _{N},\end{array} }$$
(1)

where Ω is a polygonal domain in \({\mathbb{R}}^{2}\), f(x) is a given function in L 2(Ω), the coefficient matrix a(x) is symmetric positive definite and uniformly bounded in Ω, and n is the outward unit vector normal to the boundary Γ = ∂ Ω, where \(\Gamma =\bar{ \Gamma }_{D} \cup \bar{ \Gamma }_{N}\). We assume also that the elements of the diffusion coefficient matrix a(x) are piecewise smooth functions on \(\bar{\Omega }\).

The weak formulation of the problem reads as follows: Given f ∈ L 2(Ω), find \(u \in \mathcal{V}\equiv H_{D}^{1}(\Omega ) =\{ v \in {H}^{1}(\Omega ) : v = 0\) on Γ D }, satisfying

$$\displaystyle{ \begin{array}{rcl} \mathcal{A}(u,v)& = &(f,v) :=\int _{\Omega }f(x)v(x)dx\quad \forall v \in H_{D}^{1}(\Omega ),\ \ \mbox{ where} \\ \mathcal{A}(u,v)& :=&\int _{\Omega }\mathbf{a}(x)\nabla u(x) \cdot \nabla v(x)dx.\end{array} }$$
(2)

We assume that the domain Ω is discretized by the triangulation \(\mathcal{T}_{0}\) which is obtained by a proper number of ℓ uniform refinement steps of a given coarser triangulation \(\mathcal{T}_{\ell}\). We suppose also that \(\mathcal{T}_{\ell}\) is aligned with the discontinuities of a(x) so that over each element \(T \in \mathcal{T}_{\ell}\), the entries of the coefficient matrix (diffusion tensor) a(x) are smooth functions. This assumption is mainly needed for theoretical considerations and is disregarded in the computational examples presented in Sect. 5.

The variational problem (2) is discretized using the finite element method (FEM), i.e., the continuous space \(\mathcal{V}\) is replaced by a finite-dimensional space \(\mathcal{V}_{h}\). Then the finite element formulation is the following: find \(u_{h} \in \mathcal{V}_{h}\), satisfying

$$\displaystyle{ \begin{array}{rcl} \mathcal{A}_{h}(u_{h},v_{h})& = &(f,v_{h})\quad \forall v_{h} \in \mathcal{V}_{h},\ \ \mbox{ where} \\ \mathcal{A}_{h}(u_{h},v_{h})& :=&\sum _{e\in \mathcal{T}_{h}}\int _{e}\mathbf{a}(e)\nabla u_{h} \cdot \nabla v_{h}dx.\end{array} }$$
(3)

We note that the element-by-element additive setting of \(\mathcal{A}_{h}(u_{h},v_{h})\) is applicable to both conforming and nonconforming FEM discretizations.

Here a(e) is a piecewise constant symmetric positive definite matrix, defined by the integral averaged values of a(x) over each element from the coarsest triangulation \(\mathcal{T}_{\ell}\), i.e.,

$$\displaystyle{\mathbf{a}(e) = \frac{1} {\vert e\vert }\int _{e}\mathbf{a}(x)dx,\qquad \forall e \in \mathcal{T}_{\ell}.}$$

In this way strong coefficient jumps across the boundaries between adjacent finite elements from \(\mathcal{T}_{\ell}\) are allowed.

The resulting FEM linear system of equations reads as

$$\displaystyle{ A_{h}\mathbf{u}_{h} = \mathbf{f}_{h}, }$$
(4)

with A h and f h being the corresponding global stiffness matrix and global right-hand side and h being the discretization (mesh size) parameter for the underlying triangulation \(\mathcal{T}_{0} = \mathcal{T}_{h}\) of Ω.

The stiffness matrix is symmetric, positive definite, and sparse. The sparsity property means that the number of nonzero entries in each row/column is uniformly bounded with respect to the number of the unknowns \(N = O({h}^{-2})\).

In the case of advanced real-life applications (and in the context of this paper), A h could be very large, that is, N is of order 106 up to 109. For such problems, the advantages of the iterative solution methods increase quickly with the size of the problem. The conjugate gradient (CG) method invented 60 years ago by Hestenes and Stiefel [15] is the fastest basic iterative scheme for such kind of problems. It provides a sequence of best approximations to the exact solution in the Krylov subspaces generated by the stiffness matrix. The number of CG iterations n i t C G depends on the spectral condition number of the matrix \(\kappa (A_{h})\). In the case of two-dimensional FEM elliptic systems, κ(A h ) = O(N) and \(n_{it}^{CG} = O(\sqrt{\kappa (A_{h } )}) = O({N}^{1/2})\). The aim of the preconditioning is to relax the mesh-size dependency of the iterations’ count. The following estimate characterizes the preconditioned conjugate gradient (PCG) method:

$$\displaystyle{ n_{it}^{PCG} \leq \frac{1} {2}\sqrt{\kappa \left ({B}^{-1 } A_{h } \right )}\ln \left (\frac{2} {\epsilon } \right ) + 1, }$$
(5)

where B is a symmetric and positive definite preconditioning matrix (also called preconditioner) and n i t P C G is the related number of PCG iterations sufficient to get a prescribed relative accuracy of ε > 0. The general strategy for efficient preconditioning simply follows from the estimate (5). It reads as follows: (i) The condition number of the preconditioned matrix is much less than the original one, i.e., \(\kappa \left ({B}^{-1}A\right ) <<\kappa (A)\); (ii) The computational complexity to solve the preconditioned system is much smaller than the complexity to solve the original problem, i.e., \(\mathcal{N}\left ({B}^{-1}\mathbf{v}\right ) << \mathcal{N}\left ({A}^{-1}\mathbf{v}\right )\). One could say that these conditions are contradictory. Indeed, when \(\kappa \left ({B}^{-1}A\right )\) tends to its minimal value, the preconditioner should tend to A and \(\mathcal{N}\left ({B}^{-1}\mathbf{v}\right ) \rightarrow \mathcal{N}\left ({A}^{-1}\mathbf{v}\right )\). Fortunately, such kind of reasonings are too pessimistic according to the recent state of the art of the preconditioning algorithms.

Definition 1.

The preconditioner is called optimal if the related PCG algorithm has optimal order of computational complexity \({\mathcal{N}}^{PCG} = O(N)\), that is, if \(\kappa \left ({B}^{-1}A\right ) = O(1)\) and \(\mathcal{N}\left ({B}^{-1}\mathbf{v}\right ) = O(N)\).

The existence of optimal iterative solution methods has been an open question before the early 1960s. Now, the optimal order multigrid and multilevel methods are well known in the community of researchers and engineers dealing with large-scale scientific computations and their advanced applications.

This paper is devoted to some recent achievements in the development of robust preconditioners for FEM elliptic systems belonging to the class of multilevel block factorization methods of the AMLI type. It provides a survey on robust AMLI methods for anisotropic elliptic problems, covering a significantly enriched state of the art in this field as compared to the related earlier paper [21].

Based on a sequence of nested finite element meshes, the AMLI methods were originally introduced by Axelsson and Vassilevski in [6] for the case of isotropic elliptic problems discretized by conforming linear finite elements. They are optimal with respect to the mesh parameter (problem size) and can handle straightforwardly arbitrary coefficient jumps on the coarsest mesh. The originally introduced AMLI methods are based on a hierarchical basis (HB) splitting of the stiffness matrix and a recursive application of HB two-level preconditioning. Since then the AMLI theory has evolved beyond the HB framework; see, e.g., [2, 16, 17, 25]. The construction of AMLI is always based on a recursive approximate (two-by-two) block factorization. Under rather general assumptions, the HB AMLI methods are robust in the case of linear (conforming and nonconforming) elements which does not hold for higher-order FEM. Here we present complimentary some very recent results for quadratic elements where the approximate block factorization on each level exploits an additive Schur complement approximation (ASCA), thereby avoiding the HB splitting; see [18, 20] for further details. The resulting (nonlinear) AMLI is very robust with respect to anisotropy that does not have to be aligned with the grid if it is complemented by a proper block-relaxation process. The efficiency of the interplay between these two components can be enhanced if one applies the ASCA and the block smoother on specific, augmented coarse grids (cf. Sect. 4 and [20]).

In our presentation we follow the mathematical concept of high anisotropy or orthotropy introduced in [12]. For any x ∈ Ω, we denote the eigenvalues 0 < μ 1(x) ≤ μ 2(x) and eigenvectors q j (x), j = 1, 2 (written as vector columns) of the coefficient (diffusion) matrix a(x). Then

$$\displaystyle{\mathbf{a}(x) =\mu _{1}(x)\,\mathbf{q}_{1}(x)\mathbf{q}_{1}{(x)}^{T} +\mu _{ 2}(x)\mathbf{q}_{2}(x)\mathbf{q}_{2}{(x)}^{T}.}$$

In this notation, obviously,

$$\displaystyle{\mu _{1}(x){\mathbf{q}}^{T}\mathbf{q} \leq {\mathbf{q}}^{T}<Emphasis Type="Bold">\text{a}</Emphasis>(x)\mathbf{q} \leq \mu _{ 2}(x){\mathbf{q}}^{T}\mathbf{q},\qquad \forall \mathbf{q} \in \mathrm{{ IR}}^{2}.}$$

Depending on the variation of the eigenvalues μ j (x), we may have various scenarios of highly anisotropic materials. The aspect ratio of coefficient anisotropy is introduced as

$$\displaystyle{\kappa (\mathbf{a}) =\max _{x}\frac{\mu _{2}(x)} {\mu _{1}(x)} =\max _{e}\frac{\mu _{2}(e)} {\mu _{1}(e)}.}$$

The direction of dominating anisotropy is determined by the eigenvector q 2(x).

The following simple examples illustrate the general mathematical concept of high anisotropy, where η ≫ 1: (a) In the case of orthotropic problem we have, e.g., \(\mathbf{a} = [1,0;0,\eta ]\). Then μ 1 = 1, μ 2 = η, consequently κ = η, and q 2 = [0, 1]T, i.e., the direction of dominating anisotropy is along the coordinate y-axis. (b) Let \(\mathbf{a} = [1+\eta,\eta -1;\eta -1,1+\eta ]\). Then μ 1 = 2, μ 2 = 2η, and κ = η. The direction of dominating anisotropy is determined by \(\mathbf{q}_{2} = {[1+\eta,1-\eta ]}^{T}/\sqrt{2(1 {+\eta }^{2 } )}\) where \(\mathbf{q}_{2} \rightarrow {[1,-1]}^{T}/\sqrt{2}\) when \(\eta \rightarrow \infty \).

In what follows later, two representative variants of the coefficient a(e) are considered:

  1. (a)

    The isotropic/orthotropic problem associated with

    $$\displaystyle{ \mathbf{a}(e) = \left [\begin{array}{cc} 1\;&\;0\,\,\\ 0\; & \;\varepsilon \,\,\end{array} \right ]. }$$
    (6)
  2. (b)

    The rotated diffusion problem associated with

    $$\displaystyle{ \mathbf{a}(e) = \left [\begin{array}{cc} \cos \theta &\ -\sin \theta \\ \sin \theta & \ \cos \theta \end{array} \right ]\left [\begin{array}{cc} 1&\\ &\ \varepsilon \end{array} \right ]{\left [\begin{array}{cc} \cos \theta &\ -\sin \theta \\ \sin \theta & \ \cos \theta \end{array} \right ]}^{T}, }$$
    (7)

    where ɛ > 0 and θ = θ e is a piecewise constant angle.

The setting of (7) allows to study problems with a given fixed or varying direction (angle) of anisotropy. Nongrid-aligned anisotropy in general is much more difficult to handle than orthotropy (or grid-aligned anisotropy) thus far.

The remainder of the paper is organized as follows. The theoretical background of the AMLI methods is presented next. Together with the classical formulations, Sect. 2 contains the main convergence results for linear and nonlinear AMLI methods. A complete set of robustness results for anisotropic linear FEM systems is presented in Sect. 3, where the HB AMLI method is considered. The estimates are robust with respect to coefficient and mesh anisotropy for both conforming and nonconforming elements. Section 4 is devoted to preconditioning of quadratic FEM systems. It starts with a few comments on HB splittings, which are not robust in this case. Then some very recent results are presented on an AMLI method based on ASCA. In the latter method two additional stabilizing components are incorporated, namely, augmented coarse grids and a global (block) smoothing. The numerical results in Sect. 5 demonstrate the potential of this approach for complicated and more realistic problems which are still beyond the scope of rigorous theory. The survey concludes with final remarks given in Sect. 6.

2 Algebraic Multilevel Methods

The AMLI methods have originally been introduced and studied in a multiplicative form; see [6, 7]. The presentation in this section follows [27]. Consider the linear system (4) where A h  = : A (0) is the fine-grid stiffness matrix. We assume that the standard components of a multigrid (MG) method, that is, the kth-level matrices A (k), smoothers M (k), and coarse-to-fine interpolation matrices P (k), have been defined and that the Galerkin relation \({A}^{(k+1)} ={ {P}^{(k)}}^{T}{A}^{(k)}{P}^{(k)}\) holds for \(k = 0,1,\ldots,\ell-1\).

The AMLI preconditioner B (k) is defined recursively via its inverse. On the coarsest level ℓ we set

$$\displaystyle{{ {B}^{(\ell)}}^{-1} ={ {A}^{(\ell)}}^{-1}. }$$
(8)

Then, assuming that \({{B}^{(k+1)}}^{-1}\) has already been defined for k + 1 ≤ ℓ, one constructs B (k)  − 1 in two steps. First, an approximation Z (k + 1) of A (k + 1) is defined by

$$\displaystyle{ {Z}^{(k+1)} := {A}^{(k+1)}{\left (I - {p}^{(k)}({{B}^{(k+1)}}^{-1}{A}^{(k+1)})\right )}^{-1}, }$$
(9)

where p (k) denotes a polynomial of degree ν = ν k , satisfying

$$\displaystyle{ {p}^{(k)}(0) = 1. }$$
(10)

It is important to note that in view of (10) Eq. (9) is equivalent to

$$\displaystyle{{ B_{\nu }^{(k+1)}}^{-1} :={ {Z}^{(k+1)}}^{-1} ={ {B}^{(k+1)}}^{-1}{q}^{(k)}({A}^{(k+1)}{{B}^{(k+1)}}^{-1}) }$$
(11)

where the polynomial q (k) is given by

$$\displaystyle{ {q}^{(k)}(x) = \frac{1 - {p}^{(k)}(x)} {x} }$$
(12)

showing that the application of \({B_{\nu }^{(k+1)}}^{-1} ={ {Z}^{(k+1)}}^{-1}\) requires only applications of A (k + 1) and \({{B}^{(k+1)}}^{-1}\) but not of the inverse of the coarse-level matrix A (k + 1) (as this is the case in the exact two-level method). Second, the AMLI preconditioner B (k) at level k is defined by

$$\displaystyle\begin{array}{rcl}{{ B}^{(k)}}^{-1}& :=&{ \mbox{ $\bar{{M}}^{(k)}$}}^{-1} \\ & +& \left (I -{ {M}^{(k)}}^{-T}{A}^{(k)}\right ){P}^{(k)}{B_{\nu }^{(k+1)}}^{-1}{{P}^{(k)}}^{T}\left (I - {A}^{(k)}{{M}^{(k)}}^{-1}\right ){}\end{array}$$
(13)

where \({B_{\nu }^{(k+1)}}^{-1}\) is given by (11) and \(\bar{{M}}^{(k)}\) denotes the symmetrized smoother at level k, that is,

$$\displaystyle{{ \mbox{ $\bar{{M}}^{(k)}$}}^{-1} ={ {M}^{(k)}}^{-1} +{ {M}^{(k)}}^{-T} -{ {M}^{(k)}}^{-T}{A}^{(k)}{{M}^{(k)}}^{-1}. }$$
(14)

We observe that the multilevel preconditioner defined via (11) and (13) is getting close to an exact two-level method when the polynomial (12) approximates well 1 ∕ x in which case \({B_{\nu }^{(k+1)}}^{-1} \approx { {A}^{(k+1)}}^{-1}\). In order to obtain an efficient multilevel method, the action of \({B_{\nu }^{(k+1)}}^{-1}\) on an arbitrary vector should be much cheaper to compute (in terms of the number of arithmetic operations) than the action of \({{A}^{(k+1)}}^{-1}\). Optimal order solution algorithms typically require the arithmetic work for one application of \({B_{\nu }^{(k+1)}}^{-1}\) to be of the order \(\mathcal{O}(N_{k+1})\) where N k + 1 denotes the number of unknowns at level k + 1.

In the classical AMLI method, as it has been introduced in [6, 7], the coarse-grid matrix A (k + 1) is retrieved from a (two-level) hierarchical basis transformation of A (k). The preconditioner \(\tilde{{B}}^{(k)}\) (in its multiplicative variant) then is defined by

$$\displaystyle\begin{array}{rcl}{ (\tilde{{B}}^{(k)})}^{-1}& =& \left [\begin{array}{cc} {B_{11}^{(k)}}^{-1} & 0 \\ 0 &0 \end{array} \right ] + \left [\begin{array}{c} -{ B_{11}^{(k)}}^{-1}\hat{A}_{ 12}^{(k)} \\ I \end{array} \right ]{B_{\nu }^{(k+1)}}^{-1}\left [-\hat{A}_{ 21}^{(k)}{B_{ 11}^{(k)}}^{-1},I\right ] {}\\ & =& \left [\begin{array}{cc} {B_{11}^{(k)}}^{-1} & 0 \\ 0 &0 \end{array} \right ] + {(\tilde{{L}}^{(k)})}^{T}\left [\begin{array}{c} 0 \\ I \end{array} \right ]{B_{\nu }^{(k+1)}}^{-1}\left [0,I\right ]\,\tilde{{L}}^{(k)} {}\\ \end{array}$$

where

$$\displaystyle{\tilde{{L}}^{(k)} = \left [\begin{array}{cc} I - A_{11}^{(k)}{B_{11}^{(k)}}^{-1} & 0 \\ -\hat{ A}_{21}^{(k)}{B_{11}^{(k)}}^{-1} & I \end{array} \right ].}$$

Writing the equation above in the form (13), one finds that

$$\displaystyle{{{ M}^{(k)}}^{-1} ={ {M}^{(k)}}^{-T} = \left [\begin{array}{cc} {B_{11}^{(k)}}^{-1} & 0 \\ 0 &0 \end{array} \right ] }$$
(15)

is a smoother that acts only on the hierarchical complement of the coarse space, where B 11 (k) is a proper approximation of A 11 (k). The corresponding symmetrized smoother then is given by

$$\displaystyle{{ \mbox{ $\bar{{M}}^{(k)}$}}^{-1} = \left [\begin{array}{cc} 2{B_{11}^{(k)}}^{-1} -{ B_{11}^{(k)}}^{-1}A_{11}^{(k)}{B_{11}^{(k)}}^{-1} & 0 \\ 0 &0 \end{array} \right ], }$$
(16)

and P (k) takes the simple form

$$\displaystyle{{ P}^{(k)} = \left [\begin{array}{c} 0 \\ I \end{array} \right ]. }$$
(17)

The latter is due to the fact that the (classical) AMLI preconditioner is defined for the hierarchical two-level matrix \(\hat{{A}}^{(k)}\), which contains the coarse-level matrix as a sub-matrix in its lower right block, i.e.,

$$\displaystyle{{A}^{(k+1)} = \left [0,I\right ]\hat{{A}}^{(k)}\left [\begin{array}{c} 0 \\ I \end{array} \right ].}$$

This, however, is in agreement with the Galerkin relation \({A}^{(k+1)} ={ {P}^{(k)}}^{T}{A}^{(k)}{P}^{(k)}\) as is used in (algebraic) multigrid methods.

The convergence theory of the classical AMLI methods (in the multiplicative variant) is based on the spectral equivalence of the k-th level hierarchical matrix \(\hat{{A}}^{(k)}\) and its (multiplicative) two-level preconditioner

$$\displaystyle{ \hat{{B}}^{(k)} = \left [\begin{array}{ll} B_{11}^{(k)} & 0 \\ \hat{A}_{21}^{(k)} & \hat{A}_{22}^{(k)} \end{array} \right ]\left [\begin{array}{ll} I &{B_{11}^{(k)}}^{-1}\hat{A}_{ 12}^{(k)} \\ 0 &I \end{array} \right ], }$$
(18)

that is,

$$\displaystyle{ \hat{\vartheta }_{k}\hat{{B}}^{(k)} \leq \hat{ {A}}^{(k)} \leq \hat{ {B}}^{(k)},\quad k =\ell -1,\ldots,0. }$$
(19)

Note that if \(B_{11}^{(k)} = A_{11}^{(k)}\) then \(\hat{\vartheta }_{k} = 1 -\gamma _{k}^{2}\) where γ k is the constant in the strengthened Cauchy–Bunyakovsky–Schwarz (CBS) inequality associated with the hierarchical matrix \(\hat{{A}}^{(k)}\). The subscript of γ is usually skipped when uniform estimate of the CBS constant with respect to the refinement level k is assumed (see, e.g., (35)). We conclude that the polynomial acceleration techniques described in this paper can be exploited in various implementations of AMLI preconditioners, which can be viewed as inexact two-level methods. The performance of these methods crucially depends on the particular choice of the polynomial q (k) in Eq. (11) and on two-level estimates like (19) or (31).

2.1 Condition Number Estimates for AMLI Preconditioners

Let us first summarize the main result of the analysis of the AMLI-cycle multigrid preconditioner as presented in [27].

The AMLI-cycle is a ν-fold multigrid (MG) cycle with variable ν = ν k . In the following, let ν ≥ 1 and k 0 ≥ 1 be two fixed integers. We set \(\nu _{sk_{0}} =\nu > 1\) for s = 1, 2, 3, … and ν k  = 1 otherwise. That is, we let

$$\displaystyle{{ B_{\nu }^{((s+1)k_{0})}}^{-1} ={ {B}^{((s+1)k_{0})}}^{-1}q_{\nu -1}({A}^{((s+1)k_{0})}{{B}^{((s+1)k_{0})}}^{-1}) }$$
(20)

if \(k + 1 = (s + 1)k_{0}\), and

$$\displaystyle{{ B_{\nu }^{(k+1)}}^{-1} ={ {B}^{(k+1)}}^{-1} }$$
(21)

otherwise. Then for the AMLI-cycle MG preconditioner B (k) defined in (13), the following result can be proven (cf. Theorem 5.29 in [27]).

Theorem 1 ([27]). 

With a proper choice of the parameters k 0 and ν, and for a proper choice of the polynomial \({p}^{(k)}(x) = p_{\nu }(x)\) satisfying (10),the condition number of \({{B}^{(k)}}^{-1}{A}^{(k)}\) can be uniformly bounded provided the V-cycle preconditioners with bounded level difference ℓ − k ≤ k 0 have uniformly bounded condition numbers \(K_{MG}^{\ell\mapsto k}\).

More specifically, for a fixed k 0 , and \(\nu > \sqrt{K_{MG }^{\ell\mapsto k}}\) , we can choose α > 0 such that

$$\displaystyle{\alpha K_{MG}^{\ell\mapsto k} + K_{ MG}^{\ell\mapsto k} \frac{{(1-\alpha )}^{\nu }} {{\left [\sum _{j=1}^{\nu }{(1 + \sqrt{\alpha })}^{\nu -j}{(1 -\sqrt{\alpha })}^{j-1}\right ]}^{2}} \leq 1}$$

and employ the polynomial

$$\displaystyle{p_{\nu }(x) = \frac{1 + T_{\nu }\left (\frac{1+\alpha -2x} {1-\alpha } \right )} {1 + T_{\nu }\left (\frac{1+\alpha } {1-\alpha }\right )} }$$

where T ν is the Chebyshev polynomial of the first kind of degree ν.

Alternatively, we can choose α ∈ (0,1) such that

$$\displaystyle{\alpha K_{MG}^{\ell\mapsto k} + K_{ MG}^{\ell\mapsto k} \frac{{(1-\alpha )}^{\nu }} {\sum _{j=1}^{\nu }{(1-\alpha )}^{j-1}} \leq 1}$$

and use the polynomial \(p_{\nu }(x) = {(1 - x)}^{\nu }\) to define \(q_{\nu -1}(x) := (1 - p_{\nu }(x))/x\) in (20).

Then for both choices of the polynomial p ν (respectively q ν−1 ), the resulting AMLI-cycle preconditioner B = B (0) , as defined via (8)–(13),is spectrally equivalent to the matrix A = A (0) , and the following estimate holds

$$\displaystyle{{ \mathbf{v}}^{T}A\mathbf{v} \leq {\mathbf{v}}^{T}B\mathbf{v} \leq \frac{1} {\alpha }{ \mathbf{v}}^{T}A\mathbf{v}\quad \forall \mathbf{v}, }$$
(22)

with the respective α ∈ (0,1] depending on the choice of the polynomial.

2.2 Nonlinear AMLI-Cycle Method

Consider a sequence of two-by-two block matrices

$$\displaystyle{{ A}^{(k)} = \left [\begin{array}{ll} A_{11}^{(k)} & 0 \\ A_{21}^{(k)} & {S}^{(k)} \end{array} \right ]\left [\begin{array}{ll} I &{A_{11}^{(k)}}^{-1}A_{ 12}^{(k)} \\ 0 &I \end{array} \right ] = \left [\begin{array}{ll} A_{11}^{(k)} & A_{12}^{(k)} \\ A_{21}^{(k)} & {S}^{(k)} + A_{21}^{(k)}{A_{11}^{(k)}}^{-1}A_{12}^{(k)} \end{array} \right ] }$$
(23)

associated with a (nested) sequence of meshes \(\mathcal{T}_{k}\), k = 0, 1, 2, …, ℓ, where \(\mathcal{T}_{\ell}\) denotes the coarsest mesh (and A (k) could also be in hierarchical basis). Let S (k) be the Schur complement in the exact block factorization (23) of A (k). Moreover, the following abstract (linear) multiplicative two-level preconditioner

$$\displaystyle{ \bar{{B}}^{(k)} = \left [\begin{array}{ll} B_{11}^{(k)} & 0 \\ A_{21}^{(k)} & {Q}^{(k)} \end{array} \right ]\left [\begin{array}{ll} I &{B_{11}^{(k)}}^{-1}A_{ 12}^{(k)} \\ 0 &I \end{array} \right ] = \left [\begin{array}{ll} B_{11}^{(k)} & A_{12}^{(k)} \\ A_{21}^{(k)} & {Q}^{(k)} + A_{21}^{(k)}{B_{11}^{(k)}}^{-1}A_{12}^{(k)} \end{array} \right ] }$$
(24)

to A (k) is defined at levels \(k = 0,1,2,\ldots,\ell-1\). Here B 11 (k) is a preconditioner to A 11 (k) and Q (k) is a sparse approximation of S (k). In order to relate the two sequences \(({A}^{(k)})_{k=0,1,2,\ldots,\ell-1}\) and \((\bar{{B}}^{(k)})_{k=0,1,2,\ldots,\ell-1}\) to each other, one sets

$$\displaystyle{ {A}^{(0)} := A_{ h} = A, }$$
(25)

where A h is the stiffness matrix in (4), and defines

$$\displaystyle{ {A}^{(k+1)} := {Q}^{(k)},\quad k = 0,1,2,\ldots,\ell-1. }$$
(26)

Next the nonlinear AMLI-cycle preconditioner \({B}^{(k)}[\cdot ] :\mathrm{{ IR}}^{N_{k}}\mapsto \mathrm{{IR}}^{N_{k}}\) for \(k =\ell -1,\ldots,0\) is defined recursively by

$$\displaystyle{{ {B}^{(k)}}^{-1}[\mathbf{y}] := {U}^{(k)}{D}^{(k)}[{L}^{(k)}\mathbf{y}], }$$
(27)

where

$$\displaystyle{{ L}^{(k)} := \left [\begin{array}{cc} I &0 \\ - A_{21}^{(k)}{B_{11}^{(k)}}^{-1} & I \end{array} \right ], }$$
(28)

\({U}^{(k)} ={ {L}^{(k)}}^{T}\), and

$$\displaystyle{{ D}^{(k)}[\mathbf{z}] = \left [\begin{array}{c} {B_{11}^{(k)}}^{-1}\mathbf{z}_{ 1} \\ {{Z}^{(k+1)}}^{-1}[\mathbf{z}_{2}] \end{array} \right ]. }$$
(29)

The (nonlinear) mapping \({{Z}^{(k+1)}}^{-1}[\cdot ]\) is defined by

$$\displaystyle{ \begin{array}{rcl} {{Z}^{(\ell)}}^{-1}[\cdot ]& \: = &{{A}^{(\ell)}}^{-1}, \\ {{Z}^{(k)}}^{-1}[\cdot ]& :=&{{B}^{(k)}}^{-1}[\cdot ]\quad \mbox{ if }\nu = 1\mbox{ and }k <\ell, \\ {{Z}^{(k)}}^{-1}[\cdot ]& :=&{B_{\nu }^{(k)}}^{-1}[\cdot ]\quad \mbox{ if }\nu > 1\mbox{ and }k <\ell, \end{array} }$$
(30)

with

$$\displaystyle{{B_{\nu }^{(k)}}^{-1}[\mathbf{d}] := \mathbf{x}_{ (\nu )}}$$

where \(\mathbf{x}_{(\nu )}\) is the ν-th iterate obtained when applying the generalized conjugate gradient (GCG) algorithm (see [8]) to the linear system \({A}^{(k)}\mathbf{x} = \mathbf{d}\) using B (k)[ ⋅] as a preconditioner and starting with the initial guess \(\mathbf{x}_{(0)} = \mathbf{0}\). The vector \(\boldsymbol{\nu }= {(\nu _{1},\nu _{2},\ldots,\nu _{\ell-1})}^{T}\) specifies how many inner GCG iterations are performed at each of the levels \(k =\ell -1,\ldots,1\), and \(\nu _{0} = m_{\max }\) denotes the maximum number of orthogonal search directions at level 0. Typically the algorithm is restarted after every m max iterations. If a fixed number ν of inner GCG-type iterations is performed at every intermediate level, i.e., ν k  = ν for \(k =\ell -1,\ldots,1\), the method is referred to as (nonlinear) ν-fold W-cycle AMLI method.

Next the main convergence result from [16] is presented.

Denoting by x (i) the i-th iterate generated by the nonlinear AMLI method, the goal is to derive a bound for the error reduction factor in A norm. This can be done by assuming, for example, that the two-level preconditioners (24) and the matrices (23) are spectrally equivalent, i.e.,

$$\displaystyle{ \underline{\vartheta }_{k}\bar{{B}}^{(k)} \leq {A}^{(k)} \leq \overline{\vartheta }_{ k}\bar{{B}}^{(k)},\quad k =\ell -1,\ldots,0. }$$
(31)

A slightly different approach to analyze the nonlinear AMLI-cycle method is based on the assumption that all fixed-length V-cycle multilevel methods from any coarse-level k + k 0 to level k with exact solution at level k + k 0 are uniformly convergent in k with an error reduction factor \(\delta _{k_{0}} \in [0,1)\); see [26, 27]. Both approaches, however, are based on the idea to estimate the deviation of the nonlinear preconditioner B (k)[ ⋅] from an SPD matrix \(\bar{{B}}^{(k)}\).

The following theorem (see [16, 18]) summarizes the main convergence result.

Theorem 2 ([16]). 

Consider the linear system \({A}^{(0)}\mathbf{x} ={ \mathbf{d}}^{(0)}\) where A (0) is an SPD stiffness matrix, and let x (i) be the sequence of iterates generated by the nonlinear AMLI algorithm. Further, assume that the approximation property (31) holds and let \(\vartheta :=\max _{0\leq k<\ell}\overline{\vartheta }_{k}/\underline{\vartheta }_{k}\). If ν, the number of inner GCG iterations at every coarse level (except level ℓ where \({{Z}^{(\ell)}}^{-1}[\cdot ] ={ {A}^{(\ell)}}^{-1}\)) is chosen such that

$$\displaystyle{ \delta (\nu )\text{:} ={ \left (1 - \frac{4\vartheta {(1-\epsilon )}^{2}} {{(1 +\vartheta -2\epsilon {+\vartheta \epsilon }^{2})}^{2}}\right )}^{\nu /2} \leq \epsilon }$$
(32)

for some positive ε < 1 then

$$\displaystyle{ \frac{\Vert \mathbf{x} -\mathbf{x}_{(i+1)}\Vert _{{A}^{(0)}}} {\Vert \mathbf{x} -\mathbf{x}_{(i)}\Vert _{{A}^{(0)}}} \leq \sqrt{1 - \frac{4\vartheta {(1-\epsilon )}^{2 } } {{(1 +\vartheta -2\epsilon {+\vartheta \epsilon }^{2})}^{2}}} =\delta (1) =:\delta < 1. }$$
(33)

Remark 1.

Note that the relative condition number \(\kappa ({{Q}^{(k)}}^{-1}{S}^{(k)})\) affects the approximation property (31). In the simplest case in which the multiplicative two-level preconditioner (24) is considered under the assumption \(B_{11}^{(k)} = A_{11}^{(k)}\), this results in \(\vartheta =\kappa ({{Q}^{(k)}}^{-1}{S}^{(k)})\).

2.3 Optimality Conditions

As has been stated in Theorem 2, uniform convergence of the AMLI method can be proven under the assumption (31), which guarantees that the (multiplicative) two-level preconditioner satisfies a certain approximation property. Equivalently, uniform convergence of the multilevel V-cycle preconditioner (ν = 1) with bounded level difference can be required as the basic assumption to prove uniform convergence of the AMLI method for unbounded level difference as this was done in Theorem 1 in case of the linear preconditioner. In many cases these assumptions can be verified by studying the angle between the coarse space and its hierarchical complement. In fact, and this was shown in the original convergence analysis of linear AMLI methods [7], a stabilization of the condition number of the (multiplicative) multilevel preconditioner can be achieved under the assumption

$$\displaystyle{ A_{11}^{(k)} \leq B_{ 11}^{(k)} \leq \omega A_{ 11}^{(k)} }$$
(34)

on the approximation of the pivot block A 11 (k) if

$$\displaystyle{ \frac{1} {\sqrt{1 {-\gamma }^{2}}} <\nu. }$$
(35)

Assuming now that we have a fully stabilized multilevel method, i.e., the solutions for a repeatedly refined mesh (in principle for any number of regular refinement steps) are obtained at a constant number of iterations. Then the second condition to be fulfilled for an optimal order solution process is that the computational cost of each single iteration is proportional to the total number of degrees of freedom (DOF).

The computational work (operation count) of the ν-fold W-cycle of either linear or nonlinear AMLI at level 0 (associated with the finest mesh) can be estimated by

$$\displaystyle\begin{array}{rcl}{ w}^{(0)}& \leq & c\,(N_{ 0} +\nu \, N_{1} +\ldots {+\nu }^{\ell}\,N_{\ell}) {}\\ & =& c\,N_{0}\,\left (1 + \frac{\nu } {\varrho } +{ \left (\frac{\nu } {\varrho }\right )}^{2} +\ldots +{\left (\frac{\nu } {\varrho }\right )}^{\ell}\right ) = c\,N_{0}\,\frac{1 -{\left (\frac{\nu }{\varrho }\right )}^{\ell+1}} {1 -\frac{\nu }{\varrho }}. {}\\ \end{array}$$

Assuming that the number of DOF at level k + 1 is (approximately) 1 ∕ ϱ times the number of DOF at level k, each visit of level k must induce less than ϱ visits of level k + 1 (at least in average). This means that if the coarsening ratio is, for example, four, i.e., ϱ = 4, then two but also three inner GCG iterations, or, alternatively, the employment of second- but also third-degree matrix polynomials at every intermediate level, result in a computational complexity O(N) = O(N 0) of one (outer) iteration. The condition for optimal order single iterations is thus

$$\displaystyle{ \nu <\varrho, }$$
(36)

which combined with (35) results in the (combined) optimality conditions

$$\displaystyle{ \frac{1} {\sqrt{1 {-\gamma }^{2}}} <\,\nu <\,\varrho. }$$
(37)

In what follows, we assume that the default meaning of AMLI is the multiplicative one.

Remark 2.

The optimality conditions for the symmetric preconditioner of block-diagonal (additive) form are given by

$$\displaystyle{ \sqrt{\frac{1+\gamma } {1-\gamma }} <\,\nu <\,\varrho. }$$
(38)

Stabilization techniques for additive multilevel iteration methods and nearly optimal order parameter-free block-diagonal preconditioners of AMLI type are discussed in [4, 5].

3 Linear Elements

The material selected in this section follows the spirit of the robust AMLI methods as originally presented in [3, 4, 9, 10, 22, 24] as well as the earlier survey paper [21]. The hierarchical basis approach is followed for both conforming and nonconforming elements. This allows systematically to use local constructions and analysis at the level of element and macroelement matrices.

3.1 Conforming Elements

Let us remind that the analysis for an arbitrary triangle (e) can be done on the reference triangle \((\tilde{e})\). Transforming the finite element functions between these triangles, the element bilinear form \(\mathcal{A}_{e}(.,.)\) takes the form

$$\displaystyle{ \mathcal{A}_{\tilde{e}}(\tilde{u},\tilde{v}) =\int _{\tilde{e}}\sum _{i,j}\tilde{a}_{ij} \frac{\partial \tilde{u}} {\partial \tilde{x}_{i}} \frac{\partial \tilde{v}} {\partial \tilde{x}_{j}}, }$$
(39)

where the coefficients \(\tilde{a}_{ij}\) depend on both the coordinates in e and the coefficients a i j in the differential operator.

The important conclusion is that it suffices for the local analysis to consider the (macro)element stiffness matrices for the reference triangle and arbitrary anisotropic coefficients [a i j ] or, alternatively, for the isotropic operator − Δ and an arbitrary triangle e. In this sense, the mesh and coefficient anisotropy are equivalent, which obviously holds true for any conforming or nonconforming triangular finite element.

Following the FEM assembling procedure, we write the global stiffness matrix A in the form

$$\displaystyle{ A =\sum _{e\in \mathcal{T}_{k}}R_{e}^{T}A_{ e}R_{e}, }$$
(40)

where A e is the element stiffness matrix and R e stands for the restriction mapping of the global vector of unknowns to the local one corresponding to element \(e \in \mathcal{T}_{k}\).

Consider now the Laplace operator and an arbitrary shaped linear triangular finite element (mesh anisotropy). Then, the element stiffness matrix A e can be written in the form

$$\displaystyle{ A_{e} = \frac{1} {2}\left [\begin{array}{ccc} b + c& - c & - b\\ - c &a + c & - a \\ - b & - a &a + b \end{array} \right ], }$$
(41)

where a, b, and c equal the cotangent of the angles in \(e \in \mathcal{T}_{h}\). Without loss of generality, we assume in the local analysis that | a | ≤ b ≤ c, which follows from the next lemma; see, e.g., [3].

Lemma 1.

Let \(\theta _{1},\theta _{2},\theta _{3}\) be the angles in an arbitrary triangle. Then with a = cot θ 1 , b = cot θ 2 , c = cot θ 3 , it holds

  1. (i)

    \(a = (1 - bc)/(b + c)\)

  2. (ii)

    If \(\theta _{1} \geq \theta _{2} \geq \theta _{3}\) then |a|≤ b ≤ c

  3. (iii)

    a + b > 0.

Applying Lemma 1, we simply get the scaled representation of the element stiffness matrix:

$$\displaystyle{ A_{e} = \frac{c} {2}\left [\begin{array}{ccc} \beta + 1& - 1&-\beta \\ - 1 &\alpha + 1 &-\alpha \\ -\beta & -\alpha &\alpha +\beta \end{array} \right ], }$$
(42)

\(\alpha = a/c\), \(\beta = b/c\), and (α, β) ∈ D, where

$$\displaystyle{ D =\{ (\alpha,\beta ) \in {\mathbb{R}}^{2} : -\frac{1} {2} <\alpha \leq 1,\max \{- \frac{\alpha } {\alpha +1},\vert \alpha \vert \}\leq \beta \leq 1\}. }$$
(43)

The local analysis in terms of (α, β) belonging to the convex curvilinear triangle D plays a key role in the derivation of robust estimates for anisotropic problems; see [3, 10].

Consider two consecutive meshes \(\mathcal{T}_{k+1} \subset \mathcal{T}_{k}\). A uniform refinement procedure is set as a default assumption where the current coarse triangle \(e \in \mathcal{T}_{k+1}\) is subdivided in four congruent triangles by joining the mid-edge nodes to get the macroelement \(E \in \mathcal{T}_{k}\). The related macroelement stiffness matrix consists of blocks which are 3 ×3 matrices and, the local eigenproblem to compute γ E has a reduced dimension of 2 ×2.

In the so-arising six node-points of the macroelement, we can also use hierarchical basis functions, where we keep the linear basis functions in the vertex nodes and add piecewise quadratic basis functions in the mid-edge nodes with support on the whole triangle. Let us denote by \(\hat{\gamma }_{E}\) the corresponding CBS constant. The following relation between γ E and \(\hat{\gamma }_{E}\) holds.

Theorem 3 ([23]). 

Let us consider a piecewise Laplacian elliptic problem on an arbitrary finite element triangular mesh \(\mathcal{T}_{k+1}\) , and let each element from \(\mathcal{T}_{k+1}\) be refined into four congruent elements to get \(\mathcal{T}_{k}\) . Then

$$\displaystyle{ \hat{\gamma }_{E}^{2} = \frac{4} {3}\gamma _{E}^{2}, }$$
(44)

where \(\hat{\gamma }_{E},\) γ E are the local CBS constants for the hierarchical piecewise quadratic and the piecewise linear finite elements, respectively.

Taking into account that \(\hat{\gamma }_{E} < 1\), we get the local estimate

$$\displaystyle{ \gamma _{E}^{2} < \frac{3} {4} }$$
(45)

which holds uniformly with respect to the mesh anisotropy. Then, the next fundamental result follows directly from the local estimate (45), the equivalence relation (39), and the inequality \(\gamma \leq \max _{E}\gamma _{E}\).

Theorem 4.

Consider the problem(3)discretized by conforming linear finite elements, where the coarsest grid \(\mathcal{T}_{\ell}\) is aligned with the discontinuities of the coefficient a(e), \(e \in \mathcal{T}_{\ell}\). Let us assume also that \(\mathcal{T}_{k+1} \subset \mathcal{T}_{k}\) are two consecutive meshes where each element from \(\mathcal{T}_{k+1}\) is refined into four congruent elements to get \(\mathcal{T}_{k}\). Then, the estimate

$$\displaystyle{{ \gamma }^{2} < \frac{3} {4} }$$
(46)

of the CBS constant holds uniformly with respect to the coefficient jumps, mesh or/and coefficient anisotropy, and the refinement level k.

When applicable, we will skip the superscripts of the pivot block and its approximation. Here, we will write A 11, B 11, instead of A 11 (k), B 11 (k). The construction and the analysis of the preconditioners B 11 are based on a macroelement-by-macroelement assembling procedure. Following (40), we write A 11 in the form

$$\displaystyle{ A_{11} =\sum _{E\in \mathcal{T}_{k+1}}R_{E}^{T}A_{ E:11}R_{E}. }$$
(47)

Following the scaled representation (42), we get

$$\displaystyle{ A_{E:11} = r_{T}c_{T}\left [\begin{array}{ccc} \alpha +\beta +1& - 1 & -\beta \\ - 1 &\alpha +\beta +1 & -\alpha \\ -\beta & -\alpha &\alpha +\beta +1 \end{array} \right ]. }$$
(48)

Then, the additive preconditioner of A 11 is defined as follows:

$$\displaystyle{ B_{11}^{(A)} =\sum _{ E\in \mathcal{T}_{k+1}}R_{E}^{T}B_{ E:11}^{(A)}R_{ E}, }$$
(49)

where

$$\displaystyle{ B_{E:11}^{(A)} = 2r_{ T}c_{T}\left [\begin{array}{ccc} \alpha +\beta +1& - 1 & 0\\ - 1 &\alpha +\beta +1 & 0 \\ 0 & 0 &\alpha +\beta +1 \end{array} \right ]. }$$
(50)

As one can see, the local matrix B E: 11 (A) is obtained by preserving only the strongest off-diagonal entries. Alternatively, the multiplicative preconditioner B E (M) is defined as a symmetric block Gauss–Seidel preconditioner of A 11 subject to a proper node numbering (see, e.g., [3]).

Theorem 5 ([3, 4]). 

The additive and multiplicative preconditioners of A 11 are uniform, i.e.,

$$\displaystyle{ \kappa \left ({B_{11}^{(A)}}^{-1}A_{ 11}\right ) < \frac{1} {4}(11 + \sqrt{105}) \approx 5.31, }$$
(51)
$$\displaystyle{ \kappa \left ({B_{11}^{(M)}}^{-1}A_{ 11}\right ) < \frac{15} {8} = 1.875. }$$
(52)

These condition number bounds hold independently on shape and size of each element (mesh anisotropy) and on the coefficient matrix a(e) of the FEM problem (coefficient anisotropy).

3.2 Nonconforming Elements

For the nonconforming Crouzeix–Raviart finite element, where the nodal basis functions are defined at the midpoints along the edges of the triangle rather than at its vertices (cf. Fig. 1), the natural vector spaces \(\mathcal{V}_{H}(E) :=\mathrm{ span}\,\{\phi _{I},\phi _{II},\phi _{III}\}\) and \(\mathcal{V}_{h}(E) :=\mathrm{ span}\,\{\phi _{i}\}_{i=1}^{9}\) (cf. the macroelement in Fig.1) are no longer nested, i.e., \(\mathcal{V}_{H}(E) \not\subseteq \mathcal{V}_{h}(E)\). A simple computation shows that the element stiffness matrix for the Crouzeix–Raviart (CR) element, A e CR, coincides with that of the corresponding conforming linear element up to a factor 4, i.e.,

$$\displaystyle\begin{array}{rcl} A_{e}^{\mathrm{CR}}\, =\, 2\left [\begin{array}{ccc} b + c\ & - c & - b\\ - c &\ a + c\ & - a \\ - b & - a &\ a + b \end{array} \right ],& &{}\end{array}$$
(53)

(cf., (41)). The construction of the hierarchical stiffness matrix at macroelement level starts with the assembly of four such matrices according to the numbering of the nodal points, as shown in Fig. 1. It further utilizes a transformation, which is based on a proper decomposition of the vector space \(\mathcal{V}(E) = \mathcal{V}_{h}(E)\), which is associated with the fine-grid basis functions related to this macroelement E. We consider hierarchical splittings, which make use of half-difference and half-sum basis functions. Let us denote by \(\Phi _{E}\text{:} {=\{\phi }^{(i)}\}_{i=1}^{9}\) the set of the “midpoint” basis functions of the four congruent elements in the macroelement E, as depicted in Fig. 1. The splitting of \(\mathcal{V}(E)\) can be defined in the general form (see [22]):

$$\displaystyle{ \begin{array}{l} \mathcal{V}_{1}(E)\,\text{:} =\mathrm{ span}\,\{\phi _{1},\,\phi _{2},\,\phi _{3},\,\phi _{1}^{D} +\phi _{4} -\phi _{5},\,\phi _{2}^{D} +\phi _{6} -\phi _{7},\,\phi _{3}^{D} +\phi _{8} -\phi _{9}\}\,, \\ \mathcal{V}_{2}(E)\,\text{:} =\mathrm{ span}\,\{\phi _{1}^{C} +\phi _{4} +\phi _{5},\,\phi _{2}^{C} +\phi _{6} +\phi _{7},\,\phi _{3}^{C} +\phi _{8} +\phi _{9}\}\,,\end{array} }$$
(54)

where \(\phi _{i}^{D} :=\sum _{k}d_{ik}\phi _{k}\) and \(\phi _{i}^{C} :=\sum _{k}c_{ik}\phi _{k}\) with i, k ∈ { 1, 2, 3}. The transformation matrix is given by

$$\displaystyle\begin{array}{rcl} J_{E}^{T}\, = J_{ E}^{T}(C,D)\, =\, \left [\begin{array}{ccc} I_{3} & D & C \\ 0 &J_{-}&J_{+} \end{array} \right ]\,\quad (\in {\mathbb{R}}^{9\times 9}),& &{}\end{array}$$
(55)

where I 3 denotes the 3 ×3 identity matrix and C and D are 3 ×3 matrices whose entries c i j , respectively, d i j are to be specified later. The 3 ×6 matrices

$$\displaystyle\begin{array}{rcl} J_{-}\text{:} = \frac{1} {2}{\left [\begin{array}{cccccc} 1& - 1& & & & \\ & &1 & - 1 & & \\ & & & &1& - 1 \end{array} \right ]}^{T}\ \mbox{ and}\ \ J_{ +}\text{:} = \frac{1} {2}{\left [\begin{array}{cccccc} 1&1& & & & \\ & &1 &1 & & \\ & & & &1&1 \end{array} \right ]}^{T}& &{}\end{array}$$
(56)

introduce the so-called half-difference and half-sum basis functions associated with the sides of the macroelement triangle. The matrix J E transforms the vector of the macroelement basis functions \(\phi _{E} := {(\phi }^{(i)})_{i=1}^{9}\) to the hierarchical basis vector \(\tilde{\phi }_{E} := {(\tilde{\phi }}^{(i)})_{i=1}^{9} = J_{E}^{T}\,\phi _{E}\,\), and the hierarchical stiffness matrix at macroelement level is obtained as

$$\displaystyle\begin{array}{rcl} \tilde{A}_{E}\, =\, J_{E}^{T}A_{ E}J_{E}\, =\, \left [\begin{array}{cc} \tilde{A}_{E:11} & \tilde{A}_{E:12} \\ \tilde{A}_{E:12}^{T}&\tilde{A}_{E:22} \end{array} \right ]\begin{array}{l} \} \in \mathcal{V}_{1}(E) \\ \} \in \mathcal{V}_{2}(E) \end{array}.& &{}\end{array}$$
(57)

The related global stiffness matrix is obtained as \(\tilde{A}_{h} :=\sum _{E\in \mathcal{T}_{H}}R_{E}^{T}\tilde{A}_{E}R_{E}\). The transformation matrix J = J(C, D) such that \(\tilde{\phi }= {J}^{T}\phi\) is then used for the transformation of the global matrix A h to its hierarchical form \(\tilde{A}_{h} = {J}^{T}A_{h}J\), and (by a proper permutation of rows and columns) the latter admits the 3 ×3-block representation:

$$\displaystyle\begin{array}{rcl} \tilde{A}_{h}\, =\, \left [\begin{array}{ccc} \tilde{A}_{11} & \tilde{A}_{12} & \tilde{A}_{13} \\ \tilde{A}_{12}^{T}& \tilde{A}_{22} & \tilde{A}_{23} \\ \tilde{A}_{13}^{T}&\tilde{A}_{23}^{T}&\tilde{A}_{33} \end{array} \right ]\begin{array}{l} \Bigg\} \in \mathcal{V}_{1} \\ \} \in \mathcal{V}_{2} \end{array} & &{}\end{array}$$
(58)

according to the interior, half-difference, and half-sum basis functions, which are associated with (54). The next two variants follow [9].

Definition 2 (Differences and Aggregates (DA)). 

The splitting based on differences and aggregates corresponds to D = 0 and \(\,C = \frac{1} {2}\,\mathrm{diag}(1,1,1)\).

Definition 3 (First Reduce (FR) Splitting). 

The splitting based on differences and aggregates incorporating a “first reduce” (static condensation) step is characterized by setting D = 0 and \(C = -A_{11}^{-1}\,\bar{A}_{13}\) in (55).

Theorem 6 ([22]). 

Consider the problem (3)discretized by nonconforming linear finite elements, where the multilevel meshes satisfy the conditions from Theorem 4. Then, the estimate

$$\displaystyle{ \gamma _{FR}^{2} \leq \gamma _{ DA}^{2} \leq \frac{3} {4} }$$
(59)

of the CBS constants corresponding to FR and DA splittings holds uniformly with respect to the coefficient jumps, the mesh or/and coefficient anisotropy, and the refinement level k.

The preconditioning of the pivot blocks for FR and DA splittings is studied in [10]. The structure of the related systems (after a static condensation for the case of DA) coincides with those for conforming linear elements. Although the derivation of the related condition number estimates is rather different, it is based again on a macroelement analysis in terms of (α, β) belonging to the convex curvilinear triangle D; see (43). In both FR and DA cases, the construction of the additive and multiplicative preconditioners and the related robust upper bounds are the same as in the case of conforming elements; see Theorem 6.

Fig. 1
figure 1

Macroelement composed of four Crouzeix–Raviart elements

Full size image

Let us summarize the main results in this section. The results of Theorems 4–5 for the case of conforming elements, Theorem 6 and the analogue of Theorem 5 for nonconforming elements, in combination with the optimal solvers for systems with the additive and multiplicative preconditioners for the corresponding pivot blocks (see for more details [3]), ensure the optimal complexity of the related W-cycle AMLI algorithms with polynomial degree β ∈ { 2, 3}. All presented results are robust with respect to both mesh and/or coefficient anisotropy.

4 Quadratic Elements

In [23] and [1], it has been demonstrated that the standard (P 2 to P 1) hierarchical two-level splitting of piecewise quadratic basis functions does not result in robust two- and multilevel methods for highly anisotropic elliptic problems in general. A more recent paper, [19], proves that for orthotropic problems it is possible to construct a robust two-level preconditioner for FEM discretizations using conforming quadratic elements via the HB approach. In the general setting of an arbitrary elliptic operator, however, the standard techniques, based on HB two-level splittings (cf. [13]) and on the direct assembly of local Schur complements (cf. [14]), do not result in splittings in which the angle between the coarse space and its (hierarchical) complement is uniformly bounded with respect to the mesh and/or coefficient anisotropy.

One way to overcome this problem has been suggested in [20]. The idea is to construct a multilevel approximate block factorization based on ASCA and to combine the standard (nonlinear) AMLI with a block smoother. The recursive application of ASCA on a sequence of augmented coarse grids will be described in some more detail in the remainder of this section.

4.1 Notation

Let \(H_{A} = (V _{A},E_{A})\) denote the (undirected) graph of a matrix \(A\ \in \ \mathrm{{IR}}^{N\times N}\). The set of vertices (nodes) of A is denoted by \(V _{A} :=\{ v_{i}\, :\, 1 \leq i \leq N\}\) and the set of edges by \(E_{A} :=\{ e_{ij}\, :\, 1 \leq i < j \leq N\mbox{ and }a_{ij}\neq 0\}.\)

Definition 4.

Any subgraph F of H A is referred to as a structure. The set of structures whose relevant (local) structure matrices A F satisfy the assembling property

$$\displaystyle{ \sum _{F\in \mathcal{F}}R_{F}^{T}A_{ F}R_{F} = A. }$$
(60)

is denoted by \(\mathcal{F}\).

Definition 5.

Any union G of structures \(F \in \mathcal{F}\) is referred to as a macrostructure. The set of macrostructures is denoted by \(\mathcal{G}\). It is assumed that any set of corresponding macrostructure matrices \(\mathcal{A}_{G} =\{ A_{G}\, :\, G \in \mathcal{G}\}\) has the assembling property

$$\displaystyle{ \sum _{G\in \mathcal{G}}R_{G}^{T}A_{ G}R_{G} = A. }$$
(61)

Definition 6.

If \(F_{i} \cap F_{j} = \varnothing \) (or \(G_{i} \cap G_{j} = \varnothing \)) for all i≠j, we refer to the set \(\mathcal{F}\) (or \(\mathcal{G}\)) as a nonoverlapping covering; otherwise, we call ℱ (or \(\mathcal{G}\)) an overlapping covering.

4.2 Additive Schur Complement Approximation

Let \(S = {S}^{(k)}\) be the exact Schur complement of A = A (k) that we wish to approximate on a specific (augmented) coarse grid, and let us denote the corresponding graph by H. To give an example, in case of a uniform mesh as illustrated in Fig. 3c, we construct overlapping coverings of H by structures F and macrostructures G where each macrostructure \(G \in \mathcal{G}\) is composed of nine 13-node structures \(F \in \mathcal{F}\) which overlap with half of their width or height as shown on Fig. 2.Then the following algorithm for approximating Q can be applied (see [18]):

  1. 1.

    For all \(G \in \mathcal{G}\) assemble the macrostructure matrix A G .

  2. 2.

    To each A G perform a permutation of the rows and columns according to the global two-level splitting of the DOF and compute the Schur complement:

    $$\displaystyle{S_{G} = A_{G:22} - A_{G:21}A_{G:11}^{-1}A_{ G:12}.}$$
  3. 3.

    Assemble a sparse approximation Q to the exact global Schur complement \(S = A_{22} - A_{21}{(A_{11})}^{-1}A_{12}\) from the local macrostructure Schur complements:

    $$\displaystyle{Q := S_{\mathcal{G}} =\sum _{G\in \mathcal{G}}R_{G:2}^{T}S_{ G}R_{G:2}.}$$
Fig. 2
figure 2

One macrostructure G i used in the computation of Q; G i is composed of nine overlapping structures, \(F_{i_{1}},F_{i_{2}},\ldots,F_{i_{9}}\)

Full size image
Fig. 3
figure 3

(a) Uniform mesh consisting of conforming quadratic elements, (b) standard coarse grid, and (c) augmented coarse grid

Full size image

4.3 Recursive Approximate Block Factorization on Augmented Grids

Consider a uniform fine mesh as depicted in Fig. 3a, the standard coarse grid as depicted in Fig. 3b, and the augmented coarse grid as illustrated in Fig. 3c.

Then, since the original problem is formulated on a standard (and not on an augmented) grid, as a first step, one has to define a preconditioner \(\bar{{B}}^{(0)}\) at the level of the original finite element mesh with mesh size h, i.e.,

$$\displaystyle{ \bar{{B}}^{(0)} \approx {A}^{(0)} := A_{ h} }$$
(62)

where \(\bar{{B}}^{(0)} :=\bar{ B}_{h}\) is defined by

$$\displaystyle{ \bar{B}_{h} := \left [\begin{array}{cc} I & \\ A_{ h:21}A_{h:11}^{-1} & \ I \end{array} \right ]\left [\begin{array}{cc} A_{h:11} & \\ & Q_{h} \end{array} \right ]\left [\begin{array}{cc} I\ &A_{h:11}^{-1}A_{ h:12} \\ & I \end{array} \right ]. }$$
(63)

Note that (63) involves the Schur complement approximation Q (0) : = Q h , which refers to the first augmented (coarse) grid. This is the starting point for constructing \(\bar{{B}}^{(k)}\) as defined in (24), which is used to approximate A (k) for all subsequent levels \(k = 1,2,\ldots,\ell-1\). The sequence of (approximate) two-level factorizations defines a multilevel block factorization algorithm if A (k + 1) serves as an approximation to the Schur complement of A (k), that is, A (k + 1) is used in the construction of \(\bar{{B}}^{(k)}\). Hence it is quite natural to set \({A}^{(k+1)} = {Q}^{(k)}\) where Q (k) is obtained from ASCA for all k ≥ 0. Here it is assumed that the same construction can be applied recursively using the Schur complement approximation Q (k) to define the next coarse(r) problem; see (26). At levels k ≥ 1 the use of the augmented coarse grids is advocated since it results in a very efficient combined AMLI algorithm with block (line) smoothing at every coarse level. The numerical experiments presented in Sect. 5 demonstrate that based on this approach it is possible to construct robust multilevel methods for anisotropic elliptic problems even in the more difficult situations of using quadratic elements and/or when the direction of dominating anisotropy is not aligned with the grid, and/or the diffusion tensor has large jumps which cannot be resolved on the coarsest mesh.

4.4 Remarks on the Analysis

The following theorem can be proved for the error propagation of one block Jacobi iteration; see [20].

Theorem 7.

Consider the elliptic model problem (1)with a constant diffusion coefficient \(\mathbf{a}(x) = (a_{ij})_{i,j=1}^{2}\) scaled such that a 11 = 1, and discretized on a uniform mesh with mesh size h, and Dirichlet boundary conditions. Further, let \(Q = D + L + {L}^{T}\) denote the related ASCA where D and L are the block-diagonal and lower block-triangular parts of Q. Then the following bound holds for the iteration matrix of the block Jacobi method:

$$\displaystyle{ \Vert I - {D}^{-1}Q\Vert _{ Q}^{2} \leq 1 - \frac{1} {1 + c_{0}} =: 1 - c_{1}, }$$
(64)

where \(c_{0} := (a_{22} + \vert a_{12}\vert )/(c{h}^{2})\) and hence c 1 is in the interval (0,1).

The norm of the error propagation matrix of the two-level method corresponding to the preconditioner \(\bar{B}\) as defined in (24) but with \(B_{11} = A_{11}\) satisfies

$$\displaystyle{ \Vert I -\bar{ {B}}^{-1}A\Vert _{ A}^{2} \leq 1 -\alpha \lambda _{\min }({Q}^{-1}S) \leq 1-\alpha, }$$
(65)

where α can be estimated locally.

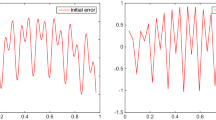
In Fig. 4 it is plotted a local estimate of the error reduction factor of the two-level method when considering grid-aligned and nongrid-aligned anisotropy. As it can be seen, in the first case, there is uniform convergence, i.e., the method is robust with respect to the parameter ɛ in (6) that has been varied in the range from 20 to 2 − 20. However, the results are worse for the rotated diffusion problem associated with (7) where the convergence estimate in general deteriorates when ɛ tends to 0. Still, for a (moderate) fixed value of ɛ, the estimate is uniform with respect to the angle of the direction of strong anisotropy.

Fig. 4
figure 4

(a) Grid-aligned anisotropy, \(\varepsilon = {2}^{-t}\), t ∈ { 0, 1, …, 20}: estimated convergence factor 1 − α plotted against t. (b) Rotated diffusion problem, \(\varepsilon \in \ \{1{0}^{-1},1{0}^{-2},1{0}^{-3}\}\),  \(\theta \in \{ {0}^{\circ },{1}^{\circ },\ldots,9{0}^{\circ }\}\): estimated convergence factor 1 − α plotted against θ

Full size image

5 Numerical Tests

In this section 2D numerical results are presented for the studied FEM discretizations based on conforming linear (P 1) and quadratic (P 2) finite elements. On the level of the coarsest discretization, the considered domain Ω = [0, 1] ×[0, 1] is split into 2 ×8 ×8 = 2 ×23 ×23 linear elements or, alternatively, into 2 ×4 ×4 = 2 ×22 ×22 quadratic elements. Dirichlet boundary conditions are imposed upon the entire boundary Γ = ∂ Ω. The finest mesh in all experiments is obtained via ℓ = 2, …, 7 steps of uniform mesh refinement resulting in \(2 \times {2}^{\ell+3} \times {2}^{\ell+3}\) linear elements or \(2 \times {2}^{\ell+2} \times {2}^{\ell+2}\) quadratic elements.

The numerical tests demonstrate the performance of the nonlinear AMLI W-cycle algorithm with 2 inner GCG iterations and an optional pre-smoothing step at every coarse level. The underlying multilevel block factorization is constructed based on the ASCA described in Sect. 4; see also [18, 20]. The following variants of complementary subspace correction are tested:

  1. (a)

    One-point Gauss–Seidel (PGS) iteration

  2. (b)

    One-line Gauss–Seidel (LGS) iteration

  3. (c)

    One-tree Gauss–Seidel (TGS) iteration

The blocks in variant (b) correspond to grid lines parallel to the x-axis. The blocks in variant (c) are constructed algebraically, by extracting strong paths from a previously computed nearly maximum spanning tree. The tree is constructed via a modified version of Kruskal’s algorithm in which the global sorting of the edges according to their weights is replaced by a partial (local) sorting (cf. [16]). For a given edge e i j  = (i, j), its weight w i j is defined by \(w_{ij} :=\vert A_{ij}\vert /\sqrt{A_{ii } A_{jj}}\) (cf. [11]). If w i j  > ρ for some threshold ρ, e.g., ρ = 0. 25, then e i j is called a strong edge.

Example 1.

In the first set of experiments we consider a permeability field with inclusions and channels on a background of conductivity one, as shown in Fig. 5. The diffusion tensor \(\mathbf{a}(x)\) equals the identity matrix outside the channels, whereas inside the channels it corresponds to highly anisotropic material and is determined by \(\{a_{11},a_{12},a_{22}\} =\{ 1{0}^{5},0,1\}\).

The results presented in Table 1 show that no additional smoothing (complementary subspace correction) is required when the direction of dominating anisotropy is aligned with the grid. The method performs absolutely robustly and very similar for both P 1 and P 2 elements, although the channels are NOT resolved on the coarsest mesh!

Example 2.

In the second set of experiments the domain is split into three nonoverlapping parts \(\Omega = \Omega _{1}\bigcup \Omega _{2}\bigcup \Omega _{3}\) where \(\Omega _{1} = [0,5/8] \times [0,1]\), \(\Omega _{2} = [5/8,11/16] \times [0,1]\), and \(\Omega _{3} = [11/16,1] \times [0,1]\) as shown on Fig. 6. We consider the rotated diffusion problem (7) where the angle \(\theta _{e} = {1}^{\circ }\) over the left and right subdomains, while in the middle one \(\theta _{e} = -8{5}^{\circ }\).

Fig. 5
figure 5

Coarse mesh and coefficient, Example 1

Full size image
Fig. 6
figure 6

Coarse mesh and direction of dominating anisotropy, Example 2

Full size image

The results in Table 2 show that while the method performs robustly without additional smoothing in case of P 1 elements, the convergence deteriorates without a complementary subspace correction step in case of P 2 elements; however, it can be improved significantly by introducing a proper block Gauss–Seidel pre-smoothing step.

Example 3.

The third set of experiments presents the performance of the nonlinear AMLI algorithm for the case of rotated diffusion problem with θ varied smoothly from the left to the right border of the domain Ω = [0, 1] ×[0, 1] according to the function \(\theta = -\pi (1 -\vert 2x - 1\vert )/6\) for x ∈ (0, 1) (Fig. 7).

Fig. 7
figure 7

Coarse mesh and direction of dominating anisotropy, Example 3

Full size image

The results are very similar to those for the second test problem. Note that all numerical experiments were designed in such a way that the coarsest mesh does not resolve the arising jumps of the coefficient (Table 3).

Table 1 Number of iterations for residual reduction by a factor 108. Nonlinear AMLI W-cycle without additional smoothing, Example 1
Full size table
Table 2 Number of iterations for residual reduction by a factor 108. Nonlinear AMLI W-cycle, Example 2
Full size table
Table 3 Number of iterations for residual reduction by a factor 108. Nonlinear AMLI W-cycle, Example 3
Full size table

6 Concluding Remarks

The theory of robust AMLI methods based on HB techniques is well established for conforming and nonconforming linear finite element discretizations of anisotropic second-order elliptic problems under the fundamental assumption that variations of the coefficient tensor can be resolved on the coarsest mesh. However, in many practical applications, this is a too strong restriction. Hence, alternative methods, e.g., based on energy-minimizing coarse spaces or robust Schur complement approximations, have recently been moving into the center of interest.

Here we describe a class of nonlinear AMLI methods that are based on ASCA and, though not fully analyzed yet, have been shown to be very efficient for problems with highly heterogeneous and anisotropic media. In case of conforming FEM and P 1 elements, this method performs robustly (even without additional smoothing). Using P 2 elements the numerical results demonstrate that in certain situations (when the convergence deteriorates) an additional smoothing step can improve the performance of the AMLI algorithm considerably. The construction of block smoothers based on graph concepts such as spanning trees seems to be very promising in this context (cf. Examples 2 and 3). The combination of an augmented coarse grid with a proper complementary subspace correction step is the key to obtain extremely efficient (oftentimes optimal or nearly optimal) solvers for strongly anisotropic problems even in case of varying and nongrid-aligned direction of dominating anisotropy and also for quadratic FEM.

Current (and future) investigations are devoted to extending the theory of this new class of methods and to improving the complementary subspace correction step(s) by refining the ideas of using (nearly maximum) spanning trees and strong paths in their construction. The latter is crucial also for the successful generalization of the new methodology to three-dimensional problems and/or discretizations on unstructured grids, where the suggested ASCA technique can be applied directly. Other topics of interest include the application to systems of partial differential equations and mixed methods.