Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

Introduction

Parametric resonance occurs in mechanical systems with external excitation when parameters of the system are at certain values. Mathematically, the equations of motion for these systems are considered as the equation with time-dependence coefficients. In the mechanical context, this means stiffness, mass, or force is changing periodically. In fact, the word “parametric” refers to parameter-dependent behavior of the system [1]. Therefore, in these systems resonances are directly connected to certain values of the parameters. It seems that Faraday [2] was the first researcher who observed parametric resonance. According to his studies, a vertically oscillating fluid with forcing frequency close to the natural frequencies of the system generates horizontal waves. A pendulum with oscillating support can be considered as a classical example of parametric resonance, where the equation of motion leads to the Mathieu [3] equation in its linear form. A great majority of studies in this regard have been conducted to model parametrically excited systems [4, 5]. This has been done on various cases including, swing, ship, pendulum and structures. In addition, controlling the vibration of the system due to parametric resonance is another subject that has a long history. For instance, Oueini and Nayfeh [6] suggested a nonlinear feedback law to control the first mode vibrations of a cantilever beam that is under principal parametric excitation. Vibration suppression of a cantilever beam when it is excited externally as well as parametrically was investigated by Eissa and Amer [7]. Similarly, they used a control law based on cubic velocity feedback to deal with the problem of vibration suppression. Although the resonance phenomenon is usually considered as a threat in mechanical applications, the concept can be utilized as an effective tool to develop mechanical and electromechanical parametric amplifiers. Parametric amplification is a well-established concept in the field of electrical engineering and has been widely implemented; however, the technique has not received enough attention in mechanical engineering context.

In mechanical and electromechanical applications, parametric amplification refers to the method for amplifying the dynamic response of a mechanical sensor by modulating system parameters, including mass, stiffness, and damping [8]. In this approach, a system parameter such as spring constant that is effective in the vibration behavior of the sensor is controlled by parametric pumping to amplify the response amplitude of the system which is directly excited. Basically, there are two types of parametric amplifiers; degenerate and nondegenerate amplifiers. The former refers to those systems where the pumping frequency is tuned at twice of the direct excitation signal. The latter is used for the system when pumping signal is locked at frequencies that are different from twice of the direct signal. In addition, frequency of the direct excitation should be sufficiently close to the values that cause resonance response. It is worth mentioning that in a nonlinear system, the resonance response exists at the natural frequency of the system as well as its harmonics (e.g., sub-harmonics and super harmonics). Parametrically excited beams are very good cases in point to study parametric amplification in mechanical and electromechanical sensors. In fact, microbeams are the most important element in almost all MEMS (Fig. 10.1). Jazar et al. [9] reviewed all important forces that affect the dynamic behavior of microbeams in MEMS and then formulated the equation of motion of the microbeam. Actually, the outcome of this study is the most general mathematical model for microbeams in MEMS. The model considers all attributes and therefore is somewhat complicated. However, this model can be simplified in different application when some terms are ignorable or a special case is going to be studied.

Fig. 10.1
figure 00101

Parametrically excited microbeams in a mass sensing device [10]

Full size image

Classically, mechanical measurements are firstly converted to electrical signals by means of transducers and then the signal is electrically amplified. However, in some cases such as atomic force microscopy it is required to amplify the mechanical motion to improve the detection sensitivity. In fact, mechanical parametric amplification is mainly functional when the inherently noisy electrical amplifiers affect the measurement accuracy [11]. Therefore, in order to accomplish low noise signal amplification, various studies have been recently conducted on this topic to develop mechanical and electromechanical resonators, especially in MEMS/NEMS [8, 9, 11–17]. In different reported works in the literature, parametric amplification has been effectively implemented when the mechanical spring constant is modulated at twice the resonance frequency by external electrostatic forces [11, 18] or mechanical pumping [19]. Rugar and Grutter [11] were among the first researchers who study the parametric amplification in mechanical domain. They investigated noise squeezing as well as low noise amplification in a micro-cantilever beam. All other works in this regard are based on this study, where parametric amplifiers were investigated for torsional micro-resonators [16, 20], coupled micro-resonators [13], electric force microscope [21], and micro-cantilevers [8, 19]. Rhoads et al. [22] analytically and experimentally studied a macro-scale cantilever beam as a pure mechanical amplifier. In this degenerate amplifier, the base excitation was considered at transverse as well as axial directions. The analysis of this model is investigated by truncating the governing equation of motion of the system such that only linear terms remain. While the above-mentioned cases are fairly well understood in the linear domain, the impact of nonlinearities on different parametric amplifiers has recently drawn many researchers attention [23]. Although in the linear analysis, the response of the system shows great performance and boundless gain for the amplifier, in a practical situation, as it was observed in experimental test of a macro-scale cantilever beam [22], the growth of the response is limited. This discrepancy between linear analysis and experimental results can be a result of inherit nonlinearities in the system that are not considered in the linearized equation of motion. Jazar et al. [9, 17] studied the dynamic behavior of an electrically actuated microcantilever. The study analyzes the steady state motion of the microcantilever with and w/o initial polarization and for linear and nonlinear condition (e.g., small and large vibration amplitude).

The main aim of this chapter is studying the behavior of the mechanical and electromechanical parametric amplifiers. Therefore, some mathematical models of mechanical and electromechanical parametric amplifiers in the literature are reviewed. To accomplish the analysis of these mathematical models, it is firstly required to acquire the necessary background about perturbation method. Therefore, the method of multiple scales is reviewed by solving a nonlinear forced oscillator as well as the Mathieu equation. Then, the nonlinear model of a classical degenerate parametric amplifier is introduced and the method of multiple scales is utilized to deal with the problem. In the next step, the stability analysis of the system is investigated. After that, in the results and discussion section, the outcomes of the perturbation solution are demonstrated and described; finally conclusion section will close the chapter.

Analytical Modeling of Mechanical and Electromechanical Parametric Amplifiers

In this section, the modeling process of some conducted studies regarding mechanical and electromechanical parametric amplifiers is briefly reported. In the scope of MEMS amplifiers, usually, the effective stiffness of the resonator is modulated electrostatically in such a way that parametric excitation arises. However, in macroscale cases base excitation can be used for this purpose. Therefore, reviewing some studies will help to get involved with the subject as well as understanding its applications.

Jazar et al. [9] have defined all important forces that affect the dynamic behavior of microbeams in MEMS and then formulated the equation of motion of the microbeam. According to this conducted study the general non-dimensionalized equation of motion of the microbeam is as following:

$$\begin{array}{lll} \ddot{Y}&+&\left( {\zeta +{a_6}\frac{r}{{1+{r^2}}}} \right)\dot{Y}+\left( {1+{b_3}-{a_7}\frac{r}{{1+{r^2}}}} \right)Y+\alpha {Y^3}\\ &+&{a_4}{Y^2}\dot{Y}+{a_5}\left( {1-Y} \right)Y=\frac{1}{{{{{\left( {1-Y} \right)}}^2}}}[\left( {\mu +\uplambda } \right)+2\sqrt{{2\mu \uplambda }}\sin \left( {r\tau } \right)-\uplambda \cos \left( {2r\tau } \right)]\end{array} $$
(10.1)

where \( Y \) stands for the lateral motion, \( \tau \) represents time, \( {a_i} \) are constant that can be calculated from the geometry and properties of the beam, \( {b_3} \) and \( \alpha \) are the terms for initial stretch and nonlinear stiffness, \( r=\frac{\omega }{{{\omega_1}}} \), \( \mu \) and \( \uplambda \) are, respectively, representatives of the polarization (\( {v_p} \)) and modulating (\( v \)) voltages in nondimensenalized form (Fig. 10.2).

Fig. 10.2
figure 00102

Schematic of electrically actuated microcantilever [9]

Full size image

This equation considers the most important forces that affect the dynamic behavior of the electrically actuated microbeam. These are inertia, rigidity, electrostatic, viscous, internal tension, squeeze film, and thermal forces. Enthusiastic readers can find detailed procedure to extract the general equation of motion (10.1) in [9]. There are some other less important forces such as fringing, van der Waals, and Casimir that are in secondary level in comparison with the considered forces. Moreover, the equation can be pruned to (10.2) if one neglects squeeze-film {\( {a_6}\frac{r}{{1+{r^2}}}\dot{Y} \) + \( {a_7}\frac{r}{{1+{r^2}}}\ Y \)}, thermal forces {\( {a_4}{Y^2}\dot{Y} \) + \( {a_5}\left( {1-Y} \right)Y \)}, and initial stretch.

$$ \ddot{Y}+\zeta \dot{Y}+Y+\alpha {Y^3}=\frac{1}{{{{{\left( {1-Y} \right)}}^2}}}(\left( {\mu +\uplambda } \right)+2\sqrt{{2\mu \uplambda }}\sin \left( {r\tau } \right)-\uplambda \cos \left( {2r\tau } \right) $$
(10.2)

Assuming no polarization voltage, the governing equation is more simplified as following:

$$ \ddot{Y}+\zeta \dot{Y}+Y+\alpha {Y^3}=\frac{1}{{{{{\left( {1-Y} \right)}}^2}}}(\uplambda -\uplambda \cos \left( {2r\tau } \right) $$
(10.3)

By expanding the electrostatic term in series form as (10.4), the complexity of this equation of motion can be reduced.

$$ \frac{1}{{{{{\left( {1-Y} \right)}}^2}}}=1+2Y+3{Y^2}+4{Y^3}+5{Y^4}+\ldots $$
(10.4)

A simple linear analysis requires expansion of the series up to \( O({Y^2}) \) provided that the term \( \alpha {Y^3} \) is also neglected from the left-hand side. On the other hand, in nonlinear analysis, due to the third order term of \( Y \) in the left-hand side, it is reasonable to expand the series term up to \( O({Y^4}) \). However, many researchers have neglected nonlinear terms of the electrostatic force while they have considered the cubic nonlinearity for stiffness of the microbeam. Although this assumption reduces the accuracy of the model, but gives a straightforward nonlinear Mathieu-type equation that eases investigation of the dynamic behavior of the system. In this condition, the microbeam is simply modeled as a mass, varying stiffness, and damper system.

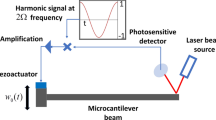
Rugar and Grutter [11] were among the first researchers who mentioned the parametric amplification in mechanical domain. In the accomplished work by them according to Fig. 10.3, the silicon microbeam is pumped electrically and a piezoelectric bimorph is used for the direct excitation. The parametric modulation is carried out by means of a capacitor with time-varying voltage \( \mathrm{V}\left( \mathrm{t} \right) \) on it. Thus, the effective stiffness of the beam is expressed as follows:

Fig. 10.3
figure 00103

The block diagram of an electromechanical parametric amplifier. Cantilever resonator is pumped by electrostatic force of the capacitor plate and the piezoelectric bimorph is used for the direct excitation [11]

Full size image
$$ k(t)={k_0}+{k_p}(t)\quad \mathrm{and}\quad k(p)=\frac{{\partial {F_e}}}{{\partial x}}=\frac{1}{2}\frac{{{\partial^2}C}}{{\partial {x^2}}}\ {{\left( {V(t)} \right)}^2} $$
(10.5)

where \( {{\mathrm{F}}_{\mathrm{e}}} \) represents electrostatic force, \( \mathrm{C} \) stands for the electrode-cantilever capacitance, and \( \mathrm{x} \) is the displacement of the beam.

The equation of motion of the cantilever beam was considered as a single degree of freedom mass, damper, and time-varying stiffness oscillator as follows:

$$ m\ddot{x}+\frac{{m{\omega_0}}}{Q}\dot{x}+\left( {{k_0}+{k_p}(t)} \right)x=F(t) $$
(10.6)

where \( \mathrm{F}\left( \mathrm{t} \right)={{\mathrm{F}}_0} \cos ({\omega_0}\mathrm{t}+\phi ) \) is the direct excitation signal, \( {k_p}(t)=\Delta k\sin 2{\omega_0}\mathrm{t} \), Q is the quality factor of resonance, \( \mathrm{x} \) is the cantilever displacement, and \( {\upomega_0} \) is the unforced resonance frequency of the cantilever beam, that is \( {\upomega_0}^2=\frac{\mathrm{k}\ }{\mathrm{m}} \). Expressing the damping factor \( \mathrm{c} \) as \( \frac{{\mathrm{m}{\upomega_0}}}{\mathrm{Q}} \) is conventional because the right condition for the occurrence of parametric resonance can be intuitively understood [10]. Generally speaking, increasing quality factor broadens the region of instability.

Zhang et al. [18] investigated an in-plane parametrically excited mass sensor with electrostatic force as the driving force. Figure 10.4 depicts a scanning electron micrograph of the oscillator. As it can be seen, there are two sets of parallel interdigitated comb finger banks on either end of the backbone and two sets of non-interdigitated comb fingers on each side. Applying a time-varying voltage to the non-interdigitated fingers as pumping signal leads to modulation of the stiffness of the system and parametric resonance.

Fig. 10.4
figure 00104

An in-plane parametrically excited oscillator. In this micrograph S indicates the folded beam springs, C demonstrates the two sets of interdigitated comb finger banks, B shows on the backbone, and N exhibits non-interdigitated comb fingers [18]

Full size image

In order to derive equation of motion of the sensor, similar to the previous case, a simple mass, spring, and damper system was considered as follows:

$$ m\ddot{x}+c\dot{x}+{F_k}(x)={F_e}\left( {t,x} \right)$$
(10.7)
$$ {F_k}(x)={k_1}x+{k_2}{x^3} $$
(10.8)
$$ {F_e}\left( {x,t} \right)=-\left( {k{r_1}x+k{r_2}{x^3}} \right){V_A}^2(1+ \cos (\omega t)) $$
(10.9)

where the letter \( \mathrm{k} \) is used for the mechanical stiffness and \( k\mathrm{r} \) represents electrostatic stiffness. Finally they have reported the following non-dimensional expression for the normalized equation of motion of the sensor.

$$ {x}^{\prime\prime}+\zeta {x}^{\prime}+(\beta +2\delta \cos\ (2\tau ))x+({\delta_3}+{{\delta^{\prime}}_3} \cos\ (2\tau )){x^3}=0 $$
(10.10)

Here, prime stands for derivative with respect to \( \uptau \). Note all the Greek letters coefficient in this nonlinear Mathieu equation are of small order (e.g., \( \mathrm{O}(\upvarepsilon ) \)), but the \( \upbeta \) that is \( \mathrm{O}(1) \).

Mahboob et al. [12] investigated a electromechanical oscillator as it is shown in Fig. 10.5. As it is observed, the resonator is a clamped–clamped microbeam with Schottky contacted two-dimensional electron systems (2DES) in clamped points. In this parametric amplifier, the stiffness modulating transducer is integrated into the mechanical element that can reduce the size of the resonator. The excitation of the oscillator is accomplished when an AC voltage is applied between the top gate and the 2DES. In fact, the piezoelectric effect leads to bending of the beam and resonance at the frequency of the applied voltage which is compatible with the fundamental mode of the beam.

Fig. 10.5
figure 00105

An out-of-plane electromechanical microbeam oscillator. Three Schottky electrodes at clamped points for parametric pumping (gate 1), resonance detection (gate 2), and direct excitation (gate 3) [12]

Full size image

In this case also the electromechanical resonator has been simplified as a mass, damper, and time-varying spring system. Thus, similar to the previous works, the governing equation of this parametric amplifier is reported to be as:

$$ \ddot{x}+\frac{{{\omega_0}}}{Q}\dot{x}+{\omega_0}^2\left( {1+\sqrt{2}C\uplambda \sin (2{\omega_0}t)} \right)x=\eta\ \sin ({\omega_0}t+\phi ) $$
(10.11)

where the \( \sqrt{2}\mathrm{C}\uplambda \sin (2{\upomega_0}\mathrm{t}) \) is pumping signal that is implemented from gate 1 (see Fig. 10.5), the \( \upeta\ \sin ({\upomega_0}\mathrm{t}+\phi ) \) is direct excitation signal via gate 3 that arises primary resonance of the beam.

Rhoads et al. [22] studied the macroscale mechanical parametric amplifiers in the case of a base excited cantilever beam. In this degenerate amplifier, the base excitation, according to Eq. (10.12), was considered at transverse (v p ) as well as axial (\( {u_p} \)) directions (Fig. 10.6).

Fig. 10.6
figure 00106

A base excited cantilever beam as a macroscale mechanical parametric amplifiers [22]

Full size image

This is carried out by installing the cantilever beam on a shaker that generates two sinusoidal signals as follows:

$$ {x_p}=A\cos\ (\Omega t+\Phi ) + B\cos\ (2\Omega t) $$
(10.12)
$$ {u_p}={x_p}\sin \alpha,\ {v_p}={x_p}\cos \alpha $$
(10.13)

where the signal with frequency \( \Omega \) is used for direct excitation and the signal with frequency \( 2\omega \) is used for parametric pumping. By using energy method that can be found in detail in [22] the governing equation of motion of the system for the first mode is reported as:

$$ \begin{array}{lll}\ddot{z}&+2\varepsilon \zeta \dot{z}+(1+\varepsilon {\uplambda_2}{\Omega^2}\cos \left( {2\Omega t} \right)+\varepsilon {\uplambda_1}{\Omega^2}\cos \left( {\Omega t+\Phi} \right))z\\ &\ \ = \varepsilon {\eta_1}{\Omega^2}\cos \left( {\Omega t+\Phi} \right)+\varepsilon {\eta_2}{\Omega^2}\cos \left( {2\Omega t} \right)\end{array} $$
(10.14)

As evident, this equation of motion is also similar to other reviewed cases in which stiffness of the mechanical resonator is modulated by a pumping signal. Therefore, the study of a general equation of motion similar to (10.6), (10.10), (10.11), and (10.14) might be useful to understand the effects of different parameters of the system on the behavior of mechanical and electromechanical parametric amplifiers. In the next sections, the general form of a classical degenerate parametric amplifier will be investigated.

Mathematical Background

In this section, prerequisite math to deal with governing equations of mechanical parametric amplifiers are introduced. For the sake of investigating these systems, one needs to have an appropriate knowledge about solving weakly nonlinear oscillators via perturbation techniques. There are various perturbation methods including Poincare, multiple scale, averaging and harmonic balance. These methods are vastly applied on oscillating systems in order to solve their nonlinear equations of motion. There is no denying that the perturbation method is useful in the case of weak nonlinearity and the resulting analytical solution is an approximation around the corresponding linear system. Due to popularity of the method of multiple scales in comparison with others, we review its basic concepts to solve weakly nonlinear equations. The enthusiastic readers can acquire deep understanding of perturbation technique by studying perturbation methods by Nayfeh [24].

The Method of Multiple Scales

The main idea of this method is that the expansion of the response is the function of multiple independent variables. This is carried out by introducing fast-scale and slow-scale variables and treating them as independent variables. It is carried out by letting:

$$ {{\mathrm{T}}_{\mathrm{n}}} = {\upvarepsilon^{\mathrm{n}}}\mathrm{t}\quad \mathrm{for}\quad \mathrm{n}=0,1,2,\ldots $$
(10.15)

Here, \( {{\mathrm{T}}_0} \) is a fast time scale and \( {{\mathrm{T}}_1} \) is a slow time scale describing variation in the response of the system. Thus, the derivative with respect to t can be expressed in the new scales by using partial derivatives as follow:

$$ \frac{\mathrm{d}}{\mathrm{d}\mathrm{t}}=\frac{{\mathrm{d}{{\mathrm{T}}_0}}}{\mathrm{d}\mathrm{t}}\frac{\partial }{{\partial {{\mathrm{T}}_0}}}+\upvarepsilon \frac{{\mathrm{d}{{\mathrm{T}}_1}}}{\mathrm{d}\mathrm{t}}\frac{\partial }{{\partial {{\mathrm{T}}_1}}}+\ldots ={{\mathrm{D}}_0}+\upvarepsilon {{\mathrm{D}}_1}+\ldots $$
(10.16)

where \( {D_{k= }}\frac{\partial }{{\partial {T_k}}} \), subsequently we have:

$$ \frac{{{{\mathrm{d}}^2}}}{{\mathrm{d}{{\mathrm{t}}^2}}}={{\mathrm{D}}_0}^2+2\upvarepsilon {{\mathrm{D}}_0}{{\mathrm{D}}_1}+\ldots $$
(10.17)

Now, one can express the response (x) in the form of new variables according to

$$ \mathrm{x}\left( {\mathrm{t},\upvarepsilon} \right) = \mathrm{x}\left( {{{\mathrm{T}}_0},{{\mathrm{T}}_1},\ldots,\ {{\mathrm{T}}_{\mathrm{n}}},\upvarepsilon} \right) = \mathop{\sum}\limits_{{\mathrm{i}=0}}^{\mathrm{n}}{\upvarepsilon^{\mathrm{i}}}\mathrm{x}\left( {{{\mathrm{T}}_0},{{\mathrm{T}}_1},\ldots,\ {{\mathrm{T}}_{\mathrm{n}}}} \right)+\mathrm{O}({\upvarepsilon^{{\mathrm{n}+1}}}) $$
(10.18)

It is worth mentioning that the number of independent variables is corresponding to the expansion order. In other words, when we expand the response to \( \mathrm{O}({\upvarepsilon^3}) \), the \( {{\mathrm{T}}_0},{{\mathrm{T}}_1} \) and \( {{\mathrm{T}}_2} \) time scales are required.

In order to use the method of multiple scale for solving equations of motion such as (10.11), it might be a wise decision to start with a directly excited oscillating systems. It is mainly because one needs to understand the different resonance cases that can be occurred in a nonlinear oscillating system under direct excitation (e.g., primary resonance, sub-harmonic and super harmonic cases). Then, we can apply the method on a simple parametrically excited system to solve the Mathieu equation. Due to the time-varying coefficient of the mathematical model regarding parametric amplifiers, this could be a useful step to acquire the required insight into their Mathieu-type nature. Finally, the combined excitation that arises in the degenerate parametric amplifiers can be easily managed.

Direct Excitation for System with Cubic Nonlinearity

Forced vibration of an oscillating system with governing equation such as (10.19) is investigated. This can be the representative of a slightly damped motion of a particle that is attached to a spring with hardening nonlinearity. For the sake of simplicity, the natural frequency of the system is considered to be unity.

$$ \ddot{\mathrm{x}} +\mathrm{x}+2\upvarepsilon \zeta \dot{x}+\upvarepsilon \alpha {x^3}=\upvarepsilon \eta \cos \Omega t $$
(10.19)

By expressing approximate solution of the system in different time scales according to the multiple scales method and expanding the response to the order of \( \mathrm{O}({\upvarepsilon^2}) \), we have:

$$ \mathrm{x}\left( {\mathrm{t},\upvarepsilon} \right) = {{\mathrm{x}}_0}\left( {{{\mathrm{T}}_0},{{\mathrm{T}}_1}} \right)+\upvarepsilon {{\mathrm{x}}_1}\left( {{{\mathrm{T}}_0},{{\mathrm{T}}_1}} \right)+\mathrm{O}({\upvarepsilon^2}) $$
(10.20)

Now, by applying new variables time derivatives and separating the terms of the resultant equation in accordance with their orders, one can obtain following equations for \( \mathrm{O}(1) \) and \( \mathrm{O}(\upvarepsilon ) \).

$$ \mathrm{O}(1):\ \ \mathrm{D}_0^2{{\mathrm{x}}_0}+{{\mathrm{x}}_0}=0 $$
(10.21)
$$ O\left( \varepsilon \right):\ \ D_0^2{x_1}+{x_1}=-2{D_0}{D_1}{x_0} - \alpha x_0^3-2\zeta {x_0}+\eta \cos \left( {\Omega {T_0}} \right) $$
(10.22)

The solution of Eq. (10.21) can be expressed as:

$$ {{\mathrm{x}}_0}=\frac{1}{2}\mathrm{A}\left( {{{\mathrm{T}}_1}} \right){{\mathrm{e}}^{{\mathrm{i}{{\mathrm{T}}_0}}}}+\mathrm{cc}. $$
(10.23)

where \( \mathrm{A}\left( {{{\mathrm{T}}_1}} \right) \) is a complex-valued quantity and cc. stands for complex conjugate of the first term. By using the above expression for \( {{\mathrm{x}}_0} \) in the second equation, the undetermined function \( \mathrm{A}\left( {{{\mathrm{T}}_1}} \right) \) is obtained. This can be accomplished when the expressions which produce secular term in Eq. (10.22) are put equal to zero. The process of eliminating secular terms depends on the frequency of the direct excitation. Up until now, we have not assumed the excitation frequency to be equal to a predefined value. This value is important for solving the above perturbation problem because different values for \( \Omega \) lead to different responses. In fact, in a nonlinear system, the resonance response exists at the natural frequency of the system as well as its harmonics. Generally speaking, there are three cases that may occur:

  • Primary Resonance Case: it refers to the situation when excitation frequency is near to the natural frequency of the system (\( \Omega \cong \omega \)).

  • Sub-Harmonic Resonance Cases: it arises when excitation frequency is near the integer multiples of the natural frequency (\( \Omega \cong \mathbf{n}\omega \) and \( \mathbf{n}=2,3,\ldots \)).

  • Super-Harmonic Resonance Cases: it is opposite concept to the previous case and occurs when the frequency of the driving excitation is close to an integer fraction of the natural frequency (\( \cong \frac{\omega }{\mathbf{n}} \) and \( \mathbf{n}=2,3,\ldots \)).

It is worth mentioning that as the nonlinearity of the system grows to higher orders, the effects of sub-harmonic and super-harmonic cases will be more noticeable. In this place, the solution is progressed for the case of primary resonance. Therefore, by substituting \( {{\mathrm{x}}_0} \) in Eq. (10.22) as well as assuming \( \Omega =1+\upvarepsilon \upsigma \), where \( \upsigma =\mathrm{O}(1) \), we will have:

$$ \begin{array}{lll}D_0^2{x_1}+{x_1}&=\{-(2i\left( {{A^{^\prime}}+\zeta A} \right)+3\alpha {A^2}\bar{A})\exp \left( {i{T_0}} \right)-\alpha {A^3}\exp \left( {3i{T_0}} \right)\nonumber\\&\quad+\frac{\eta }{2}\exp \left( {i\left( {{T_0}+\upsigma {T_1}} \right)} \right)\}+cc \end{array}$$
(10.24)

where prime denotes the derivative with respect to \( {T_1} \) (e.g., \( {A}^{\prime}={D_1}A \)) and \( \bar{A} \) is complex conjugate of \( A \). The secular term is eliminated when the terms that are the coefficient of \( \exp \left( {i{T_0}} \right) \) are put equal to zero, thus:

$$ 2i\left( {A^{\prime}+\zeta A} \right)+3\alpha {A^2}\bar{A}+\frac{\eta }{2}\exp \left( {i\upsigma {T_1}} \right)=0 $$
(10.25)

Now by expressing \( \mathrm{A} \) in polar form as

$$ \mathrm{A}=\frac{1}{2}\mathrm{a}\left( {{{\mathrm{T}}_1}} \right){{\mathrm{e}}^{{\mathrm{i}\upbeta ({{\mathrm{T}}_1})}}} $$
(10.26)

where \( \mathrm{a} \) and \( \upbeta \) are real values; by substituting it into Eq. (10.25), one can separate real and imaginary parts that lead to a set of differential equation as follows:

$$ {a}^{\prime}=-a\zeta +\frac{\eta }{2}\sin \left( {\sigma {T_1}-\beta } \right)$$
(10.27)
$$ a{\beta}^{\prime}=\frac{{3\alpha }}{8}{a^3}-\frac{\eta }{2}\cos \left( {\sigma {T_1}-\beta } \right) $$
(10.28)

Finally, the first approximate solution can be expressed as \( {{\mathrm{x}}_0}+\mathrm{O}(\upvarepsilon ) \), in which the \( \mathrm{a} \) and \( \upbeta \) are calculated from steady state solution of Eqs. (10.27) and (10.28).

Parametric Excitation of Linear Systems

We will apply the method of multiple scales on the Mathieu equation where natural frequency is a time-varying parameter according to Eq. (10.29). This parametrically excited linear oscillator can simulate small amplitude oscillations of a swing whose natural frequency is varying periodically in time.

$$ \ddot{\mathrm{x}} +\left( {{\upomega^2}+\upvarepsilon \uplambda \mathrm{cosn}t} \right)\mathrm{x}=0 $$
(10.29)

The Mathieu equation is very interesting for researchers [1, 14, 25] because an instability phenomenon occurs when natural frequency of the system (\( \omega \)) and frequency of the excitation (\( \mathrm{n} \)) are tuned at certain values. Here, we consider a special case that is \( \mathrm{n}=2 \). In this case when \( {\upomega^2}\ne {{\mathrm{m}}^2},\ \mathrm{m}=1,2,3 \), the equilibrium \( \mathrm{x}=0 \) is stable near \( \upvarepsilon =0 \); however, for some cases when \( {\upomega^2}\cong {{\mathrm{k}}^2} \), the solution is unstable [1, 4]. In this place, the case \( \mathrm{m}=1 \) that leads to \( {\upomega^2}=1+\upvarepsilon \upsigma \) when \( \upsigma =\mathrm{O}(1) \) is studied. This is mainly because we will investigate the degenerate parametric amplifiers in the next section. It is important to recall that in these types of amplifiers, the frequency of the parametric excitation is tuned at twice of the natural frequency of the system that is so-called principal resonance case of the system. Thus, Eq. (10.30) is solved by the method of multiple scales in order to discuss about \( \upsigma \) and \( \upvarepsilon \) parameters for which the instability phenomenon arises.

$$ \ddot{\mathrm{x}} +\left( {1+\upvarepsilon \upsigma +\upvarepsilon \uplambda \cos 2t} \right)\mathrm{x}=0 $$
(10.30)

By expanding the response to the order of \( \mathrm{O}({\upvarepsilon^2}) \), we have:

$$ \mathrm{x}\left( {\mathrm{t},\upvarepsilon} \right) = {{\mathrm{x}}_0}\left( {{{\mathrm{T}}_0},{{\mathrm{T}}_1}} \right)+\upvarepsilon {{\mathrm{x}}_1}\left( {{{\mathrm{T}}_0},{{\mathrm{T}}_1}} \right)+\mathrm{O}({\upvarepsilon^2}) $$
(10.31)

By substituting (10.31) into (10.30) and separating the terms of \( \mathrm{O}(1) \) and \( \mathrm{O}(\upvarepsilon ) \), one can obtain:

$$ \mathrm{D}_0^2{{\mathrm{x}}_0}+{{\mathrm{x}}_0}=0$$
(10.32)
$$ D_0^2{x_1}+{x_1}=-2{D_0}{D_1}{x_0} - (\sigma +\uplambda \cos \left( {2{T_0})} \right){x_0} $$
(10.33)

The solution of Eq. (10.32) is:

$$ {{\mathrm{x}}_0}=\frac{1}{2}\mathrm{A}\left( {{{\mathrm{T}}_1}} \right){{\mathrm{e}}^{{\mathrm{i}{{\mathrm{T}}_0}}}}+\mathrm{cc}. $$
(10.34)

In this step, by using this solution in the second equation and expressing the cosine term in its exponential form, we find:

$$ \begin{array}{lll}D_0^2{x_1}+{x_1}&=\{-i{A^{^\prime}}\exp \left( {i{T_0}} \right)-\frac{1}{2}A\sigma \exp \left( {i{T_0}} \right)\nonumber\\&\quad-\frac{A}{4}\uplambda \exp \left( {3i{T_0}} \right)-\frac{\bar{A}}{4}\uplambda \exp \left\{ {i\left( {{T_0}} \right)} \right\}+cc \end{array}$$
(10.35)

The solution for \( {{\mathrm{x}}_1} \) is periodic when the secular terms are eliminated from the above equation, which implies that:

$$ -i{A^{^\prime}}-\frac{A}{2}\sigma -\frac{\bar{A}}{4}\uplambda =0 $$
(10.36)

Now by expressing \( \mathrm{A}=\mathrm{a}+\mathrm{ib} \) and substituting it into Eq. (10.36), one can separate real and imaginary parts that lead to a set of differential equation as follows:

$$ {a}^{\prime}=\left( {-\frac{\sigma }{2}+\frac{\uplambda }{4}} \right)b $$
(10.37)
$$ {b}^{\prime}=\left( {\frac{\sigma }{2}+\frac{\uplambda }{4}} \right)a $$
(10.38)

The solutions of this set of equation are proportional to \( {{\mathrm{e}}^{{\left( {\mp s{T_1}} \right)}}} \), where \( \mathrm{s}=\frac{1}{2}\sqrt{{\frac{{{\uplambda^2}}}{4}-{\sigma^2}}} \). Hence, we find that solution is unstable or periodic solution does not exist when \( \left| \upsigma \right|<\uplambda /2 \).

The Mathieu Equation with Viscous Damping

Since there is always an amount of damping in the mechanical systems, a small viscous damping term can be considered in the Mathieu equation as:

$$ \ddot{\mathrm{x}} +\upvarepsilon \upzeta \dot{\mathrm{x}} +\left( {1+\upvarepsilon \upsigma +\upvarepsilon \uplambda \cos 2t} \right)\mathrm{x}=0 $$
(10.39)

If the solving procedure is repeated for this case, one finds that the following terms that produce secular terms should be eliminated:

$$ -i{A}^{\prime}-\frac{A}{2}\sigma -\frac{\bar{A}}{4}\uplambda -i\frac{A}{2}\upzeta =0 $$
(10.40)

Similar to the last case, if we take \( \mathrm{A}=\mathrm{a}+\mathrm{ib} \), then

$$ {a}^{\prime}=-\frac{\zeta }{2}a+\left( {\frac{\uplambda }{4}-\frac{\sigma }{2}} \right)b $$
(10.41)
$$ {b}^{\prime}=\left( {\frac{\uplambda }{4}+\frac{\sigma }{2}} \right)a-\frac{\zeta }{2}b $$
(10.42)

This leads to \( \mathrm{s}=-\frac{\zeta }{2}\mp \frac{1}{2}\sqrt{{\frac{{{\uplambda^2}}}{4}-{\sigma^2}}} \) that is the zeros of the characteristics equation; the characteristics equation is calculated from:

$$ \left| {\begin{array}{*{20}{c}} \displaystyle {s+\frac{\zeta }{2}} & \displaystyle{-\frac{\uplambda }{4}+\displaystyle\frac{\sigma }{2}} \\[6pt] \displaystyle{-\frac{\uplambda }{4}-\displaystyle\frac{\sigma }{2}} & {s+\displaystyle\frac{\zeta }{2}} \\ \end{array}} \right|=0 $$
(10.43)

Thus, the trivial solution is stable when \( \upzeta >0 \) and \( {\uplambda^2}<4\left( {{\upzeta^2}+{\upsigma^2}} \right) \). As evident, when the damping term is omitted that leads to previous condition for undamped system. The critical condition (\( \uplambda =2\sqrt{{{\upzeta^2}+{\upsigma^2}}} \)) demonstrates the curve in the \( (\upsigma, \uplambda ) \) plane that separate stable and unstable solutions; Fig. 10.7 depicts the instability bounds with and without damping in the \( (\upsigma, \uplambda ) \) plane for different values of damping. As it can be seen, when \( 0<\zeta <\frac{\uplambda }{2} \), the instability region has been shifted up, and for \( \upzeta >\frac{\uplambda }{2} \) the instability domain does not appear.

Fig. 10.7
figure 00107

First order approximation of instability bounds without and with damping

Full size image

System Model

According to governing equations of motion for reviewed mechanical and electromechanical parametric amplifiers in Sect. 10.2, the general form of governing equation for a linear degenerate amplifier may be expressed as Eq. (10.44).

$$ \ddot{\mathrm{z}} +2\upvarepsilon \upzeta \dot{\mathrm{z}} +\mathrm{z}+\upvarepsilon \uplambda \cos \left( {2\Omega \mathrm{t}} \right)\mathrm{z}=\upvarepsilon \upeta \cos \left( {\Omega \mathrm{t}+\Phi} \right) $$
(10.44)

where z represents the mechanical resonators displacement, \( \uplambda \) is the pumping signal amplitude, \( \upzeta \) considered for linear dissipation effects, \( \eta\;\ and\;\ \Omega \) represent direct excitation signal amplitude and frequency, t represents non-dimensional time variable, \( \Phi \) stands for relative phase parameter which is necessary for amplifier tuning. This simple equation is a good case in point to investigate the effects of different parameters in the response and performance of the different parametric amplifiers.

Similarly, nonlinear parametric amplifiers can be studied by this equation provided that compatible term of nonlinearity to be added to the linear equation. Since the cubic nonlinearity is a typical nonlinear term in mechanical cases, especially structural vibrations, the basic equation is amended by a cubic nonlinear term as Eq. (10.45), where \( \upalpha \) is a parameter for highlighting the order of effective nonlinearity in the system. In addition, for the sake of simplification of the analysis and according to the conducted studies [18], each of nonlinearity, dissipation, and excitation terms has been considered to be \( \mathrm{O}\left( \upvarepsilon \right) \). It is indisputable that perturbation method has proved its effectiveness for these forms of equation. It should be noted that this problem is investigated in [23] by the method of averaging. Here, similar to previous cases in this chapter, the method of multiple scales is used to deal with the problem. Furthermore, the stability analysis of the steady state solution is studied.

$$ \ddot{\mathrm{z}} +2\upvarepsilon \upzeta \dot{\mathrm{z}} +\mathrm{z}+\upvarepsilon \uplambda \cos \left( {2\Omega \mathrm{t}} \right)\mathrm{z}+\upvarepsilon \upalpha {{\mathrm{z}}^3}=\upvarepsilon \upeta \cos \left( {\Omega \mathrm{t}+\Phi} \right) $$
(10.45)

Perturbation Solution

By expanding \( \mathrm{z} \) as the following expression and substituting it into Eq. (10.45), one can obtain Eqs. (10.47) and (10.48) for terms with same order.

$$ \mathrm{z}\left( {{{\mathrm{T}}_0},{{\mathrm{T}}_1}} \right)={{\mathrm{Z}}_0}\left( {{{\mathrm{T}}_0},{{\mathrm{T}}_1}} \right)+\upvarepsilon {{\mathrm{Z}}_1}\left( {{{\mathrm{T}}_0},{{\mathrm{T}}_1}} \right)+\ldots $$
(10.46)
$$ \mathrm{O}(1): \mathrm{D}_0^2{{\mathrm{Z}}_0}+{{\mathrm{Z}}_0}=0 $$
(10.47)
$$ \begin{array}{lll}O\left( \varepsilon \right): D_0^2{Z_1}+{Z_1}&=-2{D_0}{D_1}{Z_0}-\uplambda {Z_0}\cos \left( {2\Omega {T_0}} \right)\\ &\quad - \alpha Z_0^3-2\zeta {Z_0}+\eta \cos \left( {\Omega {T_0}+\varPhi } \right) \end{array}$$
(10.48)

The solution of Eq. (10.42) can be expressed as:

$$ {{\mathrm{Z}}_0}=\frac{1}{2}\mathrm{A}\left( {{{\mathrm{T}}_1}} \right){{\mathrm{e}}^{{\mathrm{i}{{\mathrm{T}}_0}}}}+\mathrm{cc} $$
(10.49)

where \( \mathrm{A}\left( {{{\mathrm{T}}_1}} \right) \) is a complex quantity and cc. stands for complex conjugate of the first term. In addition, for the sake of investigating system behavior around its natural frequency, a detuning parameter \( (\upsigma ) \) is defined, and direct excitation frequency is considered to be \( \Omega =1+\upvarepsilon \upsigma \). By taking this measure the frequency response curves of the system can be extracted. These curves are very useful for demonstrating response variation with parameters of the system. With this in mind and substituting (10.49) into Eq. (10.48), one can find the expressions which produce secular terms are eliminated if:

$$ -2i\left[ {A^{\prime}+\zeta A} \right]-\frac{1}{2}\uplambda \bar{A}{e^{{i2\sigma {T_1}}}}-3\alpha {A^2}\bar{A}+\frac{1}{2}\eta {e^{{i(\sigma {T_1}+\Phi )}}}=0 $$
(10.50)

Consider \( A\left( {{T_1}} \right) \) in polar form as (10.51) in order to manage Eq. (10.50).

$$ \mathrm{A}=\frac{1}{2}\mathrm{a}\left( {{{\mathrm{T}}_1}} \right){{\mathrm{e}}^{{\mathrm{i}\upbeta ({{\mathrm{T}}_1})}}} $$
(10.51)

where a and \( \upbeta \) are real-valued quantities. Substituting (10.51) into Eq. (10.50), one can separate real and imaginary parts; then, a little manipulation over two equations yields:

$$ {a}^{\prime}=-\frac{1}{4}\uplambda a\sin 2\left( {\sigma {T_1}-\beta } \right)-a\zeta +\frac{1}{2}\eta \sin \left( {\sigma {T_1}-\beta +\Phi} \right) $$
(10.52)
$$ a{\beta}^{\prime}=\frac{1}{4}\uplambda a\cos 2\left( {\sigma {T_1}-\beta } \right)+\frac{{3\alpha }}{8}{a^3}-\frac{1}{2}\eta \cos \left( {\sigma {T_1}-\beta +\Phi} \right) $$
(10.53)

Next, by letting \( \gamma =\sigma {T_1}-\beta \), Eqs. (10.52) and (10.53) will be transformed into an autonomous system, the results can be expressed as:

$$ {a}^{\prime}=-\frac{1}{4}\uplambda a\sin 2\gamma -a\zeta +\frac{1}{2}\eta \sin \left( {\gamma +\Phi} \right) $$
(10.54)
$$ a{\gamma}^{\prime}=a\sigma -\frac{1}{4}\uplambda a\cos 2\gamma -\frac{{3\alpha }}{8}{a^3}+\frac{1}{2}\eta \cos \left( {\gamma +\Phi} \right) $$
(10.55)

With Eqs. (10.54) and (10.55) in hand, the steady state solution for the system of interest can be obtained by setting \( \left( {a^{\prime},{\gamma}^{\prime}} \right)=(0,0) \). Generally, one may find a closed form expression solution for pumping off (i.e., \( \uplambda =0 \)) situation in parametric amplifiers; however, steady state solution of the considered degenerate amplifier when \( \uplambda \ne 0 \) should be evaluated numerically.

Stability Analysis

In order to study the stability of steady state motion, one can impose a small perturbation to steady state solution and investigate the results by determining the nature of singular points [4]; therefore, we let,

$$ a={a_0}+{a_1} $$
(10.56)
$$ \gamma ={\gamma_0}+{\gamma_1} $$
(10.57)

where \( {a_0}\;\&\;{\gamma_0} \) represent the singular point and \( {a_1}\;\&\;{\gamma_1} \) are small perturbations over them. By substituting given expression for \( a\;\&\;\gamma \) into Eqs. (10.54) and (10.55) and knowing that \( {a_0}\;\&\;{\gamma_0} \) satisfy steady state solution as well as neglecting nonlinear terms, the following equations can be obtained.

$$ {{a^{\prime}}_1}=-\left( {\zeta +\frac{1}{4}\uplambda \sin 2{\gamma_0}} \right){a_1}+\left( {\frac{1}{2}\eta \cos \left( {{\gamma_0}+\Phi} \right)-\frac{1}{2}\uplambda {a_0}\cos 2{\gamma_0}} \right){\gamma_1} $$
(10.58)
$$ {{\gamma^{\prime}}_1}=-\left( {\frac{3}{4}\alpha {a_0}+\frac{\eta }{{2{a_0}^2}}\cos \left( {{\gamma_0}+\Phi} \right)} \right){a_1}+\left( {\frac{1}{2}\uplambda \sin 2{\gamma_0}-\frac{\eta }{{2{a_0}}}\sin \left( {{\gamma_0}+\Phi} \right)} \right){\gamma_1} $$
(10.59)

These equations can be demonstrated in matrix form such that,

$$ \left\{ {\begin{array}{*{20}{c}} {{{{a^{\prime}}}_1}} \\ {{{{\gamma^{\prime}}}_1}} \\ \end{array}} \right\}=\left[ {\begin{array}{*{20}{c}} {{{\mathrm{T}}_1}} & {{{\mathrm{T}}_2}} \\ {{{\mathrm{T}}_3}} & {{{\mathrm{T}}_4}} \\ \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{a_1}} \\ {{\gamma_1}} \\ \end{array}} \right\} $$
(10.60)

where

$$ {{\mathrm{T}}_1}=-\left( {\zeta +\frac{1}{4}\uplambda \sin 2{\gamma_0}} \right) $$
(10.61)
$$ {{\mathrm{T}}_2}=\left( {\frac{1}{2}\eta \cos \left( {{\gamma_0}+\Phi} \right)-\frac{1}{2}\uplambda {a_0}\cos 2{\gamma_0}} \right) $$
(10.62)
$$ {{\mathrm{T}}_3}=-\left( {\frac{3}{4}\alpha {a_0}+\frac{\eta }{{2{a_0}^2}}\cos \left( {{\gamma_0}+\Phi} \right)} \right) $$
(10.63)
$$ {{\mathrm{T}}_4}=\left( {\frac{1}{2}\uplambda \sin 2{\gamma_0}-\frac{\eta }{{2{a_0}}}\sin \left( {{\gamma_0}+\Phi} \right)} \right) $$
(10.64)

As it is clear, the stability of the steady state motion of an expression like \( \left\{ {X^{\prime}} \right\}=\left[ A \right]\left\{ X \right\} \) depends on the eigenvalues of the A matrix; thus, by evaluating eigenvalues (\( \mathrm{s} \)) for the T matrix in (10.60), the nature of singular points will be revealed. Hence, one needs to solve the following determinant:

$$ \left| {\begin{array}{*{20}{c}} {\mathrm{s}+\zeta +\frac{1}{4}\uplambda \sin 2{\gamma_0}} & {-\frac{1}{2}\eta \cos \left( {{\gamma_0}+\Phi} \right)+\frac{1}{2}\uplambda {a_0}\cos 2{\gamma_0}} \\ {\frac{3}{4}\alpha {a_0}+\frac{\eta }{{2{a_0}^2}}\cos \left( {{\gamma_0}+\Phi} \right)} & {\mathrm{s}-\frac{1}{2}\uplambda \sin 2{\gamma_0}+\frac{\eta }{{2{a_0}}}\sin \left( {{\gamma_0}+\Phi} \right)} \\ \end{array}} \right|=0 $$
(10.65)
$$ {{\mathrm{s}}^2}-\left( {{{\mathrm{T}}_1}+{{\mathrm{T}}_4}} \right)\mathrm{s}+\left( {{{\mathrm{T}}_1}{{\mathrm{T}}_4}-{{\mathrm{T}}_2}{{\mathrm{T}}_3}} \right)=0 $$
(10.66)
$$ \mathrm{s}=\frac{{\left( {{{\mathrm{T}}_1}+{{\mathrm{T}}_4}} \right)\pm \sqrt{{{{{\left( {{{\mathrm{T}}_1}+{{\mathrm{T}}_4}} \right)}}^2}-4\left( {{{\mathrm{T}}_1}{{\mathrm{T}}_4}-{{\mathrm{T}}_2}{{\mathrm{T}}_3}} \right)}}}}{2} $$
(10.67)

According to the above equation, the steady state motion is unstable if \( \left( {{{\mathrm{T}}_1}+{{\mathrm{T}}_4}} \right)>0 \) or \( \left( {{{\mathrm{T}}_1}{{\mathrm{T}}_4}-{{\mathrm{T}}_2}{{\mathrm{T}}_3}} \right)<0 \). Having been calculated from (10.67) for a specific singular point, a complex \( \mathrm{s} \) with negative real part means a stable solution (e.g., Stable focus); otherwise the steady state solution is unstable (e.g., Saddle point).

Similar to all linear parametrically excited systems, wedge of instability appears for the unforced linear equation of motion of the system. To extract this wedge of instability near principal resonance case, one needs to investigate Eq. (10.68).

$$ \ddot{\mathrm{z}} +2\upvarepsilon \upzeta \dot{\mathrm{z}} +\mathrm{z}+\upvarepsilon \uplambda \cos \left( {2\Omega \mathrm{t}} \right)\mathrm{z}=0 $$
(10.68)

By repeating the procedure of solving according to the method of multiple scales, one finds two equations that are identical to Eqs. (10.54) and (10.55), but in which \( \upalpha \) and \( \upeta \) are put equal to zero. As it is clear, in this condition trivial solution will be appeared, and stability analysis of the trivial solution will reveal the bounds of instability. In fact, in the case of Eq. (10.68) the secular terms are eliminated as long as:

$$ -2i\left[ {A^{\prime}+\zeta A} \right]-\frac{1}{2}\uplambda \bar{A}{e^{{i2\sigma {T_1}}}}=0 $$
(10.69)

Considering

$$ A=\frac{1}{2}(p-iq){e^{{i\sigma {T_1}}}} $$
(10.70)

where \( \mathrm{p} \) and \( \mathrm{q} \) are real. By substituting (10.70) into Eq. (10.69) and separating real and imaginary parts, one obtains:

$$ {p}^{\prime}=-\zeta p+\left( {-\sigma -\frac{\uplambda }{4}} \right)q $$
(10.71)
$$ {q}^{\prime}=\left( {\sigma -\frac{\uplambda }{4}} \right)p-\zeta q $$
(10.72)

Calculating eigenvalues of the coefficient matrix of these set of equations leads to:

$$ \mathrm{s}=-\zeta \mp \sqrt{{\frac{{{\uplambda^2}}}{16 }-{\sigma^2}}} $$
(10.73)

That implies the trivial solution is stable if:

$$ {\uplambda^2}<16({\upzeta^2}+{\upsigma^2}) $$
(10.74)

Results and Discussion

Frequency Response Curves

In the first place, the steady state solution of the linear system (\( \upalpha =0 \)) is calculated for different parameters of the system. As it can be seen in Fig. 10.8, amplitude of the system is grown by increasing the effects of pumping signal, and it becomes boundless when the pumping signal violates linear stability threshold (\( \uplambda =4\sqrt{{{\upzeta^2}+{\upsigma^2}}} \)). Figure 10.9 demonstrates the effects of damping and direct excitation on the amplitude of the amplifier. As it is expected, by increasing the direct excitation, the response of the system is magnified; and more damping reduces the amplitude of the amplifier.

Fig. 10.8
figure 00108

Linear frequency response—increasing pumping signal leads to boundless amplitude

Full size image
Fig. 10.9
figure 00109

Linear frequency response—effects of different damping (a) and direct excitation (b)

Full size image

There is no denying that for nonlinear system many stable and unstable solutions can exist. Therefore, to investigate the nature of this solution, the phase portraits of the system have been numerically calculated by solving Eqs. (10.54) and (10.55) with different initial values for \( a\;\&\;\gamma \). Figure 10.10 shows the phase plane diagrams for 3 different pumping signals when the detuning parameter is 0.1 (\( \sigma =0.1 \)). As it can be observed the number of stable and unstable solutions varies for different pumping amplitudes. While for \( \uplambda =0.035 \) there are two stable and one unstable solution, one can see three stable and two unstable solution for the \( \uplambda =0.055 \) and 0.09. For example consider phase plane diagram that has been illustrated in Fig. 10.10b, by tracking the solution routes in the phase plane diagrams, one can find three stable foci which are the feasible steady state solutions, one of the stable solutions has very small amplitude while two others have large amplitude. These stable solutions are almost identical in amplitude, but they have different phase.

Fig. 10.10
figure 001010

Phase portraits of the nonlinear amplifier at \( \sigma =0.1 \). (a) \( \uplambda =0.035 \), (b) \( \uplambda =0.055 \), (c) \( \uplambda =0.09 \)

Full size image

Figure 10.11 depicts the phase portrait with same pumping signals when detuning parameter is 0.05 and 0.01. Again, there is no equal number of stable and unstable solutions for different pumping signals as well as detuning parameters. In order to investigate this phenomenon, it is a good idea to plot frequency response curves of the system for different pumping signals to have all steady state solution in a frequency range.

Fig. 10.11
figure 001011

Phase plan diagrams of the system for different parameters. (a) \( \upsigma =0.05,\ \ \uplambda =0.035 \), (b) \( \upsigma =0.05,\ \uplambda =0.055 \), (c) \( \upsigma =0.05,\ \uplambda =0.09 \), (d) \( \upsigma =0.01,\ \ \uplambda =0.035 \), (e) \( \upsigma =0.01,\ \uplambda =0.055 \) and (f) \( \upsigma =0.01,\ \uplambda =0.09 \)

Full size image

When both \( {a}^{\prime}\;\&\;{\gamma}^{\prime} \) are considered equal to zero in (10.54) and (10.55), the steady state solutions for the system of interest can be extracted. Figures 10.12, 10.13, and 10.14 depict the amplitude and phase of the steady state solution for different parameters of the system. As expected, due to the cubic nonlinearity, the frequency response curves demonstrate a Duffing-like trend near their resonance frequency that is σ = 0. Note that frequency response curves have been calculated for three different conditions. In the first place, the steady state solutions are obtained when parameters are set in such a way that pumping amplitude is under principal resonance instability threshold, that is \( \uplambda =4\sqrt{{{\upzeta^2}+{\upsigma^2}}} \). Then, by keeping other parameter in their previous values, the pumping signal is magnified slightly and well above the instability threshold.

Fig. 10.12
figure 001012

Amplitude and phase frequency response in steady state mode when pumping amplitude is under its parametric instability threshold, (\( \boldsymbol{\Phi} =-\frac{\boldsymbol{\uppi}}{4},\ \boldsymbol{\upzeta} =0.01,\ \boldsymbol{\upalpha} =0.001,\ \boldsymbol{\upeta} =0.1\ \&\ \uplambda =0.035<4\zeta ) \). Solid lines: stable solution branches; dashed line: unstable solution branch

Full size image
Fig. 10.13
figure 001013

Amplitude and phase frequency response in steady state mode when pumping amplitude is slightly above its parametric instability threshold (\( \boldsymbol{\Phi} =-\frac{\boldsymbol{\uppi}}{4},\ \boldsymbol{\upzeta} =0.01,\ \boldsymbol{\upalpha} =0.001,\ \boldsymbol{\upeta} =0.1\ \&\ \boldsymbol{\uplambda} =0.055>4\boldsymbol{\upzeta} ) \). Solid lines: stable solution branches; dashed line: unstable solution branches

Full size image
Fig. 10.14
figure 001014

Amplitude and phase frequency response in steady state mode when pumping amplitude is far above its parametric instability threshold \( \boldsymbol{\Phi} =-\frac{\boldsymbol{\uppi}}{4},\ \boldsymbol{\upzeta} =0.01,\ \boldsymbol{\upalpha} =0.001,\ \boldsymbol{\upeta} =0.1\;\&\;\boldsymbol{\uplambda} =0.09>4\boldsymbol{\upzeta} \). Solid lines: stable solution branches; dashed line: unstable solution branches

Full size image

As it can be observed from Fig. 10.12 for under instability threshold condition (i.e., \( \uplambda <4\zeta \) when \( \upsigma =0) \), the steady state solution has three branches in a frequency band that means different steady state solutions in frequency response regime. By evaluating corresponding eigenvalues for the solutions, it is revealed that the upper and lower branches are stable solutions for this region and the middle branch is unstable steady state solution that cannot be achieved in the reality. Furthermore, Figs. 10.13 and 10.14 show that when the pumping amplitude is slightly and far above instability threshold, the frequency response solutions have five distinct branches. Therefore, they can represent five different steady state solutions; however, the stability analysis for these conditions leads to three stable solutions which are feasible and two unstable stationary points. As it is clear from Figs. 10.13 and 10.14, over a wide frequency range the amplitude of two upper stable branches is almost equal, while they have completely different phase. The other interesting phenomena about steady state solution with parameters above instability threshold is that the higher the pumping signal amplitude, the wider frequency range to have three stable solutions.

Figures 10.15 and 10.16 show the effects of nonlinear term in the amplitude of the steady state solution. As it can be seen, by increasing the order of nonlinear term, the amplitude of the amplifier is decreased, regardless of variation of pumping signal. It also leads to smaller frequency range for five steady state solutions when the pumping signal is above the linear stability threshold (Fig. 10.16).

Fig. 10.15
figure 001015

The impact of nonlinear term on the frequency response curves when pumping signal is under linear instability threshold

Full size image
Fig. 10.16
figure 001016

The effects of nonlinear term in the amplitude of the steady state solution when pumping signal is above linear instability threshold

Full size image

System Performance Metrics

An important parameter for evaluating system performance is the gain of the parametric amplifier which is defined according to Eq. (10.75). Parametric amplifier’s gain is the ratio of the steady state amplitude with pumping signal to amplitude without pumping signal. In order to study the effects of different parameters on performance of the amplifier, the gain of the system can be evaluated by changing parameters. To this end, a specific parameter of the system such as relative phase (\( \Phi \)) can be considered as variable, then by keeping other parameters as constant values, the gain is extracted. This procedure can be managed for all parameters of the system, including pumping, damping, nonlinearity, and detuning.

$$ G=\frac{{{a_{pump\ on }}}}{{{a_{pump\ \textit{off}}}}} $$
(10.75)

Firstly, the gain is calculated for linear system to examine the effects of parameters such as damping and relative excitation phase. Figure 10.17 illustrates the effects of pumping signal and damping on the gain of the system. It is clear from this figure that the gain becomes boundless when the pumping signal reaches to instability threshold. Moreover, as it can be observed, damping term does not have an effective impact on gain, but with higher damping, the pumping signal should and can be more increased to result in a better gain. Figure 10.18 shows the effects of relative phase excitation (\( \Phi \)) on gain of the linear system for different pumping signal. According to the graphs of Fig. 10.18, the excitation phase can change the gain of the system in different orders. Although the excitation phase is not such important parameter in small pumping levels, it has a great role to play when the amplitude of pumping signal is large enough and close to instability threshold. This outcome can be discussed from another point of view, in which the pumping signal is kept constant and the damping parameter is varied. In fact, when the damping decreases, the required pumping signal for high gain value that arises near instability threshold reduces. Figure 10.19 demonstrates the results for this case.

Fig. 10.17
figure 001017

The effects of pumping signal and damping on the gain of the linear system (instability restricts pumping signal)

Full size image
Fig. 10.18
figure 001018

The effects of pumping signal and relative phase excitation on the gain of the linear system (relative phase is important when the pumping signal amplitude is large enough)

Full size image
Fig. 10.19
figure 001019

The effects of damping and relative phase excitation on the gain of the linear system (relative phase is important when the pumping signal amplitude is close to instability threshold)

Full size image

In the second place, the effect of nonlinearity is examined on system performance; Fig. 10.20 shows the gain of the amplifier for nonlinearity with different orders. Calculated gains indicate that the more the level of nonlinearity, the less the effectiveness of the amplifier. Undoubtedly, as it can be seen from the results, even very small nonlinearity term can dramatically decrease system performance; therefore, analysis results with linear approximation may significantly be different for an even slightly nonlinear system. In addition, the finding reveals that nonlinear amplifiers can work well over instability threshold constraint which was previously predicted for linear systems. Furthermore, there is no denying that as long as pumping amplitude is strong enough, large gains still can be acquired.

Fig. 10.20
figure 001020

The effects of nonlinearity and pumping signal on the gain of the amplifier (meaningful nonlinear amplifiers gain over linear instability threshold that is \( \boldsymbol{\uplambda} >4\zeta \))

Full size image

The impact of relative phase is also examined for different nonlinearity orders. According to Fig. 10.21, the more the order of nonlinearity, the more distortion occurs in the gain of the amplifier. In fact, the nonlinearity term change the phase in which maximum gain occurs that is due to the imposed asymmetry on the gain versus relative phase axis diagram. In addition, investigation of different detuning parameter for system performance has revealed small changes in system performance. According to Fig. 10.22, in low pumping signal amplitude region (e.g., \( \uplambda <0.04) \), small positive detuning from resonance frequency leads to higher system gain. In contrast, in high pumping signal amplitudes (e.g., \( \uplambda =0.08 ) \), the outcome from slight negative detuning provides better performance than working at resonance frequency (\( \sigma =0 \)).

Fig. 10.21
figure 001021

Gain vs. relative phase for different nonlinearity orders (as the order of nonlinearity increases, much distortion arises)

Full size image
Fig. 10.22
figure 001022

Gain vs. pumping signal (small improvement on system performance by tuning \( \boldsymbol{\upsigma} \))

Full size image

Conclusion

Governing equations of motion for mechanical and electromechanical parametric amplifiers in the literature were reviewed. According to them, a general equation of motion for a nonlinear classical degenerate parametric amplifier was considered. The study of the parametric amplifier with a cubic nonlinearity was accomplished by means of the method of multiple scales. The stability analysis for the steady state motion of the nonlinear degenerate parametric amplifier as well as trivial solution of the unforced linear system was conducted. All the steady state solutions demonstrated a Duffing-like behavior in their frequency response curves. In addition, the stable solution branches were switched to three when pumping amplitude was increased over the instability threshold constraint for the unforced linear system. Furthermore, the effects of nonlinearity, relative phase, pumping signal amplitude, and detuning parameters were investigated on system performance. The findings indicate that even very small nonlinearity term can dramatically decrease system performance as well as changing the relative phase in which maximum gain occurs. The paper attempted to show that nonlinear amplifiers are stable and can be realized when there is no alternative to avoid working in nonlinear range; nevertheless, nonlinearities limit the maximum gains of parametric amplifiers compared with classical linear amplifiers.