Abstract
This paper is a survey on the emerging theory of truncated Toeplitz operators. We begin with a brief introduction to the subject and then highlight the many recent developments in the field since Sarason’s seminal paper (Oper. Matrices 1(4):491–526, 2007).
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Although the subject has deep classical roots, the systematic study of truncated Toeplitz operators for their own sake was only recently spurred by the seminal 2007 paper of Sarason [88]. In part motivated by several of the problems posed in the aforementioned article, the area has undergone vigorous development during the past several years [13, 14, 23, 25, 28, 35, 45, 49–52, 56, 59, 65, 88–90, 92, 93, 96]. While several of the initial questions raised by Sarason have now been resolved, the study of truncated Toeplitz operators has nevertheless proven to be fertile ground, spawning both new questions and unexpected results. In this survey, we aim to keep the interested reader up to date and to give the uninitiated reader a historical overview and a summary of the important results and major developments in this area.
Our survey commences in Sect. 2 with an extensive treatment of the basic definitions, theorems, and techniques of the area. Consequently, we shall be brief in this introduction and simply declare that a truncated Toeplitz operator is the compression \(A_{\varphi }^{u}:\mathcal{K}_{u}\to\mathcal{K}_{u}\) of a classical Toeplitz operator T φ to a shift coinvariant subspace \(\mathcal{K}_{u}:=H^{2}\ominus uH^{2}\) of the classical Hardy space H 2. Here u denotes a nonconstant inner function and we write \(A^{u}_{\varphi }f = P_{u}(\varphi f)\) where P u denotes the orthogonal projection from L 2 onto \(\mathcal{K}_{u}\). Interestingly, the study of potentially unbounded truncated Toeplitz operators, having symbols φ in L 2 as opposed to L ∞, has proven to be spectacularly fruitful. Indeed, a number of important questions in the area revolve around this theme (e.g., the results of Sect. 5).
Before proceeding, let us first recall several instances where truncated Toeplitz operators have appeared in the literature. This will not only provide a historical perspective on the subject, but it will also illustrate the fact that truncated Toeplitz operators, in various guises, form the foundations of much of modern function-related operator theory.
Let us begin with the powerful Sz.-Nagy-Foiaş model theory for Hilbert space contractions, the simplest manifestation of which is the compressed shift \(A_{z}^{u}\) [16, 77–79, 82]. To be more specific, every Hilbert space contraction T having defect indices (1,1) and such that lim n→∞ T ∗ n=0 (SOT) is unitarily equivalent to \(A_{z}^{u}\) for some inner function u. Natural generalizations of this result are available to treat contractions with arbitrary defect indices by employing the machinery of vector-valued model spaces and operator-valued inner functions.
In his approach to the Gelfand problem, that is the characterization of the invariant subspace lattice LatV of the Volterra integration operator
on L 2[0,1], Sarason noted that the Volterra operator is unitarily equivalent to the Cayley transform of the compressed shift \(A_{z}^{u}\) corresponding to the atomic inner function \(u(z) = \exp( \frac {z+1}{z-1})\) [84]. This equivalence was then used in conjunction with Beurling’s Theorem to demonstrate the unicellularity of LatV [78, 79, 84, 86]. Interestingly, it turns out that the Volterra operator, and truncated Toeplitz operators in general, are natural examples of complex symmetric operators, a large class of Hilbert space operators which has also undergone significant development in recent years [24, 35, 45–50, 54, 55, 61, 63, 71, 72, 74, 103–107]. This link between truncated Toeplitz operators and complex symmetric operators is explored in Sect. 9.
Sarason himself identified the commutant of \(A^{u}_{z}\) as the set \(\{A^{u}_{\varphi }: \varphi \in H^{\infty}\}\) of all analytic truncated Toeplitz operators. He also obtained an H ∞ functional calculus for the compressed shift, establishing that \(\varphi (A_{z}^{u}) = A_{\varphi }^{u}\) holds for all φ in H ∞ [85]. These seminal observations mark the beginning of the so-called commutant lifting theory, which has been developed to great effect over the ensuing decades [42, 80, 91]. Moreover, these techniques have given new perspectives on several classical problems in complex function theory. For instance, the Carathéodory and Pick problems lead one naturally to consider lower triangular Toeplitz matrices (i.e., analytic truncated Toeplitz operators on \(\mathcal{K}_{z^{n}}\)) and the backward shift on the span of a finite collection of Cauchy kernels (i.e., \(A_{\overline{z}}^{u}\) on a finite dimensional model space \(\mathcal{K}_{u}\)). We refer the reader to the text [1] which treats these problems in greater detail and generality.
Toeplitz matrices, which can be viewed as truncated Toeplitz operators on \(\mathcal{K}_{z^{n}}\), have long been the subject of intense research. We make no attempt to give even a superficial discussion of this immense topic. Instead, we merely refer the reader to several recent texts which analyze various aspects of this fascinating subject. The pseudospectral properties of Toeplitz matrices are explored in [100]. The asymptotic analysis of Toeplitz operators on H 2 via large truncated Toeplitz matrices is the focus of [19]. The role played by Toeplitz determinants in the study of orthogonal polynomials is discussed in [94, 95] and its relationship to random matrix theory is examined in [15, 70]. Finally, we should also remark that a special class of Toeplitz matrices, namely circulant matrices, are a crucial ingredient in many aspects of numerical computing [37].
We must also say a few words about the appearance of truncated Toeplitz operators in applications to control theory and electrical engineering. In such contexts, extremal problems posed over H ∞ often appear. It is well-known that the solution to many such problems can be obtained by computing the norm of an associated Hankel operator [43, 44]. However, it turns out that many questions about Hankel operators can be phrased in terms of analytic truncated Toeplitz operators and, moreover, this link has long been exploited [81, Eq. (2.9)]. Changing directions somewhat, we remark that the skew Toeplitz operators arising in H ∞ control theory are closely related to selfadjoint truncated Toeplitz operators [17, 18].
Among other things, Sarason’s recent article [88] is notable for opening the general study of truncated Toeplitz operators, beyond the traditional confines of the analytic (φ∈H ∞) and co-analytic (\(\overline{\varphi } \in H^{\infty}\)) cases and the limitations of the case u=z N (i.e., Toeplitz matrices), all of which are evidently well-studied in the literature. By permitting arbitrary symbols in L ∞, and indeed under some circumstances in L 2, an immense array of new theorems, novel observations, and difficult problems emerges. It is our aim in this article to provide an overview of the ensuing developments, with an eye toward promoting further research. In particular, we make an effort to highlight open problems and unresolved issues which we hope will spur further advances.
2 Preliminaries
In this section we gather together some of the standard results on model spaces and Aleksandrov-Clark measures which will be necessary for what follows. Since most of this material is familiar to those who have studied Sarason’s article [88], the following presentation is somewhat terse. Indeed, it serves primarily as a review of the standard notations and conventions of the field.
2.1 Basic Notation
Let \(\mathbb{D}\) be the open unit disk, \(\partial \mathbb{D}\) the unit circle, m=dθ/2π normalized Lebesgue measure on \(\partial \mathbb {D}\), and \(L^{p} := L^{p}( \partial \mathbb {D}, m)\) be the standard Lebesgue spaces on \(\partial \mathbb {D}\). For 0<p<∞ we use H p to denote the classical Hardy spaces on \(\mathbb{D}\) and H ∞ to denote the bounded analytic functions on \(\mathbb{D}\). As is standard, we regard H p as a closed subspace of L p by identifying each f∈H p with its m-almost everywhere defined L p boundary function
In the Hilbert space setting H 2 (or L 2) we denote the norm as ∥⋅∥ and the usual integral inner product by 〈⋅,⋅〉. On the rare occasions when we need to discuss L p norms we will use ∥⋅∥ p . We let \(\widehat{\mathbb{C}}\) denote the Riemann sphere ℂ∪{∞} and, for a set A⊆ℂ, we let A − denote the closure of A. For a subset V⊂L p, we let \(\overline{V} :=\{\overline {f}: f \in V\}\). We interpret the Cauchy integral formula
valid for all f in H 2, in the context of reproducing kernel Hilbert spaces by writing f(λ)=〈f,c λ 〉 where
denotes the Cauchy kernel (also called the Szegő kernel). A short computation now reveals that the orthogonal projection P + from L 2 onto H 2 (i.e., the Riesz projection) satisfies
for all f∈L 2 and \(\lambda\in\mathbb{D}\).
2.2 Model Spaces
Let S:H 2→H 2 denote the unilateral shift
and recall that Beurling’s Theorem asserts that the nonzero S-invariant subspaces of H 2 are those of the form uH 2 for some inner function u. Letting
denote the backward shift operator, it follows that the proper S ∗-invariant subspaces of H 2 are precisely those of the form
The subspace (5) is called the model space corresponding to the inner function u, the terminology stemming from the important role that \(\mathcal{K}_{u}\) plays in the model theory for Hilbert space contractions [79, Part C].
Although they will play only a small role in what follows, we should also mention that the backward shift invariant subspaces of the Hardy spaces H p for 0<p<∞ are also known. In particular, for 1⩽p<∞ the proper backward shift invariant subspaces of H p are all of the form
where \(H^{p}_{0}\) denotes the subspace of H p consisting of those H p functions which vanish at the origin and where the right-hand side of (6) is to be understood in terms of boundary functions on \(\partial \mathbb {D}\). For further details and information on the more difficult case 0<p<1, we refer the reader to the text [27] and the original article [4] of Aleksandrov. For p=2, we often suppress the exponent and simply write \(\mathcal{K}_{u}\) in place of \(\mathcal{K}_{u}^{2}\).
2.3 Pseudocontinuations
Since the initial definition (6) of \(\mathcal{K}_{u}^{p}\) is somewhat indirect, one might hope for a more concrete description of the functions belonging to \(\mathcal{K}_{u}^{p}\). A convenient function-theoretic characterization of \(\mathcal{K}_{u}^{p}\) is provided by the following important result.
Theorem 1
(Douglas-Shapiro-Shields [39])
If 1⩽p<∞, then f belongs to \(\mathcal{K}_{u}^{p}\) if and only if there exists a \(G \in H^{p}(\widehat{\mathbb{C}} \backslash\mathbb {D}^{-})\) which vanishes at infinity Footnote 1 such that
for almost every ζ on \(\partial \mathbb {D}\).
The function G in the above theorem is called a pseudocontinuation of f/u to \(\widehat{\mathbb{C}} \backslash\mathbb{D}^{-}\). We refer the reader to the references [5, 27, 39, 83] for further information about pseudocontinuations and their properties. An explicit function theoretic parametrization of the spaces \(\mathcal{K}_{u}^{p}\) is discussed in detail in [45].
2.4 Kernel Functions, Conjugation, and Angular Derivatives
Letting P u denote the orthogonal projection from L 2 onto \(\mathcal{K}_{u}\), we see that
for each λ in \(\mathbb{D}\). Here
denotes the reproducing kernel for \(\mathcal{K}_{u}\). In particular, this family of functions has the property that f(λ)=〈f,k λ 〉 for every \(f \in\mathcal{K}_{u}\) and \(\lambda\in\mathbb{D}\).
Each model space \(\mathcal{K}_{u}\) carries a natural conjugation (an isometric, conjugate-linear involution) \(C: \mathcal{K}_{u} \to\mathcal{K}_{u}\), defined in terms of boundary functions by
For notational convenience, we sometimes denote the conjugate Cf of f by \(\tilde{f}\). More information about conjugations in general, along with specific properties of the map (9) can be found in [45]. For the moment, we simply mention that the so-called conjugate kernels
will be important in what follows. In particular, observe that each conjugate kernel is a difference quotient for the inner function u. We therefore expect that derivatives will soon enter the picture.
Definition 1
For an inner function u and a point ζ on \(\partial \mathbb {D}\) we say that u has an angular derivative in the sense of Carathéodory (ADC) at ζ if the nontangential limits of u and u′ exist at ζ and |u(ζ)|=1.
The following theorem provides several useful characterizations of ADCs.
Theorem 2
(Ahern-Clark [3])
For an inner function u=b Λ s μ , where b Λ is a Blaschke product with zeros \(\varLambda= \{\lambda_{n}\}_{n=1}^{\infty}\), repeated according to multiplicity, s μ is a singular inner function with corresponding singular measure μ, and \(\zeta\in \partial \mathbb {D}\), the following are equivalent:
-
(i)
Every \(f \in\mathcal{K}_{u}\) has a nontangential limit at ζ.
-
(ii)
For every \(f \in\mathcal{K}_{u}\), f(λ) is bounded as λ→ζ nontangentially.
-
(iii)
u has an ADC at ζ.
-
(iv)
The function
$$ k_{\zeta}(z) = \frac{1 - \overline{u(\zeta)} u(z)}{1 - \overline {\zeta} z}, $$(11)belongs to H 2.
-
(v)
The following condition holds:
$$ \sum_{n \geq1} \frac{1 - |\lambda_{n}|^2}{|\zeta- \lambda_{n}|^2} + \int _{ \partial \mathbb {D}} \frac{d \mu(\xi)}{|\xi- \zeta|^2} < \infty. $$(12)
In fact, the preceding is only a partial statement of the Ahern-Clark result, for there are several other additional conditions which can be appended to the preceding list. Moreover, they also characterized the existence of nontangential boundary limits of the derivatives (up to a given order) of functions in \(\mathcal{K}_{u}\). An extension of Theorem 2 to the spaces \(\mathcal {K}_{u}^{p}\) is due to Cohn [32].
Among other things, Theorem 2 tells us that whenever u has an ADC at a point ζ on \(\partial \mathbb {D}\), then the functions (11), are reproducing kernels for \(\mathcal{K}_{u}\) in the sense that the reproducing property f(ζ)=〈f,k ζ 〉 holds for all f in \(\mathcal {K}_{u}\). In a similar manner, the functions
are also defined and belong to \(\mathcal{K}_{u}\) whenever u has an ADC at ζ.
2.5 Two Results of Aleksandrov
Letting H ∞ denote the Banach algebra of all bounded analytic functions on \(\mathbb{D}\), we observe that the set \(\mathcal{K}_{u}^{\infty} := \mathcal{K}_{u} \cap H^{\infty}\) is dense in \(\mathcal{K}_{u}\) since span{S ∗ n u:n=1,2,…} is dense in \(\mathcal{K}_{u}\). Another way to see that \(\mathcal{K}_{u}^{\infty}\) is dense in \(\mathcal{K}_{u}\) is to observe that each reproducing kernel (8) belongs to \(\mathcal{K}_{u}^{\infty}\) whence span{k λ :λ∈Λ} is dense in \(\mathcal{K}_{u}\) whenever Λ is a uniqueness set for \(\mathcal{K}_{u}\).
For many approximation arguments, the density of \(\mathcal {K}_{u}^{\infty}\) in \(\mathcal{K}_{u}\) is sufficient. In other circumstances, however, one requires continuity up to the boundary. Unfortunately, for many inner functions (e.g., singular inner functions) it is difficult to exhibit a single nonconstant function in \(\mathcal{K}_{u}\) which is continuous on \(\mathbb{D}^{-}\) (i.e., which belongs to the intersection of \(\mathcal{K}_{u}\) with the disk algebra \(\mathcal{A}\)). The following surprising result asserts that \(\mathcal{K}_{u} \cap\mathcal{A}\), far from being empty, is actually dense in \(\mathcal{K}_{u}\).
Theorem 3
(Aleksandrov [6])
For p∈(1,∞), \(\mathcal{K}_{u}^{p} \cap\mathcal{A}\) is dense in \(\mathcal{K}_{u}^{p}\).
A detailed exposition of Aleksandrov’s density theorem can be found in [26, p. 186]. For related results concerning whether or not \(\mathcal{K}_{u}\) contains functions of varying degrees of smoothness, the reader is invited to consult [41]. One consequence of Theorem 3 is that it allows us to discuss whether or not \(\mathcal{K}_{u}^{p}\) can be embedded in L p(μ) where μ is a measure on \(\partial \mathbb {D}\).
Theorem 4
(Aleksandrov [6])
Let u be an inner function, μ be a positive Borel measure on \(\partial \mathbb {D}\), and p∈(1,∞). If there exists a C>0 such that
then every function in \(\mathcal{K}_{u}^{p}\) has a finite nontangential limit μ-almost everywhere and (13) holds for all \(f \in \mathcal{K}_{u}^{p}\).
It is clear that every measure on \(\partial \mathbb {D}\) which is also Carleson measure (see [62]) satisfies (13). However, there are generally many other measures which also satisfy (13). For example, if u has an ADC at ζ, then the point mass δ ζ satisfies (13) with p=2.
2.6 The Compressed Shift
Before introducing truncated Toeplitz operators in general in Sect. 2.9, we should first introduce and familiarize ourselves with the most important and well-studied example. The so-called compressed shift operator is simply the compression of the unilateral shift (3) to a model space \(\mathcal{K}_{u}\):
The adjoint of \(A_{z}^{u}\) is the restriction of the backward shift (4) to \(\mathcal{K}_{u}\). Being the compression of a contraction, it is clear that \(A_{z}^{u}\) is itself a contraction and in fact, such operators and their vector-valued analogues can be used to model certain types of contractive operators [16, 77–79]. The following basic properties of \(A_{z}^{u}\) are well-known and can be found, for instance, in [78, 88].
Theorem 5
If u is a nonconstant inner function, then
-
(i)
The invariant subspaces of \(A_{z}^{u}\) are vH 2∩(uH 2)⊥, where v is an inner function which divides u (i.e., u/v∈H ∞).
-
(ii)
\(A_{z}^{u}\) is cyclic with cyclic vector k 0. That is to say, the closed linear span of \(\{(A^{u}_{z})^{n} k_{0}: n = 0, 1, 2, \ldots\}\mbox{ \textit{is equal to} }\mathcal{K}_{u}\). Moreover, \(f \in\mathcal{K}_{u}\) is cyclic for \(A^{u}_{z}\) if and only if u and the inner factor of f are relatively prime.
-
(iii)
\(A_{z}^{u}\) is irreducible (i.e., has no proper, nontrivial reducing subspaces).
To discuss the spectral properties of \(A_{z}^{u}\) we require the following definition.
Definition 2
If u is an inner function, then the spectrum σ(u) of u is the set
If u=b Λ s μ , where b is a Blaschke product with zero sequence Λ={λ n } and s μ is a singular inner function with corresponding singular measure μ, then
The following related lemma is well-known result of Moeller and we refer the reader to [78, p. 65] or [27, p. 84] for its proof.
Lemma 1
Each function in \(\mathcal{K}_{u}\) can be analytically continued across \(\partial \mathbb {D}\backslash\sigma(u)\).
An explicit description of the spectrum of the compressed shift \(A_{z}^{u}\) can be found in Sarason’s article [88, Lemma 2.5], although portions of it date back to the work of Livšic and Moeller [78, Lec. III.1].
Theorem 6
If u is an inner function, then
-
(i)
The spectrum \(\sigma(A^{u}_{z})\) of \(A_{z}^{u}\) is equal to σ(u).
-
(ii)
The point spectrum of \(\sigma_{p}(A^{u}_{z})\) of \(A_{z}^{u}\) is equal to \(\sigma(u) \cap\mathbb{D}\).
-
(iii)
The essential spectrum \(\sigma_{e}(A^{u}_{z})\) of \(A_{z}^{u}\) is equal to \(\sigma(u) \cap \partial \mathbb {D}\).
2.7 Clark Unitary Operators and Their Spectral Measures
Maintaining the notation and conventions of the preceding subsection, let us define, for each \(\alpha\in \partial \mathbb {D}\), the following operator on \(\mathcal{K}_{u}\):
In the above, the operator f⊗g, for f,g∈H 2, is given by the formula
A seminal result of Clark [29] asserts that each U α is a cyclic unitary operator and, moreover, that every unitary, rank-one perturbation of \(A^{u}_{z}\) is of the form (15). Furthermore, Clark was even able to concretely identify the corresponding spectral measures σ α for these so-called Clark operators. We discuss these results below (much of this material is presented in greater detail in the recent text [26]).
Theorem 7
(Clark)
For each \(\alpha\in \partial \mathbb {D}\), U α is a cyclic unitary operator on \(\mathcal{K}_{u}\). Moreover, any unitary rank-one perturbation of \(A^{u}_{z}\) is equal to U α for some \(\alpha\in \partial \mathbb {D}\).
The spectral theory for the Clark operators U α is well-developed and explicit. For instance, if u(0)=0, then a point ζ on \(\partial \mathbb {D}\) is an eigenvalue of U α if and only if u has an ADC at ζ and u(ζ)=α. The corresponding eigenvector is
which is simply a boundary kernel (11).
Since each U α is cyclic, there exists a measure σ α , supported on \(\partial \mathbb {D}\), so that U α is unitarily equivalent to the operator M z :L 2(σ α )→L 2(σ α ) of multiplication by the independent variable on the Lebesgue space L 2(σ α ), i.e., M z f=zf. To concretely identify the spectral measure σ α , we require an old theorem of Herglotz, which states that any positive harmonic function on \(\mathbb{D}\) can be written as the Poisson integral
of some unique finite, positive, Borel measure σ on \(\partial \mathbb {D}\) [40, Theorem 1.2].
Theorem 8
(Clark)
If σ α is the unique measure on \(\partial \mathbb {D}\) satisfying
then U α is unitarily equivalent to the operator M z :L 2(σ α )→L 2(σ α ) defined by M z f=zf.
The Clark measures \(\{\sigma_{\alpha}: \alpha\in \partial \mathbb {D}\}\) corresponding to an inner function u have many interesting properties. We summarize some of these results in the following theorem. The reader may consult [26] for further details.
Theorem 9
-
(i)
σ α is singular with respect to Lebesgue measure for each \(\alpha\in \partial \mathbb {D}\).
-
(ii)
σ α ⊥σ β when α≠β.
-
(iii)
(Nevanlinna) σ α ({ζ})>0 if and only if u(ζ)=α and u has an ADC at ζ. Moreover,
$$ \sigma_{\alpha}\bigl(\{\zeta\}\bigr) = \frac{1}{|u'(\zeta)|}. $$ -
(iv)
(Aleksandrov) For any \(f \in C( \partial \mathbb {D})\) we have
$$ \int_{ \partial \mathbb {D}} \biggl( \int_{ \partial \mathbb {D}} g(\zeta) \,d\sigma_{\alpha}(\zeta ) \biggr) \,dm(\alpha) = \int _{ \partial \mathbb {D}} g(\zeta) \,dm(\zeta). $$(17)
Condition (iv) of the preceding theorem is a special case of the Aleksandrov disintegration theorem: If g belongs to L 1, then the map
is defined for m-almost every α in \(\partial \mathbb {D}\) and, as a function of α, it belongs to L 1 and satisfies the natural analogue of (17). In fact, the Clark measures σ α are often called Aleksandrov-Clark measures in light of Aleksandrov’s deep work on the subject, which actually generalizes to measures μ α on \(\partial \mathbb {D}\) satisfying
for arbitrary functions u belonging to the unit ball of H ∞. The details and ramifications of this remarkable result are discussed in detail in [26].
2.8 Finite Dimensional Model Spaces
It is not hard to show that the model space \(\mathcal{K}_{u}\) is finite dimensional if and only if u is a finite Blaschke product. In fact, if u is a finite Blaschke product with zeros λ 1,λ 2,…,λ N , repeated according to multiplicity, then \(\dim\mathcal{K}_{u} = N\) and
With respect to the representation (18), the conjugation (9) on \(\mathcal{K}_{u}\) assumes the simple form
If the zeros of u are distinct, then the Cauchy kernels \(c_{\lambda _{i}}\) from (2) corresponding to the λ i form a basis for \(\mathcal{K}_{u}\) whence
If some of the λ i are repeated, then one must include the appropriate derivatives of the \(c_{\lambda_{i}}\) to obtain a basis for \(\mathcal{K}_{u}\).
Although the natural bases for \(\mathcal{K}_{u}\) described above are not orthogonal, a particularly convenient orthonormal basis exists. For \(\lambda\in \mathbb{D}\), let
be a disk automorphism with a zero at λ and for each 1≤n≤N let
The following important fact was first observed by Takenaka [98] in 1925, although it has been rediscovered many times since.
Theorem 10
(Takenaka)
{γ 1,γ 2,…,γ N } is an orthonormal basis for \(\mathcal{K}_{u}\).
If u is an infinite Blaschke product, then an extension, due to Walsh [78], of the preceding result tells us that {γ 1,γ 2,…} is an orthonormal basis for \(\mathcal{K}_{u}\).
Let us return now to the finite dimensional setting. Suppose that u is a finite Blaschke product with N zeros, repeated according to multiplicity. To avoid some needless technical details, we assume that u(0)=0. If {ζ 1,ζ 2,…,ζ N } are the eigenvalues of the Clark unitary operator
(i.e., the N distinct solutions on \(\partial \mathbb {D}\) to u(ζ)=α), then the corresponding eigenvectors \(\{k_{\zeta_{1}}, k_{\zeta _{2}},\ldots, k_{\zeta_{N}}\}\) are orthogonal. A routine computation shows that \(\|k_{\zeta_{j}}\| = \sqrt{|u'(\zeta)|}\) so that
is an orthonormal basis for \(\mathcal{K}_{u}\). This is called a Clark basis for \(\mathcal{K}_{u}\). Letting \(w_{j} = \exp (-\frac{1}{2}(\arg\zeta_{j} - \arg\alpha ) )\), it turns out that
is an orthonormal basis for \(\mathcal{K}_{u}\), each vector of which is fixed by the conjugation (9) on \(\mathcal{K}_{u}\) (i.e., in the terminology of [49], (21) is a C-real basis for \(\mathcal{K}_{u}\)). We refer to a basis of the form (21) as a modified Clark basis for \(\mathcal{K}_{u}\) (see [45] and [51] for further details).
2.9 Truncated Toeplitz Operators
The truncated Toeplitz operator \(A_{\varphi }^{u}\) on \(\mathcal {K}_{u}\) having symbol φ in L 2 is the closed, densely defined operator
having domainFootnote 2

When there is no danger of confusion, we sometimes write A φ in place of \(A_{\varphi }^{u}\). A detailed discussion of unbounded truncated Toeplitz operators and their properties can be found in Sect. 10. For the moment, we focus on those truncated Toeplitz operators which can be extended to bounded operators on \(\mathcal{K}_{u}\).
Definition 3
Let  denote the set of all bounded truncated Toeplitz operators on \(\mathcal{K}_{u}\).
denote the set of all bounded truncated Toeplitz operators on \(\mathcal{K}_{u}\).
For Toeplitz operators, recall that ∥T φ ∥=∥φ∥∞ holds for each φ in L ∞. In contrast, we can say little more than
for general truncated Toeplitz operators. In fact, computing, or at least estimating, the norm of a truncated Toeplitz operator is a difficult problem. This topic is discussed in greater detail in Sect. 4. However, a complete characterization of those symbols which yield the zero operator has been obtained by Sarason [88, Theorem 3.1].
Theorem 11
(Sarason)
A truncated Toeplitz operator \(A^{u}_{\varphi }\) is identically zero if and only if \(\varphi \in uH^{2} + \overline{u H^{2}}\).
In particular, the preceding result tells us that there are always infinitely many symbols (many of them unbounded) which represent the same truncated Toeplitz operator. On the other hand, since \(A_{\varphi }^{u} = A_{\psi}^{u}\) if and only if ψ−φ belongs to \(u H^{2} + \overline{u H^{2}}\), we actually enjoy some freedom in specifying the symbol of a truncated Toeplitz operator. The following corollary makes this point concrete.
Corollary 1
If
A
belongs to
 , then there exist
φ
1
and
φ
2
in
\(\mathcal{K}_{u}\)
such that
\(A = A_{\varphi _{1} + \overline{\varphi _{2}}}\). Furthermore, φ
1
and
φ
2
are uniquely determined if we fix the value of one of them at the origin.
, then there exist
φ
1
and
φ
2
in
\(\mathcal{K}_{u}\)
such that
\(A = A_{\varphi _{1} + \overline{\varphi _{2}}}\). Furthermore, φ
1
and
φ
2
are uniquely determined if we fix the value of one of them at the origin.
To some extent, the preceding corollary can be reversed. As noted in [14], if we assume that  has a symbol \(\varphi _{1} + \overline{\varphi _{2}}\), where φ
1 and φ
2 belong to \(\mathcal{K}_{u}\) and φ
2(0)=0, then we can recover φ
1 and φ
2 by knowing the action of A on the reproducing kernels k
λ
and the conjugate reproducing kernels Ck
λ
. Indeed, one just needs to solve the following linear system in the variables φ
1(λ) and \(\overline{\varphi _{2}(\lambda)}\):
has a symbol \(\varphi _{1} + \overline{\varphi _{2}}\), where φ
1 and φ
2 belong to \(\mathcal{K}_{u}\) and φ
2(0)=0, then we can recover φ
1 and φ
2 by knowing the action of A on the reproducing kernels k
λ
and the conjugate reproducing kernels Ck
λ
. Indeed, one just needs to solve the following linear system in the variables φ
1(λ) and \(\overline{\varphi _{2}(\lambda)}\):

With more work, one can even obtain an estimate of max{∥φ 1∥,∥φ 2∥} [14].
Letting C denote the conjugation (9) on \(\mathcal{K}_{u}\), a direct computation confirms the following result from [49]:
Theorem 12
(Garcia-Putinar)
For any
 , we have
A=CA
∗
C.
, we have
A=CA
∗
C.
In particular, Theorem 12 says each truncated Toeplitz operator is a complex symmetric operator, a class of Hilbert space operators which has undergone much recent study [24, 35, 45–50, 54, 55, 61, 63, 71, 72, 74, 103–107]. In fact, it is suspected that truncated Toeplitz operators might serve as some sort of model operator for various classes of complex symmetric operators (see Sect. 9). For the moment, let us simply note that the matrix representation of a truncated Toeplitz operator \(A_{\varphi }^{u}\) with respect to a modified Clark basis (21) is complex symmetric (i.e., self-transpose). This was first observed in [49] and developed further in [45].
An old theorem of Brown and Halmos [20] says that a bounded operator T on H 2 is a Toeplitz operator if and only if T=STS ∗. Sarason recently obtained a version of this theorem for truncated Toeplitz operators [88, Theorem 4.1].
Theorem 13
(Sarason)
A bounded operator
A
on
\(\mathcal{K}_{u}\)
belongs to
 if and only if there are functions
\(\varphi , \psi\in\mathcal{K}_{u}\)
such that
if and only if there are functions
\(\varphi , \psi\in\mathcal{K}_{u}\)
such that
When \(\mathcal{K}_{u}\) is finite dimensional, one can get more specific results using matrix representations. For example, if u=z
N, then {1,z,…,z
N−1} is an orthonormal basis for \(\mathcal{K}_{z^{N}}\). Any operator in  represented with respect to this basis yields a Toeplitz matrix and, conversely, any N×N Toeplitz matrix gives rise to a truncated Toeplitz operator on \(\mathcal{K}_{z^{N}}\). Indeed the matrix representation of \(A_{\varphi }^{z^{N}}\) with respect to {1,z,…,z
N−1} is the Toeplitz matrix \((\widehat{\varphi }(j - k))_{j, k=0}^{N-1}\). For more general finite Blaschke products we have the following result from [28].
represented with respect to this basis yields a Toeplitz matrix and, conversely, any N×N Toeplitz matrix gives rise to a truncated Toeplitz operator on \(\mathcal{K}_{z^{N}}\). Indeed the matrix representation of \(A_{\varphi }^{z^{N}}\) with respect to {1,z,…,z
N−1} is the Toeplitz matrix \((\widehat{\varphi }(j - k))_{j, k=0}^{N-1}\). For more general finite Blaschke products we have the following result from [28].
Theorem 14
(Cima-Ross-Wogen)
Let
u
be a finite Blaschke product of degree
n
with distinct zeros
λ
1,λ
2,…,λ
n
and let
A
be any linear transformation on the
n-dimensional space
\(\mathcal{K}_{u}\). If
\(M_{A} = (r_{i, j})_{i,j=1}^{n}\)
is the matrix representation of
A
with respect to the basis
\(\{k_{\lambda_{1}},k_{\lambda_{2}}, \ldots, k_{\lambda_{n}}\}\), then
 if and only if
if and only if
for 1⩽i,j⩽n and i≠j.
Although the study of general truncated Toeplitz operators appears to be difficult, there is a distinguished subset of these operators which are remarkably tractable. We say that \(A_{\varphi }^{u}\) is an analytic truncated Toeplitz operator if the symbol φ belongs to H ∞, or more generally, to H 2. It turns out that the natural polynomial functional calculus \(p(A_{z}^{u}) = A_{p}^{u}\) can be extended to H ∞ in such a way that the symbol map \(\varphi \mapsto \varphi (A_{z}^{u}) := A_{\varphi }^{u}\) is linear, contractive, and multiplicative. As a broad generalization of Theorem 6, we have the following spectral mapping theorem [78, p. 66], the proof of which depends crucially on the famous Corona Theorem of L. Carleson [21].
Theorem 15
If φ∈H ∞, then
-
(i)
\(\sigma(A_{\varphi }^{u}) = \{ \lambda: \inf_{z\in\mathbb{D} }(|u(z)| + | \varphi (z) - \lambda|)=0 \}\).
-
(ii)
If \(\varphi \in H^{\infty} \cap C( \partial \mathbb {D})\), then \(\sigma(A_{\varphi }^{u}) = \varphi (\sigma(u))\).
We conclude this section by remarking that vector-valued analogues are available for most of the preceding theorems. However, these do not concern us here and we refer the reader to [78] for further details.
3
 as a Linear Space
as a Linear Space
Recent work of Baranov, Bessonov, and Kapustin [13] has shed significant light on the structure of  as a linear space. Before describing these results, let us first recount a few important observations due to Sarason. The next theorem is [88, Theorem 4.2].
as a linear space. Before describing these results, let us first recount a few important observations due to Sarason. The next theorem is [88, Theorem 4.2].
Theorem 16
(Sarason)
 is closed in the weak operator topology.
is closed in the weak operator topology.
It is important to note that  is not an operator algebra, for the product of truncated Toeplitz operators is rarely itself a truncated Toeplitz operator (the precise conditions under which this occurs were found by Sedlock [92, 93]). On the other hand,
is not an operator algebra, for the product of truncated Toeplitz operators is rarely itself a truncated Toeplitz operator (the precise conditions under which this occurs were found by Sedlock [92, 93]). On the other hand,  contains a number of interesting subsets which are algebras. The details are discussed in Sect. 7, followed in Sect. 8 by a brief discussion about C
∗-algebras generated by truncated Toeplitz operators.
contains a number of interesting subsets which are algebras. The details are discussed in Sect. 7, followed in Sect. 8 by a brief discussion about C
∗-algebras generated by truncated Toeplitz operators.
In order to better frame the following results, first recall that there are no nonzero compact Toeplitz operators on H 2 [20]. In contrast, there are many examples of finite rank (hence compact) truncated Toeplitz operators. In fact, the rank-one truncated Toeplitz operators were first identified by Sarason [88, Theorem 5.1].
Theorem 17
(Sarason)
For an inner function u, the operators
-
(i)
\(k_{\lambda} \otimes C k_{\lambda} = A^{u}_{\frac{\overline {u}}{\overline{z} - \overline{\lambda}}}\) for \(\lambda\in\mathbb{D}\),
-
(ii)
\(C k_{\lambda} \otimes k_{\lambda}= A^{u}_{\frac{u}{z - \lambda }}\) for \(\lambda\in\mathbb{D}\),
-
(iii)
\(k_{\zeta} \otimes k_{\zeta} = A^{u}_{k_{\zeta} + \overline {k_{\zeta}} - 1}\) where u has an ADC at \(\zeta\in \partial \mathbb {D}\),
are truncated Toeplitz operators having rank one. Moreover, any truncated Toeplitz operator of rank one is a scalar multiple of one of the above.
We should also mention the somewhat more involved results of Sarason [88, Theorems 6.1 & 6.2] which identify a variety of natural finite rank truncated Toeplitz operators. Furthermore, the following linear algebraic description of  has been obtained [88, Theorem 7.1] in the finite dimensional setting.
has been obtained [88, Theorem 7.1] in the finite dimensional setting.
Theorem 18
(Sarason)
If \(\dim\mathcal{K}_{u} = n\), then
-
(i)
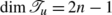 ,
, -
(ii)
If λ 1,λ 2,…,λ 2n−1 are distinct points of \(\mathbb{D}\), then the operators \(k_{\lambda_{j}}^{u} \otimes\tilde{k}_{\lambda_{j}}^{u}\) for j=1,2,…,2n−1 form a basis for
 .Footnote 3
.Footnote 3
When confronted with a novel linear space, the first questions to arise concern duality. Baranov, Bessonov, and Kapustin recently identified the predual of  and discussed the weak-∗ topology on
and discussed the weak-∗ topology on  [13]. Let us briefly summarize some of their major results. First consider the space
[13]. Let us briefly summarize some of their major results. First consider the space
with norm
It turns out that
and that each element of \(\mathcal{X}_{u}\) can be written as a linear combination of four elements of the form \(f \overline{g} \), where f and g belong to \(\mathcal{K}_{u}\). The importance of the space \(\mathcal{X}_{u}\) lies in the following important theorem and its corollaries.
Theorem 19
(Baranov-Bessonov-Kapustin [13])
For any inner function
u, \(\mathcal{X}_{u}^{*}\), the dual space of
\(\mathcal{X}_{u}\), is isometrically isomorphic to
 via the dual pairing
via the dual pairing

Furthermore, if
 denotes the compact truncated Toeplitz operators, then
denotes the compact truncated Toeplitz operators, then
 , the dual of
, the dual of
 , is isometrically isomorphic to
\(\mathcal{X}_{u}\).
, is isometrically isomorphic to
\(\mathcal{X}_{u}\).
Corollary 2
(Baranov-Bessonov-Kapustin)
-
(i)
The weak topology and the weak-∗ topology on
 are the same.
are the same. -
(ii)
The norm closed linear span of the rank-one truncated Toeplitz operators is
 .
. -
(iii)
 is weakly dense in
is weakly dense in
 .
.
For a general inner function u, we will see below that not every bounded truncated Toeplitz operator on \(\mathcal{K}_{u}\) has a bounded symbol (see Sect. 5). On the other hand, the following corollary holds in general.
Corollary 3
(Baranov-Bessonov-Kapustin)
The truncated Toeplitz operators with bounded symbols are weakly dense in
 .
.
This leaves open the following question.
Question 1
Are the truncated Toeplitz operators with bounded symbols norm dense in  ?
?
4 Norms of Truncated Toeplitz Operators
Recall that for φ in L ∞ we have the trivial estimates (22) on the norm of a truncated Toeplitz operator, but little other general information concerning this quantity. For φ in L 2, we may also consider the potentially unbounded truncated Toeplitz operator \(A_{\varphi }^{u}\). Of interest is the quantity
which we regard as being infinite if \(A_{\varphi }^{u}\) is unbounded. For \(A_{\varphi }^{u}\) bounded, (23) is simply the operator norm of \(A_{\varphi }^{u}\) in light of Theorem 3. Evaluation or estimation of (23) is further complicated by the fact that the representing symbol φ for \(A^{u}_{\varphi }\) is never unique (Theorem 11).
If u is a finite Blaschke product (so that the corresponding model space \(\mathcal{K}_{u}\) is finite dimensional) and φ belongs to H ∞, then straightforward residue computations allow us to represent \(A^{u}_{\varphi }\) with respect to any of the orthonormal bases mentioned earlier (i.e., the Takenaka (19), Clark (20), or modified Clark (21) bases). For \(\mathcal {K}_{z^{n}}\), the Takenaka basis is simply the monomial basis {1,z,z 2,…,z n−1} and the matrix representation of \(A_{\varphi }^{u}\) is just a lower triangular Toeplitz matrix. In any case, one can readily compute the norm of \(A^{u}_{\varphi }\) by computing the norm of one of its matrix representations. This approach was undertaken by the authors in [51]. One can also approach this problem using the theory of Hankel operators (see [81, Eq. (2.9)] and the method developed in [23]).
Let us illustrate the general approach with a simple example. If φ belongs to H ∞ and u is the finite Blaschke product with distinct zeros λ 1,λ 2,…,λ n , then the matrix representation for \(A^{u}_{\varphi }\) with respect to the modified Clark basis (21) is
In particular, observe that this matrix is complex symmetric, as predicted by Theorem 12. As a specific example, consider the Blaschke product
and the H ∞ function
The parameters in (24) are

which yields

On a somewhat different note, it is possible to obtain lower estimates of \(\|A_{\varphi }^{u}\|\) for general φ in L 2. This can be helpful, for instance, in determining whether a given truncated Toeplitz operator is unbounded. Although a variety of lower bounds on \(\| A_{\varphi }^{u} \|\) are provided in [52], we focus here on perhaps the most useful of these. We first require the Poisson integral
of a function φ in L 1. In particular, recall that \(\lim_{r \to1^{-}}(\mathfrak{P}\varphi )(r \zeta) = \varphi (\zeta)\) whenever φ is continuous at a point \(\zeta\in \partial \mathbb {D}\) [69, p. 32] or more generally, when ζ is a Lebesgue point of φ.
Theorem 20
(Garcia-Ross)
If φ∈L 2 and u is inner, then
where the supremum is regarded as 0 if u never vanishes on \(\mathbb{D}\).
Corollary 4
If φ belongs to \(C( \partial \mathbb {D})\) and u is an inner function whose zeros accumulate almost everywhere on \(\partial \mathbb {D}\), then \(\| A_{\varphi }^{u} \| = \| \varphi \|_{\infty}\).
A related result on norm attaining symbols can be found in [51].
Theorem 21
(Garcia-Ross)
If u is inner, φ∈H ∞, and \(A^{u}_{\varphi }\) is compact, then \(\|A^{u}_{\varphi }\| = \|\varphi \|_{\infty}\) if and only if φ is a scalar multiple of the inner factor of a function from \(\mathcal{K}_{u}\).
It turns out that the norm of a truncated Toeplitz operator can be related to certain classical extremal problems from function theory. For the following discussion we require a few general facts about complex symmetric operators [45, 49, 50]. Recall that a conjugation on a complex Hilbert space \(\mathcal{H}\) is a map \(C: \mathcal{H} \to\mathcal {H}\) which is conjugate-linear, involutive (i.e., C
2=I), and isometric (i.e., 〈Cx,Cy〉=〈y,x〉). A bounded linear operator \(T: \mathcal{H} \to\mathcal{H}\) is called C-symmetric if T=CT
∗
C and complex symmetric if there exists a conjugation C with respect to which T is C-symmetric. Theorem 12 asserts that each operator in  is C-symmetric with respect to the conjugation C on \(\mathcal{K}_{u}\) defined by (9). The following general result from [51] relates the norm of a given C-symmetric operator to a certain extremal problem (as is customary, |T| denotes the positive operator \(\sqrt{T^{*}T}\)).
is C-symmetric with respect to the conjugation C on \(\mathcal{K}_{u}\) defined by (9). The following general result from [51] relates the norm of a given C-symmetric operator to a certain extremal problem (as is customary, |T| denotes the positive operator \(\sqrt{T^{*}T}\)).
Theorem 22
(Garcia-Ross)
If \(T:\mathcal{H}\to\mathcal{H}\) is a bounded C-symmetric operator, then
-
(i)
∥T∥=sup∥x∥=1|〈Tx,Cx〉|.
-
(ii)
If ∥x∥=1, then ∥T∥=|〈Tx,Cx〉| if and only if Tx=ω∥T∥Cx for some unimodular constant ω.
-
(iii)
If T is compact, then the equation Tx=∥T∥Cx has a unit vector solution. Furthermore, this unit vector solution is unique, up to a sign, if and only if the kernel of the operator |T|−∥T∥I is one-dimensional.
Applying the Theorem 22 to \(A_{\varphi }^{u}\) we obtain the following result.
Corollary 5
For inner u and φ∈L ∞
For φ in H ∞, the preceding supremum can be taken over H 2.
Corollary 6
For inner u and φ∈H ∞
The preceding corollary relates the norm of a truncated Toeplitz operator to a certain quadratic extremal problem on H 2. We can relate this to a classical linear extremal problem in the following way. For a rational function ψ with no poles on \(\partial \mathbb {D}\) we have the well-studied classical H 1 extremal problem [40, 62]:
On the other hand, basic functional analysis tells us that
Following [51], we recall that the extremal problem Λ(ψ) has an extremal function F e (not necessarily unique). It is also known that F e can be taken to be outer and hence F e =f 2 for some f in H 2. Therefore the linear extremal problem Λ(ψ) and the quadratic extremal problem
have the same value. The following result from [51], combined with the numerical recipes discussed at the beginning of this section, permit one to explicitly evaluate many specific extremal problems. Before doing so, we remark that many of these problems can be attacked using the theory of Hankel operators, although in that case one must compute the norm of a finite-rank Hankel operator acting on an infinite-dimensional space. In contrast, the truncated Toeplitz approach employs only n×n matrices.
Corollary 7
Suppose that ψ is a rational function having no poles on \(\partial \mathbb {D}\) and poles λ 1,λ 2,…,λ n lying in \(\mathbb{D}\), counted according to multiplicity. Let u denote the associated Blaschke product whose zeros are precisely λ 1,λ 2,…,λ n and note that φ=uψ belongs to H ∞. We then have the following:
-
(i)
\(\|A^{u}_{\varphi }\| = \varGamma(\psi) = \varLambda(\psi)\).
-
(ii)
There is a unit vector \(f \in\mathcal{K}_{u}\) satisfying \(A^{u}_{\varphi } f = \|A^{u}_{\varphi }\| C f\) and any such f is an extremal function for Γ(ψ). In other words,
$$ \biggl \vert \frac{1}{2 \pi i} \oint_{ \partial \mathbb {D}} \psi f^2 \, dz \biggr \vert = \bigl\|A^u_{\varphi }\bigr\|. $$ -
(iii)
Every extremal function f for Γ(ψ) belongs to \(\mathcal{K}_{u}\) and satisfies
$$ A^u_{\varphi } f = \|A_{ \varphi }\| C f. $$ -
(iv)
An extremal function for Γ(ψ) is unique, up to a sign, if and only if the kernel of the operator \(|A^{u}_{\varphi }| - \|A^{u}_{\varphi }\| I\) is one-dimensional.
We refer the reader to [51] for several worked examples of classical extremal problems Λ(ψ) along with a computation of several extremal functions F e . For rational functions ψ with no poles on \(\partial \mathbb {D}\), we have seen that the linear (25) and the quadratic (26) extremal problems have the same value. Recent work of Chalendar, Fricain, and Timotin shows that this holds in much greater generality.
Theorem 23
(Chalendar-Fricain-Timotin [23])
For each ψ in L ∞, Γ(ψ)=Λ(ψ).
It is important to note that for general ψ in L ∞ an extremal function for Λ(ψ) need not exist (see [51] for a relevant discussion). Nevertheless, for ψ in L ∞, Chalendar, Fricain, and Timotin prove that Λ(ψ)=Γ(ψ) by using the fact that Λ(ψ)=∥H ψ ∥, where H ψ :H 2→L 2⊖H 2 is the corresponding Hankel operator H ψ f=P −(ψf). Here P − denotes the orthogonal projection from L 2 onto L 2⊖H 2. We certainly have the inequality
When equality holds in the preceding, we say that the symbol ψ is norm attaining. The authors of [23] prove the following.
Theorem 24
(Chalendar-Fricain-Timotin)
If ψ∈L ∞ is norm attaining then ψ has constant modulus and there exists an extremal outer function for Λ(ψ).
Before proceeding, we should also mention the fact that computing the norm of certain truncated Toeplitz operators and solving their related extremal problems have been examined for quite some time in the study of H ∞ control theory and skew-Toeplitz operators [17, 18, 43, 44]. In the scalar setting, a skew-Toeplitz operator is a truncated Toeplitz operator \(A^{u}_{\varphi }\), where the symbol takes the form
making \(A_{\varphi }^{u}\) self-adjoint. In H ∞ control theory, the extremal problem
where ψ is a rational function belonging to H ∞, plays an important role. From the preceding results, we observe that \(\|A^{u}_{\psi}\| = \mbox{dist}(\psi, u H^{\infty})\).
5 The Bounded Symbol and Related Problems
Recall that  denotes the set of all truncated Toeplitz operators \(A_{\varphi }^{u}\), densely defined on \(\mathcal{K}_{u}\) and having symbols φ in L
2, that can be extended to bounded operators on all of \(\mathcal{K}_{u}\). As a trivial example, if φ belongs to L
∞, then clearly \(A_{\varphi }^{u}\) belongs to
denotes the set of all truncated Toeplitz operators \(A_{\varphi }^{u}\), densely defined on \(\mathcal{K}_{u}\) and having symbols φ in L
2, that can be extended to bounded operators on all of \(\mathcal{K}_{u}\). As a trivial example, if φ belongs to L
∞, then clearly \(A_{\varphi }^{u}\) belongs to  . A major open question involved the converse. In other words, if \(A_{\varphi }^{u}\) is a bounded truncated Toeplitz operator, does there exist a symbol φ
0 in L
∞ such that \(A_{\varphi }^{u} = A_{\varphi _{0}}^{u}\)? This question was recently resolved in the negative by Baranov, Chalendar, Fricain, Mashreghi, and Timotin [14]. We describe this groundbreaking work, along with important related contributions by Baranov, Bessonov, and Kapustin [13], below.
. A major open question involved the converse. In other words, if \(A_{\varphi }^{u}\) is a bounded truncated Toeplitz operator, does there exist a symbol φ
0 in L
∞ such that \(A_{\varphi }^{u} = A_{\varphi _{0}}^{u}\)? This question was recently resolved in the negative by Baranov, Chalendar, Fricain, Mashreghi, and Timotin [14]. We describe this groundbreaking work, along with important related contributions by Baranov, Bessonov, and Kapustin [13], below.
For symbols φ in H 2, a complete and elegant answer to the bounded symbol problem is available. In the following theorem, the implication (i) ⇔ (ii) below is due to Sarason [85]. Condition (iii) is often referred to as the reproducing kernel thesis for \(A_{\varphi }^{u}\).
Theorem 25
(Baranov, Chalendar, Fricain, Mashreghi, Timotin [14])
For φ∈H 2, the following are equivalent.
-
(i)
 .
. -
(ii)
\(A_{\varphi }^{u} = A_{\varphi _{0}}^{u}\) for some φ 0∈H ∞.
-
(iii)
\(\sup_{\lambda\in\mathbb{D}} \Vert A_{\varphi }^{u} \frac {k_{\lambda }}{\|k_{\lambda}\|}\Vert < \infty\).
Furthermore, there exists a universal constant
C>0 so that any
 with
φ∈H
2, has a bounded symbol
φ
0
such that
with
φ∈H
2, has a bounded symbol
φ
0
such that
The following result demonstrates the existence of bounded truncated Toeplitz operators with no bounded symbol (a small amount of function theory, discussed below, is required to exhibit concrete examples). Recall from Theorem 17 that for ζ in \(\partial \mathbb {D}\), the rank one operator k
ζ
⊗k
ζ
belongs to  if and only if u has an ADC at ζ. Using two technical lemmas from [14] (Lemmas 5.1 and 5.2), they prove the following theorem.
if and only if u has an ADC at ζ. Using two technical lemmas from [14] (Lemmas 5.1 and 5.2), they prove the following theorem.
Theorem 26
(Baranov, Chalendar, Fricain, Mashreghi, Timotin)
If u has an ADC at \(\zeta\in \partial \mathbb {D}\) and p∈(2,∞), then the following are equivalent:
-
(i)
k ζ ⊗k ζ has a symbol in L p.
-
(ii)
k ζ ∈L p.
Consequently, if
k
ζ
∉L
p
for some
p∈(2,∞), then
k
ζ
⊗k
ζ
belongs to
 and has no bounded symbol.
and has no bounded symbol.
From Theorem 2 we know that if u=b Λ s μ , where b is a Blaschke product with zeros \(\varLambda= \{\lambda_{n}\}_{n = 1}^{\infty}\) (repeated according to multiplicity) and s μ is a singular inner function with corresponding singular measure μ, then
This was extended [3, 32] to p∈(1,∞) as follows:
Based upon this, one can arrange it so that k ζ belongs to H 2 but not to H p for any p>2. This yields the desired example of a bounded truncated Toeplitz operator which cannot be represented using a bounded symbol. We refer the reader to the article [14] where the details and further examples are considered.
Having seen that there exist bounded truncated Toeplitz operators which lack bounded symbols, it is natural to ask if there exist inner functions u so that every operator in  has a bounded symbol? Obviously this holds when u is a finite Blaschke product. Indeed, in this case the symbol can be taken to be a polynomial in z and \(\overline{z}\). A more difficult result is the following (note that the initial symbol φ belongs to L
2, as opposed to H
2, as was the case in Theorem 25).
has a bounded symbol? Obviously this holds when u is a finite Blaschke product. Indeed, in this case the symbol can be taken to be a polynomial in z and \(\overline{z}\). A more difficult result is the following (note that the initial symbol φ belongs to L
2, as opposed to H
2, as was the case in Theorem 25).
Theorem 27
(Baranov, Chalendar, Fricain, Mashreghi, Timotin)
If a>0, \(\zeta\in \partial \mathbb {D}\), and
then the following are equivalent for φ∈L 2:
-
(i)
 .
. -
(ii)
\(A_{\varphi }^{u} = A_{\varphi _{0}}^{u}\) for some φ 0∈L ∞.
-
(iii)
\(\sup_{\lambda\in\mathbb{D}} \Vert A_{\varphi }^{u} \frac {k_{\lambda }}{\|k_{\lambda}\|}\Vert < \infty\).
Furthermore, there exists a universal constant
C>0 so that any
 with
φ∈L
2, has a bounded symbol
φ
0
such that
with
φ∈L
2, has a bounded symbol
φ
0
such that
In light of Theorems 25 and 27, one might wonder whether condition (iii) (the reproducing kernel thesis) is always equivalent to asserting that \(A_{\varphi }^{u}\) belongs to  . Unfortunately, the answer is again negative [14, Sect. 5].
. Unfortunately, the answer is again negative [14, Sect. 5].
On a positive note, Baranov, Bessonov, and Kapustin recently discovered a condition on the inner function u which ensures that every operator in  has a bounded symbol [13]. After a few preliminary details, we discuss their work below.
has a bounded symbol [13]. After a few preliminary details, we discuss their work below.
Definition 4
For p>0, let \(\mathcal{C}_{p}(u)\) denote the finite complex Borel measures μ on \(\partial \mathbb {D}\) such that \(\mathcal{K}_{u}^{p}\) embeds continuously into L p(|μ|).
Since S ∗ u belongs to \(\mathcal{K}_{u}\), it follows from Aleksandrov’s embedding theorem (Theorem 4) that for each μ in \(\mathcal {C}_{2}(u)\), the boundary values of u are defined |μ|-almost everywhere. Moreover, it turns out that |u|=1 holds |μ|-almost everywhere [6, 13]. For \(\mu\in\mathcal{C}_{2}(u)\) the quadratic form
is continuous and so, by elementary functional analysis, there is a bounded operator \(\mathcal{A}_{\mu}: \mathcal{K}_{u} \to\mathcal{K}_{u}\) such that
The following important result of Sarason [88, Theorem 9.1] asserts that each such \(\mathcal{A}_{\mu}\) is a truncated Toeplitz operator.
Theorem 28
(Sarason)
 whenever
\(\mu\in\mathcal{C}_{2}(u)\).
whenever
\(\mu\in\mathcal{C}_{2}(u)\).
A natural question, posed by Sarason [88, p. 513], is whether the converse holds. In other words, does every bounded truncated Toeplitz operator arise from a so-called u-compatible measure [88, Sect. 9]? This question was recently settled in the affirmative by Baranov, Bessonov, and Kapustin [13].
Theorem 29
(Baranov-Bessonov-Kapustin [13])
 if and only if
\(A = \mathcal{A}_{\mu}\)
for some
\(\mu \in\mathcal{C}_{2}(u)\).
if and only if
\(A = \mathcal{A}_{\mu}\)
for some
\(\mu \in\mathcal{C}_{2}(u)\).
The measure μ above is called the quasi-symbol for the truncated Toeplitz operator. For φ∈L ∞ we adopt the convention that \(\mathcal {A}_{\varphi \, d m}^{u} := A_{\varphi }^{u}\) so that every bounded symbol is automatically a quasi-symbol.
It turns out that \(\mathcal{C}_{1}(u^{2}) \subseteq\mathcal{C}_{2}(u) = \mathcal{C}_{2}(u^{2})\) always holds. Baranov, Bessonov, and Kapustin showed that equality is the precise condition which ensures that every  can be represented using a bounded symbol.
can be represented using a bounded symbol.
Theorem 30
(Baranov-Bessonov-Kapustin)
An operator
 has a bounded symbol if and only if
\(A = \mathcal{A}_{\mu}\)
for some
\(\mu\in\mathcal{C}_{1}(u^{2})\). Consequently, every operator in
has a bounded symbol if and only if
\(A = \mathcal{A}_{\mu}\)
for some
\(\mu\in\mathcal{C}_{1}(u^{2})\). Consequently, every operator in
 has a bounded symbol if and only if
\(\mathcal{C}_{1}(u^{2}) = \mathcal{C}_{2}(u)\).
has a bounded symbol if and only if
\(\mathcal{C}_{1}(u^{2}) = \mathcal{C}_{2}(u)\).
Recall that each function F in H 1 can be written as the product F=fg of two functions in H 2. Conversely, the product of any pair of functions in H 2 lies in H 1. For each \(f, g \in\mathcal{K}_{u}\) we note that
whence \(f g \in H^{1} \cap\overline{z} u^{2} \overline{H^{1}_{0}}\). Moreover, one can show that finite linear combinations of pairs of products of functions from \(\mathcal{K}_{u}\) form a dense subset of \(H^{1} \cap\overline{z} u^{2} \overline {H^{1}_{0}}\). As a consequence, this relationship between \(\mathcal{K}_{u}\) and \(H^{1} \cap\overline{z} u^{2} \overline{H^{1}_{0}}\) is sometimes denoted
For certain inner functions, one can say much more.
Theorem 31
(Baranov-Bessonov-Kapustin)
For an inner function u the following statements are equivalent.
-
(i)
\(\mathcal{C}_{1}(u^{2}) = \mathcal{C}_{2}(u)\).
-
(ii)
For each \(f \in H^{1} \cap\overline{z} u^{2} \overline{H^{1}_{0}}\) there exists sequences g j ,h j in \(\mathcal{K}_{u}\) such that ∑ j ∥g j ∥∥h j ∥<∞ and
$$ f = \sum_{j} g_j h_j. $$Moreover, there exists a universal C>0, independent of f, such that the g j ,h j can be chosen to satisfy ∑ j ∥g j ∥∥h j ∥⩽C∥f∥1.
As we have seen, the condition \(\mathcal{C}_{1}(u^{2}) = \mathcal {C}_{2}(u)\) is of primary importance. Unfortunately, it appears difficult to test whether or not a given inner function has this property. On the other hand, the following related geometric condition appears somewhat more tractable.
Definition 5
An inner function u is called a one-component inner function if the set \(\{z \in\mathbb{D}: |u(z)| < \epsilon\}\) is connected for some ϵ>0.
One can show, for instance, that for the atomic inner functions \(s_{\delta_{\zeta}}\) (where δ ζ denotes the point mass at a point ζ on \(\partial \mathbb {D}\)), the set {|u|<ϵ} is a disk internally tangent to \(\partial \mathbb {D}\) at ζ. In other words, these inner functions are one-component inner functions. The relevance of one-component inner functions lies in the following result of Aleksandrov.
Theorem 32
(Aleksandrov [7])
If u is inner, then
-
(i)
u is a one-component inner function if and only if
$$ \sup_{\lambda\in\mathbb{D}} \frac{\|k_{\lambda}\|_{\infty}}{\| k_{\lambda }\|} < \infty. $$ -
(ii)
If u is a one-component inner function, then \(\mathcal{C}_{p_{1}}(u) = \mathcal{C}_{p_{2}}(u)\) for all p 1,p 2>0.
There is also a related result of Treil and Volberg [102]. We take a moment to mention that W. Cohn [32] has described the set \(\mathcal{C}_{2}(u)\) in the case where u is a one component inner function.
Theorem 33
(Cohn)
If u is a one component inner function and μ is a positive measure on \(\partial \mathbb {D}\) for which \(\mu(\sigma(u) \cap \partial \mathbb {D}) = 0\), then \(\mu\in\mathcal{C}_{2}(u)\) if and only if there is a constant C>0 such that
for all z in \(\mathbb{D}\).
Note that if u is a one-component inner function, then so is u 2. Combining the preceding results we obtain the following.
Corollary 8
If
u
is a one-component inner function, then every operator in
 has a bounded symbol.
has a bounded symbol.
Of course the natural question now (and conjectured in [14]) is the following:
Question 2
Is the converse of the preceding corollary true?
It turns out that there is an interesting and fruitful interplay between the material discussed above and the family of Clark measures \(\{\sigma_{\alpha}: \alpha\in \partial \mathbb {D}\}\), defined by (16), associated with an inner function u. To be more specific, Aleksandrov showed in [6] that if \(\mathcal{C}_{1}(u^{2}) = \mathcal {C}_{2}(u^{2})\) (the equivalent condition for every operator in  to have a bounded symbol), then every Clark measure is discrete. This leads to the following corollary.
to have a bounded symbol), then every Clark measure is discrete. This leads to the following corollary.
Corollary 9
Let
u
be an inner function. If for some
\(\alpha\in \partial \mathbb {D}\)
the Clark measure
σ
α
is not discrete, then there is an operator in
 without a bounded symbol.
without a bounded symbol.
Since any singular measure μ (discrete or not) is equal to σ
1 for some inner function u [26], it follows that if we let μ be a continuous singular measure, then the corollary above yields an example of a truncated Toeplitz operator space  which contains operators without a bounded symbol.
which contains operators without a bounded symbol.
6 The Spatial Isomorphism Problem
For two inner functions u
1 and u
2, when is  spatially isomorphic to
spatially isomorphic to  ? In other words, when does there exist a unitary operator \(U: \mathcal{K}_{u_{1}} \to\mathcal{K}_{u_{2}}\) such that
? In other words, when does there exist a unitary operator \(U: \mathcal{K}_{u_{1}} \to\mathcal{K}_{u_{2}}\) such that  ? This is evidently a stronger condition than isometric isomorphism since one insists that the isometric isomorphism is implemented in a particularly restrictive manner.
? This is evidently a stronger condition than isometric isomorphism since one insists that the isometric isomorphism is implemented in a particularly restrictive manner.
A concrete solution to the spatial isomorphism problem posed above was given in [25]. Before discussing the solution, let us briefly introduce three basic families of spatial isomorphisms between truncated Toeplitz operator spaces. If \(\psi: \mathbb{D}\to\mathbb{D}\) is a disk automorphism, then one can check that the weighted composition operator
is unitary. In particular, this implies that the map

which satisfies the useful relationship \(\varLambda_{\psi }(A^{u}_{\varphi }) = A^{u \circ\psi}_{\varphi \circ\psi}\), implements a spatial isomorphism between  and
and  .
.
Another family of spatial isomorphisms arises from the so-called Crofoot transforms [34] (see also [88, Sect. 13]). For \(a \in\mathbb{D}\) and \(\psi_{a} = \frac{z - a}{1 - \overline{a} z}\), one can verify that the operator
is unitary. In particular, the corresponding map

implements a spatial isomorphism between  and
and  .
.
Finally, let us define
The operator \(U_{\#}: \mathcal{K}_{u} \to\mathcal{K}_{u^{\#}}\) is unitary and if

then \(\varLambda_{\#}(A^{u}_{\varphi }) = A^{u^{\#}}_{\overline{\varphi ^{\#}}}\) whence  is spatially isomorphic to
is spatially isomorphic to  . Needless to say, the three classes of unitary operators U
ψ
, U
a
, and U
# introduced above should not be confused with the Clark operators U
α
(15), which play no role here.
. Needless to say, the three classes of unitary operators U
ψ
, U
a
, and U
# introduced above should not be confused with the Clark operators U
α
(15), which play no role here.
It turns out that any spatial isomorphism between truncated Toeplitz operator spaces can be written in terms of the three basic types described above [25].
Theorem 34
(Cima-Garcia-Ross-Wogen)
For two inner functions
u
1
and
u
2
the spaces
 and
and
 are spatially isomorphic if and only if either
u
1=ψ∘u
2∘φ
or
\(u_{1} = \psi\circ u_{2}^{\#} \circ \varphi \)
for some disk automorphisms
φ,ψ. Moreover, any spatial isomorphism
are spatially isomorphic if and only if either
u
1=ψ∘u
2∘φ
or
\(u_{1} = \psi\circ u_{2}^{\#} \circ \varphi \)
for some disk automorphisms
φ,ψ. Moreover, any spatial isomorphism
 can be written as
Λ=Λ
a
Λ
ψ
or
Λ
a
Λ
#
Λ
ψ
, where we allow
a=0 or
ψ(z)=z.
can be written as
Λ=Λ
a
Λ
ψ
or
Λ
a
Λ
#
Λ
ψ
, where we allow
a=0 or
ψ(z)=z.
The preceding theorem leads immediately to the following question.
Question 3
Determine practical conditions on inner functions u 1 and u 2 which ensure that u 1=ψ∘u 2∘φ or \(u_{1} = \psi\circ u_{2}^{\#} \circ \varphi \) for some disk automorphisms φ,ψ. For instance, do this when u 1 and u 2 are finite Blaschke products having the same number of zeros, counted according to multiplicity.
In the case where one of the inner functions is z n, there is a complete answer [25].
Corollary 10
For a finite Blaschke product
u
of order
n,  is spatially isomorphic to
is spatially isomorphic to
 if and only if either
u
has one zero of order
n
or
u
has
n
distinct zeros all lying on a circle
Γ
in
\(\mathbb{D}\)
with the property that if these zeros are ordered according to increasing argument on
Γ, then adjacent zeros are equidistant in the hyperbolic metric.
if and only if either
u
has one zero of order
n
or
u
has
n
distinct zeros all lying on a circle
Γ
in
\(\mathbb{D}\)
with the property that if these zeros are ordered according to increasing argument on
Γ, then adjacent zeros are equidistant in the hyperbolic metric.
7 Algebras of Truncated Toeplitz Operators
Recall that  is a weakly closed subspace of \(\mathcal{B}(\mathcal{H})\) (see Sect. 3). Although
is a weakly closed subspace of \(\mathcal{B}(\mathcal{H})\) (see Sect. 3). Although  is not an algebra, there are many interesting algebras contained within
is not an algebra, there are many interesting algebras contained within  . In fact, the recent thesis [92] and subsequent paper of Sedlock [93] described them all. We discuss the properties of these so-called Sedlock algebras below, along with several further results from [59].
. In fact, the recent thesis [92] and subsequent paper of Sedlock [93] described them all. We discuss the properties of these so-called Sedlock algebras below, along with several further results from [59].
To begin with, we require the following generalization (see [88, Sect. 10]) of the Clark unitary operators (15):
where the parameter a is permitted to vary over the closed unit disk \(\mathbb{D}^{-}\) (we prefer to reserve the symbol α to denote complex numbers of unit modulus). The operators \(S_{u}^{a}\) turn out to be fundamental to the study of Sedlock algebras. Before proceeding, let us recall a few basic definitions.
For  , the commutant {A}′ of A is defined to be the set of all bounded operators on \(\mathcal{K}_{u}\) which commute with A. The weakly closed linear span of {A
n:n≥0} will be denoted by \(\mathcal{W}(A)\). Elementary operator theory says that \(\mathcal{W}(A) \subseteq\{A\}'\) holds and that {A}′ is a weakly closed subset of \(\mathcal{B}(\mathcal{K}_{u})\). The relevance of these concepts lies in the following two results from [88, p. 515] and [59], respectively.
, the commutant {A}′ of A is defined to be the set of all bounded operators on \(\mathcal{K}_{u}\) which commute with A. The weakly closed linear span of {A
n:n≥0} will be denoted by \(\mathcal{W}(A)\). Elementary operator theory says that \(\mathcal{W}(A) \subseteq\{A\}'\) holds and that {A}′ is a weakly closed subset of \(\mathcal{B}(\mathcal{K}_{u})\). The relevance of these concepts lies in the following two results from [88, p. 515] and [59], respectively.
Theorem 35
(Sarason)
For each
\(a \in\mathbb{D}^{-}\),  .
.
Theorem 36
(Garcia-Ross-Wogen)
For each \(a \in\mathbb{D}^{-}\), \(\{S_{u}^{a}\}' = \mathcal{W}(S_{u}^{a})\).
The preceding two theorems tell us that \(\mathcal{W}(S_{u}^{a})\) and \(\mathcal{W}((S_{u}^{b})^{*})\), where a,b belong to \(\mathbb{D}^{-}\), are algebras contained in  . We adopt the following notation introduced by Sedlock [93]:
. We adopt the following notation introduced by Sedlock [93]:

Note that  is the algebra of analytic truncated Toeplitz operators (i.e.,
is the algebra of analytic truncated Toeplitz operators (i.e.,  ) and that
) and that  is the algebra of co-analytic truncated Toeplitz operators (i.e.,
is the algebra of co-analytic truncated Toeplitz operators (i.e.,  ). The following theorem of Sedlock asserts that the algebras
). The following theorem of Sedlock asserts that the algebras  for \(a \in\widehat{\mathbb{C}}\) are the only maximal abelian algebras in
for \(a \in\widehat{\mathbb{C}}\) are the only maximal abelian algebras in  .
.
Theorem 37
(Sedlock [93])
If
 , then
, then
 if and only if
if and only if
 for some
\(a \in\widehat{\mathbb {C}}\). Consequently, every weakly closed algebra in
for some
\(a \in\widehat{\mathbb {C}}\). Consequently, every weakly closed algebra in
 is abelian and is contained in some
is abelian and is contained in some
 .
.
Let us gather together a few facts about the Sedlock algebras  , all of which can be found in Sedlock’s paper [93]. First we note that
, all of which can be found in Sedlock’s paper [93]. First we note that

and

Most importantly, we have the following concrete description of  .
.
Theorem 38
(Sedlock [93])
If \(a \in\mathbb{D}\), then

Furthermore, if φ,ψ∈H ∞, then we have the following product formula
In particular, if \(a \in\widehat{\mathbb{C}} \setminus \partial \mathbb {D}\), then every operator in  is a truncated Toeplitz operator which can be represented using a bounded symbol. On the other hand, if a belongs to \(\partial \mathbb {D}\), then there may be operators in
is a truncated Toeplitz operator which can be represented using a bounded symbol. On the other hand, if a belongs to \(\partial \mathbb {D}\), then there may be operators in  which do not have bounded symbols. In fact, if u has an ADC at some ζ in \(\partial \mathbb {D}\), then k
ζ
⊗k
ζ
belongs to
which do not have bounded symbols. In fact, if u has an ADC at some ζ in \(\partial \mathbb {D}\), then k
ζ
⊗k
ζ
belongs to  . From here, one can use the example from the remarks after Theorem 26 to produce an operator in
. From here, one can use the example from the remarks after Theorem 26 to produce an operator in  which has no bounded symbol.
which has no bounded symbol.
Let us now make a few remarks about normal truncated Toeplitz operators. For a in \(\partial \mathbb {D}\) the Sedlock algebra  is generated by a unitary operator (i.e., a Clark operator) and is therefore an abelian algebra of normal operators. When \(a \in\widehat{\mathbb{C}} \setminus \partial \mathbb {D}\), the situation drastically changes [59].
is generated by a unitary operator (i.e., a Clark operator) and is therefore an abelian algebra of normal operators. When \(a \in\widehat{\mathbb{C}} \setminus \partial \mathbb {D}\), the situation drastically changes [59].
Theorem 39
(Garcia-Ross-Wogen)
If
\(a \in\widehat{\mathbb{C}} \setminus \partial \mathbb {D}\), then
 is normal if and only if
A∈ℂI.
is normal if and only if
A∈ℂI.
In Sect. 6, we characterized all possible spatial isomorphisms between truncated Toeplitz operator spaces. In particular, recall that the basic spatial isomorphisms Λ ψ ,Λ #,Λ a played a key role. Let us examine their effect on Sedlock algebras. The following result is from [59].
Theorem 40
(Garcia-Ross-Wogen)
For u inner, \(a \in\widehat{\mathbb{C}}\), and \(c \in\mathbb{D}\), we have

where
For a in \(\widehat{\mathbb{C}} \setminus \partial \mathbb {D}\), the preceding theorem follows from direct computations based upon Theorem 38. When a belongs to \(\partial \mathbb {D}\), however, a different proof is required. One can go even further and investigate when two Sedlock algebras are spatially isomorphic. The following results are from [59].
Theorem 41
(Garcia-Ross-Wogen)
If
u(z)=z
n
and
\(a, a' \in\mathbb{D}\), then
 is spatially isomorphic to
is spatially isomorphic to
 if and only if |a|=|a′|.
if and only if |a|=|a′|.
Theorem 42
(Garcia-Ross-Wogen)
If
and
\(a, a' \in\mathbb{D}\), then
 is spatially isomorphic to
is spatially isomorphic to
 if and only if
a=a′.
if and only if
a=a′.
Before moving on, let us take a moment to highlight an interesting operator integral formula from [88, Sect. 12] which is of some relevance here. Recall that for α in \(\partial \mathbb {D}\), the operator \(S_{u}^{\alpha}\) given by (29) is unitary, whence \(\varphi (S_{u}^{\alpha})\) is defined by the functional calculus for φ in L
∞. By Theorem 35 we see that \(\varphi (S_{u}^{\alpha})\) belongs to  . Using the Aleksandrov disintegration theorem (Theorem 9), one can then prove that
. Using the Aleksandrov disintegration theorem (Theorem 9), one can then prove that
which can be written in the more compact and pleasing form
A similar formula exists for symbols φ in L 2, but the preceding formulae must be interpreted carefully since the operators \(\varphi (S_{u}^{\alpha })\) may be unbounded.
Recall that for each φ in L ∞, the Cesàro means of φ are trigonometric polynomials φ n which approximate φ in the weak-∗ topology of L ∞. From the discussion above and Corollary 3 we know that
is weakly dense in  . When u is a finite Blaschke product, it turns out that we can do much better. The following result can be found in [28], although it can be gleaned from [88, Sect. 12].
. When u is a finite Blaschke product, it turns out that we can do much better. The following result can be found in [28], although it can be gleaned from [88, Sect. 12].
Theorem 43
Let u be a Blaschke product of degree N and let \(\alpha_{1}, \alpha_{2} \in \partial \mathbb {D}\) with α 1≠α 2. Then for any φ∈L 2, there are polynomials p,q of degree at most N so that \(A_{\varphi} = p(S_{u}^{\alpha_{1}}) + q(S_{u}^{\alpha_{2}})\).
8 Truncated Toeplitz C ∗-Algebras
In the following, we let \(\mathcal{H}\) denote a separable complex Hilbert space. For each  , let
, let  denote the unital C
∗-algebra generated by
denote the unital C
∗-algebra generated by  . In other words,
. In other words,  is the closure, in the norm of \(\mathcal{B}(\mathcal{H})\), of the unital algebra generated by the operators in
is the closure, in the norm of \(\mathcal{B}(\mathcal{H})\), of the unital algebra generated by the operators in  and their adjoints. Since we are frequently interested in the case where
and their adjoints. Since we are frequently interested in the case where  is a singleton, we often write C
∗(A) in place of C
∗({A}) in order to simplify our notation.
is a singleton, we often write C
∗(A) in place of C
∗({A}) in order to simplify our notation.
Recall that the commutator ideal
 of
of  , is the smallest closed two-sided ideal which contains the commutators
, is the smallest closed two-sided ideal which contains the commutators
where A and B range over all elements of  . Since the quotient algebra
. Since the quotient algebra  is an abelian C
∗-algebra, it is isometrically ∗-isomorphic to C(Y), the set of all continuous functions on some compact Hausdorff space Y [33, Theorem 1.2.1]. We denote this relationship
is an abelian C
∗-algebra, it is isometrically ∗-isomorphic to C(Y), the set of all continuous functions on some compact Hausdorff space Y [33, Theorem 1.2.1]. We denote this relationship

Putting this all together, we have the short exact sequence

where  is the inclusion map and
is the inclusion map and  is the composition of the quotient map with the isometric ∗-isomorphism which implements (30).
is the composition of the quotient map with the isometric ∗-isomorphism which implements (30).
The Toeplitz algebra
C
∗(T
z
), where T
z
denotes the unilateral shift on the classical Hardy space H
2, has been extensively studied since the seminal work of Coburn in the late 1960s [30, 31]. Indeed, the Toeplitz algebra is now one of the standard examples discussed in many well-known texts (e.g., [10, Sect. 4.3], [36, Chap. V.1], [38, Chap. 7]). In this setting, we have  , the ideal of compact operators on H
2, and \(Y = \partial \mathbb {D}\), so that the short exact sequence (31) takes the form
, the ideal of compact operators on H
2, and \(Y = \partial \mathbb {D}\), so that the short exact sequence (31) takes the form

In other words, C
∗(T
z
) is an extension of  by \(C( \partial \mathbb {D})\). It also follows that
by \(C( \partial \mathbb {D})\). It also follows that

and, moreover, that each element of C ∗(T z ) enjoys a unique decomposition of the form T φ +K [10, Theorem 4.3.2]. As a consequence, we see that the map \(\pi:C^{*}(T_{z})\to C( \partial \mathbb {D})\) is given by π(T φ +K)=φ.
Needless to say, the preceding results have spawned numerous generalizations and variants over the years. For instance, one can consider C
∗-algebras generated by matrix-valued Toeplitz operators or Toeplitz operators acting on other Hilbert function spaces (e.g., the Bergman space [11]). As another example, if  denotes the truncated Toeplitz operators whose symbols are both piecewise and left continuous on \(\partial \mathbb{D}\), then Gohberg and Krupnik proved that
denotes the truncated Toeplitz operators whose symbols are both piecewise and left continuous on \(\partial \mathbb{D}\), then Gohberg and Krupnik proved that  and obtained the short exact sequence
and obtained the short exact sequence

where Y is the cylinder \(\partial \mathbb {D}\times[0, 1]\), endowed with a nonstandard topology [64].
In the direction of truncated Toeplitz operators, we have the following analogue of Coburn’s work.
Theorem 44
If u is an inner function, then
-
(i)
 , the algebra of compact operators on
\(\mathcal{K}_{u}\),
, the algebra of compact operators on
\(\mathcal{K}_{u}\), -
(ii)
 is isometrically ∗-isomorphic to
\(C(\sigma(u) \cap \partial \mathbb {D})\),
is isometrically ∗-isomorphic to
\(C(\sigma(u) \cap \partial \mathbb {D})\), -
(iii)
If \(\varphi \in C( \partial \mathbb {D})\), then \(A_{\varphi }^{u}\) is compact if and only if \(\varphi (\sigma(u)\cap \partial \mathbb {D}) = \{0\}\),
-
(iv)
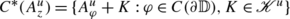 ,
, -
(v)
If \(\varphi \in C( \partial \mathbb {D})\), then \(\sigma_{e}(A^{u}_{\varphi }) = \varphi (\sigma_{e}(A_{z}^{u}))\),
-
(vi)
For \(\varphi \in C( \partial \mathbb {D})\), \(\|A^{u}_{\varphi }\|_{e} = \sup\{ |\varphi (\zeta)| : \zeta\in\sigma(u)\cap \partial \mathbb {D}\}\).
In recent work [60], the authors and W. Wogen were able to provide operator algebraic proofs of the preceding results, utilizing an approach similar in spirit to the original work of Coburn. However, it should also be noted that many of the statements in Theorem 44 can be obtained using the explicit triangularization theory developed by Ahern and Clark in [2] (see the exposition in [78, Lec. V]).
9 Unitary Equivalence to a Truncated Toeplitz Operator
A significant amount of evidence is mounting that truncated Toeplitz operators may play a significant role in some sort of model theory for complex symmetric operators [25, 56, 96]. At this point, however, it is still too early to tell what exact form such a model theory should take. On the other hand, a surprising array of complex symmetric operators can be concretely realized in terms of truncated Toeplitz operators (or direct sums of such operators), without yet even venturing to discuss vector-valued truncated Toeplitz operators.
Before discussing unitary equivalence, however, we should perhaps say a few words about similarity. A number of years ago, D.S. Mackey, N. Mackey, and Petrovic asked whether or not the inverse Jordan structure problem can be solved in the class of Toeplitz matrices [75]. In other words, given any Jordan canonical form, can one find a Toeplitz matrix which is similar to this form? A negative answer to this question was subsequently provided by Heinig in [67]. On the other hand, it turns out that the inverse Jordan structure problem is always solvable in the class of truncated Toeplitz operators, for we have the following theorem [25, Theorem 6.2].
Theorem 45
(Cima-Garcia-Ross-Wogen)
Every operator on a finite dimensional space is similar to a co-analytic truncated Toeplitz operator.
In light of the preceding theorem, it is clear that simple, purely algebraic, tools will be insufficient to settle the question of whether every complex symmetric operator can be represented in some fashion using truncated Toeplitz operators. We turn our attention now toward unitary equivalence.
Let us begin by recalling an early result of Sarason, who observed that the Volterra integration operator (1), a standard example of a complex symmetric operator [45, 49, 50], is unitarily equivalent to a truncated Toeplitz operator acting on the \(\mathcal{K}_{u}\) space corresponding to the atomic inner function \(u(z) = \exp( \frac {z+1}{z-1})\) [84] (although the term “truncated Toeplitz operator” was not yet coined). Detailed computations using the theory of model operators and characteristic functions can be found in [79, p. 41].
What was at first only an isolated result has recently begun to be viewed as a seminal observation. More recently, a number of standard classes of complex symmetric operators have been identified as being unitarily equivalent to truncated Toeplitz operators. Among the first observed examples are
-
(i)
rank-one operators [25, Theorem 5.1],
-
(ii)
2×2 matrices [25, Theorem 5.2],
-
(iii)
normal operators [25, Theorem 5.6],
-
(iv)
for k∈ℕ∪{∞}, the k-fold inflation of a finite Toeplitz matrix [25, Theorem 5.7].
This last item was greatly generalized by Strouse, Timotin, and Zarrabi [96], who proved that a remarkable array of inflations of truncated Toeplitz operators are themselves truncated Toeplitz operators. In addition, a variety of related results concerning tensor products, inflations, and direct sums are given in [96]. The key to many of these results lies in the fact that if B is an inner function, then
extends linearly to a unitary operator \(\varOmega_{B}: \mathcal {K}_{B}\otimes L^{2} \to L^{2}\) and, moreover, this operator maps \(\mathcal{K}_{B} \otimes H^{2}\) onto H 2. Letting \(\omega_{B}: \mathcal{K}_{B}\otimes\mathcal{K}_{u} \to\mathcal{K}_{u\otimes B}\) denote the restriction of Ω B to \(\mathcal{K}_{B}\otimes \mathcal{K}_{u}\), one can obtain the following general theorem.
Theorem 46
(Strouse-Timotin-Zarrabi [96])
Let B and u be inner functions, and suppose that ψ,φ belong to L 2 and satisfy the following conditions:
-
(i)
The operators \(A_{\overline{B}^{j} \psi}^{B}\) are bounded, and nonzero only for a finite number of j∈ℤ.
-
(ii)
\(A_{\varphi }^{u}\) is bounded.
-
(iii)
ψ(φ∘B)∈L 2.
Then \(A_{\psi(\varphi \circ B)}^{u\circ B}\) is bounded and
We state explicitly only a few more results from [96], hoping to give the reader the general flavor of this surprising work. In the following, we say that the inner function B is of order n if B is a finite Blaschke product of degree n, and of order infinity otherwise.
Theorem 47
(Strouse-Timotin-Zarrabi)
Suppose that u is an inner function, that φ∈L 2, and that B is an inner function of order k for some k∈ℕ∪{∞}. Assume also that \(A_{\varphi }^{u}\) is bounded. Then \(A_{\varphi \circ B}^{u\circ B}\) is bounded and unitarily equivalent to \(I_{k} \otimes A_{\varphi }^{u}\).
Theorem 48
(Strouse-Timotin-Zarrabi)
If ψ is an analytic function, \(A_{\psi}^{B}\) is bounded, and R is a non-selfadjoint operator of rank one, then \(A_{\psi}^{B} \otimes R\) is unitarily equivalent to a truncated Toeplitz operator.
Theorem 49
(Strouse-Timotin-Zarrabi)
Suppose u is inner, φ∈H ∞, and \((A_{\varphi }^{u})^{2}\allowbreak = 0\). If \(k = \dim\mathcal{K}_{u} \ominus\ker A_{\varphi }^{u}\), then \(A_{\varphi }^{u} \oplus 0_{k}\) is unitarily equivalent to a truncated Toeplitz operator.
Although a few results concerning matrix representations of truncated Toeplitz operators have been obtained [25, 28, 96], the general question of determining whether a given matrix represents a truncated Toeplitz operator, with respect to some orthonormal basis of some \(\mathcal{K}_{u}\) space, appears difficult. On the other hand, it is known that every truncated Toeplitz operator is unitarily equivalent to a complex symmetric matrix [45, 49], a somewhat more general issue which has been studied for its own independent interest [12, 57, 58, 99, 101].
The main result of [56] is the following simple criterion for determining whether or not a given matrix is unitarily equivalent to a truncated Toeplitz operator having an analytic symbol.
Theorem 50
(Garcia-Poore-Ross)
Suppose M∈M n (ℂ) has distinct eigenvalues λ 1,λ 2,…,λ n with corresponding unit eigenvectors x 1,x 2,…,x n . Then M is unitarily equivalent to an analytic truncated Toeplitz operator, on some model space \(\mathcal{K}_{u}\) if and only if there are distinct points z 1,z 2,…,z n−1 in \(\mathbb{D}\) such that
holds for 1⩽i⩽j<n.
The method of Theorem 50 is constructive, in the sense that if (33) is satisfied, then one can construct an inner function u and a polynomial φ such that M is unitarily equivalent to \(A_{\varphi }^{u}\). In fact, u is the Blaschke product having zeros at z 1,z 2,…,z n−1 and z n =0. Using Theorem 50 and other tools, one can prove the following result from [56].
Theorem 51
(Garcia-Poore-Ross)
Every complex symmetric operator on a 3-dimensional Hilbert space is unitarily equivalent to a direct sum of truncated Toeplitz operators.
Taken together, these results from [25, 56, 96] yield a host of open questions, many of which are still open, even in the finite dimensional setting.
Question 4
Is every complex symmetric matrix M∈M n (ℂ) unitarily equivalent to a direct sum of truncated Toeplitz operators?
Question 5
Let n≥4. Is every irreducible complex symmetric matrix M∈M n (ℂ) unitarily equivalent to a truncated Toeplitz operator?
Recently, the first author and J. Tener [53] showed that every finite complex symmetric matrix is unitarily equivalent to a direct sum of (i) irreducible complex symmetric matrices or (ii) matrices of the form A⊕A T where A is irreducible and not unitarily equivalent to a complex symmetric matrix (such matrices are necessarily 6×6 or larger). This immediately suggests the following question.
Question 6
For A∈M n (ℂ), is the matrix A⊕A T∈M 2n (ℂ) unitarily equivalent to a direct sum of truncated Toeplitz operators?
One method for producing complex symmetric matrix representations of a given truncated Toeplitz operator is to use modified Clark bases (21) for \(\mathcal{K}_{u}\).
Question 7
Suppose that M∈M n (ℂ) is complex symmetric. If M is unitarily equivalent to a truncated Toeplitz operator, does there exist an inner function u, a symbol φ∈L ∞, and a modified Clark basis for \(\mathcal{K}_{u}\) such that M is the matrix representation of \(A_{\varphi }^{\varTheta}\) with respect to this basis? In other words, do all such unitary equivalences between complex symmetric matrices and truncated Toeplitz operators arise from Clark representations?
10 Unbounded Truncated Toeplitz Operators
As we mentioned earlier (Sect. 2.9), for a symbol φ in L 2 and an inner function u, the truncated Toeplitz operator \(A^{u}_{\varphi }\) is closed and densely defined on the domain

in \(\mathcal{K}_{u}\). In particular, the analytic function P
u
(φf) can be defined on \(\mathbb{D}\) by writing the formula (7) as an integral. In general, we actually have \(CA^{u}_{\varphi } C = A^{u}_{\overline{\varphi }}\), and, when \(A^{u}_{\varphi }\) is bounded (i.e.,  ), we have \(A^{u}_{\overline{\varphi }} = (A^{u}_{\varphi })^{*}\). Let us also recall an old and important result of Sarason [85] which inspired the commutant lifting theorem [97].
), we have \(A^{u}_{\overline{\varphi }} = (A^{u}_{\varphi })^{*}\). Let us also recall an old and important result of Sarason [85] which inspired the commutant lifting theorem [97].
Theorem 52
(Sarason)
The bounded operators on \(\mathcal{K}_{u}\) which commute with \(A^{u}_{\overline{z}}\) are \(\{A^{u}_{\overline{\varphi }}: \varphi \in H^{\infty}\}\).
In the recent papers [89, 90], Sarason studied unbounded Toeplitz operators (recall that a Toeplitz operator on H 2 is bounded if and only if the symbol is bounded) as well as unbounded truncated Toeplitz operators. We give a brief survey of these results.
In the following, N denotes the Nevanlinna class, the set of all quotients f/g where f and g belong to H ∞ and g is non-vanishing on \(\mathbb {D}\). The Smirnov class N + denotes the subset of N for which the denominator g is not only non-vanishing on \(\mathbb{D}\) but outer. By [90] each φ in N + can be written uniquely as \(\varphi = \frac{b}{a}\) where a and b belong to H ∞, a is outer, a(0)>0, and |a|2+|b|2=1 almost everywhere on \(\partial \mathbb {D}\). Sarason calls this the canonical representation of φ.
For φ in N
+ define the Toeplitz operator T
φ
as multiplication by φ on its domain  . In particular, observe that there is no projection involved in the preceding definition.
. In particular, observe that there is no projection involved in the preceding definition.
Theorem 53
(Sarason [90])
For
φ=b/a∈N
+, written in canonical form, T
φ
is a closed operator on
H
2
with dense domain
 .
.
There is no obvious way to define the co-analytic Toeplitz operator \(T_{\overline{\varphi }}\) on H 2 for φ∈N +. Of course we can always define \(T_{\overline{\varphi }}\) to be \(T_{\varphi }^{*}\) and this makes sense when φ belongs to H ∞. In order to justify the definition \(T_{\overline{\varphi }} := T_{\varphi }^{*}\) for φ∈N +, however, we need to take care of some technical details.
As the preceding theorem shows, if φ∈N
+, then T
φ
is a closed operator with dense domain aH
2. Basic functional analysis tells us that its adjoint \(T_{\varphi }^{*}\) is also closed and densely defined. In fact, one can show that  is the associated deBranges-Rovnyak space \(\mathcal{H}(b)\) [90]. In order to understand \(T_{\overline{\varphi }}\) we proceed, at least formally, as we do when examining \(T_{\overline{\varphi }}\) when φ is bounded. Let φ and f have Fourier expansions
is the associated deBranges-Rovnyak space \(\mathcal{H}(b)\) [90]. In order to understand \(T_{\overline{\varphi }}\) we proceed, at least formally, as we do when examining \(T_{\overline{\varphi }}\) when φ is bounded. Let φ and f have Fourier expansions
Formal series manipulations show that

This suggests that if \(\varphi = \sum_{n = 0}^{\infty} \varphi _{n} z^{n}\) is the power series representation for φ in N +, then we should define, for each function \(f(z) = \sum_{n = 0}^{\infty} f_{n} z^{n}\) analytic in a neighborhood of \(\mathbb{D}^{-}\),
It turns out that \(t_{\overline{\varphi }} f\), so defined, is an analytic function on \(\mathbb{D}\). The following result indicates that this is indeed the correct approach to defining \(T_{\varphi }^{*}\).
Theorem 54
(Sarason [90])
If φ∈N +, then \(t_{\overline{\varphi }}\) is closable and \(T_{\varphi }^{*}\) is its closure.
In light of the preceding theorem, for φ in N + we may define \(T_{\overline{\varphi }}\) to be \(T_{\varphi }^{*}\). More generally, we can define, for each φ in N + and u inner, the truncated Toeplitz operator \(A^{u}_{\overline{\varphi }}\) by

We gather up some results about \(A^{u}_{\overline{\varphi }}\) from [90].
Theorem 55
(Sarason)
If φ=b/a∈N + is in canonical form and u is inner, then
-
(i)
\(A^{u}_{\overline{\varphi }}\) is closed and densely defined.
-
(ii)
\(A^{u}_{\overline{\varphi }}\) is bounded if and only if dist(b,uH ∞)<1.
From Theorem 12 we know that A=CA
∗
C whenever  . Therefore it makes sense for us to define
. Therefore it makes sense for us to define
for φ∈N
+. It turns out that  and that the operator \(A^{u}_{\varphi }\) is closed and densely defined. Fortunately this definition makes sense in terms of adjoints.
and that the operator \(A^{u}_{\varphi }\) is closed and densely defined. Fortunately this definition makes sense in terms of adjoints.
Theorem 56
(Sarason)
For inner u and φ∈N +, the operators A φ and \(A_{\overline{\varphi }}\) are adjoints of each other.
What is the analog of Theorem 52 for of unbounded truncated Toeplitz operators? In [89] Sarason showed that
holds for f in  and thus one might be tempted to think that the closed densely defined operators which commute with \(A^{u}_{\overline{z}}\) are simply \(\{A_{\overline{\varphi }}: \varphi \in N^{+}\}\). Unfortunately the situation is more complicated and one needs to define \(A^{u}_{\overline{\varphi }}\) for a slightly larger class of symbols than N
+. Sarason works out the details in [89] and identifies the closed densely defined operators on \(\mathcal{K}_{u}\) which commute with \(A^{u}_{\overline{z}}\) as the operators \(A^{u}_{\overline{\varphi }}\) where the symbols φ come from a so-called local Smirnov class
\(N^{+}_{u}\). The details are somewhat technical and so we therefore leave it to the reader to explore this topic further in Sarason paper [89].
and thus one might be tempted to think that the closed densely defined operators which commute with \(A^{u}_{\overline{z}}\) are simply \(\{A_{\overline{\varphi }}: \varphi \in N^{+}\}\). Unfortunately the situation is more complicated and one needs to define \(A^{u}_{\overline{\varphi }}\) for a slightly larger class of symbols than N
+. Sarason works out the details in [89] and identifies the closed densely defined operators on \(\mathcal{K}_{u}\) which commute with \(A^{u}_{\overline{z}}\) as the operators \(A^{u}_{\overline{\varphi }}\) where the symbols φ come from a so-called local Smirnov class
\(N^{+}_{u}\). The details are somewhat technical and so we therefore leave it to the reader to explore this topic further in Sarason paper [89].
11 Smoothing Properties of Truncated Toeplitz Operators
Let us return to Theorem 2, an important result of Ahern and Clark which characterizes those functions in the model space \(\mathcal{K}_{u}\) which have a finite angular derivative in the sense of Carathéodory (ADC) at some point ζ on \(\partial \mathbb {D}\). In particular, recall that every function in \(\mathcal{K}_{u}\) has a finite nontangential limit at ζ precisely when u has an ADC at ζ. The proof of this ultimately relies on the fact that this statement is equivalent to the condition that \((I - \overline{\lambda} A^{u}_{z})^{-1} P_{u} 1\) is bounded as λ approaches ζ nontangentially. One can see this by observing that
holds for all f in \(\mathcal{K}_{u}\). If one replaces P u 1 in the formula above with P u h for some h in H ∞, then a routine calculation shows that
for all f in \(\mathcal{K}_{u}\). An argument similar to that employed by Ahern and Clark shows that \((A^{u}_{\overline{h}} f)(\lambda)\) has a finite nontangential limit at ζ for each f in \(\mathcal{K}_{u}\) if and only if \((I - \overline{\lambda} A^{u}_{z})^{-1} P_{u} h\) is bounded as λ approaches ζ nontangentially.
Let us examine the situation when u is an infinite Blaschke product with zeros {λ n } n≥1, repeated according to multiplicity. Recall that the Takenaka basis {γ n } n≥1, defined by (19), is an orthonormal basis for \(\mathcal{K}_{u}\). For each ζ in \(\partial \mathbb {D}\), a calculation from [65] shows that \(A^{u}_{\overline{h}} \gamma_{n}\) is a rational function (and so can be defined at any \(\zeta\in \partial \mathbb {D}\)). From this one can obtain the following analogue of the Ahern-Clark result [65].
Theorem 57
(Hartmann-Ross)
If u is a Blaschke product with zeros {λ n } n≥1 and h∈H ∞, then every function in \(\operatorname {ran}A^{u}_{\overline{h}}\) has a finite nontangential limit at \(\zeta\in \partial \mathbb {D}\) if and only if
From here one can see the smoothing properties of the co-analytic truncated Toeplitz operator \(A^{u}_{\overline{h}}\). If u happens to be an interpolating Blaschke product, then the condition in the above theorem reduces to
The following open problem now suggests itself.
Question 8
Obtain extensions of Theorem 57 to general inner functions u and symbols h∈L 2.
12 Nearly Invariant Subspaces
We conclude this survey with a few remarks about truncated Toeplitz operators which act on a family of spaces that are closely related to the model spaces \(\mathcal{K}_{u}\). To be more precise, we say that a (norm closed) subspace \(\mathcal{M}\) of H 2 is nearly invariant if the following divisibility condition holds
These spaces were first considered and characterized in [68, 87] and they continue to be the focus of intense study [8, 9, 22, 66, 73, 76].
The link between nearly invariant subspaces of H 2 and model spaces is supplied by a crucial result of Hitt [68], which asserts that there is a unique solution g to the extremal problem
and moreover, that there is an inner function u so that
and such that the map \(W_{g}: \mathcal{K}_{u} \to\mathcal{M}\) defined by
is unitary. The function g is called the extremal function for the nearly invariant subspace \(\mathcal{M}\). It is important to observe that since g belongs to \(\mathcal{M}= g\mathcal{K}_{u}\), the inner function u must satisfy u(0)=0. We remark that the content of these observations is nontrivial, for the set \(g\mathcal{K}_{u}\), for arbitrary g in H 2 and u inner, is not necessarily even a subspace of H 2 since it may fail to be closed.
In the other direction, Sarason showed that if u is an inner function which satisfies u(0)=0, then every isometric multiplier from \(\mathcal{K}_{u}\) into H 2 takes the form
where a and b are in the unit ball of H ∞ satisfy |a|2+|b|2=1 a.e. on \(\partial \mathbb {D}\) [87]. Consequently, one sees that \(\mathcal{M}=g \mathcal{K}_{u}\) is a (closed) nearly invariant subspace of H 2 with extremal function g as in (35).
The next natural step towards defining truncated Toeplitz operators on the nearly invariant subspace \(\mathcal{M}= g \mathcal{K}_{u}\) is to understand \(P_{\mathcal{M}}\), the orthogonal projection of L 2 onto \(\mathcal{M} \). The following lemma from [65] provides an explicit formula relating \(P_{\mathcal{M}}\) and P u .
Lemma 2
If \(\mathcal{M}=g\mathcal{K}_{u}\) is a nearly invariant subspace with extremal function g and associated inner function u satisfying u(0)=0, then
for all f in \(\mathcal{M}\). Consequently, the reproducing kernel for \(\mathcal{M}\) is given by
Now armed with the preceding lemma, we are in a position to introduce truncated Toeplitz operators on nearly invariant subspaces. Certainly whenever φ is a bounded function we can use Lemma 2 to see that the operator \(A_{\varphi }^{\mathcal{M}}:\mathcal{M}\to \mathcal{M}\)
is well-defined and bounded. More generally, we may consider symbols φ such that |g|2 φ belongs to L 2. In this case, for each h in \(\mathcal{K}_{u}^{\infty}:=\mathcal{K}_{u}\cap H^{\infty}\), the function |g|2 φh is in L 2 whence P u (|g|2 φh) belongs to \(\mathcal{K}_{u}\). By the isometric multiplier property of g on \(\mathcal{K}_{u}\), we see that
Note that by the isometric property of g, the set \(g\mathcal{K}_{u}^{\infty}\) is dense in \(g\mathcal{K}_{u}\) by Theorem 3. Thus in this setting the operator \(A^{\mathcal{M}}_{\varphi }\) is densely defined. We refer to any such operator as a truncated Toeplitz operator on \(\mathcal{M}\). We denote by  the set of all such densely defined truncated Toeplitz operators which have bounded extensions to \(\mathcal{M}\). The following theorem from [65], which relies heavily upon the unitarity of the map (36), furnishes the explicit link between
the set of all such densely defined truncated Toeplitz operators which have bounded extensions to \(\mathcal{M}\). The following theorem from [65], which relies heavily upon the unitarity of the map (36), furnishes the explicit link between  and
and  .
.
Theorem 58
(Hartmann-Ross)
If \(\mathcal{M}=g\mathcal{K}_{u}\) is a nearly invariant subspace with extremal function g and associated inner function u satisfying u(0)=0, then for any Lebesgue measurable φ on \(\partial \mathbb {D}\) with |g|2 φ∈L 2 we have
In light of the preceding theorem, we see that the map
is a spatial isomorphism between  and
and  . In particular, we have
. In particular, we have

One can use the preceding results to prove the following facts about  , all of which are direct analogues of the corresponding results on
, all of which are direct analogues of the corresponding results on  .
.
-
(i)
 is a weakly closed linear subspace of \(\mathcal{B}(\mathcal{M})\).
is a weakly closed linear subspace of \(\mathcal{B}(\mathcal{M})\). -
(ii)
\(A^{\mathcal{M}}_{\varphi } \equiv0\) if and only if \(|g|^{2} \varphi \in u H^{2} + \overline{u H^{2}}\).
-
(iii)
\(C_{g} := W_{g} C W_{g}^{*}\) defines a conjugation on \(\mathcal {M}\) and A=C g A ∗ C g for every
 .
. -
(iv)
If \(S_{g} := W_{g} A_{z} W_{g}^{*}\), then a bounded operator A on \(\mathcal{M}\) belongs to
 if and only if there are functions \(\varphi _{1}, \varphi _{2} \in\mathcal{M}\) so that $$ A - S_{g} A S_{g}^{*} = \bigl( \varphi _1 \otimes k^{\mathcal{M}}_{0}\bigr) + \bigl(k^{\mathcal{M}}_{0} \otimes \varphi _2\bigr). $$
if and only if there are functions \(\varphi _{1}, \varphi _{2} \in\mathcal{M}\) so that $$ A - S_{g} A S_{g}^{*} = \bigl( \varphi _1 \otimes k^{\mathcal{M}}_{0}\bigr) + \bigl(k^{\mathcal{M}}_{0} \otimes \varphi _2\bigr). $$ -
(v)
The rank-one operators in
 are constant multiples of $$ gk_{\lambda}\otimes gCk_{\lambda}, \qquad gCk_{\lambda}\otimes gk_{\lambda}, \qquad gk_{\zeta}\otimes gk_{\zeta}. $$
are constant multiples of $$ gk_{\lambda}\otimes gCk_{\lambda}, \qquad gCk_{\lambda}\otimes gk_{\lambda}, \qquad gk_{\zeta}\otimes gk_{\zeta}. $$ -
(vi)
 is spatially isomorphic to
is spatially isomorphic to  if and only if either u
1=ψ∘u
2∘φ or \(u_{1} = \psi\circ\overline {u_{2}(\overline{z})} \circ \varphi \) for some disk automorphisms φ,ψ. In particular, this is completely independent of the corresponding extremal functions g
1 and g
2 for \(\mathcal{M}_{1}\) and \(\mathcal{M}_{2}\).
if and only if either u
1=ψ∘u
2∘φ or \(u_{1} = \psi\circ\overline {u_{2}(\overline{z})} \circ \varphi \) for some disk automorphisms φ,ψ. In particular, this is completely independent of the corresponding extremal functions g
1 and g
2 for \(\mathcal{M}_{1}\) and \(\mathcal{M}_{2}\).
Notes
- 1.
Equivalently, \(G(1/z) \in H^{p}_{0}\).
- 2.
Written as an integral transform, P u can be regarded as an operator from L 1 into \(\mbox{Hol}(\mathbb{D})\).
- 3.
Recall that we are using the notation \(\widetilde{f} := C f\) for \(f \in\mathcal {K}_{u}\).
References
Agler, J., McCarthy, J.E.: Pick Interpolation and Hilbert Function Spaces. Graduate Studies in Mathematics, vol. 44. Am. Math. Soc., Providence (2002)
Ahern, P.R., Clark, D.N.: On functions orthogonal to invariant subspaces. Acta Math. 124, 191–204 (1970)
Ahern, P.R., Clark, D.N.: Radial limits and invariant subspaces. Amer. J. Math. 92, 332–342 (1970)
Aleksandrov, A.B.: Invariant subspaces of the backward shift operator in the space H p (p∈(0, 1)). Zap. Nauchn. Sem. Leningr. Otdel. Mat. Inst. Steklov. (LOMI) 92, 7–29 (1979), also see p. 318. Investigations on linear operators and the theory of functions, IX
Aleksandrov, A.B.: Invariant subspaces of shift operators. An axiomatic approach. Zap. Nauchn. Sem. Leningr. Otdel. Mat. Inst. Steklov. (LOMI), 113, 7–26 (1981), also see p. 264. Investigations on linear operators and the theory of functions, XI
Aleksandrov, A.B.: On the existence of angular boundary values of pseudocontinuable functions. Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklov. (POMI) 222, 5–17 (1995), also see p. 307 (Issled. po, Linein. Oper. i Teor. Funktsii. 23)
Aleksandrov, A.B.: Embedding theorems for coinvariant subspaces of the shift operator. II. Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklov. (POMI) 262, 5–48 (1999), also see p. 231 (Issled. po, Linein. Oper. i Teor. Funkts. 27)
Aleman, A., Korenblum, B.: Derivation-invariant subspaces of C ∞. Comput. Methods Funct. Theory 8(1–2), 493–512 (2008)
Aleman, A., Richter, S.: Simply invariant subspaces of H 2 of some multiply connected regions. Integral Equ. Oper. Theory 24(2), 127–155 (1996)
Arveson, W.: A Short Course on Spectral Theory. Graduate Texts in Mathematics, vol. 209. Springer, New York (2002)
Axler, S., Conway, J.B., McDonald, G.: Toeplitz operators on Bergman spaces. Can. J. Math. 34(2), 466–483 (1982)
Balayan, L., Garcia, S.R.: Unitary equivalence to a complex symmetric matrix: geometric criteria. Oper. Matrices 4(1), 53–76 (2010)
Baranov, A., Bessonov, R., Kapustin, V.: Symbols of truncated Toeplitz operators. J. Funct. Anal. 261, 3437–3456 (2011)
Baranov, A., Chalendar, I., Fricain, E., Mashreghi, J.E., Timotin, D.: Bounded symbols and reproducing kernel thesis for truncated Toeplitz operators. J. Funct. Anal. 259(10), 2673–2701 (2010)
Basor, E.L.: Toeplitz determinants, Fisher-Hartwig symbols, and random matrices. In: Recent Perspectives in Random Matrix Theory and Number Theory. London Math. Soc. Lecture Note Ser., vol. 322, pp. 309–336. Cambridge University Press, Cambridge (2005)
Bercovici, H.: Operator Theory and Arithmetic in H ∞. Mathematical Surveys and Monographs, vol. 26. Am. Math. Soc., Providence (1988)
Bercovici, H., Foias, C., Tannenbaum, A.: On skew Toeplitz operators. I. In: Topics in Operator Theory and Interpolation. Oper. Theory Adv. Appl., vol. 29, pp. 21–43. Birkhäuser, Basel (1988)
Bercovici, H., Foias, C., Tannenbaum, A.: On skew Toeplitz operators. II. In: Nonselfadjoint Operator Algebras, Operator Theory, and Related Topics, Oper. Theory Adv. Appl., vol. 104, pp. 23–35. Birkhäuser, Basel (1998)
Böttcher, A., Silbermann, B.: Introduction to Large Truncated Toeplitz Matrices. Universitext. Springer, New York (1999)
Brown, A., Halmos, P.R.: Algebraic properties of Toeplitz operators. J. Reine Angew. Math. 213, 89–102 (1963/1964)
Carleson, L.: Interpolations by bounded analytic functions and the corona problem. Ann. Math. (2) 76, 547–559 (1962)
Chalendar, I., Chevrot, N., Partington, J.R.: Nearly invariant subspaces for backwards shifts on vector-valued Hardy spaces. J. Oper. Theory 63(2), 403–415 (2010)
Chalendar, I., Fricain, E., Timotin, D.: On an extremal problem of Garcia and Ross. Oper. Matrices 3(4), 541–546 (2009)
Chevrot, N., Fricain, E., Timotin, D.: The characteristic function of a complex symmetric contraction. Proc. Am. Math. Soc. 135(9), 2877–2886 (2007) (electronic)
Cima, J.A., Garcia, S.R., Ross, W.T., Wogen, W.R.: Truncated Toeplitz operators: spatial isomorphism, unitary equivalence, and similarity. Indiana Univ. Math. J. 59(2), 595–620 (2010)
Cima, J.A., Matheson, A.L., Ross, W.T.: The Cauchy Transform. Mathematical Surveys and Monographs, vol. 125. Am. Math. Soc., Providence (2006)
Cima, J.A., Ross, W.T.: The Backward Shift on the Hardy Space. Mathematical Surveys and Monographs, vol. 79. Am. Math. Soc., Providence (2000)
Cima, J.A., Ross, W.T., Wogen, W.R.: Truncated Toeplitz operators on finite dimensional spaces. Oper. Matrices 2(3), 357–369 (2008)
Clark, D.N.: One dimensional perturbations of restricted shifts. J. Anal. Math. 25, 169–191 (1972)
Coburn, L.A.: The C ∗-algebra generated by an isometry. Bull. Am. Math. Soc. 73, 722–726 (1967)
Coburn, L.A.: The C ∗-algebra generated by an isometry. II. Trans. Am. Math. Soc. 137, 211–217 (1969)
Cohn, W.: Radial limits and star invariant subspaces of bounded mean oscillation. Amer. J. Math. 108(3), 719–749 (1986)
Conway, J.B.: A Course in Operator Theory. Graduate Studies in Mathematics, vol. 21. Am. Math. Soc., Providence (2000)
Crofoot, R.B.: Multipliers between invariant subspaces of the backward shift. Pac. J. Math. 166(2), 225–246 (1994)
Danciger, J., Garcia, S.R., Putinar, M.: Variational principles for symmetric bilinear forms. Math. Nachr. 281(6), 786–802 (2008)
Davidson, K.R.: C ∗-Algebras by Example. Fields Institute Monographs, vol. 6. Am. Math. Soc., Providence (1996)
Davis, P.J.: Circulant Matrices. Wiley, New York (1979). A Wiley-Interscience Publication, Pure and Applied Mathematics
Douglas, R.G.: Banach Algebra Techniques in Operator Theory, 2nd edn. Graduate Texts in Mathematics, vol. 179. Springer, New York (1998)
Douglas, R.G., Shapiro, H.S., Shields, A.L.: Cyclic vectors and invariant subspaces for the backward shift operator. Ann. Inst. Fourier (Grenoble) 20, 37–76 (1970)
Duren, P.L.: Theory of H p Spaces. Academic Press, New York (1970)
Dyakonov, K., Khavinson, D.: Smooth functions in star-invariant subspaces. In: Recent Advances in Operator-Related Function Theory. Contemp. Math., vol. 393, pp. 59–66. Am. Math. Soc., Providence (2006)
Foias, C., Frazho, A.E.: The Commutant Lifting Approach to Interpolation Problems. Operator Theory: Advances and Applications, vol. 44. Birkhäuser, Basel (1990)
Foias, C., Tannenbaum, A.: On the Nehari problem for a certain class of L ∞-functions appearing in control theory. J. Funct. Anal. 74(1), 146–159 (1987)
Foias, C., Tannenbaum, A.: On the Nehari problem for a certain class of L ∞ functions appearing in control theory. II. J. Funct. Anal. 81(2), 207–218 (1988)
Garcia, S.R.: Conjugation and Clark operators. In: Recent Advances in Operator-Related Function Theory. Contemp. Math., vol. 393, pp. 67–111. Am. Math. Soc., Providence (2006)
Garcia, S.R.: Aluthge transforms of complex symmetric operators. Integral Equ. Oper. Theory 60(3), 357–367 (2008)
Garcia, S.R., Poore, D.E.: On the closure of the complex symmetric operators: compact operators and weighted shifts. Preprint. arXiv:1106.4855
Garcia, S.R., Poore, D.E.: On the norm closure problem for complex symmetric operators. Proc. Am. Math. Soc., to appear. arXiv:1103.5137
Garcia, S.R., Putinar, M.: Complex symmetric operators and applications. Trans. Am. Math. Soc. 358(3), 1285–1315 (2006) (electronic)
Garcia, S.R., Putinar, M.: Complex symmetric operators and applications. II. Trans. Am. Math. Soc. 359(8), 3913–3931 (2007) (electronic)
Garcia, S.R., Ross, W.T.: A nonlinear extremal problem on the Hardy space. Comput. Methods Funct. Theory 9(2), 485–524 (2009)
Garcia, S.R., Ross, W.T.: The norm of a truncated Toeplitz operator. CRM Proc. Lect. Notes 51, 59–64 (2010)
Garcia, S.R., Tener, J.E.: Unitary equivalence of a matrix to its transpose. J. Oper. Theory 68(1), 179–203 (2012)
Garcia, S.R., Wogen, W.R.: Complex symmetric partial isometries. J. Funct. Anal. 257(4), 1251–1260 (2009)
Garcia, S.R., Wogen, W.R.: Some new classes of complex symmetric operators. Trans. Am. Math. Soc. 362(11), 6065–6077 (2010)
Garcia, S.R., Poore, D.E., Ross, W.: Unitary equivalence to a truncated Toeplitz operator: analytic symbols. Proc. Am. Math. Soc. 140, 1281–1295 (2012)
Garcia, S.R., Poore, D.E., Tener, J.E.: Unitary equivalence to a complex symmetric matrix: low dimensions. Lin. Alg. Appl. 437, 271–284 (2012)
Garcia, S.R., Poore, D.E., Wyse, M.K.: Unitary equivalence to a complex symmetric matrix: a modulus criterion. Oper. Matrices 4(1), 53–76 (2010)
Garcia, S.R., Ross, W., Wogen, W.: Spatial isomorphisms of algebras of truncated Toeplitz operators. Indiana Univ. Math. J. 59, 1971–2000 (2010)
Garcia, S.R., Ross, W., Wogen, W.: C ∗-algebras generated by truncated Toeplitz operators. Oper. Theory. Adv. Appl., to appear
Garcia, S.R.: The eigenstructure of complex symmetric operators. In: Recent Advances in Matrix and Operator Theory. Oper. Theory Adv. Appl., vol. 179, pp. 169–183. Birkhäuser, Basel (2008)
Garnett, J.: Bounded Analytic Functions, 1st edn. Graduate Texts in Mathematics, vol. 236. Springer, New York (2007)
Gilbreath, T.M., Wogen, W.R.: Remarks on the structure of complex symmetric operators. Integral Equ. Oper. Theory 59(4), 585–590 (2007)
Gohberg, I.C., Krupnik, N.Ja.: The algebra generated by the Toeplitz matrices. Funkc. Anal. Ego Prilož. 3(2), 46–56 (1969)
Hartmann, A., Ross, W.T.: Boundary values in range spaces of co-analytic truncated Toeplitz operators. Publ. Mat. 56, 191–223 (2012)
Hartmann, A., Sarason, D., Seip, K.: Surjective Toeplitz operators. Acta Sci. Math. (Szeged) 70(3–4), 609–621 (2004)
Heinig, G.: Not every matrix is similar to a Toeplitz matrix. In: Proceedings of the Eighth Conference of the International Linear Algebra Society, Barcelona, 1999, vol. 332/334, pp. 519–531 (2001)
Hitt, D.: Invariant subspaces of H 2 of an annulus. Pac. J. Math. 134(1), 101–120 (1988)
Hoffman, K.: Banach Spaces of Analytic Functions. Prentice-Hall Series in Modern Analysis. Prentice-Hall, Englewood Cliffs (1962)
Johansson, K.: Toeplitz determinants, random growth and determinantal processes. In: Proceedings of the International Congress of Mathematicians, Beijing, 2002, vol. III, pp. 53–62. Higher Ed. Press, Beijing (2002)
Jung, S., Ko, E., Lee, J.: On scalar extensions and spectral decompositions of complex symmetric operators. J. Math. Anal. Appl. 379, 325–333 (2011)
Jung, S., Ko, E., Lee, M., Lee, J.: On local spectral properties of complex symmetric operators. J. Math. Anal. Appl. 379, 325–333 (2011)
Kiselev, A.V., Naboko, S.N.: Nonself-adjoint operators with almost Hermitian spectrum: matrix model. I. J. Comput. Appl. Math. 194(1), 115–130 (2006)
Li, C.G., Zhu, S., Zhou, T.: Foguel operators with complex symmetry. Preprint
Mackey, D.S., Mackey, N., Petrovic, S.: Is every matrix similar to a Toeplitz matrix? Linear Algebra Appl. 297(1–3), 87–105 (1999)
Makarov, N., Poltoratski, A.: Meromorphic inner functions, Toeplitz kernels and the uncertainty principle. In: Perspectives in Analysis. Math. Phys. Stud., vol. 27, pp. 185–252. Springer, Berlin (2005)
Nikolski, N.: Operators, Functions, and Systems: An Easy Reading. Vol. 1. Mathematical Surveys and Monographs, vol. 92
Nikolski, N.: Treatise on the Shift Operator. Springer, Berlin (1986)
Nikolski, N.: Operators, Functions, and Systems: An Easy Reading. Vol. 2 Mathematical Surveys and Monographs, vol. 93. Am. Math. Soc., Providence (2002). Model operators and systems, Translated from the French by Andreas Hartmann and revised by the author
Partington, J.R.: Linear Operators and Linear Systems: An Analytical Approach to Control Theory. London Mathematical Society Student Texts, vol. 60. Cambridge University Press, Cambridge (2004)
Peller, V.V.: Hankel Operators and Their Applications. Springer Monographs in Mathematics. Springer, New York (2003)
Rosenblum, M., Rovnyak, J.: Hardy Classes and Operator Theory. Oxford Mathematical Monographs. The Clarendon Press/Oxford University Press, New York (1985). Oxford Science Publications
Ross, W.T., Shapiro, H.S.: Generalized Analytic Continuation. University Lecture Series, vol. 25. Am. Math. Soc., Providence (2002)
Sarason, D.: A remark on the Volterra operator. J. Math. Anal. Appl. 12, 244–246 (1965)
Sarason, D.: Generalized interpolation in H ∞. Trans. Am. Math. Soc. 127, 179–203 (1967)
Sarason, D.: Invariant Subspaces. Topics in Operator Theory, pp. 1–47. Am. Math. Soc., Providence (1974). Math. Surveys, No. 13
Sarason, D.: Nearly invariant subspaces of the backward shift. In: Contributions to Operator Theory and Its Applications, Mesa, AZ, 1987. Oper. Theory Adv. Appl., vol. 35, pp. 481–493. Birkhäuser, Basel (1988)
Sarason, D.: Algebraic properties of truncated Toeplitz operators. Oper. Matrices 1(4), 491–526 (2007)
Sarason, D.: Unbounded operators commuting with restricted backward shifts. Oper. Matrices 2(4), 583–601 (2008)
Sarason, D.: Unbounded Toeplitz operators. Integral Equ. Oper. Theory 61(2), 281–298 (2008)
Sarason, D.: Commutant lifting. In: A Glimpse at Hilbert Space Operators. Oper. Theory Adv. Appl., vol. 207, pp. 351–357. Birkhäuser, Basel (2010)
Sedlock, N.: Properties of truncated Toeplitz operators. Ph.D. Thesis, Washington University in St. Louis, ProQuest LLC, Ann Arbor, MI (2010)
Sedlock, N.: Algebras of truncated Toeplitz operators. Oper. Matrices 5(2), 309–326 (2011)
Simon, B.: Orthogonal Polynomials on the Unit Circle. Part 1 American Mathematical Society Colloquium Publications, vol. 54. Am. Math. Soc., Providence (2005). Classical theory. MR 2105088 (2006a:42002a)
Simon, B.: Orthogonal Polynomials on the Unit Circle. Part 2 American Mathematical Society Colloquium Publications, vol. 54. Am. Math. Soc., Providence (2005). Spectral theory. MR 2105089 (2006a:42002b)
Strouse, E., Timotin, D., Zarrabi, M.: Unitary equivalence to truncated Toeplitz operators. Indiana U. Math. J., to appear. http://arxiv.org/abs/1011.6055
Sz.-Nagy, B., Foias, C., Bercovici, H., Kérchy, L.: Harmonic Analysis of Operators on Hilbert Space, 2nd edn. Universitext. Springer, New York (2010)
Takenaka, S.: On the orthonormal functions and a new formula of interpolation. Jpn. J. Math. 2, 129–145 (1925)
Tener, J.E.: Unitary equivalence to a complex symmetric matrix: an algorithm. J. Math. Anal. Appl. 341(1), 640–648 (2008)
Trefethen, L.N., Embree, M.: Spectra and Pseudospectra: The Behavior of Nonnormal Matrices and Operators. Princeton University Press, Princeton (2005)
Vermeer, J.: Orthogonal similarity of a real matrix and its transpose. Linear Algebra Appl. 428(1), 382–392 (2008)
Volberg, A.L., Treil, S.R.: Embedding theorems for invariant subspaces of the inverse shift operator. Zap. Nauchn. Sem. Leningr. Otdel. Mat. Inst. Steklov. (LOMI) 149, 38–51 (1986), also see pp. 186–187 (Issled. Linein. Teor. Funktsii. XV)
Wang, X., Gao, Z.: A note on Aluthge transforms of complex symmetric operators and applications. Integral Equ. Oper. Theory 65(4), 573–580 (2009)
Wang, X., Gao, Z.: Some equivalence properties of complex symmetric operators. Math. Pract. Theory 40(8), 233–236 (2010)
Zagorodnyuk, S.M.: On a J-polar decomposition of a bounded operator and matrix representations of J-symmetric, J-skew-symmetric operators. Banach J. Math. Anal. 4(2), 11–36 (2010)
Zhu, S., Li, C.G.: Complex symmetric weighted shifts. Trans. Am. Math. Soc., to appear
Zhu, S., Li, C., Ji, Y.: The class of complex symmetric operators is not norm closed. Proc. Am. Math. Soc. 140, 1705–1708 (2012)
Acknowledgements
First author partially supported by National Science Foundation Grant DMS-1001614. Second author partially supported by National Science Foundation Grant DMS-1001614.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer Science+Business Media New York
About this chapter
Cite this chapter
Garcia, S.R., Ross, W.T. (2013). Recent Progress on Truncated Toeplitz Operators. In: Mashreghi, J., Fricain, E. (eds) Blaschke Products and Their Applications. Fields Institute Communications, vol 65. Springer, Boston, MA. https://doi.org/10.1007/978-1-4614-5341-3_15
Download citation
DOI: https://doi.org/10.1007/978-1-4614-5341-3_15
Publisher Name: Springer, Boston, MA
Print ISBN: 978-1-4614-5340-6
Online ISBN: 978-1-4614-5341-3
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)




 as a Linear Space
as a Linear Space ,
, .
. are the same.
are the same. .
. is weakly dense in
is weakly dense in
 .
. .
. .
. , the algebra of compact operators on
, the algebra of compact operators on
 is isometrically ∗-isomorphic to
is isometrically ∗-isomorphic to
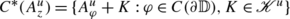 ,
, is a weakly closed linear subspace of
is a weakly closed linear subspace of  .
. if and only if there are functions
if and only if there are functions  are constant multiples of
are constant multiples of  is spatially isomorphic to
is spatially isomorphic to  if and only if either u
1=ψ∘u
2∘φ or
if and only if either u
1=ψ∘u
2∘φ or