The Discretizable Molecular Distance Geometry Problem seems Easier on Proteins

Abstract

Distance geometry methods are used to turn a set of interatomic distances given by Nuclear Magnetic Resonance (NMR) experiments into a consistent molecular conformation. In a set of papers (see the survey [8]) we proposed a Branch-and-Prune (BP) algorithm for computing the set X of all incongruent embeddings of a given protein backbone. Although BP has a worst-case exponential running time in general, we always noticed a linear-like behaviour in computational experiments. In this chapter we provide a theoretical explanation to our observations. We show that the BP is fixed-parameter tractable on protein-like graphs and empirically show that the parameter is constant on a set of proteins from the Protein Data Bank.

1 3.1 Introduction

We consider the following decision problem [9]:

Discretizable Molecular Distance Geometry Problem (DMDGP). Given a simple weighted undirected graph G = (V, E, d) where $d : E \rightarrow {\mathbb{R}}_{+}$, V is ordered so that $V = [n] =\{ 1,\ldots ,n\}$, and the following assumptions hold:

• 1. For all v > 3 and $u \in V$ with $1 \leq v - u \leq 3$, $\{u,v\} \in E$ (discretization).

• 2. Strict triangular inequalities ${d}_{v-2,v} < {d}_{v-2,v-1} + {d}_{v-1,v}$ hold for all v > 2 (non-collinearity)

and given an embedding $x{^\prime} :\{ 1,2,3\} \rightarrow {\mathbb{R}}^{3}$, is there an embedding $x : V \rightarrow {\mathbb{R}}^{3}$ extending x′, such that

$$\forall \{u,v\} \in E\quad \|{x}_{u} - {x}_{v}\| = {d}_{uv}\;?$$

(3.1)

An embedding x on V extends an embedding x′ on $U \subseteq V$ if x′, as a function, is the restriction of x to U; an embedding is feasible if it satisfies (3.1). We also consider the following problem variants:

• DMDGP${}_{K}$, i.e. the family of decision problems (parametrized by the positive integer K) obtained by replacing each symbol ‘3’ in the DMDGP definition by the symbol ‘K’.

• The ${}^{<Emphasis FontCategory="SansSerif">\text{ K}</Emphasis>}$DMDGP, where K is given as part of the input (rather than being a fixed constant as in the DMDGP${}_{K}$).

In both variants, strict triangular inequalities are replaced by strict simplex inequalities, see Eq. (11) in [7]. We remark that $\mbox{ DMDGP} ={ \mbox{ DMDGP}}_{3}$. Other related problems also exist in the literature, such as the discretizable distance geometry problem (DDGP) [18], where the discretization axiom is relaxed to require that each vertex v > K has at least K adjacent predecessors. The original results in this chapter, however, only refer to the DMDGP and its variants.

Statements such as “$\forall p \in P\;F(p)$ holds with probability 1”, for some uncountable set P and valid sentence F, actually mean that there is a Lebesgue-measurable $Q \subseteq P$ with Lebesgue measure 1 w.r.t. P such that $\forall p \in Q\;F(p)$ holds. This notion is less restrictive than genericity based on algebraic independence [2]. We also point out that a statement might hold with probability 1 with respect to a set which has itself Lebesgue measure 0 in a larger set. For example, we will show that the set of ${}^{<Emphasis FontCategory="SansSerif">\text{ K}</Emphasis>}$DMDGP instances having an incongruent solution set X with $\vert X\vert = {2}^{\mathcal{l}}$ for some $\mathcal{l} \in \mathbb{N}$ has measure 1 into the set of all YES instances, which itself is a set of measure 0 in the set of all ${}^{<Emphasis FontCategory="SansSerif">\text{ K}</Emphasis>}$DMDGP instances.

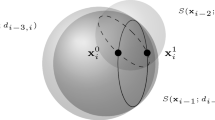
The discretization axiom guarantees that the locus of the points that embed v in ${\mathbb{R}}^{3}$ is the intersection of the three spheres centred at v − 3, v − 2, v − 1 with radii ${d}_{v-3,v},{d}_{v-2,v},{d}_{v-1,v}$. If this intersection is non-empty, then it contains two points with probability 1. The complementary zero-measure set contains instances that do not satisfy the non-collinearity axiom and which might yield loci for v with zero or uncountably many points. We remark that if the intersection of the three spheres is empty, then the instance is a NO one. We solve ${}^{<Emphasis FontCategory="SansSerif">\text{ K}</Emphasis>}$DMDGP instances using a recursive algorithm called Branch-and-Prune (BP) [13]: at level v, the search is branched according to the (at most two) possible positions for v. The BP generates a (partial) binary search tree of height n, each full branch of which represents a feasible embedding for the given graph. The BP has exponential worst-case complexity.

The ${}^{<Emphasis FontCategory="SansSerif">\text{ K}</Emphasis>}$DMDGP and its variants are related to the molecular distance geometry problem (MDGP), i.e. find an embedding in ${\mathbb{R}}^{3}$ of a given simple weighted undirected graph. We denote the K-dimensional generalization of the MDGP (with K part of the input) by distance geometry problem (DGP) and the variant with K fixed by DGP _K . The MDGP is a good model for determining the structure of molecules given a set of interatomic distances [11, 14], which are usually given by nuclear magnetic resonance (NMR) experiments [21], a technique which allows the detection of interatomic distances below 5.5Å. The DGP has applications to wireless sensor networks [5], statics, robotics and graph drawing among others. In general, the MDGP and DGP implicitly require a search in a continuous Euclidean space [14]. ${}^{<Emphasis FontCategory="SansSerif">\text{ K}</Emphasis>}$DMDGP instances describe rigid graphs [6], in particular Henneberg type I graphs [12].

The DMDGP is a model for protein backbones. For any atom $v \in V$, the distances ${d}_{v-1,v}$ and ${d}_{v-2,v-1}$ are known because they refer to covalent bonds. Furthermore, the angle between v − 2, v − 1 and v is known because it is adjacent to two covalent bonds, which implies that ${d}_{v-2,v}$ is also known by triangular geometry. In general, the distance ${d}_{v-3,v}$ is smaller than 5Å and can therefore be assumed to be known by NMR experiments; in practice, there are ways to find atomic orders which ensure that ${d}_{v-3,v}$ is known [7]. There is currently no known protein with ${d}_{v-3,v-1}$ being exactly equal to ${d}_{v-3,v-2} + {d}_{v-2,v-1}$ [13].

Over the years, we noticed that the CPU time behaviour of the BP on protein instances looked more linear than exponential. In this chapter we give a theoretical motivation for this observation. More precisely, there are cases where BP is actually fixed-parameter tractable (FPT), and we empirically verify on 45 proteins from the Protein Data Bank (PDB) [1] that they belong to these cases, and always with the parameter value set to the constant 4. The strategy is as follows: we first show that DMDGP${}_{K}$ is NP-hard (Sect. 3.3), then we show that the number of leaf nodes in the BP search tree is a power of 2 with probability 1 (Sect. 3.4.2), and finally we use this information to construct a directed acyclic graph (DAG) representing the number of leaf nodes in function of the graph edges (Sect. 3.5). This DAG allows us to show that the BP is FPT on a class of graphs which provides a good model for proteins (Sect. 3.5.1).

2 3.2 The BP Algorithm

For all $v \in V$ we let $N(v) =\{ u \in V \;\vert \;\{u,v\} \in E\}$ be the set of vertices adjacent to $v$. An embedding of a subgraph of $G$ is called a partial embedding of G. Let X be the set of embeddings (modulo translations and rotations) solving a given ${}^{<Emphasis FontCategory="SansSerif">\text{ K}</Emphasis>}$DMDGP instance.

Since vertex v can be placed in at most two possible positions (the intersection of K spheres in ${\mathbb{R}}^{K}$), the BP algorithm tests each in turn and calls itself recursively for every feasible position. BP exploits other edges (than those granted by the discretization axiom) in order to prune branches: a position might be feasible with respect to the distances to the K immediate predecessors $v - 1,\ldots ,v - K$ but not necessarily with distances to other adjacent predecessors.

For a partial embedding $\bar{x}$ of G and $\{u,v\} \in E$ let ${S}_{uv}^{\bar{x}}$ be the sphere centered at ${x}_{u}$ with radius ${d}_{uv}$.

The BP algorithm is BP(K + 1, x′, $\varnothing$) (see Alg. 1), where x′ is the initial embedding of the first K vertices mentioned in the ${}^{<Emphasis FontCategory="SansSerif">\text{ K}</Emphasis>}$DMDGP definition. By the ${}^{<Emphasis FontCategory="SansSerif">\text{ K}</Emphasis>}$DMDGP axioms, | T | ≤ 2. At termination, X contains all embeddings (modulo rotations and translations) extending x′ [9, 13]. Embeddings x ∈ X can be represented by sequences $\chi (x) \in \{-1,{1\}}^{n}$ representing left/right choices when traversing a branch from root to leaf of the search tree. More precisely, (i) $\chi {(x)}_{i} = 1$ for all i ≤ K; (ii) for all i > K, $\chi {(x)}_{i} = -1$ if $a{x}_{i} < {a}_{0}$ and $\chi {(x)}_{i} = 1$ if $a{x}_{i} \geq {a}_{0}$, where $ax = {a}_{0}$ is the equation of the hyperplane through ${x}_{i-K},\ldots ,{x}_{i-1}$. For an embedding $x \in X$, $\chi (x)$ is the chirality [3] of x (the formal definition of chirality actually states $\chi {(x)}_{0} = 0$ if $a{x}_{i} = {a}_{0}$, but since this case holds with probability 0, we do not consider it here).

The BP (Alg. 1) can be run to termination to find all possible embeddings of G, or stopped after the first leaf node at level n is reached, in order to find just one embedding of G. In the last few years we have conceived and described several BP variants targeting different problems [8], including, very recently, problems with interval-type uncertainties on some of the distance values [10]. The BP algorithm is currently the only method which is able to find all incongruent embeddings for a given protein backbone. Compared to continuous search algorithms (e.g. [17]), the performance of the BP algorithm is impressive from the point of view of both efficiency and reliability.

3 3.3 Complexity

Any class of YES instances where each vertex v only has distances to the K immediate predecessors provides a full BP binary search tree (after level K), and therefore shows that the BP is an exponential-time algorithm in the worst case. One remarkable feature of the computational experiments conducted on our BP implementation [19] on protein instances is that the exponential-time behaviour of the BP algorithm was never noticed empirically.

Restricting d to only take integer values, the DGP${}_{1}$ is NP-complete by reduction from Subset-Sum, the DGP${}_{K}$ is (strongly) NP-hard by reduction from 3-SAT, and the DGP is (strongly) NP-hard by induction on K [20]. Only the DGP${}_{1}$ is known to be NP-complete, because if d takes integer values then the YES-certificate x (the embedding) can be chosen to have integer values too.

The DMDGP is NP-hard by reduction from Subset-Sum (Theorem 3 in [9]). We generalize this result to the ${}^{<Emphasis FontCategory="SansSerif">\text{ K}</Emphasis>}$DMDGP.

Theorem 3.1.

The DMDGP ${}_{K}$ is NP-hard for all $K \geq 2$ .

Proof.

Let $a = ({a}_{1},\ldots ,{a}_{N})$ be an instance of Subset-Sum consisting of positive integers, and define an instance of DMDGP${}_{K}$ where $V =\{ 0,\ldots ,KN\}$, E includes $\{i,i + j\}$ for all j ∈ { 1, …, K} and $i \in \{ 0,\ldots ,KN - j\}$, and

$$\begin{array}{rcl} \forall i \in \{ 0,\ldots ,KN - 1\}\quad {d}_{i,i+1}& =& {a}_{\lfloor i/K\rfloor } \end{array}$$

(3.2)

$$\begin{array}{rcl}\forall j \in \{ 2,\ldots ,K\},i \in \{ 0,\ldots ,KN - j\}\quad {d}_{i,i+j}& =& \sqrt{{\sum \nolimits }_{\mathcal{l}=1}^{j}{d}_{i+\mathcal{l}-1,i+\mathcal{l}}^{2}}\end{array}$$

(3.3)

$$\begin{array}{rcl} {d}_{0,KN}& =& 0. \end{array}$$

(3.4)

Let $s \in \{-1,{1\}}^{N}$ be a solution of the Subset-Sum instance a. We let ${x}_{0} = 0$ and for all $i = K(\mathcal{l} - 1) + j > 0$ we let ${x}_{i} = {x}_{i-1} + {s}_{\mathcal{l}}{a}_{\mathcal{l}}{e}_{j}$, where ${e}_{j}$ is the vector with a one in component j and zero elsewhere. Because ${\sum \nolimits }_{\mathcal{l}\leq N}{s}_{\mathcal{l}}{a}_{\mathcal{l}} = 0$, if s solves the Subset-Sum instance a, then, by inspection, x solves the corresponding DMDGP instance Eqs. (3.2)–(3.4). Conversely, let x be an embedding that solves Eqs. (3.2)–(3.4), where we assume without loss of generality that ${x}_{0} = 0$. Then Eq. (3.3) ensures that the line through ${x}_{i},{x}_{i-1}$ is orthogonal to the line through ${x}_{i-1},{x}_{i-2}$ for all i > 1, and again we assume without loss of generality that, for all $j \in \{ 1,\ldots ,K\}$, the lines through ${x}_{j-1},{x}_{j}$ are parallel to the ith coordinate axis. Now consider the chirality $\chi$ of x: because all distance segments are orthogonal, for each $j \leq K$ the jth coordinate is given by ${x}_{KN,j} =\mathop{ \sum }\limits_{i \mathbin{\rm mod}\,\,K=j}{\chi }_{i}{a}_{\lfloor i/K\rfloor }$. Since ${d}_{0,KN} = 0$, for all $j \leq K$, we have $0 = {x}_{KN,j} ={ \sum \nolimits }_{\mathcal{l}\leq N}{\chi }_{K(\mathcal{l}-1)+j}{a}_{\mathcal{l}}$, which implies that, for all $j \leq K$, ${s}^{j} = ({\chi }_{K(\mathcal{l}-1)+j}\;\vert \;1 \leq \mathcal{l} \leq N)$ is a solution for the Subset-Sum instance a. $\square$

Corollary 3.1.

The ${}^{\mathsf{K}}$ DMDGP is NP-hard.

Proof.

Every specific instance of the ${}^{<Emphasis FontCategory="SansSerif">\text{ K}</Emphasis>}$DMDGP specifies a fixed value for K and hence belongs to the DMDGP${}_{K}$. Hence the result follows by inclusion. $\square$

4 3.4 Partial Reflection Symmetries

The results in this section are also found in [16], but the presentation below, which is based on group theory, is new and (we hope) clearer. We partition E into the sets ${E}_{D} =\{\{ u,v\}\;\vert \;\vert v - u\vert \leq K\}$ and ${E}_{P} = E \ {E}_{D}$. We call E _D the discretization edges and E _P the pruning edges. Discretization edges guarantee that a DGP instance is in the ${}^{<Emphasis FontCategory="SansSerif">\text{ K}</Emphasis>}$DMDGP. Pruning edges are used to reduce the BP search space by pruning its tree. In practice, pruning edges might make the set T in Alg. 1 have cardinality 0 or 1 instead of 2. We assume G is a YES instance of the ${}^{<Emphasis FontCategory="SansSerif">\text{ K}</Emphasis>}$DMDGP.

4.1 3.4.1 The Discretization Group

Let ${G}_{D} = (V,{E}_{D},d)$ and X _D be the set of embeddings of ${G}_{D}$; since ${G}_{D}$ has no pruning edges, the BP search tree for ${G}_{D}$ is a full binary tree and $\vert {X}_{D}\vert = {2}^{n-K}$. The discretization edges arrange the embeddings so that, at level $\mathcal{l}$, there are ${2}^{\mathcal{l}-K}$ possible positions for the vertex v with rank $\mathcal{l}$. We assume that | T |  = 2 (see Alg. 1) at each level v of the BP tree, an event which, in absence of pruning edges, happens with probability 1 — thus many results in this section are stated with probability 1. Let therefore $T =\{ {x}_{v}^{0},{x}_{v}^{1}\}$ be the two possible embeddings of v at a certain recursive call of Alg. 1 at level v of the BP tree; then because T is an intersection of K spheres, ${x}_{v}^{1}$ is the reflection of ${x}_{v}^{0}$ through the hyperplane defined by ${x}_{v-K},\ldots ,{x}_{v-1}$. Denote this reflection operator by ${R}_{x}^{v}$.

Theorem 3.2 (Cororollary 4.6 and Theroem 4.9 in [16]). 

With probability 1, for all v > K and u < v − K there is a set H ^uv , with |H ^uv | = 2 ^v−u−K , of real positive values such that for each $x \in X$ we have $\|{x}_{v} - {x}_{u}\| \in {H}^{uv}$ . Furthermore, $\forall x \in X\;\|{x}_{v} - {x}_{u}\| =\| {R}_{x}^{u+K}({x}_{v}) - {x}_{u}\|$ and $\forall x{^\prime} \in X$ , if ${x}_{v}{^\prime}\not\in \{{x}_{v},{R}_{x}^{u+K}({x}_{v})\}$ then $\|{x}_{v} - {x}_{u}\|\not =\|{x{^\prime}}_{v} - {x}_{u}\|$ .

We sketch the proof in Fig. 3.1 for K = 2; the solid circles at levels 3, 4, 5 mark equidistant levels from 1. The dashed circles represent the spheres ${S}_{uv}^{x}$ (see Alg. 1). Intuitively, two branches from level 1 to level 4 or 5 will have equal segment lengths but different angles between consecutive segments, which will cause the end nodes to be at different distances from the node at level 1.

Fig. 3.1

A pruning edge {1, 4} prunes either ${\nu }_{6},{\nu }_{7}$ or ${\nu }_{5},{\nu }_{8}$

For any nonzero vector $y \in {\mathbb{R}}^{K}$ let ${\rho }^{y}$ be the reflection operator through the hyperplane passing through the origin and normal to y. If y is normal to the hyperplane defined by ${x}_{v-K},\ldots ,{x}_{v-1}$, then ${\rho }^{y} = {R}_{x}^{v}$.

Lemma 3.1.

Let $x\not =y \in {\mathbb{R}}^{K}$ and $z \in {\mathbb{R}}^{K}$ such that z is not in the hyperplanes through the origin and normal to x,y. Then ${\rho }^{x}{\rho }^{y}z = {\rho }^{{\rho }^{x}y }{\rho }^{x}z$ .

Proof.

Fig. 3.2 gives a proof sketch for K = 2. By considering the reflection ${\rho }^{{\rho }^{x}y }$ of the map ${\rho }^{y}$ through ${\rho }^{x}$, we get $\|z - {\rho }^{y}z\| =\| {\rho }^{x}z - {\rho }^{{\rho }^{x}y }{\rho }^{x}z\|$. By reflection through ${\rho }^{x}$ we get $\|O - z\| =\| O - {\rho }^{x}z\|$ and $\|O - {\rho }^{y}z\| =\| O - {\rho }^{x}{\rho }^{y}z\|$. By reflection through ${\rho }^{y}$ we get $\|O - z\| =\| O - {\rho }^{y}z\|$. By reflection through ${\rho }^{{\rho }^{x}y }$ we get $\|O - {\rho }^{x}z\| =\| O - {\rho }^{{\rho }^{x}y }{\rho }^{x}z\|$. The triangles $\bigtriangleup (z,O,{\rho }^{y}z)$ and $\bigtriangleup ({\rho }^{x}z,O,{\rho }^{{\rho }^{x}y }{\rho }^{x}z)$ are then equal because the side lengths are pairwise equal. Also, reflection of $\bigtriangleup (z,O,{\rho }^{y}z)$ through ${\rho }^{x}$ yields $\bigtriangleup (z,O,{\rho }^{y}z) = \bigtriangleup ({\rho }^{x}z,O,{\rho }^{x}{\rho }^{y}z)$, whence ${\rho }^{{\rho }^{x}y }{\rho }^{x}z = {\rho }^{x}{\rho }^{y}z$. $\square$

For v > K and $x \in X$ we now define partial reflection operators:

$${g}_{v}(x) = ({x}_{1},\ldots ,{x}_{v-1},{R}_{x}^{v}({x}_{ v}),\ldots ,{R}_{x}^{v}({x}_{ n})).$$

(3.5)

The ${g}_{v}$’s map an embedding x to its partial reflection with first branch at v. It is easy to show that the ${g}_{v}$’s are injective with probability 1 and idempotent. Further, the ${g}_{v}$’s commute.

Lemma 3.2.

For $x \in X$ and $u,v \in V$ such that u,v > K, ${g}_{u}{g}_{v}(x) = {g}_{v}{g}_{u}(x)$ .

Proof.

Assume without loss of generality u < v. Then:

$$\begin{array}{rcl}{ g}_{u}{g}_{v}(x)& =& {g}_{u}({x}_{1},\ldots ,{x}_{v-1},{R}_{x}^{v}({x}_{ v}),\ldots ,{R}_{x}^{v}({x}_{ n})) \\ & =& ({x}_{1}\ldots ,{x}_{u-1},{R}_{{g}_{v}(x)}^{u}({x}_{ u}),\ldots ,{R}_{{g}_{v}(x)}^{u}{R}_{ x}^{v}({x}_{ v}),\ldots ,{R}_{{g}_{v}(x)}^{u}{R}_{ x}^{v}({x}_{ n})) \\ & =& ({x}_{1}\ldots ,{x}_{u-1},{R}_{x}^{u}({x}_{ u}),\ldots ,{R}_{{g}_{u}(x)}^{v}{R}_{ x}^{u}({x}_{ v}),\ldots ,{R}_{{g}_{u}(x)}^{v}{R}_{ x}^{u}({x}_{ n})) \\ & =& {g}_{v}({x}_{1},\ldots ,{x}_{u-1},{R}_{x}^{u}({x}_{ u}),\ldots ,{R}_{x}^{u}({x}_{ n})) \\ & =& {g}_{v}{g}_{u}(x), \\ \end{array}$$

where ${R}_{{g}_{v}(x)}^{u}{R}_{x}^{v}({x}_{w}) = {R}_{{g}_{u}(x)}^{v}{R}_{x}^{u}({x}_{w})$ for each $w \geq v$ by Lemma 3.1. □ 

We define the discretization group to be the group ${\mathcal{G}}_{D} =\langle {g}_{v}\;\vert \;v > K\rangle$ generated by the g _v ’s.

Corollary 3.2.

With probability 1, ${\mathcal{G}}_{D}$ is an Abelian group isomorphic to ${C}_{2}^{n-K}$ (the Cartesian product consisting of n − K copies of the cyclic group of order 2).

For all v > K let ${\gamma }_{v} = (1,\ldots ,1,-{1}_{v},\ldots ,-1)$ be the vector consisting of one’s in the first v − 1 components and − 1 in the last components. Then the ${g}_{v}$ actions are naturally mapped onto the chirality functions.

Lemma 3.3.

For all x ∈ X, $\chi ({g}_{v}(x)) = \chi (x) \circ {\gamma }_{v}$ , where $\circ$ is the Hadamard (i.e. component-wise) product.

This follows by definition of ${g}_{v}$ and of chirality of an embedding.

Fig. 3.2

Reflecting through ${\rho }^{y}$ first and ${\rho }^{x}$ later is equivalent to reflecting through ${\rho }^{x}$ first and (the reflection of ${\rho }^{y}$ through ${\rho }^{x}$) later

Because, by Alg. 1, each $x \in X$ has a different chirality, for all $x,x{^\prime} \in X$ there is $g \in {\mathcal{G}}_{D}$ such that x′ = g(x), i.e. the action of ${\mathcal{G}}_{D}$ on X is transitive. By Theorem 3.2, the distances associated to the discretization edges are invariant with respect to the discretization group.

4.2 3.4.2 The Pruning Group

Consider a pruning edge $\{u,v\} \in {E}_{P}$. By Theroem 3.2, with probability 1 we have ${d}_{uv} \in {H}^{uv}$, otherwise G cannot be a YES instance (against the hypothesis). Also, again by Theroem 3.2, ${d}_{uv} =\| {x}_{u} - {x}_{v}\|\not =\|{g}_{w}{(x)}_{u} - {g}_{w}{(x)}_{v}\|$ for all $w \in \{ u + K + 1,\ldots ,v\}$ (e.g. the distance $\|{\nu }_{1} - {\nu }_{9}\|$ in Fig. 3.1 is different from all its reflections $\|{\nu }_{1} - {\nu }_{h}\|$, with $h \in \{ 10,11,12\}$, w.r.t. ${g}_{4},{g}_{5}$). We therefore define the pruning group

$${\mathcal{G}}_{P} =\langle {g}_{w}\;\vert \;w > K \wedge \forall \{u,v\} \in {E}_{P}\;(w\not\in \{u + K + 1,\ldots ,v\})\rangle .$$

By definition, ${\mathcal{G}}_{P} \leq {\mathcal{G}}_{D}$ and the distances associated with the pruning edges are invariant with respect to ${\mathcal{G}}_{P}$.

Theorem 3.3.

The action of ${\mathcal{G}}_{P}$ on X is transitive with probability 1.

Proof.

This theorem follows from Theorem 5.4 in [15], but here is another, hopefully simpler, proof. Let $x,x{^\prime} \in X$, we aim to show that $\exists g \in {\mathcal{G}}_{P}$ such that x′ = g(x) with probability 1. Since the action of ${\mathcal{G}}_{D}$ on X is transitive, $\exists g \in {\mathcal{G}}_{D}$ with x′ = g(x). Now suppose $g\not\in {\mathcal{G}}_{P}$, then there is a pruning edge $\{u,v\} \in {E}_{P}$ and an $\mathcal{l} \in \mathbb{N}$ s.t. $g ={ \prod \nolimits }_{h=1}^{\mathcal{l}}{g}_{{v}_{h}})$ for some vertex set $\{{v}_{1},\ldots ,{v}_{\mathcal{l}} > K\}$ including at least one vertex $w \in \{ u + K + 1,\ldots ,v\}$. By Theorem 3.2, as remarked above, this implies that ${d}_{uv} =\| {x}_{u} - {x}_{v}\|\not =\|{g}_{w}{(x)}_{u} - {g}_{w}{(x)}_{v}\|$ with probability 1. If the set $Q =\{ {v}_{1},\ldots ,{v}_{\mathcal{l}}\} \cap \{ u + K + 1,\ldots ,v\}$ has cardinality 1, then ${g}_{w}$ is the only component of g not fixing ${d}_{uv}$, and hence $x{^\prime} = g(x)\not\in X$, against the hypothesis. Otherwise, the probability of another $z \in Q \{ w\}$ yielding $\|{x}_{u} - {x}_{v}\| =\| {g}_{z}{g}_{w}{(x)}_{u} - {g}_{z}{g}_{w}{(x)}_{v}\|$, notwithstanding the fact that $\|{g}_{w}{(x)}_{u} - {g}_{w}{(x)}_{v}\|\not =\|{x}_{u} - {x}_{v}\|\not =\|{g}_{z}{(x)}_{u} - {g}_{z}{(x)}_{v}\|$, is zero; and by induction this also covers any cardinality of Q. Therefore $g \in {\mathcal{G}}_{P}$ and the result follows. $\square$

Theorem 3.4.

With probability 1, $\exists \mathcal{l} \in \mathbb{N}\;\vert X\vert = {2}^{\mathcal{l}}$ .

Proof.

Since ${\mathcal{G}}_{D}\cong{C}_{2}^{n-K}$, $\vert {\mathcal{G}}_{D}\vert = {2}^{n-K}$. Since ${\mathcal{G}}_{P} \leq {\mathcal{G}}_{D}$, $\vert {\mathcal{G}}_{P}\vert$ divides the order of $\vert {\mathcal{G}}_{D}\vert$, which implies that there is an integer $\mathcal{l}$ with $\vert {\mathcal{G}}_{P}\vert = {2}^{\mathcal{l}}$. By Theorem 3.3, the action of ${\mathcal{G}}_{P}$ on X only has one orbit, i.e. ${\mathcal{G}}_{P}x = X$ for any $x \in X$. By idempotency, for $g,g{^\prime} \in {\mathcal{G}}_{P}$, if gx = g′x then g = g′. This implies $\vert {\mathcal{G}}_{P}x\vert = \vert {\mathcal{G}}_{P}\vert$. Thus, for any $x \in X$, $\vert X\vert = \vert {\mathcal{G}}_{P}x\vert = \vert {\mathcal{G}}_{P}\vert = {2}^{\mathcal{l}}$. □ 

5 3.5 Bounded Treewidth

The results of the previous section allow us to express the number of nodes at each level of the BP search tree in function of the level rank and the pruning edges. Fig. 3.3 shows a DAG ${\mathcal{D}}_{uv}$ that represents the number of valid BP search tree nodes in function of pruning edges between two vertices $u,v \in V$ such that v > K and u < v − K. The first line shows different values for the rank of v w.r.t. u; an arc labelled with an integer i implies the existence of a pruning edge {u + i, v} (arcs with ∨ -expressions replace parallel arcs with different labels). An arc is unlabelled if there is no pruning edge {w, v} for any $w \in \{ u,\ldots ,v - K - 1\}$. The vertices of the DAG are arranged vertically by BP search tree level and are labelled with the number of BP nodes at a given level, which is always a power of two by Theroem 3.4. A path in this DAG represents the set of pruning edges between u and v, and its incident vertices show the number of valid nodes at the corresponding levels. For example, following unlabelled arcs corresponds to no pruning edge between u and v and leads to a full binary BP search tree with 2^v − K nodes at level v.

Fig. 3.3

Number of valid BP nodes (vertex label) at level $u + K + \mathcal{l}$ (column) in function of the pruning edges (path spanning all columns)

5.1 3.5.1 Fixed-Parameter Tractable Behaviour

For a given G _D , each possible pruning edge set E _P corresponds to a path spanning all columns in ${\mathcal{D}}_{1n}$. Instances with diagonal (Proposition 3.1) or below-diagonal (Proposition 3.2) E _P paths yield BP trees whose width is bounded by $O({2}^{{v}_{0}})$ where ${v}_{0}$ is small w.r.t. n.

Proposition 3.1.

If $\exists {v}_{0} > K$ s.t.  $\forall v > {v}_{0}\exists u < v - K$ with $\{u,v\} \in {E}_{P}$ then the BP searchtreewidth is bounded by ${2}^{{v}_{0}-K}$ .

This corresponds to a path ${<Emphasis FontCategory="SansSerif">\text{ p}</Emphasis>}_{0} = (1,2,\ldots ,{2}^{{v}_{0}-K},\ldots ,{2}^{{v}_{0}-K})$ that follows unlabelled arcs up to level ${v}_{0}$ and then arcs labelled ${v}_{0} - K - 1$, ${v}_{0} - K - 1 \vee {v}_{0} - K$ and so on, leading to nodes that are all labelled with ${2}^{{v}_{0}-K}$ (Fig. 3.4, left).

Fig. 3.4

A path ${<Emphasis FontCategory="SansSerif">\text{ p}</Emphasis>}_{0}$ yielding treewidth 4 (above) and another path below ${<Emphasis FontCategory="SansSerif">\text{ p}</Emphasis>}_{0}$ (below)

Proposition 3.2.

If $\exists {v}_{0} > K$ such that every subsequence s of consecutive vertices $>\!\! {v}_{0}$ with no incident pruning edge is preceded by a vertex ${v}_{s}$ such that ∃u _s < v _s  (v _s − u _s ≥|s|∧{ u _s ,v _s } ∈ E _P ), then the BP searchtreewidth is bounded by ${2}^{{v}_{0}-K}$ .

This situation corresponds to a below-diagonal path, Fig. 3.4 (right). In general, for those instances for which the BP searchtreewidth has a $O({2}^{{v}_{0}}\log n)$ bound, the BP has a worst-case running time $O({2}^{{v}_{0}}L{2}^{\log n}) = O(Ln)$, where L is the complexity of computing T. Since L is typically constant in n [4], for such cases the BP runs in time $O({2}^{{v}_{0}}n)$. Let $V {^\prime} =\{ v \in V \;\vert \;\exists \mathcal{l} \in \mathbb{N}\;(v = {2}^{\mathcal{l}})\}$.

Proposition 3.3.

If $\exists {v}_{0} > K$ s.t. for all $v \in V \ V {^\prime}$ with $v > {v}_{0}$ there is $u < v - K$ with $\{u,v\} \in {E}_{P}$ then the BP searchtreewidth at level n is bounded by ${2}^{{v}_{0}}n$ .

This corresponds to a path along the diagonal ${2}^{{v}_{0}}$ apart from logarithmically many vertices in V (those in V′), at which levels the BP doubles the number of search nodes (Fig. 3.5). For a pruning edge set E _P as in Proposition 3.3, or yielding a path below it, the BP runs in $O({2}^{{v}_{0}}{n}^{2})$.

5.2 3.5.2 Empirical Verification

We consider a set of 45 protein instances from the PDB. Since PDB data include the Euclidean embedding of the protein, we compute all distances, then filter all those that are longer than 5.5Å, which is a reasonable estimate for NMR measures [21]. We then form the weighted graph and embed it with our implementation of the BP algorithm [19]. It turns out that 40 proteins satisfy Proposition. 3.1 and five proteins satisfy Proposition. 3.2, all with ${v}_{0} = 4$ (see Table 3.1). This is consistent with the computational insight [9] that BP empirically displays a polynomial (specifically, linear) complexity on real proteins.

Fig. 3.5

A path yielding treewidth O(n)

Table 3.1 Computation of minimum v ₀ in PDB instances

6 3.6 Conclusion

In this chapter we provide a theoretical basis to the empirical observation that the BP never seems to attain its exponential worst-case time bound on DMDGP instances from proteins. Other original contributions include a generalization of an NP-hardness proof to the ${}^{<Emphasis FontCategory="SansSerif">\text{ K}</Emphasis>}$DMDGP and a new presentation, based on group theory and involving new proofs, of the fact that the cardinality of the solution set of YES instances of the ${}^{<Emphasis FontCategory="SansSerif">\text{ K}</Emphasis>}$DMDGP is a power of two with probability 1.