Revisiting the Tail Asymptotics of the Double QBD Process: Refinement and Complete Solutions for the Coordinate and Diagonal Directions

Abstract

We consider a two-dimensional skip-free reflecting random walk on a nonnegative integer quadrant. We are interested in the tail asymptotics of its stationary distribution, provided its existence is assumed. We derive exact tail asymptotics for the stationary probabilities on the coordinate axis. This refines the asymptotic results in the literature and completely solves the tail asymptotic problem on the stationary marginal distributions in the coordinate and diagonal directions. For this, we use the so-called analytic function method in such a way that either generating functions or moment-generating functions are suitably chosen. The results are exemplified by a two-node network with simultaneous arrivals.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

Introduction

We are concerned with a two-dimensional reflecting random walk on a nonnegative integer quadrant, which is the set of two-dimensional vectors (i, j) such that i, j are nonnegative integers. We assume that it is skip free in all directions, that is, its increments in each coordinate direction are at most one in absolute value. The boundary of the quadrant is partitioned into three faces: the origin and the two coordinate axes in the quadrant. We assume that the transition probabilities of this random walk are homogeneous on each boundary face, but they may change on different faces or the interior of the quadrant, that is, inside of the boundary.

This reflecting random walk is referred to as a double quasi-birth-and-death (QBD) process in [18]. This process can be used to describe a two-node queueing network under various settings such as server collaboration and simultaneous arrivals and departures, and its stationary distribution is important for the performance evaluation of such a network model. The existence of the stationary distribution, that is, stability, is nicely characterized, but the stationary distribution is hard to obtain analytically except for some special cases. Because of this and its own importance, research interest has been directed at its tail asymptotics.

Until now, the tail asymptotics for the double QBD have been obtained in terms of its modeling primitives under the most general setting by Miyazawa [18], while less explicit results have been obtained for more general two-dimensional reflecting random walks by Borovkov and Mogul’skii [2]. Foley and McDonald [10, 11] studied the double QBD under some limitations. Recently, Kobayashi and Miyazawa [13] modified the double QBD process in such a way that upward jumps may be unbounded; they also studied its tail asymptotics. This process, called a double M/G/1 type, includes the double QBD process as a special case. For special cases such as tandem and priority queues, the tail asymptotics were recently investigated in Guillemin and Leeuwaarden [12] and Li and Zhao [14, 15]. Li and Zhao [16] challenged the general double QBD process (see additional note at the end of this section).

Tail asymptotic problems have also been studied for a semimartingale reflecting Brownian motion (SRBM), which is a continuous-time-and-state counterpart of a reflecting random walk. For the two-dimensional SRBM, the rate function for large deviations was obtained under a certain extra assumption in Avram et al. [1]. Dai and Miyazawa [3] derived more complete answers but for stationary marginal distributions.

Thus, we now have many studies of the tail asymptotics for two-dimensional reflecting and related processes (see, e.g., Miyazawa [19] for a survey). Nevertheless, many problems remain unsolved even for the double QBD process. The exact tail asymptotics of the stationary marginal distributions in the coordinate directions are one such problem. Here, a sequence of nonnegative numbers {p(n); n = 0, 1, 2} is said to have exact tail asymptotic {h(n); n = 0, 1, …} if its ratio p(n) ∕ h(n) converges to a positive constant as n goes to infinity. We also write this asymptotic as

$$\begin{array}{rcl} p(n) \sim h(n).& & \\ \end{array}$$

We will find $h(n) = {n}^{\kappa }{a}^{-n}$ or ${n}^{\kappa }(1 + b{(-1)}^{n}){a}^{-n}$ with constants $\kappa = -\frac{3} {2},-\frac{1} {2},0,1$, a > 1 and | b | ≤ 1 for marginal distributions (and for stationary probabilities on the boundaries).

We aim to completely solve the exact tail asymptotics of stationary marginal distributions in the coordinate and diagonal directions, provided a stationary distribution exists. It is known that the tail asymptotics of the stationary probabilities on each coordinate axis are one of their key features (e.g., see Miyazawa [19]). These asymptotics are studied by Borovkov and Mogul’skii [2] and Miyazawa [18]. The researchers used Markov additive processes generated by removing one of the boundary faces that is not the origin and related their asymptotics. However, there are some limitations in that approach.

In this chapter, we revisit the double QBD process using a different approach that has been recently developed [3, 13, 20]. This approach is purely analytic and is called an analytic function method. It is closely related to the kernel method used in various studies [12, 14, 15]. Its details and related topics are reviewed by Miyazawa [19].

The analytic function method [3, 13, 20] only uses moment-generating functions because they have nice analytic properties including convexity. However, a generating function is more convenient for a distribution of integers because they are polynomials. Thus, generating functions have been used in the kernel method.

In this chapter, we use both generating functions and moment-generating functions. We first consider the convergence domain of the moment-generating function of a stationary distribution, which is two-dimensional. This part mainly refers to recent results from Kobayashi and Miyazawa [13]. Once the domain is obtained, we switch from a moment-generating function to a generating function and consider analytic behaviors around its dominant singular points. A key is the so-called kernel function. We derive inequalities for it (Lemma 8.8), adapting the idea presented by Dai and Mayazawa [3]. This is a crucial step in the present approach, which enables us to apply analytic extensions not using the Riemann surface that has been typically used in the kernel method. We then apply the inversion technique for generating functions and derive the exact tail asymptotics of the stationary tail probabilities on the coordinate axes.

The asymptotic results are exemplified by a two-node queueing network with simultaneous arrivals. This model is an extension of a two-parallel-queue model with simultaneous arrivals. For the latter, the tail asymptotics of its stationary distribution in the coordinate directions are obtained in from Flatto and Hahn [8] and Flatto and McKean [9]. We modify this model in such a way that a customer who has completed service may be routed to another queue with a given probability. Thus, our model is more like a Jackson network, but it does not have a product-form stationary distribution because of simultaneous arrivals. We will discuss how we can see the tail asymptotics from the modeling primitives.

This chapter is composed of seven sections. In the section “Double QBD Process and the Convergence Domain,” we introduce the double QBD process and summarize existence results using moment-generating functions. The section “Analytic Function Method” considers generating functions for stationary probabilities on the coordinate axes. Analytic behaviors around their dominant singular points are studied. We then apply the inversion technique and derive exact asymptotics in the sections “Exact Tail Asymptotics for the Nonarithmetic Case” and “Exact Tail Asymptotics for the Arithmetic Case.” An example for simultaneous arrivals is considered in the section “Application to a Network with Simultaneous Arrivals.” We discuss some remaining problems in “Concluding Remarks.”

(Additional note) After the first submission of this chapter, we have learned that Li and Zhao [16] studied the same exact tail asymptotic problem, including the case where the tail asymptotics is periodic. This periodic case was absent in our original submission and added in the present chapter. Thus, we benefited from Li and Zhao’s work. However, our approach is different from theirs, although both use analytic functions and its asymptotic inversions. That is, the crucial step in Li and Zhao’s case [16] is analytic extensions on a Riemann surface studied by Fayoelle et al. [6], whereas we use the convergence domain obtained by Kobayashi and Miyazawa [13] and the key lemma. Another difference is in the sorting of tail asymptotic results. Their presentation is purely analytic while we use the geometrical classifications of [13, 18] (see also Miyazawa [19]).

Double QBD Process and the Convergence Domain

The double QBD process was introduced and studied by Miyazawa [18]. Here we briefly introduce it and present results of the tail asymptotics of its stationary distribution. We use the following set of numbers:

$$\begin{array}{rcl} & & \mathbb{Z} = \mbox{ the set of all integers},\qquad \qquad {\mathbb{Z}}_{+} =\{ j \in \mathbb{Z};j \geq 0\}; \\ & & \mathbb{U} =\{ (i,j) \in {\mathbb{Z}}^{2};i,j = 0,1,-1\}; \\ & & \mathbb{R} = \mbox{ the set of all real numbers},\qquad {\mathbb{R}}_{+} =\{ x \in \mathbb{R};x \geq 0\}; \\ & & \mathbb{C} = \mbox{ the set of all complex numbers}.\end{array}$$

Let $S = {\mathbb{Z}}_{+}^{2}$, which is a state space for the double QBD process. Define the boundary faces of S as

$$\begin{array}{rcl}{ S}_{0} =\{ (0,0)\},\quad {S}_{1} =\{ (i,0) \in {\mathbb{Z}}_{+}^{2};i \geq 1\},\quad {S}_{ 2} =\{ (0,i) \in {\mathbb{Z}}_{+}^{2};i \geq 1\}.& & \\ \end{array}$$

Let $\partial S = {\cup }_{i=0}^{2}{S}_{i}$ and ${S}_{+} = S \setminus \partial S$. We refer to ∂S and S ₊ as the boundary and interior of S, respectively.

Let $\{{\mathbf{Y}}_{\mathcal{l}};\mathcal{l} = 0,1,\ldots \}$ be a skip-free random walk on ℤ². That is, its increments ${\mathbf{X}}_{\mathcal{l}}^{(+)} \equiv {\mathbf{Y}}_{\mathcal{l}} -{\mathbf{Y}}_{\mathcal{l}-1}$ take values in $\mathbb{U}$ and are independent and identically distributed. By ${\mathbf{X}}^{(+)}$ we simply denote a random vector that has the same distribution as ${\mathbf{X}}_{\mathcal{l}}^{(+)}$. Define a discrete-time Markov chain $\{{\mathbf{L}}_{\mathcal{l}}\}$ with state space S by the following transition probabilities:

$$\begin{array}{rcl} P({\mathbf{L}}_{\mathcal{l}+1} = \mathbf{j}\vert {\mathbf{L}}_{\mathcal{l}} = \mathbf{i}) = \left \{\begin{array}{ll} P({\mathbf{X}}^{(+)} = \mathbf{j} -\mathbf{i}),&\mathbf{j} \in S,\mathbf{i} \in {S}_{ +}, \\ P({\mathbf{X}}^{(k)} = \mathbf{j} -\mathbf{i}), &\mathbf{j} \in S,\mathbf{i} \in {S}_{k},k = 0,1,2, \end{array} \right.& & \\ \end{array}$$

where ${\mathbf{X}}^{(k)}$ is a random vector taking values in $\{({i}_{1},{i}_{2}) \in \mathbb{U};{i}_{3-k} \geq 0\}$ for k = 1, 2 and in $\{({i}_{1},{i}_{2}) \in \mathbb{U};{i}_{1},{i}_{2} \geq 0\}$ for k = 0. Hence, we can write

$$\begin{array}{rcl}{ \mathbf{L}}_{\mathcal{l}+1} ={ \mathbf{L}}_{\mathcal{l}} +{ \sum \limits_{k=0,1,2,+}}{\mathbf{X}}_{\mathcal{l}}^{(k)}1({\mathbf{L}}_{ \mathcal{l}} \in {S}_{k}),\qquad \mathcal{l} = 0,1,2,\ldots, & &\end{array}$$

(8.1)

where 1( ⋅) is the indicator function of the statement “ ⋅” and ${\mathbf{X}}_{\mathcal{l}}^{(k)}$ has the same distribution as that of ${\mathbf{X}}^{(k)}$ for each $k = 0,1,2,+$, and is independent of everything else.

Thus, $\{{\mathbf{L}}_{\mathcal{l}}\}$ is a skip-free reflecting random walk on the nonnegative integer quadrant S, which is called a double QBD process because its QBD transition structure is unchanged when the level and background states are exchanged.

We denote the moment-generating functions of ${\mathbf{X}}^{(k)}$ by γ _k , that is, for $\mathbf{\theta } \equiv ({\theta }_{1},{\theta }_{2}) \in {\mathbb{R}}^{2}$,

$$\begin{array}{rcl}{ \gamma }_{k}(\mathbf{\theta }) = E({\mathrm{e}}^{\langle \mathbf{\theta },{\mathbf{X}}^{(k)}\rangle }),\qquad k = 0,1,2,+,& & \\ \end{array}$$

where $\langle \mathbf{a},\mathbf{b}\rangle = {a}_{1}{b}_{1} + {a}_{2}{b}_{2}$ for $\mathbf{a} = ({a}_{1},{a}_{2})$ and $\mathbf{b} = ({b}_{1},{b}_{2})$. As usual, ℝ² is considered to be a metric space with Euclidean norm $\|\mathbf{a}\| \equiv \sqrt{\langle \mathbf{a}, \mathbf{a}\rangle }$. In particular, a vector $\mathbf{c}$ is called a directional vector if $\|\mathbf{c}\| = 1$. In this chapter, we assume that

• (i) The random walk $\{{\mathbf{Y}}_{\mathcal{l}}\}$ is irreducible,

• (ii) The reflecting process $\{{\mathbf{L}}_{\mathcal{l}}\}$ is irreducible and aperiodic, and

• (iii) Either E(X ₁ ^( + ))≠0 or E(X ₂ ^( + ))≠0 for ${\mathbf{X}}^{(+)} = ({X}_{1}^{(+)},{X}_{2}^{(+)})$.

Remark 8.1.

If $E({X}_{1}^{(+)}) = E({X}_{2}^{(+)}) = 0$, then it is known that the stationary distribution of $\{{\mathbf{L}}_{\mathcal{l}}\}$ cannot have a light tail, that is, it cannot geometrically (or exponentially) decay in all directions (see Fayoelle et al. [5] and Remark 3.1 of Kobayashi and Miyazawa [13]). Thus, assumption (iii) is not a restrictive assumption for considering the light tail.

Under these assumptions, tractable conditions are obtained for the existence of the stationary distribution in the book [5]. They recently have been corrected by Kobayashi and Miyazawa [13]. We refer to this corrected version below.

Lemma 8.1 (Lemma 2.1 of [13]). 

Assume conditions (i)–(iii), and let

$$\begin{array}{rcl} \mathbf{m}& & = (E({X}_{1}^{(+)}),E({X}_{ 2}^{(+)})), \\ {\mathbf{m}}_{\perp }^{(1)}& & = (E({X}_{ 2}^{(1)}),-E({X}_{ 1}^{(1)})), \\ {\mathbf{m}}_{\perp }^{(2)}& & = (-E({X}_{ 2}^{(2)}),E({X}_{ 1}^{(2)})).\end{array}$$

Then the reflecting random walk $\{{\mathbf{L}}_{\mathcal{l}}\}$ has a stationary distribution if and only if any one of the following three conditions holds [13]).

$$\begin{array}{rcl} & & {m}_{1} < 0,{m}_{2} < 0,\langle \mathbf{m},{\mathbf{m}}_{\perp }^{(1)}\rangle < 0,\langle \mathbf{m},{\mathbf{m}}_{ \perp }^{(2)}\rangle < 0;\end{array}$$

(8.2)

$$\begin{array}{rcl} & & {m}_{1} \geq 0,{m}_{2} < 0,\langle \mathbf{m},{\mathbf{m}}_{\perp }^{(1)}\rangle < 0;\ \mbox{ in addition},\ {m}_{ 2}^{(2)} < 0\ \mbox{ is needed if}\ {m}_{ 1}^{(2)} = 0;\end{array}$$

(8.3)

$$\begin{array}{rcl} & & {m}_{1} < 0,{m}_{2} \geq 0,\langle \mathbf{m},{\mathbf{m}}_{\perp }^{(2)}\rangle < 0;\mbox{ in addition},\ {m}_{ 1}^{(1)} < 0\ \mbox{ is needed if}\ {m}_{ 2}^{(1)} = 0.\quad \end{array}$$

(8.4)

Throughout the chapter, we also assume this stability condition. That is,

• (iv) Any one of (8.2), (8.3), or (8.4) holds.

In addition to conditions (i)–(iv), we will use the following conditions to distinguish some periodical nature of the tail asymptotics:

(v-a):

$P({\mathbf{X}}^{(+)} \in \{ (1,1),(-1,1),(0,0),(1,-1),(-1,-1)\}) < 1$.

(v-b):

$P({\mathbf{X}}^{(1)} \in \{ (1,1),(0,0),(-1,1)\}) < 1$.

(v-c):

$P({\mathbf{X}}^{(2)} \in \{ (1,1),(0,0),(1,-1)\}) < 1$.

These conditions are said to be nonarithmetic in the interior and boundary faces 1, 2, respectively, while the conditions under which they do not hold are called arithmetic. The remark below explains why they are so called.

Remark 8.2.

To see the meaning of these conditions, let us consider random walk $\{{\mathbf{Y}}_{\mathcal{l}}\}$ on ℤ². We can view this random walk as a Markov additive process in the kth coordinate direction if we consider the kth entry of ${\mathbf{Y}}_{\mathcal{l}}$ as an additive component and the other entry as a background state (k = 1, 2). Then, condition (v-a) is exactly the nonarithmetic condition of this Markov additive process in each coordinate direction (see [21] for a definition of the period of a Markov additive process). For random walk $\{{\mathbf{Y}}_{\mathcal{l}}\}$, if the Markov additive process in one direction is nonarithmetic, then the one in the other direction is also nonarithmetic.

We can give similar interpretations for (v-b) and (v-c). That is, for each k = 1, 2 consider a random walk with increments subject to the same distribution as ${\mathbf{X}}^{(k)}$. This random walk is also viewed as a Markov additive process with an additive component in the kth coordinate direction. Then, (v-b) and (v-c) are the nonarithmetic conditions of this Markov additive process for k = 1, 2, respectively.

Remark 8.3.

These conditions were recently studied by Li and Zhao in [16]. The authors of that study call a probability distribution on $\mathbb{U} \equiv \{ (i,j);i,j = -1,0,1\}$ X-shaped if its support is included in

$$\{(1,1),(-1,1),(0,0),(1,-1),(-1,-1)\}.$$

Thus, conditions (v-a), (v-b), and (v-c) are for ${\mathbf{X}}^{(+)}$, ${\mathbf{X}}^{(1)}$, and ${\mathbf{X}}^{(2)}$, respectively, not X-shaped.

We denote the stationary distribution of $\{{\mathbf{L}}_{\mathcal{l}};\mathcal{l} = 0,1,\ldots \}$ by ν and let $\mathbf{L}$ be a random vector subject to ν. Then, it follows from (8.1) that

$$\begin{array}{rcl} \mathbf{L} \simeq \mathbf{L} +{ \sum \limits_{k=0,1,2,+}}{\mathbf{X}}^{(k)}1(\mathbf{L} \in {S}_{ k}),& &\end{array}$$

(8.5)

where “ ≃ ” stands for the equality in distribution. We introduce four moment-generating functions concerning ν. For $\mathbf{\theta } \in {\mathbb{R}}^{2}$,

$$\begin{array}{rcl} \varphi (\mathbf{\theta })& & = E({\mathrm{e}}^{\langle \mathbf{\theta },\mathbf{L}\rangle }), \\ {\varphi }_{+}(\mathbf{\theta })& & = E({\mathrm{e}}^{\langle \mathbf{\theta },\mathbf{L}\rangle }1(\mathbf{L} \in {S}_{ +})), \\ {\varphi }_{k}({\theta }_{k})& & = E({\mathrm{e}}^{{\theta }_{k}{L}_{k} }1(\mathbf{L} \in {S}_{k})),\qquad k = 1,2.\end{array}$$

Then, from (8.5) and the fact that

$$\begin{array}{rcl} \varphi (\mathbf{\theta }) = {\varphi }_{+}(\mathbf{\theta }) +{ \sum \limits_{k=1}^{2}}{\varphi }_{ k}({\theta }_{k}) + \nu (\mathbf{0})& & \\ \end{array}$$

we can easily derive the stationary equation

$$\begin{array}{lr} (1 - {\gamma }_{+}(\mathbf{\theta })){\varphi }_{+}(\mathbf{\theta }) + (1 - {\gamma }_{1}(\mathbf{\theta })){\varphi }_{1}({\theta }_{1}) \\ \quad\quad + (1 - {\gamma }_{2}(\mathbf{\theta })){\varphi }_{2}({\theta }_{2}) + (1 - {\gamma }_{0}(\mathbf{\theta }))\nu (\mathbf{0}) = 0\qquad \end{array}$$

(8.6)

as long as $\varphi (\mathbf{\theta })$ is finite. Clearly, this finiteness holds for $\mathbf{\theta } \leq \mathbf{0}$.

To find the maximal region for (8.6) to be valid, we define the convergence domain of φ as

$$\begin{array}{rcl} \mathcal{D} = \mbox{ the interior of }\{\mathbf{\theta } \in {\mathbb{R}}^{2};\varphi (\mathbf{\theta }) < \infty \}.& & \\ \end{array}$$

This domain is obtained by Kobayashi and Miyazawa [13]. To present this result, we introduce notations.

From (8.6) we can see that the curves $1 - {\gamma }_{k}(\mathbf{\theta }) = 0$ for $k = +,1,2$ are keys for $\varphi (\mathbf{\theta })$ to be finite. Thus, we let

$$\begin{array}{rcl} {\Gamma }_{k}& & =\{ \mathbf{\theta } \in {\mathbb{R}}^{2};{\gamma }_{ k}(\mathbf{\theta }) < 1\}, \\ \partial {\Gamma }_{k}& & =\{ \mathbf{\theta } \in {\mathbb{R}}^{2};{\gamma }_{ k}(\mathbf{\theta }) = 1\},\qquad k = 1,2,+.\end{array}$$

We denote the closure of Γ _k by ${\overline{\Gamma }}_{k}$. Since γ _k is a convex function, Γ _k and ${\overline{\Gamma }}_{k}$ are convex sets. Furthermore, condition (i) implies that Γ ₊ is bounded, that is, it is included in a ball in ℝ². Let

$$\begin{array}{rcl}{ \mathbf{\theta }}^{(k,\mathrm{r})}& =& {\arg }_{\mathbf{ \theta }\in {\mathbb{R}}^{2}}\sup \{{\theta }_{k};\mathbf{\theta } \in {\Gamma }_{+} \cap {\Gamma }_{k}\},\quad k = 1,2, \\ {\mathbf{\theta }}^{(k,\mathrm{min})}& =& {\arg }_{\mathbf{ \theta }\in {\mathbb{R}}^{2}}\inf \{{\theta }_{k};\mathbf{\theta } \in {\Gamma }_{+}\}, \\ { \mathbf{\theta }}^{(k,\max )}& =& {\arg }_{\mathbf{ \theta }\in {\mathbb{R}}^{2}}\sup \{{\theta }_{k};\mathbf{\theta } \in {\Gamma }_{+}\}.\end{array}$$

These extreme points play key roles in obtaining the convergence domain. It is notable that ${\mathbf{\theta }}^{(k,\mathrm{r})}$ is not the zero vector $\mathbf{0}$ because stability condition (iv) implies that, for each k = 1, 2, Γ ₊ ∩ Γ _k contains $\mathbf{\theta } = ({\theta }_{1},{\theta }_{2})$ such that θ _k  > 0 (see Lemma 2.2 of [13]).

We further need the following points:

$$\begin{array}{rcl}{ \mathbf{\theta }}^{(k,\Gamma )} = \left \{\begin{array}{ll} {\mathbf{\theta }}^{(k,\mathrm{r})},\quad &{\gamma }_{ k}({\mathbf{\theta }}^{(k,\max )}) > 1, \\ {\mathbf{\theta }}^{(k,\max )},\quad &{\gamma }_{k}({\mathbf{\theta }}^{(k,\max )}) \leq 1, \end{array} \right.\qquad k = 1,2.& & \\ \end{array}$$

According to Miyazawa [18] (see also [3]), we classify the model into the following three categories:

• Category I θ₁ ^(2, Γ) < θ₁ ^(1, Γ) and θ₂ ^(1, Γ) < θ₂ ^(2, Γ),

• Category II θ₁ ^(2, Γ) < θ₁ ^(1, Γ) and θ₂ ^(1, Γ) ≥ θ₂ ^(2, Γ),

• Category III θ₁ ^(2, Γ) ≥ θ₁ ^(1, Γ) and θ₂ ^(1, Γ) < θ₂ ^(2, Γ).

Note that it is impossible to have θ₁ ^(2, Γ) ≥ θ₁ ^(1, Γ) and θ₂ ^(1, Γ) ≥ θ₂ ^(2, Γ) at once because θ₁ ^(2, Γ) ≥ θ₁ ^(1, Γ) and the convexity of Γ ₊ imply that θ₂ ^(1, Γ) ≤ θ₂ ^(2, Γ) (see Sect. 4 of [18]). We further note that θ₂ ^(1, Γ) ≥ θ₂ ^(2, Γ) can be replaced by θ₂ ^(1, Γ) = θ₂ ^(2, Γ) in category II. Similarly, θ₁ ^(2, Γ) ≥ θ₁ ^(1, Γ) can be replaced by θ₁ ^(2, Γ) = θ₁ ^(1, Γ) in category III.

Define the vector τ as

$$\begin{array}{rcl} \mathbf{\tau } = \left \{\begin{array}{ll} ({\theta }_{1}^{(1,\Gamma )},{\theta }_{2}^{(2,\Gamma )}),\quad &\mbox{ for category I}, \\ ({\overline{\xi }}_{1}({\theta }_{2}^{(2,\mathrm{r})}),{\theta }_{2}^{(2,\mathrm{r})}),\quad &\mbox{ for category II}, \\ ({\theta }_{1}^{(1,\mathrm{r})},{\overline{\xi }}_{2}({\theta }_{1}^{(1,\mathrm{r})})),\quad &\mbox{ for category III}, \end{array} \right.& & \\ \end{array}$$

where ${\overline{\xi }}_{k}({\theta }_{3-k}) =\sup \{ {\theta }_{k};({\theta }_{1},{\theta }_{2}) \in {\Gamma }_{+}\}$. This definition of τ shows that categories I–III are convenient.

We are now ready to present results on the convergence domain $\mathcal{D}$ and the tail asymptotics obtained by Kobayashi and Miyazawa [13]. As was mentioned in the section “Introduction,” they are obtained for the more general reflecting random walk. Thus, some of their conditions automatically hold for the double QBD process (Fig. 8.1).

Fig. 8.1

The light-green areas are domains $\mathcal{D}$ for categories I and II

Lemma 8.2 (Theorem 3.1 of [13]). 

$$\begin{array}{rcl} \mathcal{D} =\{ \mathbf{\theta } \in {\mathbb{R}}^{2};\mathbf{\theta } < \mathbf{\tau }\mbox{\it and }\exists \mathbf{\theta }^{\prime} \in {\Gamma }_{ +}\mbox{\it such that }\mathbf{\theta } < \mathbf{\theta }^{\prime}\}.& &\end{array}$$

(8.7)

Theorem 8.1 (Theorem 4.2 of [13]). 

Under conditions (i)–(iv), we have, for k = 1,2,

$$ \begin{array}{rcl} {\lim \limits_{n\rightarrow \infty }}\frac{1} {n}\log P({L}_{k} \geq n,{L}_{3-k} = 0) = -{\tau }_{k},& &\end{array}$$

(8.8)

and, for any directional vector $\mathbf{c} \geq \mathbf{0}$,

$$ \begin{array}{rcl} {\lim \limits_{n\rightarrow \infty }}\frac{1} {x}\log P(\langle \mathbf{c},\mathbf{L}\rangle \geq x) = -{\alpha }_{\mathbf{c}},& &\end{array}$$

(8.9)

where we recall that ${\alpha }_{\mathbf{c}} =\sup \{ x \geq 0;x\mathbf{c} \in \mathcal{D}\}$ . Furthermore, if $\gamma ({\alpha }_{\mathbf{c}}\mathbf{c}) = 1$ and if ${\gamma }_{k}({\alpha }_{\mathbf{c}}\mathbf{c})\neq 1$ and ${\alpha }_{\mathbf{c}}{c}_{k}\neq {\theta }_{kk}^{(\infty )}$ for k = 1,2, then we have the following exact asymptotics:

$$ \begin{array}{rcl} {\lim \limits_{x\rightarrow \infty }}{\mathrm{e}}^{{\alpha }_{\mathbf{c}}x}P(\langle \mathbf{c},\mathbf{L}\rangle \geq x) = {b}_{\mathbf{ c}}.& &\end{array}$$

(8.10)

In this chapter, we aim to refine these asymptotics to be exact when $\mathbf{c}$ is (1, 0), (0, 1), or (1, 1). Recall that a sequence of nonnegative numbers {p(n); n ∈ ℤ ₊} is said to have the exact asymptotic $(1 + b{(-1)}^{n}){n}^{-\kappa }{\alpha }^{-n}$ for constants κ and α > 1 if there exist real numbers b ∈ [ − 1, 1] and a positive constant c such that

$$ \begin{array}{rcl} {\lim \limits_{n\rightarrow \infty }}(1 + b{(-1)}^{n}){n}^{\kappa }{\alpha }^{n}p(n) = c.& &\end{array}$$

(8.11)

We note that, if b = 0, then this asymptotic is equivalent to

$$ \begin{array}{rcl} {\lim \limits_{n\rightarrow \infty }}(1 + b{(-1)}^{n}){n}^{\kappa }{\alpha }^{n}{ \sum \limits_{\mathcal{l}=n}^{\infty }}p(\mathcal{l}) = c^{\prime}& &\end{array}$$

(8.12)

for some c′ > 0. Thus, if b = 0, then there is no difference on the exact asymptotic between P(L _k  ≥ n) and P(L _k  = n). In what follows, we are mainly concerned with the latter type of exact asymptotics.

Analytic Function Method

Our basic idea for deriving exact asymptotics is to adapt the method used in [3], which extends the moment-generating functions to complex variable analytic functions and obtains the exact tail asymptotics from analytic behavior around their singular points. A similar method is called a kernel method in some literature [12, 14–16]. Here we call it an analytic function method because our approach uses the convergence domain $\mathcal{D}$ heavily, which is not the case for the kernel method. See [19] for more details.

There is one problem in adapting the method of [3] because the moment-generating functions ${\gamma }_{k}(\mathbf{\theta })$ are not polynomials, while the corresponding functions of SRBM are polynomial. If they are not polynomials, the analytic function approach is hard to apply. This problem is resolved if we use generating functions instead of moment-generating functions. We here thanks for the skip-free assumption.

Convergence Domain of a Generating Function

Let us convert results on moment-generating functions to those on generating function using a mapping from $\mathbf{z} \equiv ({z}_{1},{z}_{2}) \in \mathbb{C}$ to $\mathbf{g}(\mathbf{z}) \equiv ({\mathrm{e}}^{{z}_{1}},{\mathrm{e}}^{{z}_{2}}) \in \mathbb{C}$. In particular, for $\mathbf{\theta } \in {\mathbb{R}}^{2}$, $\mathbf{g}(\mathbf{\theta }) \in {({\mathbb{R}}_{+}^{\mathrm{o}})}^{2}$, where ${\mathbb{R}}_{+}^{\mathrm{o}} = (0,\infty )$. We use the following notations for k = 1, 2:

$$\begin{array}{rcl} & & \left ({u}_{1}^{(k,\mathrm{min})},{u}_{ 2}^{(k,\mathrm{min})}\right ) = \mathbf{g}\left ({\mathbf{\theta }}^{(k,\mathrm{min})}\right ),\qquad \left ({u}_{ 1}^{(k,\max )},{u}_{ 2}^{(k,\max )}\right ) = \mathbf{g}\left ({\mathbf{\theta }}^{(k,\max )}\right ); \\ & & \left ({u}_{1}^{(k,\mathrm{r})},{u}_{ 2}^{(k,\mathrm{r})}\right ) = \mathbf{g}\left ({\mathbf{\theta }}^{(k,\mathrm{r})}\right ),\qquad \qquad \quad \left ({u}_{ 1}^{(k,\Gamma )},{u}_{ 2}^{(k,\Gamma )}\right ) = \mathbf{g}\left ({\mathbf{\theta }}^{(k,\Gamma )}\right ). \\ & & \left (\tilde{{\tau }}_{1},\tilde{{\tau }}_{2}\right ) = \mathbf{g}(\mathbf{\tau }), \\ \end{array}$$

We now transfer the results on the moment-generating functions in the section “Double QBD Process and the Convergence Domain” to those on the generating functions. For this, we define

$$\begin{array}{rcl} & & \tilde{\mathcal{D}} =\{ \mathbf{g}(\mathbf{\theta }) \in {\mathbb{R}}_{+}^{2};\mathbf{\theta } \in \mathcal{D}\}, \\ & & \tilde{{\Gamma }}_{k} =\{ \mathbf{g}(\mathbf{\theta }) \in {\mathbb{R}}_{+}^{2};\mathbf{\theta } \in {\Gamma }_{ k}\},\quad k = 1,2,+.\end{array}$$

Define the following generating functions. For $k = 0,1,2,+$

$$\begin{array}{rcl} \tilde{{\gamma }}_{k}(\mathbf{z}) = E\left ({z}_{1}^{{X}_{1}^{(k)} }{z}_{2}^{{X}_{2}^{(k)} }\right ),\quad \mathbf{z} \equiv ({z}_{1},{z}_{2}) \in {\mathbb{C}}^{2},& & \\ \end{array}$$

which exists except for z ₁ = 0 or z ₂ = 0. Similarly,

$$\begin{array}{rcl} & & \tilde{\varphi }(\mathbf{z}) = E({z}_{1}^{{L}_{1} }{z}_{2}^{{L}_{2} }), \\ & & \tilde{{\varphi }}_{+}(\mathbf{z}) = E({z}_{1}^{{L}_{1} }{z}_{2}^{{L}_{2} }1(\mathbf{L} \in {S}_{+})), \\ & & \tilde{{\varphi }}_{k}({z}_{k}) = E({z}_{k}^{{L}_{k} }1(\mathbf{L} \in {S}_{k})),\qquad k = 1,2.\end{array}$$

as long as they exist.

Obviously, these generating functions are obtained from the corresponding moment-generating functions using the inverse mapping ${\mathbf{g}}^{-1}$:

$$\begin{array}{rcl} & & \tilde{{\gamma }}_{k}(\mathbf{z}) = {\gamma }_{k}(\log {z}_{1},\log {z}_{2}),\quad k = 0,1,2,+,\qquad \\ & & \tilde{\varphi }(\mathbf{z}) = \varphi (\log {z}_{1},\log {z}_{2}), \\ & & \tilde{{\varphi }}_{+}(\mathbf{z}) = {\varphi }_{+}(\log {z}_{1},\log {z}_{2}), \\ & & \tilde{{\varphi }}_{k}(z) = {\varphi }_{k}(\log z),\qquad k = 1,2.\end{array}$$

Then stationary Eq. (8.6) can be written as

$$\begin{array}{lr} (1 -\tilde{ {\gamma }}_{+}(\mathbf{z}))\tilde{{\varphi }}_{+}(\mathbf{z}) + (1 -\tilde{ {\gamma }}_{1}(\mathbf{z}))\tilde{{\varphi }}_{1}({z}_{1}) \\ \quad\quad + (1 -\tilde{ {\gamma }}_{2}(\mathbf{z}))\tilde{{\varphi }}_{2}({z}_{2}) + (1 -\tilde{ {\gamma }}_{0}(\mathbf{z}))\nu (\mathbf{0}) = 0.\qquad \end{array}$$

(8.13)

It is easy to see that

$$\begin{array}{rcl} & & \tilde{{\Gamma }}_{k} \equiv \{\mathbf{u} \in {\mathbb{R}}_{+}^{2};\mathbf{u} >\mathbf{0},\tilde{{\gamma }}_{ k}(\mathbf{u}) < 1\},\quad k = 1,2,+, \\ & & \tilde{\mathcal{D}}\equiv \{\mathbf{u} \in {\mathbb{R}}_{+}^{2};\mathbf{u} >\mathbf{0},\tilde{\varphi }(\mathbf{u}) < \infty \}.\end{array}$$

These sets may not be convex because two-dimensional generating functions may not be convex (Fig. 8.2).Nevertheless, they still have nice properties because the generating functions are polynomials with nonnegative coefficients. To make this specific, we introduce the following terminology.

Fig. 8.2

Examples of $\mathcal{D}$ and the corresponding $\tilde{\mathcal{D}}$, which may not be convex, where $({p}_{21},{p}_{01},{p}_{11}) = (0.1,0.1,0.7),({p}_{20},{p}_{00},{p}_{10}) = (1.5,0.5,0.5),({p}_{22},{p}_{02},{p}_{12}) = (2,3,1)$ for ${p}_{ij} = P({\mathbf{X}}^{(+)} = (i,j))$

Definition 8.1.

A subset A of ℝ² is said to be nonnegative-directed (or coordinate-directed) convex if $\lambda \mathbf{x} + (1 - \lambda )\mathbf{y} \in A$ for any number λ ∈ [0, 1] and any $\mathbf{x},\mathbf{y} \in A$ such that $\mathbf{y} -\mathbf{x} \geq \mathbf{0}$ (or $\mathbf{y} -\mathbf{x}$ in either one of the coordinate axes, respectively).

We then immediately have the following facts.

Lemma 8.3.

$\tilde{\mathcal{D}}$ is nonnegative-directed convex, and $\tilde{{\Gamma }}_{k}$ is coordinate-directed convex for $k = +,0,1,2$.

Note that (8.13) is valid for $\mathbf{z} \in {\mathbb{C}}^{2}$ satisfying $\vert \mathbf{z}\vert \in \tilde{\mathcal{D}}$ because $\vert \tilde{\varphi }(\mathbf{z})\vert \leq \tilde{ \varphi }(\vert \mathbf{z}\vert )$. Furthermore,

$$\begin{array}{lrr} \left \{\mathbf{z} \in {\mathbb{C}}^{2};\vert \mathbf{z}\vert \in \tilde{\mathcal{D}}\right \} = \left \{\mathbf{z} \in {\mathbb{C}}^{2};E({\mathrm{e}}^{{L}_{1}\log \vert {z}_{1}\vert +{L}_{2}\log \vert {z}_{2}\vert }) < \infty \right \}&& \\ \ \ = \left \{\mathbf{g}(\log \vert {z}_{1}\vert + i\arg {z}_{1},\log \vert {z}_{2}\vert + i\arg {z}_{2});\mathbf{z} \in {\mathbb{C}}^{2},(\log \vert {z}_{ 1}\vert, \log \vert {z}_{2}\vert ) \in \mathcal{D}\right \} \\ \ \ = \mathbf{g}(\{\mathbf{z} \in {\mathbb{C}}^{2},(\mathfrak{R}{z}_{ 1},\mathfrak{R}{z}_{2}) \in \mathcal{D}\}), \\ \end{array}$$

where $\vert \mathbf{z}\vert = (\vert {z}_{1}\vert, \vert {z}_{2}\vert )$. Hence, the domain $\mathcal{D}$ is well transferred to $\tilde{\mathcal{D}}$. We will work on $\tilde{\mathcal{D}}$ to find the analytic behaviors of $\tilde{{\varphi }}_{1}(z)$ and $\tilde{{\varphi }}_{2}(z)$ around their dominant singular points. This is different from the kernel method, which works directly on the set of complex vectors $\mathbf{z}$ satisfying $\tilde{{\gamma }}_{+}(\mathbf{z}) = 1$ and applies deeper complex analysis such as analytic extension on a Riemann surface (e.g., see [6]). We avoid it using the domain $\tilde{\mathcal{D}}$.

A Key Function for Analytic Extension

Once the domain $\tilde{\mathcal{D}}$ is obtained, the next step is to study the analytic behaviors of the generating function $\tilde{{\varphi }}_{k}$ for k = 1, 2. For this, we use a relation between them by letting $\tilde{{\gamma }}_{+}(\mathbf{z}) - 1 = 0$ in stationary Eq. (8.13), which removes $\tilde{{\varphi }}_{+}(\mathbf{z})$. For this, let us consider the solution u ₂ > 0 of $\tilde{{\gamma }}_{+}({u}_{1},{u}_{2}) = 1$ for each fixed u ₁ > 0. Since this equation is quadratic concerning u ₂ and $\tilde{\mathcal{D}}\subset {({\mathbb{R}}^{\mathrm{o}})}_{+}^{2}$, it has two positive solutions for each u ₁ satisfying

$$\begin{array}{rcl}{ u}_{1}^{(1,\mathrm{min})} \leq {u}_{ 1} \leq {u}_{1}^{(1,\max )}.& & \\ \end{array}$$

Denote these solutions by ${\underline \zeta_2} (u_1)$ and ${\overline{\zeta }}_{2}({u}_{1})$ such that ${\underline{\zeta }}_{2}({u}_{1}) \leq {\overline{\zeta }}_{2}({u}_{1})$. Similarly, ${\underline \zeta_1} (u_2)$ and ${\overline{\zeta }}_{1}({u}_{2})$ are defined for u ₂ satisfying

$$\begin{array}{rcl}{ u}_{2}^{(2,\mathrm{min})} \leq {u}_{ 2} \leq {u}_{2}^{(2,\max )}.& & \\ \end{array}$$

One can see these facts also applying the mapping $\mathbf{g}$ to the convex bounded set $\mathcal{D}$ (Lemma 8.3).

We now adapt the arguments in [3]. For this, we first examine the function ${\underline \zeta_2}$. Let

$$\begin{array}{rcl} & & {p}_{{_\ast}k}(u) = E({u}^{{X}_{1}^{(+)} }1({X}_{2}^{(+)} = k)), \\ & & {p}_{k{_\ast}}(u) = E({u}^{{X}_{2}^{(+)} }1({X}_{1}^{(+)} = k)),\quad k = 0,1,-1.\qquad \\ \end{array}$$

Then $\tilde{{\gamma }}_{+}({u}_{1},{u}_{2}) = 1$ can be written as

$$\begin{array}{rcl}{ u}_{2}^{2}{p}_{ {_\ast}1}({u}_{1}) - {u}_{2}(1 - {p}_{{_\ast}0}({u}_{1})) + {p}_{{_\ast}-1}({u}_{1}) = 0.& &\end{array}$$

(8.14)

Hence, we have, for u ∈ [u ₁ ^(1, min), u ₁ ^(1, max)],

$$\begin{array}{rcl}{ \underline{\zeta }}_{2}(u) = \frac{1 - {p}_{{_\ast}0}(u) -\sqrt{{D}_{2 } (u)}} {2{p}_{{_\ast}1}(u)}, & &\end{array}$$

(8.15)

where

$$\begin{array}{rcl}{ D}_{2}(u) = {(1 - {p}_{{_\ast}0}(u))}^{2} - 4{p}_{ {_\ast}1}(u){p}_{{_\ast}-1}(u) \geq 0.& & \\ \end{array}$$

Since ${D}_{2}({u}_{1}^{(1,\mathrm{min})}) = {D}_{2}({u}_{1}^{(1,\max )}) = 0$ and u ² D ₂(u) is a polynomial of order 4 at most and order 2 at least by condition (i), u ² D ₂(u) can be factorized as

$$\begin{array}{rcl}{ u}^{2}{D}_{ 2}(u) = (u - {u}_{1}^{(1,\mathrm{min})})({u}_{ 1}^{(1,\max )} - u){h}_{ 2}(u),& & \\ \end{array}$$

where h ₂(u)≠0 for u ∈ (u ₁ ^(1, min), u ₁ ^(1, max)). This fact can be verified by the mapping $\mathbf{g}$ from Γ ₊ to $\tilde{{\Gamma }}_{+}$.

To obtain tail asymptotics, we will use analytic functions. So far, we would like to analytically extend the function ${\underline \zeta_2}$ from the real interval to a sufficiently large region in the complex plane ℂ. For this, we prepare a series of lemmas. We first note the following fact.

Lemma 8.4 (Lemma 2.3.8 of [6]). 

All the solutions of z ² D ₂ (z) = 0 for z ∈ ℂ are real numbers.

In the light of the preceding arguments, this lemma immediately leads to the following fact.

Lemma 8.5.

z ² D ₂ (z) = 0 for z ∈ ℂ has no solution in the region such that |z|∈ (u ₁ ^{(1,min )} ,u ₁ ^{(1,max )} ).

We will also use the following two lemmas, which show how the periodic nature of the random walk $\{{\mathbf{Y}}_{\mathcal{l}}\}$ is related to the branch points (see Remark 8.2 on the periodic nature). They are proved in the appendices “Proof of Lemma 8.6” and “Proof of Lemma 8.7,” respectively.

Lemma 8.6.

The equation

$$\begin{array}{rcl}{ D}_{2}(z) = 0,\qquad \vert z\vert = {u}_{1}^{(1,\max )},\;z \in \mathbb{C},& &\end{array}$$

(8.16)

has only one solution z = u ₁ ^{(1,max )} if and only if (v-a) holds. Otherwise, it has two solutions z = ±u ₁ ^{(1,max )} , and u ² D ₂ (u) is an even function.

Lemma 8.7.

There are x,y > 0 such that

$$\begin{array}{rcl} \tilde{{\gamma }}_{+}(x,y) = 1,\qquad \tilde{{\gamma }}_{+}(-x,-y) = 1& &\end{array}$$

(8.17)

if and only if (v-a) does not hold.

Remark 8.4.

Lemma 8.6 is essentially the same as Remark 3.1 of [16], which is obtained as a corollary of their Lemma 3.1, which is immediate from Lemmas 2.3.8 of [6].

By Lemmas 8.4 and 8.5, ${\underline \zeta_2} (u)$ on (u ₁ ^(1, min), u ₁ ^(1, max)) is extendable as an analytic function of a complex variable to the region $\tilde{{\mathcal{G}}}_{0}({u}_{1}^{(1,\mathrm{min})},{u}_{1}^{(1,\max )})$, where

$$\begin{array}{rcl} \tilde{{\mathcal{G}}}_{0}(a,b) =\{ z \in \mathbb{C};z\not\in (-\infty, a] \cup [b,\infty )\},\qquad a,b \in \mathbb{R},& & \\ \end{array}$$

and has a single branch point u ₁ ^(1, max) on | z |  = u ₁ ^(1, max) if (v-a) holds and two branch points ± u ₁ ^(1, max) there otherwise by Lemmas 8.6 and 8.5. Both branch points have order 2. We denote this extended analytic function by ${\underline \zeta_2}(z)$. That is, we use the same notation for an analytically extended function. We identify it by its argument. The following lemma is a key for our arguments. The idea of this lemma is similar to Lemma 6.3 of [3], but its proof is entirely different from that lemma.

Lemma 8.8.

• (a) ${\underline \zeta_2}$ of (8.15) is analytically extended on $\tilde{{\mathcal{G}}}_{0}({u}_{1}^{(1,\mathrm{min})},{u}_{1}^{(1,\max )})$.

• (b) For z ∈ ℂ satisfying |z|∈ (u ₁ ^{(1,min )} ,u ₁ ^{(1,max )} ],

  $$\begin{array}{rcl} \vert {\underline{\zeta }}_{2}(z)\vert \leq {\underline{\zeta }}_{2}(\vert z\vert ) \leq {u}_{2}^{(1,\max )},& & \end{array}$$

  (8.18)

  where the second inequality is strict if |z| < u ₁ ^{(1,max )}.

• (c) If either m ₂ ⁽¹⁾ = 0 or (v-b) holds, then

  $$\begin{array}{rcl} \tilde{{\gamma }}_{1}(z,{\underline{\zeta }}_{2}(z)) = 1,\qquad \vert z\vert = {u}_{1}^{(1,\mathrm{r})},& & \end{array}$$

  (8.19)

  has no solution other than z = u ₁ ^{(1,r )}.

• (d) Equation (8.19) has two solutions z = ±u ₁ ^{(1,r )} if and only if m ₂ ⁽¹⁾ = 0, (v-a), and (v-b) do not hold.

Proof.

We have already proved (a). Thus, we only need to prove (b)–(d). We first prove (b). For this, it is sufficient to prove (8.18) for |z| < u ₁ ^{(1,max )} by the continuity of ${\underline \zeta_2}(z)$ for |z|≤ u ₁ ^{(1,max )} at z = u ₁ ^{(1,max )} . Substituting complex numbers z ₁ and z ₂ into u ₁ and u ₂ of (8.14), we have

$$\begin{array}{rcl}{ z}_{2}^{2}{p}_{ {_\ast}1}({z}_{1}) + {z}_{2}{p}_{{_\ast}0}({z}_{1}) + {p}_{{_\ast}-1}({z}_{1}) = {z}_{2}.& &\end{array}$$

(8.20)

Obviously, this equation has the following solutions for each fixed z ₁ such that |z ₁ |∈ (u ₁ ^{(1,min )} ,u ₁ ^{(1,max )} ):

$$\begin{array}{rcl}{ z}_{2} ={ \underline{\zeta }}_{2}({z}_{1}),\quad {\overline{\zeta }}_{2}({z}_{1}).& &\end{array}$$

(8.21)

We next take the absolute values of both sides of (8.20); then

$$\begin{array}{rcl} \vert {z}_{2}{\vert }^{2}{p}_{ {_\ast}1}(\vert {z}_{1}\vert ) + \vert {z}_{2}\vert {p}_{{_\ast}0}(\vert {z}_{1}\vert ) + {p}_{{_\ast}-1}(\vert {z}_{1}\vert ) \geq \vert {z}_{2}\vert.& & \\ \end{array}$$

Thus, we get

$$\begin{array}{rcl} \vert {z}_{2}\vert (\tilde{{\gamma }}_{+}(\vert {z}_{1}\vert, \vert {z}_{2}\vert ) - 1) \geq 0.& & \\ \end{array}$$

By the definitions of ${\underline \zeta_2}(|z_1|)$ and ${\overline{\zeta }}_{2}(\vert {z}_{1}\vert )$ , this inequality can be written as

$$\begin{array}{rcl} (\vert {z}_{2}\vert -{\underline{\zeta }}_{2}(\vert {z}_{1}\vert ))(\vert {z}_{2}\vert -{\overline{\zeta }}_{2}(\vert {z}_{1}\vert )) = \vert {z}_{2}\vert (\tilde{{\gamma }}_{+}(\vert {z}_{1}\vert, \vert {z}_{2}\vert ) - 1) \geq 0.& & \\ \end{array}$$

Hence, ${\underline{\zeta }}_{2}(\vert {z}_{1}\vert ) \leq {\overline{\zeta }}_{2}(\vert {z}_{1}\vert )$ implies

$$\begin{array}{rcl} \vert {z}_{2}\vert \leq {\underline{\zeta }}_{2}(\vert {z}_{1}\vert )\quad \mbox{ or }\quad {\overline{\zeta }}_{2}(\vert {z}_{1}\vert ) \leq \vert {z}_{2}\vert.& &\end{array}$$

(8.22)

By (8.21), we can substitute ${z_2} = {\underline \zeta_2}(z_1)$ into (8.22) and get

$$\begin{array}{rcl} \vert {\underline{\zeta } }_{2 } ({z}_{1})\vert \leq {\underline{\zeta }}_{2}(\vert {z}_{1}\vert )\quad \mbox{ or}\quad {\overline{\zeta }}_{2}(\vert {z}_{1}\vert ) \leq \vert {\underline{\zeta }}_{2}({z}_{1})\vert, \qquad \vert {z}_{1}\vert \in ({u}_{1}^{(1,\mathrm{min})},{u}_{ 1}^{(1,\max )}).\quad & &\end{array}$$

(8.23)

Thus, (b) is obtained if we show that ${\overline{\zeta }}_{2}(\vert {z}_{1}\vert ) \leq \vert {\underline{\zeta }}_{2}({z}_{1})\vert$ is impossible. Suppose the contrary of this, then there is a z ₁ ⁽⁰⁾ such that

$$\begin{array}{rcl}{ \underline{\zeta }}_{2}(\vert {z}_{1}^{(0)}\vert ) < \vert {\underline{\zeta }}_{ 2}({z}_{1}^{(0)})\vert, \qquad \vert {z}_{ 1}^{(0)}\vert \in ({u}_{ 1}^{(1,\mathrm{min})},{u}_{ 1}^{(1,\max )}).& &\end{array}$$

(8.24)

Since $|{\underline \zeta_2}(z)|$ is continuous and converges to ${\underline \zeta_2}(|{z_{1}^{(0)}}|)$ as z goes to |z ₁ ⁽⁰⁾ | on the path where |z| = |z ₁ ⁽⁰⁾ |, there must be a z ₁ ⁽¹⁾ such that |z ₁ ⁽¹⁾ | = |z ₁ ⁽⁰⁾ | and

$$\begin{array}{rcl}{ \underline{\zeta }}_{2}(\vert {z}_{1}^{(1)}\vert ) < \vert {\underline{\zeta }}_{ 2}({z}_{1}^{(1)})\vert <{ \overline{\zeta }}_{ 2}(\vert {z}_{1}^{(1)}\vert ).& & \\ \end{array}$$

Since |z ₁ ⁽¹⁾ | = |z ₁ ⁽⁰⁾ |∈ (u ₁ ^{(1,min )} ,u ₁ ^{(1,max )} ), this contradicts (8.23), which proves (b).

We next prove (c). Let

$$\begin{array}{rcl}{ p}_{{_\ast}k}^{(1)}(z) = E({z}^{{X}_{1}^{(1)} }1({X}_{2}^{(1)} = k)),\qquad k = 0,1.& & \\ \end{array}$$

First, assume that m ₂ ⁽¹⁾ = 0. This implies p _∗1 ⁽¹⁾ (z) = 0, and therefore (8.19) is reduced to p _∗0 ⁽¹⁾ (z) = 1. Hence, its solution is z = 1 or $z = {p}_{-10}^{(1)}/{p}_{10}^{(1)} \geq 0$ if p ₁₀ ⁽¹⁾ ≠0 (otherwise, z = 1 is the only solution). Both are nonnegative numbers, and therefore (8.19) has no solution z such that

$$\begin{array}{rcl} \vert z\vert = {u}_{1}^{(1,\mathrm{r})},\qquad z\neq {u}_{ 1}^{(1,\mathrm{r})}.& &\end{array}$$

(8.25)

We next assume that m ₂ ⁽¹⁾ ≠0, which implies p _∗1 ⁽¹⁾ (z)≠0. Since (8.19) can be written as

$$\begin{array}{rcl}{ \underline{\zeta }}_{2}(z){p}_{{_\ast}1}^{(1)}(z) + {p}_{ {_\ast}0}^{(1)}(z) = 1& &\end{array}$$

(8.26)

and $1 \leq \vert w\vert + \vert 1 - w\vert$ for any w ∈ ℂ, we have

$$\begin{array}{rcl} \vert {\underline{\zeta }}_{2}(z)\vert = \left \vert \frac{1 - {p}_{{_\ast}0}^{(1)}(z)} {{p}_{{_\ast}1}^{(1)}(z)} \right \vert \geq \frac{1 -\vert {p}_{{_\ast}0}^{(1)}(z)\vert } {\vert {p}_{{_\ast}1}^{(1)}(z)\vert } \geq \frac{1 - {p}_{{_\ast}0}^{(1)}(\vert z\vert )} {{p}_{{_\ast}1}^{(1)}(\vert z\vert )} ={ \underline{\zeta }}_{2}(\vert z\vert ).& &\end{array}$$

(8.27)

If (8.25) holds, then both sides of this inequality are identical for z = γpmu ₁ ^(1,r) if and only if (v-b) does not hold. Hence, if (v-b) holds, then $|{\underline \zeta_2}(z)| > {\underline \zeta_2}(|z|)$, and therefore (8.19) has no solution satisfying (8.25) because of (8.18).

We finally prove (d). For this we assume that neither m ₂ ⁽¹⁾ = 0 nor (v-b) holds. In this case, ${p}_{01}^{(1)} = {p}_{(-1)0}^{(1)} = {p}_{10}^{(1)} = 0$ , so it follows from (8.26) that

$$\begin{array}{rcl}{ \underline{\zeta }}_{2}(z) = \frac{(1 - {p}_{00}^{(1)})z} {{p}_{-11}^{(1)} + {p}_{11}^{(1)}{z}^{2}}.& & \\ \end{array}$$

Hence, if (8.25) holds, then we must have $z = -{u}_{1}^{(1,\mathrm{r})}$ because of (8.18) and (8.27). By the preceding equation, we also have ${\underline{\zeta }}_{2}(-{u}_{1}^{(1,\mathrm{r})}) = -{\underline{\zeta }}_{2}({u}_{1}^{(1,\mathrm{r})})$ . Hence, we need to check whether $(-{u}_{1}^{(1,\mathrm{r})},-{\underline{\zeta }}_{2}({u}_{1}^{(1,\mathrm{r})}))$ is the solution of ${\gamma }_{+}(x,y) = 1$ . By Lemma 8.7, $z = -{u}_{1}^{(1,\mathrm{r})}$ is the solution of (8.19) if and only if (v-a) does not hold. Combining this with (b) and (c) completes the proof of (d). □

For the convenience of later reference, we summarize the results in (c) and (d) of Lemma 8.8 in Table 8.1. Similar results can be obtained in the direction of the second axes using (v-b) and m ₁ ⁽²⁾ = 0 instead of (v-a) and m ₂ ⁽¹⁾ = 0. Since the results are symmetric, we omit them. We remark that Li and Zhao [16] have not considered the cases m ₁ ⁽²⁾ = 0 and m ₂ ⁽¹⁾ = 0, which seems to be overlooked.

Table 8.1 The solutions of (8.16) and (8.19), where ○ , ×, and − indicate “yes,” “no,” and “‘irrelevant”

Nature of the Dominant Singularity

We consider the complex variable functions $\tilde{{\varphi }}_{1}({z}_{1})$ and $\tilde{{\varphi }}_{2}({z}_{2})$. Recall that

$$\begin{array}{rcl} \tilde{\varphi }(\mathbf{z}) =\tilde{ {\varphi }}_{+}(\mathbf{z}) +\tilde{ {\varphi }}_{1}({z}_{1}) +\tilde{ {\varphi }}_{2}({z}_{2}) + \nu (\mathbf{0}).& &\end{array}$$

(8.28)

Obviously, $\tilde{\varphi }(\mathbf{z})$ is analytic for $\mathbf{z} \in {\mathbb{C}}^{2}$, such that $(\vert {z}_{1}\vert, \vert {z}_{2}\vert ) \in \tilde{\mathcal{D}}$, and singular on the boundary of $\tilde{\mathcal{D}}$. This implies that $\tilde{{\varphi }}_{i}({z}_{i})$ is analytic for $\vert {z}_{i}\vert <\tilde{ {\tau }}_{i}$ and has a point on the circle $\vert z\vert =\tilde{ {\tau }}_{i}$. This is easily seen from (8.28) with z _j  = 0 for $j = 3 - i$. Furthermore, ${z}_{i} =\tilde{ {\tau }}_{i}$ must be a singular point for i = 1, 2 by Pringsheim’s theorem (see, e.g., Theorem 17.13 in volume 1 of [17]). In addition to this point, we need to find all singular points on $\vert z\vert =\tilde{ {\tau }}_{i}$ to get the tail asymptotics, as we will see. As expected from Lemma 8.6, $z = -\tilde{{\tau }}_{i}$ may be another singular point, which occurs only when (v-a) does not hold.

We focus on these singular points instead of searching for singular points on $\vert z\vert =\tilde{ {\tau }}_{i}$ and show that there is no other singular point on the circle because of the analytic behavior of $\tilde{{\varphi }}_{i}(z)$. Since the results are symmetric for $\tilde{{\varphi }}_{1}(z)$ and $\tilde{{\varphi }}_{2}(z)$, we only consider $\tilde{{\varphi }}_{1}(z)$ in this section.

For this, we use stationary Eq. (8.13), which is valid on $\tilde{\mathcal{D}}$. Plugging ${\underline \zeta_2}$ into (8.13) yields, for $\vert z\vert \in ({u}_{1}^{(1,\mathrm{min})},\tilde{{\tau }}_{1})$,

$$\begin{array}{rcl} \tilde{{\varphi }}_{1}(z) = \frac{(\tilde{{\gamma }}_{2}(z,{\underline{\zeta }}_{2}(z)) - 1)\tilde{{\varphi }}_{2}({\underline{\zeta }}_{2}(z))} {1 -\tilde{ {\gamma }}_{1}(z,{\underline{\zeta }}_{2}(z))} + \frac{(\tilde{{\gamma }}_{0}(z,{\underline{\zeta }}_{2}(z)) - 1)\nu (\mathbf{0})} {1 -\tilde{ {\gamma }}_{1}(z,{\underline{\zeta }}_{2}(z))}.& &\end{array}$$

(8.29)

In light of this equation, the dominant singularity of $\tilde{{\varphi }}_{1}(z)$ is caused by ${\underline\zeta}_{2}(z)$, $\tilde{{\varphi }}_{2}({\underline{\zeta }}_{2}(z))$, or

$$\begin{array}{rcl} \tilde{{\gamma }}_{1}(z,{\underline{\zeta }}_{2}(z)) = 1.& &\end{array}$$

(8.30)

In addition to $\tilde{{\mathcal{G}}}_{0}(a,b)$, we will use the following sets to consider analytic regions (Fig. 8.3):

$$\begin{array}{rcl} & & \tilde{{C}}_{\delta }(u) =\{ z \in \mathbb{C};u - \delta < \vert z\vert < u + \delta, z\neq u\},\qquad u,\delta >0, \\ & & \tilde{{\mathcal{G}}}_{\delta }^{+}(u) =\tilde{ {\mathcal{G}}}_{ 0}({u}_{1}^{(1,\mathrm{min})},u) \cap \tilde{ {C}}_{ \delta }(u),\qquad {u}_{1}^{(1,\mathrm{min})} < u, \\ & & \tilde{{\mathcal{G}}}_{\delta }^{-}(u) =\tilde{ {\mathcal{G}}}_{ 0}(u,-{u}_{1}^{(1,\mathrm{min})}) \cap \tilde{ {C}}_{ \delta }(u),\qquad u < -{u}_{1}^{(1,\mathrm{min})}.\end{array}$$

Fig. 8.3

Shaded area: $\tilde{{\mathcal{G}}}_{\delta }^{-}(-{u}_{1}^{(1,\max )}) \cap \tilde{{\mathcal{G}}}_{\delta }^{+}({u}_{1}^{(1,\max )})$

Remark 8.5.

One may wonder whether (8.18) in Lemma 8.8 is sufficient for verifying the analyticity of $\tilde{{\varphi }}_{1}(z)$ in $\tilde{{\mathcal{G}}}_{\delta }^{+}({u}_{1}^{(1,\max )})$ when $\tilde{{\tau }}_{1} = {u}_{1}^{(1,\max )}$. This will turn out to be no problem because of (8.29).

In what follows, we first consider the case where (v-a) holds, then we consider the other case.

Singularity for the Nonarithmetic Case

Assume the nonarithmetic condition (v-a). We consider the analytic behavior of $\tilde{{\varphi }}_{1}(z)$ around the singular point $z =\tilde{ {\tau }}_{1}$. This behavior will show that there is no other singular point on $\vert z\vert =\tilde{ {\tau }}_{1}$. We separately consider the three causes discussed above.

(8Ia) The solution of (8.30): This equation has six solutions at most because it can be written as a polynomial equation of order 6. z = 1, u ₁ ^(1, r) are clearly the solutions. Because $\tilde{{\varphi }}_{1}(z)$ of (8.29) is analytic for $\vert z\vert <\tilde{ {\tau }}_{1}$, (8.30) cannot have a solution such that $\vert z\vert <\tilde{ {\tau }}_{1}$, except for the points where the numerator of the right-hand side of (8.29) vanishes. This must be finitely many because the numerator vanishes otherwise by the uniqueness of analytic extension. On the other hand, (8.30) has no solution on the circle | z |  = u ₁ ^(1, r), except for z = u ₁ ^(1, r), by Lemma 8.8.

Thus, the compactness of the circle implies that, if $\tilde{{\tau }}_{1} = {u}_{1}^{(1,\mathrm{r})} < {u}_{1}^{(1,\max )}$, then (8.30) has no solution on $\tilde{{C}}_{\delta }({u}_{1}^{(1,\mathrm{r})})$ for some δ > 0. Hence, we have the following fact from (8.29).

Lemma 8.9.

Assume that $\tilde{{\tau }}_{1} = {u}_{1}^{(1,\mathrm{r})} < {u}_{1}^{(1,\max )}$ and $\tilde{{\varphi }}_{2}({\underline{\zeta }}_{2}(z))$ is analytic at |z| = u ₁ ^{(1,r )} . Then, $\tilde{{\varphi }}_{1}(z)$ has a simple pole at z = u ₁ ^{(1,r )} and is analytic on $\tilde{{C}}_{\delta }({u}_{1}^{(1,\mathrm{r})})$.

Remark 8.6.

For categories I and III, the analytic condition on $\tilde{{\varphi }}_{2}({\underline{\zeta }}_{2}(z))$ in this lemma is always satisfied because Lemma 8.8 and the category condition, ${\underline{\zeta }}_{2}(\tilde{{\tau }}_{1}) <\tilde{ {\tau }}_{2}$, imply, for | z |  = u ₁ ^(1, r),

$$\begin{array}{rcl} \vert \tilde{{\varphi }}_{2}({\underline{\zeta }}_{2}(z))\vert \leq \tilde{ {\varphi }}_{2}(\vert {\underline{\zeta }}_{2}(z)\vert ) \leq \tilde{ {\varphi }}_{2}({\underline{\zeta }}_{2}(\vert z\vert )) =\tilde{ {\varphi }}_{2}({u}_{2}^{(1,\mathrm{r})}) < \infty.& & \\ \end{array}$$

If $\tilde{{\tau }}_{1} = {u}_{1}^{(1,\mathrm{r})} = {u}_{1}^{(1,\max )}$, then the analytic behavior of $\tilde{{\varphi }}_{1}(z)$ around z = u ₁ ^(1, r) is a bit complicated because ${\underline\zeta}_{2}(z)$ is also singular there. We will consider this case in the section “Exact Tail Asymptotics for the Nonarithmetic Case.”

(8Ib) The singularity of ${\underline\zeta}_{2}(z)$: By Lemma 8.8, this function is analytic on $\tilde{{\mathcal{G}}}_{0}({u}_{1}^{(1,\mathrm{min})},{u}_{1}^{(1,\max )})$ and singular at z = u ₁ ^(1, max), which is a branch point.

(8Ic) The singularity of $\tilde{{\varphi }}_{2}({\underline{\zeta }}_{2}(z))$: This function is singular at $z =\tilde{ {\tau }}_{1}$ if ${\underline{\zeta }}_{2}(\tilde{{\tau }}_{1}) =\tilde{ {\tau }}_{2}$. Otherwise, it is singular at z = u ₁ ^(1, max) because ${\underline\zeta}_{2}(z)$ is singular there. Furthermore, we may simultaneously have ${\underline{\zeta }}_{2}(\tilde{{\tau }}_{1}) =\tilde{ {\tau }}_{2}$ and $\tilde{{\tau }}_{1} = {u}_{1}^{(1,\max )}$. Thus, we need to consider these three cases: $\tilde{{\tau }}_{1} = {u}_{1}^{(1,\max )}$ for categories I and III, and $\tilde{{\tau }}_{1} < {u}_{1}^{(1,\max )}$ or $\tilde{{\tau }}_{1} = {u}_{1}^{(1,\max )}$ for category II. For this, we will use the following fact, which is essentially the same as Lemma 4.2 of [20].

Lemma 8.10.

${\overline{\zeta }}_{1}({\mathrm{e}}^{\theta })$ is a concave function of θ ∈ [θ ₂ ^{(2,min )} ,θ ₂ ^{(2,max )} ], ${\overline{\zeta }}_{1}^{\prime}({u}_{2}^{(1,\max )}) = 0$, ${\overline{\zeta }}_{1}^{\prime\prime}({u}_{2}^{(1,\max )}) <\ 0$ , and

$$\begin{array}{rcl}{ \qquad \lim \limits_{{ z\rightarrow {u}_{1}^{(1,\max )} \atop z\in \tilde{{\mathcal{G}}}_{0}({u}_{1}^{(1,\mathrm{min})},{u}_{1}^{(1,\max )})} }} \frac{{u}_{2}^{(1,\max )} -{\underline{\zeta }}_{2}(z)} {{({u}_{1}^{(1,\max )} - z)}^{\frac{1} {2} }} = \frac{\sqrt{2}} {\sqrt{-{\overline{\zeta } }_{1 } ^{\prime\prime}({u}_{2 }^{(1,\max ) })}}.& &\end{array}$$

(8.31)

Proof.

The first part is immediate from the facts that Γ ₊ is a convex set and ${u}_{1}^{(1,\max )} ={ \mathrm{e}}^{{\theta }_{1}^{(1,\max )} }$ . By Taylor expansion of ${\overline{\zeta }}_{1}({z}_{2})$ at z ₂ = u ₂ ^{(1,max )} < u ₂ ^{(2,max )},

$$\begin{array}{rcl}{ \overline{\zeta }}_{1}({z}_{2}) = {u}_{1}^{(1,\max )} + \frac{1} {2}{\overline{\zeta }}_{1}^{\prime\prime}({u}_{2}^{(1,\max )}){({z}_{ 2} - {u}_{2}^{(1,\max )})}^{2} + o(\vert {z}_{ 2} - {u}_{2}^{(1,\max )}{\vert }^{2}).& & \\ \end{array}$$

Letting ${z_2} = {\underline\zeta}_{2}(z)$ in this equation yields (8.31) since ${\overline{\zeta }}_{1}({\underline{\zeta }}_{2}(z)) = z$ for z to be sufficiently close to u ₁ ^{(1,max )} . □

Another useful asymptotic is as follows.

Lemma 8.11.

If u ₁ ^{(1,max )} = u ₁ ^{(1,r )} , then for any δ > 0,

$$ \begin{array}{rcl} {\lim \limits_{{ z\rightarrow {u}_{1}^{(1,\max )} \atop z\in \tilde{{\mathcal{G}}}_{\delta }^{+}({u}_{1}^{(1,\max )})} }} \frac{{({u}_{1}^{(1,\max )} - z)}^{\frac{1} {2} }} {1 -\tilde{ {\gamma }}_{1}(z,{\underline{\zeta }}_{2}(z))} = \frac{\sqrt{-{\overline{\zeta } }_{1 } ^{\prime\prime}({u}_{2 }^{(1,\max ) })}} {\sqrt{2}{p}_{{_\ast}1}^{(1)}({u}_{1}^{(1,\mathrm{r})})}.& &\end{array}$$

(8.32)

Proof.

By the condition u ₁ ^(1, max) = u ₁ ^(1, r), we have

$$\begin{array}{rcl} 1 -\tilde{ {\gamma }}_{1}(z,{\underline{\zeta }}_{2}(z)) =\tilde{ {\gamma }}_{1}({\mathbf{u}}^{(1,\max )}) -\tilde{ {\gamma }}_{ 1}(z,{\underline{\zeta }}_{2}(z))\quad && \\ & & = ({u}_{2}^{(1,\max )} -{\underline{\zeta }}_{ 2}(z)){p}_{{_\ast}1}^{(1)}({u}_{ 1}^{(1,\mathrm{r})}) \\ & & \;\;\;+{\underline{\zeta }}_{2}(z)({p}_{{_\ast}1}^{(1)}({u}_{ 1}^{(1,\mathrm{r})}) - {p}_{ {_\ast}1}^{(1)}(z)) + {p}_{ {_\ast}0}^{(1)}({u}_{ 1}^{(1,\mathrm{r})}) - {p}_{ {_\ast}0}^{(1)}(z).\end{array}$$

Hence, if we divide both sides by ${({u}_{1}^{(1,\max )} - z)}^{\frac{1} {2} }$, then Lemma 8.10 yields (8.31) because p _∗ 1 ⁽¹⁾(z) and p _∗ 0 ⁽¹⁾(z) are analytic except for z = 0. □ 

We now consider the three cases separately.

(8Ic-1) ${\underline{\zeta }}_{2}(\tilde{{\tau }}_{1}) <\tilde{ {\tau }}_{2}$, equivalently, categories I or III, and $\tilde{{\tau }}_{1} = {u}_{1}^{(1,\max )}$: In this case, $\tilde{{\varphi }}_{2}(z)$ is analytic for $z \in \tilde{ {C}}_{\delta }({u}_{2}^{(1,\max )})$ for some δ > 0 because ${u}_{2}^{(1,\max )} ={ \underline{\zeta }}_{2}({u}_{1}^{(1,\max )}) ={ \underline{\zeta }}_{2}(\tilde{{\tau }}_{1}) <\tilde{ {\tau }}_{2}$. Hence, by Taylor expansion, we have, for $\vert z\vert <\tilde{ {\tau }}_{2}$,

$$\begin{array}{rcl} \tilde{{\varphi }}_{2}(z) =\tilde{ {\varphi }}_{2}({u}_{2}^{(1,\max )}) +\tilde{ {\varphi }}_{ 2}^{\prime}({u}_{2}^{(1,\max )})(z - {u}_{ 2}^{(1,\max )}) + o(\vert z - {u}_{ 2}^{(1,\max )}\vert ).& &\end{array}$$

(8.33)

Thus, the analytic behavior of $\tilde{{\varphi }}_{2}({\underline{\zeta }}_{2}(z))$ around z = u ₁ ^(1, max) is determined by that of ${\underline\zeta}_{2}(z) - {U_{2}^{(1,{\text max})}}$. Since ${u}_{2}^{(1,\max )} ={ \underline{\zeta }}_{2}({u}_{1}^{(1,\max )}) <\tilde{ {\tau }}_{2}$ by the conditions of (8Ic-1), Lemma 8.10 yields

$$\begin{array}{rl} \quad \tilde{{\varphi }}_{2}({\underline{\zeta }}_{2}(z)) =\tilde{ {\varphi }}_{2}({u}_{2}^{(1,\max )}) - \frac{\sqrt{2}\tilde{{\varphi }}_{2}^{\prime}({u}_{2}^{(1,\max )})} {\sqrt{-{\overline{\zeta } }_{1 } ^{\prime\prime}({u}_{2 }^{(1,\max ) })}}{({u}_{1}^{(1,\max )} - z)}^{\frac{1} {2} } \\ +o(\vert z - {u}_{2}^{(1,\max )}{\vert }^{\frac{1} {2} }).\end{array}$$

(8.34)

Thus, $\tilde{{\varphi }}_{2}({\underline{\zeta }}_{2}(z))$ has a branch point of order 2 at $z =\tilde{ {\tau }}_{1} = {u}_{1}^{(1,\max )}$ and is analytic on $\tilde{{\mathcal{G}}}_{\delta }^{+}({u}_{1}^{(1,\max )})$ for some δ > 0.

(8Ic-2) ${\underline{\zeta }}_{2}(\tilde{{\tau }}_{1}) =\tilde{ {\tau }}_{2}$ and $\tilde{{\tau }}_{1} < {u}_{1}^{(1,\max )}$: This is only for category II. Hence, $\tilde{{\tau }}_{2} = {u}_{2}^{(2,\mathrm{r})} < {u}_{2}^{(2,\max )}$, and therefore the $\tilde{{\varphi }}_{2}$-version of Lemma 8.9 is available. Thus, $\tilde{{\varphi }}_{2}(z)$ has a simple pole at z = u ₂ ^(2, r). Here, that u ₂ ^(2, r) is the solution of the equation

$$\begin{array}{rcl} \tilde{{\gamma }}_{2}({\underline{\zeta }}_{1}(z),z) = 1& &\end{array}$$

(8.35)

is crucial. Furthermore, ${\underline\zeta}_{2}(z)$ is analytic at $z =\tilde{ {\tau }}_{1}$. Hence, $\tilde{{\varphi }}_{2}({\underline{\zeta }}_{2}(z))$ has a simple pole at $z =\tilde{ {\tau }}_{1}$ and is analytic on $\tilde{{C}}_{\delta }({u}_{1}^{(1,\max )})$ for some δ > 0.

(8Ic-3) ${\underline{\zeta }}_{2}(\tilde{{\tau }}_{1}) =\tilde{ {\tau }}_{2}$ and $\tilde{{\tau }}_{1} = {u}_{1}^{(1,\max )}$: This is also only for category II. This case is similar to (8Ic-2) except that ${\underline\zeta}_{2}(z)$ has a branch point at $z =\tilde{ {\tau }}_{1} = {u}_{1}^{(1,\max )}$. Since $\tilde{{\varphi }}_{2}(z)$ has a simple pole at $z =\tilde{ {\tau }}_{2}$, we have, by Lemma 8.10,

$$\begin{array}{rcl} \tilde{{\varphi }}_{2}({\underline{\zeta }}_{2}(z)) \sim {({u}_{1}^{(1,\max )} - z)}^{-\frac{1} {2} },& & \\ \end{array}$$

and $\tilde{{\varphi }}_{2}({\underline{\zeta }}_{2}(z))$ is analytic on $\tilde{{\mathcal{G}}}_{\delta }^{+}({u}_{1}^{(1,\max )})$ for some δ > 0.

Singularity for the Arithmetic Case

We next consider the case where (v-a) does not hold. That is, the Markov additive process for the interior is arithmetic. In this case, the singularity of $\tilde{{\varphi }}_{1}(z)$ at $z =\tilde{ {\tau }}_{1}$ occurs similarly to its occurrence in the section “Singularity for the Nonarithmetic Case.” In addition to this singular point, we may have another singular point $-\tilde{{\tau }}_{1}$, as can be seen in Table 8.1. For this, we separately consider two subcases:

• (B1) Either (v-b) or m ₂ ⁽¹⁾ = 0 holds. (B2) Neither (v-b) nor m ₂ ⁽¹⁾ = 0 holds.

In some cases, we need further classification:

• (C1) Either (v-c) or m ₁ ⁽²⁾ = 0 holds. (C2) Neither (v-b) nor m ₁ ⁽²⁾ = 0 holds.

Consider (B1). From Table 8.1, the solutions of (8.16) are z =  ± u ₁ ^(1, max), and the solution of (8.19) is z = u ₁ ^(1, r). There is no other solution. We consider cases similar to (8Ia), (8Ib), (8Ic-2), (8Ic-1), and (8Ic-3) of the section “Singularity for the Nonarithmetic Case.”

• (8Ia’) The solution of (8.30): This case is exactly the same as in the section “Singularity for the Nonarithmetic Case” because $z = -{u}_{1}^{(1,\mathrm{r})}$ is not the solution of (8.19). Hence, Lemma 8.9 also holds true.

• (8Ib’) The singularity of ${\underline\zeta}_{2}(z)$ at | z |  = u ₁ ^(1, max): It is singular at z =  ± u ₁ ^(1, max).

• (8Ic’) The singularity of $\tilde{{\varphi }}_{2}({\underline{\zeta }}_{2}(z))$ at $\vert z\vert =\tilde{ {\tau }}_{1}$: For $z =\tilde{ {\tau }}_{1}$, the story is the same as in the section “Singularity for the Nonarithmetic Case.” Hence, we only consider the case where $z = -\tilde{{\tau }}_{1}$. From (8.15) and the condition that (v-a) does not hold, we have

  $$\begin{array}{rcl}{ \underline{\zeta }}_{2}(-\tilde{{\tau }}_{1}) = - \frac{1 - {p}_{00}} {2({p}_{-11} + {p}_{11}\tilde{{\tau }}_{1}^{2})}\tilde{{\tau }}_{1} = -{\underline{\zeta }}_{2}(\tilde{{\tau }}_{1}).& & \end{array}$$

  (8.36)

  Hence, $\vert {\underline{\zeta }}_{2}(-\tilde{{\tau }}_{1})\vert ={ \underline{\zeta }}_{2}(\tilde{{\tau }}_{1}) > 0$, and

  $$\begin{array}{rcl} \vert {\underline{\zeta }}_{1}({\underline{\zeta }}_{2}(-\tilde{{\tau }}_{1}))\vert = \vert {\underline{\zeta }}_{1}(-{\underline{\zeta }}_{2}(\tilde{{\tau }}_{1}))\vert ={ \underline{\zeta }}_{1}({\underline{\zeta }}_{2}(\tilde{{\tau }}_{1})).& & \\ \end{array}$$

  Since ${\underline{\zeta }}_{1}({\underline{\zeta }}_{2}(\tilde{{\tau }}_{1})) <\tilde{ {\tau }}_{1}$, $\tilde{{\varphi }}_{1}({\underline{\zeta }}_{1}({\underline{\zeta }}_{2}(z)))$ is analytic around $z = -\tilde{{\tau }}_{1}$. Furthermore, Lemma 8.10 and (8.34) are still valid if we replace u _i ^(1, max) by − u _i ^(1, max) for i = 1, 2. However, this $z = -\tilde{{\tau }}_{1}$ cannot be the solution of (8.30) because of (B1). Thus, we must partially change the arguments in the section “Singularity for the Nonarithmetic Case.”

  • (8Ic’-1) ${\underline{\zeta }}_{2}(\tilde{{\tau }}_{1}) <\tilde{ {\tau }}_{2}$ and $\tilde{{\tau }}_{1} = {u}_{1}^{(1,\max )}$: This is only for categories I and III, and $\tilde{{\varphi }}_{2}({\underline{\zeta }}_{2}(z))$ has a branch point of order 2 at $z = -{u}_{1}^{(1,\max )}$ and is analytic on $\tilde{{\mathcal{G}}}_{\delta }^{-}(-{u}_{1}^{(1,\max )}) \cap \tilde{{\mathcal{G}}}_{\delta }^{+}({u}_{1}^{(1,\max )})$ for some δ > 0 because it also has a branch point at z = u ₁ ^(1, max).

  • (8Ic’-2) ${\underline{\zeta }}_{2}(\tilde{{\tau }}_{1}) =\tilde{ {\tau }}_{2}$ and $\tilde{{\tau }}_{1} < {u}_{1}^{(1,\max )}$: This is only for category II. Since ${\underline\zeta}_{2}(z)$ is analytic at $z =\tilde{ {\tau }}_{1}$, $\tilde{{\varphi }}_{2}({\underline{\zeta }}_{2}(z))$ is analytic at $z = -\tilde{{\tau }}_{1}$ if (C1) holds. Otherwise, if (C2) holds, it has a simple pole at $z = -\tilde{{\tau }}_{1}$ because ${\underline{\zeta }}_{2}(-\tilde{{\tau }}_{1}) = -{\underline{\zeta }}_{2}(\tilde{{\tau }}_{1})$ is the solution of (8.35).

  • (8Ic’-3) ${\underline{\zeta }}_{2}(\tilde{{\tau }}_{1}) =\tilde{ {\tau }}_{2}$ and $\tilde{{\tau }}_{1} = {u}_{1}^{(1,\max )}$: This is only for category II, and the situation is similar to (8c’-2), except that the singularity is caused by ${\underline\zeta}_{2}(z)$ at $z = -\tilde{{\tau }}_{1}$. To verify this fact, we rework $\tilde{{\varphi }}_{2}({\underline{\zeta }}_{2}(z))$. Similarly to (8.29), we have, for $\vert z\vert \in ({u}_{2}^{2,\mathrm{min})},\tilde{{\tau }}_{2})$,

    $$\begin{array}{rcl} \tilde{{\varphi }}_{2}(z) = \frac{(\tilde{{\gamma }}_{1}({\underline{\zeta }}_{1}(z),z) - 1)\tilde{{\varphi }}_{1}({\underline{\zeta }}_{1}(z))} {1 -\tilde{ {\gamma }}_{2}({\underline{\zeta }}_{1}(z),z)} + \frac{(\tilde{{\gamma }}_{0}({\underline{\zeta }}_{2}(z),z) - 1)\nu (\mathbf{0})} {1 -\tilde{ {\gamma }}_{2}({\underline{\zeta }}_{1}(z),z)}.& & \\ \end{array}$$

    Substituting ${\underline\zeta}_{2}(z)$ into z of this equation, we have

    $$\begin{array}{rl} \quad \tilde{{\varphi }}_{2}({\underline{\zeta }}_{2}(z)) = \frac{(\tilde{{\gamma }}_{1}({\underline{\zeta }}_{1}({\underline{\zeta }}_{2}(z)),{\underline{\zeta }}_{2}(z)) - 1)\tilde{{\varphi }}_{1}({\underline{\zeta }}_{1}({\underline{\zeta }}_{2}(z)))} {1 -\tilde{ {\gamma }}_{2}({\underline{\zeta }}_{1}({\underline{\zeta }}_{2}(z)),{\underline{\zeta }}_{2}(z))} \\ + \frac{(\tilde{{\gamma }}_{0}({\underline{\zeta }}_{2}({\underline{\zeta }}_{2}(z)),{\underline{\zeta }}_{2}(z)) - 1)\nu (\mathbf{0})} {1 -\tilde{ {\gamma }}_{2}({\underline{\zeta }}_{1}({\underline{\zeta }}_{2}(z)),{\underline{\zeta }}_{2}(z))}. \end{array}$$

    (8.37)

    By the assumptions of (8c-3), if (C2) holds, then $\tilde{{\varphi }}_{2}(z)$ has a simple pole at $z = -\tilde{{\tau }}_{2}$, and therefore $\tilde{{\varphi }}_{2}({\underline{\zeta }}_{2}(z)) \sim {(-{u}_{1}^{(1,\max )} - z)}^{-\frac{1} {2} }$ around $z = -{u}_{1}^{(1,\max )}$ by Lemma 8.10. Otherwise, if (C1) holds, then we need to consider $\tilde{{\varphi }}_{1}({\underline{\zeta }}_{1}({\underline{\zeta }}_{2}(z)))$ in (8.37) due to the singularity of ${\underline\zeta}_{2}(z)$ at $z = -\tilde{{\tau }}_{1} = -{u}_{1}^{(1,\max )}$, where $\tilde{{\varphi }}_{1}({\underline{\zeta }}_{1}(z))$ is analytic at $z = -{u}_{2}^{(1,\max )} = -{\underline{\zeta }}_{2}({u}_{1}^{(1,\max )})$ because

    $$\vert {\underline{\zeta }}_{1}({\underline{\zeta }}_{2}(-\tilde{{\tau }}_{1}))\vert = \vert {\underline{\zeta }}_{1}({\underline{\zeta }}_{2}(\tilde{{\tau }}_{1}))\vert <\tilde{ {\tau }}_{1}.$$

    Hence, $\tilde{{\varphi }}_{1}({\underline{\zeta }}_{1}({\underline{\zeta }}_{2}(z))) -\tilde{ {\varphi }}_{1}(-{\underline{\zeta }}_{1}({u}_{2}^{(1,\max )})) \sim {(-{u}_{1}^{(1,\max )} - z)}^{\frac{1} {2} }$. On the other hand, $\tilde{{\gamma }}_{1}({\underline{\zeta }}_{1}({\underline{\zeta }}_{2}(z)),{\underline{\zeta }}_{2}(z)) - 1 \sim {(-{u}_{1}^{(1,\max )} - z)}^{\frac{1} {2} }$ because (v-a) does not hold. Combining these asymptotics in (8.37), we have $\tilde{{\varphi }}_{2}({\underline{\zeta }}_{2}(z)) -\tilde{ {\varphi }}_{2}(-\tilde{{\tau }}_{2}) \sim {(-{u}_{1}^{(1,\max )} - z)}^{\frac{1} {2} }$ around $z = -{u}_{1}^{(1,\max )}$ by Lemma 8.10.

We next consider (B2). From Table 8.1, the solutions of (8.16) are z =  ± u ₁ ^(1, max), and the solutions of (8.19) are z =  ± u ₁ ^(1, r). In this case, the arguments for $z = -\tilde{{\tau }}_{1}$ are completely parallel to those for $z =\tilde{ {\tau }}_{1}$ except for the cases (8Ic’-2) and (8Ic’-3). The latter two cases are also parallel if (C2) holds. Otherwise, $\tilde{{\varphi }}_{2}(z)$ is analytic at $z = -\tilde{{\tau }}_{2}$.

Asymptotic Inversion Formula

From these singularities, we derive exact tail asymptotics of the stationary distribution. For this, we use a Tauberian-type theorem for generating functions.

Lemma 8.12 (Theorem VI.5 of [7]). 

Let f be a generating function of a sequence of real numbers {p(n);n = 0,1,…}. If f(z) is singular at finitely many points a ₁ ,a ₂ ,…,a _m on the circle |z| = ρ for some ρ > 0 and positive integer m and analytic on the set

$$\begin{array}{rcl}{ \Delta }_{i} \equiv \{ z \in \mathbb{C};\vert z\vert < {r}_{i},z\neq {a}_{i},\vert \arg (z - {a}_{i})\vert >{\omega }_{i}\},\quad i = 1,2,\ldots, m,& & \\ \end{array}$$

for some ω _i and r _i such that ρ < r _i and $0 \leq {\omega }_{i} < \frac{\pi } {2}$ , and if

$$ \begin{array}{rcl} {\lim }_{{\Delta }_{i}\ni z\rightarrow {a}_{i}}{({a}_{i} - z)}^{{\kappa }_{i} }f(z) = {b}_{i},\qquad i = 1,2,\ldots, m,& &\end{array}$$

(8.38)

for ${\kappa }_{i}\not\in \{0,-1,-2,\ldots \}$ and some constant b _i ∈ ℝ, then

$$ \begin{array}{rcl} {\lim \limits_{n\rightarrow \infty }}{\left ({\sum \nolimits }_{i=1}^{m}\frac{{n}^{{\kappa }_{i}-1}} {\Gamma ({\kappa }_{i})}{a}_{i}^{-n}\right )}^{-1}p(n) = b& &\end{array}$$

(8.39)

for some real number b, where Γ(z) is the gamma function for complex number z (see Sect. 52 of volume II of [17]).

Recall the asymptotic notation “ ∼ ” introduced in the introduction. With this notation, (8.39) can be written as

$$\begin{array}{rcl} p(n) \sim {\sum \limits_{i=1}^{m}}\frac{{n}^{{\kappa }_{i}-1}} {\Gamma ({\kappa }_{i})}{a}_{i}^{-n},& & \\ \end{array}$$

where $\Gamma (\frac{1} {2}) = \sqrt{\pi }$ and $\Gamma (-\frac{1} {2}) = -2\sqrt{\pi }$.

We will apply Lemma 8.12 in the following cases: For m = 1, a ₁ = u ₁ ^(1, r), and κ₁ = 1, 2, a ₁ = u ₁ ^(1, max) and ${\kappa }_{1} = \pm \frac{1} {2}$. For m = 2, a ₁ =  ± u ₁ ^(1, r), and κ₁ = 1, 2, a ₁ =  ± u ₁ ^(1, max) and ${\kappa }_{1} = -\frac{1} {2}$.

Exact Tail Asymptotics for the Nonarithmetic Case

Throughout this section, we assume the nonarithmetic condition (v-a). We first derive exact asymptotics for the stationary probabilities ν(n, 0) and ν(0, n) on the boundary faces. Because of symmetry, we are only concerned with ν(n, 0).

Boundary Probabilities for Nonarithmetic Case

We separately consider the two cases where u ₂ ^(1, Γ) < u ₂ ^(2, Γ) and u ₂ ^(1, Γ) ≥ u ₂ ^(2, Γ), which correspond to categories I (or III) and II, respectively. In this subsection, we prove the following two theorems.

Theorem 8.2.

Under conditions (i)–(iv) and (v-a), for categories I and III, $\tilde{{\tau }}_{1} = {u}_{1}^{(1,\Gamma )}$ , and $P({L}_{1} = n,{L}_{2} = 0)$ has the following exact asymptotic h ₁ (n):

$$\begin{array}{rcl}{ h}_{1}(n) = \left \{\begin{array}{ll} \tilde{{\tau }}_{1}^{-n},\quad &{u}_{1}^{(1,\Gamma )}\not ={u}_{1}^{(1,\max )}, \\ {n}^{-\frac{1} {2} }\tilde{{\tau }}_{1}^{-n},\quad &{u}_{1}^{(1,\Gamma )} = {u}_{1}^{(1,\max )} = {u}_{1}^{(1,\mathrm{r})}, \\ {n}^{-\frac{3} {2} }\tilde{{\tau }}_{1}^{-n},\quad &{u}_{1}^{(1,\Gamma )} = {u}_{1}^{(1,\max )}\neq {u}_{1}^{(1,\mathrm{r})}. \end{array} \right.& &\end{array}$$

(8.40)

By symmetry, the corresponding results are also obtained for $P({L}_{1} = 0,{L}_{2} = n)$ for categories I and II.

Theorem 8.3.

Under conditions (i)–(iv) and (v-a), for category II, $\tilde{{\tau }}_{2} = {u}_{2}^{(2,\mathrm{r})}$ , and $P({L}_{1} = n,{L}_{2} = 0)$ has the following exact asymptotic h ₁ (n):

$$\begin{array}{rcl}{ h}_{1}(n) = \left \{\begin{array}{ll} \tilde{{\tau }}_{1}^{-n},\quad &\tilde{{\tau }}_{1} < {u}_{1}^{(1,\Gamma )},\mbox{ or } \\ &\tilde{{\tau }}_{1} = {u}_{1}^{(1,\Gamma )} = {u}_{1}^{(1,\max )} = {u}_{1}^{(1,\mathrm{r})}, \\ n\tilde{{\tau }}_{1}^{-n},\quad &\tilde{{\tau }}_{1} = {u}_{1}^{(1,\Gamma )}\not ={u}_{1}^{(1,\max )}, \\ {n}^{-\frac{1} {2} }\tilde{{\tau }}_{1}^{-n},\;&\tilde{{\tau }}_{1} = {u}_{1}^{(1,\Gamma )} = {u}_{1}^{(1,\max )}\neq {u}_{1}^{(1,\mathrm{r})}. \end{array} \right.& &\end{array}$$

(8.41)

By symmetry, the corresponding results are also obtained for $P({L}_{1} = 0,{L}_{2} = n)$ for categories III.

Remark 8.7.

Theorems 8.2 and 8.3 exactly correspond with Theorem 6.1 of [4] (see also Theorems 2.1 and 2.3 of [3]). This is not surprising because of the similarity of the stationary equations, although moment-generating functions are used in [3, 4].

Remark 8.8.

These theorems fill missing cases for the exact asymptotics of Theorem 4.2 of [18]. Furthermore, they correct two errors there. Both of them are for category II. The exact asymptotic is geometric for $\tilde{{\tau }}_{1} = {u}_{1}^{(1,\Gamma )} = {u}_{1}^{(1,\max )} = {u}_{1}^{(1,\mathrm{r})}$ and not geometric for $\tilde{{\tau }}_{1} = {u}_{1}^{(1,\Gamma )}\not ={u}_{1}^{(1,\max )}$ (Theorem 8.3). However, in Theorem 4.2 of [18], they are not geometric [see (43d3) there] and geometric [see (4c) there], respectively. Thus, these should be corrected.

Proof of Theorem 8.2. We assume category I or III. This is equivalent to u ₂ ^(1, Γ) < u ₂ ^(2, Γ) and $\tilde{{\tau }}_{1} = {u}_{1}^{(1,\Gamma )}$. Furthermore, we always have ${\underline{\zeta }}_{2}({u}_{1}^{(1,\Gamma )}) = {u}_{2}^{(1,\Gamma )} <\tilde{ {\tau }}_{2}$, and therefore $\tilde{{\varphi }}_{2}({\underline{\zeta }}_{2}(z))$ is analytic at z = u ₁ ^(1, Γ). We consider three cases separately.

(8IIa) u ₁ ^(1, Γ) < u ₁ ^(1, max): This case implies that u ₁ ^(1, r) < u ₁ ^(1, max) and $\tilde{{\gamma }}_{1}({\mathbf{u}}^{(1,\max )}) > 1$, and therefore ${\mathbf{u}}^{(1,\mathrm{r})} ={ \mathbf{u}}^{(1,\Gamma )}$. Hence, by Lemma 8.9, $\tilde{{\varphi }}_{1}$ of (8.29) satisfies the conditions of Lemma 8.12 under the setting (8.38) with a ₁ = u ₁ ^(1, r), κ = 1. Thus, letting

$$\begin{array}{rcl} b = \frac{(\tilde{{\gamma }}_{2}({\mathbf{u}}^{(1,\mathrm{r})}) - 1)\tilde{{\varphi }}_{2}({u}_{2}^{(1,\mathrm{r})}) + (\tilde{{\gamma }}_{0}({\mathbf{u}}^{(1,\mathrm{r})}) - 1)\nu (\mathbf{0})} { \frac{\mathrm{d}} {\mathrm{d}u}\tilde{{\gamma }}_{1}(u,{\underline{\zeta }}_{2}(u)){\vert }_{u={u}_{1}^{(1,\mathrm{r})}}}, & & \\ \end{array}$$

which must be positive by (8.39) and the fact that $\tilde{{\varphi }}_{1}(z)$ is singular at z = u ₁ ^(1, r), we have

$$ \begin{array}{rcl} {\lim \limits_{n\rightarrow \infty }}\tilde{{\tau }}_{1}^{n}P({L}_{ 1} = n,{L}_{2} = 0) = b.& & \\ \end{array}$$

(8IIb) u ₁ ^(1, Γ) = u ₁ ^(1, max), u ₁ ^(1, r) = u ₁ ^(1, max): In this case, category III is impossible, and $\tilde{{\gamma }}_{1}({\mathbf{u}}^{(1,\max )}) = 1$. On the other hand, $\tilde{{\varphi }}_{2}(z)$ is analytic at $z ={ \underline{\zeta }}_{2}({u}_{1}^{(1,\max )}) <\tilde{ {\tau }}_{2}$ because of category I. Hence, we can use the Taylor expansion (8.33), and therefore (8.29), (8.34), and Lemma 8.11 yield, for some δ > 0,

$$ \begin{array}{rcl} {\lim \limits_{\tilde{{\mathcal{G}}}_{\delta }^{+}({u}_{1}^{(1,\max )})\ni z\rightarrow {u}_{1}^{(1,\max )}}}{({u}_{1}^{(1,\max )} - z)}^{\frac{1} {2} }\tilde{{\varphi }}_{1}(z) = b,& &\end{array}$$

(8.42)

where

$$\begin{array}{rcl} b = \left((\tilde{{\gamma }}_{2}({\mathbf{u}}^{(1,\max )}) - 1)\tilde{{\varphi }}_{ 2}({u}_{2}^{(1,\max )}) + (\tilde{{\gamma }}_{ 0}({\mathbf{u}}^{(1,\max )}) - 1)\nu (\mathbf{0})\right) \frac{\sqrt{-{\overline{\zeta } }_{1 } ^{\prime\prime}({u}_{2 }^{(1,\max ) })}} {\sqrt{2}{p}_{{_\ast}1}^{(1)}({u}_{1}^{(1,\mathrm{r})})}.& & \\ \end{array}$$

Hence, $\tilde{{\varphi }}_{1}$ satisfies the conditions of Lemma 8.12 under the setting (8.38) with a ₁ = u ₁ ^(1, max) and ${\kappa }_{1} = \frac{1} {2}$, and therefore we have

$$ \begin{array}{rcl} {\lim \limits_{n\rightarrow \infty }}{n}^{\frac{1} {2} }\tilde{{\tau }}_{1}^{n}P({L}_{1} = n,{L}_{2} = 0) = \frac{b} {\sqrt{\pi }},& & \\ \end{array}$$

where the positivity of b is checked, similarly to case (8a) [see also case (8c) below].

(8IIc) u ₁ ^(1, Γ) = u ₁ ^(1, max), u ₁ ^(1, r) ≠ u ₁ ^(1, max): In this case, category III is also impossible, and $\tilde{{\gamma }}_{1}({\mathbf{u}}^{(1,\max )})\not =\ 1$. Thus, we consider the setting (8.38) with ${\kappa }_{1} = -\frac{1} {2}$. From (8.29) we have

$$\begin{array}{rcl} \tilde{{\varphi }}_{1}(z) -\tilde{ {\varphi }}_{1}({u}_{1}^{(1,\max )})&& \\ & & = \frac{(\tilde{{\gamma }}_{2}(z,{\underline{\zeta }}_{2}(z)) - 1)\tilde{{\varphi }}_{2}({\underline{\zeta }}_{2}(z)) + (\tilde{{\gamma }}_{0}(z,{\underline{\zeta }}_{2}(z)) - 1)\nu (\mathbf{0})} {1 -\tilde{ {\gamma }}_{1}(z,{\underline{\zeta }}_{2}(z))} -\tilde{ {\varphi }}_{1}({u}_{1}^{(1,\max )}) \\ & & = \frac{(\tilde{{\gamma }}_{2}(z,{\underline{\zeta }}_{2}(z)) - 1)(\tilde{{\varphi }}_{2}({\underline{\zeta }}_{2}(z)) -\tilde{ {\varphi }}_{2}({u}_{2}^{(1,\max )}))} {1 -\tilde{ {\gamma }}_{1}(z,{\underline{\zeta }}_{2}(z))} \\ & & \quad + \frac{(\tilde{{\gamma }}_{2}(z,{\underline{\zeta }}_{2}(z)) -\tilde{ {\gamma }}_{2}({\mathbf{u}}^{(1,\max )}))\tilde{{\varphi }}_{2}({u}_{2}^{(1,\max )})} {1 -\tilde{ {\gamma }}_{1}(z,{\underline{\zeta }}_{2}(z))} + \frac{(\tilde{{\gamma }}_{0}(z,{\underline{\zeta }}_{2}(z)) -\tilde{ {\gamma }}_{0}({\mathbf{u}}^{(1,\max )}))\nu (\mathbf{0})} {1 -\tilde{ {\gamma }}_{1}(z,{\underline{\zeta }}_{2}(z))} \\ & & \quad + \left[ \frac{(\tilde{{\gamma }}_{2}({\mathbf{u}}^{(1,\max )}) - 1)\tilde{{\varphi }}_{2}({u}_{2}^{(1,\max )})} {(1 -\tilde{ {\gamma }}_{1}(z,{\underline{\zeta }}_{2}(z)))(1 -\tilde{ {\gamma }}_{1}({\mathbf{u}}^{(1,\max )}))} + \frac{(\tilde{{\gamma }}_{0}({\mathbf{u}}^{(1,\max )}) - 1)\nu (\mathbf{0})} {(1 -\tilde{ {\gamma }}_{1}(z,{\underline{\zeta }}_{2}(z)))(1 -\tilde{ {\gamma }}_{1}({\mathbf{u}}^{(1,\max )}))}\right] \\ & & \qquad \times \left (\tilde{{\gamma }}_{1}(z,{\underline{\zeta }}_{2}(z)) -\tilde{ {\gamma }}_{1}({\mathbf{u}}^{(1,\max )})\right ). \end{array}$$

(8.43)

We recall (8.34) that

$$\begin{array}{rcl} \tilde{{\varphi }}_{2}({\underline{\zeta }}_{2}(z)) -\tilde{ {\varphi }}_{2}({u}_{2}^{(1,\max )}) = -{({u}_{ 1}^{(1,\max )} - z)}^{\frac{1} {2} } \frac{\sqrt{2}\tilde{{\varphi }}_{2}^{\prime}({u}_{2}^{(1,\max )})} {\sqrt{-{\overline{\zeta } }_{1 } ^{\prime\prime}({u}_{2 }^{(1,\max ) })}} + o(\vert {u}_{1}^{(1,\max )} - z{\vert }^{\frac{1} {2} }).& & \\ \end{array}$$

From (8.31) we have

$$\begin{array}{rcl} \tilde{{\gamma }}_{0}(z,{\underline{\zeta }}_{2}(z)) -\tilde{ {\gamma }}_{0}({\mathbf{u}}^{(1,\max )}) = ({\underline{\zeta }}_{ 2}(z) -{\underline{\zeta }}_{2}({u}_{1}^{(1,\max )})){p}_{ {_\ast}1}^{(0)}(z)\quad && \\ & & \quad +{ \underline{\zeta }}_{2}({u}_{1}^{(1,\max )})({p}_{ {_\ast}1}^{(0)}(z) - {p}_{ {_\ast}1}^{(0)}({u}_{ 1}^{(1,\max )})) + {p}_{ {_\ast}0}^{(0)}(z) - {p}_{ {_\ast}0}^{(0)}({u}_{ 1}^{(1,\max )}) \\ & & = -\frac{\sqrt{2}{p}_{{_\ast}1}^{(0)}({u}_{1}^{(1,\max )})} {\sqrt{-{\overline{\zeta } }_{1 } ^{\prime\prime}({u}_{2 }^{(1,\max ) })}} {({u}_{1}^{(1,\max )} - z)}^{\frac{1} {2} } + o(\vert {u}_{1}^{(1,\max )} - z{\vert }^{\frac{1} {2} }).\end{array}$$

Similarly,

$$\begin{array}{rcl} & & \tilde{{\gamma }}_{1}(z,{\underline{\zeta}}_{2}(z)) -\tilde{ {\gamma }}_{1}({\mathbf{u}}^{(1,\max )}) \\ & & \quad = -\frac{\sqrt{2}{p}_{{_\ast}1}^{(1)}({u}_{1}^{(1,\max )})} {\sqrt{-{\overline{\zeta } }_{1 } ^{\prime\prime}({u}_{2 }^{(1,\max ) })}} {({u}_{1}^{(1,\max )} - z)}^{\frac{1} {2} } + o(\vert {u}_{1}^{(1,\max )} - z{\vert }^{\frac{1} {2} }), \\ & & \qquad \tilde{{\gamma }}_{2}(z,{\underline{\zeta }}_{2}(z)) -\tilde{ {\gamma }}_{2}({\mathbf{u}}^{(1,\max )}) \\ & & \quad = -\frac{\sqrt{2}\left({p}_{{_\ast}1}^{(2)}({u}_{1}^{(1,\max )}) -\frac{{p}_{{_\ast}-1}^{(2)}({u}_{1}^{(1,\max )})} { \left( {u}_{2}^{(1,\max )}\right)}^{2} \right)} {\sqrt{-{\overline{\zeta } }_{1 } ^{\prime\prime}({u}_{2 }^{(1,\max ) })}} {({u}_{1}^{(1,\max )} - z)}^{\frac{1} {2} } + o(\vert {u}_{1}^{(1,\max )} - z{\vert }^{\frac{1} {2} }).\end{array}$$

With the notation

$$\begin{array}{rcl} & & {c}_{1} = \frac{\sqrt{2}} {\left(1 -\tilde{ {\gamma }}_{1}({\mathbf{u}}^{(1,\max )})\right)\sqrt{-{\overline{\zeta } }_{1 } ^{\prime\prime}({u}_{2 }^{(1,\max ) })}}, \\ & & {d}_{k} ={ \left. \frac{\partial } {\partial v}\tilde{{\gamma }}_{k}({u}_{1}^{(1,\max )},v)\right \vert }_{ v={\underline{\zeta }}_{2}({u}_{1}^{(1,\max )})}, \\ \end{array}$$

(8.43) yields, as z → u ₁ ^(1, max) satisfying that $z \in \tilde{{\mathcal{G}}}_{\delta }^{+}({u}_{1}^{(1,\max )})$ for some δ > 0,

$$\begin{array}{lll} \quad \tilde{{\varphi }}_{1}(z) -\tilde{{\varphi }}_{1}({u}_{1}^{(1,\max )}) &= -{c}_{ 1}{({u}_{1}^{(1,\max)} - z)}^{\frac{1} {2}} \left(\left(\tilde{{\gamma}}_{2}({\mathbf{u}}^{(1,\max )}) - 1\right)\tilde{{\varphi}}_{2}^{\prime}({u}_{2}^{(1,\max )})\right. \\ &\left.+{d}_{2}\tilde{{\varphi }}_{2}({u}_{2}^{(1,\max )}) + {d}_{ 0}\nu(\mathbf{0}) + {d}_{1}\tilde{{\varphi }}_{1}({u}_{1}^{(1,\max)})\right) + o(\vert {u}_{ 1}^{(1,\max )} - z{\vert }^{\frac{1} {2}}).\end{array}$$

(8.44)

Let

$$\begin{array}{rcl} b = -\left(\left(\tilde{{\gamma }}_{2}({\mathbf{u}}^{(1,\max )}) - 1\right)\tilde{{\varphi }}_{ 2}^{\prime}({u}_{2}^{(1,\max )}) + {d}_{ 2}\tilde{{\varphi }}_{2}({u}_{2}^{(1,\max )}) + {d}_{ 0}\nu (\mathbf{0}) +{d}_{1}\tilde{{\varphi }}_{1}({u}_{1}^{(1,\max )})\right).& & \\ \end{array}$$

Then, taking u ₁ which is sufficiently close to u ₁ ^(1, max) from below in (8.44), we can see that this b must be negative because $\tilde{{\varphi }}_{1}({u}_{1})$ is strictly increasing in u ₁ ∈ [0, u ₁ ^(1, max)). Thus, (8.38) holds for the setting of (8.38) with ${\kappa }_{1} = -\frac{1} {2}$, and therefore (8.39) leads to

$$ \begin{array}{rcl} {\lim \limits_{n\rightarrow \infty }}{n}^{\frac{3} {2} }\tilde{{\tau }}_{1}^{n}P({L}_{1} = n,{L}_{2} = 0) = - \frac{b} {2\sqrt{\pi }} > 0.& & \\ \end{array}$$

Thus, we have obtained all the cases of (8.40), and the proof is completed. □ 

Proof of Theorem 8.3. Assume category II. In this case, $\tilde{{\tau }}_{2} ={ \underline{\zeta }}_{2}(\tilde{{\tau }}_{1})$, and $\tilde{{\varphi }}_{2}(z)$ has a simple pole at $z =\tilde{ {\tau }}_{2}$ because of category II [see (8Ic-2)]. We need to consider the following cases.

(8IIa’): $\tilde{{\tau }}_{1} < {u}_{1}^{(1,\Gamma )}$: In this case, $\tilde{{\varphi }}_{2}({\underline{\zeta }}_{2}(z))$ has a simple pole at $z =\tilde{ {\tau }}_{1}$. Since $\tilde{{\varphi }}_{1}(z)$ has no other singularity on $\vert z\vert =\tilde{ {\tau }}_{1}$, it has a simple pole at $z =\tilde{ {\tau }}_{1}$.

(8IIb’): $\tilde{{\tau }}_{1} = {u}_{1}^{(1,\Gamma )}$: This case is further partitioned into the following subcases:

• (8IIb’-1) u ₁ ^(1, Γ) ≠ u ₁ ^(1, max): In this case, $\tilde{{\tau }}_{1} = {u}_{1}^{(1,\mathrm{r})} < {u}_{1}^{(1,\max )}$, and therefore it is easy to see from (8.29) that $\tilde{{\varphi }}_{1}(z)$ has a double pole at $z =\tilde{ {\tau }}_{1}$. Hence, we can apply the setting (8.38) with a ₁ = u ₁ ^(1, r) and κ = 2.

• (8IIb’-2) u ₁ ^(1, Γ) = u ₁ ^(1, max)≠u ₁ ^(1, r): (8.30) does not hold, and therefore (8.31) and the fact that $\tilde{{\varphi }}_{2}(z)$ has a simple pole at $z =\tilde{ {\tau }}_{2}$ yield the same asymptotic as (8.42) but with a different b. Hence, we apply (8.38) with ${\kappa }_{1} = \frac{1} {2}$.

• (8IIb’-3) ${u}_{1}^{(1,\Gamma )} = {u}_{1}^{(1,\max )} = {u}_{1}^{(1,\mathrm{r})}$: In this case, we note the following facts.

  • (8IIb’-3-1) $\tilde{{\varphi }}_{2}(z)$ has a simple pole at $z =\tilde{ {\tau }}_{2}$, and therefore Lemma 8.10 yields

    $$\begin{array}{rcl} \tilde{{\varphi }}_{2}({\underline{\zeta }}_{2}(z)) \sim {({u}_{1}^{(1,\max )} - z)}^{-\frac{1} {2} }.& & \\ \end{array}$$

  • (8IIb’-3-2) By Lemma 8.11, $1 -\tilde{ {\gamma }}_{1}(z,{\underline{\zeta }}_{2}(z)) \sim {({u}_{1}^{(1,\max )} - z)}^{\frac{1} {2} }$.

  Hence, (8.29) yields $\tilde{{\varphi }}_{1}(z) \sim {({u}_{1}^{(1,\max )} - z)}^{-1}$, and therefore we apply (8.38) with a ₁ = u ₁ ^(1, r) and κ = 1.

Thus, similar to Theorem 8.2, we can obtain (8.41), which completes the proof. □ 

Marginal Distributions for the Nonarithmetic Case

We consider the asymptotics of $P(\langle \mathbf{c},\mathbf{L}\rangle = x)$ as x → ∞ for $\mathbf{c} = (1,0),(0,1),(1,1)$. For them, we use the generating functions $\tilde{{\varphi }}_{+}(z,1)$, $\tilde{{\varphi }}_{+}(1,z)$, and $\tilde{{\varphi }}_{+}(z,z)$. For simplicity, we denote them by ψ₁₀(z), ψ₀₁(z), ψ₁₁(z), respectively. We note that generating functions are not useful for the other direction $\mathbf{c}$ because we cannot appropriately invert them. For general $\mathbf{c} > 0$, we should use moment-generating functions instead of generating functions. However, in this case, we need finer analytic properties to apply asymptotic inversion (e.g., see Appendix C of [3]). Thus, we leave it for future study.

From (8.13) and (8.28) we have, for $\mathbf{z} \in {\mathbb{C}}^{2}$ satisfying $(\vert {z}_{1}\vert, \vert {z}_{2}\vert ) \in \tilde{\mathcal{D}}$,

$$\begin{array}{rcl} \tilde{\varphi }(\mathbf{z}) = \left (1+ \frac{\tilde{{\gamma }}_{1}(\mathbf{z})-1} {1-\tilde{{\gamma }}_{+}(\mathbf{z})}\right )\tilde{{\varphi }}_{1}({z}_{1})+\frac{\tilde{{\gamma }}_{2}(\mathbf{z})-\tilde{{\gamma }}_{+}(\mathbf{z})} {1-\tilde{{\gamma }}_{+}(\mathbf{z})} \tilde{{\varphi }}_{2}({z}_{2})+\frac{\tilde{{\gamma }}_{0}(\mathbf{z})-\tilde{{\gamma }}_{+}(\mathbf{z})} {1-\tilde{{\gamma }}_{+}(\mathbf{z})} \nu (\mathbf{0}).\qquad & &\end{array}$$

(8.45)

Hence, the asymptotics of $P(\langle \mathbf{c},\mathbf{L}\rangle = x)$ can be obtained for $\mathbf{c} = (1,0),(0,1),(1,1)$ by the analytic behavior of ψ₁₀(z), ψ₀₁(z), ψ₁₁(z), respectively, around the singular points on the circles with radii ${\rho }_{\mathbf{c}}$, where

$$\begin{array}{rcl} & & {\rho }_{(1,0)} =\sup \{ u \geq 0;(u,1) \in \tilde{\mathcal{D}}\},\quad {\rho }_{(0,1)} =\sup \{ u \geq 0;(1,u) \in \tilde{\mathcal{D}}\}, \\ & & {\rho }_{(1,1)} =\sup \{ u \geq 0;(u,u) \in \tilde{\mathcal{D}}\}.\end{array}$$

Since ψ₁₀(z) and ψ₀₁(z) are symmetric, we only consider ψ₁₀(z) and ψ₁₁(z). From (8.45) we have

$$\begin{array}{rcl}{ \psi }_{10}(z)& =& \left (1 + \frac{\tilde{{\gamma }}_{1}(z,1) - 1} {1 -\tilde{ {\gamma }}_{+}(z,1)}\right )\tilde{{\varphi }}_{1}(z) + \frac{\tilde{{\gamma }}_{2}(z,1) -\tilde{ {\gamma }}_{+}(z,1)} {1 -\tilde{ {\gamma }}_{+}(z,1)} \tilde{{\varphi }}_{2}(1) \\ & & \;\;+\frac{\tilde{{\gamma }}_{0}(z,1) -\tilde{ {\gamma }}_{+}(z,1)} {1 -\tilde{ {\gamma }}_{+}(z,1)} \nu (\mathbf{0}), \end{array}$$

(8.46)

$$\begin{array}{rcl}{ \psi }_{11}(z)& =& \left (1 + \frac{\tilde{{\gamma }}_{1}(z,z) - 1} {1 -\tilde{ {\gamma }}_{+}(z,z)}\right )\tilde{{\varphi }}_{1}(z) + \frac{\tilde{{\gamma }}_{2}(z,z) -\tilde{ {\gamma }}_{+}(z,z)} {1 -\tilde{ {\gamma }}_{+}(z,z)} \tilde{{\varphi }}_{2}(z)\quad \\ & & \;\;+\frac{\tilde{{\gamma }}_{0}(z,z) -\tilde{ {\gamma }}_{+}(z,z)} {1 -\tilde{ {\gamma }}_{+}(z,z)} \nu (\mathbf{0}). \end{array}$$

(8.47)

We first consider the tail asymptotics for $\mathbf{c} = (1,0)$ under nonarithmetic condition (v-a). From (8.46) the singularity of ψ₁₁(z) on the circle | z |  = ρ_(1, 0) occurs by either that of $\tilde{{\varphi }}_{1}(z)$ or the solution of the following equation:

$$\begin{array}{rcl} \tilde{{\gamma }}_{+}(z,1) = 1.& &\end{array}$$

(8.48)

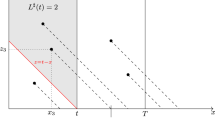
Since this equation is quadratic and the domain $\tilde{\mathcal{D}}$ contains vectors $\mathbf{x} > \mathbf{1} \equiv (1,1)$, Eq. (8.48) has a unique real solution greater than 1. We denote it by σ₊. We then have the following asymptotics (see also Fig. 8.4).

Fig. 8.4

Left: ${\overline{\zeta }}_{2}({u}_{1}^{(1,\Gamma )}) < 1$; right: ${\overline{\zeta }}_{2}({u}_{1}^{(1,\Gamma )}) > 1$ and ${\underline\zeta}_{2} (u_{1}^{(1,{\Gamma})}) \neq 1$

Theorem 8.4.

Under conditions (i)–(iv) and (v-a), let h ₁ (n) be the exact asymptotic function given in Theorems 8.2 and 8.3; then P(L ₁ = n) has the following exact asymptotic g ₁ (n) as n →∞:

• (a) If ${\overline{\zeta }}_{2}({u}_{1}^{(1,\Gamma )}) < 1$ , then ${g}_{1}(n) = {\sigma }_{+}^{-n}$.

• (b) If ${\overline{\zeta }}_{2}({u}_{1}^{(1,\Gamma )}) > 1$ and ${\underline\zeta}_{2} (u_{1}^{(1,{\Gamma})}) \neq 1$, then g ₁ (n) = h ₁ (n).

• (c) If ${\overline{\zeta }}_{2}({u}_{1}^{(1,\Gamma )}) > 1 ={ \underline{\zeta }}_{2}({u}_{1}^{(1,\Gamma )})$ , then ${g}_{1}(n) =\tilde{ {\tau }}_{1}^{-n}$.

• (d) If ${\overline{\zeta }}_{2}({u}_{1}^{(1,\Gamma )}) = 1 ={ \underline{\zeta }}_{2}({u}_{1}^{(1,\Gamma )})$ , then ${g}_{1}(n) =\tilde{ {\tau }}_{1}^{-n}$.

• (e) If ${\overline{\zeta }}_{2}({u}_{1}^{(1,\Gamma )}) = 1 >{ \underline{\zeta }}_{2}({u}_{1}^{(1,\Gamma )})$ , then ${g}_{1}(n) = n\tilde{{\tau }}_{1}^{-n}$.

Remark 8.9.

The corresponding but less complete results are obtained using moment-generating functions in Corollary 4.3 of [18].

Before proving this theorem, we present asymptotics for the marginal distribution in the diagonal direction. Let σ_d be the real solution of

$$\begin{array}{rcl} \tilde{{\gamma }}_{+}(u,u) = 1,\qquad u > 1,& & \\ \end{array}$$

which can be shown to be unique (Fig. 8.6). Because of symmetry, we assume without loss of generality that $\tilde{{\tau }}_{1} \leq \tilde{ {\tau }}_{2}$. See Fig. 8.5 for the location of this point.

Fig. 8.5

Left: ${\overline{\zeta }}_{2}({u}_{1}^{(1,\Gamma )}) > 1$ and ${\underline\zeta}_{2} (u_{1}^{(1,{\Gamma})}) = 1$; right: ${\overline{\zeta }}_{2}({u}_{1}^{(1,\Gamma )}) ={ \underline{\zeta }}_{2}({u}_{1}^{(1,\Gamma )}) = 1$

Fig. 8.6

Left: ${\sigma }_{\mathrm{d}} <\tilde{ {\tau }}_{1}$, Right: ${\sigma }_{\mathrm{d}} >\tilde{ {\tau }}_{1}$

Theorem 8.5.

Under conditions (i)–(iv), (v-a), and $\tilde{{\tau }}_{1} \leq \tilde{ {\tau }}_{2}$ , let h ₁ (n) be the exact asymptotic function given in Theorems 8.2 and 8.3; then $P({L}_{1} + {L}_{2} = n)$ has the following exact asymptotic g ₊ (n) as n →∞:

• (a) If ${\sigma }_{\mathrm{d}} <\tilde{ {\tau }}_{1}$ , then ${g}_{+}(n) = {\sigma }_{\mathrm{d}}^{-n}$.

• (b) If ${\sigma }_{\mathrm{d}} >\tilde{ {\tau }}_{1}$ , then ${g}_{+}(n) = {h}_{1}(n)$.

• (c) If ${\sigma }_{\mathrm{d}} =\tilde{ {\tau }}_{1}\neq {u}_{1}^{(1,\max )}$ , then ${g}_{+}(n) = n{\sigma }_{\mathrm{d}}^{-n}$.

• (d) If ${\sigma }_{\mathrm{d}} =\tilde{ {\tau }}_{1} = {u}_{1}^{(1,\max )} =\tilde{ {\tau }}_{2}$ , then ${g}_{+}(n) = n{\sigma }_{\mathrm{d}}^{-n}$

• (e) If ${\sigma }_{\mathrm{d}} =\tilde{ {\tau }}_{1} = {u}_{1}^{(1,\max )}\neq \tilde{{\tau }}_{2}$ , then ${g}_{+}(n) = {\sigma }_{\mathrm{d}}^{-n}$.

In what follows, we prove Theorem 8.4. The proof of Theorem 8.5 is similar, so we only outline it briefly.

Proof of Theorem 8.4. Let

$$\begin{array}{rcl} \xi (z) = (\tilde{{\gamma }}_{2}(z,1) -\tilde{ {\gamma }}_{+}(z,1))\tilde{{\varphi }}_{2}(1) + (\tilde{{\gamma }}_{0}(z,1) -\tilde{ {\gamma }}_{+}(z,1))\nu (\mathbf{0});& & \\ \end{array}$$

then (8.46) can be written as

$$\begin{array}{rcl}{ \psi }_{10}(z) = \left (1 + \frac{\tilde{{\gamma }}_{1}(z,1) - 1} {1 -\tilde{ {\gamma }}_{+}(z,1)}\right )\tilde{{\varphi }}_{1}(z) + \frac{\xi (z)} {1 -\tilde{ {\gamma }}_{+}(z,1)}.& &\end{array}$$

(8.49)

Since $\tilde{{\gamma }}_{2}(u,1) > 1,\tilde{{\gamma }}_{0}(u,1) > 1$ for u > 0 and

$$\begin{array}{rcl}{ \left. \frac{\partial } {\partial u}\tilde{{\gamma }}_{1}(u,1)\right \vert }_{u={\sigma }_{1}} < 0,\qquad {\left. \frac{\partial } {\partial u}\tilde{{\gamma }}_{+}(u,1)\right \vert }_{u={\sigma }_{+}} >0\;\mbox{ if}\ {\underline{\zeta }}_{2}({\sigma }_{+}) = 0,& & \\ \end{array}$$

where σ₁ is a positive number satisfying that $\tilde{{\gamma }}_{1}({\sigma }_{1},1) = 1$, ξ(σ₊) > 0, and ${\sigma }_{+} = {\sigma }_{1}$ implies that the prefactor of $\tilde{{\varphi }}_{1}(z)$ is positive at $z = {\sigma }_{+}$ if ${\underline{\zeta }}_{2}({\sigma }_{+}) = 0$. With these observations in mind, we prove each case.

• (a) Assume that ${\overline{\zeta }}_{2}({u}_{1}^{(1,\Gamma )}) < 1$. This occurs if and only if ${\sigma }_{+} = {\rho }_{10} <\tilde{ {\tau }}_{1}$ (see the left-hand picture of Fig. 8.4). In this case, ψ₁₀(z) must be singular at $z = {\sigma }_{+}$ because it is on the boundary of the convergence domain $\tilde{\mathcal{D}}$. Hence, it has a simple pole at $z = {\sigma }_{+}$, and therefore we have the exact geometric asymptotic.

• (b) Assume that ${\overline{\zeta }}_{2}({u}_{1}^{(1,\Gamma )}) > 1$ and ${\underline\zeta}_{2} (u_{1}^{(1,{\tau})}) \neq 1$. This case occurs if and only if ${\sigma }_{+}\neq {\rho }_{10} =\tilde{ {\tau }}_{1}$ (see the right-hand picture of Fig. 8.4). In this case, $\tilde{{\gamma }}_{1}(\tilde{{\tau }}_{1},1)\neq 1$, $\tilde{{\gamma }}_{+}(\tilde{{\tau }}_{1},1)\neq 1$, and $\tilde{{\gamma }}_{1}(\tilde{{\tau }}_{1},1) - 1$ has the same sign as $1 -\tilde{ {\gamma }}_{+}(\tilde{{\tau }}_{1},1)$. Hence, the prefactor of $\tilde{{\varphi }}_{1}(z)$ is analytic at $z =\tilde{ {\tau }}_{1}$, and the singularity of ψ₁₀(z) is determined by $\tilde{{\varphi }}_{1}(z)$. Thus, we have the same asymptotics as in Theorems 8.2 and 8.3.

• (c) Assume that ${\overline{\zeta }}_{2}({u}_{1}^{(1,\Gamma )}) > 1$ and ${\underline\zeta}_{2} (u_{1}^{(1,{\tau})}) \neq 1$ (see the left-hand figure of Fig. 8.5). In this case, $\tilde{{\gamma }}_{+}(\tilde{{\tau }}_{1},1) =\tilde{ {\gamma }}_{1}(\tilde{{\tau }}_{1},1) = 1$, and category II is impossible, and therefore, from (8.49) and Theorem 8.2, we have the exact geometric asymptotic.

• (d) Assume that ${\overline{\zeta }}_{2}({u}_{1}^{(1,\Gamma )}) = 1 ={ \underline{\zeta }}_{2}({u}_{1}^{(1,\Gamma )})$ (see the right-hand figure of Fig. 8.5). In this case, $\tilde{{\tau }}_{1} = {\sigma }_{+} = {u}_{1}^{(1,\max )}$, and therefore $\tilde{{\gamma }}_{+}(\tilde{{\tau }}_{1},1) = 1$. We need to consider two subcases, u ₁ ^(1, r) = u ₁ ^(1, max) and u ₁ ^(1, r)≠u ₁ ^(1, max). If u ₁ ^(1, r) = u ₁ ^(1, max), then $\tilde{{\gamma }}_{1}(\tilde{{\tau }}_{1},1) = 1$ and $\tilde{{\varphi }}_{1}(z) \sim {(\tilde{{\tau }}_{1} - z)}^{-\frac{1} {2} }$ by Theorem 8.2. Thus, we have ${\psi }_{10}(z) \sim {(\tilde{{\tau }}_{1} - z)}^{-1}$ due to the second term of (8.49). Otherwise, if u ₁ ^(1, r)≠u ₁ ^(1, max), then $\tilde{{\gamma }}_{1}(\tilde{{\tau }}_{1},1)\neq 1$ implies that the prefactor of $\tilde{{\varphi }}_{1}(z)$ in (8.46) has a single pole at $z =\tilde{ {\tau }}_{1}$ and that $\tilde{{\varphi }}_{1}(z) -\tilde{ {\varphi }}_{1}({u}_{1}^{(1,\max )}) \sim {(\tilde{{\tau }}_{1} - z)}^{\frac{1} {2} }$. Again, from (8.49), we have ${\psi }_{10}(z) \sim {(\tilde{{\tau }}_{1} - z)}^{-1}$. Thus, we have the exact geometric asymptotic in both cases.

• (e) Assume that ${\overline{\zeta }}_{2}({u}_{1}^{(1,\Gamma )}) = 1 >{ \underline{\zeta }}_{2}({u}_{1}^{(1,\Gamma )})$. In this case, $\tilde{{\tau }}_{1} = {\sigma }_{+} = {u}_{1}^{(1,\mathrm{r})} < {u}_{1}^{(1,\max )}$, and we must have category I or III. Since $\tilde{{\gamma }}_{+}(\tilde{{\tau }}_{1},1) = 1$, $\tilde{{\gamma }}_{1}(\tilde{{\tau }}_{1},1) > 1$, and $\tilde{{\varphi }}_{1}(z)$ has a single pole at $z =\tilde{ {\tau }}_{1}$, ψ₁₀(z) in (8.46) has a double pole at $z =\tilde{ {\tau }}_{1}$. This yields the desired asymptotic. □ 

The proof of Theorem 8.5 is more or less similar to that of P(L ₁ ≥ n). From Figs. 8.6 and 8.7, we can see how the dominant singular point is located. Since its derivation is routine, we omit the detailed proof.

Fig. 8.7

Left: ${\sigma }_{\mathrm{d}} =\tilde{ {\tau }}_{1} = {u}_{1}^{(1,\max )} =\tilde{ {\tau }}_{2}$; right: ${\sigma }_{\mathrm{d}} =\tilde{ {\tau }}_{1} = {u}_{1}^{(1,\max )}\neq \tilde{{\tau }}_{2}$

Exact Tail Asymptotics for the Arithmetic Case

Throughout this section, we assume that (v-a) does not hold. As in the section “Singularity for the Arithmetic Case,” we separately consider two cases: (B1) either (v-b) or m ₂ ⁽¹⁾ = 0 holds, and (B2) neither (v-b) nor m ₂ ⁽¹⁾ = 0 holds, according to Table 8.1. In some cases, we need: (C1) either (v-c) or m ₁ ⁽²⁾ = 0 holds, and (C2) neither (v-c) nor m ₁ ⁽²⁾ = 0 holds.

Boundary Probabilities for Arithmetic Case with (B1)

In this case, we have the following asymptotics.

Theorem 8.6.

Under conditions (i)–(iv) and (B1), if (v-a) does not hold, then for categories I and III $\tilde{{\tau }}_{1} = {u}_{1}^{(1,\Gamma )}$ , and $P({L}_{1} = n,{L}_{2} = 0)$ has the following exact asymptotic h ₂ (n). For some constant b ∈ [−1,1]

$$\begin{array}{rcl}{ h}_{2}(n) = \left \{\begin{array}{ll} \tilde{{\tau }}_{1}^{-n},\quad &{u}_{1}^{(1,\Gamma )}\not ={u}_{1}^{(1,\max )}, \\ {n}^{-\frac{1} {2} }\tilde{{\tau }}_{1}^{-n},\quad &{u}_{1}^{(1,\Gamma )} = {u}_{1}^{(1,\max )} = {u}_{1}^{(1,\mathrm{r})}, \\ {n}^{-\frac{3} {2} }\left (1 + b{(-1)}^{n}\right )\tilde{{\tau }}_{1}^{-n},\quad &{u}_{1}^{(1,\Gamma )} = {u}_{1}^{(1,\max )}\neq {u}_{1}^{(1,\mathrm{r})}. \end{array} \right.& &\end{array}$$

(8.50)

By symmetry, the corresponding results are also obtained for $P({L}_{1} = 0,{L}_{2} = n)$ for categories I and II.

Theorem 8.7.

Under conditions (i)–(iv) and (B1), if (v-a) does not hold, then, for category II, $\tilde{{\tau }}_{1} ={ \underline{\zeta }}_{2}(\tilde{{\tau }}_{2})$, $\tilde{{\tau }}_{2} = {u}_{2}^{(2,\mathrm{r})}$ , and $P({L}_{1} = n,{L}_{2} = 0)$ has the following exact asymptotic h ₂ (n). For some constant b ∈ [−1,1]

$$\begin{array}{rcl}{ h}_{2}(n) = \left \{\begin{array}{ll} \tilde{{\tau }}_{1}^{-n},\quad &\tilde{{\tau }}_{1} < {u}_{1}^{(1,\Gamma )}\mbox{ or } \\ &\tilde{{\tau }}_{1} = {u}_{1}^{(1,\Gamma )} = {u}_{1}^{(1,\max )} = {u}_{1}^{(1,\mathrm{r})}, \\ n\tilde{{\tau }}_{1}^{-n},\quad &\tilde{{\tau }}_{1} = {u}_{1}^{(1,\Gamma )}\not ={u}_{1}^{(1,\max )}, \\ {n}^{-\frac{1} {2} }\tilde{{\tau }}_{1}^{-n},\; &\tilde{{\tau }}_{1} = {u}_{1}^{(1,\Gamma )} = {u}_{1}^{(1,\max )}\neq {u}_{1}^{(1,\mathrm{r})}, \\ &\mbox{\it and (C1) holds}. \\ {n}^{-\frac{1} {2} }(1 + b{(-1)}^{n})\tilde{{\tau }}_{1}^{-n},\;&\tilde{{\tau }}_{1} = {u}_{1}^{(1,\Gamma )} = {u}_{1}^{(1,\max )}\neq {u}_{1}^{(1,\mathrm{r})}, \\ &\mbox{\it and (C2) holds}.\\ \end{array} \right.& &\end{array}$$

(8.51)

By symmetry, the corresponding results are also obtained for $P({L}_{1} = 0,{L}_{2} = n)$ for category III.

Remark 8.10.

As we will see in the proofs of these theorems, the asymptotics can be refined for those with the same geometric decay term $\tilde{{\tau }}_{1}^{-n}$. There is no difficulty in finding them, but they are cumbersome because we need additional cases. Thus, we omit their details.

Remark 8.11.

One may wonder whether b =  ± 1 can occur in Theorems 8.6 and 8.7. If this is the case, then the tail asymptotics are purely periodic. Closely look at the coefficients of the asymptotic expansion of the terms in (8.37); it is unlikely to occur because $\vert \tilde{{\varphi }}_{2}(-{\underline{\zeta }}_{2}(\tilde{{\tau }}_{1}))\vert <\tilde{ {\varphi }}_{2}({\underline{\zeta }}_{2}(\tilde{{\tau }}_{1}))$. Thus, we conjecture that | b |  < 1 is always the case.

By Table 8.1, $\tilde{{\varphi }}_{1}(z)$ may be singular at $z = -\tilde{{\tau }}_{1}$ on $\vert z\vert =\tilde{ {\tau }}_{1}$. On the other hand, $\tilde{{\varphi }}_{1}(z)$ has the same singularity at $z =\tilde{ {\tau }}_{1}$ as in the nonarithmetic case, so we can only focus on the singularity at $z = -\tilde{{\tau }}_{1}$. We note that $z = -{u}_{1}^{(1,\mathrm{r})}$ cannot be the solution of (8.19) under the assumptions of Theorems 8.6 and 8.7. With this fact in mind, we give proofs.

Proof of Theorem 8.6. We consider the singularity of $\tilde{{\varphi }}_{1}(z)$ at $z = -\tilde{{\tau }}_{1}$ by (8.29) using the arguments in the sections “Singularity for the Arithmetic Case” and “Exact Tail Asymptotics for the Nonarithmetic Case.” Note that $\tilde{{\tau }}_{1} = {u}_{1}^{(1,\Gamma )}$ because the category is either I or III. We need to consider the following three cases.

• (8IIIa) u ₁ ^(1, Γ)≠u ₁ ^(1, max): This case is equivalent to u ₁ ^(1, Γ) < u ₁ ^(1, max), and it follows from (8.29) that $\tilde{{\varphi }}_{1}(z)$ is analytic at $z = -{u}_{1}^{(1,\mathrm{r})}$. Hence, there is no singularity contribution by $z = -{u}_{1}^{(1,\mathrm{r})}$.

• (8IIIb) u ₁ ^(1, Γ) = u ₁ ^(1, max), u ₁ ^(1, r) = u ₁ ^(1, max): In this case, as z → − u ₁ ^(1, max) in such a way that $z \in \tilde{{\mathcal{G}}}_{\delta }^{+}(-{u}_{1}^{(1,\max )})$ for some δ > 0,

  $$\begin{array}{rcl} \tilde{{\varphi }}_{2}\left ({\underline{\zeta }}_{2}(z)\right ) -\tilde{ {\varphi }}_{2}\left ({\underline{\zeta }}_{2}(-{u}_{1}^{(1,\max )})\right ) \sim {\left (-{u}_{ 1}^{(1,\max )} - z\right )}^{\frac{1} {2} },& & \\ \end{array}$$

  but $1 -\tilde{ {\gamma }}_{1}(z,{\underline{\zeta }}_{2}(z))$ does not vanish at $z = -{u}_{1}^{(1,\max )}$, and therefore

  $$\begin{array}{rcl} \tilde{{\varphi }}_{1}(z) -\tilde{ {\varphi }}_{1}\left (-{u}_{1}^{(1,\max )}\right ) \sim {\left (-{u}_{ 1}^{(1,\max )} - z\right )}^{\frac{1} {2} }.& & \\ \end{array}$$

  This yields the asymptotic function ${n}^{-\frac{3} {2} }\tilde{{\tau }}_{1}^{-n}$, but this function is dominated by the slower asymptotic function ${n}^{-\frac{1} {2} }\tilde{{\tau }}_{1}^{-n}$ due to the singularity at z = u ₁ ^(1, max).

• (8IIIc) u ₁ ^(1, Γ) = u ₁ ^(1, max), u ₁ ^(1, r) ≠ u ₁ ^(1, max): In this case, the solution of (8.19) has no essential role, so $\tilde{{\varphi }}_{1}(z)$ has the same analytic behavior at $z = -{u}_{1}^{(1,\max )}$ as at z = u ₁ ^(1, max) in (8IIc) in the proof of Theorem 8.2.

Thus, combining with the asymptotics in Theorem 8.2, we complete the proof. □ 

Proof of Theorem 8.7. Because of category II, ${\tau }_{2} ={ \underline{\zeta }}_{2}(\tilde{{\tau }}_{1})$, and therefore ${\underline{\zeta }}_{2}(-\tilde{{\tau }}_{1}) = -{\underline{\zeta }}_{2}(\tilde{{\tau }}_{1}) = -\tilde{{\tau }}_{2}$ by the assumption that (v-a) does not hold. We consider the singularity at $z = -\tilde{{\tau }}_{1}$ for the following cases with this in mind.

• (8IIIa’) $\tilde{{\tau }}_{1} < {u}_{1}^{(1,\Gamma )}$: This case is included in (8Ic’-2). Hence, if (C1) holds, then $\tilde{{\varphi }}_{2}({\underline{\zeta }}_{2}(z))$, and therefore $\tilde{{\varphi }}_{1}(z)$ are analytic at $z = -{u}_{1}^{(1,\mathrm{r})}$. Otherwise, if (C2) holds, then $\tilde{{\varphi }}_{2}({\underline{\zeta }}_{2}(z))$ has a simple pole at $z = -{u}_{1}^{(1,\mathrm{r})}$. However, in (8.29), $\tilde{{\varphi }}_{2}({\underline{\zeta }}_{2}(z))$ has the prefactor $\tilde{{\gamma }}_{2}(z,{\underline{\zeta }}_{2}(z)) - 1$, which vanishes at $z = -{u}_{1}^{(1,\mathrm{r})}$ because of (C2). Hence, the pole of $\tilde{{\varphi }}_{2}({\underline{\zeta }}_{2}(z))$ is cancelled, and therefore $\tilde{{\varphi }}_{1}(z)$ is analytic at $z = -{u}_{1}^{(1,\mathrm{r})}$. Thus, neither case has a contribution by $z = -{u}_{1}^{(1,\mathrm{r})}$.

• (8IIIb’) $\tilde{{\tau }}_{1} = {u}_{1}^{(1,\Gamma )}\neq {u}_{1}^{(1,\max )}$: In this case, $\tilde{{\tau }}_{1} = {u}_{1}^{(1,\mathrm{r})}$. If (C2) holds, then $\tilde{{\varphi }}_{2}(z)$ has a simple pole at $z = -\tilde{{\tau }}_{2}$, and therefore, as in (8IIIb’-3-1),

  $$\begin{array}{rcl} \tilde{{\varphi }}_{2}\left ({\underline{\zeta }}_{2}(z)\right ) \sim {\left (-{u}_{1}^{(1,\max )} - z\right )}^{-\frac{1} {2} },& & \\ \end{array}$$

  but (8IIb’-3-2) is not the case, and therefore this yields the asymptotic function ${n}^{-\frac{1} {2} }\tilde{{\tau }}_{1}^{-n}$. However, this asymptotic term is again dominated by $\tilde{{\tau }}_{1}^{-n}$ due to the singularity at z = u ₁ ^(1, max). On the other hand, if (C1) holds, then there is no singularity contribution by $z = -\tilde{{\tau }}_{1}$. Hence, we have the same asymptotics as in the corresponding case of Theorem 8.3.

• (8IIIc’) $\tilde{{\tau }}_{1} = {u}_{1}^{(1,\Gamma )} = {u}_{1}^{(1,\max )}$: This is the case of (8c’-3). As we discussed there, if (C2) holds, then $\tilde{{\varphi }}_{2}({\underline{\zeta }}_{2}(z)) \sim {(-{u}_{1}^{(1,\max )} - z)}^{-\frac{1} {2} }$ around $z = -{u}_{1}^{(1,\max )}$. Because of (B1), there is no other singularity contribution in (8.29), and therefore we also have $\tilde{{\varphi }}_{1}(z) \sim {(-{u}_{1}^{(1,\max )} - z)}^{-\frac{1} {2} }$ around $z = -{u}_{1}^{(1,\max )}$. This results in the asymptotic ${n}^{-\frac{1} {2} }\tilde{{\tau }}_{1}^{-n}$. On the other hand, if (C1) holds, we similarly have $\tilde{{\varphi }}_{1}(z) -\tilde{ {\varphi }}_{1}(-{u}_{1}^{(1,\max )}) \sim {(-{u}_{1}^{(1,\max )} - z)}^{\frac{1} {2} }$. This implies the asymptotic ${n}^{-\frac{3} {2} }\tilde{{\tau }}_{1}^{-n}$. To combine this with the corresponding asymptotics obtained in Theorem 8.3, we consider two subcases.

  • (8IIIc’-1) u ₁ ^(1, max) = u ₁ ^(1, r): In this case, the asymptotics caused by $z =\tilde{ {\tau }}_{1}$ is $n\tilde{{\tau }}_{1}^{-n}$, and therefore the asymptotic due to $z = -{u}_{1}^{(1,\max )}$ is ignorable.

  • (8IIIc’-2) u ₁ ^(1, max)≠u ₁ ^(1, r): In this case, the asymptotic caused by $z =\tilde{ {\tau }}_{1}$ is ${n}^{-\frac{1} {2} }\tilde{{\tau }}_{1}^{-n}$. Hence, we have two different cases. If (C1) holds, then the contribution by $z = -\tilde{{\tau }}_{1}$ is ignorable. Otherwise, if (C2) holds, then we have an additional asymptotic term: ${(-1)}^{n}{n}^{-\frac{1} {2} }\tilde{{\tau }}_{1}^{-n}$.

Thus, the proof is completed. □ 

Boundary Probabilities for Arithmetic Case with (B2)

We next consider case (B2). As noted in the section “Singularity for the Arithmetic Case,” in this case, $\tilde{{\varphi }}_{1}(z)$ is singular at z =  ± u ₁ ^(1, r), and both singular points have essentially the same properties. Thus, we have the following theorems.

Theorem 8.8.

Under conditions (i)–(iv) and (B2), if (v-a) does not hold, then for categories I and III, $\tilde{{\tau }}_{1} = {u}_{1}^{(1,\Gamma )}$ , and $P({L}_{1} = n,{L}_{2} = 0)$ has the following exact asymptotic h ₃ (n). For some constants b _i ∈ [−1,1] for i = 1,2,3

$$\begin{array}{rcl}{ h}_{3}(n) = \left \{\begin{array}{ll} (1 + {b}_{1}{(-1)}^{n})\tilde{{\tau }}_{1}^{-n},\quad &{u}_{1}^{(1,\Gamma )}\not ={u}_{1}^{(1,\max )}, \\ {n}^{-\frac{1} {2} }(1 + {b}_{2}{(-1)}^{n})\tilde{{\tau }}_{1}^{-n},\quad &{u}_{1}^{(1,\Gamma )} = {u}_{1}^{(1,\max )} = {u}_{1}^{(1,\mathrm{r})}, \\ {n}^{-\frac{3} {2} }(1 + {b}_{3}{(-1)}^{n})\tilde{{\tau }}_{1}^{-n},\quad &{u}_{1}^{(1,\Gamma )} = {u}_{1}^{(1,\max )}\neq {u}_{1}^{(1,\mathrm{r})}. \end{array} \right.& &\end{array}$$

(8.52)

By symmetry, the corresponding results are also obtained for $P({L}_{1} = 0,{L}_{2} = n)$ for categories I and II.

Theorem 8.9.

Under conditions (i)–(iv) and (B2), if (v-a) does not hold, then, for category II, $\tilde{{\tau }}_{2} = {u}_{2}^{(2,\mathrm{r})}$ , and $P({L}_{1} = n,{L}_{2} = 0)$ has the following exact asymptotic h ₃ (n). For some constants b _i ∈ [−1,1] for i = 1,2,3

$$\begin{array}{rcl}{ h}_{3}(n) = \left \{\begin{array}{ll} (1 + {b}_{1}{(-1)}^{n})\tilde{{\tau }}_{1}^{-n},\quad &\tilde{{\tau }}_{1} < {u}_{1}^{(1,\Gamma )}\mbox{ or } \\ &\tilde{{\tau }}_{1} = {u}_{1}^{(1,\Gamma )} = {u}_{1}^{(1,\max )} = {u}_{1}^{(1,\mathrm{r})}, \\ n(1 + {b}_{2}{(-1)}^{n})\tilde{{\tau }}_{1}^{-n},\quad &\tilde{{\tau }}_{1} = {u}_{1}^{(1,\Gamma )}\not ={u}_{1}^{(1,\max )}, \\ {n}^{-\frac{1} {2} }(1 + {b}_{3}{(-1)}^{n})\tilde{{\tau }}_{1}^{-n},\;&\tilde{{\tau }}_{1} = {u}_{1}^{(1,\Gamma )} = {u}_{1}^{(1,\max )}\neq {u}_{1}^{(1,\mathrm{r})}. \end{array} \right.& &\end{array}$$

(8.53)

By symmetry, the corresponding results are also obtained for $P({L}_{1} = 0,{L}_{2} = n)$ for categories III.

Marginal Distributions for Arithmetic Case

Under the arithmetic condition that (v-a) does not hold, we consider the tail asymptotics of the marginal distributions. Basically, the results are the same as in Theorems 8.4 and 8.5, in which Theorems 8.2 and 8.3 should be replaced by Theorems 8.6 and 8.7 for case (B1) and Theorems 8.8 and 8.9 for case (B2). Thus, we omit their details.

Application to a Network with Simultaneous Arrivals

In this section, we apply the asymptotic results to a queueing network with two nodes numbered 1 and 2. Assume that customers simultaneously arrive at both nodes from the outside subject to the Poisson process at the rate λ. For i = 1, 2, service times at node i are independent and identically distributed with the exponential distribution with mean μ _i ^− 1. Customers who have finished their services at node 1 go to node 2 with probability p. Similarly, customers departing from queue 2 go to queue 1 with probability q. This routing is independent of everything else. Customers what are not routed to the other queue leave the network. We refer to this queueing model as a two-node Jackson network with simultaneous arrival.

Obviously, this network is stable, that is, it has a stationary distribution, if and only if

$$\begin{array}{rcl} \frac{\lambda (1 + q)} {1 - pq} < {\mu }_{1},\qquad \frac{\lambda (1 + p)} {1 - pq} < {\mu }_{2}.& &\end{array}$$

(8.54)

This fact can also be checked by stability condition (iv).

We are interested in how the tail asymptotics of the stationary distribution of this network are changed. If $p = q = 0$, this model is studied in [8, 9]. As we will see subsequently, this model can be described by a double QBD process, and therefore we know the solutions to the tail asymptotic problem. However, this does not mean that the solutions are analytically tractable. Thus, we will consider what kind of difficulty arises in applications of our tail asymptotic results.

Let L _i (t) be the number of customers at node i at time t. It is easy to see that {(L ₁(t), L ₂(t)); t ∈ ℝ ₊} is a continuous-time Markov chain. Because the transition rates of this Markov chain are uniformly bounded, we can construct a discrete-time Markov chain given by uniformization, which has the same stationary distribution. We denote this discrete-time Markov chain by $\{{\mathbf{L}}_{n} = ({L}_{1\mathcal{l}},{L}_{2\mathcal{l}});\mathcal{l} \in {\mathbb{Z}}_{+}\}$, where it is assumed without loss of generality that

$$\begin{array}{rcl} \lambda + {\mu }_{1} + {\mu }_{2} = 1.& & \\ \end{array}$$

Obviously, $\{{\mathbf{L}}_{n};\mathcal{l} \in {\mathbb{Z}}_{+}\}$ is a double QBD process. We denote a random vector subject to the stationary distribution of this process by $\mathbf{L} \equiv ({L}_{1},{L}_{2})$, as we did in the section “Double QBD Process and the Convergence Domain.”

To apply our asymptotic results, we first compute generating functions. For $\mathbf{u} = ({u}_{1},{u}_{2}) \in {\mathbb{R}}^{2}$

$$\begin{array}{rcl} & & \quad \tilde{{\gamma }}_{+}(\mathbf{u})=\lambda {u}_{1}{u}_{2}+{\mu }_{1}p{u}_{1}^{-1}{u}_{ 2}+{\mu }_{2}q{u}_{1}{u}_{2}^{-1}+{\mu }_{ 1}(1-p){u}_{1}^{-1}+{\mu }_{ 2}(1-q){u}_{2}^{-1},\quad \end{array}$$

(8.55)

$$\begin{array}{rcl} & & \quad \tilde{{\gamma }}_{1}(\mathbf{u}) = \lambda {u}_{1}{u}_{2} + {\mu }_{1}p{u}_{1}^{-1}{u}_{ 2} + {\mu }_{1}(1 - p){u}_{1}^{-1} + {\mu }_{ 2},\quad \end{array}$$

(8.56)

$$\begin{array}{rcl} & & \quad \tilde{{\gamma }}_{2}(\mathbf{u}) = \lambda {u}_{1}{u}_{2} + {\mu }_{2}q{u}_{1}{u}_{2}^{-1} + {\mu }_{ 2}(1 - q){u}_{2}^{-1} + {\mu }_{ 1}.\qquad \end{array}$$

(8.57)

We next find the extreme point ${\mathbf{u}}^{(1,\mathrm{r})} = ({u}_{1}^{(1,\mathrm{r})},{u}_{2}^{(1,\mathrm{r})})$. This is obtained as the solution to the equations

$$\begin{array}{rcl} \tilde{{\gamma }}_{+}(\mathbf{u}) =\tilde{ {\gamma }}_{1}(\mathbf{u}) = 1.& & \\ \end{array}$$

Applying (8.55) and (8.56) to the first equation we have

$$\begin{array}{rcl}{ u}_{2} = {u}_{1}q + (1 - q).& &\end{array}$$

(8.58)

Substituting (8.58) into $\tilde{{\gamma }}_{1}(\mathbf{u}) = 1$ we have

$$\begin{array}{rcl} \lambda {u}_{1}^{2}({u}_{ 1}q + 1 - q) + {\mu }_{1}p({u}_{1}q + 1 - q) + {\mu }_{1}(1 - p) + {\mu }_{2}{u}_{1} = {u}_{1}.& & \\ \end{array}$$

Assume that q > 0. Then u ₁ has the following solutions:

$$\begin{array}{rcl}{ u}_{1} = 1, \frac{-\lambda \pm \sqrt{{\lambda }^{2 } + 4\lambda q{\mu }_{1 } (1 - pq)}} {2\lambda q}.& & \\ \end{array}$$

We are only interested in the solution u ₁ > 1, which must be u ₁ ^(1, r), that is,

$$\begin{array}{rcl}{ u}_{1}^{(1,\mathrm{r})} = \frac{-\lambda + \sqrt{{\lambda }^{2 } + 4\lambda q{\mu }_{1 } (1 - pq)}} {2\lambda q}.& &\end{array}$$

(8.59)

We next consider the maximal point ${\mathbf{u}}^{(1,\max )}$ of $\tilde{\gamma }(\mathbf{u}) = 1$. This can be obtained to solve the equations

$$\begin{array}{rcl} \tilde{{\gamma }}_{+}(\mathbf{u}) = 1,\quad \frac{\mathrm{d}{u}_{1}} {\mathrm{d}{u}_{2}} = 0.& & \\ \end{array}$$

These equations are equivalent to

$$\begin{array}{rcl} & & \lambda {u}_{1} + {\mu }_{1}p{u}_{1}^{-1} - {\mu }_{ 2}q{u}_{1}{u}_{2}^{-2} - {\mu }_{ 2}(1 - q){u}_{2}^{-2} = 0,\end{array}$$

(8.60)

$$\begin{array}{rcl} & & \lambda {u}_{1}{u}_{2} + {\mu }_{1}p{u}_{1}^{-1}{u}_{ 2} + {\mu }_{2}q{u}_{1}{u}_{2}^{-1} + {\mu }_{ 1}(1 - p){u}_{1}^{-1} + {\mu }_{ 2}(1 - q){u}_{2}^{-1} = 1.\end{array}$$

(8.61)

Theoretically we know that these equations have two solutions such that $\mathbf{u} > \mathbf{0}$, which must be ${\mathbf{u}}^{(1,\mathrm{min})}$ and ${\mathbf{u}}^{(1,\max )}$. We can numerically obtain them, but their analytic expressions are not easy to obtain. Furthermore, even if they are obtained, they would be analytically intractable.

To circumvent this difficulty, we propose to draw figures. Today we have at our disposal excellent software such as Mathematica to draw two-dimensional figures. Then we can manipulate figures and could discover how modeling parameters change the tail asymptotics. This is essentially the same as numerical computations. However, figures are more informative to see how changes occur (see, e.g., Fig. 8.8).

Fig. 8.8

Effect of the arrival rate: λ is changed from 1 to 1. 2 and 1. 5 (thicker curves), while μ₁ = 5, μ₂ = 4, p = 0. 25, q = 0. 4 are unchanged

We finally consider a simpler case to find analytically tractable results. Assume that q = 0 but p > 0. q = 0 implies that

$$\begin{array}{rcl}{ \mathbf{u}}^{(1,\mathrm{r})} = ({\rho }_{ 1}^{-1},1),& & \\ \end{array}$$

where ${\rho }_{1} = \frac{{\lambda }_{1}} {{\mu }_{1}}$. Obviously, ρ₁ must be the decay rate of P(L ₁ = n). This can be also verified by Theorem 8.4. However, it may not be the decay rate of $P({L}_{1} = n,{L}_{2} = 0)$. In fact, we can derive

$$\begin{array}{rcl}{ \left.\frac{\mathrm{d}{u}_{1}} {\mathrm{d}{u}_{2}}\right \vert }_{\mathbf{u}={\mathbf{u}}^{(1,\mathrm{r})}} = \frac{{\mu }_{2} - ({\mu }_{1} + \lambda p)} {\lambda (1 - {\rho }_{1}^{-1})} & & \\ \end{array}$$

on the curve $\tilde{{\gamma }}_{+}(\mathbf{u}) = 1$. Hence, u ₁ ^(1, Γ) = u ₁ ^(1, r) if and only if

$$\begin{array}{rcl}{ \mu }_{2} \geq {\mu }_{1} + \lambda {p}_{1}.& &\end{array}$$

(8.62)

Thus, if (8.62) holds, then $P({L}_{1} = n,{L}_{2} = 0)$ has an exact geometric asymptotic. Otherwise, we have, by Theorem 8.2,

$$ \begin{array}{rcl} {\lim \limits_{n\rightarrow \infty }}{n}^{-\frac{3} {2} }{({u}_{1}^{(1,\max )})}^{-n}P({L}_{1} = n,{L}_{2} = 0) = b.& &\end{array}$$

(8.63)

We can see that ρ₁ ^− 1 < u ₁ ^(1, max), but u ₁ ^(1, max) is only numerically obtained by solving (8.60) and (8.61).

Concluding Remarks

We derived the exact asymptotics for a stationary distribution applying the analytic function method based on the convergence domain. We here discuss which problems can be studied by this method and what is needed to develop it further.

Technical issue.:

In the analytic function method, a key ingredient is that the function ${\underline\zeta}_{2}(z)$ is analytic and suitably bounded for an appropriate region, as we showed in Lemma 8.8. For this, we use the fact that ${\underline\zeta}_{2}(z)$ is the solution of a quadratic equation, which is equivalent for the random walk to be skip free in the interior of the quadrant. The quadratic equation (or polynomial equation in general) is also a key for the alternative approach based on an analytic extension on a Riemann surface. If the random walk is not skip free, then it would be harder to get a right analytic function. However, the non-skip-free case is also interesting. Thus, it is challenging to overcome this difficulty. A completely different approach might be needed here.

Probabilistic interpretation.:

We employed a purely analytic method and gave no stochastic interpretations except a few, although the asymptotic results are stochastic. However, probabilistic interpretations may be helpful. For example, one might wonder what the probabilistic meanings of the function ${\underline\zeta}_{2}$ and (8.29) are. We believe there should be something here. If sound meanings are provided, then we may better explain Lemma 8.8 and may resolve the technical issues discussed previously.

Modeling extensions.:

We think the present approach is applicable to a higher-dimensional model as well as a generalized reflecting random walk proposed in [19] as long as the skip-free assumption is satisfied. One might also consider relaxing the irreducibility condition on the random walk in the interior of the quadrant. However, this is essentially equivalent to reducing the dimension, so there should be no difficulty in considering it. Another extension is to modulate the double QBD process or multidimensional reflecting random walk in general by a background Markov chain. The tail asymptotic problem becomes harder, but there should be a way to use the present analytic function approach at least for the two-dimensional case with finitely many background states. Related discussions can be found in [19].

Applicability.:

As we saw in the section “Application to a Network with Simultaneous Arrivals,” analytic results on the tail asymptotics may not be easy to apply to each specific application because they are not analytically tractable. To fill this gap between theory and application, we have proposed using geometric interpretations instead of analytic formulas. However, this is currently more or less like having numerical tables. We should here make clear what we want to do using tail asymptotics. Once a problem is set up, we might consider solving it using geometric interpretations. There would probably be a systematic way to do this that did not depend on a specific problem. This is also challenging.

Appendix

Proof of Lemma 8.6

Note that u ² D ₂(u) is a polynomial of order 2 at least and order 4 at most. For k = 1, 3, let c _k be the coefficients of u ^k in the polynomial u ² D ₂(u). Then,

$$\begin{array}{rcl} & & {c}_{1} = -2(1 - {p}_{00}){p}_{(-1)0} - 4({p}_{(-1)(-1)}{p}_{01} + {p}_{(-1)1}{p}_{0(-1)}) \leq 0, \\ & & {c}_{3} = -2(1 - {p}_{00}){p}_{10} - 4({p}_{1(-1)}{p}_{01} + {p}_{11}{p}_{0(-1)}) \leq 0. \end{array}$$

Hence, if both u ₁ ^(1, max) and − u ₁ ^(1, max) are the solutions of u ² D ₂(u) = 0, then

$$\begin{array}{rcl} 2({c}_{1}{u}_{1}^{(1,\max )} + {c}_{ 3}{({u}_{1}^{(1,\max )})}^{3}) = {({u}_{ 1}^{(1,\max )})}^{2}({D}_{ 2}({u}_{1}^{(1,\max )}) - {D}_{ 2}(-{u}_{1}^{(1,\max )})) = 0.& & \\ \end{array}$$

Since u ₁ ^(1, max) > 0, this holds true if and only if ${c}_{1} = {c}_{3} = 0$, which is equivalent to ${p}_{01} = {p}_{0(-1)} = {p}_{(-1)0} = {p}_{10} = 0$ because p ₀₀ = 1 is impossible. Hence, u ² D ₂(u) = 0 has the two solutions u ₁ ^(1, max) and − u ₁ ^(1, max) if and only if (v-a) does not hold. In this case, we have ${c}_{1} = {c}_{3} = 0$, which implies that u ² D ₂(u) is an even function. Since u ² D ₂(u) = 0 has only real solutions including u ₁ ^(1, max) by Lemmas 8.4 and 8.5, we complete the proof. □ 

Proof of Lemma 8.7

By (8.17), we have

$$\begin{array}{rcl} {\sum \limits_{i\in \{-1,0,1\}}}{ \sum \limits_{j\in \{-1,0,1\}}}{p}_{ij}{x}^{i}{y}^{j} = 1,\qquad {\sum \limits_{i\in \{-1,0,1\}}}{ \sum \limits_{j\in \{-1,0,1\}}}{(-1)}^{i+j}{p}_{ ij}{x}^{i}{y}^{j} = 1.& & \\ \end{array}$$

Subtracting both sides of these equations we have

$$\begin{array}{rcl}{ p}_{10}x + {p}_{01}y + {p}_{0(-1)}{y}^{-1} + {p}_{ (-1)0}{x}^{-1} = 0.& & \\ \end{array}$$

Since x, y are positive, this equation holds true if and only if

$$\begin{array}{rcl}{ p}_{10} = {p}_{01} = {p}_{0(-1)} = {p}_{(-1)0} = 0.& & \\ \end{array}$$

This is the condition that (v-a) does not hold. □