Keywords

Introduction

The quality of mathematical thinking of coming generations has been a serious concern of many educators for a number of years. Since the middle of the twentieth century, mathematicians have emphasised (as in the rest of this chapter) the essential meaning of problem solving , reasoning, and the construction of communicative tools for the understanding of the nature of mathematical thought (see, for example Polya 1945; Freudenthal 1973; Lakatos 1976; Sfard 2008, to name just a few). In mathematics education in schools all over the world, however, there is nevertheless a strong emphasis on the mastery of number operations and on the formation of skills in faultless arithmetic .

Indeed, important changes have taken place in mathematics classrooms in the past few decades. Context-based problem solving has become a part of regular classroom practice for developing mathematical proficiency in pupils, but still the dominant focus is set on instruction for skill acquisition, avoiding serious efforts in promoting pupils’ problem solving (Kolovou 2011) and deep conceptual understanding (Bruin-Muurling 2010). Considering the worldwide interest in accountability of schools, effective education, and skill mastery, there is no reason as yet to stop being concerned. Skill acquisition is still the main criterion in the testing of children’s mathematical development , while deep conceptual understanding, argumentation, and creative problem solving more and more seem to be reserved for the gifted pupils.

Many studies, however, show that the concepts and approaches for promoting children’s abilities of dealing in mathematically consistent ways with reality are not exhausted (see, for example Sfard 2008). Particularly, studies on young children’s thinking and learning give reasons to assume that “mathematising” (organising experience for mathematical purposes) may be rooted in early childhood education (see, for example Pound 1999). Picking up on young children’s abilities and assisting them in their ways of dealing with number (Munn 1998), emergent notions of quantity (Carruthers and Worthington 2006), drawing (van Oers 1994, 2004), and collective reasoning (Krummheuer 2011) may provide good starting points for gradual improvements of children’s mathematising abilities, beyond mere technically operating with numbers and number symbols.

In the present chapter, I will unfold an approach to early mathematics education based on a theory of playful activities , drawing from the perspective of cultural-historical activity theory (CHAT/Vygotskij) . From this perspective, I will demonstrate how direct instruction of mathematical operations can be reconciled with productive mathematical problem solving . Starting out from the CHAT, I will argue that productive mathematising is to be conceived as an essentially playful activity that has its roots in young children’s playful participation in cultural practices . Within this context, instruction of useful mathematical operations can be taught and practised, as long as it can be meaningfully embedded in children’s activity. The approach that will be presented here is becoming increasingly popular in Dutch primary schools that have adopted the Vygotskian concept of Developmental Education (see van Oers 2012a).

What is Productive Mathematising?

The notion of “mathematising” has been introduced by Freudenthal (1973) for referring to mathematics as a human activity of organising a field (be it conceptual or material) into a structure that is accessible for mathematical refinement (Freudenthal 1973, p. 133). Organising a field of mathematical objects like circles, ellipses, parabola, etc. into the category of conic sections or quadratic functions is an example of mathematising , as well as the recognition of the growth of a plant in early childhood classrooms as a measurement problem. Mathematising is the activity of producing structured objects that allow further elaborations in mathematical terms through problem solving and (collective) reasoning/argumentation. It is the type of dialogic, inquisitive, and productive thinking that was once described as mathematical discovery by Lakatos (1976). Hence, as an expression, “productive mathematising” is basically pleonastic, but it is a useful way to contrast this mathematical activity with the re-productive activity of applying mathematical rules or operations for the solution of instructional tasks . By itself, there is nothing wrong, though, with reproduction in the context of mathematising (as, for example, anyone proficient in mathematics does, when immediately applying specific knowledge , e.g. the square root of, say, 81, in solving a specific problem or doing a specific task). However, reducing mathematics education to the mastery of these types of reproductions is like cutting the heart out of mathematics as mathematising.

In terms of the CHAT, mathematising can be further specified as a complex of specific human tool-mediated actions driven by a motive to know the world and organised by a series of (emergent) goals. Developing mathematical thinking from this perspective can be conceived of as a process of producing new or improved tools for the understanding and analysis of quantitative or spatial dimensions of reality that are acceptable for the mathematical community (van Oers 2001). It would not make much sense here to further characterise mathematising as an ongoing activity by specifying its goals and tools , as these latter elements always depend on the specific type of problem a person tries to solve. Rather, on a more general level, it is possible to characterise the format of the activity of mathematising. A format of activity refers to the general characteristics of the way an activity is carried out (see van Oers 2012b)Footnote 1. First of all a cultural activity can be more or less strictly rule-driven, by object-bound rules, technical rules, and/or social rules. The number and nature of the rules determine the nature of the activity to a great extent. As a matter of fact, the rules featuring in mathematising strongly depend on the type of problem a person tries to solve, and on the mathematical rules and socio-mathematical norms available in the person. However, what basically makes an activity a form of mathematising are at least the rules of intersubjectivity and consistency, and the rules that a newly constructed object should be acceptable for the mathematical community and be accessible for further mathematical elaboration. A mathematical activity that requires strict obedience to rules has a format which is different from a mathematical activity that is based on ill-defined rules that have to be interpreted and specified by the pupils. Both are basically different mathematical activities.

A second characteristic of the format of cultural activities is the level of involvement of the agent. Activity settings differ as to the conditions they provide to get actors involved. At one extreme pole, an agent can be forced to carry out a procedure of specific actions (without personal involvement, as often happens in the reproduction or recitation script of schooling); at the other extreme, the activity is carried out from an intrinsic motivation and the authentic will to achieve a specific goal. Low levels of involvement require high levels of extrinsic motivation to make and keep the process going; high levels of involvement encourage pupils to get engaged in (collaborative) problem solving , to be creative, and to endure. Characteristically, mathematising is an activity that is driven by personal engagement with a personally acknowledged query that requires creativity and endurance.

Finally, the format of human activity can be characterised by more or less degrees of freedom allowed to the actor in the choice of goals, tools , or rules. Activities without any degrees of freedom are performances like in drill, strictly sanctioned practices, or training. On the other hand, activities that require creativity and imagination by definition require at least some degrees of freedom for the actor. As a problem-solving activity, mathematising can only be successful and productive if the problem solver is allowed to act tentatively, to make mistakes, try and re-try, and feels allowed to make wild guesses.

Hence, analysing productive mathematising as a human activity leads to the picture of this activity as a goal-oriented, tool-mediated human activity that is characterised by specific mathematical rules and socio-mathematical norms, by high involvement of the agent, and by at least some degrees of freedom in the choice of rules, tools , and goals. This characterisation of the general nature of cultural activities does not preclude or contradict a further microgenetic analysis of these activities in (Leont’evian) terms of motives, actions, objects, goals, tools, and operations. As said before, such analysis would only make sense when it refers to a specific task (e.g. using a number line for estimating the position of the value 17/23). I will not pursue this type of microgenetic analyses here (how illustrative and interesting they may be), as it is not necessary to complete the general argument concerning the roots of mathematising in young children’s play .

Mathematics Learning and Play

On the basis of my previous research in early years’ classrooms, I will argue that the activity format of mathematising as described above, can be interpreted as a specimen of a more general kind of human activity called “play” . In my studies of play as a kind of human behaviour and as a context for learning, I have argued that play is basically an activity that is carried out in a specific format, i.e. as an activity that implies obeying self-acknowledged rules, requires high engagement, and allows at least some degrees of freedom (see for van Oers 2010a, 2012b). As a result, I defend the proposition that mathematising is basically a form of playful mathematics, embedded in young children’s play. In playful activities, children can encounter situations that require special attention for the quantitative of spatial dimensions of their activity (e.g. when trading money in a supermarket play); in order to deal effectively with these aspects, children need to learn new actions that can be considered mathematical from a cultural point of view. Hence, mathematics arises in the context of play through the mathematisation of children’s actions and utterances by more knowledgeable others (adults or peers). Mathematics emerges in children’s development , not as an elaboration of implicit mathematics in play, but as an attribution from outside of mathematical meanings to children’s actions or utterances (see van Oers 2012c).

The format of the traditional mathematics classroom activity is typically characterised by strict rules, little or no involvement of the pupils, and no degrees of freedom in the choice of tasks , objects, and rules or operations. Traditionally, the mathematical task prescribes which operations have to be carried out. This classroom gives little or no room for playing and mathematising as a productive activity .

Socioconstructivist and activity theory approaches to human learning emphasise the importance of the active involvement of pupils in their (mathematical) learning activities (see, for example Darling-Hammond 2008; Schoenfeld 2008; Leontev 1978). In the wake of the socioconstructivist approach to mathematics, several attempts have been made to make mathematics classrooms more engaging for children , particularly by introducing moments of play in the classroom. Popular versions of such attempts can be seen in the introduction of realistic contexts (like supermarkets) into the classroom, which require pupils to deal with trading money (addition, subtraction) But many other examples can be found: children sharing a pizza at parties (to evoke thinking about division), or all kinds of board games (to engage young children in counting), etc. No doubt, this has made the mathematics classes in primary schools more playful, but play in these cases was still just embedded in task-based classroom work within an otherwise strict classroom script that focused mainly on the mastery of operations; play functioned here merely as a stepping stone for further practising the mathematical operations outside the play contexts that initiated them.

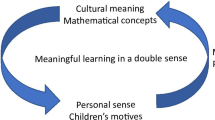
Starting out from a cultural-historical activity point of view, a new approach is developed towards a play-based curriculum that does not just allow children to play sometimes, in addition to their task-related work, but which fundamentally implements the play format in all pupils’ activities. This is essentially different from the previously described approach of integrating play and mathematics (see Fig. 8.1). In a genuine play-based curriculum, mathematising is provoked and encouraged in children as a way of dealing (collaboratively) with the quantitative and spatial dimensions of reality which surface during their participation in engaging and meaningful cultural practices. Looking for solutions to emerging problems regarding quantitative or spatial dimensions in such practices may lead to the enhancement of a child’s possibilities of participating in this practice. Guided problem solving through mathematising as well as improving (mathematical) skills through practising are functional and meaningful for children’s participation in this practice. In a play-based curriculum problem, solving and practising are not taken out of a playful activity , but remain functional parts of the playfully formatted practice, improving the participants’ abilities to take part in this practice.

Fig. 8.1
figure 1

Different relationships between mathematics and play. a Mathematics classrooms that follow the direct-instruction script. b Mathematics classrooms that follow a problem-solving script

Full size image

Figure 8.1 summarises the major difference between (a) mathematics classrooms that follow the direct-instruction script (with incidentally embedded games), evoking at best reproductive mathematising, and (b) mathematics classrooms that follow a problem-solving script, requiring productive mathematising, interrupted by dispersed moments of meaningful, and functional instructions.

Mathematics Learning Within Play?

When participating playfully in an engaging practice (like a restaurant, a construction site, gardener’s practice, a post office, etc.), young children encounter numerous problems that demand a mathematical approach (e.g. paying three stamps in the post office, finding and comparing the dimensions of a building, figuring out the number of chocolates needed for a party, etc). In the play-based curriculum, children work out solutions to these problems collaboratively under the guidance of the teacher or a more knowledgeable peer. There are probably different dimensions of activity involved in the emergence of mathematising from playful activities . In this chapter, I will elaborate on two dimensions that we have found in our research in the past decade.

Learning to Communicate on Mathematical Aspects of Reality

An obvious feature of children’s behaviour when facing a (mathematical) problem in their play is their wish to suggest solutions, to try out different solutions, to discuss different solutions, in short: to communicate about possible solutions. The first thing that children need in cases, where they face a problem regarding quantitative or spatial aspects of their play, is a proper language to communicate about number and spatial positions or relations. Learning to communicate mathematically is an important process to stimulate in children’s play , as it is the main prerequisite for the development of mathematising in play and as play. Many researchers have already discussed the importance of language for the development of mathematical thinking (e.g. Pimm 1987, 1995), and have been able to demonstrate empirically that relationships do exist between mathematical thinking and narrative competence (see Burton 2003; Krummheuer 2011; van Houten 2011). With regard to mathematical reasoning and the construction of a mathematical space for focused communication, a number of researchers have pointed at the relevance of gestures (gesticulations) as means for communication in a mathematical discourse or teaching process (see among others Bjuland et al. 2008; Yoon et al. 2011). Similar suggestions have recently been forwarded with regard to picture books as a communicative medium for the stimulation of young children’s mathematical thinking (see, for example Elia et al. 2010). Inventing or looking for symbolic means to support communication about number, number operations, or space is common practice in many play activities of young children.

In one of my classroom visits, I witnessed two 5-year-old boys’ cooperative activity of building a castle on the basis of a schematic construction plan provided by the teacher. The plan showed the floor plan of the castle and depicted the direction of the blocks and the numbers of blocks on top of each other for the reconstruction of the towers and walls of the castle (see Fig. 8.2). The teacher helped the two boys with interpreting the construction plan correctly. After that, the boys started building the castle.

Fig. 8.2
figure 2

Construction plan of a castle

Full size image

However, during the re-construction of the castle the boys ran out of blocks and had to change the teacher’s design for building a castle that looked similar to the teacher’s design. After finalising their castle, the teacher discussed it with the boys and showed her approval. She suggested that the boys should make a drawing of their castle that could help other children build such a nice castle too. The boys liked the idea. Actually, the teacher’s request put them in the position to communicate the relevant information about their castle to other children they did not even know by then.

The boys adopted the basic idea from the teacher’s construction plan, but they also had to invent new communicative tools , for their castle was not exactly like the teacher’s. From the perspective of learning to communicate about number, this was an interesting process to observe. One of the boys started of with drawing the blocks in the walls and towers in the way the teacher had done. However, he had trouble writing the number symbols. Immediately, he changed to an analogical representation indicating the number of blocks by corresponding quantities of small circles. So 4 was represented by four small circles. In this process, the boy was using a one-to-one correspondence rule, and he used it consistently. At a certain moment, he drew five circles in a wall with four blocks, but immediately crossed out one. These phenomena demonstrate that the boy was tentatively finding out appropriate ways to communicate about the numbers in the castle to inform future constructors.

This example of mathematical communication grew meaningfully out of the children’s play . Many similar examples of children’s efforts to create proper means of communication about number can be found in the work of Carruthers and Worthington (2006).

In our research programme for the study of children’s symbolisations and construction of schematic representations, we have studied processes like the one described above in many early years’ classrooms. We have evidence to conclude that children can produce much more sophisticated schematic representations of quantities and their relationships as long as it is meaningful for the children (and functional in the context of their play). The evolution of these representations with communicative purposes is a demonstration of how mathematising emerges in play on the basis of learning how to communicate about number (relationships). Mathematising in play develops as a playful activity , and may flourish with appropriate help towards playful mathematics. In an experimental study of Poland (see Poland et al. 2009), the researcher could demonstrate that engaging young (6-year-olds) children in this type of playful mathematising (particularly focusing on schematising) facilitates their transition into more formal mathematics in the early grades of primary school (ages 6 and 7).

Embedded Mathematics Teaching in the Context of Play

Involving children in mathematical communications in the context of their play activities is a powerful way of getting them involved in meaningful productive mathematising. Not every child, however, will immediately pick up the structure of mathematical operations through schematising alone, as some of them will not always immediately understand the action-regulating function of schematic representations or algorithms. In those cases, more stepwise instruction , explanation, and practice will be needed. Moreover, developing proficiency in mathematical communication also requires the development of automatised operations that can be used in problem solving regarding the mathematical objects or relations. Both for the support of slow learning pupils and for the development of automatised operations in all children , instruction may be unavoidable. The mastery of mathematical operations (i.e. reproductive mathematising) most of the time contributes to young children’s ability to participate in role play with other children (e.g. when tending the counter of a shop).

From one of our classroom observation studies, we can report examples of both cases. In an early years’ classroom (populated with pupils aged 5–7 years) a shoe shop was set up in which children were playing all kinds of shoe-shop related roles. One 6-year-old girl (who was known by the teacher to be a slow learner in maths) was highly involved in the play, and as a customer in the shop, she has bought two pairs of boots which cost € 60 each. The girl was insecure if she had enough money and said to the boy at the counter: “Wait a moment; I have to figure out, if I can pay it.” She withdrew from the scene and set herself on a small bench at some distance from the counter, but next to the teacher. The teacher, however, decided to leave her alone for a moment to give her a chance to sort it out for herself. The girl opened her purse, put all her money next to her on the bank, and started counting , but she mostly had notes (notes of 50 and 10), so there was little to count: she had to calculate by adding and subtracting how much she had to pay, and find out if she had enough money. It took her a while of fiddling around with the money, but apparently she could not solve the problem on her own. The teacher had observed her from a distance and finally decided to offer help. The teacher sat next to the girl and started a conversation about her money, but she did not immediately ask what the precise problem was. The teacher started with structuring the girl’s money in batches of 100, and showing that two times 50 is 100. With the girl, she explored different amounts of money, structured with the help of her notes of 50 and 10. Only after some examples of how to structure amounts of money with notes of 50 and 10, she addressed the girl’s real problem. With some help and instruction, the girl figures out that 60 can be composed as 50 + 10, and two times 60 can be structured as two times 50 (the girl knew this was hundred) and two notes of ten. The teacher’s instruction was useful for the girl, as it strengthened her ability to participate in the play.

In the same classroom, there was a small group of children interested in the shop’s stock of shoes. The teacher translated this interest in a role of a book-keeper who must keep an eye on the stock of shoes available in the shop. The teacher suggests that a book-keeper must be good at calculation and should keep on practising calculations. She said: “If you want to be the book-keepers, we can play the book-keeper game. It will help you to play shop play activities in a more easy way.” The children agreed and sat at the table to play the game. The teacher explained the game: there were two decks of cards (reds and greens, each with a number on it; numbers were faced down): reds are for buying shoes, greens are for selling shoes. The children understood that when you sell shoes you will earn money, but also may run out of shoes at some moment. All children are allowed 10 turns, and at each turn a child must take one card from the deck (a red or a green one). The game starts with each child drawing a red card from the deck. One child after the other may draw a card of his/her choice. They had to calculate his/her stock with the information on this card and write it down on a piece of paper as a + or a − sum. For example, one paper looked like this

5 (start quantity) − 3 − 1 + 1 + 2 + 4 − 3 etc.

The teacher was sitting at the table too, checked if it went well, that no mistakes were made; she offered help where needed for each child’s successful participation in this game. For an outsider, the game may look like a traditional instruction lesson for automatisation of the elementary operations of addition and subtraction. Actually, the children performed their actions as part of their role of a book-keeper of the shoe shop. They experienced their actions as meaningful, but basically were practising addition and abstraction as well. Although from the outside the scene may look like a playful moment in an otherwise traditional mathematics classroom , it was actually experienced by the children as an instruction and practice moment in a play activity (see again Fig. 8.1).

The bottom line of the two examples above is that a playful activity including mathematical actions does not prohibit embedded instructions as long as these contribute to the child’s interest in participating in the play as good as possible. Mathematising requires productive construction , but also instruction and practice. Each dimension can be made a meaningful part of coherent children’s play.

Fostering a Mathematising Culture in the Classroom

Is this enough for an optimal stimulation of pupils’ proficiency in mathematics? Pupils cannot keep on playing in shoe shops, restaurants, hospitals, racetracks, etc. forever. Embedding mathematising as a playful part of children’s role play turns out to be a rich context for meaningful learning. However, appropriate conditions must be created for play to evolve into new activities that can be playfully formatted. By the same token, conditions must also be created to give children the chance to learn to play the role of mathematical expert who can do mathematics as an independent practice, just for the sake of mathematics, just for his/her interest in mathematics! Finally, we want pupils to master mathematical operations and understandings as meaningful “stand alone operations”, originally rooted in everyday practices but finally winded up as independent accomplishments in the context of an emancipated mathematical discipline.

We are still in the middle of reflecting this issue and consider that it is even unsure that all pupils can or need to reach that high a level of disciplinary expertise for proficient participation in society and for their future jobs. Theorising on this topic from CHAT , we may conceive of this process of “emancipation” of mathematics from everyday practice as another specimen of the division of labour, an intrinsic potential of all cultural practices. In fact, the history of mathematics exemplifies this process, if we think about the origins of mathematics in practical geometry and music.

At this moment, we hypothesise that the formation of a new and autonomous positive mathematical attitude in pupils is an important condition for fostering the transition of functional mathematics in play into a playfully functioning mathematical discipline. Much is still to be found out on this issue, and elaborating deeply on this issue would go way beyond the scope of this chapter. In our approach to primary schools (“Developmental Education”), we contribute to this development by creating from the youngest grades (4-year-olds) a mathematical culture in classrooms, i.e. a culture in which communicating about number, spatial relations, mathematical games, and mathematical objects is accepted and positively valued (see for example van Oers, 2010b). Teachers try to contribute to such a culture by frequently asking questions like, “Are you sure?” (see van Oers 1996, 2001).

In Conclusion

Our argument winds up in claiming that mathematical thinking should start out as mathematics in play (rather than direct instruction on elementary mathematical operations), and be fostered into mathematics as play . Inventing and improving ways to communicate about number and spatial aspects of reality turns out to be a core issue in this process.

However, from our observations in classrooms involved in play, it is also clear that both creative construction and sensitive instruction are necessary elements for a developmentally productive organisation of play and the development of mathematical thinking . From an activity theory point of view, the differences between the two can be explained on the basis of varying degrees of freedom that are allowed to the actors (“players”). Both construction and instruction can be seen as attempts by an actor to execute his or her actions on the basis of personally and socially acceptable rules. In the instruction case, an actor receives the rules from teacher, textbook, or memory and carries out the actions strictly according to the prescriptions that follow from this rule. The girl from the example above re-constructs the conventional rule (with the help of the teacher) of how to sum 50 and 50 etc. She had no choice as to how to define the rules, but—importantly—she acknowledged the relevance of the rules for her ability to participate in the shoe shop play. The example of the book-keepers was similar: the players applied the rules as given, with minimal degrees of freedom (note that the degrees of freedom in this activity were at an another level of activity: which colour to choose?). In the construction case, the actor is more free to make decisions about how to regulate his or her actions, and to invent appropriate symbolic equipment for communication. But, here too, there is no absolute freedom due to the communicative function of the constructed symbols, or how to use the rules (see the example of the analogically represented one-to-one correspondence between quantity of blocks and the number of circles). The freedom here regards the choice of the rules or symbols to use for communication. It is important to emphasise at this point that in both cases, the actions were based on personally acknowledged (and meaningful) rules.

In the context of play and the embedded processes of creative construction and rule-driven instruction, it is important to take care that any embedded action (be it instruction or construction) is meaningful for the children and related to the psychological functions they are supposed to fulfil within the play activity (communication or mastery). The nature of the actions embedded in play can vary with respect to their degrees of freedom allowed, as long as the activity as a whole remains a playful activity , i.e. is based on personally acknowledged rules, is engaging, and preserves some degrees of freedom for the player.

Only to the extent that we succeed in doing this in our schools and families, and only to the extent that teachers and parents can receptively and purposefully participate in children’s play without impairing this activity as play, we may hope that we really have harvested the best from the richness of play, and have made a start with fostering autonomous critical mathematical thinking in our children.