Keywords

9.1 Introduction

Adhesively bonded joints, especially composite laminated joints, have been widely used in automotive and aerospace industry nowadays. Various kinds of failure modes have been identified in everyday use, among which delamination is the most life-limiting mechanism in bonding joint. The analysis of adhesive joint is usually based on through-thickness averages of stress and strain, then, the basic variables are the peel stress, σ, the shear stress, τ, the opening distance, w, and the shear deformation, v, of the adhesive layer. The shear loading case for adhesive joint has been studied in Nassar et al. [1], current study will focus on the peel loading case using Double Cantilever Beam (DCB) model.

The adhesively bonded joint loaded in peel has been intensively studied. Whitney [2] carried out experiments on composite joint and discussed a number of approaches for data reduction schemes, El-Zein [3] tested a composite joint in elevated temperature and proposed a theory for determining critical load, the developed model only took adherend into account, and crack tip opening was neglect. Hashemi et al. [4] analyzed some DCB composite joints using corrected beam theory, Johnson et al. [5] investigated the environmental durability of a series of bonded systems, Shindo et al. [6]experimentally and analytically investigated the cryogenic Mode I interlaminar fracture behavior and toughness of SL-E woven glass-epoxy laminate, Jyoti et al. [7] experimentally explored the effect of adhesive layer to the critical energy release rate of specimen, Xie et al. [8] discussed methodologies and techniques used for characterizing metal/epoxy interfaces, latter, Pradeep et al. [9] used the evaluation methodologies for assessing the interfacial integrity using FEA, the methodology considered the effect of adhesive properties such as Young’s modulus and thickness, however the crack tip rotation wasn’t taken into account. In contrary to the above mentioned researches, increasing number of researches (Barenblatt [10], Yang et al. [11], Andersson et al. [12] and Andersson et al. [13], Ouyang et al. [14]) used cohesive zone model (CZM) to solve the adhesively bonded joint. The CZM was critically dependent on accurate constitutive models, i.e. stress-elongation (σ-w) relation of adhesive layer, it had been proven very hard to correlate the bulk properties of adhesives with their behavior in a thin and constrained layer [15], also, a stress-elongation relation works fine for this adherend material may not work for other adherend material, hence repeated works were need to determine stress-elongation relation for other adherend material,

It’s well known that the fracture energy and morphology varies with the thickness of the adhesive layer [16], previous studies either neglect the existence of adhesive layer [2, 5, 17], or model the adhesive layer as spring [18–20], or neglect the crack tip rotation [9, 17], others using stress-elongation relation to represent the property of adhesive layer [12–14], they were suitable for modeling very thin adhesive or interfacial behavior of adhesively bonded joint, however, due to the lack of consideration about the adhesive material properties and geometry properties, the results obtained by previous were very limited to specific cases. In this study, a model is developed which takes into account of the adhesive material properties and adhesive thickness and their geometry configuration, also a novel parameter c is introduced, and it’s determined by solving a nonlinear equation, in addition, crack tip rotation is considered. Various cases were compared and discussed to verify the novel developed model. The effective of each key parameter in the model is discussed.

9.2 Analytical Model

The geometric model for the analysis is presented in Fig. 9.1. Two adherends with same size, length l, height h, and width b are bonded by an adhesive layer with one end leaving unbounded and this end is subjected to peel load P as in Fig. 9.1a. The adhesive layer has a thickness of h a , and length l-a. the coordinate is originated at the center of left end in Fig.9.1a. The free body diagram of adherend is shown in Fig. 9.1b.

Fig. 9.1
figure 1

Schematic of analysis model

Full size image

For the unbounded adherend portion, the moment is expressed as

$$ M(x) = P(l - x)\quad \quad l - a \le x \le l $$
(9.1)

For the bonded ahderend portion, the moment can be given as

$$ M(x) = P(l - x) - b\int_0^{{l - a - x}} {s\sigma (x + s)ds}\quad \quad 0 \le x \le l - a $$
(9.2)

as can be seen in Fig. 9.1b, s is a new coordinate parallels with x-axis, and originated at x.

Force equilibrium of upper adherend gives

$$ b\int_0^{{l - a}} {\sigma (x)dx = P} $$
(9.3)

where \( \sigma (x) \)is the stress distribution along the bonding interface, and it is assumed to be

$$ \sigma (x) = {\sigma_0}{e^{{c(x - l + a)}}} $$
(9.4)

where \( {\sigma_0} \) is the stress at the crack tip, and c is the material parameter.

From Eqs.9.3 and 9.4,

$$ \frac{{b{\sigma_0}}}{c}\left[ {1 - {e^{{c(a - l)}}}} \right] = P $$
(9.5)

The moment and deflection relationship of adherend can be give as

$$ w\prime \prime (x) = - \frac{{M(x)}}{{E_x^{{(1)}}I}} $$
(9.6)

where \( E_x^{{(1)}} \) is the adherend Young’s modulus in x direction. \( I \) is the Moment of Inertia.

9.2.1 Modeling of Bonded Region ( \( \bf {0 \le x \le l - a} \) )

For the upper half adhesive, the elongation in y direction is obtained as

$$ w(x) = - \frac{{{h_a}}}{2}\frac{{\sigma (x)}}{{E_y^{{(2)}}}}\quad \quad 0 \le x \le l - a $$
(9.7)

where \( E_y^{{(2)}} \) is the adhesive Young’s modulus in y direction.

First derivative of Eq. 9.7 gives

$$ w\prime (x) = - \frac{{{h_a}c}}{{2E_y^{{(2)}}}}\sigma (x)\quad \quad 0 \le x \le l - a $$
(9.8)

Substitute Eq. 9.2 into Eq. 9.6, and using Eqs. 9.4 and 9.5, one obtains,

$$ \displaystyle \frac{{\displaystyle \left( {\frac{1}{{c{e^{{c(l - a)}}}}} + \frac{{E_x^{{(1)}}I{h_a}}}{{2E_y^{{(2)}}{e^{{c(l - a)}}}}}\frac{{{c^3}}}{b}} \right){e^{{cx}}} - x + l - a - \frac{1}{c}}}{{1 - {e^{{c(a - l)}}}}} = l - x $$
(9.9)

From Eq. 9.9, c is depended on x. Following Nayfeh et al. [21], a continuum mixture format is carried out to eliminating the x-dependence by integrating both side of Eq. 9.9 from 0 to l-a, and divided by l-a, then, a nonlinear equation can be obtained from Eq. 9.9 for determining parameter c as follows

$$ \frac{1}{{{c^2}(l - a)}} + \frac{{E_x^{{(1)}}I{h_a}}}{{2E_y^2}}\frac{{{c^2}}}{{b(l - a)}} + \frac{{\displaystyle \frac{1}{2}\left( {l - a} \right) - \frac{1}{c}}}{{1 - {e^{{c(a - l)}}}}} = \frac{1}{2}\left( {l + a} \right) $$
(9.10)

Equation 9.10 can be solved by Newton–Raphson method. Theoretically, there are four solutions for this equation, but the realistic one should be real number, and not far away from 0, otherwise it will cause numerical problem.

9.2.2 Modeling of Unbounded Region ( \( \bf{l - a \le x \le l} \) )

From Eqs. 9.1 and 9.6

$$ E_x^{{(1)}}Iw\prime= \frac{1}{2}P{x^2} - Plx + {B_1} $$
(9.11)
$$ E_x^{{(1)}}Iw = \frac{1}{6}P{x^3} - \frac{1}{2}Pl{x^2} + {B_1}x + {B_2} $$
(9.12)

\( {B_1} \) and \( {B_2} \) are constant, to be determined by boundary condition. The continuity condition at \( x = l - a \) gives

$$ \frac{1}{2}P{\left( {l - a} \right)^2} - Pl\left( {l - a} \right) + {B_1} = - \frac{{E_x^{{(1)}}I{h_a}}}{{2E_y^{{(2)}}}}c{\sigma_0} $$
(9.13)
$$ \frac{1}{6}P{\left( {l - a} \right)^3} - \frac{1}{2}Pl{\left( {l - a} \right)^2} + {B_1}\left( {l - a} \right) + {B_2} = - \frac{{E_x^{{(1)}}I{h_a}}}{{2E_y^{{(2)}}}}{\sigma_0} $$
(9.14)

Equations 9.13 and 9.14 give the value of \( {B_1} \) and \( {B_2} \) as

$$ {B_1} = - \frac{{E_x^{{(1)}}I{h_a}}}{{2E_y^{{(2)}}}}c{\sigma_0} - \frac{1}{2}P{\left( {l - a} \right)^2} + Pl\left( {l - a} \right) $$
(9.15)
$$ {B_2} = - \frac{{E_x^{{(1)}}I{h_a}}}{{2E_y^{{(2)}}}}{\sigma_0}\left[ {1 - c(l - a)} \right] + \frac{1}{3}P{\left( {l - a} \right)^3} - \frac{1}{2}Pl{\left( {l - a} \right)^2} $$
(9.16)

Then, the deflection of unbounded region of adherend can be determined as

$$ \begin{array}{ccc} w = \frac{1}{{E_x^{{(1)}}I}}\left\{ {\frac{1}{6}P{x^3} - \frac{1}{2}Pl{x^2} + \left[ { - \frac{{E_x^{{(1)}}I{h_a}}}{{2E_y^2}}c{\sigma_0} - \frac{1}{2}P{{\left( {l - a} \right)}^2} + Pl\left( {l - a} \right)} \right]x} \right. \\\left.- \frac{{E_x^{{(1)}}I{h_a}}}{{2E_y^{{(2)}}}}{\sigma_0}\left[ {1 - c(l - a)} \right] + \frac{1}{3}P{{\left( {l - a} \right)}^3} - \frac{1}{2}Pl{{\left( {l - a} \right)}^2} \right\}\quad \quad l - a \le x \le l \end{array} $$
(9.17)

9.2.3 Joint Fracture Properties

The loadline deflection will be given by

$$ {w_P} = - \frac{1}{{E_x^{{(1)}}I}}\left[ {\frac{{E_x^{{(1)}}I{h_a}}}{{2E_y^{{(2)}}}}{\sigma_0}(ca + 1) + \frac{1}{3}P{l^3} + P{{(l - a)}^2}l - P{l^2}(l - a) - \frac{1}{3}P{{(l - a)}^3}} \right] $$
(9.18)

The Crack Open Displacement COD of loadline for the joint is obtained as

$$ COD = \frac{2}{{E_x^{{(1)}}I}}\left[ {\frac{{E_x^{{(1)}}I{h_a}}}{{2E_y^{{(2)}}}}{\sigma_0}(ca + 1) + \frac{1}{3}P{l^3} + P{{(l - a)}^2}l - P{l^2}(l - a) - \frac{1}{3}P{{(l - a)}^3}} \right] $$
(9.19)

and Crack Tip Opening Displacement CTOD is

$$ CTOD = \frac{{{h_a}{\sigma_0}}}{{E_y^{{(2)}}}}{ } $$
(9.20)

From Eqs. 9.5 and 9.9, the compliance of the joint can be obtained. In the determination of c, the continuum mixture theory is used, which eliminates the x-dependence of c. A closed examination finds that using the continuum mixture theory, the prediction tends to deviate from experiment, the deviation is related to crack length and joint length as (l-a)/l/k, which is called the correction factor in this paper, and k is a constant, which can be determined experimentally or using FEA method. With the correction factor in consideration for bonded joint region, the compliance of the joint can be expressed as

$$ C = \frac{2}{{E_x^{{(1)}}I}}\left[ {\frac{{E_x^{{(1)}}I{h_a}c(ca + 1)(l - a)}}{{2E_y^{{(2)}}b[1 - {e^{{c(a - l)}}}]lk}} + \frac{1}{3}{l^3} + {{(l - a)}^2}l - {l^2}(l - a) - \frac{1}{3}{{(l - a)}^3}} \right] $$
(9.21)

The Strain Energy Release Rate (SERR) of the joint can be given as

$$ {G_I} = \frac{{{P^2}}}{{2b}}\frac{{dC}}{{da}} = \frac{{{P^2}}}{{E_x^{{(1)}}Ib}}\left\{ {\frac{{E_x^{{(1)}}I{h_a}{c^2}(l - a)}}{{2E_y^{{(2)}}blk}}\frac{{1 + ca{e^{{c(a - l)}}}}}{{{{[1 - {e^{{c(a - l)}}}]}^2}}} + {a^2}} \right\} $$
(9.22)

In Eqs. 9.21 and 9.22, the correction factor is incorporated directly after derivation.

Compared to previous studies (shown in Table 9.1, Summary of different theories), such as beam theory (crack tip rotation is not considered), El-Zein [3], more variables are taken in to account, such as Young’s modulus of adhesive material and thickness of adhesive layer, although Penado [18] considered these parameters, he modeled the adhesive layer as spring, while our model treated the adhesive layer more naturally as continuum material, and the parameter c is introduced in the model, in addition, the crack tip rotation is taken into account. The advantages of introducing these variables will be illustrated subsequently.

Table 9.1 Summary of different theories
Full size table

9.3 Results and Discussion

One distinct difference of current theory is the introduction of c, which will be determined by Eq. 9.10 using Newton–Raphson method. Another one is k in the correction factor, FEA method is used, and it’s determined as k = 22.

To compare various theories listed in Table 9.1 Summary of different theories with current theory, three joints are considered. The experimental results are obtained from various sources, the material properties of each components are listed in Table 9.2 Material properties, and specimens configuration are shown in Table 9.3 specimen geometry, unit: mm In regards to the APC-2/AS4-CFRP composite joint, the adhesive properties was unspecified [22], E = 12.5415 MPa, and ν =0.4 is assumed.

Table 9.2 Material properties
Full size table
Table 9.3 Specimen geometry, unit: mm
Full size table

9.3.1 Critical Load

Critical load of APC-2/AS4-CFRP joint predicted by different theories is shown in Table 9.4. Note that the adhesive thickness is relatively thick in this case. From Table 9.4, all the theories give closed prediction with experiment result [22] except Penado’s theory [18], and the current theory is the most closed one.

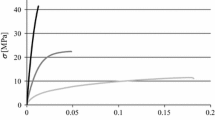
Table 9.4 Comparison of different theories in calculating of critical load and Critical SERR for APC-2/AS4-CFRP joint
Full size table

For Al/FM®73 M/Al joint, the critical load predicted is shown in Fig. 9.2. From Fig. 9.2, Beam theory and Pradeep’s theory give prediction almost double the experimental result at small crack length, however, with the increase of crack length, the results predicted by these two theories improve a lot. On the other hand, El-Zein and Penado’s theory overestimate the result at small crack length, but underestimated the result at larger crack length. Compared to the other theories, current theory improves a lot for the whole examined crack length region.

Fig. 9.2
figure 2

Critical load determined by various theories for Al/FM-73 M/Al joint, EXP. is the experimental result from [5]

Full size image

In regards to Titanium/FM-X5/Titanium joint, the results are shown in Fig. 9.3, From Fig. 9.3, Beam theory, El-Zein and Pradeep’s theories overestimated the critical load about 70% at small crack length, with the increase of crack length, prediction improves greatly. Current theory gives the best agreement with experiment result.

Fig. 9.3
figure 3

Critical load determined by various theories for Titanium/FM-X5/Titanium joint, EXP. is the experimental result from [5]

Full size image

9.3.2 Strain Energy Release Rate

Critical SERR of APC-2/AS4-CFRP joint is listed in Table 9.4. From Table 9.4, current theory gives the critical SERR very close to Pradeep, El-Zein, and beam theory. For Al/FM-73 M/Al joint, the results are listed in Table 9.5, the critical SERR varies a little with crack length, the average critical SERR is about 2.88 × 103 J/m2 from experiment, current theory and Penado’s theory are closer to experimental one. For Titanium/FM-X5/Titanium joint (see Table 9.6), current theory is even better than Penado’s theory.

Table 9.5 Strain energy release rate calculated by various theories for Al/FM-73 M/Al joint, original experiment data from [5], Unit: 103 J/m2
Full size table
Table 9.6 Energy release rate calculated by various theories for Titanium/FM-X5/Titanium joint, original experiment data from [5], Unit: 103 J/m2
Full size table

From the above comparison, current theory has wider application than others. El-Zein, and beam theory doesn’t consider the adhesive Young’s modulus and thickness, the predictions given by these theories are poor when adhesive Young’s modulus is relatively high, for example, the Titanium/FM-X5/Titanium joint, Pradeep’s theory doesn’t take the crack tip rotation into account, the application into studied case is not good as shown above, Penado modeled the adhesive as spring, while the adhesive is relatively thick, the result is very bad as for APC-2/AS4-CFRP joint.

In order to investigate the effect of various variables on the model prediction, parametric study is conducted, and Al/FM-73 M/Al joint mentioned above is used in the study.

9.3.3 Effect of Adhesive Young’s Modulus

Figure 9.4 shows the effect of adhesive Young’s modulus on critical SERR, with x-axis showing the Young’s modulus ratio of adherend to adhesive, and y-axis showing the critical SERR normalized by its initial value. The Young’s modulus ratio of adherend to adhesive is accomplished by changing the adhesive Young’s modulus, and keep adherend’s constant. From Fig. 9.4, the adhesive Young’s modulus affects the critical SERR differently at different crack length. When the crack length is relatively small compared to joint length, the change of adhesive Young’s modulus affects the joint’s critical SERR significantly, increase of E a decreases the critical SERR nonlinearly. However, the influence of E a tends to disappear with the increase of crack length. At a/l = 0.38, the change of E a almost have no impact on the critical SERR, and further increase of crack length, the curves seems to be overlapping as in Fig. 9.4. The result indicates that adhesive Young’s modulus is necessary to be considered when the crack length is relatively small, however, in a large crack length joint, the adhesive Young’s modulus is almost irrelevant.

Fig. 9.4
figure 4

Effect of Young’s modulus on critical SERR

Full size image

9.3.4 Effect of Adhesive Thickness

Effect of adhesive thickness is investigated by changing the adhesive thickness at fixed adherend thickness. The result shown in Fig. 9.5 is obtained at crack length a = 69.81 mm. From Fig. 9.5, the change of adhesive thickness h a has almost no influence on critical SERR when the thickness ratio of adherend to adhesive is below about 100, beyond which, however, the influence becomes significant, decrease of h a greatly increases critical SERR. In real application, the thickness ratio of adherend to adhesive is rare beyond 100, current study provides a theoretical support for other theories which neglect the effect of adhesive thickness.

Fig. 9.5
figure 5

Effect of adhesive thickness on critical SERR

Full size image

9.3.5 Effect of Crack Length

Joint compliance C versus crack length a is shown in Fig. 9.6. It is illustrated in the figure that joint compliance increases nonlinearly with the extension of crack length, the increase rate becomes larger as crack length increase. This indicates that the load is going to decrease as crack propagates as shown in Fig. 9.2, meanwhile, the critical SERR almost keeps unchanged as can been seen in Table 9.5, this is in agreement with the statement in [23].

Fig. 9.6
figure 6

Effect of crack length on joint compliance

Full size image

9.3.6 Effect of k in the Correction Factor

The introduction of correction factor is mainly due to the using of continuum mixture theory for reduction of x-dependence of c. The effect of k in the correction factor is investigated. Figures 9.7 and 9.8 show, respectively, the effect of k in correction factor on the joint compliance and critical SERR. From these figures, the joint compliance is in inverse proportion to k, increase of k decreases joint compliance at a given crack length, and results in an increased nonlinearity compliance versus crack length curve, meanwhile, the curves becomes much closer. On the contrary, the critical SERR is in direct proportion to k, increase of k increases critical SERR, while the rate of increase is decreased as the tangent of the curve decrease.

Fig. 9.7
figure 7

Effect of k in correction factor on the joint compliance

Full size image
Fig. 9.8
figure 8

Effect of k in correction factor on the critical SERR

Full size image

9.4 Conclusion

Analytical model is developed to characterize the fracture behavior of an adhesively bonded joint loaded in peel. The model takes various variables into account, and continuum mixture theory is used for determining new introduced parameter c, also, the crack tip rotation is considered. The model has been applied to 3 different joints, current prediction has a better agreement with experiment compared with other theories. The parametric study leads to the following conclusion.

Adhesive Young’s modulus is necessary to be considered when the crack length is relatively small (less than 20% of joint length), however, in a large crack length joint (above 38% of joint length), the adhesive Young’s modulus is almost irrelevant.

The adhesive thickness has little influence on the critical SERR when h/h a is approximately less than 100, but significant effect is observed beyond this value. Although it rarely happens in real application that thickness ratio of adherend to adhesive is bigger than 100, current study does provide a justification for other theories which neglect the effect of adhesive thickness.

Crack length affect joint compliance in direct proportion. With the increase of crack length, joint compliance goes up.

Constant k in the correction factor affects the joint compliance in inverse proportion at a given crack length, however, it affects the SERR in direct proportion.