Keywords

7.1 Introduction

There are several methods to determine the coefficient of elasticity of a pavement’s sub grade soil from dynamic load non destructive tests. The frequency sweep method [1] uses the driving point frequency response to correlate to the static response of a pavement from a plate load test. The frequency sweep method uses a weighted average of the driving point frequency response to determine the equivalent static response. A previous paper by this author [2] correlated the uniform beam response from a dynamic test to the static response from a conventional test but uses the zero frequency response of the dynamic test to compare to the static response of a conventional test. This paper shows that after introducing viscous damping into the equations of motion, the coefficient of elasticity remains constant but the dynamic response is dependent on two additional constants, a stiffness proportional constant and a mass proportional constant. The stiffness proportional constant is dependent on the material and the mass proportional constant is dependent on the system. Using the zero frequency response of the dynamic test as the equivalent static response, static data system identification methods are now possible.

7.2 Simple Models of Viscoelastic Behavior

In the simplest models of viscoelastic behavior, elastic behavior is represented by a spring while viscous behavior is represented by a dashpot. In the Kelvin-Voight model, the spring and dashpot are arranged in parallel so that under load, the same strain applies to both elements and the response is

$$ \sigma = E\varepsilon + c\frac{{d\varepsilon }}{{dt}} $$
(7.1)

For the creep test, the strain is found by solving the ordinary differential equation with the boundary condition that the stress is constant for positive time.

$$ \varepsilon = \frac{{{{\sigma }_0}}}{E}\left[ {1 - {{e}^{{ - \frac{t}{{{{t}_1}}}}}}} \right] $$
(7.2)

The retardation time is

$$ {{t}_1} = \frac{c}{E} $$
(7.3)

In the Maxwell model, the spring and dashpot are arranged in series so that under load, the same stress applies to both elements and the response is

$$ \frac{{d\varepsilon }}{{dt}} = \frac{1}{E}\frac{{d\sigma }}{{dt}} + \frac{\sigma }{c} $$
(7.4)

For the relaxation test, the stress is found by solving the ordinary differential equation with the boundary condition that the strain is constant for positive time.

$$ \sigma = E{{\varepsilon }_0}{{e}^{{ - \frac{t}{{{{t}_2}}}}}} $$
(7.5)

The relaxation time is

$$ {{t}_2} = \frac{c}{E} $$
(7.6)

For the generalized Kelvin-Voight model, where multiple parallel spring and dashpot are arranged in series, the total strain is

$$ \mathop{\sum }\nolimits {{\varepsilon }_i} = \mathop{\sum }\nolimits \frac{{\sigma - {{c}_i}\mathop{{{{\varepsilon }_i}}}\limits^{.} }}{{{{E}_i}}} $$
(7.7)

The stress is

$$ \sigma = \frac{1}{{\mathop{\sum }\nolimits \frac{1}{{{{E}_i}}}}}\left[ {\mathop{\sum }\nolimits \frac{1}{{{{E}_i}}}\left( {{{E}_i}{{\varepsilon }_i} + {{c}_i}\mathop{{{{\varepsilon }_i}}}\limits^{.} } \right)} \right] $$
(7.8)

For the creep test,

$$ \varepsilon = \mathop{\sum }\nolimits \frac{{{{\sigma }_0}}}{{{{E}_i}}}\left( {1 - {{e}^{{ - \frac{t}{{{{t}_{{1i}}}}}}}}} \right) $$
(7.9)

For the generalized Maxwell model, where multiple series of spring and dashpot are arranged in parallel, the total stress is

$$ \mathop{\sum }\nolimits {{\sigma }_i} = \mathop{\sum }\nolimits {{c}_i}\dot{\varepsilon } - \mathop{\sum }\nolimits \frac{{{{c}_i}}}{{{{E}_i}}}\mathop{{{{\sigma }_i}}}\limits^{.} $$
(7.10)

The strain is

$$ \dot{\varepsilon } = \frac{{\mathop{\sum }\nolimits {{c}_i}\left( {\frac{1}{{{{E}_i}}}\mathop{{{{\sigma }_i}}}\limits^{.} + \frac{1}{{{{c}_i}}}{{\sigma }_i}} \right)}}{{\mathop{\sum }\nolimits {{c}_i}}} $$
(7.11)

For the relaxation test,

$$ \sigma = \mathop{\sum }\nolimits {{E}_i}{{\varepsilon }_0}{{e}^{{ - \frac{t}{{{{t}_{{2i}}}}}}}} $$
(7.12)

More details are available in reference [3].

7.3 Uncoupled Axial Equations of Motion of Beam with Viscous Damping

The equilibrium of a differential beam element in axial deformation is

$$ F + {{F}_{{inertial}}}dx - \left[ {F + \frac{{\partial F}}{{\partial x}}dx} \right] + {{F}_{{damping}}}dx - {{F}_{{external}}}dx = 0 $$
(7.13)
$$ {{F}_{{inertial}}} = m(x)\ddot{u} $$
(7.14)
$$ {{F}_{{damping}}} = c(x)\dot{u}\;\;{\text{Generalized damping}} $$
(7.15)
$$ Let\ c(x) = {{t}_0}m(x)\;\;{\text{Mass proportional damping}} $$
(7.16)
$$ F = \sigma A(x) = \left[ {{{u}^{^\prime}} + {{t}_1}{{{\dot{u}}}^{^\prime}}} \right]EA(x)\;\;{\text{Using Kelvin}} - {\text{Voight material model}}. $$
(7.17)

\( u\left( {x,t} \right) \) can be transformed from the geometric displacement coordinates to the modal amplitudes or normal coordinates.

$$ u\left( {x,t} \right) = \mathop{\sum }\limits_i^{\infty } {{\varnothing }_i}(x){{U}_i}(t) $$
(7.18)

The \( {{\varnothing }_i}(x) \) functions are orthogonal. Substituting the above equation into the force equilibrium and multiplying by \( {{\varnothing }_n}(x) \) and integrating over the beam length gives the uncoupled axial equations of motion of beam with viscous damping.

$$ {{M}_n}\mathop{{{{{\ddot{U}}}_n}}}\limits + {{C}_n}\mathop{{{{{\dot{U}}}_n}}}\limits + {{K}_n}{{U}_n} = \mathop{\int }\nolimits_0^L {{\varnothing }_n}{{F}_{{external}}}dx $$
(7.19)
$$ {{M}_n} = \mathop{\int }\nolimits_0^L \varnothing_n^{2}m(x)dx $$
(7.20)
$$ {{K}_n} = - \mathop{\int }\nolimits_0^L {{\varnothing }_n}\frac{\partial }{{\partial x}}\left[ {\varnothing_n^{^\prime}EA(x)} \right]dx $$
(7.21)
$$ {{C}_n} = {{t}_0}{{M}_n} + {{t}_1}{{K}_n} $$
(7.22)

\( {{t}_0} \ and \ {{t}_1} \) should be constant for all modes if the model is valid.

More details are available in reference [4].

7.4 Uncoupled Torsional Equations of Motion of Beam with Viscous Damping

The equilibrium of a differential beam element in torsion is similar to axial deformation

$$ T + {{T}_{{inertial}}}dx - \left[ {T + \frac{{\partial T}}{{\partial x}}dx} \right] + {{T}_{{damping}}}dx - {{T}_{{external}}}dx = 0 $$
(7.23)
$$ {{T}_{{inertial}}} = m(x)J(x)\ddot{\theta } $$
(7.24)
$$ {{T}_{{damping}}} = c(x)\dot{\theta }\;\; {\text{Generalized damping}} $$
(7.25)
$$ Let\ c(x) = {{t}_0}m(x)J(x)\;\;{\text{Mass proportional damping}} $$
(7.26)
$$ T = \tau J(x) = \left[ {{{\theta }^{^\prime}} + {{t}_1}{{{\dot{\theta }}}^{^\prime}}} \right]GJ(x)\;\;{\text{Using Kelvin}} - {\text{Voight material model}}. $$
(7.27)
$$ \theta \left( {x,t} \right) = \mathop{\sum }\nolimits {{\varnothing }_i}(x){{\mathop{{\bar{\theta }}}\limits }_i}(t)\;\;{\text{Normal coordinate transformation}} $$
(7.28)
$$ {{M}_n}\mathop{{{{{\mathop{{\ddot{\bar \theta }}}\limits }}_n}}}\limits + {{C}_n}\mathop{{{{{\mathop{{\dot{\bar \theta }}}\limits }}_n}}}\limits + {{K}_n}{{\mathop{\bar \theta }\limits }_n} = \mathop{\int }\nolimits_0^L {{\varnothing }_n}{{T}_{{external}}}dx $$
(7.29)
$$ {{M}_n} = \mathop{\int }\nolimits_0^L \varnothing_n^{2}m(x)J(x)dx $$
(7.30)
$$ {{K}_n} = - \mathop{\int }\nolimits_0^L {{\varnothing }_n}\frac{\partial }{{\partial x}}\left[ {\varnothing_n^{^\prime}GJ(x)} \right]dx $$
(7.31)
$$ {{C}_n} = {{t}_0}{{M}_n} + {{t}_1}{{K}_n} $$
(7.32)

7.5 Uncoupled Flexural Equations of Motion of Beam with Viscous Damping

The vertical force equilibrium of a differential flexural beam element is

$$ \mathop{{\bar{V}}}\limits - {{\mathop{{\bar{V}}}\limits }_{{inertial}}}dx - \left[ {\mathop{{\bar{V}}}\limits + \frac{{\partial \mathop{{\bar{V}}}\limits }}{{\partial x}}dx} \right] - {{\mathop{{\bar{V}}}\limits }_{{damping}}}dx + {{\mathop{{\bar{V}}}\limits }_{{external}}}dx = 0 $$
(7.33)
$$ {{\mathop{{\bar{V}}}\limits }_{{inertial}}} = m(x)\ddot{v} $$
(7.34)
$$ {{\mathop{{\bar{V}}}\limits }_{{damping}}} = c(x)\dot{v}\;\; {\text{Generalized damping}} $$
(7.35)
$$ Let\ c(x) = {{t}_0}m(x)\;\;{\text{Mass proportional damping}} $$
(7.36)

The moment equilibrium of a differential flexural beam element is

$$ \mathop{{\bar{M}}}\limits + \mathop{{\bar{V}}}\limits dx - \left[ {\mathop{{\bar{M}}}\limits + \frac{{\partial \mathop{{\bar{M}}}\limits }}{{\partial x}}dx} \right] = 0 $$
(7.37)

and ignoring rotational inertia

$$ \mathop{{\bar{V}}}\limits = \frac{{\partial \mathop{{\bar{M}}}\limits }}{{\partial x}} and \frac{{\partial \mathop{{\bar{V}}}\limits }}{{\partial x}} = \frac{{{{\partial }^2}\mathop{{\bar{M}}}\limits }}{{\partial {{x}^2}}} $$
(7.38)

Assuming normal strains vary linearly over the beam cross section and using the axial stress strain relationship from the Kelvin-Voight material model the moment curvature is

$$ \mathop{{\bar{M}}}\limits = EI(x)\left[ {v^{\prime\prime} + {{t}_1}\dot{v}^{\prime\prime}} \right] $$
(7.39)
$$ v\left( {x,t} \right) = \mathop{\sum }\nolimits {{\varnothing }_i}(x){{V}_i}(t)\;\;{\text{Normal coordinate transformation}} $$
(7.40)

As with the axial deformation the uncoupled flexural equation of motion is

$$ {{M}_n}\mathop{{{{{\ddot{V}}}_n}}}\limits + {{C}_n}\mathop{{{{{\dot{V}}}_n}}}\limits + {{K}_n}{{V}_n} = \mathop{\int }\nolimits_0^L {{\varnothing }_n}{{\mathop{{\bar{V}}}\limits }_{{external}}}dx $$
(7.41)
$$ {{M}_n} = \mathop{\int }\nolimits_0^L \varnothing_n^2m(x)dx $$
(7.42)
$$ {{K}_n} = \mathop{\int }\nolimits_0^L {{\varnothing }_n}\frac{{{{\partial }^2}}}{{\partial {{x}^2}}}\left[ {\varnothing_n^{{^{\prime\prime}}}EI(x)} \right]dx $$
(7.43)
$$ {{C}_n} = {{t}_0}{{M}_n} + {{t}_1}{{K}_n} $$
(7.44)

7.6 Dynamic Modal Model

The response of a multiple degree of freedom system under forced harmonic vibration [4–6], given by the general dynamic modal model is

$$ {{x}_s}(t) = \sum\limits_{{n = 1}}^N {\frac{{{{\phi }_{{sn}}}\sum\limits_{{n = 1}}^N {{{\phi }_{{dn}}}{{F}_d}} }}{{{{K}_n} - {{\omega }^2}{{M}_n} + i\omega {{C}_n}}}} {{e}^{{i\omega t}}} $$
(7.45)

For the special case when there is only one harmonic load at the sth degree of freedom and the mode shapes are normalized with respect to that location of the load, then \( {{\phi }_{{sn}}} \) = 1 for n = 1,2,…,N and \( {{F}_d} \) = 0 for all d <> s and \( {{F}_d} \) = \( F \) when d = s. The driving point response is

$$ x(t) = H(i\omega )F{{e}^{{i\omega t}}} $$
(7.46)
$$ H(i\omega ) = \sum\limits_{{n = 1}}^N {{{H}_n}(i\omega )} $$
(7.47)
$$ {{H}_n}(i\omega ) = \frac{1}{{{{K}_n} - {{\omega }^2}{{M}_n} + i\omega {{C}_n}}} $$
(7.48)

The driving point response can be written as the sum of the magnitudes and phases of the individual modes

$$ x(t) = \sum\limits_{{n = 1}}^N {\left| {{{H}_n}(i\omega )} \right|} {{e}^{{i(\omega t + {{\theta }_n})}}} $$
(7.49)
$$ {{\left| {{{H}_n}(i\omega )} \right|}^2} = \frac{1}{{{{{\left( {{{K}_n} - {{\omega }^2}{{M}_n}} \right)}}^2} + {{{\left( {\omega {{C}_n}} \right)}}^2}}} $$
(7.50)
$$ {{\theta }_n} = - {{\tan }^{{ - 1}}}\left( {\frac{{\omega {{C}_n}}}{{{{K}_n} - {{\omega }^2}{{M}_n}}}} \right) $$
(7.51)

The driving point response can also be written directly as the total system magnitude and phase

$$ x(t) = \left| {H(i\omega )} \right|F{{e}^{{i(\omega t + \theta )}}} $$
(7.52)
$$ {{\left| {H(i\omega )} \right|}^2} = real{{\left( {H(i\omega )} \right)}^2} + imaginary{{\left( {H(i\omega )} \right)}^2} $$
(7.53)
$$ \theta = {{\tan }^{{ - 1}}}\left( {\frac{{imaginary\left( {H(i\omega )} \right)}}{{real\left( {H(i\omega )} \right)}}} \right) $$
(7.54)
$$ real\left( {H(i\omega )} \right) = \sum\limits_{{n = 1}}^N {\frac{{{{K}_n} - {{\omega }^2}{{M}_n}}}{{{{{\left( {{{K}_n} - {{\omega }^2}{{M}_n}} \right)}}^2} + {{{\left( {\omega {{C}_n}} \right)}}^2}}}} $$
(7.55)
$$ imaginary\left( {H(i\omega )} \right) = - \sum\limits_{{n = 1}}^N {\frac{{\omega {{C}_n}}}{{{{{\left( {{{K}_n} - {{\omega }^2}{{M}_n}} \right)}}^2} + {{{\left( {\omega {{C}_n}} \right)}}^2}}}} $$
(7.56)

When the load is harmonic, the response is harmonic and the magnitude and phase of the response has contributions from the individual modes. In theory, the magnitude of the frequency response at a frequency of zero corresponds to the static deflection due to a unit force. The zero frequency response [7] is defined as

$$ H(0) = \left| {H(0)} \right| = \sum\limits_{{n = 1}}^N {\frac{1}{{{{K}_n}}}} $$
(7.57)

The zero frequency response is equivalent to the static deflection (flexibility) under a unit load of N springs in series where the spring constants, \( {{K}_n} \), n = 1,2,…N, are the modal spring constants. The system stiffness is simply the inverse of the zero frequency response.

7.7 Static Response of Uniform Beam

The basic mechanical tension, compression, torsion and bending tests of uniform beams to determine the coefficient of elasticity are based on the following equations of static equilibrium [8].

Axial Tension/Compression

$$ w = \frac{{FL}}{{EA}} $$
(7.58)

Torsion

$$ \vartheta = \frac{{TL}}{{GJ}} $$
(7.59)

3 Point Bending at mid span

$$ w = \frac{{F{{L}^3}}}{{48EI}} $$
(7.60)

Poisson’s Ratio can be determined by the relation

$$ \nu = \frac{E}{{2G}} - 1 $$
(7.61)

7.8 Dynamic Response of Uniform Beam in Bending

From the available frequency equation of a simply supported uniform beam bending at mid span [4–6]46

$$ \omega_n^2 = \frac{{{{K}_n}}}{{{{M}_n}}} = \frac{{{{n}^4}{{\pi }^4}EI}}{{{{L}^4}m}} $$
(7.62)
$$ {{M}_n} = \frac{{mL}}{2} $$
(7.63)
$$ {{K}_n} = \frac{{{{n}^4}{{\pi }^{{{{4}}}}}EI}}{{2{{L}^3}}} $$
(7.64)
$$ {{\phi }_n} = \sin \left( {\frac{{n\pi x}}{L}} \right) $$
(7.65)
$$ H(0) = \sum\limits_{{n = 1}}^{\infty } {\frac{{\phi_n^2}}{{{{K}_n}}}} $$
(7.66)

The static response is equal to the zero frequency response of the simply supported uniform beam in bending at mid span and can be expressed as a function of the first modal stiffness [2]

$$ \frac{{{{L}^3}}}{{48EI}} = \frac{{{{\pi }^4}}}{{96{{K}_1}}} $$
(7.67)

The coefficient of elasticity as a function of the first modal stiffness is

$$ E = \frac{{2{{L}^3}{{K}_1}}}{{{{\pi }^4}I}} $$
(7.68)

7.9 Dynamic Response of Uniform Beam in Axial Deformation

For axial deformation the available frequency equation [4–6]46 for a beam fixed at x = 0 and free at x = L is

$$ \omega_n^2 = \frac{{{{K}_n}}}{{{{M}_n}}} = \frac{{{{\pi }^2}{{{\left( {2n - 1} \right)}}^2}EA}}{{4m{{L}^2}}} $$
(7.69)
$$ {{M}_n} = \frac{{mL}}{2} $$
(7.70)
$$ {{K}_n} = \frac{{{{\pi }^2}{{{\left( {2n - 1} \right)}}^2}EA}}{{8L}} $$
(7.71)
$$ {{\phi }_n} = \sin \left( {(2n - 1)\frac{\pi }{2}\frac{x}{L}} \right) $$
(7.72)

The static response is equal to the zero frequency response of the beam and can be expressed as a function of the first modal stiffness

$$ \frac{L}{{EA}} = \frac{{{{\pi }^2}}}{{8{{K}_1}}} $$
(7.73)

The coefficient of elasticity as a function of the first modal stiffness is

$$ E = \frac{{8L{{K}_1}}}{{{{\pi }^2}A}} $$
(7.74)

Dynamic Response of Uniform Beam in Torsion

For torsion the frequency equation [4–6]46 for a cylindrical beam fixed at x = 0 and free at x = L is similar to the axial frequency equation

$$ \omega_n^2 = \frac{{{{K}_n}}}{{{{M}_n}}} = \frac{{{{\pi }^2}{{{\left( {2n - 1} \right)}}^2}GJ}}{{4m{{L}^2}}} $$
(7.75)
$$ G = \frac{{8L{{K}_1}}}{{{{\pi }^2}J}} $$
(7.76)

Knowing \( E \) and \( G \), Poisson’s ratio can be determined as

$$ \nu = \frac{{J{{K}_{{1axial}}}}}{{2A{{K}_{{1torsion}}}}} - 1 $$
(7.77)

7.10 Uniform Beam in Bending Quarter Span

When \( {{x}_d} = \frac{L}{2} \) and \( {{x}_s} = \frac{L}{4} \) then the zero frequency response is

$$ \sum\limits_{{n = 1}}^{\infty } {\frac{{\left( {\displaystyle\frac{{\sin \left( {\frac{{n\pi }}{4}} \right)}}{{\sin \left( {\frac{{n\pi }}{2}} \right)}}} \right)}}{{\left( \displaystyle{\frac{{{{K}_n}}}{{\sin {{{\left( {\frac{{n\pi }}{2}} \right)}}^{2}}}}} \right)}}} $$
(7.78)

and includes modes where \( \sin \left( {\frac{{n\pi }}{4}} \right) < > 0 \)

When \( {{x}_d} = {{x}_s} = \frac{L}{4} \) then the zero frequency response is

$$ \sum\limits_{{n = 1}}^{\infty } {\frac{1}{{\left( {\frac{{{{K}_n}}}{{\sin {{{\left( {\frac{{n\pi }}{4}} \right)}}^2}}}} \right)}}} $$
(7.79)
$$ {\text{So}}\;{\text{measured}}\;{{K}_n} = \frac{{{{K}_n}}}{{\sin {{{\left( {\frac{{n\pi }}{4}} \right)}}^2}}} $$
(7.80)
$$ {{K}_n}\left( {{{x}_d} = {{x}_s} = \frac{L}{4}} \right) = \frac{{{{K}_n}\left( {{{x}_d} = {{x}_s} = \frac{L}{2}} \right)}}{{\sin {{{\left( {\frac{{n\pi }}{4}} \right)}}^2}}} $$
(7.81)

From statics [8], the quarter span elastic deformation is related to the mid span elastic deformation

$$ w\left( {{{x}_d} = {{x}_s} = \frac{L}{4}} \right) = \frac{9}{{16}}w\left( {{{x}_d} = {{x}_s} = \frac{L}{2}} \right) $$
(7.82)

So

$$ \sum\limits_{{n = 1}}^{\infty } {\frac{{\sin {{{\left( {\frac{{n\pi }}{4}} \right)}}^2}}}{{{{n}^4}}}} = \frac{{{{\pi }^4}}}{{96}}\frac{9}{{16}} $$
(7.83)

Reciprocity is valid because the zero frequency response when \( {{x}_d} = \frac{L}{4} \) and \( {{x}_s} = \frac{L}{2} \) is equal to the zero frequency response when \( {{x}_d} = \frac{L}{2} \) and \( {{x}_s} = \frac{L}{4} \)

The zero frequency response is

$$ \sum\limits_{{n = 1}}^{\infty } {\frac{{\left( \displaystyle{\frac{{\sin \left( {\frac{{n\pi }}{2}} \right)}}{{\sin \left( {\frac{{n\pi }}{4}} \right)}}} \right)}}{{\left( \displaystyle{\frac{{{{K}_n}}}{{\sin {{{\left( {\frac{{n\pi }}{4}} \right)}}^2}}}} \right)}}} = \sum\limits_{{n = 1}}^{\infty } {\frac{{\left( \displaystyle{\frac{{\sin \left( {\frac{{n\pi }}{4}} \right)}}{{\sin \left( {\frac{{n\pi }}{2}} \right)}}} \right)}}{{\left( {\displaystyle\frac{{{{K}_n}}}{{\sin {{{\left( {\frac{{n\pi }}{2}} \right)}}^2}}}} \right)}}} $$
(7.84)

From statics [8], the quarter span deformation due to the load at the mid span is related to the mid span elastic deformation.

$$ w\left( {{{x}_d} = \frac{L}{2},{{x}_s} = \frac{L}{4}} \right) = \frac{{11}}{{16}}w\left( {{{x}_d} = {{x}_s} = \frac{L}{2}} \right) $$
(7.85)

So

$$ \sum\limits_{{n = 1}}^{\infty } {\frac{{\sin \left( {\frac{{n\pi }}{2}} \right)\sin \left( {\frac{{n\pi }}{4}} \right)}}{{{{n}^4}}}} = \frac{{{{\pi }^4}}}{{96}}\frac{{11}}{{16}} $$
(7.86)

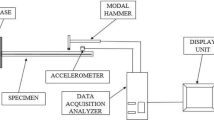
7.11 Experimental Modal Analysis

From experimental modal analysis the frequency, damping, poles and residues can be estimated. From the damped frequencies and residues the zero frequency response can be determined. The partial fraction form of the frequency response function for a single force at \( {{x}_d} \) and the response at \( {{x}_s} \)

$$ {{H}_{{sd}}}\left( {i\omega } \right) = \mathop{\sum }\nolimits \frac{{{{\varnothing }_{{sn}}}{{\varnothing }_{{dn}}}}}{{{{M}_n}\left( {i\omega - {{s}_n}} \right)\left( {i\omega - s_n^{*}} \right)}} = \mathop{\sum }\nolimits \left( {\frac{{{{A}_n}}}{{i\omega - {{s}_n}}} + \frac{{A_n^{*}}}{{i\omega - s_n^{*}}}} \right) $$
(7.87)
$$ {{s}_n} = - \frac{{{{C}_n}}}{{2{{M}_n}}} + i\sqrt{\frac{{{{K}_n}}}{{{{M}_n}}} - {{{\left({\frac{{{{C}_n}}}{{2{{M}_n}}}} \right)}}^{2}}} $$
(7.88)
$$ {{A}_n} = \frac{{{{\varnothing }_{{sn}}}{{\varnothing }_{{dn}}}}}{i2{{M}_n}\sqrt {{\frac{{{{K}_n}}}{{{{M}_n}}} - {{{\left( {\frac{{{{C}_n}}}{{2{{M}_n}}}} \right)}}^{2}}} }} $$
(7.89)

Setting the frequency to zero, it can be shown that

$$ {{H}_{{sd}}}(0) = \mathop{\sum }\nolimits \left( {\frac{{{{A}_n}}}{{ - {{s}_n}}} + \frac{{A_n^{*}}}{{ - s_n^{*}}}} \right) = \mathop{\sum }\nolimits \frac{{{{\varnothing }_{{sn}}}{{\varnothing }_{{dn}}}}}{{{{K}_n}}} $$
(7.90)

To get the stiffness proportional constant and mass proportional constant use the following equation. Since there are usually more modal frequencies than the two unknowns, the solution requires the pseudo inverse.

$$ {{\phi }_n} = \frac{{ - real({{s}_n})}}{{{{\omega }_n}}} = \frac{{{{t}_0}}}{{2{{\omega }_n}}} + \frac{{{{t}_1}{{\omega }_n}}}{2} $$
(7.91)

Where \( {{\omega }_n} = \left| {{{s}_n}} \right| \).

7.12 Element Stiffness Identification from Equivalent Static Test Data

The procedure for element stiffness identification follows that of [9] with a modification to use the complex variable semi-analytical method instead of the finite difference method in approximating the derivatives of the sensitivity matrix [10].

Using the zero frequency response as the equivalent static response, the global experimental stiffness matrix can be determined from inverting the flexibility matrix where

$$ u(x = {{x}_s} = {{x}_d}) = \mathop{\sum }\nolimits \frac{{\varnothing_n^2}}{{{{K}_n}}} \ {\rm and} \ u\left( {x = {{x}_s} \ne {{x}_d}} \right) = \mathop{\sum }\nolimits \frac{{{{\varnothing }_{{sn}}}{{\varnothing }_{{dn}}}}}{{{{K}_n}}} $$
(7.92)
$$ {{K}^e} = {{u}^{{ - 1}}} $$
(7.93)

The stiffness matrix derived from the finite element method matrix must be partitioned into four sub matrices.

$$ \left[ {\begin{array}{lll} {{{F}_m}} \\{{{F}_u}} \\\end{array} } \right] = \left[ {\begin{array}{lll} {{{K}_{{mm}}}} & {{{K}_{{mu}}}} \\{{{K}_{{um}}}} & {{{K}_{{uu}}}} \\\end{array} } \right]\left[ {\begin{array}{lll} {{{U}_m}} \\{{{U}_u}} \\\end{array} } \right] $$
(7.94)

The \( m \) subscript indicates the degrees of freedom which represent the measured force, stiffness and displacement. The \( u \) subscript indicates the unmeasured degrees of freedom. The global analytical stiffness matrix is

$$ {{K}^a} = {{K}_{{mm}}} - {{K}_{{mu}}}K_{{uu}}^{{ - 1}}{{K}_{{um}}} $$
(7.95)

By adjusting the experimental and analytical stiffness matrices into vectors that match the unknown parameters that are to be identified and minimizing the error norm between the two vectors, an estimate for the parameters can be made. Since the analytical stiffness vector of unknown parameters is non linear, a first order Taylor series expansion is used.

$$ {{k}^a}\left( {p + \Delta p} \right) \cong {{k}^a}(p) + s(p)\Delta p \ where\ s(p) = \frac{\partial }{{\partial p}}{{k}^a}(p) $$
(7.96)
$$ S(p) = \frac{\partial }{{\partial p}}{{K}^a}(p) = \frac{\partial }{{\partial p}}{{K}_{{mm}}} - \left( {\frac{\partial }{{\partial p}}{{K}_{{mu}}}} \right)K_{{uu}}^{{ - 1}}{{K}_{{um}}} + {{K}_{{mu}}}K_{{uu}}^{{ - 1}}\left( {\frac{\partial }{{\partial p}}{{K}_{{uu}}}} \right)K_{{uu}}^{{ - 1}}{{K}_{{um}}} - {{K}_{{mu}}}K_{{uu}}^{{ - 1}}\left( {\frac{\partial }{{\partial p}}{{K}_{{um}}}} \right) $$
(7.97)

Placing the values of \( S(p) \) into the vector \( s(p) \).

$$ J\left( {\Delta p} \right) = {{\left[ {e(\Delta p)} \right]}^T}\left[ {e(\Delta p)} \right] \ where\ \left[ {e(\Delta p)} \right] = {{k}^e} - {{k}^a}\left( {p + \Delta p} \right) = {{k}^e} - {{k}^a}(p) - s(p)\Delta p $$
(7.98)
$$ Setting \ \frac{{\partial J(\Delta p)}}{{\partial p}} = 0 \ the \ relationship \ s(p)\Delta p = \Delta k(p) \ can \ be \ derived \ where \ \Delta k(p) = {{k}^e} - {{k}^a}(p). $$
(7.99)

An iterative procedure for parameter identification can now be used.

$$ {{p}^{{i + 1}}} = {{p}^i} + \Delta p \ where\ \Delta p = {{\left[ {s{{{(p)}}^T}s(p)} \right]}^{{ - 1}}}s{{(p)}^T}\Delta k(p) $$
(7.100)

The partial derivatives can be solved analytically, finite differences, or by complex variable semi analytical method. The CVSAM has several numerical advantages and a brief description follows.

A Taylor series expansion of a function in the complex plane is

$$ f\left( {x + i\Delta x} \right) = f(x) + i\Delta x{{f}^{^\prime}}(x) - \frac{{\Delta {{x}^2}{{f}^{{^{\prime\prime}}}}(x)}}{{2!}} - \frac{i\Delta {{x}^3}{{f}^{{^{\prime\prime\prime}}}(x)}}{{3!}} + \ldots $$
(7.101)

Grouping the real and imaginary parts, the first order derivative can be obtained as

$$ {{f}^{^\prime}}(x) = \frac{{imag(f\left( {x + i\Delta x} \right))}}{{\Delta x}} + O(\Delta {{x}^2}) $$
(7.102)

Note the calculation of the first order derivative does not involve the subtraction of two numbers and using the above approximation avoids the subtractive cancellation errors that plague the finite difference approach.

7.13 A 2 Node Isotropic Beam Element

Considering the well known 2 node, 6 degree of freedom isotropic beam element, the analytic stiffness matrix for a cantilever beam element is as follows, where the free end is at x = 0 and the fixed end at x = L and there are 2 degrees of freedom which are considered to be measured, the axial and flexural at x = 0 and where the unknown parameter is the coefficient of elasticity.

$$ {{K}_{{mm}}} = \left[ {\begin{array}{lll} {\frac{{AE}}{L}} & 0 \\0 & {\frac{{12EI}}{{{{L}^3}}}} \\\end{array} } \right] \ and\ \frac{{\partial {{K}_{{mm}}}}}{{\partial E}} = \left[ {\begin{array}{lll} {\frac{A}{L}} & 0 \\0 & {\frac{{12I}}{{{{L}^3}}}} \\\end{array} } \right] $$
(7.103)
$$ {{K}_{{um}}} = \left[ {\begin{array}{lll} 0 & {\frac{{6EI}}{{{{L}^2}}}} \\\end{array} } \right] \ and \ \frac{{\partial {{K}_{{um}}}}}{{\partial E}} = \left[ {\begin{array}{lll} 0 & {\frac{{6I}}{{{{L}^2}}}} \\\end{array} } \right] \ and\ {{K}_{{mu}}} = K_{{um}}^T \ and \ \frac{{\partial {{K}_{{mu}}}}}{{\partial E}} = \frac{{\partial K_{{um}}^T}}{{\partial E}} $$
(7.104)
$$ {{K}_{{uu}}} = \frac{{4EI}}{L} \ and\ \frac{{\partial {{K}_{{uu}}}}}{{\partial E}} = \frac{{4I}}{L} \ and\ K_{{uu}}^{{ - 1}} = \frac{L}{{4EI}} $$
(7.105)

Using CVSAM, the first derivative approximation for this element is equal to the analytic first derivative.

$$ \frac{{\partial {{K}_{{mm}}}}}{{\partial E}} = \frac{{imag\left[ {\begin{array}{lll} {\frac{{A(E + i\Delta E)}}{L}} & 0 \\0 & {\frac{{12(E + i\Delta E)I}}{{{{L}^3}}}} \\\end{array} } \right]}}{{\Delta E}} = \left[ {\begin{array}{lll} {\frac{A}{L}} & 0 \\0 & {\frac{{12I}}{{{{L}^3}}}} \\\end{array} } \right] $$
(7.106)
$$ S(E) = \left[ {\begin{array}{lll} {\frac{A}{L}} & 0 \\0 & {\frac{{3I}}{{{{L}^3}}}} \\\end{array} } \right] \ and\ {{K}^a} = \left[ {\begin{array}{lll} {\frac{{AE}}{L}} & 0 \\0 & {\frac{{3EI}}{{{{L}^3}}}} \\\end{array} } \right] $$
(7.107)

After some manipulation,

$$ {{E}^{{i + 1}}} = {{E}^i} + \frac{{\frac{A}{L}\left( {{{k}_x} - \frac{{A{{E}^i}}}{L}} \right) + \frac{{3I}}{{{{L}^3}}}({{k}_y} - \frac{{3{{E}^i}I}}{{{{L}^3}}})}}{{{{{\left( {\frac{A}{L}} \right)}}^2} + {{{\left( {\frac{{3I}}{{{{L}^3}}}} \right)}}^2}}} $$
(7.108)

7.14 A 2 Node Orthotropic Beam Element

Considering the 2 node, 6 degree of freedom orthotropic beam element [11], the analytic stiffness matrix for a cantilever beam element is as follows, where the free end is at x = 0 and the fixed end at x = L and there are 2 degrees of freedom which are considered to be measured, the axial and flexural at x = 0 and where the unknown parameter is the fiber angle.

The stress strain relations for an orthotropic material in plane stress are as follows

$$ \frac{{\partial u}}{{\partial x}} = {{\varepsilon }_x} = {{a}_{{11}}}{{\sigma }_x} + {{a}_{{12}}}{{\sigma }_y} + {{a}_{{16}}}{{\sigma }_{{xy}}} $$
(7.109)
$$ \frac{{\partial v}}{{\partial y}} = {{\varepsilon }_y} = {{a}_{{12}}}{{\sigma }_x} + {{a}_{{22}}}{{\sigma }_y} + {{a}_{{26}}}{{\sigma }_{{xy}}} $$
(7.110)
$$ \frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial x}} = {{\varepsilon }_{{xy}}} = {{a}_{{16}}}{{\sigma }_x} + {{a}_{{26}}}{{\sigma }_y} + {{a}_{{66}}}{{\sigma }_{{xy}}} $$
(7.111)
$$ m = cos\theta \ and\ n = sin\theta $$
$$ {{S}_{{11}}} = \frac{1}{{{{E}_1}}} \ and\ {{S}_{{12}}} = - \frac{{{{v}_{{12}}}}}{{{{E}_1}}} \ and\ {{S}_{{22}}} = \frac{1}{{{{E}_2}}} \ and\ {{S}_{{66}}} = \frac{1}{{{{G}_{{12}}}}} $$
(7.112)
$$ {{a}_{{11}}} = {{S}_{{11}}}{{m}^4} + \left( {2{{S}_{{12}}} + {{S}_{{66}}}} \right){{m}^2}{{n}^2} + {{S}_{{22}}}{{n}^4} $$
(7.113)
$$ {{a}_{{12}}} = {{S}_{{12}}}({{m}^4} + {{n}^4}) + \left( {{{S}_{{11}}} + {{S}_{{22}}} - {{S}_{{66}}}} \right){{m}^2}{{n}^2} $$
(7.114)
$$ {{a}_{{22}}} = {{S}_{{11}}}{{n}^4} + \left( {2{{S}_{{12}}} + {{S}_{{66}}}} \right){{m}^2}{{n}^2} + {{S}_{{22}}}{{m}^4} $$
(7.115)
$$ {{a}_{{16}}} = (2{{S}_{{11}}} - 2{{S}_{{12}}} - {{S}_{{66}}})n{{m}^3} - (2{{S}_{{22}}} - 2{{S}_{{12}}} - {{S}_{{66}}}){{n}^3}m $$
(7.116)
$$ {{a}_{{26}}} = (2{{S}_{{11}}} - 2{{S}_{{12}}} - {{S}_{{66}}})m{{n}^3} - (2{{S}_{{22}}} - 2{{S}_{{12}}} - {{S}_{{66}}}){{m}^3}n $$
(7.117)
$$ {{a}_{{66}}} = 2(2{{S}_{{11}}} + 2{{S}_{{22}}} - 4{{S}_{{12}}} - {{S}_{{66}}}){{n}^2}{{m}^2} - {{S}_{{66}}}({{n}^4} + {{m}^4}) $$
(7.118)

The deflection equation in the symmetry axis of the beam, y = 0 is

$$ v = \frac{P}{I}\frac{{{{a}_{{11}}}}}{6}\left( {{{x}^3} - 3{{L}^2}x + 2{{L}^3}} \right) \ and\ v\left( {x = 0} \right) = \frac{P}{I}\frac{{{{a}_{{11}}}{{L}^3}}}{3} $$
(7.119)
$$ When \ \theta = {{0}^0}, v\left( {x = 0} \right) = \frac{{P{{L}^3}}}{{3{{E}_1}I}} \ and\ when\ \theta = {{90}^0}, v\left( {x = 0} \right) = \frac{{P{{L}^3}}}{{3{{E}_2}I}} $$
(7.120)
$$ {{K}_{{mm}}} = \left[ {\begin{array}{lll} {\frac{A}{{L{{a}_{{11}}}}}} & 0 \\0 & {\frac{{12I}}{{{{L}^3}{{a}_{{11}}}}}} \\\end{array} } \right] $$
(7.121)
$$ {{K}_{{um}}} = \left[ {\begin{array}{lll} 0 & {\frac{{6I}}{{{{L}^2}{{a}_{{11}}}}}} \\\end{array} } \right] \ and\ {{K}_{{mu}}} = K_{{um}}^T\ and\ \frac{{\partial {{K}_{{mu}}}}}{{\partial E}} = \frac{{\partial K_{{um}}^T}}{{\partial E}} $$
(7.122)
$$ {{K}_{{uu}}} = \frac{{4I}}{{L{{a}_{{11}}}}} \ and\ K_{{uu}}^{{ - 1}} = \frac{{L{{a}_{{11}}}}}{{4I}} $$
(7.123)

Using CVSAM requires evaluating

$$ \frac{{\partial {{a}_{{11}}}}}{{\partial \theta }} \cong \frac{{imag\left[ {{{S}_{{11}}}{\text{co}}{{\text{s}}^4}(\theta + i\Delta \theta ) + \left( {2{{S}_{{12}}} + {{S}_{{66}}}} \right){\text{co}}{{\text{s}}^2}(\theta + i\Delta \theta ){\text{si}}{{\text{n}}^2}(\theta + i\Delta \theta ) + {{S}_{{22}}}{\text{si}}{{\text{n}}^4}(\theta + i\Delta \theta )} \right]}}{{\Delta \theta }} $$
(7.124)

7.15 Summary

When the frequency equation is known, the elastic properties of uniform beams can be determined from knowledge of the first modal stiffness. If the frequency equation is not known then the elastic properties can be determined by inverse identification methods using finite elements with the zero frequency response as the equivalent static response. The modal stiffness is derived from parameter estimation using experimental modal data [12]. The experimental modal data can be from any dynamic test using a time domain or frequency domain parameter estimation technique. After introducing viscous damping into the equations of motion, the coefficient of elasticity remains constant but the dynamic response is dependent on two additional constants, a stiffness proportional constant and a mass proportional constant. The stiffness proportional constant is dependent on the material and the mass proportional constant is dependent on the system. The two constants can be estimated by the pseudo inverse of a matrix based on the modal frequency and damping.