Keywords

1 Introduction

The advent of dynamic geometry systems (DGSs) has dramatically changed the possible scenario of geometrical experiences at school. The transition from the traditional graphic environment based on paper and pencil, to the virtual graphic environment based on figures on the screen, realized by graphical tools and transformed by acting through the mouse, has the potential of deeply affecting the way students conceive and reason upon geometrical figures.

Line segments that stretch and points that move relative to each other are not trivially the same objects that one treats in the familiar synthetic geometry, and this suggests new styles of reasoning. (Goldenberg 1995, p. 220)

DGSs for computers and calculators, such as the Geometer’s Sketchpad (Jackiw 2009) and Cabri géométre (Laborde and Bellemain 1995), have been at the core of a number of studies claiming the potential to impact the teaching and learning of school geometry (Healy and Hoyles 2001; Hölzl 2001; Jones 2000; Laborde 2000; Mariotti 2000; Sträßer 2001; and for an extensive review, see Battista 2007; Laborde et al. 2006) . Since the very beginning of their appearance research studies have highlighted the potential offered by DGSs in supporting students’ solution of geometrical problems:

[…] the changes in the solving process brought by the dynamic possibilities of Cabri come from an active and reasoning visualisation, from what we call an interactive process between inductive and deductive reasoning. (Laborde and Laborde 1991, p. 185)

Specifically, studies have investigated the support provided by a DGS in the solution of open problems that require the formulation of a conjecture. These types of tasks have been discussed to claim their didactic potential, not only with respect to the use of a DGS (Hadas et al. 2000; Boero et al. 2007; Pedemonte 2008) .

The use of a DGS, like Cabri, in the generation of conjectures is based on the interpretation of the dragging function in terms of logical control that involves converting perceptual data into a conditional statement . During the conjecturing process, the way of transforming and observing screen images is directed by the intention of revealing a significant relationship between geometric properties, a relationship that may be formulated in the statement of a conjecture.

Elaborating on the seminal work of Arzarello, Olivero, and colleagues (Arzarello et al. 2002; Olivero 2001, 2002), the potential offered by a DGS not only in supporting conjecturing processes but also in mediating the mathematical meaning of conjecture and specifically of conditional statement in the geometry context is discussed .

The following discussion is framed within the theory of semiotic mediation (TSM) as it has been introduced by Bartolini Bussi and Mariotti (2008) . In this specific theoretical framework, the semiotic potential of particular modalities of dragging with respect to the notion of conditionality is discussed. Any dragging mode can be considered as a specific artifact used to solve an open problem, meanings emerging from this use may be referred to the mathematical meaning of conjecture, that is, of a conditional statement expressing the logical dependency between a premise and a conclusion .

A brief outline of the TSM and specifically of the notion of semiotic potential and that of didactic cycle is given , then specific dragging modalities explaining how they can be related to the mathematical meanings of premise, conclusion, and conditional link between them are analyzed . Some illustrative examples are given, drawn from a recent study carried out at the upper secondary level, focusing on a particular process of conjecture generation (Baccaglini-Frank 2010a, 2010b; Baccaglini-Frank et al. 2009; Baccaglini-Frank and Mariotti 2010) .

2 The Theory of Semiotic Mediation

In relation to the use of particular tools, specifically in relation to the use of new computer-based technologies in school practice, the term mediation has become widely present in the current mathematic education literature (Meira 1998; Radford 2003; Noss and Hoyles 1996; Borba and Villarreal 2005) . However, the term “mediation” has been often employed in an unclear way, mixing up two interrelated potentialities of a given tool. On the one hand, the tool may be used and it may successfully contribute to the accomplishment of a task, and on the other hand, the use of the tool may foster learning processes concerning mathematical ideas.

What remains unaddressed is the epistemological issue concerning the relationship between the accomplishment of a task and the student’s learning. This leaves implicit the key elements of the mediation processFootnote 1, which is triggered by the use of a specific tool and that is related to particular mathematical knowledge.

The TSM elaborated in Bartolini Bussi and Mariotti (2008) addresses this issue, combining a semiotic and an educational perspective and considering the crucial role of human mediation (Kozulin 2003, p. 19) in the teaching–learning process.

Starting from the notion of semiotic mediation introduced by Vygotsky (1978) , we analyze the role of tools and of their functioning in the solution of specific tasks, and outline a model that describes how a specific tool can be exploited by the teacher as a means to enhance the teaching–learning process seen as effect of social and cultural interaction.

In the following, a short introduction of the model is provided, strictly finalized to clarifying the analysis of the dragging tool and the subsequent discussion of the examples that constitute the core of this contribution (for a full discussion and more references, see Bartolini Bussi and Mariotti 2008 and Mariotti 2009) .

Following Vygotsky, we used the semiotic lens to describe individual knowledge construction in terms of internalization (Vygotsky 1981, p. 162) that constitutes the unifying element of description (Wertsch and Addison Stone 1985) . The basic assumption concerns the claim that internalization is essentially a social process based on the communication dimension and on the asymmetric role played by the main interlocutors: the teacher and the students.

Specifically, the social use of a certain tool in accomplishing a task makes meanings emerge and these are shared via different semiotic means (verbal, gestural, etc.). Such meanings directly refer to the tool and its use in the context of the task; however, if observed from the point of view of an expert, they may also be related to specific mathematical content. Following Hoyles (1993), we can consider the relation between the tool’s use and mathematics as evoked knowledge: for an expert, the teacher for instance, the use of a tool may evoke the mathematics knowledge that one has to resort to in order to solve a specific task. In this sense, one says that a DGS may evoke the classic “ruler and compass” geometry or the abacus may evoke the positional notation for numbers.

Hence, a double semiotic relationship is recognizable: (1) between a tool and meanings emerging in the accomplishment of the task and (2) between the tool and the meanings related to specific mathematical content evoked by that use and recognizable by an expert. We define (Bartolini Bussi and Mariotti 2008) this double semiotic link as the semiotic potential specific to the tool .

A double relationship may occur between an artifact and on the one hand the personal meanings emerging from its use to accomplish a task (instrumented activity), and on the other hand the mathematical meanings evoked by its use and recognizable as mathematics by an expert. (op. cit., p. 754)

On the basis of the distinction between meanings emerging from the use of the tool and shared in a social interaction and mathematical meanings related to specific mathematical content, we can interpret the teaching–learning activity as organized around the goal of making students’ personal meanings evolve into mathematical meanings. In other terms, we can see the educational intervention as a way of exploiting the semiotic potential of a specific tool. On the one hand, the teacher organizes didactic situations where students use the tool and consequently are expected to generate specific personal meanings. On the other hand, the teacher organizes social interactions in order to support the transformation of the personal meanings that emerged in the artifact-centered activities into the mathematical meanings that constitute the teaching objectives.

Thus any artifact will be referred to as tool of semiotic mediation as long as it is (or it is conceived to be) intentionally used by the teacher to mediate a mathematical content through a designed didactical intervention. (Bartolini Bussi and Mariotti 2008, p. 758)

The complex semiotic processes of the emergence and transformation of personal meanings, evolving toward mathematical meanings can be developed through the design and implementation of the so-called didactical cycle (op. cit., p. 754 ff). Because of the specific focus of this contribution, the description of any more detail on this part of the model will not be dealt with.

Of course, in order to make use of a tool as a tool of semiotic mediation, the teacher needs to be aware of its semiotic potential both in terms of personal meanings that are expected to emerge when students are involved in specific tasks, and of the mathematical meanings that may be evoked by these activities. This asks for a careful a priori analysis, from both a cognitive and an epistemological perspective, of the use of a specific tool with respect to specific mathematical meanings that are educationally significant.

The discussion developed in the following section concerns the semiotic potential of a DGS with respect to the didactic goal of introducing students to conjecturing and developing the mathematical meaning of conditional statement, i.e., a logical dependency between premise and conclusion .

3 Transforming Figures in a DGS: Dragging and Invariants

Dynamic geometry provides, besides the traditional classic graphic representation, a new dimension—dynamism—that leads to a potentially quite powerful representation. The basic rationale behind dynamic geometry is that geometrical objects and properties can be presented in a dynamic format, which means that any figure that has been constructed using specific primitives can be acted upon by using the mouse .

This last action, generally referred to as “dragging” modality, constitutes the true novelty of such environments, and determines the well-known phenomenon of moving figures that gave the name to this category of softwares. After a construction is accomplished, the user may activate the dragging tool and determine the movement of the figure on the screen.

Perceiving the movement of the figure actually originates from the visual effect produced by a rapid sequence of images that are produced one after the other by the system according to the variation of the input (a new position of the dragged point) and the construction procedure given by the original sequence of the graphical tools. The perception of a moving figure comes from the fact that there is something that changes and something that is preserved: what is preserved—that is invariant—constitutes the identity of the object/figure in contrast to the changes that determines its transformation and consequently its movement.

Dynamic geometry exteriorizes the duality invariant/variable in a tangible way by means of motion in the space of the plane. (Laborde 2005, p. 22)

The invariants correspond to the properties that are preserved and allow the observer to recognize the sequence of images as the same element in movement. The interplay between variation and invariants is the core of the process of categorization, what allows us to recognize quite different objects as belonging to the same category, somewhat like recognizing a friend’s face over time.

But which are the “invariants” that are at the basis of the movement of figures in a DGS?

Actually, in a DGS like Cabri, there are two kinds of invariants appearing simultaneously as the dynamic figure is acted upon, and therefore “moves”: first, there are the invariants determined by the geometrical relations defined by the commands used to accomplish the construction, we call them direct invariants, and second, there are the invariants that are derived—indirect invariants—as a consequence within the theory of Euclidean geometry (Laborde and Sträßer 1990) .

The relationship of logical dependency between the two types of invariants corresponds to an asymmetry between the two types of invariants, an asymmetry that can also be recognized in the relative movement of the different elements of a figure. Dragging is accomplished by acting on the basic points, those from which the construction originates, but their movement will determine the motion of the other elements of the figure obtained through the construction. Thus, there are fundamentally two different types of movements that, as we will see in the following, are worth distinguishing and analyzing carefully: direct motion and indirect motion .

The direct motion of a basic element (for instance, a point) consists in the variation of this element in the plane under the direct control of the mouse.

The indirect motion of an element (a point of any other element of a figure) consists in the variation of this element as a consequence of the direct variation that can occur after a construction has been accomplished.

Therefore, the experience of dragging constructed figures allows the user to distinguish between direct invariants and indirect invariants, because the action of dragging can allow the user to “feel” motion dependency, which can be interpreted in terms of logical dependency. The distinction between direct and indirect invariants can be interpreted in terms of logical consequence between properties within the geometrical context. Consistently with this analysis, previous studies showed how the semiotic potential of dragging and constructions in Cabri could be exploited with the aim of introducing pupils to a theoretical perspective (Mariotti 2000, 2001, 2007, 2009) .

Starting from this phenomenological analysis of the dragging tool, we now focus on the specific task of conjecture generation to analyze the semiotic potential of specific dragging modalities that can be used to solve it . Our discussion is consistent with classic results coming from previous studies where the dragging strategies were described (Arzarello 2000; Hölzl 1996; Leung and Lopez-Real 2000; Leung and Lopez-Real 2002; Lopez-Real and Leung 2006; Healy 2000) , and aims to elaborate on them within the frame of the theory of semiotic mediation.

Specifically, we discuss how different dragging modalities can be used to produce a conditional statement . First, we consider the case of exploring the consequences of a certain set of premises, then we consider the case of finding under which conditions a given configuration takes on a certain property (as in Arzarello et al. 2002; Olivero 2002) .

4 Dragging to Produce a Conditional Statement

The term “open problem” is common in mathematics education literature (Arsac and Mante 1983; Silver 1995) to express a task that poses a question without revealing or suggesting the expected answer. In the geometry context, open problems can consist of tasks requiring the formulation of a conjecture starting from a given configuration, i.e., a figure of which specific properties are given . The solver is let free to explore the possible significant properties that are compatible with the original configuration and to formulate a conditional statement linking the given properties and their possible consequences. As the previous analysis highlights, dragging for producing a conjecture requires a complex interpretation of perceptual data coming from the screen; clearly, such an interpretation presents a higher complexity as compared to, for example, dragging to test the correctness of a construction. It is not enough to observe the figure and its movement globally, but it is also necessary to analyze and decompose the image appearing on the screen, according to its elements and their properties, in order to recognize a geometrically significant relationship between them.

4.1 Dragging to Search for Consequences

In this case, the statement of a conjecture is generated by the interpretation of perceived invariants taking into account their logical hierarchy induced by the original construction. Consider the following example .

ABCD is a quadrilateral in which D is chosen on the parallel line to BC through A, and the perpendicular bisectors of AD and BC are constructed (Fig. 9.1).

Fig. 9.1
figure 1

ABCD as a result of the construction described in the earlier example

Full size image

Dragging any of the free points, the constructed parallelism and perpendicularity are preserved, but it also happens that the parallelism between the two perpendicular bisectors is preserved. Complexity resides in being aware of the hierarchy induced on the different invariants, in spite of the fact that they are simultaneously perceived, and interpreting such a hierarchy as a logical dependency between properties of the “geometric figure.” In the earlier example, the exploration by dragging can lead to the following conjecture: “if two sides of the quadrilateral are parallel, then the corresponding perpendicular bisectors are parallel ” (Fig. 9.2).

Fig. 9.2
figure 2

The figures show the effect of dragging ABCD’s basic point C while trying to maintain the coincidence of the perpendicular bisectors

Full size image

In other words, what appears on the screen while dragging, that is, the fact that a specific relationship between invariants is preserved, corresponds to the general validity of a logical implication between properties of a geometrical figure.

The distinction between direct and indirect movements plays a key role in identifying and discerning the given properties and their consequences. As far as dragging is concerned, a dynamic figure moves when its basic points are acted upon. In the earlier example, A, B, and C are basic points of the dynamic figure and they can be dragged to any place on the screen (in this case, we speak of free dragging), while D can only be dragged along the parallel line to BC through A. The perpendicular bisectors, as dependent elements of the construction, cannot be directly acted upon, but they will move indirectly and their parallelism will be an indirect invariant . The different status of the elements of the figure, basic or dependent, as can be experienced through dragging, corresponds to the different logical status of the geometrical properties, premises, or consequences of a conditional statement . Therefore, we claim that the dragging tool used in solving a conjecture-production task has a semiotic potential recognizable in the relationship between:

  • Direct and indirect invariants and premise and conclusion of a conditional statement and

  • The dynamic sensation of dependence between the two types of invariants and the geometrical meaning of logical dependence between premise and conclusion.

4.2 Dragging to Search for a Premise

As shown by many studies in the literature, exploring the consequences of a certain set of premises is not the only possible use of dragging for generating conjectures. A different way involves the induction of a specific property by a “constrained” type of dragging. This way of dragging produces a new kind of invariant, which has been classified as a soft invariant, as opposed to a robust invariant that refers to direct invariants induced by a construction .

A soft invariant is a property “purposely constructed by eye, allowing the locus of permissible figures to be built up in an empirical manner under the control of the student” (Healy 2000; Laborde 2005) . The use of soft invariants in the solution of conjecture problems has been observed in previous studies and described with different names, like lieu muet or dummy locus dragging (Arzarello et al. 2002) . In a recent study, it has been referred to as maintaining dragging (Baccaglini-Frank 2010; Baccaglini-Frank and Mariotti 2010).

As explained earlier, the control of the status of the different kinds of invariants is based on an enacted distinction between direct and indirect movements. This distinction leads to consider the new type of invariant, emerging from the specific goal-oriented dragging as indirectly induced invariant: A property occurs because of the movement of a basic point. Such a movement is direct, but controlled by the objective of causing a specific property to occurFootnote 2 (Baccaglini-Frank 2010; Baccaglini-Frank and Mariotti 2010) .

Consider the following example. Given a quadrilateral, construct the bisector of its sides, their intersections generate a new quadrilateral. Dragging freely, one observes that in some circumstances the internal quadrilateral collapses in one point. This may represent an interesting property for the solver, thus he/she decides to explore under which circumstances this may happen. In the earlier example, it is possible to try to induce the soft invariant “coinciding perpendicular bisectors” and search for a specific condition under which such property occurs.

Using maintaining dragging, the special movement of a basic point intentionally induces the occurrence of a selected property and makes the figure assume a specific configuration as the consequence of a geometrical condition corresponding to the goal-oriented movement .

Once again we have the simultaneity of two invariants; however, they have a different status that comes from the different control exerted by the solver acting upon the figure. The haptic sensation of causality can be referred to the conditionality relating the unknown condition realized by the direct movement and the selected property indirectly induced as invariant, the first corresponding to the premise and the second to the conclusion of a conditional statement .

The different status of the two invariants is clearly discernible by their characteristics related to the exploration process carried out by the solver.

On the one hand, the indirectly induced invariant that will become the conclusion of the conjecture has the following characteristics that make it clearly recognizable :

It is a property that is intentionally selected and may be induced indirectly as (soft) invariant by moving a basic point.

On the other hand, the condition destined to originate the premise has the following characteristics:

It is searched for in response to the questions “what might cause the Indirectly Induced Invariant?”, it is recognizable in the constrained movement performed during the maintaining dragging.

In summary, the asymmetry of the relationship between invariants in a DGS offers a great potential with respect to distinguishing the logical status of the properties that determines their belonging to the premise or the conclusion . Thus, according to our analysis it is possible to outline the following semiotic potential of the maintaining dragging tool in solving a conjecture-production task, recognizable in the relationship between

  • The indirectly induced invariant, i.e., the property the solver intends to achieve, and the conclusion of the conjecture statement.

  • The invariant constrained by the specific goal-oriented movement, i.e., the property that must be assumed in order to obtain the induced invariant, and the premise of the conjecture statement.

  • The haptic sensation of causality relating the direct and indirect movements and the geometrical meaning of logical dependence between premise and conclusion .

5 The Teaching Experiment

As part of a broader research study (Baccaglini-Frank 2010) , a teaching experiment was carried out with students of scientific high schools (licei scientifici) (a total of 31: 14 pairs and 3 single students.). The students had been using a DGS, specifically Cabri, for at least 1 year prior to the study. Different dragging modalities were explicitly introduced during two 1-hour introductory lessons (for details, see Baccaglini-Frank 2010) . Specifically, we introduced the maintaining dragging in relation to exploring a configuration to formulate conjectures. Subsequently, pairs of students were observed during a problem-solving session where four different open problems were proposed .

During these interview sessions, we intended to observe and describe the relationship between students’ use of the different modalities of dragging, in particular of the maintaining dragging, and the production of conjectures.

Data collected included: audio and video tapes and transcriptions of the introductory lessons; Cabri files worked on by the instructor and the students during the classroom activities; audio and video tapes, screenshots of the students’ explorations, transcriptions of the task-based interviews, and the students’ work on paper that was produced during the interviews.

Among other results (for a full discussion, see Baccaglini-Frank 2010) , the analysis of the collected data provides evidence supporting the previous analysis concerning the semiotic potential of the dragging tool and in particular of maintaining dragging with respect to conjecture tasks . In the following section, we discuss two examples drawn from this corpus of data .

6 The Unfolding of the Semiotic Potential

During the interviews, pairs of students were observed while solving open problems in which the production of a conjecture was required . The use of different modalities of dragging and specifically the maintaining dragging modality was promoted so that we could observe the relationship between the enactment of dragging and the emergence of meanings related to it . The following examples illustrate students’ actions and their interpretations of their experiences with the images on the screen. The analysis of students’ behavior will be related to the mathematical meanings discussed earlier. We will observe how the semiotic potential of dragging modalities unfolds. For the reader’s convenience, the examples that we present will refer to the same open problem, which is reported subsequently .

Problem

  • Draw three points: A, M, and K.

  • Construct point B as the symmetric image of A with respect to M and C as the symmetric image of A with respect to K.

  • Construct the parallel line l to BC through A.

  • Construct the perpendicular to l through C, and construct D as the point of intersection of these two lines.

  • Consider the quadrilateral ABCD.

Make conjectures about the types of quadrilaterals that can emerge, and try to describe all the ways in which it can become a particular type of quadrilateral.

6.1 Dragging to Search for Consequence

The following excerpt concerns the kind of exploration carried out at the very beginning of the solving process. We can observe how two students (Pie and Ale) notice and describe an indirect invariant, after free dragging of a basic point .

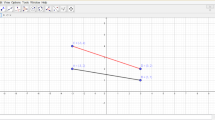
In the following excerpt, students are referring to the screen image which is shown in Fig. 9.3.

Fig. 9.3
figure 3

A screen shot from the students’ exploration in Cabri

Full size image

Excerpt 1

Transcript

Analysis

[1] Pie: the segment BC … if it varies what does it depend on?

Student’s attention focuses on one of the elements of the figure—segment BC—and he asks himself what does its variation depend on

[2] Pie: So, point B is the symmetric image of A …

In order to identify dependency, the student comes back to the given properties that determine the original configuration

[3] Ale: I think that the segment [pointing to BC] is fixed

[4] Pie: …and C is the symmetric image of A with respect to K. Therefore if I vary A, C varies too

[5] Pie: because…they are…I mean A has influence over both B and C

[6] Ale: But the distance between B and C always stays the same

In the exchange between the two students, the main elements come out: the identification of an invariant and the explicit expression of the dependence between basic points and constructed points. Ale identifies an invariant, Pie tries to link such invariance to the given properties, at the same time expressing such link in terms of dependency on the variation of basic points: “Therefore if I vary A, C varies too. […] I mean A has influence over both B and C”

[7] Pie: Here there is basically AK and KC, which are the same and AM and BM are always the same

[8] Ale: Yes, try to move it?

[9] Pie: yes

[10] Ale: Hmm

[11] I: What are you looking at?

[12] Ale: No, nothing, just that…I wanted to…now we can also put [Ale refers to the statement that they are asked to write as a conjecture ] that the distance between B and C always stays the same…in any case it does not vary

More invariants are identified. It seems that Ale is looking for geometrical reasons for their appearance, though he does not immediately see them. The control by dragging is invoked to verify them and decide to include them in the conjecture

However, dragging a basic point is invoked to check whether a certain property is a consequence; provided that it is invariant, a property should appear in the conjecture (“we can also put …”)

The main elements come out: the identification of an invariant and the explicit expression of the dependence between basic points and constructed points . When Ale identifies an invariant Pie tries to link it to the given properties [3–4], and expresses such links in terms of dependency on the variation of basic points: “Therefore if I vary A, C varies too. […] I mean A has influence over both B and C.”

This is a good example of how dragging is combined with the control over the direct and indirect movements of points, and of how this combination may be associated with logical dependency between properties, orienting the recognition of the status of premises and derived properties .

6.2 Dragging to Search for a Premise

Let us now consider an example of using the maintaining dragging modality . Here, after a first phase of exploration by free dragging, a pair of students start a more systematic investigation using the maintaining dragging mode, as it was introduced in the classroom. As we will see, they start searching for a condition to make the quadrilateral become a rectangle. It is possible to observe how this use of maintaining dragging allows the students to distinguish the status of the different properties involved.

The exploration of Fab and Gus

The problem is the same as in the previous example. After dealing with a first conjecture concerning the fact that the “quadrilateral is always a right trapezium,” the students notice the particular configuration “ABCD is a rectangle” and start dragging the basic point M trying to maintain this property, which we therefore refer to as the intentionally induced invariant . At the same time, Fab and Gus start to search for the condition that might be the cause that makes this property occur .

Excerpt 2.a

Transcript

Analysis

10 Fab: Ok, should we drag M now?

11 Fab: Let’s try to get a rectangle first

12 Fab: How was it?

13 Fab: Like this. Now let’s try to maintain …

14 Interviewer: rectangle

15 Fab: The property rectangle

16 Gus: Eh, going up

17 I: Slowly, slowly

…

20 Fab: No, no, it changes. It moves too much…

21 Fab: Should we try to do trace so we can see?

…

28 Fab: It looks like a curve

29 Gus: It would look like a nice circle again

30 Fab: Like this

31 Fab: It is not a straight line, for sure!

…

42 Fab: It looks like it goes through A

43 Gus: and through K

44 Fab: where?

45 Gus: It looks like a circle with diameter AK

46 Fab: Yes, it looks like a circle with diameter AK!

….

The solvers decide to activate the maintaining dragging on point M to induce the property “ABCD rectangle”

It is clear that for the students the direct motion has to cause the invariance of the property “ABCD rectangle”

Students are searching for regularities in the direct motion and in order to detect them the students decide to activate trace on M, as they say “so we can see”

The haptic sensation of dependency appears in the utterances 16–21, when modifications of the action of dragging is invoked after perceiving that maintaining is violated

After the use of trace, the direct motion—causing the property of being a rectangle to occur—is reified in the trajectory produced by the trace tool. The solvers recognize such trajectory as a circle and specifically as the circle of diameter AK

The first property “ABCD is a rectangle” is identified and fixed at the very beginning, while the condition slowly emerges through the enacted goal-oriented dragging process. In this case, as in others, the use of the trace tool is combined with the maintaining dragging; this leads to the reification of the direct movement of the basic point, facilitating the recognition of the searched condition. A trace of the haptic sensation of causality is expressed by the students’ verbal commentary to the dragging (16–21) .

Both the properties in focus (“ABCD rectangle” and “M on circle”) constitute soft invariants; the first is controlled “by eye” with a certain tolerance, the second emerges and is recognized after its reification in the trajectory produced by the trace tool. It is expressed as “the point M moves on the circle of diameter AK.”

In the following episode, we can find confirmation of students’ awareness of the different status of the two soft invariants .

Excerpt 2.b

Transcript

Analysis

50 Fab: So let’s draw the circle AK…

51 Interviewer: that you thought appeared

52 Fab: exactly, but first we need to…I mean I need to give it a centre, right?

53 Fab & Gus: So let’s construct the midpoint of AK. (They label it Z)

…

Fab suggests to construct robustly the circle identified in the product of the trace

64 Fab: I need to link M to the circle.

…

66 Fab: Because I am trying to maintain the

property rectangle dragging M along this circle…

Point M is linked to the constructed circle through the command “redefine object,” and Fab explains his goal “66 I’m trying to maintain ….”. It is clear that this robust property, obtained by construction, is recognized as the cause of the property “ABCD is rectangle”

69 Fab: That means, if M belongs to the circle with radius AZ and center Z …

70 Fab: then ABCD is a rectangle

Finally, the conjecture is given (69–70) in the form “if … than…”

The students construct the circle that was identified in the product of the trace, then point M is linked to it. Fab summarizes the interpretation of their phenomenological experience referring to the initial activity of exploration “66. Fab: I’m trying to maintain ….” It seems clear that they interpret the new directly induced invariant “M on the circle” as a cause of the indirectly induced invariant “ABCD rectangle .” All that finally (69–70) is expressed in a conditional statement, a conjecture of the form “if … then …”

Immediately after that, the conjecture is tested through constructing the premise and accomplishing a free dragging; the simultaneous appearance of the two robust invariants, confirms the conjecture .

We advance the hypothesis that as the solvers induce the invariants, the type of control that they experience over them can help them to perceive the asymmetry of their status in spite of the fact that they appear simultaneously. This may lead the students to interpret the dynamic relationship between the invariants as a conditional relationship between properties. Thus, perception of invariants together with the sensation of the causal relationship between them may be transformed into a conditional statement relating geometrical properties .

7 Conclusions

Though one should not under-evaluate the difficulty that students face in perceiving and interpreting dynamic phenomena occurring on the screen, the deep educational value of such activities motivates the effort requested in fostering it through adequate teaching interventions (Talmon and Yerushalmy 2004; Restrepo 2008; Baccaglini-Frank et al. 2009; Mariotti and Maracci 2010) .

However, with this contribution I want to go a step further: it is claimed that not only the use of different dragging modalities may lead students to successfully solve conjecture-generation tasks, supporting them in producing conditional statements, but also the dragging modalities offer a semiotic potential that can be exploited by the teacher to make the mathematical meaning of conditional statement evolve from haptic experience of direct and indirect movements, and the related different status of invariant properties .

Simultaneity, combined with the control of direct and indirect movements, makes the different status of each kind of invariant emerge as well as the counterpart of the logical dependency between a premise, corresponding to the constructed invariants and a conclusion, corresponding to the derived invariants. Specifically, the two kinds of invariants can be characterized referring to their specific status in the exploratory activity, their specific characteristics make them clearly recognizable by the students and they can be used by the teacher to exploit the semiotic potential of maintaining dragging .

In summary, different meanings emerging from the semantic of the DGS can be exploited to mediate the mathematical meaning of premise and conclusion and generally speaking, the mathematical notion of conditional statement. Specifically, the two kinds of invariants can be characterized referring to their specific status in the exploratory activity, their specific characteristics make them clearly recognizable by the students and they can be used by the teacher to exploit the semiotic potential of maintaining dragging.

The model elaborated in the TSM (Bartolini Bussi and Mariotti 2008) describes the main components of the process that starts with the student’s use of an artifact to accomplish a task and leads to the student’s appropriation of a particular mathematical content. Taking a semiotic perspective, such a description is provided in terms of transformation of signs: personal signs, referring to meanings emerging from students’ activities with the artifact, are expected to be transformed into mathematical signs. Such a transformation is not spontaneous, rather it has to be fostered by the teacher through organizing specific social activities designed to exploit the semiotic potential of the artifact. Collective mathematical discussions (Bartolini Bussi 1998) constitute the core of these activities, on which teaching and learning is based. The whole class is engaged: taking into account individual contributions and exploiting the semiotic potentialities coming from the use of a particular artifact, the teacher’s action aims at fostering the transformations from personal meanings to mathematical meanings (Mariotti 2009; Mariotti and Maracci 2010) .

Further investigations are necessary to explore the whole process of semiotic mediation related to the different dragging modalities. Teaching experiments designed according to a specific didactic organization (didactical cycle) described in the TSM (Bartolini Bussi and Mariotti 2008) have been planned, and are in progress, in order to collect evidence of how the semiotic potential of different dragging modalities can be exploited in classroom activities and how the transformation of signs might actually be realized. However, this will be the theme of another paper.