Abstract
In this chapter, we will first introduce the basics of geolocation techniques that are based on Time of Arrival (TOA), Time Difference of Arrival (TDOA), Angle of Arrival (AOA), and Received Signal Strength (RSS). Then we introduce the major challenges to accurate localization: multipath propagation and non-line-of-sight conditions where we will focus on the two most popular ranging techniques, TOA and RSS, and evaluate how the accuracy of localization is affected by these physical challenges. We will further highlight the relationship between the accuracy of estimation and the signal to noise ratio and bandwidth parameters through the well-known Cramer-Rao Lower Bound (CRLB) equations. Finally, we will introduce measurement and modeling of the RSS/TOA ranging that will highlight the impact of multipath and NLOS on the accuracy of ranging systems.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
In this chapter, we will first introduce the basics of geolocation techniques that are based on Time of Arrival (TOA), Time Difference of Arrival (TDOA), Angle of Arrival (AOA), and Received Signal Strength (RSS). Then we introduce the major challenges to accurate localization: multipath propagation and non-line-of-sight conditions where we will focus on the two most popular ranging techniques, TOA and RSS, and evaluate how the accuracy of localization is affected by these physical challenges. We will further highlight the relationship between the accuracy of estimation and the signal to noise ratio and bandwidth parameters through the well-known Cramer-Rao Lower Bound (CRLB) equations. Finally, we will introduce measurement and modeling of the RSS/TOA ranging that will highlight the impact of multipath and NLOS on the accuracy of ranging systems.
2.1 Basics of Geolocation
Classical geolocation techniques (non-survey based) depend on geometrical relationships between the coordinates of the reference points (satellites in GPS technology) and the associated range/angle measurements. Typically, reference points are wireless devices with known location information (e.g. x- and y-coordinates) either pre-programmed or obtained through GPS. The mobile device (seeking its own position information) exchanges RF signals with the reference points to estimate the distance or angle to each of the reference points. Equipped with the range measurements and the coordinates of the reference points, the mobile device can solve for the unknown position through a variety of techniques (geometrical, optimization, etc.). The accuracy of the location information is affected by three major factors: the accuracy of the reference points’ position, the accuracy of range/angle estimates, and the geometrical configuration of the reference points and the unknown position. The non-survey geolocation techniques computes location estimates through two steps: range/angle estimation and tri-lateration/angulation. Figure 2.1 illustrates the two-step procedure.
Classical geolocation system. Range or angle information is extracted from received RF signals. Location is then estimated by lateration/angulation techniques
In this section we will introduce the most popular geolocation techniques: TOA, TDOA, AOA, and RSS and provide an evaluation of the achieved accuracy through the well-known Cramer-Rao Lower Bound (CRLB) analysis.
2.1.1 TOA-Based Techniques
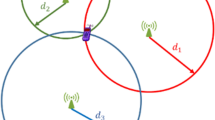
Once distance/range measurements to at least 3(4) reference points are available the 2(3)-dimensional position estimate can be obtained. The set of distance measurements from the reference points to the mobile terminal forms a set of nonlinear equations that can be solved to estimate the position. Here, it is assumed that the mobile terminals exchanging range measurements are time synchronized and that they are all in LOS condition (no obstruction between the mobile device and the base stations). Figure 2.2 illustrates the basic concept of tri-lateration.
TOA-based tri-lateration. Range measurements to at least three base stations make up a set of nonlinear equations that can be solved to estimate the position of a mobile device. Black points are base stations with a priori known position information while the intersection of the circles is the position estimate of the mobile device
The range measurements can be used to estimate the position of a mobile device through several techniques that are generally grouped under Maximum Likelihood (ML) and Least-Squares (LS) Techniques. In ML techniques, the solution is the position that maximizes the conditional probability density function or
where \( {\hat{\varvec{\theta }}} = [\hat{x},\hat{y}]^{T} \) and \( {\varvec{\theta}} = [x,y]^{T} \) are the estimated and true position coordinates, respectively. \( {\hat{\mathbf{d}}} = {\mathbf{d}} + {\mathbf{w}} \) is the measured/estimated distance vector to each base station or \( {\hat{\mathbf{d}}} = \left[ {\begin{array}{*{20}c} {\hat{d}_{1} } & {\hat{d}_{2} } & \ldots & {\hat{d}_{{n_{B} }} } \\ \end{array} } \right]^{T} \), \( {\mathbf{w}} \) is zero-mean Gaussian measurement noise and \( n_{B} \) is the number of base stations. Assuming that the noise measurements are independent and identically distributed (i.i.d), then the conditional distribution is given by
where \( \sigma_{i}^{2} \) is the variance of the ith measurement noise. There are two major problems with this ML approach. The first is that conditional PDF requires the knowledge of the exact distances, which is not available in practice. The second is that solving for the position using the maximization approach requires a search over all possible locations which is neither practical nor computationally efficient (Guvenc and chong 2009). There are also some variants of the original ML technique which are the two-step ML and the approximate ML (AML). The interested reader can find more details about the ML techniques in Guvenc et al. (2006), Chan and Ho (1994).
The other class of TOA-based localization algorithms is based on the LS techniques. The range measurements to the reference points form a set of nonlinear equations of which the solution is the mobile position. The LS techniques are further subdivided into nonlinear LS (NL-LS) and the linearized LS (L-LS). The NL-LS technique estimates the position by minimizing a residual error function (Caffery and Stuber 1998) or
Thus the residual, \( R_{\text{es}} \left( {\varvec{\theta}} \right) \), is a measure of error between the measured distances, \( \hat{d}_{i} \), and the estimated distance obtained from computing the Euclidean distance between the reference points and the estimated position, \( \left\| {{\varvec{\theta}} - {\varvec{\theta}}_{i} } \right\| \). \( \beta_{i} \) is a weight that can be used to emphasize range estimates which is proportional to the degree of confidence in the measurement. The L-LS solution is obtained by linearizing the nonlinear equations formed by the \( n_{B} \)distances given by
where \( \left[ {x_{n} ,y_{n} } \right] \) are the coordinates of the nth base station. The linearization is obtained through the well-known Taylor series expansion around \( {\varvec{\theta}}_{0} \) given by \( {\mathbf{F}}\left( {\varvec{\theta}} \right) \approx {\mathbf{F}}\left( {{\varvec{\theta}}_{0} } \right) + {\mathbf{J}}\left( {{\varvec{\theta}} - {\varvec{\theta}}_{0} } \right) \) Kay (1993) where \( {\mathbf{J}}\left( {{\varvec{\theta}} - {\varvec{\theta}}_{0} } \right) \) is the Jacobian of \( {\mathbf{F}} \) evaluated at \( {\varvec{\theta}}_{0} \) and it is given by
and the L-LS solution (mobile position estimate) is then given by Kay (1993)
where H is the Hermitian operation. Typically, the accuracy of localization is affected by the accuracy of the base station location; the statistics of the range measurements and the geometry of the base stations with respect to the mobile terminal. The performance of TOA-based localization can be examined by evaluating the Cramer-Rao Lower Bound (CRLB), which provides the lower bound on the variance of the estimate or Kay (1993)
where \( {\mathbf{I}}({\varvec{\theta}}) \) is the Fisher Information Matrix (FIM) and \( E[ \bullet ] \) is the expectation operation. The FIM is given by Kay (1993)
where \( f({\hat{\mathbf{d}}}|{\varvec{\theta}}) \) is the joint PDF of \( {\hat{\mathbf{d}}} \) condition on the unknown parameters. The measured distances are modeled by
where \( {\mathbf{d}} \) is the vector containing the actual (exact) distances between the mobile device and the BS and \( {\mathbf{w}} \) is the zero-mean Gaussian measurement noise. Since the joint PDF is a function of \( {\mathbf{d}} \) which is a function of \( {\varvec{\theta}} \), then from the chain rule
So (2.7) can be rewritten as
where \( {\mathbf{J}} \) is the Jacobian given in (2.4) or explicitly
or alternatively
where \( \phi_{n} \) is the angle between the mobile device and the nth BS. The joint PDF of the distance measurements is given by
where \( {\varvec{\Upsigma}} \) is the covariance. \( {\mathbf{I}}_{{\mathbf{d}}} \) can then be easily derived and it is given by
The CRLB for the mobile device position is then given by
Another popular metric to characterize the accuracy of localization is the Geometric Dilution of Precision (GDOP) which describes the amplification of the errors in range measurements to the location error (Patwari et al. 2003) and it is given by
where \( \sigma_{x}^{2} \) and \( \sigma_{y}^{2} \) the variances of the position estimate and \( \sigma_{r} \) is the standard deviation of the range measurement error. An alternative expression for the GDOP could be derived to emphasize the geometrical relationship between the BSs and the mobile device Spirito (2001)
where \( \phi_{ij} \) is the angle between the ith and jth BSs.
Although the CRLB derivations in this subsection assumed single-path ideal propagation (simplified zero-mean Gaussian noise model) it can provide a starting point to evaluate the performance and understand the main factors that can affect the accuracy. Different CRLB derivations that address the NLOS problem can be found in Qi et al. (2006), Dardari et al. (2006), Shen et al. (2007). The accuracy of the TOA-based techniques relies heavily on the measurement noise and the multipath condition of the channel. Thus the CRLB will only be meaningful when the models are realistic in that they reflect the actual propagation conditions. In addition it is common to assume that the BS and the mobile device are synchronized, but this is not the case in practice.
2.1.2 TDOA Techniques
Time Difference of Arrival (TDOA) technique is based on the idea that the position of the mobile device can be determined by examining the difference in time at which the signal arrives at multiple reference points (Liu et al. 2007). Adopting this technique is useful in practical scenarios where synchronization between mobile devices is not available. Each TDOA measurement constrains the location of the mobile device to be on a hyperboloid with a constant range difference between the two reference points. For two-dimensional position estimation three reference points are required. Figure 2.3 illustrates the localization technique based on TDOA measurements.
TDOA localization. At least three BS are required for two-dimensional localization. The time (range) differences \( d_{2} - d_{1} \) and \( d_{3} - d_{1} \) form two hyperboloids of which the intersection (solution) is the estimated position
A TDOA measurement between BS1 and BS2 can be given by Sayed et al. (2005)
where \( t_{0} \) is the clock time of the mobile device, \( t_{1} \) and \( t_{2} \) are the TOA between the mobile device and BS1 and BS2 respectively. The equation can be written in terms of distance through speed of light scaling or \( d_{21} = \left( {t_{2} - t_{1} } \right)c \). Thus the time difference (or range difference) is \( d_{21} = d_{2} - d_{1} \) where \( d_{2}^{2} = \left( {x_{2} - x} \right)^{2} + \left( {y_{2} - y} \right)^{2} \) and \( d_{1}^{2} = \left( x\right)^{2} + \left( y\right)^{2} \). Without loss of generality, the latter equation is valid with the assumption that the x- and y-coordinates of BS1 are \( \left( {0\hbox{,0}} \right) \). The range difference equation can be rearranged to \( d_{21} + d_{1} = d_{2} \). The TDOA equation can then be obtained by squaring both sides or
Using \( K_{2}^{2} = x_{2}^{2} + y_{2}^{2} \) the above equation simplifies to
which can be further rearranged to solve for the unknowns or
Two equations are required to solve for the two unknowns and the second TDOA equation between BS3 and BS1 can be similarly obtained
The equations can be arranged in matrix form given by Sayed et al. (2005)
where \( {\mathbf{a}} = \left[ {\begin{array}{*{20}c} { - d_{21} } \\ { - d_{31} } \\ \end{array} } \right] \), \( {\mathbf{b}} = \frac{1}{2}\left[ {\begin{array}{*{20}c} {K_{2}^{2} - d_{21}^{2} } \\ {K_{3}^{2} - d_{31}^{2} } \\ \end{array} } \right] \). Solving for θ we have
Extension to more reference points and three dimensions is trivial and more details can be found in Sayed et al. (2005).
The performance of TDOA-based localization can be similarly examined by evaluating the CRLB. A similar derivation of the CRLB for TDOA localization follows from (2.7). In fact it can be shown that the TDOA CRLB is given by Qi et al. (2006)
where
where \( \phi_{n} \) is the angle between the mobile device and the nth BS.
2.1.3 AOA-Based Techniques
Localization using angle-of-arrival is simpler than time-based techniques in that only two angle measurements are required, as opposed to three range measurements, in order to estimate the two-dimensional position. However the challenge is presented when obtaining accurate angle of arrival estimation using wireless devices. In typical scenarios, the base stations are equipped with K antenna array elements spaced by \( \Updelta \) which are capable of estimating the angle of arrival which is then used to locate the mobile device. Figure 2.4 illustrates the basic concept of AOA localization.
AOA positioning (angulation). The AOA estimate from 2 base stations to the mobile terminal can be used to estimate the position
The relationship between the coordinates and the angles is given by
These equations can be combined to estimate the position of the mobile terminal as Dempster (2006)
The CRLB for AOA can be similarly obtained from the formulation in (2.6) and (2.7), but with specific models for the angle measurements. In practice, the antenna array is capable of measuring a function of the angle or Qi et al. (2006)
where \( n \) is the index identifying the BS and \( w_{n} \) is a zero mean Gaussian noise with a variance given by Qi et al. (2006)
where \( {\mathbf{a}}_{n} (\varphi_{n} ) \) is the steering vector for a specific antenna array configuration and \( \Upupsilon \) is the Signal to Noise Ratio (SNR). For an antenna array with K elements spaced by \( \Updelta \) the steering vector is given by
where \( \varphi_{n} = 2\pi \Updelta \cos \phi_{n} \). The variance of the estimation error is then given by Qi et al. (2006)
Given the above model parameters of the AOA localization system the CRLB can be given by Qi et al. (2006)
where
and
The performance of AOA positioning techniques in LOS conditions is satisfactory. However, in severe NLOS multipath conditions the reliability and accuracy of AOA techniques suffers considerably. As a result in these unfavorable propagation conditions, TOA- or RSS-based techniques are preferred. Furthermore, hybrid positioning techniques can be used to incorporate the advantages of two different techniques which usually outperform the individual techniques.
2.1.4 Received Signal Strength Localization
Localization using Received Signal Strength (RSS) is very similar to TOA-based technique in that the distances to \( n_{B} \) base stations are used in a tri-lateration approach to estimate the position. The difference is the method in which the distance is estimated. For a mobile device and \( n_{B} \) base stations, the unknown location can be estimated using the LS method similar to that of the TOA presented in (2.5) or
The difference between (2.37) and (2.5) is the estimated distance vector. For RSS-based localization the distance can be estimated through the power–distance relationship that is very well known for wireless propagation in different environments. The RSS between the mobile device and the nth base station is modeled by
where \( \gamma \) is the pathloss exponent (governing the rate of power decay with distance), \( S_{n} \) is the log-normal shadow fading component with variance \( \sigma_{{S_{n} }}^{2} \) and \( d_{n} \) is the distance between the mobile devices and the nth base station. The ML estimate of the distance is given by \( \hat{d}_{n} = 10^{{\left( { - P_{r} } \right)/\left( {10\gamma } \right)}} \) Patwari et al. (2003). Then the distance vector in (2.37) is given by \( {\hat{\mathbf{d}}}_{\text{RSS}} = [\hat{d}_{1} ,\hat{d}_{2} , \ldots ,\hat{d}_{{n_{B} }} ]^{T} \). The CRLB for RSS-based localization can be similarly derived from (2.6) to (2.7) (Qi et al. 2006)
where
and
2.2 The Multipath Problem
The presence of multipath fading in harsh propagation environments can have a significant impact on the performance of TOA-, RSS-, or AOA-based ranging and localization systems. Multipath is the reception of multiple copies of the transmitted signal—each arriving from different propagation paths—which combine in either a constructive or destructive manner that distorts the received signal. The transmitted signal undergoes reflections and diffractions along different propagation paths to the receiver. At the receiver, replicas of the transmitted signal arrive attenuated, phase-shifted, and time-delayed. For RSS-based systems, multipath causes the well-known fast fading phenomenon, where the received power in a given location fluctuates significantly due to constructive and destructive interference of incoming multipath signals. For TOA-based systems, the multipath impacts the distance estimation directly by adding a random bias to the estimation. In this section, we will introduce the multipath problem and highlight its impact on RSS- and TOA-based ranging/localization systems.
In order to appreciate the impact of multipath, it is important to analyze it in LOS environments, since multipath is the major error contributor. LOS propagation can behave drastically different based on the environment. For example, performance in outdoor open-field LOS, outdoor urban LOS, and indoor LOS can exhibit different TOA estimation behavior. In outdoor open-field LOS, the direct path between the transmitter and receiver is unobstructed and there is at least a single ground reflection at the receiver. In urban LOS or indoor LOS, there may be many signals arriving at the receiver that were reflected or diffracted from the surrounding buildings or objects. Figure 2.5 illustrates different possible LOS multipath scenarios.
LOS multipath channels. a Outdoor open space—single bounce model, b urban LOS, c indoor LOS
In outdoor open space, the multipath structure is mainly composed of the direct path signal and a single-bounce ground reflection (see Fig. 2.5a). In urban LOS, reflections from the surrounding buildings make up the multipath environment (see Fig. 2.5b). The density of the buildings and surrounding obstacles will dictate the structure of the multipath environment. Finally, in indoor LOS environments, the multipath structure can be significantly different as there are reflections from the many cluttering objects and also reflections from walls, doors, and windows with closer interarrival of multipath components at the receiver (see Fig. 2.5c). This creates an environment that is very different from the urban environment.
Formally, the multipath can be modeled by
where \( L_{p} \) is the number of MPCs, \( \alpha_{k} \) and, \( \phi_{k} \) and \( \tau_{k} \) are amplitude, phase and propagation delay of the kth path, respectively (Pahlavan and Levesque 2005; Rappaport 1996). The received waveform is then given by \( r(t) = h(t) * s(t) \) where \( s(t) \) is the transmitted signal waveform and (*) is the convolution operator.
2.2.1 TOA-Based Ranging in LOS Multipath Channels
The basic idea behind TOA-based ranging is to estimate the distance between a transmitter and a receiver through measuring the signal propagation delay. For a transmitter at location \( (x_{1} ,y_{1} ) \) and a receiver at location \( (x_{2} ,y_{2} ) \) the Euclidean distance is given by \( d = \sqrt {(x_{1} - x_{2} )^{2} + (y_{1} - y_{2} )^{2} } \). In practice the distance can be calculated from the speed of light/propagation delay relationship given by \( c = d/\tau \), where \( c \) is the speed of signal propagation (in free space \( c = 3e8\,\text{m/s} \)) and \( \tau \) is the propagation delay. But in realistic applications, the propagation delay estimates are always corrupted by noise—additive white Gaussian noise (AWGN). Thus, the measured distance can be written as \( \hat{d} = c \times \tau + w = d + w \). Here \( w \) is a zero-mean Gaussian noise. In practice, the delay can be estimated using two methods: one-way TOA ranging or two-way TOA ranging. The latter requires no synchronization and it is the basic ranging technique proposed in IEEE 802.15.4a (IEEE 802.15.TG4a). The former requires strict synchronization since the distance is estimated from the received waveform. This is practically challenging for two reasons. The first is that extracting the TOA of the first path arrival is difficult (Lee and Scholtz 2002; Guvenc and sahinoglu 2005). The second is that synchronization of wireless devices in multipath environments is very difficult to achieve and is in fact an open research area. The main challenges are due to the clock drift over time and the effect of temperature and humidity on the accuracy of clock frequency (Sundararaman et al. 2005). Two-way TOA ranging techniques are the most popular due to the fact that they do not require synchronization and the protocols are very simple. For treatment of one-way TOA ranging further details can be found in (Guvenc and sahinoglu 2005). Two-way TOA ranging is achieved by noting the time that the ranging reference signal is sent out with the time it takes to receive it. Figure 2.6 illustrates an example where Device 1 is attempting to estimate the distance to Device 2.
Two-way TOA ranging. Devices 1 and 2 exchange transmit and receive time information. With these four time stamps, the propagation delay (distance) between the devices can be estimated
Device 1 initiates the two-way ranging by sending a ranging packet (signal) to Device 2 and noting the time as \( t_{TX1} \). Device 2 receives the signal at \( t_{RX2} \) and prepares its own ranging signal (after a processing delay) and sends out a response ranging signal at time \( t_{TX2} \). Finally Device 1 receives the response at \( t_{RX1} \). Given that Device 2 shares the time stamp information \( t_{RX2} \) and \( t_{TX2} \) with Device 1 it is now possible to estimate the propagation delay (distance) between the two devices by
where \( t_{\text{total}} = 2\tau + t_{\text{round - trip}} \) is the total time it takes for the two-way ranging and \( t_{\text{round - trip}} \) is the round-trip delay at Device 2. The assumptions regarding this two-way TOA ranging are overly simplistic and not valid in practice. In reality, the clocks of the two devices are not synchronized and not perfect. This means that with time the clocks will drift and the delay estimation will not be accurate (biased). Recently, researchers have investigated this problem and proposed some practical techniques to estimate the delay in non-ideal scenarios (clock drift and bias) (Zheng and Wu 2010; Wu et al. 2011).
The performance of TOA estimation in single path AWGN ideal scenario is usually analyzed using the Cramer Rao Lower Bound, which is a statistical approach to quantifying the variance of TOA estimation. Essentially any algorithm, in theory, can achieve the CRLB given that both the CRLB and algorithm follow the same assumptions (for example LOS single path model and same noise variance). The variance of TOA estimation \( \sigma_{\text{TOA}}^{2} \) is bounded by the CRLB given by Gezici et al. (2005),
where \( T \) is the signal observation time, \( \Upupsilon \) is the SNR, \( f_{0} \) is the frequency of operation, and \( B \) is the system bandwidth. This relationship highlights that the accuracy of TOA estimation can be improved by either increasing the SNR—since higher signal level will enable the estimation of the direct path signal with greater accuracy—or increasing the system bandwidth—since higher system bandwidth means higher time–domain resolution leading to better range estimates. The increase in time–domain resolution of the channel can be attributed to narrower time–domain signals/pulses. This makes it possible to discriminate or resolve the different multipath arrivals and improve the TOA estimation. Multipath signals (especially in dense cluttered environment) tend to arrive fairly close to the direct path. If the interarrival time between the multipath components is much smaller than the time–domain resolution of the system (low bandwidth systems) then at the receiver those multiple signals will combine to create a new cluster. The TOA estimate (from the receiver’s point of view) will then be the peak of the cluster. In order to clarify this phenomenon, Fig. 2.7 illustrates a power delay profile example and the resulting envelope. A power delay profile is a representation of the channel impulse response where the power from different arrival paths can be measured and analyzed. In the figure there are ten multipath components where the first multipath component is the strongest and, in this case, is the LOS or direct path. The multipath components arriving after the direct path fall in close proximity to each other (because of the nature of the propagation environment). For this narrowband system, the multipath components arrive and combine (due to low time–domain resolution) and appear at the receiver as four multipath components (the peaks of the blue envelope). As a result, the peaks will ultimately be detected as path arrivals. The first path arrival will be estimated as the LOS path and thus used for distance estimation. It is clear in this case that the actual TOA is not equal to the estimated TOA. This difference in estimation is the multipath error.
Power delay profile highlighting the multipath error corrupting TOA-based range estimates
For higher system bandwidths, the multipath error in LOS environments is usually smaller. For example, Fig. 2.8 illustrates a measured channel impulse response (measurement systems will be described in detail later in the chapter) for 200 MHz bandwidth in a typical LOS office environment.
Measured power delay profile highlighting TOA estimation in indoor LOS office at 200 MHz bandwidth
As can be seen from the figure, the actual/expected TOA is very close to the peak of the measured TOA of the first path. Also, note that there are about 15 multipath components for a noise threshold of –85 dBm. These non-direct multipath components can originate from wall reflections, furniture diffractions, and scattering from other objects in the office.
One way to assess the performance of TOA-based ranging is to analyze the ranging error. In LOS environments, the ranging error could be attributed to both multipath and measurement noise. Let \( \alpha_{1}^{\text{DP}} \) and \( \tau_{1}^{\text{DP}} \)denote the DP amplitude and propagation delay, respectively. The distance between the transmitter and the receiver is \( d^{\text{DP}} = \nu \times \tau_{1}^{\text{DP}} \), where \( \nu \) is the speed of signal propagation. Then ranging error which is defined as the difference between the estimated and the actual distance or,
In a general LOS multipath environment, the ranging device will experience varying error behavior depending on the structure of the propagation environment and the system bandwidth. In LOS, the distance estimate can be modeled by
where \( \varepsilon_{\text{DP}} = \tilde{b}_{m} (B) \) is a bias induced by the multipath and it is a function of the system bandwidth and \( w \) is a zero-mean additive measurement noise. As we will later discuss, the statistics of the multipath bias can be modeled differently. One popular approach is to model it spatially as a zero-mean Gaussian (Alavi and Pahlavan 2003). This means that an ensemble of LOS measurements in a given LOS environment will generally result in a Gaussian distribution. The variance of the distribution will be directly related to the variation in the multipath structure in a given environment. For example, the spatial variance in an indoor office environment is typically higher than the variance in an outdoor, flat terrain.
An analytical treatment of the performance of TOA estimation in multipath environments can be found in (Dardari et al. 2009) where Ziv-Zakai Bounds are introduced for realistic propagation environments.
2.2.2 RSS-Based Ranging in LOS Multipath Environments
Unlike TOA-based ranging, RSS-based ranging depends on an a priori power–distance relationship or pathloss model. The power–distance relationship has been investigated extensively in wireless communications for different technologies (Pahlavan and Levesque 2005; Rappaport 1996). In many of the experimental findings, the distance is related to the power law. For a narrowband transmitted signal in free-space with transmitted power \( P_{t} \), the received signal power \( P_{r} \) is given by Pahlavan and Levesque (2005)
where \( G_{t} \) and \( G_{r} \) are the transmitter and receiver antenna gains, respectively. \( \lambda \) is the wavelength of the transmitted signal and \( d \) is the distance between the transmitter and receiver. A reference received power at distance \( d = 1\,\text{m}\) is usually defined as \( P_{0} = P_{t} G_{t} G_{r} (\lambda /4\pi )^{2} \) then the distance–power relationship in free space can be given by
RSS ranging is based on models which assume an a priori relationship between the distance and the received power (or pathloss of the signal). A popular model in LOS channels relates the received power to the transmitted power by the following equation
where \( \gamma \) is the pathloss exponent that determines the rate of power loss with increasing distance. Note that this is equivalent to (2.48) for \( \gamma = 2 \). If we define pathloss to be the ratio of received power to transmitted power then the above power–distance relationship can be rewritten in terms of pathloss \( L \) given by
where \( L_{0} = 10\log_{10} P_{t} - 10\log_{10} P_{0} \) and \( L = 10\log_{10} P_{t} - 10\log_{10} P_{r} \). In order to model the power–distance relationship more accurately, a random component that models the shadow (slow) fading is included or
where \( S \) is a normally distributed random variable in the log domain and it models the fluctuation of the signal away from the median pathloss. This fluctuation stems from the presence of different obstructions between the transmitter and receiver which “shadow” the signal. RSS-ranging is mainly affected, however, by fast-fading (Pahlavan and Levesque 2005; Rappaport 1996). At the receiver, the attenuated and phase shifted replicas of the transmitted signal combine either constructively or destructively. The effect is a fast fluctuation of power at a given distance. One way to deal with this fast fading problem is to collect more RSS measurements and “average out” the fluctuations by taking the mean of the measurements. Then, for a given pathloss exponent and \( P_{0} \), the Maximum Likelihood Estimate (MLE) of the distance between a transmitter and a receiver can be estimated from the measured received power as Patwari et al. (2003)
The major weakness with RSS-based distance estimation is the assumption that the pathloss exponent (pathloss model) is known a priori when in fact the exponent changes between multipath environments—and even within the same environment. Furthermore, the accuracy of the range estimate cannot be improved by averaging the received signal power alone. Averaging of the RSS prior to estimating the distance will only remove the small-scale fading (fast fading) due to the multipath but not the shadow fading (which is more common in NLOS environments). Typical values for the pathloss exponent in LOS multipath environments range between 1 and 2 (Pahlavan and Levesque 2005). There are approaches that attempt to estimate the pathloss exponent prior to the localization stage, but that approach presents some challenges as well (Li 2006). The statistical performance of RSS ranging can be analyzed through the well-known CRLB given by Qi and Kobayashi (2003)
where \( \sigma_{S}^{2} \) is the variance of the shadow fading term. This relationship indicates that RSS-based ranging estimation is affected by the pathloss exponent and the variance of the shadow-fading in addition to the distance. As the distance increases, RSS estimation degrades. More importantly, as the variance of the shadow fading increases, the variance of RSS ranging also increases. This basic, yet powerful relationship highlights the challenges of RSS-based ranging. In typical multipath environments, the shadow fading variance is significant and thus reliable estimation of the distance can be difficult. In addition, the inverse dependency on the pathloss exponent indicates that performance of RSS ranging in LOS environments (lower pathloss exponent ~1–2) is expected to be much better than NLOS environments (typical pathloss exponents ~3–5). These challenges to RSS-based ranging make it a more practical, but inaccurate option for localization.
2.3 The NLOS Problem
This section introduces the NLOS problem and describes the impact of NLOS channels on TOA- and RSS-based ranging. For the former, NLOS affects the estimation of the direct path signal. Since in most cases the direct path will not be detectible, ranging is achieved through non-direct path components which bias TOA-based estimation. For the latter, NLOS introduces the problem of shadow fading, where RSS is attenuated randomly as the mobile device moves from one area to the other.
2.3.1 TOA-Based Ranging in NLOS Multipath Environments
In the previous section, the basics of TOA-based ranging in LOS environments were introduced. A natural extension of the LOS case is a more challenging and complex situation where the transmitter and receiver experience an NLOS multipath channel. Specifically, when considering NLOS cases, there is an obstruction in the path of the transmitter and receiver. Depending on the type of obstruction and the relative distances of the transmitter/receiver to the obstruction, the channel behavior can vary significantly. There are two specific NLOS cases that occur in typical obstructed environments. The first is when the direct path (DP) signal is attenuated but detected (albeit weak SNR). This situation can arise naturally when the transmitter and receiver are separated by “light” obstructions such as a glass or a wooden door. Indeed, in this scenario TOA estimates can be obtained with good accuracy due to the detection of the DP signal. The second NLOS case is when there is a “heavy” or severe obstruction between the transmitter and receiver, where the direct path is severely attenuated and “buried” under the noise floor of the receiver, making it undetectable. The first non-Direct path (NDP) component is then used for TOA estimation. This results in a significant bias that corrupts the TOA estimation and ultimately the position estimate. In this severe NLOS condition, the variance of TOA estimation with time is usually large due to the fact that the estimated first arrival path varies significantly due to the shadowing problem. For a quasi-static channel, the first path can be detected. However, when some perturbation is introduced to the multipath structure (another person moves around/close to the TX-RX path), then the estimation of the first path arrival will fluctuate significantly. It is clear, then, that NLOS does not only introduce a bias, but also introduces significant TOA estimation perturbations that can degrade the real-time distance estimation.
Formally stated, in the absence of the DP, ranging is achieved using the amplitude and propagation delay of the first Non-Direct Path (NDP) component—denoted as \( \alpha_{1}^{\text{NDP}} \) and \( \tau_{1}^{\text{NDP}} \) respectively—resulting in a longer distance \( d^{\text{NDP}} = \nu \times \tau_{1}^{\text{NDP}} \), where \( d^{\text{NDP}} > d^{\text{DP}} \). In order for the receiver to successfully identify the DP, the ratio of the strongest multipath component to that of the DP, given by
must be less than the receiver dynamic range, \( \kappa \), and the power of the DP must be greater than the receiver sensitivity, \( \varphi \). These constraints are given by
where \( P_{\text{DP}} = 20\log_{10} \left( {\alpha_{1}^{\text{DP}} } \right) \).
In an indoor environment the mobile device will experience varying error behavior depending on the availability of the DP and, in the case of its absence, on the characteristics of the DP blockage. It is possible to categorize the error based on the following ranging states (Alsindi et al. 2009). In the presence of the DP, both the constraints above are met and the distance estimate is accurate, yielding
where \( \tilde{b}_{m} \) is the zero-mean random bias induced by the multipath, \( b_{\text{pd}} \) is the bias corresponding to the propagation delay caused by NLOS conditions and \( w \) is a zero-mean additive measurement noise. It has been shown that \( \tilde{b}_{m} \) is indeed a function of the bandwidth and signal to noise ratio (SNR) (Pahlavan et al. 1998), while \( b_{\text{pd}} \) is dependent on the medium of the obstacles (Gentile and Kik2007). In the more severe case, the DP is completely attenuated and the requirement that \( \kappa_{1} \le \kappa \) is not met because the DP is shadowed by some obstacle, burying its power under the dynamic range of the receiver. In this situation, the ranging estimate experiences a larger error compared to the LOS condition. Emphasizing that ranging is achieved through the first arriving NDP component, the estimate is then given by
where \( b_{\text{NDP}} \) is a deterministic additive bias representing the nature of the blockage. Unlike the multipath biases, and similar to biases induced by propagation delay, the dependence of \( b_{\text{NDP}} \) on the system bandwidth and SNR has its own limitations, as reported in Pahlavan et al. (1998). Figure 2.9 illustrates the two specific conditions occurring in NLOS environments.
Indoor NLOS multipath channels. a “Light” NLOS—the DP is attenuated but can be detected b Severe NLOS—the DP is not detected
An example of the measured channel profiles in the NLOS conditions is shown in Figs. 2.10 and 2.11.
Measurement of a “light” NLOS channel—the DP is attenuated but can be detected
Sample measurement of a Severe NLOS multipath channel—the DP is not detected
It is clear from the figures that in NLOS channel conditions large ranging errors are possible, highlighting the major limitation to deploying accurate geolocation systems in urban and indoor environments. The impact of NLOS range measurements on the localization performance can be evaluated through CRLB-type bounds. Given that the statistics of the NLOS biases are available then it is possible to derive the Generalized-CRLB which integrates the statistical information. The analytical treatment of this problem can be found in Qi et al. (2006).
2.3.2 RSS-Based Ranging in NLOS Multipath Environments
In the previous section, RSS-based ranging in LOS multipath environment was introduced and it was illustrated how a simple pathloss model can be used to estimate the distance. Besides the limitation due to the unknown parameters of the pathloss model, the challenge of RSS ranging in NLOS is exacerbated by the fact that obstructions between the transmitter and receiver can further complicate the distance–power relationship, making it difficult to directly estimate the distance accurately. For example, consider a mobile station moving away from a base station in a typical LOS environment. The pathloss model for this scenario is a typical LOS propagation model with pathloss exponent around 1–2 and minimal shadowing variance. However, as the mobile moves behind a wall, cabinet, or even an elevator, the power suddenly fluctuates and severe attenuation perturbs the LOS distance–power relationship. It then becomes very difficult to achieve accurate distance estimation in light of this problem. Although Li (2006) proposed a technique to estimate the pathloss exponent in real-time, the limitations still affect the accuracy and practicality of this approach. As a result, numerous research efforts have focused instead on an alternative RSS-based localization technique, namely fingerprinting-based localization, an approach to which Chap. 4 of this book is completely dedicated.
In NLOS environments the pathloss model introduced earlier for LOS environments can be further extended
where \( \gamma^{\text{NLOS}} \) and \( S^{\text{NLOS}} \) is the pathloss exponent and shadow fading parameters for NLOS. Usually \( \gamma^{\text{NLOS}} > \gamma^{\text{LOS}} \), with \( \gamma^{\text{NLOS}} \) ranging between 3 and 6 (Pahlavan and Levesque 2005). The NLOS pathloss model will be significantly different when considering the type and number of obstructions separating the transmitter and receiver. For example in indoor NLOS environments, the number of walls between the transmitter and receiver can significantly change the pathloss behavior. An additional parameter to incorporate the wall effect has been modeled in the literature as
where \( W_{n} \) is the attenuation specific to a type of wall (Durantini and Cassioli 2005). It is clear that, in practice, it is very difficult to have an accurate pathloss model that can be used to estimate the distance accurately for all the environments.
2.4 Empirical Evaluation of the Multipath and NLOS Problems
In order to understand the impact of the propagation channel on the effectiveness of existing TOA-based and RSS-based algorithms and to appreciate the limitations that they face, it is necessary to empirically characterize the radio propagation channel for the ranging- or geolocation-specific application. The TOA- and RSS-specific propagation studies help to shed light on the fundamental aspects of the ranging technique and the parameters that control its performance. In this section, we will provide an overview of the measurement techniques, results, and modeling efforts that have been carried out for TOA- and RSS-based ranging. The aim of this section is to introduce the reader to the methodologies used to measure and characterize the wireless channel for geolocation applications. This will serve as a foundation through which it is possible to understand the limitations facing some of the popular ranging and localization techniques that will be introduced in the later chapters.
2.4.1 Channel Measurement Systems
In order to characterize the behavior of TOA- or RSS-based ranging in multipath environments, the channel impulse response (CIR) or the power delay profile of the channel must be measured. The CIR is the time-delay characterization of the multipath and it provides the amplitude/delay relationship of the arriving multipath components. In practice the CIR can be measured directly by either using a time–domain measurement system or indirectly by using a frequency–domain measurement system. For geolocation-specific measurements and modeling, either systems can be used to extract relevant information for TOA-based ranging. Specifically, the measurement systems can be used to measure the large-scale, spatial characteristics of the direct path, mainly the \( \hat{\alpha }_{1}^{\text{DP}} \) and the \( \hat{\tau }_{1}^{\text{DP}} \), which can be used to examine the ranging coverage (pathloss characterization) and accuracy, respectively. In the absence of the DP, it is possible to measure the first detected path, \( \hat{\tau }_{1}^{\text{NDP}} \), and analyze the probability of blockage and the error statistics in this condition. These TOA-based parameters can be extracted directly from the measured CIR.
2.4.1.1 Time Domain Systems
One way to capture the channel multipath profile is through the well-known time domain measurement system. The channel is captured by transmitting a known waveform (with special autocorrelation properties) and post-processing the received waveform by cross-correlation with the known template. Since the arriving waveform will be a superposition of shifted and attenuated replicas of the original signal, then the output of the cross-correlation will contain “peaks” at the delay values of the multipath components. A typical time domain measurement system is depicted in Fig. 2.12.
Time domain measurement system block diagram
Typically, the template waveform can be either pulses or PN-sequences, employed in direct-sequence spread spectrum systems (Ciccognani et al. 2005). After amplification, the received waveform is captured by a digital sampling oscilloscope and stored for post-processing (Cassioli et al. 2002). Depending on the waveform type, the multipath profile can be extracted from the received waveform. In the case of the PN-sequence waveform, the received signal is correlated (after demodulation) with a replica of the transmitted sequence (Janssen and Vriens 1991). Note that for this measurement system the signal generator must be “synchronized” with the digitally sampling oscilloscope. That is a trigger signal is typically used to trigger the events for correlation purposes.
2.4.1.2 Frequency Domain Systems
One of the most popular and practical methods to measure the wireless channel is through the use of the frequency-domain measurement system. For such measurement systems a generic vector network analyzer (VNA) can be used. Frequency-domain measurement techniques have been previously employed to characterize the channel impulse response (Ghassemzadeh et al. 2004); Chong and Yong (2005), Pahlavan and Levesque (2005), Howard and Pahlavan (1990) but for modeling the communication channel—characterizing RMS delay spread and power-distance relationships. The frequency measurement system captures the channel transfer function (CTF) and the time domain CIR can then be obtained by the inverse Fourier Transform (IFT).
The core of the measurement system is the VNA, which is used to sweep the frequency spectrum of a desirable system bandwidth with a certain sampling interval. The CTF can be captured by measuring the S21 S-parameter on the VNA which are samples of the frequency domain of the channel. Figure 2.13 illustrates an example measurement system setup. Further details of the measurement system can be found in Ghassemzadeh et al. (2004), Pahlavan and Levesque (2005) and Alsindi et al. (2009).
Frequency-domain measurement system block diagram
The CIR is then obtained by an IFT process and Fig. 2.14 highlights the system block diagram of the post-processing stage.
Measurement post-processing and CIR generation
The uncalibrated measured CTF from the VNA is passed through a post-measurement calibration process that removes the channel response of the cables, LNA and PA. The CIR is then obtained by the IFT or the Chirp-Z transform which has a signal processing “zooming” capability. The time and amplitude of the multipath delays are then extracted by passing the raw estimated CIR through a peak detection algorithm, that essentially identifies the peaks in the profile that are greater than a certain noise threshold (typically −120 to −110 dBm).
The frequency domain measurement parameters are related to the time domain channel impulse response. The parameters that can be controlled in the VNA when measuring the frequency response are the swept frequencies (bandwidth), the number of samples, and the transmitted power. The frequency spacing is determined by the number of samples in a given bandwidth. For a CTF measurement \( H(f) = H(f_{1} ,f_{2} ) \) the VNA can be configured to measure a certain bandwidth between \( f_{1} \) and \( f_{2} \), or \( B = f_{2} - f_{1} \). Selecting the number of points will dictate the frequency spacing \( \Updelta f \). The relationship between the number of measured frequency samples, \( N_{f} \), and the frequency spacing, \( \Updelta f \) is \( N_{f} = ({{f_{2} - f_{1} }) \mathord{\left/ {\vphantom {{f_{2} - f_{1} } {\Updelta f}}} \right. \kern-\nulldelimiterspace} {\Updelta f}} \). The frequency samples on the VNA directly affect the time domain CIR. The measured bandwidth \( B \) controls the time domain resolution \( \Updelta t \) and the frequency spacing \( \Updelta f \) controls the maximum time delay, \( \tau_{\max } \), that can be measured. Figure 2.15 and Table 2.1 illustrate and summarize the relationship.
Frequency domain measurement system—parameter relationships between the frequency and time domain signals
The collected measurement data can be then used to extract the TOA or RSS parameters for analysis. In the next subsectionss we introduce some of the models developed for the indoor environment.
2.4.2 Alavi Models
One of the earliest TOA-based ranging measurements and modeling was conducted by Alavi and Pahlavan (2006). The focus of the measurement and modeling was to characterize the impact of multipath on the accuracy of range estimation. The measurements and modeling provided an analysis of the impact of system bandwidth on the multipath-induced error. In addition, the TOA-specific measurements errors were analyzed under different NLOS conditions. Specifically, in this work, ranging error was referred to as Distance Measurement Error (DME) and it is given by
where \( d \) is the ground-truth distance, \( \hat{d}_{B} \) is the measured distance, and its dependence on system bandwidth is explicitly given by the subscript \( B \). As a result, the error is a function of the distance between the transmitter and receiver and the bandwidth. Furthermore, depending on the condition of the indoor channel, the error can be significantly different: in LOS environments, multipath is the dominant source of error while in NLOS the absence of the DP—also known as Undetected Direct Path (UDP)—dominates the error. UDP is essentially severe NLOS where the DP cannot be detected due to a large obstruction between the transmitter and receiver which causes the DP path to be buried under the receiver noise floor. The models were obtained by conducting frequency domain measurements using the VNA described in the previous subsections. Figures 2.8 and 2.11 illustrate LOS versus NLOS with undetected DP.
By comparing the two measured profiles, it is clear that the error in UDP conditions contains a combination of the multipath error and a “UDP” error, which is essentially a bias in the time delay estimation. Note from the figure that the direct path is severely attenuated and lies below the noise threshold, which makes its detection very difficult. Based on the measurements in an indoor environment, Alavi introduced a model that incorporates the different ranging conditions. Specifically, the error is modeled as
where \( \varepsilon_{M,B} (d) \) is the multipath error, \( \varepsilon_{U,B} (d) \) is the UDP error or bias, and \( \xi_{B} (B) \) is a random variable that takes the value of “1” when a UDP condition occurs and “0” otherwise. The model also includes \( \varepsilon \), which is an error that models the inaccuracies occurring during measurement of the actual distance between the transmitter and receiver. Typically, this error can be assumed zero-mean Gaussian with a variance that depends on the accuracy of the measurement error. Since \( \varepsilon \) cannot be separated from the multipath error, it is assumed that \( \varepsilon + \varepsilon_{M,B} (d) \approx \varepsilon_{M,B} (d) \), which simplifies the model to
The multipath error \( \varepsilon_{M,B} (d) \) can been modeled by
where \( X(m_{M,\,B} ,\sigma_{M,\,B} ) \) is a Gaussian random variable with mean \( m_{M,\,B} \) and standard deviation \( \sigma_{M,\,B} \). The UDP error component was similarly modeled as Gaussian \( X(m_{U,B} ,\sigma_{U,B} ) \). As a result, the overall model is given by
The random variable \( \xi_{B} (d) \) can be modeled as
The proposed models have been verified to fit actual data in Alavi and Pahlavan (2006).
The work in Alavi and Pahlavan (2006) also investigated the impact of the system bandwidth on the DME. Basically, as the system bandwidth increases, the error decreases due to enhanced time resolution. The finding further supports the idea that one way to mitigate the multipath problem is to increase the system bandwidth. This observation was also highlighted in Gentile and Kik (2007).
2.4.3 Alsindi Models
As stated earlier, the Alavi models were the first models developed for TOA-based ranging that analyzed the impact of LOS/NLOS and system bandwidth on the accuracy. The results of these models highlighted the fundamental limitations and challenges facing TOA-based ranging in harsh multipath environments. The measurements and models, however, were limited in scope since they were based on a single floor/office of an indoor environment and thus lacked comprehensive analysis in different buildings/environments. In addition, the models do not provide any indication of the coverage aspect of the ranging systems. As a continuation of the modeling efforts, Alsindi’s work focused on developing models for Ultra-Wideband (UWB) TOA-based systems that characterize in detail some of the fundamental parameters such as ranging coverage, ranging error in LOS, NLOS-presence of DP, and NLOS-absence of DP (Alsindi et al. 2009). UWB is defined as any system operating with a bandwidth of 500 MHz or with a bandwidth exceeding 20 % of the center frequency.
The objective of the measurement campaign was to develop models for fire-fighter/soldier TOA-based ranging/localization in hostile indoor environments. In such scenarios, beacons or anchors were placed surrounding a given building in order to aid firefighters/soldiers to localize and navigate themselves in an indoor environment through cooperative localization using wireless sensor networks (WSN). Cooperative localization is dealt with in Chaps. 6 and 7 where centralized and distributed techniques will be discussed in more detail. Figure 2.16 illustrates the localization scenario that was considered for the measurement campaign.
Firefighter/soldier localization scenario in hostile indoor environments
In order to develop reliable systems operating in these challenging environments, it is necessary to understand the propagation characteristics that impact ranging and localization accuracy. It is clear from the figure that three distinct ranging scenarios are possible: Indoor-to-Indoor (ITI), Outdoor-to-Indoor (OTI) and Roof-to-Indoor (RTI). In addition four different building types were investigated: old office (Atwater Kent—AK), new office (Fuller Labs), residential (Schussler) and manufacturing floor (Norton). All the buildings are in Worcester, MA, USA. From this application point of view, it is then interesting to investigate the following issues:
-
For the outdoor beacons (OTI & RTI), how far can the devices reliably provide TOA-based ranging estimates? What is the ranging coverage?
-
What is the probability of DP blockage in NLOS environments?
-
What are the ranging error characteristics in ITI, OTI and RTI?
-
How is the ranging/localization performance impacted for different building types: residential, office, etc.?
For the firefighter/soldier localization scenario, the multipath and NLOS problems can be difficult challenges that will impact the accuracy of the localization directly. Figure 2.17 highlights the NLOS challenges facing OTI/RTI and ITI scenarios.
NLOS challenges facing the firefighter localization application
For OTI/RTI scenarios, the signal propagating through the external walls of the building typically undergoes significant attenuation because the walls are usually thick in construction and are composed of brick and steel material. As a result, the ranging coverage can be limited significantly and, in most cases, is much less than the ITI scenarios. For ITI scenarios the ranging coverage, although higher than OTI/RTI, is significantly different for LOS and NLOS scenarios.
Alsindi’s models focused on characterizing the ranging coverage and ranging error in these different scenarios and environments. For the former the distance–power relationship of the Direct Path (DP) signal provides an empirical evaluation of the ranging coverage which is the maximum distance where the DP can be detected. For the latter the spatial distribution of the ranging error in different scenarios and environments provides an empirical evaluation of the physical limitation facing indoor geolocation.
In indoor environments, the distance-dependence of the received power, which can be used to determine the communication coverage, is usually predicted from experimental pathloss models of the total signal energy in different environments and scenarios (Durgin et al. 1998; Molisch 2005; Ghassemzadeh et al. 2004). Similarly, the distance-dependence behavior of the power of the DP can be used to determine the ranging coverage. Unlike communication coverage which is related to the received power of all the multipath components at a given distance, ranging coverage is related to the received power of the DP component. For a given system dynamic range, \( \kappa \), ranging coverage, \( R_{r} \), is defined as the distance in which the maximum tolerable average pathloss of the DP is within \( \kappa \) (Alsindi et al. 2009). This is represented by
where \( \overline{{L_{p}^{\text{DP}} }} \) is the average pathloss of the DP and \( \gamma \) is the pathloss exponent. The pathloss behavior of the DP is distance-dependant, but because of the attenuation and energy removed by scattering, its intensity decreases more rapidly with distance compared with the total signal energy (Siwiak et al. 2003). This means that for typical indoor multipath scattering environment, communication coverage is greater than ranging coverage, \( R_{c} > R_{r} \). Operating out of ranging coverage causes large TOA estimation errors and performance degradation (always in NLOS-NDP condition). The characterization of ranging error in different scenarios has been introduced earlier in the chapter and it is summarized in Table 2.2 for convenience.
2.4.3.1 Modeling the Pathloss: Ranging Coverage
Using the same established pathloss modeling approach used in the literature, (Ghassemzadeh et al. 2004; Pahlavan and Levesque 2005), Alsindi characterized the distance–power dependence of the measured DP (Alsindi et al. 2009) and compared it to the distance–power relationship of the total received power (RSS). The pathloss exponent is determined from measurement data through least-square (LS) linear regression. The pathloss relationship is provided in (2.61) but an additional factor attributed to the power loss due to penetration through walls can be incorporated as \( L_{X} \) (which is depending on the ranging scenario OTI, RTI, etc.). Thus the modified expression is given by
All the parameters of the model in (2.70) are a function of the building type/propagation environment. Figures 2.18, 2.19 and 2.20 show sample measured scatter plots of the pathloss as a function of TX-RX separation for different buildings and ranging scenarios.
Pathloss scatter plots in Fuller ITI LOS at 3 GHz bandwidth
Pathloss scatter plots in Norton OTI at 500 MHz bandwidth
Pathloss scatter plots in AK RTI at 500 MHz
The pathloss model parameters are summarized in Table 2.3.
Several observations can be made from the table and the figures. The first is that for all the measurement data the pathloss exponent is higher for the DP relative to the total signal power, which is consistent with the modeling approach. Second, the DP power experiences greater fluctuations around the mean pathloss as compared with the total signal counterpart. This observation makes sense because small variations on the transmitter location affect the DP power more than the total power. Third, \( L_{X} \) changes for the different penetration scenarios. In ITI scenarios Schussler NLOS suffers 6 dB penetration loss due to the walls compared to 7.5 in AK. Norton ITI measurements are a mixture of LOS/NLOS because the manufacturing floor contained scattered machines. The impact can be clearly seen on the pathloss exponent when the bandwidth increases, hence higher attenuation. Results of OTI measurements show that Fuller and AK exhibit the largest penetration loss mainly because the signal had to penetrate a thicker building construction when compared with Norton and Schussler. In addition, the pathloss exponents in AK are large mainly because the measurement locations were conducted inside a metal shop on the edge of the building and between concrete corridors and rooms. AK in general imposes a very challenging environment for ranging because of the building material and dense cluttering. RTI measurements experienced the largest penetration loss and high pathloss exponent. Finally, note that the harsher the indoor environment, the higher the pathloss exponent difference when moving to a higher system bandwidth. This is mainly due to the fact that larger system bandwidths provide better time domain resolution at the cost of reduced power per multipath component. This implies that the advantage of higher time domain resolution comes at a cost of shorter ranging coverage.
2.4.3.2 Modeling the Ranging Error
The spatial characteristics of the ranging errors are determined through the behavior of the biases, which are random due to the unknown structure of the indoor environment and the relative location of the user to them. Since the errors are highly dependent on the absence or the presence of the DP, the models introduced by Alsindi are based on the classification in Table 2.2. Further, in order to model and compare the behavior in different building environments and scenarios, the normalized ranging error was modeled instead as
The range error observed in an indoor environment can then be modeled by combining the conditions in Table 2.2 through the following expression
where \( \psi_{m} \) is the normalized multipath error that exists in both the presence and absence of the DP. \( \psi_{\text{pd}} \) is the normalized propagation delay-induced error, and \( \psi_{\text{NDP}} \) is the normalized error due to DP blockage. In order to distinguish between the error behavior in LOS and NLOS, a Bernoulli random variable, \( G \) was used. That is,
where \( p\left( {G = 0} \right) = p\left( {\text{LOS}} \right) \) is the probability of being in LOS and \( p\left( {G = 1} \right) = p\left( {\text{NLOS}} \right) \) is the probability of being in NLOS. Similarly, \( X \) is a Bernoulli random variable that models the occurrence of DP blockage and is given by
where \( p\left( {X = 0} \right) = p\left( {\zeta_{1} } \right) \) denote the probability of detecting a DP, while \( p\left( {X = 1} \right) = p\left( {\zeta_{2} } \right) \) denotes the probability of the occurrence of blockage. It is important to emphasize that Alsindi’s modeling approach focuses on the DP and not the traditional definition of NLOS used for communications. This means that a mobile station and a base station separated by a wall, for instance, is considered NLOS, but does not necessarily imply the absence of the DP. In the remainder of the chapter, ranging error, bias, and normalized error will be used interchangeably.
The results of the measurement and modeling also revealed a significant difference in the probability of DP blockage among the different environments, which is highlighted in Table 2.4.
Several observations can be concluded. First, a positive correlation between the system bandwidth and the blockage probability \( p\left( {\zeta_{2} } \right) \) exists due to lower energy per MPCs in higher system bandwidths. Second, as expected, DP blockage increases from ITI, to OTI, and RTI. Attenuation due to penetration from exterior walls and ceiling results in higher \( p\left( {\zeta_{2} } \right) \). Third, blockage is highly correlated with the building type. In residential environments, blockage probability is low since the interior is composed of wooden structures with few metallic objects (e.g. a fridge, laundry room, etc.). Office buildings, however, pose harsher conditions with thicker walls, metallic beams, vending machines, metallic cabinets, shelves, and elevator shafts, resulting in a substantial blockage up to 90 %, see Fuller and AK (ITI/OTI). Also, ITI measurements on the manufacturing floor highlight the impact of occasional clutter of machineries. Finally, it is worth mentioning that these results were measured using a 120 dB dynamic range provided by the external amplifiers and LNA extending the measured range. In realistic UWB systems, unfortunately, this would be prohibitively high in terms of implementation expense, which means that the results here can be seen as a lower bound.
The models also analyze the behavior of ranging error in the presence and in the absence of the DP. The measurement results of the ranging error in LOS scenarios revealed that the impact of the multipath can be modeled through a normal distribution since the DP is available and the error deviates in both directions relative to the actual distance. In addition, normality of the ranging error in this condition has been reported in Alavi and Pahlavan (2003, 2006). The error distribution can then be explicitly modeled as,
with mean \( \mu_{\text{LOS}} \) and standard deviation \( \sigma_{\text{LOS}} \) specific to the LOS multipath-induced errors. Figure 2.21 further confirms the normality of errors in this condition.
Norton ITI at 500 MHz bandwidth: confirming the normality of the biases in LOS conditions
A similar observation of the multipath effect in indoor LOS environments has been reported through measurements (Alavi and Pahlavan 2006). In NLOS scenarios, when the DP is present, the amount of propagation delay and multipath due to obstructing objects such as wooden walls causes the biases to be more positive. The results show (see Fig. 2.22) that the spatial characteristics retain the statistics of the LOS counterpart but with a higher mean and standard deviation.
Schussler ITI NLOS—mean of biases is larger than LOS
According to these results, the normalized ranging error is modeled similar to (2.75), but with emphasis on the condition. This is given by,
The subscripts in (2.76) specify the contributing error factors. Table 2.5 provides the modeling parameters of all the scenarios and environments in the presence of the DP.
The results show a positive correlation between the statistics of the normal distribution with the complexity of environment and/or ranging scenario. Negative correlation can be seen between the statistics and the system bandwidth due to reduction of multipath error in higher bandwidths.
The ranging error behavior in the absence of the DP is significantly different. The shadowing of the DP impacts the error behavior in several ways. First, only positive errors occur, since the blockage induces a higher positive bias that dominates compared to the multipath counterpart. Second, there are occasionally large positive range errors that occur due to heavier indoor constructions such as elevator shafts, clustering of cabinets, or even metallic doors. Third, the diversity of blocking material in indoor environments means that the spatial distribution of errors will in general exhibit a heavier positive tail. By examining the PDF of the errors in this condition, it is observed that different subsets of the data showed varying tail behavior. The “heaviness” of the tail depended on the ranging environment and scenario. Thus harsher blockage conditions, i.e., higher number of blocked MPCs, exhibited heavier tails. As a result, the ranging error in this condition was modeled as log-normally distributed. The lognormal model is then given by,
where \( \mu_{\text{NLOS - NDP}} \) and \( \sigma_{\text{NLOS - NDP}} \) are the mean and standard deviation of the ranging error’s logarithm. The subscripts emphasize the contributing factors. Figure 2.23 provides a sample measurement result confirming the lognormal behavior of the error.
Schussler OTI at 3 GHz bandwidth—confirming the lognormality of the measured normalized ranging error
The estimated parameters of the lognormal distribution, obtained using Maximum Likelihood (ML) estimation techniques, for different ranging scenarios and environments, are given in Table 2.6. Similar observations compared with earlier models can be observed for the correlation between the error statistics with bandwidth and ranging conditions.
However, there are several scenarios where the extent of the correlation diminishes. For example, Fuller OTI and ITI contain measurements in severe NLOS conditions and increasing system bandwidth has a limited impact on the parameters of the model. This is mainly due to ranging conditions that induce large blockage errors which are effectively insensitive to bandwidth changes, e.g., elevator shafts.
The measurement and modeling introduced in this section provides realistic insight into these challenges, which is necessary for performance evaluation through CRLB and algorithm design and development.
2.5 Conclusion
The development of location-enabled services is mainly hindered by the realities of harsh propagation in environments where the devices are to be deployed—typically the dense urban and indoor environments. These environments pose serious challenges to system designers and engineers developing next generation location enabled devices. Specifically, multipath and NLOS are the two main physical limitations that need to be resolved in order to enable accurate and reliable localization. In this chapter we have first introduced the basics of geolocation techniques such as TOA, TDOA, AOA, and RSS. Then the multipath and NLOS problems for TOA- and RSS-based ranging techniques were presented.
Through channel measurements and modeling, the impact of multipath on TOA-based ranging as a function of bandwidth was investigated. It was shown that an increase in system bandwidth can reduce the multipath error significantly. For RSS-based ranging systems, however, the bandwidth does not play a major role in mitigating the multipath problem. Instead, averaging can remove the fast-fading variations of power due to multipath, yielding better distance estimation. With regard to the NLOS problem, both RSS- and TOA-based ranging suffer from the physical limitations. For the former, large power variations (shadow fading) affect the power–distance relationship and make it difficult to accurately estimate the distance; for the latter, NLOS introduces biases that corrupt the distance estimation and cause large errors that can affect the accuracy of any localization algorithm. In the next chapter, we will investigate popular techniques to mitigate the multipath and NLOS problems.
References
A. Durantini, D. Cassioli, A multi-wall pathloss model for indoor UWB propagation. in Proceedings of Vehicular Technology Conference (VTC), pp. 30–34, May 2005
B. Alavi, K. Pahlavan, Modeling of the TOA-based distance measurement error using UWB indoor radio measurements. IEEE Commun. Lett. 10(4), 275–277 (2006)
N. Alsindi, B. Alavi, K. Pahlavan, Measurement and modeling of ultrawideband TOA-based ranging in indoor multipath environments. IEEE Trans. Veh. Technol. 58(3), 1046–1058 (2009)
B. Alavi, K. Pahlavan, Modeling of the distance error for indoor geolocation. in Proceedings of IEEE Wireless Communications and Networking (WCNC), vol 1 New Orleans, LA, USA, (2003), pp. 668–672
B. Alavi, K. Pahlavan, Studying the effect of bandwidth on performance of UWB positioning systems. in Proceedings of IEEE Wireless Communications and Networking Conference (WCNC) (Las Vegas, NV, USA, 2006), pp. 884–889
C. Gentile, A. Kik, A comprehensive evaluation of indoor ranging using ultra-wideband technology. EURASIP J. Wirel. Commun. Netw. 2007, Article ID 86031 (2007)
J. J. Caffery, G. L. Stuber, Overview of radiolocation in CDMA cellular systems. IEEE Commun. Mag. 36(4), 38–45 (1998)
D. Cassioli, M. Z. Win, A. F. Molisch, The UWB indoor channel: from statistical model to simulations. IEEE J. Select. Areas Commun. 20(6), 1247–1257 (2002)
C.–C. Chong, S. K. Yong, A generic statistical-based UWB channel mode for high-rise apartments. IEEE Trans. Antennas Propag. 53(8), 2389–2399 (2005)
Y. T. Chan, K. C. Ho, A simple and efficient estimator for hyperbolic location. IEEE Trans. Signal Process. 42(8), 1905–1915 (1994)
W. Ciccognani, A. Durantini, D. Cassioli, Time domain propagation measurements of the UWB indoor channel using PN-sequence in the FCC-compliant band 3.6–6 GHz. IEEE Trans. Antennas Propag. 53(4), 1542–1549 (2005)
D. Dardari, C.-C. Chong, M. Z. Win, Improved lower bounds on time of arrival estimation error in realistic UWB channels. in Proceedings of IEEE 2006 Conference On Ultra-Wideband, pp. 531–537, 2006
D. Dardari, A. Conti, U. Ferner, A. Giorgetti, M. Z. Win, Ranging with ultrawide bandwidth signals in multipath environments. Proc. IEEE 97(2), 404–426 (2009)
A. G. Dempster, Dilution of precision in angle-of-arrival positioning systems. Electron. Lett. 42(5), 291–292 (2006)
G. Durgin, T.S. Rappaport, H. Xu, Measurements and models for radio pathloss and penetration loss in and around homes and trees at 5.85 GHz. IEEE Trans. Commun. 46(11), 1484–1496 (1998)
G. Janssen, J. Vriens, High resolution coherent radiochannel measurements using direct sequence spread spectrum modulation. in Proceedings of 6th Mediterranean IEEE Electrotechnical Conference, vol 1, 1991, pp. 720–727
S. Gezici, Z. Tian, G. B. Giannakis, H. Kobayashi, A. F. Molisch, H. V. Poor, Z. Sahinoglu, Localization via ultra-wideband radios. IEEE Signal Process. Mag. (Special Issue on Signal Processing for Positioning and Navigation with Applications to Communications) 22(4), 70–84 (2005)
S. S. Ghassemzadeh, R. Jana, C. W. Rice, W. Turin, V. Tarokh, Measurement and modeling of an ultra-wide bandwidth indoor channel. IEEE Trans. Commun. 52(10), 1786–1796 (2004)
I. Guvenc, C.-C Chong, A survey on TOA based wireless localization and NLOS mitigation techniques. IEEE Commun. Surv. Tutor. 11(3), 3rd Quarter (2009)
I. Guvenc, Y.T. Chan, H.Y.C. Hang, P.C. Ching, Exact and approximate maximum likelihood localization algorithms. IEEE Trans. Veh. Technol. 55(1), 10–16 (2006)
H. Liu, H. Darabi, P. Banerjee, J. Liu, Survey of wireless indoor positioning techniques and systems. IEEE Trans. Sys. Man Cybern. Part C Appl Rev 37(6), 1067–1080 (2007)
S. J. Howard, K. Pahlavan, Measurement and analysis of the indoor radio channel in the frequency domain. IEEE Trans. Instrum. Meas. 39(5), 751–755 (1990)
I. Guvenc, Z. Sahinoglu, Threshold-based TOA estimation for impulse radio UWB systems. in Proceedings of International Conference on Ultra-Wideband, (2005)
J. Zheng, Y.-C Wu, Joint time synchronization and localization of an unknown node in wireless sensor networks. IEEE Trans. Signal Proces. 58(3), 1309–1320 (2010)
J. Y. Lee, R. A. Scholtz, Ranging in a dense multipath environment using an UWB radio link. IEEE Trans. Select. Areas Commun. 20(9), 1677–1683 (2002)
S. M. Kay, Fundementals of Statistical Signal Processing: Estimation Theory (Prentice Hall, Upper Saddle River, 1993)
X. Li, RSS-based location estimation with unknown pathloss model. IEEE Trans. Wirel. Commun. 5(12), 3626–3633 (2006)
A. F. Molisch, Ultrawideband propagation channel-theory, measurement and modelling. IEEE Trans. Veh. Technol. 54(5), 1528–1545 (2005)
K. Pahlavan, P. Krishnamurthy, J. Beneat, Wideband radio channel modeling for indoor geolocation applications. IEEE Commun. Mag. 36(4), 60–65 (1998)
K. Pahlavan, A. Levesque, Wireless Information Networks, 2nd edn. Wiley (2005)
N. Patwari, A. O. Hero, M. Perkins, N. S. Correal, R. J. O’Dea, Relative location estimation in wireless sensor network. IEEE Trans. Signal Process. 51(8), 2137–2148 (2003)
Y. Qi, H. Kobayashi, H. Suda, Analysis of wireless geolocation in a non-line-of-sight environment. IEEE Trans. Wirel. Commun. 5(3), 672–681 (2006)
A. H. Sayed, A. Tarighat, N. Khajehnouri, Network-based wireless location: challenges faced in developing techniques for accurate wireless location information. IEEE Signal Process. Mag. 22(4), 24–40 (2005)
K. Siwiak, H. Bertoni, S. M. Yano, Relation between multipath and wave propagation attenuation. IEE Electron. Lett. 39(1), 142–143 (2003)
M. A. Spirito, On the accuracy of cellular mobile station location estimation. IEEE Trans. Veh.r Tech. 50(3), 674–685 (2001)
B. Sundararaman, U. Buy, A. Kshemkalyani, Clock synchronization for wireless sensor networks: a survey. Ad Hoc Netw. (Elsevier) 3(3), 281–323 (2005)
T. S. Rappaport, Wireless Communications: Principles and Practice (Prentice-Hall 1996)
IEEE 802.15.TG4a official web page, http://www.ieee802.org/15/pub/TG4a.html
Y. Qi, H. Kobayashi, On relation among time delay and signal strength based geolocation methods. in Proceedings of IEEE Global Telecommunications Conference (GLOBECOM03), vol 7, (San Francisco, CA, 2003), pp. 40794083
Y. Shen, M. Z. Win, Fundamental limits of wideband localization accuracy via Fisher Information. in Proceedings of IEEE Wireless Communications and Networking Conference (WCNC), pp. 3046–3051, March 2007
Y.-C Wu, Q. Chaudhari, E. Serpedin, Clock synchronization of wireless sensor networks. IEEE Signal Proces. Mag., 28(1), 124–138 (2011)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2013 Springer Science+Business Media New York
About this chapter
Cite this chapter
Gentile, C., Alsindi, N., Raulefs, R., Teolis, C. (2013). Ranging and Localization in Harsh Multipath Environments. In: Geolocation Techniques. Springer, New York, NY. https://doi.org/10.1007/978-1-4614-1836-8_2
Download citation
DOI: https://doi.org/10.1007/978-1-4614-1836-8_2
Published:
Publisher Name: Springer, New York, NY
Print ISBN: 978-1-4614-1835-1
Online ISBN: 978-1-4614-1836-8
eBook Packages: EngineeringEngineering (R0)