Coloring Clean and K ₄-Free Circle Graphs

Abstract

A circle graph is the intersection graph of chords drawn in a circle. The best-known general upper bound on the chromatic number of circle graphs with clique number k is $50 \cdot {2}^{k}$. We prove a stronger bound of 2k−1 for graphs in a simpler subclass of circle graphs, called clean graphs. Based on this result, we prove that the chromatic number of every circle graph with clique number at most 3 is at most 38.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Recall that the chromatic number of a graph G, denoted χ(G), is the minimum size of a partition of V (G) into independent sets. A clique is a set of pairwise adjacent vertices, and the clique number of G, denoted ω(G), is the maximum size of a clique in G.

Vertices in a clique must receive distinct colors, so $\chi (G) \geq \omega (G)$ for every graph G. In general, χ(G) cannot be bounded above by any function of ω(G). Indeed, there are triangle-free graphs with arbitrarily large chromatic number [4, 18].

When graphs have additional structure, it may be possible to bound the chromatic number in terms of the clique number. A family of graphs $\mathcal{G}$ is χ-bounded if there is a function f such that $\chi (G) \leq f(\omega (G))$ for each $G \in \mathcal{G}$. Some families of intersection graphs of geometric objects have been shown to be χ-bounded (see e.g. [8, 11, 12]). Recall that the intersection graph of a family of sets has a vertex for each set in the family, with vertices adjacent if and only if the corresponding sets intersect. Possibly the simplest example is the class $\mathcal{I}$ of interval graphs, i.e., the class of intersection graphs of intervals in a line. Interval graphs are perfect graphs; i.e., $\chi (G) = \omega (G)$ for every interval graph G. Another interesting family is the family $\mathcal{C}$ of circle graphs, that is, the intersection graphs of families of chords of a circle. This family is more complicated than $\mathcal{I}$: Although the problem of recognition of a circle graph is polynomial (Bouchet [2]) and so are the problems of finding maximum cliques and maximum independent sets in circle graphs (Gavril [7, 8]), the problems of finding the chromatic number (Garey et al. [6]) and clique covering number (Keil and Stewart [14]) are NP-complete. Circle graphs naturally arise in a number of combinatorial problems: from sorting problems to studying planar graphs to continuous fractions (see, e.g., [3, 5, 8]).

A graph G is a circle graph if and only if it is an overlap graph: The vertices of such a graph are closed intervals in the real line, and two intervals are adjacent if they overlap, that is, intersect and neither of them contains the other. To see this, observe that given a family of chords on a circle representing a circle graph, cutting the circle at a point and unrolling gives an overlap representation for the same graph.

The above-mentioned complexity results on circle graphs make interesting upper bounds on the chromatic number of circle graphs in terms of their clique number, especially if the proofs yield polynomial-time algorithms for corresponding colorings. There was a series of results in this direction. Karapetyan [13] showed that $\chi (G) \leq 8$ when G is a triangle-free circle graph. Gyárfás [9, 10] proved that $\chi (G) \leq {k}^{2}{2}^{k}({2}^{k} - 2)$ when G is a circle graph with clique number k. The bound was improved in [17] to $\chi (G) \leq k(k + 2){2}^{k}$, and in [16] to $\chi (G) \leq 50 \cdot {2}^{k} - 32k - 64$. The best-known lower bound for the maximum chromatic number of circle graphs with clique number k is only 0. 5k(lnk − 2) [15, 17]. The exponential gap has remained open for 25 years.

Exact results are known only for circle graphs with clique number at most 2. Kostochka [17] showed that χ(G) ≤ 5 for every such graph G, and Ageev [1] constructed a triangle-free circle graph with chromatic number 5.

The purpose of this chapter is twofold. First, we consider a simple subclass of circle graphs, the clean graphs. A family of intervals X is clean if no interval is contained in the intersection of two overlapping intervals in X. A circle graph is clean if it is the overlap graph of a clean family of intervals. Since the structure of clean graphs is much simpler than that of general circle graphs, we are able to prove a much better bound for clean graphs.

Theorem 1.1.

For every clean circle graph G with clique number k, $\chi (G) \leq 2k - 1$.

Moreover, the proof yields a polynomial-time algorithm that, for each clean circle graph G with clique number k, finds a (2k − 1)-coloring of a special type, a good coloring that will be defined later. On the other hand, we show that for every k, there exists a clean circle graph G with clique number k that needs 2k − 1 colors for a good coloring.

We use Theorem 1.1 to derive an upper bound on the chromatic number of K ₄-free circle graphs. For such graphs G, the general bound in [17] implies that $\chi (G) \leq 120$. Our second main results follows.

Theorem 1.2.

For every circle graph G with clique number at most 3, $\chi (G) \leq 38$.

It can be checked that the proof of Theorem 1.2 yields a polynomial-time algorithm for coloring K ₄-free circle graphs using at most 38 colors. In the next section, we introduce notation and basic concepts. In Sect. 3, we prove Theorem 1.1, and in the last section, we prove Theorem 1.2.

2 Preliminaries

Recall that a circle graph is the intersection graph of a set of chords of a circle. Before proceeding, we clarify a minor technical point. Suppose a set of chords share a common endpoint p on the circle but are otherwise internally disjoint. Should these chords be considered pairwise intersecting or pairwise disjoint? Fortunately, the answer does not matter: Without affecting other intersection relationships, one can spread the common endpoints over a small portion of the circle near p so that the chords either intersect or are disjoint, as desired. Therefore, we may (and will) assume that the endpoints of all chords are distinct.

By the discussion in the previous section, for every circle graph F, there exists an overlap representation of F, that is, a family X of intervals in the real line such that F is the overlap graph of X. In this case, we also will write that F = G(X). Since the endpoints of chords in a circle representation are distinct, the intervals in X have distinct endpoints.

Definition 2.1.

An interval $\left[a,b\right]$ is a left-neighbor of $\left[c,d\right]$ if a < c < b < d. We use L _X (u) to denote the set of all left-neighbors of an interval u in a family X, or simply L(u) when X is clear from the context. Similarly, $\left[a,b\right]$ is a right-neighbor of $\left[c,d\right]$ if c < a < d < b, and R _X (u) denotes the set of all right-neighbors of u. We also define the closed left- and right-neighborhoods via ${\overline{L}}_{X}(u) = {L}_{X}(u) \cup \left\{u\right\}$ and ${\overline{R}}_{X}(u) = {R}_{X}(u) \cup \left\{u\right\}$. For each interval u, we use l(u) to denote the left endpoint of u and r(u) to denote the right endpoint of u.

The inclusion order is defined by containment. The endpoint order is defined by putting x ≤ y if and only if $l(x) \leq l(y)$ and $r(x) \leq r(y)$. Note that x ≤ y in the endpoint order if and only if x comes before y in both the left-endpoint order and the right-endpoint order. Note that any two distinct intervals are comparable in exactly one of the inclusion order and the endpoint order.

Definition 2.2.

If S is a set of intervals, then the center of S is the intersection of the intervals in S. A family of intervals X is clean if no interval is contained in the intersection of two overlapping intervals. A circle graph is clean if it is the overlap graph of a clean family of intervals.

A set S of vertices in a graph G is a cutset if G − S is disconnected. When S is a cutset in G, the graphs induced by the union of S and the vertices of a component of G − S are S-lobes. To color G, it suffices to color the S-lobes so that the colorings agree on S. To ensure that S is colored in the same way in all S-lobes, our inductive hypothesis prescribes the way in which S is colored.

Definition 2.3.

A subset A of a poset P is a downset if y ∈ A whenever y ≤ x for some x ∈ A, and A is an upset if y ∈ A whenever y ≥ x for some x ∈ A. For an element z ∈ P, we use D[z] to denote the downset $\left\{y \in P : \,\,y \leq z\right\}$ and D(z) to denote the downset $\left\{y \in P : \,\,y < z\right\}$. Similarly, U[z] denotes the upset $\{y \in P : \,y \geq z\}$ and U(z) denotes the upset $\{y \in P : \,y > z\}$. The height of an element x ∈ X is the size of a maximum chain in D[x] and the depth of x is the size of a maximum chain in U[x]. When X is a family of intervals, we define h _X (x) [or simply h(x) when X is clear from the context] to be the height of x in the endpoint order on X. The canonical coloring of a family X of intervals assigns h(x) to each interval x ∈ X. A coloring f of a family X of intervals is canonical, and we say that f is canonical on X if the color classes of f form the same partition of X as the color classes of the canonical coloring.

Note that the canonical coloring is a proper coloring; if x and y overlap, then they are comparable in the endpoint order, and therefore $h(x)\neq h(y)$.

3 Clean Circle Graphs

Definition 3.1.

A coloring f of a family of intervals X is good if, for each w ∈ X, f is canonical on $\overline{R}(w)$.

Note that if f is a good coloring of X, then it follows that f is a proper coloring. While some families of intervals do not admit good colorings with any number of colors, clean families have good colorings. The goal of this section is to prove the following refinement of Theorem 1.1.

Theorem 3.2.

If X is a clean family of intervals with clique number k ≥ 1, then there is a good coloring f of G(X) using at most 2k − 1 colors.

Proposition 3.3.

In a clean family of intervals, let x be an interval with h(x) ≥ 2. If y is chosen from D(x) to maximize l(y), then $h(x) = h(y) + 1$.

Proof.

Let k = h(x); we use induction on k. When k = 2, the statement is trivial. Suppose k ≥ 3. Since h(y) < h(x), it suffices to show that $h(y) \geq h(x) - 1$. Since h(x) = k, there is a chain ${z}_{1},\ldots,{z}_{k}$ with z _k  = x. We may assume that $y\neq {z}_{k-1}$, so the choice of y yields $l({z}_{k-1}) < l(y)$. Therefore, $l({z}_{k-2}) < l({z}_{k-1}) < l(y)$. Consider the order of r(y) and $r({z}_{k-2})$. If $r(y) < r({z}_{k-2})$, then y is contained in ${z}_{k-1} \cap {z}_{k-2}$, contradicting that the family is clean. Otherwise, $r(y) > r({z}_{k-2})$; now y > z _{k − 2} and $h(y) \geq k - 1$. $\square$

Proposition 3.4.

Let X be a clean family, and let x be an interval in X that contains another interval in X. If $Y = X -\{ x\}$ , then ${h}_{Y }(u) = {h}_{X}(u)$ for all u ∈ Y.

Proof.

Let z be an interval in X that is contained in x. Because X is clean, y < x implies y < z, and y > x implies y > z. Therefore, if C is a chain containing x, then substituting z for x in C yields another chain of the same size. Hence, ${h}_{Y }(u) \geq {h}_{X}(u)$ for all u ∈ Y, and the other inequality holds since $Y \subseteq X$. $\square$

Proposition 3.5.

If X is a family of intervals that share a common point a and the overlap graph G(X) has clique number k, then the canonical coloring on X uses exactly k colors.

Proof.

Because the canonical coloring is proper, it uses at least k colors. For the other direction, if the canonical coloring uses r colors, then there is a chain C of size r in the endpoint order on X. It follows that C is an independent set in the inclusion order on X. Hence, no two intervals in C are related by containment. However, C is pairwise intersecting because every member of X contains a. It follows that the intervals in C pairwise overlap, and so k ≥ r. $\square$

Proposition 3.6.

If f is canonical on X, and Y is a downset of X in the endpoint order, then f is canonical on Y.

Proof.

Because Y is a downset in X, we have ${h}_{X}(x) = {h}_{Y }(x)$ for each x ∈ Y. $\square$

Let X be a family of intervals and let u ∈ X be an interval that is not inclusion-minimal, where u = [a, b]. We define the subordinate of u to be the interval with the rightmost right endpoint among all intervals contained in u. Let v be the subordinate of u, where v = [c, d], and define the modified subordinate to be the interval v′, where v′ = [c, b]. The right-push operation on u produces the families Y and Y′ and a map ϕ : Y → Y′, where $Y = X - u$, $Y ^{\prime} = Y - v + v^{\prime}$, and ϕ(x) = x for x≠v and ϕ(v) = v′. When $S \subseteq X$, we write ϕ(S) for $\{\phi (w): \,w \in S\}$.

Lemma 3.7.

Let X be a family of intervals, let u ∈ X be an interval that is not inclusion-minimal, and let Y, Y ′, and ϕ : Y → Y ′ be produced by the right-push operation on u. If X is clean, then the following hold:

• (1) The map ϕ preserves the order of the left and right endpoints. That is, l(x) < l(y) if and only if $l(\phi (x)) < l(\phi (y))$ for each x,y ∈ Y. Similarly, r(x) < r(y) if and only if $r(\phi (x)) < r(\phi (y))$.

• (2) Y and Y ′ are clean.

• (3) The clique numbers of Y and Y ′ are both at most the clique number of X.

• (4) For each w ∈ Y with w≠v, we have $\phi ({\overline{R}}_{Y }(w)) ={ \overline{R}}_{Y ^{\prime}}(\phi (w))$.

• (5) $\phi ({\overline{R}}_{Y }(v)) \subseteq {\overline{R}}_{Y ^{\prime}}(\phi (v))$ and $\phi ({\overline{R}}_{Y }(v))$ is a downset of ${\overline{R}}_{Y ^{\prime}}(\phi (v))$ in the endpoint order.

Proof.

Define a, b, c, d so that u = [a, b] and v = [c, d].

• (1) Note that no interval in X has its right endpoint strictly between d and b. Indeed, if there were such an interval w, then either w is contained in u, in which case v is not the subordinate of w, or $\left\{w,u\right\}$ is a 2-clique whose center contains v, contradicting that X is clean. In passing from Y to Y ’, the right endpoint of v is moved from d to b to form a new interval v′. Doing so preserves the order of the left and right endpoints.

• (2) Because $Y \subseteq X$ and X is clean, we have that Y is clean. Note that x is contained in the center of a 2-clique with $\left\{y,z\right\}$ with y ≤ z if and only if l(y) < l(z) < l(x) and r(x) < r(y) < r(z). Hence, the property of being clean is determined by the order of the left endpoints and the order of right endpoints. Because ϕ preserves these orders, Y′ is also clean.

• (3) Let k be the clique number of X. Because $Y \subseteq X$, the clique number of Y is at most k. Let $\left\{{x}_{1},\ldots,{x}_{t}\right\}$ be a clique S in Y′ with ${x}_{1} < \cdots < {x}_{t}$, and note that $l({x}_{1}) < \cdots < l({x}_{t}) < r({x}_{1}) < \cdots < r({x}_{t})$. Suppose for a contradiction that t > k. We have that x _j  = v′ for some j, or else S is a clique in Y. If j > 1, then x _{j − 1} cannot have its right endpoint between d and b. Because d < b and r(x _j ) = b, it follows that $r({x}_{j-1}) < d < r({x}_{j})$. But d = r(v), and so $S - v^{\prime} + v$ is a clique of size t in Y, a contradiction. Hence, it must be that j = 1. Recalling that $r({x}_{1}) = r(u) = b$, we have that $l(u) < l({x}_{2}) < \cdots < l({x}_{t}) < r(u) < r({x}_{2}) < \cdots < r({x}_{t})$, which implies that $S - v^{\prime} + u$ is a clique of size t in X, another contradiction.

• (4) If $x \in {\overline{R}}_{Y }(w)$, then passing from x to ϕ(x) leaves the left endpoint fixed and possibly increases the right endpoint. Because w≠v and ϕ(w) = w, it follows that $\phi (x) \in {\overline{R}}_{Y ^{\prime}}(\phi (w))$ and so $\phi ({\overline{R}}_{Y }(w)) \subseteq {\overline{R}}_{Y ^{\prime}}(\phi (w))$. Conversely, if $\phi (x) \in {\overline{R}}_{Y ^{\prime}}(\phi (w))$, then passing from ϕ(x) to x leaves the left endpoint fixed and possibly decreases the right endpoint. However, the right endpoint of ϕ(x) must remain greater than the right endpoint of ϕ(w), and so $x \in {\overline{R}}_{Y }(w)$. It follows that ${\overline{R}}_{Y ^{\prime}}(\phi (w)) \subseteq \phi ({\overline{R}}_{Y }(w))$.

• (5) Passing from v to v′ increases the right endpoint of v, but in doing so, the right endpoint never crosses the right endpoint of another interval. Hence, each right-neighbor of v in Y is a right-neighbor of v′ in Y′, and therefore $\phi ({\overline{R}}_{Y }(v)) \subseteq {\overline{R}}_{Y ^{\prime}}(\phi (v))$. To see that $\phi ({\overline{R}}_{Y }(v))$ is a downset of ${\overline{R}}_{Y ^{\prime}}(v^{\prime})$, note that a right-neighbor x of v′ in Y′ is also a right-neighbor of v in Y if and only if l(x) < d. $\square$

Note that because the endpoint order on X only depends on the order of the left endpoints and that of the right endpoints, a consequence of Lemma 3.7 is that ϕ is a poset isomorphism from Y to Y′ under the endpoint order.

Proposition 3.8.

Let X be a clean family of intervals and let u ∈ X be a nonminimal element in the inclusion order. If v is chosen from $\left\{w \in X\, :\, w \subseteq u\right\}$ to minimize the left endpoint, then ${h}_{X}(u) = {h}_{X}(v)$.

Proof.

We argue that w < u if and only if w < v. If w < u, then also w < v or else $\left\{w,u\right\}$ is a 2-clique with v in the center, contradicting that X is clean. Conversely, if w < v, then the extremality of v implies that w < u. $\square$

Lemma 3.9.

If X is a clean family and f is the canonical coloring on X, then f is good.

Proof.

Let z ∈ X, let $S ={ \overline{R}}_{X}(z)$, and let h _S (resp., h _X ) be the height function for the endpoint order on S (resp., X). We show that ${h}_{S}(u) = {h}_{S}(v)$ if and only if ${h}_{X}(u) = {h}_{X}(v)$ for each u, v ∈ S. For each $k \geq 1$, let ${T}_{k} = \left\{w \in S\, :\, {h}_{S}(w) = k\right\}$. Fix a positive integer k. Because all elements in T _k have the same height, they are not comparable in the endpoint order, and therefore T _k is a chain in the inclusion order. Index the elements of T _k as ${u}_{1},\ldots,{u}_{n}$ so that ${u}_{1} \subsetneq {u}_{2} \subsetneq \cdots \subsetneq {u}_{n}$, and fix j < n. We claim there are no intervals in X whose left endpoint is between l(u _j ) and l(u _{j + 1}). Indeed, if there are such intervals, then let v be one that minimizes the left endpoint. Note that $v \subsetneq {u}_{j+1}$, or else $\left\{{u}_{j+1},v\right\}$ is a 2-clique with u _j in the center. Also, v ∉ S, or else applying Proposition 3.8 to u _{j + 1} and v in the family S would give that ${h}_{S}(v) = {h}_{S}({u}_{j+1}) = k$, and hence v ∈ T _k , a contradiction because no interval in T _k has a left endpoint between a left endpoints of u _j and u _{j + 1}. But now $v\not\in S$ implies that v is in the center of the 2-clique $\left\{z,{u}_{j+1}\right\}$, a contradiction. A final application of Proposition 3.8 to u _{j + 1} and u _j in X gives that ${h}_{X}({u}_{j+1}) = {h}_{X}({u}_{j})$. It follows that all intervals in T _k have the same height in X.

For the converse, suppose that T _k and T _k′ with k < k′ have the property that all elements in ${T}_{k} \cup {T}_{k^{\prime}}$ have the same height in the endpoint order on X. Fix $u \in {T}_{k^{\prime}}$. Because ${h}_{S}(u) = k^{\prime}$ and k < k′, there is an interval v ∈ S with v < u and h _S (v) = k. It follows that v ∈ T _k . But now v and u are comparable in the endpoint order, so they cannot have the same height in X. $\square$

Lemma 3.10.

Let X be a clean family of intervals, let u be a nonminimal element in the inclusion order on X, and obtain Y,Y ′, and ϕ from the right-push operation on u. If g′ is a good coloring of Y ′, then $g^{\prime} \circ \phi$ is a good coloring of Y.

Proof.

Consider w ∈ Y. Because g′ is good on Y′, we have that g′ is canonical on ${\overline{R}}_{Y ^{\prime}}(\phi (w))$. By Lemma 3.7, we have that $\phi ({\overline{R}}_{Y }(w))$ is a downset of ${\overline{R}}_{Y ^{\prime}}(\phi (w))$ in the endpoint order (even equality holds when w≠v). By Proposition 3.6, we have that g′ is canonical on $\phi ({\overline{R}}_{Y }(w))$. But ϕ : Y → Y′ is an isomorphism of the endpoint orders on Y and Y′, so g′ ∘ ϕ is canonical on ${\overline{R}}_{Y }(w)$. $\square$

If $a \in \mathbb{R}$, then X ^a denotes the subfamily of X consisting of all intervals that contain a in their interior, X ^{> a} denotes $\{[c,d] \in X : \,c > a\}$, and X ^{< a} denotes $\{[c,d] \in X : \,d < a\}$.

Proposition 3.11.

Let f be a good coloring of X, let α and β be colors, let a be a point on the real line, and suppose that $f(u)\not\in \left\{\alpha,\beta \right\}$ for each u ∈ X ^a . If f′ is the coloring of X obtained from f by interchanging α and β on the intervals in X ^>a , then f′ is also good.

Proof.

Let w ∈ X and define c, d so that w = [c, d]. If d > a, then every interval in ${\overline{R}}_{X}(w)$ with a color in $\left\{\alpha,\beta \right\}$ is in X ^{> a}, and so the change in colors does not alter the partition on ${\overline{R}}_{X}(w)$ given by the color classes of f. Similarly, if d < a, then every interval in ${\overline{R}}_{X}(w)$ with a color in $\left\{\alpha,\beta \right\}$ is in X ^{< a}, and so none of these intervals changes colors. If d = a, then increase a by a small amount and apply the proposition again. $\square$

We are now ready to prove Theorem 3.2.

Proof.

By induction on $\left\vert X\right\vert$; we may assume $\left\vert X\right\vert \geq 1$ and k ≥ 2. Let x be the interval in X that minimizes l(x). If $R(x) = \varnothing$, then x has no neighbors. Let $Y = X - x$, apply induction to Y to obtain a good coloring g of Y, and extend g to a coloring f of X by assigning an arbitrarily chosen color to x. Clearly, f is canonical on each right-neighborhood.

Therefore, we may assume that x has right-neighbors. Choose y ∈ R(x) to minimize l(y), and define a and b so that $y = \left[a,b\right]$. Let ${Y }_{1} = \left\{z \in X : \,l(z) \leq b\right\}$ and ${Y }_{2} = \left\{z \in X : \,r(z) \geq b\right\}$. Note that $x\not\in {Y }_{2}$ and therefore ${Y }_{2} \subsetneq X$. If also ${Y }_{1} \subsetneq X$, then we may apply induction to Y ₁ and Y ₂ to obtain respective good colorings g ₁ and g ₂. Note that ${Y }_{1} \cap {Y }_{2} = \left\{z \in X : \,l(z) \leq b \leq r(z)\right\}$, and because y is inclusion-maximal, ${Y }_{1} \cap {Y }_{2} ={ \overline{R}}_{X}(y)$. Consequently, all right-neighbors of y survive in Y ₁ and Y ₂, and hence ${\overline{R}}_{X}(y) ={ \overline{R}}_{{Y }_{1}}(y) ={ \overline{R}}_{{Y }_{2}}(y)$, which implies that g ₁ and g ₂ are canonical on ${Y }_{1} \cap {Y }_{2}$. Hence, after relabeling the color names, we obtain a coloring g of X that is a common extension of g ₁ and g ₂. Clearly, g uses at most 2k − 1 colors; it remains to show that g is canonical on each right-neighborhood. Consider u ∈ X. If r(u) ≤ b, then ${\overline{R}}_{X}(u) \subseteq {Y }_{1}$ and so ${\overline{R}}_{X}(u) ={ \overline{R}}_{{Y }_{1}}(u)$, which implies that g is canonical on ${\overline{R}}_{X}(u)$. Otherwise, ${\overline{R}}_{X}(u) \subseteq {Y }_{2}$, and so ${\overline{R}}_{X}(u) ={ \overline{R}}_{{Y }_{2}}(u)$, which again implies that g is canonical on ${\overline{R}}_{X}(u)$.

Hence, we may assume X = Y ₁. Next, we consider the case that x is not inclusion-minimal. Let v be the subordinate of x, let v′ be the modified subordinate of x, and obtain Y, Y′, and ϕ from the right-push operation on x. By Lemma 3.7, we have that Y and Y′ are clean with clique number at most k. By induction and Lemma 3.10, we obtain good colorings g′ of Y′ and g ₀ = g′ ∘ ϕ of Y using at most 2k − 1 colors. Extend g ₀ to a coloring g of X by defining g(w) = g ₀(w) for w≠x and $g(x) = {g}_{0}(v) = g^{\prime}(v^{\prime})$. Clearly, g uses at most 2k − 1 colors. We claim that g is a good coloring. First, note that because x minimizes l(x), we have that $x \in {\overline{R}}_{X}(w)$ implies that w = x. Therefore, g inherits the canonical coloring of g ₀ on ${\overline{R}}_{X}(w)$ whenever w≠x. Finally, note that because X is clean, we have that ${R}_{X}(x) = {R}_{Y ^{\prime}}(v^{\prime})$ and hence g inherits the canonical coloring on ${\overline{R}}_{X}(x)$ from the canonical coloring of g′ on ${\overline{R}}_{Y ^{\prime}}(v^{\prime})$.

Hence, we may assume that x is inclusion-minimal; it follows that $y \in {\overline{R}}_{X}(w)$ implies that $w \in \left\{x,y\right\}$. Next, we consider the case that y is not inclusion-minimal. Let v be the subordinate of y, let v′ be the modified subordinate, and obtain Y, Y′ and ϕ from the push operation. By Lemma 3.7, we have that Y and Y′ are clean with clique number at most k. By induction and Lemma 3.10, obtain good colorings g′ of Y′ and ${g}_{0} = g^{\prime} \circ \phi$ of Y using at most 2k − 1 colors. We use g ₀ to construct a good coloring of X. Because $Y = X - x$, to extend a good coloring of Y to a good coloring of X, we must assign a color to y so that the coloring remains canonical on each closed right-neighborhood. Because y is only in the closed right-neighborhood of x and y, we need only verify that the coloring is canonical on ${\overline{R}}_{X}(x)$ and ${\overline{R}}_{X}(y)$.

We consider two subcases. First, suppose that y is inclusion-minimal in ${\overline{R}}_{X}(x)$. Because y is chosen from ${\overline{R}}_{X}(x)$ to minimize l(y), it follows that x < y < z for every $z \in {\overline{R}}_{X}(x) -\left\{x,y\right\}$. With ${Z}_{1} ={ \overline{R}}_{X}(x)$ and ${Z}_{2} ={ \overline{R}}_{Y }(x) ={ \overline{R}}_{X}(x) -\left\{y\right\}$, this implies that two elements have the same height in Z ₂ if and only if they have the same height in Z ₁, and y is the only element of height 1 in Z ₁. Consequently, an extension of g ₀ to X is canonical on ${\overline{R}}_{X}(x)$ if and only if it assigns y a color that is not used on any other interval in ${\overline{R}}_{X}(x)$. Similarly, y < z for each $z \in {\overline{R}}_{X}(y) -\left\{y\right\}$ and hence an extension of g ₀ to X is canonical on ${\overline{R}}_{X}(y)$ if and only if y is assigned a color that is not used on any other interval in ${\overline{R}}_{X}(y)$. Because g ₀ is canonical on ${\overline{R}}_{Y }(x)$ and the clique number of ${\overline{R}}_{Y }(x)$ is at most k − 1 [indeed, every maximal clique in ${\overline{R}}_{X}(x)$ contains y], it follows that g ₀ uses at most $k - 1$ colors on ${\overline{R}}_{Y }(x)$. Also, g′ uses at most k colors on ${\overline{R}}_{Y ^{\prime}}(v^{\prime})$, and hence g ₀ uses at most k − 1 colors on R _X (y) [indeed, g′(v′) is used on $v^{\prime} \in {\overline{R}}_{Y ^{\prime}}(v^{\prime})$ but is not used on any interval in R _X (y)]. Because 2k − 1 colors are available and at most 2k − 2 provide conflicts, one color remains available for assignment to y.

The second subcase is that y is not inclusion-minimal in ${\overline{R}}_{X}(x)$. Let z be the interval that minimizes l(z) among all intervals in ${\overline{R}}_{X}(x)$ that are contained in y. Note that z is also the interval that minimizes l(z) among all that are contained in y. Let α = g ₀(z). By Proposition 3.8, the height of y and the height of z are the same in all subsets of X containing z and y. By induction, we have that g ₀ is canonical on ${\overline{R}}_{X}(x) - y$. Applying Proposition 3.4 to ${\overline{R}}_{X}(x)$, an extension of g ₀ to X is canonical on ${\overline{R}}_{X}(x)$ if and only if y is assigned color α. Also, an extension of g ₀ to X is canonical on ${\overline{R}}_{X}(y)$ if and only if y is assigned a color different from every other interval in ${\overline{R}}_{X}(y)$. If α is not used on R _X (y), then we may assign α to y. Otherwise, we first modify g ₀ before extending to X. Note that z is inclusion-maximal in Y, and let a be a point slightly to the right of r(z). Because z is inclusion-maximal in Y, every interval in Y that contains a is in R _Y (z). Let A be the set of colors that g ₀ uses on intervals containing a. Because g ₀ is canonical on ${\overline{R}}_{Y }(z)$, at most k colors are used on these intervals; because g ₀ uses $\alpha$ on $z \in {\overline{R}}_{Y }(z)$, we have α ∉ A and hence $\left\vert A\right\vert \leq k - 1$. Let B be the set of colors that g ₀ uses on intervals in R _X (y). Because g′ is canonical on ${\overline{R}}_{Y ^{\prime}}(v^{\prime})$, ${R}_{X}(y) ={ \overline{R}}_{Y ^{\prime}}(v^{\prime}) -\left\{v^{\prime}\right\}$, and v′ overlaps with every other interval in ${\overline{R}}_{Y ^{\prime}}(v^{\prime})$, we have that $\left\vert B\right\vert \leq k - 1$. Let β be a color that g ₀ uses but is not contained in A ∪B. Obtain g ₁ from g ₀ by applying Proposition 3.11 with colors $\left\{\alpha,\beta \right\}$ at point a. Note that because β ∉ B, we have that g ₁ does not use α on any interval in R _X (y). Also, g ₁(z) = α and an extension of g ₁ to X is canonical on ${\overline{R}}_{X}(x)$ if and only if y is assigned color α. Therefore, we obtain a good coloring of X from g ₁ by assigning y the color α.

Hence, we may assume that both x and y are inclusion-minimal. By Lemma 3.9, the canonical coloring on X is good. Because $X - x ={ \overline{R}}_{X}(y)$ and Proposition 3.5 implies that the canonical coloring uses at most k colors on ${\overline{R}}_{X}(y)$, the canonical coloring on X uses at most k + 1 colors in total. $\square$

Theorem 3.12.

For each k ≥ 1, there is a clean circle graph G with ω(G) = k such that every good coloring of G uses at least 2k − 1 colors.

Proof.

We construct G in stages. Our construction uses a set of k − 1 intervals V that induce a clique in the overlap graph and a set of k − 1 intervals V′ that form a chain under inclusion. These intervals are represented by solid lines in Fig. 1, which presents the construction for k = 5. Let $V =\{ {v}_{1},\ldots,{v}_{k-1}\}$ and let $V ^{\prime} =\{ {v^{\prime}}_{1},\ldots,{v^{\prime}}_{k-1}\}$, indexed so that ${v}_{1} < \cdots < {v}_{k-1}$ and ${v^{\prime}}_{1} \supseteq \cdots \supseteq {v^{\prime}}_{k-1}$. The left endpoint of v′ _j is placed slightly to the left of l(v _j ), and the right endpoints of intervals in V′ satisfy $r({v^{\prime}}_{1}) \geq \cdots \geq r({v^{\prime}}_{k-1})$. Next, add v ₀ so that v ₀ is a left-neighbor of all intervals in V ∪V′, and add v′ ₀ so that v′ ₀ is a right-neighbor of all intervals in V and is contained in all intervals in V′.

Because a good coloring must be canonical on $\overline{R}({v}_{0})$, it follows that a good coloring assigns the same color to v _j and v′ _j for j ≥ 1, and hence k − 1 distinct colors are assigned to intervals in V′. Since v′ ₀ is a right-neighbor of each interval in V, it follows that k distinct colors are assigned to intervals in $V ^{\prime} \cup \{ {v^{\prime}}_{0}\}$. These intervals form an independent set in the overlap graph.

In the second stage, we add a set S of k − 1 pairwise overlapping intervals such that each interval in S overlaps with intervals in $V ^{\prime} \cup \{ {v^{\prime}}_{0}\}$ and no others. Intervals in S are represented by dashed lines in Fig. 1. A good coloring must use k − 1 new colors on S, and hence at least 2k − 1 colors in total. $\square$

Fig. 1

Construction in Theorem 3.12

4 Chromatic Number of K ₄-Free Circle Graphs

In this section, we study the chromatic number of circle graphs with clique number at most 3. By Theorem 3.2, it follows that a clean K ₄-free circle graph has chromatic number at most 5. We need a lemma that provides 5-colorings of other circle graphs. Recall that if a is a point in $\mathbb{R}$, then X ^a is the set of all intervals in X that contain a.

Lemma 4.1.

Let ${a}_{1},\ldots,{a}_{k}$ and ${b}_{1},\ldots,{b}_{k}$ be points with ${a}_{1} < {b}_{1} < {a}_{2} < {b}_{2} < \cdots < {a}_{k} < {b}_{k}$ , and let ${S}_{j} =\{ {a}_{j},{b}_{j}\}$ . Let X be a family of intervals, each of which has nonempty intersection with exactly one of the sets in $\{{S}_{1},\ldots,{S}_{k}\}$ . If $\omega (G(X)) \leq 3$ and $\omega (G({X}^{c})) \leq 2$ for each $c \in \{ {a}_{1},\ldots,{a}_{k}\} \cup \{ {b}_{1},\ldots,{b}_{k}\}$ , then there is a proper 5-coloring of G(X) with a distinguished color α such that every interval assigned color α is disjoint from $\{{a}_{1},\ldots,{a}_{k}\}$ , and for each $c \in \{ {a}_{1},\ldots,{a}_{k}\} \cup \{ {b}_{1},\ldots,{b}_{k}\}$ , at most 4 colors are used on intervals in X ^c.

Proof.

Partition X into ${A}_{1},{B}_{1},\ldots,{A}_{k},{B}_{k}$ as follows. If S _j is the unique set in $\{{S}_{1},\ldots,{S}_{k}\}$ that has a nonempty intersection with x, then we assign x to the set A _j if a _j  ∈ x or to the set B _j otherwise. Note that for all $1 \leq i,j \leq k$, we have $\omega (G({A}_{i})) \leq 2$ and $\omega (G({B}_{j})) \leq 2$, and hence the endpoint orders on A _i and B _j are posets of height at most 2.

The canonical coloring is defined with respect to height in the endpoint order. The dual-canonical coloring of a family of intervals colors each interval with its depth in the endpoint order. When the interval order on Z has height at most t, the $({\beta }_{1},\ldots,{\beta }_{t})$-canonical coloring on Z assigns to an interval z ∈ Z the color β _j , where j is the height of z in the endpoint order. Similarly, the $({\beta }_{1},\ldots,{\beta }_{t})$-dual-canonical coloring on Z assigns to an interval z ∈ Z the color β _j , where j is the depth of z in the endpoint order. We color each A _j canonically, and we color each B _j with a dual-canonical coloring.

We use $\{1,2,3,4,\alpha \}$ as our set of colors. If j is odd, then we use the (2, 1)-canonical coloring on A _j and the (α, 3)-dual-canonical coloring on B _j . If j is even, then we use the (4, 3)-canonical coloring on A _j and the (α, 1)-dual-canonical coloring on B _j . First, note that if x has color α, then x is in some B _j , which implies that x contains b _j but not a _j , and therefore x does not contain any of the points in $\{{a}_{1},\ldots,{a}_{k}\}$.

Note that for each j, at most 4 colors are used on intervals in ${A}_{j} \cup {B}_{j}$. It follows that for each $c \in \{ {a}_{1},\ldots,{a}_{k}\} \cup \{ {b}_{1},\ldots,{b}_{k}\}$, at most 4 colors are used on intervals in X ^c. It remains to check that the coloring is proper. Note that the colors used on A _j are disjoint from the colors used on B _j . Since the coloring is proper on A _j and on B _j , it follows that the coloring is proper on ${A}_{j} \cup {B}_{j}$. Moreover, if $x \in {A}_{i} \cup {B}_{i}$ and $y \in {A}_{j} \cup {B}_{j}$ overlap, it follows that | i − j | ≤ 1 and y overlap, since each interval in X meets exactly one of the sets in $\{{S}_{1},\ldots,{S}_{k}\}$.

Suppose that $x \in {A}_{i} \cup {B}_{i}$ and $y \in {A}_{j} \cup {B}_{j}$ overlap. If i = j, then x and y receive different colors since the coloring is proper on ${A}_{i} \cup {B}_{i}$. Hence, we may assume that $j = i + 1$. Note that a _j  ∈ y, since otherwise a _j would separate x and y. It follows that y ∈ A _j . If y has height 0 in A _j , then the color assigned to y is not used for intervals in ${A}_{i} \cup {B}_{i}$, and hence x and y receive different colors. If y has height 1 in A _j , then the color β assigned to y is used only for the intervals in ${A}_{i} \cup {B}_{i}$ that have depth 1 in B _i . Suppose for a contradiction that x also receives color β. Since x has depth 1 in B _i , there exists $x^{\prime} \in {B}_{i}$ with x < x′ in the endpoint order. Similarly, since y has height 1 in A _j , there exists y′ ∈ A _j with y′ < y in the endpoint order. Moreover, $l(x^{\prime}) < {b}_{i} < l(y)$ and $r(x^{\prime}) < {a}_{3} < r(y^{\prime})$, and, therefore, x′ < y′ in the endpoint order. But then $\{x,x^{\prime},y^{\prime},y\}$ is a 4-clique in G(X) since x < x′ < y′ < y in the endpoint order and x and y overlap. $\square$

Example 4.2.

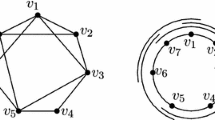
The complement of the cycle on 7 vertices, denoted $\overline{{C}_{7}}$, is the overlap graph of a family of intervals that satisfies the hypotheses of Lemma 4.1 with carefully chosen points a ₁ and b ₁ (see Fig. 2). Consequently, Lemma 4.1 cannot be improved by more than one color.

Fig. 2

$\overline{{C}_{7}}$ as the overlap graph of a family of intervals

Our next task is to explore the structure of segments. A segment of a family X is an inclusion-maximal interval in the set of all centers of 2-cliques in X.

Lemma 4.3.

Let X be a family of intervals. If [a,b] and [c,d] are overlapping segments of X with a < c < b < d, then there exists x ∈ X with l(x) ∈ [a,c) and r(x) ∈ (b,d].

Proof.

Let y ₁ and y ₂ be overlapping intervals in X with ${y}_{1} < {y}_{2}$ and center [a, b]. Let z ₁ and z ₂ be overlapping intervals in X with ${z}_{1} < {z}_{2}$ and center [c, d]. Note that $l({y}_{2}) = a$ and $r({z}_{1}) = d$. We claim that either $r({y}_{2}) \in (b,d]$ or $l({z}_{1}) \in [a,c)$. Because $r({y}_{2}) > b$ and $l({z}_{1}) < c$, failure requires $r({y}_{2}) > d$ and l(z ₁) < a. But then we have $l({z}_{1}) < l({y}_{2}) = a < d = r({z}_{1}) < r({y}_{2})$, which implies that z ₁ and y ₂ are overlapping intervals in X with center [a, d], contradicting that [a, b] and [c, d] are segments. Hence, either y ₂ or z ₁ is as required. $\square$

Lemma 4.4.

Let X be a family of intervals. If ${u}_{1},\ldots,{u}_{t}$ are overlapping segments of X with ${u}_{1} < {u}_{2} < \cdots < {u}_{t}$ , then $\left[l({u}_{t}),r({u}_{1})\right]$ is the center of a (t + 1)-clique in X.

Proof.

For 1 ≤ j < t, apply Lemma 4.3 to the segments u _j and u _{j + 1} to obtain z _j  ∈ X with $l({z}_{j}) \in [l({u}_{j}),l({u}_{j+1}))$ and $r({z}_{j}) \in (r({u}_{j}),r({u}_{j+1})]$. Of the overlapping pair of intervals in X whose center is u ₁, let z ₀ be the leftmost in the endpoint order. Similarly, of the overlapping pair of intervals in X whose center is u _t , let z _t be the rightmost in the endpoint order. It follows that $l({z}_{0}) < l({z}_{1}) < \cdots < l({z}_{t}) < r({z}_{0}) < r({z}_{1}) < \cdots < r({z}_{t})$ and so $\left\{{z}_{0},\ldots,{z}_{t}\right\}$ is a (t + 1)-clique in X with center $[l({u}_{t}),r({u}_{1})]$. $\square$

As a consequence of Lemma 4.4, if X has clique number k and U is the family of segments of X, then U has clique number at most k − 1. Moreover, by definition, each interval in U is inclusion-maximal. Hence, the endpoint order on U is a chain. If X has clique number at most 3, then every component of the overlap graph of U is a chain.

We need the following lemma due to Gyárfás [9].

Lemma 4.5.

Let X be a of intervals such that G(X) is connected, let x ₀ be the interval in X that minimizes l(x ₀ ), and for each k ≥ 0, let X _k be the set of all intervals at distance k from x in G(X). Let k be a positive integer, and let [a,b] be an interval such that $[a,b] \subseteq \bigcup\nolimits_{x\in {X}_{k}}x$. If $z \in {S}_{k-1}$ and one endpoint of z is in [a,b], then the other endpoint of z is outside [a,b].

Our next lemma ties together the two separate coloring strategies given by Theorem 3.2 and Lemma 4.1 and is at the heart of our proof. The clean part of a family of intervals X is the set of intervals in X that are not contained in a segment of X. Note that the clean part of a family of intervals is clean. In the following, we fix disjoint color sets A and B of sizes 10 and 9, respectively.

Lemma 4.6.

Let X be a family of intervals such that no interval is contained in the center of a 3-clique, G(X) is connected, and $\omega (G(X)) \leq 3$ . Let x ₀ be the interval in X that minimizes l(x ₀ ), and for k ≥ 0, let X _k be the set of intervals at distance k from x ₀ . Let Y _k be the clean part of X _k , and let Z _k be the complement ${X}_{k} - {Y }_{k}$.

For each nonnegative integer k, there are a set P _k of points and a proper (A ∪ B)-coloring of $G({X}_{0} \cup \ldots \cup {X}_{k})$ with the following properties.

• (1) If j > k and x ∈ X _j , then x and P _k are disjoint.

• (2) Every interval in Z _k contains a point in P _k.

• (3) The colors used on Y _k are contained in a subset A′ of A with |A′|≤ 5.

• (4) The colors used on Z _k are contained in B.

• (5) Let I be an inclusion-maximal interval in $\mathbb{R} - {P}_{k}$ . There exists a subset B′ of B with |B′|≤ 5 such that every interval in Z _k that overlaps I has a color in B′, and there is a color $\beta \in B^{\prime}$ such that z overlaps I on the left whenever z ∈ Z _k overlaps I and has color β.

Proof.

For k = 0, we let ${P}_{0} = \varnothing$ and color the single interval x ₀ in X ₀ with an arbitrary color in A. Since ${Y }_{0} =\{ {x}_{0}\}$ and ${Z}_{0} = \varnothing$, conditions (1)–(5) are satisfied.

For k ≥ 1, we obtain a set of points P _{k − 1} and a proper (A ∪B)-coloring of $G({X}_{0} \cup \ldots \cup {X}_{k-1})$ with conditions (1)–(5) by induction. We first extend the coloring to $G({X}_{0} \cup \ldots \cup {X}_{k})$. Note that an interval in X _k overlaps only with intervals in ${X}_{k-1} \cup {X}_{k}$. Since property (3) implies that at most 5 colors are used on intervals in Y _{k − 1} and | A |  = 10, there is a set A′ of 5 colors in A, none of which appears on intervals in Y _{k − 1}. Since Y _k is clean, Theorem 3.2 implies that Y _k has a proper 5-coloring. We use the colors in A′ to color Y _k .

Every interval in Z _k is contained in a segment of X _k . Let ${u}_{1},\ldots,{u}_{s}$ be the segments of X _k , indexed so that ${u}_{1} < \cdots < {u}_{s}$ in the endpoint order. For each segment u _j , we define a left-pina _j and a right-pinb _j . Let $\epsilon$ be a positive real number that is less than the minimum distance between two endpoints of intervals in X. When there are intervals in X _{k − 1} that overlap u _j on the left, we define a _j to be $\max \{r(x): \,x \in {X}_{k-1}$ and x overlaps u _j on the left}. When there are no such intervals, we define a _j to be $r({u}_{j-1}) + \epsilon$ when u _{j − 1} exists and overlaps u _j and $l({u}_{j}) + \epsilon$ otherwise. Similarly, when there are intervals in X _{k − 1} that overlap u _j on the right, we define b _j to be $\min \{l(x): \,x \in {X}_{k-1}\ \text{ and}\ x\ \text{ overlaps}\ {u}_{j}\ \text{ on the right}\}$. When there are no such intervals, we define b _j to be $l({u}_{j+1}) - \epsilon$ when u _{j + 1} exists and overlaps u _j and $r({u}_{j}) - \epsilon$ otherwise.

Note that no pin is in more than one segment. If some pin $c \in \{ {a}_{1},\ldots,{a}_{s},{b}_{1},$ …, b _s } were contained in u _j and u _{j + 1}, it follows from the definition of c that there is an interval x ∈ X _{k − 1} with c as an endpoint. Moreover, Lemma 4.4 implies that there is a 3-clique $\{{x}_{1},{x}_{2},{x}_{3}\}$ in X _k whose center is the same as the center of $\{{u}_{j},{u}_{j+1}\}$. Since c is in the center of $\{{x}_{1},{x}_{2},{x}_{3}\}$, Lemma 4.5 implies that the other endpoint of x is outside ${x}_{1} \cup {x}_{2} \cup {x}_{3}$, and so x overlaps each interval in $\{{x}_{1},{x}_{2},{x}_{3}\}$. Therefore, $\{{x}_{1},{x}_{2},{x}_{3},x\}$ is a 4-clique in X, a contradiction.

Next, we argue that every interval z ∈ Z _k contains some pin in its interior. Since z ∈ Z _k , it follows that z is contained in some segment u _j . Since z is at distance k from x ₀ in G(X), it follows that z overlaps with an interval x at distance k − 1 from x ₀ in G(X). Suppose that x overlaps z to the left, so that r(x) is in the interior of z. We claim that z contains the left-pin of u _j . Since $x \in {X}_{k-1}$, it follows that ${a}_{j} \geq r(x) > l(z)$. Let x′ be the interval in X _{k − 1} whose right endpoint is a _j , and let x ₁ and x ₂ be the intervals in X _k whose center is the segment u _j . Lemma 4.5 implies that the left endpoint of x′ is outside ${x}_{1} \cup {x}_{2}$, which implies that $\{x^{\prime},{x}_{1},{x}_{2}\}$ is a 3-clique in X. Since z is contained in the center of x ₁ and x ₂ and z is not contained in a 3-clique of X, it must be that z is not contained in x′, which implies that ${a}_{j} = r(x^{\prime}) < r(z)$. Hence, $l(z) < {a}_{j} < r(z)$. Similarly, if x overlaps z on the right, then z contains the right-pin of u _j .

For each j with $1 \leq j \leq s$, let ${S}_{j} =\{ {a}_{j},{b}_{j}\}$. Since an interval z ∈ Z _k is contained in some segment u _j and u _j contains only the pins a _j and b _j , it follows that z has nonempty intersection with exactly one of the sets in $\{{S}_{1},\ldots,{S}_{s}\}$. We claim that if c is a pin, then $\omega (G({Z}_{k}^{c})) \leq 2$. This is immediate if c is an endpoint of an interval in X _{k − 1}. Otherwise, let c′ be the other pin associated with the segment containing c, and note that ${Z}_{k}^{c} \subseteq {Z}_{k}^{c^{\prime}}$. If c′ is an endpoint of an interval in X _{k − 1}, then we have $\omega (G({Z}_{k}^{c})) \leq \omega (G({Z}_{k}^{c^{\prime}})) \leq 2$. If neither c nor c′ is the endpoint of an interval in X _{k − 1}, then it must be that ${Z}_{k}^{c} = {Z}_{k}^{c^{\prime}} = \varnothing$. Therefore, every subset of Z _k satisfies the hypotheses of Lemma 4.1 with respect to the points ${a}_{1},\ldots,{a}_{s}$ and ${b}_{1},\ldots,{b}_{s}$.

It remains to color Z _k . Let I be an inclusion-maximal interval of $\mathbb{R} - {P}_{k-1}$, and let L be the set of intervals in Z _k that are contained in I. Since intervals in distinct inclusion-maximal intervals of $\mathbb{R} - {P}_{k-1}$ do not overlap, we may color L independently of the rest of Z _k .

By property (5), there exists ${B}_{0} \subseteq B$ with | B ₀ | ≤ 5 such that every interval in Z _{k − 1} that overlaps I has a color in B ₀, and there is a distinguished color α ∈ B ₀ such that if $z \in {Z}_{k-1}$ overlaps I and has color α, then z overlaps I on the left. Let $B^{\prime} = B - {B}_{0} \cup \{ \alpha \}$, and note that | B′ |  = 5.

Using the colors in B′ and the distinguished color α, apply Lemma 4.1 to color L. We claim that the coloring remains proper. If not, then there are intervals z ∈ L and z′ ∈ X _{k − 1} that overlap and have the same color. Since the color of z is in B′, the color of z′ is also in B′, which implies that $z^{\prime} \in {Z}_{k-1}$. By property (2), we have that z′ contains a point in P _{k − 1}, and it follows that z′ overlaps I. Hence, property (5) implies that the color of z′ is in B ₀. Since ${B}_{0} \cap B^{\prime} =\{ \alpha \}$, it follows that the common color of z and z′ is α. It now follows that z′ overlaps I on the left. Since z′ is an interval in X _{k − 1} that overlaps z on the left, it follows that z contains the left-pin a _j of the segment u _j containing z, contradicting that each interval in L with color α is disjoint from $\{{a}_{1},\ldots,{a}_{s}\}$.

We have obtained a proper (A ∪B)-coloring of $G({X}_{0} \cup \cdots \cup {X}_{k})$. Let P _k be the union of P _{k − 1} and the points in $\{{a}_{1},\ldots,{a}_{s},{b}_{1},\ldots,{b}_{s}\}$ that are endpoints of intervals in X _{k − 1}. It remains to check that the coloring and P _k satisfy properties (1)–(5). Note that if x has distance k − 1 from x ₀ and x′ has distance at least k + 1, then x′ does not contain either endpoint of x. Since every point in ${P}_{k} - {P}_{k-1}$ is an endpoint of some interval in X _{k − 1}, it follows that no interval in X _j for j > k contains a point in P _k , which implies property (1). If z ∈ Z _k , then z overlaps some interval x ∈ X _{k − 1}. Let u be the segment of X _k containing z. If x overlaps z on the left, then z contains the left-pin of u, which is the endpoint of an interval in X _{k − 1}. Otherwise, if x overlaps z on the right, then z contains the right-pin of u, which is the endpoint of an interval in X _{k − 1}. In either case, z contains a point in P _k , and therefore property (2) is satisfied. It is clear from our coloring that properties (3) and (4) are satisfied.

Let I be an inclusion-maximal interval in $\mathbb{R} - {P}_{k}$. Since ${P}_{k-1} \subseteq {P}_{k}$, it follows that I is contained in an inclusion-maximal interval I′ in $\mathbb{R} - {P}_{k-1}$. Let L be the set of intervals in Z _k that are contained in I′, and let B′ be the set of 5 colors in B that are used to color intervals in L. Clearly, every interval in Z _k that overlaps I has a color in B′. Let c be the right endpoint of I. By Lemma 4.1, at most 4 colors are used on intervals in L ^c. It follows that there is a color $\beta \in B^{\prime}$ such that every interval in L with color β that overlaps I does so on the left. It follows that property (5) is satisfied. $\square$

With Lemma 4.6, we are now able to complete our upper bound on the chromatic number of a circle graph with clique number at most 3.

Proof of Theorem 1.2.

We may assume that G(X) is connected. Let x ₀ be the interval in X that minimizes l(x ₀), and for k ≥ 0, let X _k be the set of intervals that are at distance k from x ₀ in G(X).

Note that no interval in X _k is contained in the center of a 3-clique of X _k . This is immediate if k = 0 since ${X}_{0} =\{ {x}_{0}\}$. For k ≥ 1, if some interval x were contained in the center of a 3-clique $\{{x}_{1},{x}_{2},{x}_{3}\}$ in X _k , then there is an interval x′ in X _{k − 1} that overlaps x, and Lemma 4.5 would imply that $\{{x}_{1},{x}_{2},{x}_{3},x^{\prime}\}$ is a 4-clique in G(X), a contradiction.

Therefore, Lemma 4.6 implies that $\chi (G({X}_{k})) \leq 19$. Using disjoint color sets for ${X}_{0} \cup {X}_{2} \cup \cdots$ and ${X}_{1} \cup {X}_{3} \cup \cdots$, we have that $\chi (G(X)) \leq 38$. $\square$

Addendum.Subsequent to our current work but prior to publication, we learned that Gleb Nenashev has improved on Theorem 1.2 by showing that χ(G) ≤ 30 when G is a K ₄-free circle graph.