Keywords

Many software reliability models have been proposed to help software developers and managers understand and analyze the software development process, estimate the development cost, and assess the level of software reliability. Among these software reliability models, models based on the nonhomogeneous Poisson process (NHPP) have been successfully applied to model the software failure processes that possess certain trends such as reliability growth or deterioration. NHPP models seem to be useful to predict software failures and software reliability in terms of time and to determine when to stop testing and release the software [1].

Currently most existing NHPP software reliability models have been carried out through the fault intensity rate function and the mean-value functions (MVF) m(t) within a controlled operating environment [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55]. Obviously, different models use different assumptions and therefore provide different mathematical forms for the mean-value function m(t). Table 25.1 shows a summary of several existing models appearing in the software reliability engineering literature [14]. Generally, these models are applied to software testing data and then to make predictions of software failures and reliability in the field. The underlying assumption for this application is that the field environments are the same as, or close to, a testing environment; this is valid for some software systems that are only used in one environment throughout their entire lifetime. However, this assumption is not valid for many applications where a software program may be used in many different locations once it is released.

Table 25.1 Summary of NHPP software reliability models [44, 50]
Full size table

The operating environments for the software in the field are quite different. The randomness of the field environment will affect software failure and software reliability in an unpredictable way. Yang and Xie [15] mentioned that the operational reliability and testing reliability are often different from each other, but they assumed that the operational failure rate is still close to the testing failure rate, and hence that the difference between them is that the operational failure rate decreases with time, while the testing failure rate remains constant. Zhang et al. [16] proposed an NHPP software reliability calibration model by introducing a calibration factor. This calibration factor, K, obtained from software failures in both the testing and field operation phases will be a multiplier to the software failure intensity. This calibrated software reliability model can be used to assess and adjust the predictions of software reliability in the operation phase.

Instead of relating the operating environment to the failure intensity λ, in this chapter we assume that the effect of the operating environment is to multiply the unit failure-detection rate b(t) achieved in the testing environment using the concept of the proportional hazard approach suggested by Cox [56]. If the operating environment is more liable to software failure, then the unit fault-detection rate increases by some factor η greater than 1. Similarly, if the operating environment is less liable to software failure, then the unit fault-detection rate decreases by some positive factor η less than 1.

This chapter describes a model based on the NHPP model framework for predicting software failures and evaluating the software reliability in random field environments. A generalized random field environment (RFE) model incorporating both the testing phase and operating phase in the software development cycle with Vtub-shaped fault-detection rate is discussed. An explicit solution of the mean value function for this model is derived. Numerical results of some selected NHPP models are also discussed based on existing criteria such as mean squared error (MSE), predictive power, predictive-ratio risk, and normalized criteria distance from a set of software failure data.

Based on this model, developers and engineers can further develop specific software reliability models customized to various applications.

Notations

R(t)

Software reliability function

η

Random environmental factor

G(η)

Cumulative distribution function of η

γ

Shape parameter of gamma distributions

θ

Scale parameter of gamma distributions

α, β

Parameters of beta distributions

N(t)

Counting process which counts the number of software failures discovered by time t

m(t)

Expected number of software failures detected by time t, m(t) = E[N(t)]

a(t)

Expected number of initial software faults plus introduced faults by time t

m1(t)

Expected number of software failures in testing by time t

m2(t)

Expected number of software failures in the field by time t

a1(t)

Expected number of initial software faults plus introduced faults discovered in the testing by time t

a

Number of initial software faults at the beginning of testing phase, is a software parameter that is directly related to the software itself

T

Time to stop testing and release the software for field operations

aF

Number of initial software faults in the field (at time T)

b(t)

Failure detection rate per fault at time t, is a process parameter that is directly related to testing and failure process

p

Probability that a fault will be successfully removed from the software

q

Error introduction rate at time t in the testing phase

MLE

Maximum likelihood estimation

RFE-model

Software reliability model subject to a random field environment

γ-RFE

Software reliability model with a gamma distributed field environment

β-RFE

Software reliability model with a beta distributed field environment

NHPP

Nonhomogeneous Poisson process

SRGM

Software reliability growth model

HD

Hossain–Ram

PNZ

Pham–Nordman–Zhang

G–O

Goel–Okumoto

MLE

Maximum likelihood estimation

RFE

Random field environment

1 A Generalized NHPP Software Reliability Model

A generalized NHPP model studied by Zhang et al. [7] can be formulated as follows:

$$ {m}^{\prime }(t)=\eta b(t)\left[a(t)- pm(t)\right], $$
(25.1)
$$ {a}^{\prime }(t)=q\cdot {m}^{\prime }(t), $$
(25.2)

where m(t) is the number of software failures expected to be detected by time t. If the marginal conditions are given as m(0) = 0 and a(0) = a, then for a specific environmental factor η, the solutions to (25.1) and (25.2) are, given in [7], as follows

$$ {m}_{\eta }(t)=a\int_0^t\eta b(u){\mathrm{e}}^{-{\int}_{\!\!0}^{u}\eta \left(p-q\right)b\left(\tau \right)\mathrm{d}\tau}\mathrm{d}u, $$
(25.3)
$$ {a}_{\eta }(t)=a\left[1+\int_0^t\eta qb(u){\mathrm{e}}^{-{\int}_{\!\!0}^{u}\eta \left(p-q\right)\cdot b\left(\tau \right)\mathrm{d}\tau}\mathrm{d}u\right]. $$
(25.4)

This is the generalized form of the NHPP software reliability model. When p = 1, η = 1, and q = 0, then for any given function a(t) and b(t), all the functions listed in Table 25.1 can easily be obtained.

2 Generalized Random Field Environment (RFE) Model

The testing environment is often a controlled environment with much less variation compared to the field environments, which may be quite different for the field application software. Once a software program is released, it may be used in many different locations and various applications in industries. The operating environments for the software are quite different. Therefore, the randomness of the field environment will affect the cumulative software failure data in an unpredictable way.

Figure 25.1 shows the last two phases of the software life cycle: in-house testing and field operation [18]. If T is the time to stop testing and release the software for field operations, then the time period 0 ≤ t ≤ T refers to the time period ofsoftware testing, while the time period T ≤ t refers to the postrelease period – field operation.

Fig. 25.1
figure 1

Testing versus field environment where T is the time to stop testing and release the software

Full size image

The environmental factor η is used to capture the uncertainty about the environment and its effects on the software failure rate. In general, software testing is carried out in a controlled environment with very small variations, which can be used as a reference environment where η is constant and equals to 1. For the field operating environment, the environmental factor η is assumed to be a non-negative random variable (RV) with probability density function (PDF) f(η), that is,

$$ \eta =\left\{\begin{array}{ll}1& t\le T\\ {}\mathrm{RV}\ \mathrm{with}\ \mathrm{PDF}\ f\!\left(\eta \right)& t\ge T\end{array}.\right. $$
(25.5)

If the value of η is less than 1, this indicates that the conditions are less favorable to fault detection than that of testing environment. Likewise, if the value of η is greater than 1, it indicates that the conditions are more favorable to fault detection than that of the testing environment.

From (25.3) and (25.5), the mean-value function and the function a1(t) during testing can be obtained as

$$ {\displaystyle \begin{aligned}&{m}_1(t)=a\int_0^tb(u){\mathrm{e}}^{-{\int}_{\!\!0}^{u}\left(p-q\right)b\left(\tau \right)\mathrm{d}\tau}\mathrm{d}u\, t\le T,\\ &{a}_1(t)=a\left[1+\int_0^t qb(u)\times {\mathrm{e}}^{-{\int}_{\!\!0}^{u}\left(p-q\right)\cdot b\left(\tau \right)\mathrm{d}\tau}\mathrm{d}u\right]\, t\le T.\end{aligned}} $$
(25.6)

For the field operation where t ≥ T, the mean-value function can be represented as

$$ {\displaystyle \begin{aligned}{m}_2(t)=&\,{m}_1(T)+\int_0^{\infty }{m}_{\eta }(t)f\!\left(\eta \right)\mathrm{d}\eta={m}_1(T) \\ &+\int_0^{\infty}\left[{a}_{\mathrm{F}}\int_T^t\eta b(u)\times {\mathrm{e}}^{-{\int}_T^u\eta \left(p-q\right)b\left(\tau \right)\mathrm{d}\tau}\mathrm{d}u\right]f\!\left(\eta \right)\!\mathrm{d}\eta \, t\ge T\\ =&\,{m}_1(T)+\int_T^t{a}_{\mathrm{F}}b(u)\left[\int_0^{\infty}\eta \times {\mathrm{e}}^{-\eta {\int}_T^u\left(p-q\right)b\left(\tau \right)\mathrm{d}\tau }f\!\left(\eta \right)\!\mathrm{d}\eta \right]\mathrm{d}u,\end{aligned}} $$
(25.7)

where aF is the number of faults in the software at time T. Using the Laplace transform formula, the mean-value function can be rewritten as

$$ {\displaystyle \begin{aligned}&{m}_2(t)={m}_1(T)\!\!+\!\!\int_T^t{a}_{\mathrm{F}}b(u)\!\times\! \left(\!\!-{\left.\frac{\mathrm{d}{F}^{\ast }(s)}{\mathrm{d}s}\right|}_{s\,{=}\,{\int}_{\!\!0}^{u}\left(p-q\right)b\left(\tau \right)\mathrm{d}\tau}\right)\mathrm{d}u,\\ &t\ge T\\ &\!=\!{m}_1(T)\!+\!\frac{a_{\mathrm{F}}}{\left(p-q\right)}\times \int_T^t\left\{-\mathrm{d}{F}^{\ast}\left[\left(p-q\right)\int_T^ub\left(\tau \right)\mathrm{d}\tau \right]\right\},\end{aligned}} $$

where F*(s) is the Laplace transform of the PDF f(x) and

$$ \int_0^{\infty }x{\mathrm{e}}^{-x\cdot s}f(x)\mathrm{d}x=-\frac{\mathrm{d}{F}^{\ast }(s)}{\mathrm{d}s} $$

or, equivalently,

$$ {\displaystyle \begin{array}{c}{m}_2(t)={m}_1(T)-\frac{a_{\mathrm{F}}}{\left(p-q\right)}\times {F}^{\ast }{\left.\left[\left(p-q\right)\int_T^ub\left(\tau \right)\mathrm{d}\tau \right]\right|}_T^t,\;\; t\le T\\[4pt] ={m}_1(T)+\frac{a_{\mathrm{F}}}{\left(p-q\right)}\times \left\{{F}^{\ast }(0)-{F}^{\ast}\left[\left(p-q\right)\right.\right.\\[4pt]\left.\left.\int_T^tb\left(\tau \right)\mathrm{d}\tau \right]\right\}.\end{array}} $$

Notice that \( {F}^{\ast }(0)={\int}_{\!\!0}^{\infty }{\mathrm{e}}^{-0x}f(x)\mathrm{d}x=1 \), so

$$ \begin{aligned}{m}_2(t)=&\,{m}_1(T)+\frac{a_{\mathrm{F}}}{\left(p-q\right)}\\ &\times \left\{1-{F}^{\ast}\left[\left(p-q\right)\int_T^tb\left(\tau \right)\mathrm{d}\tau \right]\right\}\, t\ge T.\end{aligned} $$

The expected number of faults in the software at time T is given by

$$ {\displaystyle \begin{aligned}{a}_{\mathrm{F}}&={a}_1(T)-{pm}_1(T)\\ &=a\left[1-\int_0^t\left(p-q\right)b(u){\mathrm{e}}^{-{\int}_{\!\!0}^u\left(p-q\right)\cdot b\left(\tau \right)\mathrm{d}\tau}\mathrm{d}u\right]\\ &=a{\mathrm{e}}^{-{\int}_{\!\!0}^t\left(p-q\right)b\left(\tau \right)\mathrm{d}\tau }.\end{aligned}} $$

The generalized RFE model can be obtained as

$$ { {m(t)=\left\{\begin{array}{l}\frac{a}{\left(p-q\right)}\left(1-{\mathrm{e}}^{-\left(p-q\right){\int}_{\!\!0}^ub\left(\tau \right)\mathrm{d}\tau}\right)\, t\le T\\ {}\frac{a}{\left(p-q\right)}\left\{1-{\mathrm{e}}^{-\left(p-q\right){\int}_{\!\!0}^Tb\left(\tau \right)\mathrm{d}\tau}\right.\times {F}^{\ast}\left[{\left(p-q\right)}^{\int_T^tb\left(\tau \right)\mathrm{d}\tau}\right]\;\, t\ge T.\end{array}\right.}} $$
(25.8)

The model in (25.8) is a generalized software reliability model subject to random field environments. The next section presents specific RFE models for the gamma and beta distributions of the random field environmental factor η.

3 RFE Software Reliability Models

Obviously, the environmental factor η must be non-negative. Any suitable non-negative distribution may be used to describe the uncertainty about η. In this section, we present two RFE models. The first model is a γ-RFE model, based on the gamma distribution, which can be used to evaluate and predict software reliability in field environments where the software failure-detection rate can be either greater or less than the failure detection rate in the testing environment. The second model is a β-RFE model, based on the beta distribution, which can be used to predict software reliability in field environments where the software failure detection rate can only be less than the failure detection rate in the testing environment.

3.1 γ-RFE Model

In this model, we use the gamma distribution to describe the random environmental factor η. This model is called the γ-RFE model.

Assume that η follows a gamma distribution with a probability density function as follows:

$$ {f}_{\gamma}\!\left(\eta \right)=\frac{\theta^{\gamma }{\eta}^{\gamma -1}{\mathrm{e}}^{-\theta \cdot \eta }}{\Gamma \left(\gamma \right)},\gamma, \theta >0;\eta \ge 0. $$
(25.9)

The gamma distribution has sufficient flexibility and has desirable qualities with respect to computations [18]. Figure 25.2 shows an example of the gamma density probability function. The gamma function seems to be reasonable to describe a software failure process in those field environments where the software failure-detection rate can be either greater (i.e., η > 1) or less than (i.e., η < 1) the failure-detection rate in the testing environment.

Fig. 25.2
figure 2

A gamma density function

Full size image

The Laplace transform of the probability density function in (25.9) is

$$ {F}^{\ast }(s)={\left(\frac{\theta }{\theta +s}\right)}^{\gamma }. $$
(25.10)

Assume that the error-detection rate function b(t) is given by

$$ b(t)=\frac{b}{1+c{\mathrm{e}}^{-b\cdot t}}. $$
(25.11)

where b is the asymptotic unit software-failure detection rate and c is the parameter defining the shape of the learning curve, then from (25.8) the mean-value function of the γ-RFE model can be obtained as follows

$$ { { {m}_{\gamma }(t)=\left\{\begin{array}{l}\frac{a}{\left(p-q\right)}\left[1-{\left(\frac{1+c}{{\mathrm{e}}^{bt}+c}\right)}^{\left(p-q\right)}\right]\, t\le T,\\ \\ {}\frac{a}{\left(p-q\right)}\left[1-{\left(\frac{1+c}{{\mathrm{e}}^{bT}+c}\right)}^{\left(p-q\right)}\times {\left(\frac{\theta }{\theta +\left(p-q\right)\ln \left(\frac{c+{\mathrm{e}}^{bt}}{c+{\mathrm{e}}^{bT}}\right)}\right)}^{\gamma}\right]\, t\ge T.\end{array}\right.}}\nonumber\\ $$
(25.12)

3.2 β-RFE Model

This section presents a model using the beta distribution that describes the random environmental factor η, called the β-RFE model.

The beta PDF is

$$ {f}_{\beta}\!\left(\eta \right)=\frac{\Gamma\! \left(\alpha +\beta \right)}{\Gamma\! \left(\alpha \right)\Gamma\! \left(\beta \right)}{\eta}^{\alpha -1}{\left(1-\eta \right)}^{\beta -1},\nonumber\\ \alpha >0,\beta >0;\, 0\le \eta \le 1. $$
(25.13)

Figure 25.3 shows an example of the beta density function. It seems that the β-RFE model is a reasonable function to describe a software failure process in those field environments where the software failure-detection rate can only be less than the failure-detection rate in the testing environment. This is not uncommon in the software industry because, during software testing, the engineers generally test the software intensely and conduct an accelerated test on the software in order to detect most of the software faults as early as possible.

Fig. 25.3
figure 3

A PDF curve of the beta distribution

Full size image

The Laplace transform of the PDF in (25.13) is

$$ {F}_{\beta}^{\ast }(s)={\mathrm{e}}^{-s}\cdot \mathrm{HG}\left(\left[\beta \right],\left[\alpha +\beta \right],s\right), $$
(25.14)

where HG([β], [α + β], s) is a generalized hypergeometric function such that

$$ {\displaystyle \begin{array}{l}\mathrm{HG}\left(\left[{a}_1,{a}_2,\dots, {a}_m\right],\left[{b}_1,{b}_2,\dots, {b}_n\right],s\right)\\[3pt] {}\quad\quad =\sum \limits_{k=0}^{\infty}\left(\frac{s^k\prod \limits_{i=1}^m\frac{\Gamma\! \left({a}_i+k\right)}{\Gamma\! \left({a}_i\right)}}{\prod \limits_{i=1}^n\frac{\Gamma\! \left({b}_i+k\right)}{\Gamma\! \left({b}_i\right)}k!}\right).\end{array}} $$

Therefore,

$$ {\displaystyle \begin{array}{rcl}{F}_{\beta}^{\ast }(s)&=&\displaystyle {\mathrm{e}}^{-s}\sum \limits_{k=0}^{\infty}\left(\frac{\Gamma\! \left(\alpha +\beta \right)\Gamma\! \left(\beta +k\right){s}^k}{\Gamma\! \left(\beta \right)\Gamma\! \left(\alpha +\beta +k\right)k!}\right)\\ {}&=&\displaystyle\sum \limits_{k=0}^{\infty}\left(\frac{\Gamma\! \left(\alpha +\beta \right)\Gamma\! \left(\beta +k\right)}{\Gamma\! \left(\beta \right)\Gamma\! \left(\alpha +\beta +k\right)}\frac{s^k{\mathrm{e}}^{-s}}{k!}\right)\\ {}&=&\displaystyle\sum \limits_{k=0}^{\infty}\left(\frac{\Gamma\! \left(\alpha +\beta \right)\Gamma\! \left(\beta +k\right)}{\Gamma\! \left(\beta \right)\Gamma\! \left(\alpha +\beta +k\right)}\mathrm{Poisson}\left(k,s\right)\right).\end{array}} $$

where the Poisson PDF is given by

$$ \mathrm{Poisson}\left(k,s\right)=\frac{s^k{\mathrm{e}}^{-s}}{k!}. $$

Using the same error-detection rate function in (25.11) and replacing F*(s) by Fβ*(s), the mean-value function of the β-RFE model is

$$ { { {m}_{\beta }(t)\,{=}\,\left\{\begin{array}{l}\frac{a}{\left(p-q\right)}\left[1-{\left(\frac{1+c}{{\mathrm{e}}^{bt}+c}\right)}^{\left(p-q\right)}\right]\, t\le T,\\ {}\frac{a}{\left(p-q\right)}\left[1-{\left(\frac{1+c}{{\mathrm{e}}^{bT}+c}\right)}^{\left(p-q\right)}\!\times\! \sum \limits_{k=0}^{\infty}\left(\frac{\Gamma\! \left(\alpha +\beta \right)\Gamma\! \left(\beta +k\right)\mathrm{Poisson}\left(k,s\right)}{\Gamma\! \left(\beta \right)\Gamma\! \left(\alpha +\beta +k\right)}\right)\right]\; t\ge T.\end{array}\right.}} $$
(25.15)

where

$$ s=\left(p-q\right)\left[\ln \left(\frac{c+{\mathrm{e}}^{bt}}{c+{\mathrm{e}}^{bT}}\right)\right]. $$

The next section will discuss the parameter estimation and illustrate the applications of these two RFE software reliability models using software failure data.

4 Parameter Estimation

4.1 Maximum Likelihood Estimation (MLE)

We use the MLE method to estimate the parameters in these two RFE models. Let yi be the cumulative number of software faults detected up to time ti, i = 1, 2,…, n. Based on the NHPP, the likelihood function is given by

$$ L=\prod \limits_{i=1}^n\frac{{\left[m\left({t}_i\right)-m\left({t}_{i-1}\right)\right]}^{y_i-{y}_{i-1}}}{\left({y}_i-{y}_{i-1}\right)!}{\mathrm{e}}^{-\left[m\left({t}_i\right)-m\left({t}_{i-1}\right)\right]}. $$
(25.16)

The logarithmic form of the above likelihood function is

$$ \ln L=\sum \limits_{i=1}^n\left\{{y}_i-{y}_{i-1}\right\}\ln\left[m\left({t}_i\right)-m\left({t}_{i-1}\right)\right]\\ \quad -\left[m\left({t}_i\right)-m\left({t}_{i-1}\right)\right]-\ln\left[\left({y}_i-{y}_{i-1}\right)!\right].\nonumber\\ $$
(25.17)

In this analysis, the error-removal efficiency p is given. Each model has five unknown parameters. For example, in the γ-RFE model, we need to estimate the following five unknown parameters: a, b, q, γ, and θ. For the β-RFE model, we need to estimate: a, b, q, α, and β. By taking derivatives of (25.17) with respect to each parameter and setting the results equal to zero, we can obtain five equations for each RFE model. After solving all those equations, we obtain the maximum likelihood estimates (MLEs) of all parameters for each RFE model.

Table 25.2 shows a set of failure data from a telecommunication software application during software testing [16]. The column “Time” shows the normalized cumulative time spent in software testing for this telecommunication application, and the column “Failures” shows the normalized cumulative number of failures occurring in the testing period up to the given time.

Table 25.2 Normalized cumulative failures and times during software testing
Full size table

The time to stop testing is T = 0.0184. After the time T, the software is released for field operations. Table 25.3 shows the field data for this software release. Similarly, the column “Time” shows the normalized cumulative time spent in the field for this software application, and the time in Table 25.3 is continued from the time to stop testing T. The column “Failures” shows the normalized cumulative number of failures found after releasing the software for field operations up to the given time. The cumulative number of failures is the total number of software failures since the beginning of software testing.

Table 25.3 Normalized cumulative failures and their times in operation
Full size table

To obtain a better understanding of the software development process, we show the actual results of the MLE solutions instead of the normalized results. In this study, let us assume that testing engineers have a number of years of experience of this particular product and software development skills and therefore conducted perfect debugging during the test. In other word, p = 1. The maximum likelihood estimates of all the parameters in the γ-RFE model are obtained as shown in Table 25.4.

Table 25.4 MLE solutions for the γ-RFE model
Full size table

Similarly, set p = 1, the MLE of all the parameters in the β-RFE model are obtained as shown in Table 25.5.

Table 25.5 MLE solutions for the β-RFE model
Full size table

For both RFE models, the MLE results can be used to obtain more insightful information about the software development process. In this example, at the time to stop testing the software T = 0.0184, the estimated number of remaining faults in the system is aF = a − (p − q)m(T) = 55.

4.2 Mean-Value Function Fits

After we obtain the MLEs for all the parameters, we can plot the mean-value function curve fits for both the γ-RFE and β-RFE models based on the MLE parameters against the actual software application failures.

Table 25.6 shows the mean-value function curve fits for both the models where the columns mγ(t) and mβ(t) show the mean-value function for the γ-RFE model and the β-RFE model, respectively.

Table 25.6 The mean-value functions for both RFEs models
Full size table

The γ-RFE and β-RFE models yield very close fits and predictions on software failures. Figure 25.4 shows the mean-value function curve fits for both the γ-RFE model and β-RFE model. Both models appear to be a good fit for the given data set. Since we are particularly interested in the fits and the predictions for software failure data during field operation, we also plot the detailed mean-value curve fits for both the γ-RFE model and the β-RFE model in Fig. 25.5.

Fig. 25.4
figure 4

Mean-value function curve fits for both RFE models

Full size image
Fig. 25.5
figure 5

Mean-value function fitting comparisons

Full size image

For the overall fitting of the mean-value function against the actual software failures, the MSE is 23.63 for the γ-RFE model fit and is 23.69 for the β-RFE model. We can also obtain the fits and predictions for software failures by applying some existing NHPP software reliability models to the same set of failure data. Since all these existing models assume a constant failure-detection rate throughout both the software testing and operation periods, we only apply the software testing data to the software models and then predict the software failures in the field environments.

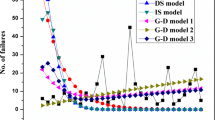
Figure 25.6 shows the comparisons of the mean-value function curve fits between the two RFE models and some existing NHPP software reliability models. It appears that the two models that include consideration of the field environment on the software failure-detection rate perform better in terms of the predictions for software failures in the field.

Fig. 25.6
figure 6

Model comparisons

Full size image

4.3 Software Reliability

Once the MLEs of all the parameters in (25.12) and (25.14) are obtained, the software reliability within (t, t + x) can be determined as

$$ R\!\left(x|t\right)={\mathrm{e}}^{-\left[m\left(t+x\right)-m(t)\right]}. $$
(25.18)

Let T = 0.0184, and change x from 0 to 0.004, then we can compare the reliability predictions between the two RFE models and some other NHPP models that assume a constant failure-detection rate for both software testing and operation. The reliability prediction curves are shown in Fig. 25.7. From Fig. 25.7, we can see that the NHPP models without consideration of the environmental factor yield much lower predictions for software reliability in the field than the two proposed RFE software reliability models.

Fig. 25.7
figure 7

Reliability prediction comparisons

Full size image

4.4 Confidence Interval

4.4.1 γ-RFE Model

To see how good the reliability predictions given by the two RFE models are, in this section we describe how to construct confidence intervals for the prediction of software reliability in the random field environments. From Tables 25.4 and 25.5, the MLEs of c and q are equal to zero and, if p is set to 1, then the model in (25.12) becomes

$$ m(t)=\left\{\begin{array}{ll}a\left(1-{\mathrm{e}}^{-b\cdot t}\right)& t\le T,\\[3pt] {}a\left[1-{\mathrm{e}}^{-b\cdot t}{\left(\frac{\theta }{\theta +b\left(t-T\right)}\right)}^{\gamma}\right]& t\ge T.\end{array}\right. $$
(25.19)

This model leads to the same MLE results for the parameters a, b, γ, and θ and also yields exactly the same mean-value function fits and predictions as the model in (25.12). To obtain the confidence interval for the reliability predictions for the γ-RFE model, we derive the variance–covariance matrix for all the maximum likelihood estimates as follows.

If we use xi, i = 1, 2, 3, and 4, to denote all the parameters in the model, or

$$ {x}_1\to a\, {x}_2\to b\, {x}_3\to \theta \, {x}_4\to \gamma . $$

The Fisher information matrix H can be obtained as

$$ H=\left(\begin{array}{llll}{h}_{11}& {h}_{12}& {h}_{13}& {h}_{14}\\ {}{h}_{21}& {h}_{22}& {h}_{23}& {h}_{24}\\ {}{h}_{31}& {h}_{32}& {h}_{33}& {h}_{34}\\ {}{h}_{41}& {h}_{42}& {h}_{43}& {h}_{44}\end{array}\right), $$

where

$$ {h}_{ij}=E\left(-\frac{\partial^2L}{\partial {x}_i\partial {x}_j}\right)i,j=1,\dots, 6. $$

where L is the log-likelihood function in (25.18).

If we denote z(tk) = m(tk) − m(tk–1) and Δyk  = yk − yk–1, k = 1, 2,…, n, then we have

$$ \frac{\partial^2L}{\partial {x}_i\partial {x}_j}=\sum \limits_{k=1}^n\left[-\frac{\Delta {y}_k}{z{\left({t}_k\right)}^2}\frac{\partial z\left({t}_k\right)}{\partial {x}_i}\cdot \frac{\partial z\left({t}_k\right)}{\partial {x}_j}\right.\\ \left.\quad +\left(\frac{\Delta {y}_k-z\left({t}_k\right)}{z\left({t}_k\right)}\cdot \frac{\partial^2z\left({t}_k\right)}{\partial {x}_i\partial {x}_j}\right)\right]. $$

Then we can obtain each element in the Fisher information matrixH. For example,

$$ {\displaystyle \begin{array}{rcl}{h}_{11}&=&E\left(-\frac{\partial^2L}{\partial {x}_1^2}\right)\\[-5pt] \\ {}&=&\sum \limits_{k=1}^n\left\{\sum \limits_{\Delta {y}_k=0}^{\infty}\left[\frac{\Delta {y}_k}{z{\left({t}_k\right)}^2}{\left(\frac{\partial z\left({t}_k\right)}{\partial a}\right)}^2\right]\times \frac{{\left[z\left({t}_k\right)\right]}^{\Delta {y}_k}{\mathrm{e}}^{-z\left({t}_k\right)}}{\left(\Delta {y}_k\right)!}\right\}\\[-5pt] \\ {}&=&\sum \limits_{k=1}^n\left\{\sum \limits_{\Delta {y}_k=0}^{\infty}\left[\frac{\Delta {y}_k}{z{\left({t}_k\right)}^2}{\left(\frac{z\left({t}_k\right)}{a}\right)}^2\right]\times \frac{{\left[z\left({t}_k\right)\right]}^{\Delta {y}_k}{\mathrm{e}}^{-z\left({t}_k\right)}}{\left(\Delta {y}_k\right)!}\right\}\\[-5pt] \\ {}&=&\sum \limits_{k=1}^n\left(\frac{1}{a^2}\sum \limits_{\Delta {y}_k=0}^{\infty}\Delta {y}_k\frac{{\left[z\left({t}_k\right)\right]}^{\Delta {y}_k}{\mathrm{e}}^{-z\left({t}_k\right)}}{\left(\Delta {y}_k\right)!}\right)\\[-5pt] \\ {}&=&\sum \limits_{k=1}^n\left[\frac{1}{a^2}\cdot z\left({t}_k\right)\right]\\ \\ {}&=&\frac{1}{a^2}m\left({t}_n\right).\end{array}} $$

The variance matrix, V, can also be obtained

$$ V={(H)}^{-1}=\left(\begin{array}{llll}{v}_{11}& {v}_{12}& {v}_{13}& {v}_{14}\\ {}{v}_{21}& {v}_{22}& {v}_{23}& {v}_{24}\\ {}{v}_{31}& {v}_{32}& {v}_{33}& {v}_{34}\\ {}{v}_{41}& {v}_{42}& {v}_{43}& {v}_{44}\end{array}\right). $$

The variances of all the estimate parameters are given by

$$ {\displaystyle \begin{array}{l}\mathrm{Var}\!\left(\hat{a}\right)=\mathrm{Var}\!\left({x}_1\right)={v}_{11},\\ {}\mathrm{Var}\!\left(\hat{b}\right)\!=\mathrm{Var}\!\left({x}_2\right)={v}_{22},\\ {}\mathrm{Var}\!\left(\hat{\gamma}\right)=\mathrm{Var}\!\left({x}_3\right)={v}_{33},\\ {}\mathrm{Var}\!\left(\hat{\theta}\right)=\mathrm{Var}\!\left({x}_4\right)={v}_{44}.\end{array}} $$

The actual numerical results for the γ-RFE model variance matrix are

$$ { {V\gamma =\left(\begin{array}{llll}703.8472& -0.005387& -88.6906& -2.6861\\ {}-0.005387& 7.3655\times {10}^{-8}& 1.11\times {10}^{-3}& 3.097\times {10}^{-5}\\ {}-88.6906& 1.11\times {10}^{-3}& 92.4287& 1.1843\\ {}-2.6861& 3.097\times {10}^{-5}& 1.1843& 0.0238\end{array}\right).}} $$

4.4.2 β-RFE Model

The model in (25.14) can also be simplified given that the estimates of both q and c are equal to zero and p is set to 1. The mean-value function becomes

$$ { {{m}_{\beta }(t)=\left\{\begin{array}{ll}a\left(1-{\mathrm{e}}^{- bt}\right)& t\le T,\\[3pt] {}a\left[1-{\mathrm{e}}^{- bT}\times \sum \limits_{k=0}^{\infty}\left(\frac{\Gamma\! \left(\alpha +\beta \right)\Gamma\! \left(\beta +k\right)\mathrm{Poisson}\left[k,b\left(t-T\right)\right]}{\Gamma\! \left(\beta \right)\Gamma\! \left(\alpha +\beta +k\right)}\right)\right]& t\ge T.\end{array}\right.}} $$

This model leads to the same MLE results for the parameters a, b, α, and β and also yields exactly the same mean-value function fits and predictions. To obtain the confidence interval for the reliability predictions for the β-RFE model, we need to obtain the variance–covariance matrix for all the maximum likelihood estimates.

If we use xi, i = 1, 2, 3, and 4, to denote all the parameters in the model, or

$$ {x}_1\to a\, {x}_2\to b\, {x}_3\to \alpha \, {x}_4\to \beta, $$

and go through similar steps as for the γ-RFE model, the actual numerical results for the β-RFE model variance matrix can be obtained as

$$ { {{V}_{\beta }=\left(\begin{array}{cccc}691.2& -0.00536& -2.728& -66.2172\\ {}-0.00536& 7.4485\times {10}^{-8}& 2.671\times {10}^{-5}& 0.00085\\ {}-2.7652& 2.671\times {10}^{-5}& 0.01820& 0.8295\\ {}-66.2172& 0.00085& 0.8295& 60.5985\end{array}\right)}} $$

4.4.3 Confidence Interval of the Reliability Predictions

If we define a partial derivative vector for the reliability R(x | t) in (25.18) as

$$ vR\left(x|t\right)=\left(\frac{\partial R\!\left(x|t\right)}{\partial {x}_1},\frac{\partial R\!\left(x|t\right)}{\partial {x}_2},\frac{\partial Rb\!\left(x|t\right)}{\partial {x}_3},\frac{\partial R\!\left(x|t\right)}{\partial {x}_4}\right) $$

then the variance of R(x | t) in (25.18) can be obtained as

$$ \mathrm{Var}\ \left[R\!\left(x|t\right)\right]= vR\!\left(x|t\right)V{\left[ vR\!\left(x|t\right)\right]}^{\mathrm{T}}. $$

Assume that the reliability estimation follows a normal distribution, then the 95% confidence interval for the reliability predictionR(x | t) is

$$ \left[R\left(x|t\right)-1.96\times \sqrt{\mathrm{Var}\ \left[R\left(x|t\right)\right]},R\left(x|t\right)\right.\\ \quad \left. +\ 1.96\times \sqrt{\mathrm{Var}\ \left[R\left(x|t\right)\right]}\right]. $$

Figures 25.8 and 25.9 show the 95% confidence interval of the reliability predicted by the γ-RFE and β-RFE models, respectively.

Fig. 25.8
figure 8

γ-RFE model reliability growth curve and its 95% confidence interval

Full size image
Fig. 25.9
figure 9

β-RFE model reliability growth prediction and its 95% confidence interval

Full size image

We plot the reliability predictions and their 95% confidence interval for both the γ-RFE model and the β-RFE model in Fig. 25.10. For this given application data set, the reliability predictions for the γ-RFE model and the β-RFE model are very close to each other, as are their confidence intervals. Therefore, it would not matter too much which one of the two RFE models was used to evaluate the software reliability for this application. However, will these two RFE models always yield similar reliability predictions for all software applications? or which model should one choose for applications if they are not always that close to each other? We will try to answer these two questions in the next section. Figure 25.11 shows the 95% confidence interval for the mean-value function fits and predictions from the γ-RFE model.

Fig. 25.10
figure 10

Reliability growth prediction curves and their 95% confidence intervals for the γ-RFE model and the β-RFE model

Full size image
Fig. 25.11
figure 11

Mean-value function curve fit and its 95% confidence intervals for the γ-RFE mode

Full size image

4.5 Concluding and Remarks

Table 25.7 shows all the maximum likelihood estimates of all the parameters and other fitness measures. The maximum likelihood estimates (MLEs) on common parameters, such as a – the initial number of faults in the software and b – the unit software failure-detection rate during testing, are consistent for both models. Both models provide very close predictions for software reliability and also give similar results for the mean and variance of the random environment factor η.

Table 25.7 MLEs and fitness comparisons
Full size table

The underlying rationale for this phenomenon is the similarity between the gamma and beta distributions when the random variable η is close to zero. In this application, the field environments are much less liable to software failure than the testing environment. The random field environmental factor, η, is mostly much less than 1 with mean (η) ≈ 0.02.

Figure 25.12 shows the PDF curves of the environmental factorη based on the MLEs of all the parameters for both the γ-RFE model and the β-RFE model. We observe that the PDF curves for the beta and gamma distributions are also very close to each other. The two RFEs models give similar results because this software application is much less likely to fail in the field environment, with mean (η) = 0.02. If the mean (η) is not so close to 0, then we would expect to have different prediction results from the γ-RFE model and the β-RFE model.

Fig. 25.12
figure 12

PDF curves comparison for the environmental factor η

Full size image

We suggest the following criteria as ways to select between the two models discussed in this chapter for predicting the software reliability in the random field environments:

  1. 1.

    Software less liable to failure in the field than in testing, that is, η ≤ 1

    In the γ-RFE model, the random field environmental factor, η following a gamma distribution, ranges from 0 to +∞. For the β-RFE model, the random field environmental factor, η following a beta distribution, ranging from 0 to 1. Therefore, the β-RFE model will be more appropriate for describing field environments in which the software application is likely to fail than in the controlled testing environment.

    For this given application, we notice that when the field environmental factor η is much less than 1 [mean(η) = 0.02], the γ-RFE model yields similar results to the β-RFE model. However, we also observe that the γ-RFE model does not always yield similar results to the β-RFE model when η is not close to 0. In this case, if we keep using the γ-RFE model instead of the β-RFE model, we would expect to see a large variance in the maximum likelihood estimates for all the unknown parameters, and hence a wider confidence interval for the reliability prediction.

  2. 2.

    Smaller variance of the RFE factor η

    A smaller variance of the random environmental factor η will generally lead to a smaller confidence interval for the software reliability prediction. It therefore represents a better prediction in the random field environments.

  3. 3.

    Smaller variances for the common parameters a and b

    The software parameter a and the process parameter b are directly related to the accuracy of reliability prediction. They can also be used to investigate the software development process. Smaller variances of a and b would lead, in general, to smaller confidence intervals for the mean-value function predictions and reliability predictions.

  4. 4.

    Smaller MSE of the mean-value function fits

    A smaller MSE for the mean-value function fits means a better fit of the model to the real system failures. This smaller MSE will usually lead to a better prediction of software failures in random field environments.

The above criteria can be used with care to determine which RFE model should be chosen in practice. They may sometime provide contradictory results. In the case of contradictions, practitioners can often consider selecting the model with the smaller confidence interval for the reliability prediction.

5 A RFE Model with Vtub-Shaped Fault-Detection Rate

In this section, we present a specific RFE model with Vtub-shaped fault-detection rate. Numerical results of some selected NHPP models based on MSE, predictive power, predictive-ratio risk, and normalized criteria distance from a set of software failure data are discussed.

Here we assume that a detected fault will be 100% successfully removed from the software during the software testing period and the software fault-detection rate per unit time, h(t), with a Vtub-shaped function [22], is as follows:

$$ h(t)=b\ln (a){t}^{b-1}{a}^{t^b}\, \mathrm{for}\, a>1,b>0 $$
(25.20)

We also assume that the random variable η as defined in (25.1) has a gamma distribution with parameters α and β, that is, η ∼ gamma(α, β) where the PDF of η is given by

$$ g(x)=\frac{\beta^{\alpha }{x}^{\alpha -1}{\mathrm{e}}^{-\beta x}}{\Gamma\! \left(\alpha \right)}\, \mathrm{for}\, \alpha, \beta >0;x\ge 0 $$
(25.21)

From Eq. (25.1), we can obtain the expected number of software failures detected by time t subject to the uncertainty of the environments as follows:

$$ m(t)=N\left(1-{\left(\frac{\beta }{\beta +{a}^{t^b}-1}\right)}^{\alpha}\right) $$
(25.22)

where N is the expected number of faults that exists in the software before testing.

5.1 Model Criteria

We briefly discuss some common criteria such as MSE, predictive-ratio risk (PRR), and predictive power (PP) that will be used to compare the performance of some selected models from Table 25.1 to illustrate the modeling analysis.

The MSE measures the difference between the estimated values and the actual observation and is defined as:

$$ \mathrm{MSE}=\frac{\sum \limits_{i=1}^n{\left(\hat{m}\left({t}_i\right)-{y}_i\right)}^2}{n-k} $$
(25.23)

where yi = total number of actual failures at time ti; \( \hat{m}\left({t}_i\right) \) = the estimated cumulative number of failures at time ti for i = 1, 2,…, n; and n and k = number of observations and number of model parameters, respectively.

The predictive-ratio risk (PRR) measures the distance of model estimates from the actual data against the model estimate and is defined as [22]:

$$ \mathrm{PRR}=\sum \limits_{i=1}^n{\left(\frac{\hat{m}\left({t}_i\right)-{y}_i}{\hat{m}\left({t}_i\right)}\right)}^2 $$
(25.24)

The predictive power (PP) measures the distance of model estimates from the actual data against the actual data [22]:

$$ \mathrm{PP}=\sum \limits_{i=1}^n{\left(\frac{\hat{m}\left({t}_i\right)-{y}_i}{y_i}\right)}^2 $$
(25.25)

For all these three criteria – MSE, PRR, and PP – the smaller the value, the better the model fits.

Pham [28] discussed a normalized criteria distance, or NCD criteria, to determine the best model from a set of performance criteria. The NCD criteria is defined as follows:

$$ {D}_i=\sum \limits_{j=1}^d\left\{\left(\sqrt{\left[\sum \limits_{i=1}^2{\left(\frac{C_{ijk}}{\sum \limits_{i=1}^s{C}_{ijk}}\right)}^2\right]}\right){w}_j\right\} $$
(25.26)

where s and d are the total number of models and criteria, respectively.

  • wj = the weight of the jth criteria for j = 1, 2, ... ,d

  • \( k=\left\{\begin{array}{ll}1& \mathrm{represent}\, \mathrm{criteria}\, j\, \mathrm{value}\\ {}2& \mathrm{represent}\, \mathrm{criteria}\, j\, \mathrm{ranking}\end{array}\right\} \)

  • Cij1 = the ranking based on specified criterion of model i with respect to (w.r.t.) criteria j

  • Cij2 = criteria value of model i w.r.t. criteria j where i = 1, 2, ..., s and j = 1, 2, ... ,d

Obviously the smaller the NCD value, Di, it represents the better rank.

5.2 Model Analysis

A set of system test data which is referred to as Phase 2 data set [22] is used to illustrate the model performance in this subsection. In this data set, the number of faults detected in each week of testing is found and the cumulative number of faults since the start of testing is recorded for each week. This data set provides the cumulative number of faults by each week up to 21 weeks.

Table 25.8 summarizes the result as well as the ranking of nine selected models from Table 25.1 based on MSE, PRR, PP, and NCD criteria. It is worth to note that one can use the NCD criterion to help in selecting the best model from among model candidates. Table 25.8 shows the NCDs and its corresponding ranking for w1 = 2, w2 = 1.5, and w3 = 1 with respect to MSE, PRR, and PP, respectively.

Table 25.8 [28, page 1488]: Parameter estimation and model comparison when w1 = 2, w2 = 1.5, w3 = 1
Full size table

Based on the results as shown in Table 25.8, the Vtub-shaped fault-detection rate model seems to provide the best fit based on the normalized criteria distance method.