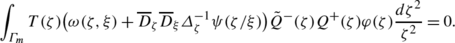Fermions Acting on Quasi-local Operators in the XXZ Model

Abstract

This is a survey about the construction of fermions which act on the space of quasi-local operators in the XXZ model. We also include a proof of the anti-commutativity of fermionic creation operators.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In this article, we give an exposition of the ‘fermionic basis’ found in [1, 2] for the space of operators in the XXZ spin chain. In order to explain the problem, let us begin with some historical background.

Quite generally, in integrable models one is given a large family of commuting operators which act on the space of states. The first issue is then to describe their spectra. In the case of the XXZ chain, the space of states is simply a tensor product V ^⊗N, where V=ℂ². The generating function of the commuting operators is the transfer matrix of the underlying six vertex model, and the standard machinary of the Bethe ansatz enables one to study its spectra in great detail.

The second issue is to describe expectation values of local operators

This is a problem far more involved than the first. It has been known for some time that, for the XXZ chain in the thermodynamic limit N→∞, the expectation values of the standard basis elements (products of matrix units) are given by certain multiple integrals [3–6]. Subsequently it has been recognised, on many examples, that actually these integrals can be reduced to sums of products of one-dimensional integrals, with complicated rational functions as coefficients [7–10]. These findings suggested that, if one passes from the standard basis of local operators to a suitable new basis, then the corresponding expectation values simplify drastically.

It turns out to be convenient to introduce a parameter α and consider in place of End V ^⊗m the space of expressions of the form

where $\sigma^{3}_{j}$ is a Pauli matrix at site j and $\mathcal{O}$ is a local operator in the usual sense. We shall call such operators ‘quasi-local’ (see Sect. 3 below). The parameter α plays a role of regularisation which helps removing degeneracies from the formulas.

In [1], we have defined certain fermions $\mathbf{b}_{p},\mathbf{c}_{p},\mathbf{b}^{*}_{p},\mathbf{c}^{*}_{p}$, p≥1, which act on the space of all quasi-local operators. Together with the adjoint action of the integrals of motion $\mathbf{t}^{*}_{p}$, these operators act on q ^2αS(0) and create a basis which we call ‘fermionic’. We have shown in [2] that for these basis elements the expectation values are given by determinants involving only two basic functions ρ(ζ) and ω(ζ,ξ) (see Sect. 6, Theorem 2). This clarifies the reason for the simplification of the integrals mentioned above.

The aim of the present paper is to outline the construction of the fermions, leaving the proofs to the original papers. The construction is purely algebraic. It can be viewed as a sophisticated version of the algebraic Bethe ansatz, but there are new features. In particular it is applied to the spaces End V ^⊗m rather than V ^⊗m. Also, essential use is made of representations of the Borel subalgebra $U_{q}\mathfrak{b}$ of $U_{q}\widehat{\mathfrak{sl}}_{2}$. Taking this opportunity, we supply a proof of the anti-commutativity of fermionic creation operators which has not been published in the previous papers.

The text is organised as follows. In Sect. 2 we collect preliminary materials about the transfer matrix and Baxter’s Q-matrices, thereby introducing our notation. In Sect. 3 we consider the action of integrals of motion on the space of quasi-local operators. In Sect. 4 we define the fermionic annihilation and creation operators, and in Sect. 5 explain their properties. In Sect. 6 we consider the expectation values. The main statement is that the expectation values of operators created by fermions from ‘the primary operator’ can be computed as a determinant. We give an explicit formula for the function ω(ζ,ξ) in Appendix A. Appendix B is devoted to the proof of anti-commutativity of creation operators.

Throughout the text we shall assume that q is not a root of unity.

2 Transfer Matrix and Q-Matrices

In this section, we fix our notation and review the standard construction of the transfer matrix of the six vertex model and Baxter’s Q-matrices.

Let V=ℂ², and let v ₊,v ₋ be the standard basis. Let V _j (j∈ℤ) be copies of V, and set V _[K,L]=V _K ⊗⋯⊗V _L for an interval [K,L]⊂ℤ. The transfer matrix is an element of  EndV _[K,L] defined by

(1)

Here the operator $\mathcal{L}$ is the image of the universal R matrix of $U_{q}\widehat{\mathfrak{sl}}_{2}$ in the two-dimensional evaluation representation $\pi_{a,\zeta}:U_{q}\widehat{\mathfrak{sl}}_{2}\to\mathrm{End}\,V_{a}$,

(2)

It has the weight preserving property

(3)

We have also introduced an arbitrary parameter α, which will play a key role later on.

Due to the Yang-Baxter relation, for each fixed α the transfer matrices (1) mutually commute,

We note also

where

In addition to the transfer matrices, there are also Baxter’s Q-matrices among the commuting family. As we shall see below, the latter are more fundamental objects than the former.

For the construction of Q-matrices one uses representations of the Borel subalgebra $U_{q}\mathfrak{b}$ of $U_{q}\widehat{\mathfrak{sl}}_{2}$ [12] in place of the two-dimensional ‘auxiliary space’ V _a . More specifically, consider the following operators a,a ^∗,q ^±D on the vector space W=⨁ _k∈ℤℂ|k〉:

They satisfy the so-called q-oscillator algebra relations

Then the formulas

give a representation $\varpi^{+}_{A,\zeta}:U_{q}\mathfrak{b}\to\mathrm{End}\,W^{+}$, where W ⁺=⨁ _k≥0ℂ|k〉. Interchanging the indices 0 and 1, one defines another representation $\varpi^{-}_{A,\zeta}$ on the quotient space W ⁻=W/W ⁺. (We use the letter A for ‘auxiliary’. The representations $\varpi^{\pm}_{A,\zeta}$ are the two types of fundamental representations of $U_{q}\mathfrak{b}$, see [13].) Accordingly we define

where $\pm2D_{A}=\varpi^{\pm}_{A}(h_{1})$ and

(4)

In the above, Tr is understood as analytic continuation from |q ^±2α|<1, e.g., $\mathrm{Tr}_{W^{\pm}}(q^{2\alpha D})=\pm 1/(1-q^{2\alpha})$.

The Q-matrices commute among themselves as well as with T _[K,L](ζ,α) and S _[K,L],

In fact, the transfer matrix and its ‘higher’ analogs are all expressible as quadratic combinations of the Q-matrices. For instance, dropping the suffix [K,L] we have

These ‘Wronskian’ like relations follow from the analysis of the composition factors of $W_{A,\zeta_{1}}^{+}\otimes W_{A,\zeta_{2}}^{-}$ [12]. They entail in particular Baxter’s TQ relation

(5)

which corresponds to the exact sequence of $U_{q}\mathfrak{b}$-modules

(6)

Here, for a $U_{q}\mathfrak{b}$-module W, W[m] means the $U_{q}\mathfrak{b}$-module structure on W where $q^{h_{1}}$ acts by $q^{m}\times q^{h_{1}}$.

3 Quasi-local Operators

Our main concern in this note is not the space of states V _[K,L], but rather the space of operators  EndV _[K,L]. We wish to consider them all at once by letting −K,L→∞ while keeping only local operators, i.e., only those elements $\mathcal{O}$ which have finite support. Here, by support $\mathrm{supp}\,\mathcal{O}$ of $\mathcal{O}$, we mean the minimal interval [k ₀,l ₀]⊂ℤ such that $\mathcal{O}$ acts as identity on V _j for all $j\not\in [k_{0},l_{0}]$. When $\mathrm{supp}\,\mathcal{O}\subset [k,l]$, we indicate this fact by putting a suffix and writing $\mathcal{O}_{[k,l]}$. We shall also say that $\mathcal{O}$ has spin s∈ℤ if $\mathbb{S}(\mathcal{O})=s\mathcal{O}$, where $\mathbb{S}(\cdot)=[S_{(-\infty,\infty)},\cdot]$.

Let us look at the action of the transfer matrix on an element $\mathcal{O}\in \mathop{\mathrm{End}}{V_{[K,L]}}$,

It is a simple consequence of the weight-preserving property (3) that, if $\mathop{\mathrm{supp}}\mathcal{O}\subset [k,l]$, then

(7)

Namely, apart from the ‘tail’ $q^{\alpha(\sigma^{3}_{K}+\cdots+\sigma^{3}_{k-1})}$, there is a reduction of the action of the operator t ^∗ to the left of the support [k,l] of the operand $\mathcal{O}_{[k,l]}$. Although there is no such simple reduction to the right, the following stability takes place. Consider the Taylor expansion at ζ ²=1,

Then for each fixed p the coefficient $\mathbf{t}^{*}_{[k,L],p} (\mathcal{O}_{[k,l]} )$ becomes independent of L if L is chosen large enough.

These properties suggest that, instead of naïvely taking −K,L→∞, it is more natural to introduce a formal element

and to consider expressions of the form

(8)

The shift of α depending on the spin s is introduced for convenience. Let $\mathcal{W}_{\alpha-s,s}$ be the set of all elements (8), and set

We shall say that an element of $\mathcal{W}^{(\alpha)}$ is a quasi-local operator. We call $q^{2\alpha S(0)}\in \mathcal{W}_{\alpha,0}$ the primary operator. Abusing the language we define the support of (8) to be $\mathop{\mathrm{supp}}\mathcal{O}$.

From the foregoing discussions it is clear that for each p≥1 the limit

has a well-defined meaning as an operator acting on $\mathcal{W}^{(\alpha)}$. We shall use the generating series

(9)

From the definition it is equally clear that the operators $\{\mathbf{t}^{*}_{p}\}_{p\ge1}$ mutually commute. However we are not interested in their diagonalisation. Indeed, the question does not even make sense because their action on $\mathcal{W}^{(\alpha)}$ turns out to be free. They generate one half of the Heisenberg algebra, and we shall use them as a part of operators which create a basis of $\mathcal{W}^{(\alpha)}$ from the primary operator q ^2αS(0), see Sect. 5 below.

4 Introducing Fermions

In this section we shall introduce fermions which act on the space $\mathcal{W}^{(\alpha)}$.

Going back to the setting of a finite interval [K,L], let us re-examine the derivation of the TQ relation (5). For definiteness we consider only $W_{A,\zeta}^{+}$ and omit the superfix +. The exact sequence (6) tells that, with an appropriate matrix F _a,A of base change in V _a,ζ ⊗W _A,ζ , the product of the two $\mathcal{L}$ operators (2), (4) can be brought to a block triangular form

where the suffix a refers to the block structure in V _a . Introducing

we consider its action on an element X∈ End(V _[K,L]) by

If we take the trace of both sides on V _a,ζ ⊗W _A,ζ , then we obtain an  EndV _[K,L] version of the TQ relation (5). Here we proceed differently and define a new operator by looking at the lower left block,

(10)

For each X, the operator (10) is a rational function in ζ ² apart from an overall power ζ ^α. It has poles at ζ ²=1,q ^±2 in the ζ ²-plane. Hence one can write the partial fraction decomposition

(11)

demanding that ζ ²=1 is the only pole of

(There is an ambiguity about how to share the possible polynomial part among them. The prescription is given in [1], Sect. 2.7.) We define further

(12)

Notice that the right hand side is the combination which appears in the TQ relation (5). Although we are not able to give a logical explanation to the formula (12), it turns out that this operator enjoys various nice properties.

We supplement (11), (12) by giving two more definitions,

where $N=q^{-1}(q^{-\alpha+\mathbb{S}+1}-q^{\alpha-\mathbb{S}-1})$ is a normalisation and

is an operator which flips the spin.

It can be shown that the operators b _[K,L], c _[K,L], $\mathbf{b}^{*}_{[K,L]}$, $\mathbf{c}^{*}_{[K,L]}$ introduced above have reduction properties similar to (7). The left reduction takes the form

(13)

where the + sign is chosen for x=c,b ^∗ and − for x=b,c ^∗. (The change of α in (13) is the reason why we introduced the shift in the definition (8) of quasi-local operators.) In addition, b ^∗, c ^∗ share with t ^∗ the same stability properties to the right. For x=b,c the situation is even simpler, since

As it was explained for $\mathbf{t}^{*}_{p}$, these properties allow us to consider the limit −K,L→∞ of b _[K,L](ζ,α) and so forth. We end up with the formal series

(14)

(15)

whose coefficients $\mathbf{b}_{p},\mathbf{c}_{p},\mathbf{b}^{*}_{p},\mathbf{c}^{*}_{p}$ are well-defined operators on $\mathcal{W}^{(\alpha)}$. We shall not use the zeroth coefficients b ₀,c ₀ because they are not independent from b _p ,c _p , p≥1.

5 Properties of Fermions

So far we have introduced the operators

(16)

which act on $\mathcal{W}^{(\alpha)}$ in the following manner:

In this section we summarize their basic properties.

Commutation Relations

Among the operators in the list (16), $\mathbf{t}^{*}_{p}$ are central:

(17)

The rest of the operators obey the canonical anti-commutation relations

(18)

(19)

(20)

The proof of (18), (19) requires quite a heavy computation which occupies a large part of [1]. We give a proof of (20) when the target space is $\mathcal{W}_{\alpha,0}$ in Appendix B.

Later on we shall use (19) in the form of generating series,

where ψ(ζ,α) is a Cauchy kernel defined by

Support Property

By acting with b _p ,c _p the support of an operator does not enlarge. Namely if $X\in \mathcal{W}^{(\alpha)}$ satisfies  suppX⊂[k,l], then

(21)

(22)

In particular, we have

(23)

These properties justify calling b _p ,c _p annihilation operators.

In contrast, the support is enlarged by $\mathbf{t}^{*}_{p}, \mathbf{b}^{*}_{p},\mathbf{c}^{*}_{p}$ according to the rule

(24)

We call $\mathbf{t}^{*}_{p},\mathbf{b}^{*}_{p},\mathbf{c}^{*}_{p}$ creation operators.

Fermionic Basis

The following set is a basis of $\mathcal{W}^{(\alpha)}$ [11]:

(25)

Hence $\mathcal{W}^{(\alpha)}$ may be regarded as a tensor product of Fock spaces of one boson and two kinds of fermions. (However we do not know how to construct the annihilation partner to $\mathbf{t}^{*}_{p}$.)

As we shall explain in the next section, it is in this fermionic basis that the calculation of expectation values simplify drastically.

6 Expectation Values

We now move on to the discussion of expectation values in the six vertex model. Dealing with the infinite lattice limit one has to be specific about the range of the parameters. From now on we assume that q=e ^πiν, 1/2<ν<1, $\nu\not\in\mathbb{Q}$.

Let us consider an infinite cylinder extending to the horizontal direction. We take finitely many rows, numbered say from 1 to n, and denote them collectively by M (the letter M stands for ‘Matsubara’). To each row m=1,…,n attach a parameter τ _m and set

Further, on each vertical edge j between the n-th and the (n+1)-st row, i.e., the first row in the cyclic boundary condition, we assign a ‘field’ $q^{(\kappa+\alpha)\sigma^{3}_{j}}$, j≤0 or $q^{\kappa\sigma^{3}_{j}}$, j>0 (see Fig. 1).

Fig. 1

Six vertex model with fields $\times=q^{(\kappa+\alpha)\sigma^{3}_{j}}$, $\circ=q^{\kappa\sigma^{3}_{j}}$. Insertion of a local field $E^{\varepsilon_{1}',\varepsilon_{1}}_{1} E^{\varepsilon_{2}',\varepsilon_{2}}_{2}$ corresponds to introducing defects (filled circles)

We introduce the expectation value of a quasi-local operator $q^{2\alpha S(0)}\mathcal{O}$ as the limit of the ratio

(26)

It is a linear functional $Z^{\kappa}:\mathcal{W}^{(\alpha)}\to\mathbb{C}$ so normalised that Z ^κ{q ^2αS(0)}=1. The numerator which appears in the right hand side is the partition function corresponding to a lattice with ‘defects’ specified by $\mathcal{O}$.

It is convenient to introduce a slightly more general object than Z ^κ. Consider the transfer matrix corresponding to a column

We call it the ‘Matsubara’ transfer matrix. Fix an eigencovector 〈Φ| of T _M (ζ,κ+α) (resp. eigenvector |Ψ〉 of T _M (ζ,κ)) with eigenvalue T(ζ,κ+α) (resp. T(ζ,κ)),

We assume that

(27)

and in particular that they have the same spin. For an element $q^{2\alpha S(0)}\mathcal{O}\in \mathcal{W}_{\alpha,0}$, choose −K,L>0 so that $\mathrm{supp}\,\mathcal{O}\subset [K,L]$, and set

(28)

Then the right hand side is independent of the choice of K,L. If 〈Φ|=〈κ+α|, |Ψ〉=|κ〉 are the maximal eigenvectors, then by the Perron-Frobenius theorem the expectation value (26) considered above reduces to (28):

It is not difficult to see that

where

A more interesting example of (28) is

The function ω(ζ,ξ) is determined from the data about the eigenvectors 〈Φ|, |Ψ〉. An explicit formula for ω(ζ,ξ) is given in Appendix A.

We are now in a position to state the ‘Ward identities’ regarding the expectation values.

Theorem 1

For any $X\in \mathcal{W}^{(\alpha)}$ the following relations hold:

In the left hand side, we have the action of creation operators. In the right hand side, it becomes reduced to that of the annihilation operators. The proof given in [2] makes use of a q-difference analog of Abelian integrals on hyperelliptic Riemann surfaces.

The formulas in Theorem 1, combined with the annihilation property (23), allow one to calculate the expectation values of operators inductively. We thus arrive at the following main result of [2], which says that the calculation of $Z_{\varPhi,\varPsi}^{\kappa}$ on the fermionic base vectors in (25) can be performed by using the ordinary Wick theorem for fermions.

Theorem 2

Notation being as above, we have

7 Concluding Remarks

In this article we have outlined the construction of fermions acting on the space $\mathcal{W}^{(\alpha)}$ of quasi-local operators. In this basis the expectation values take a very simple form (Theorem 2).

As long as the number of sites n in the Matsubara direction is kept finite, ρ(ζ) and (ζ/ξ)^−α ω(ζ,ξ) are rational functions (see Appendix A below). The main virtue of such a formula is that, in passing to various limits, it is enough to do that for these two functions alone. For example, for the ground state average in the XXZ spin chain, the limit n→∞ can be taken in a straightforward manner. Moreover, on the infinite lattice any operator of the form $\mathbf{t}^{*}_{p}(X)$ (p≥2) has vanishing expectation value, so ρ(ζ) does not appear in the result. This explains the fact that the original multiple integral formula can be simplified using only one transcendental function (the limit of ω(ζ,ξ)).

In a sense, the main formula is only an existence theorem, since the transition matrix between the standard basis and the fermionic basis remains unknown in general. Nevertheless, it has non-trivial implications in the continuous limit to conformal field theory and the sine-Gordon theory. For these topics the reader is referred to [15–18].

Appendices

Appendix A: Formula for ω(ζ,ξ)

We quote an explicit formula for the function ω(ζ,ξ) from [2], Sect. 7. For that purpose we need to prepare some notation.

As in the text, we fix an eigencovector 〈Φ| of T _M (ζ,κ+α) and an eigenvector |Ψ〉 of T _M (ζ,κ) satisfying 〈Φ|Ψ〉≠0. Denote their eigenvalues and those for the Q-matrices as follows:

Introduce q-difference operators Δ _ζ , $\overline{D}_{\zeta}$ by

Hereafter we shall use the shorthand

Set

(29)

and define ω _sym(ζ,ξ) by

As a function of ζ, ω(ζ,ξ) is characterised by the following two conditions.

• 1. ζ ^−α T(ζ)(ω(ζ,ξ)−ω _sym(ζ,ξ)) is a polynomial in ζ ² of degree n,

• 2. It satisfies the normalisation conditions for m=0,1,…,n:

  

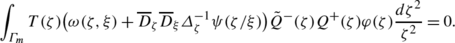
  Here Γ ₀ is a contour around ζ ²=0, and for m=1,…,n, Γ _m is a contour encircling $\zeta^{2}=\tau_{m}^{2}, q^{-2}\tau_{m}^{2}$.

As it is explained in [2], Sect. 5, the integral in (ii) does not depend on a particular choice of the ‘q-primitive’ $\varDelta ^{-1}_{\zeta}\psi(\zeta/\xi)$.

To be more explicit, consider the function

Then it has the form

where $p^{+}_{m}(\zeta^{2})$ is a polynomial in ζ ² of degree 2n. Using them we introduce (n+1)×(n+1) matrices $\mathcal{A}$, $\mathcal{B}$ by

The formula for ω(ζ,ξ) reads

where v ^±(ζ) denote column vectors with entries v ^±(ζ) _j =ζ ^±α+2j.

For the purpose of studying various limits, it is more convenient to use an alternative expression in terms of solutions to integral equations [19]. The relevant formula can be found in [15], (3.11) (the function ω(ζ,ξ) in the present paper is denoted ω _rat(ζ,ξ) there, see [15], (2.11)). In this connection one should mention the recent paper [20] where a Riemann-Hilbert problem has been formulated.

Appendix B: Anti-commutativity of Fermionic Creation Operators

In this appendix we prove the following anti-commutation relations between the creation operators.

Theorem 3

For all p,p′≥1, we have

(30)

(31)

Since the proofs are similar, we shall concentrate on the case (31).

The next Proposition says that the anti-commutation relation (31) holds in the sense of expectation values.

Proposition 1

Assume (27). Then for any $X\in \mathcal{W}_{\alpha,0}$ we have

Proof

Abbreviating $Z^{\kappa}_{\varPhi,\varPsi}$ to Z, we apply the Ward identities for the expectation values in Theorem 1,

In the second line we used the known anti-commutation relations between the creation and annihilation operators.

Similarly one calculates

Using the known anti-commutativity of b(ξ ₂) and c(ξ ₁), we arrive at

which is equivalent to the assertion of Proposition. □

Before proceeding, we recall a few facts from the algebraic Bethe ansatz. Normalising the $\mathcal{L}$ operator as

we set

Let $|0\rangle=v_{+}^{\otimes n}$, $\langle 0 |=(v^{*}_{+})^{\otimes n}$ be the reference vector and covector respectively, where v ₊,v ₋ is the standard basis of ℂ² and $v_{+}^{*},v_{-}^{*}$ is the dual basis. Let further l∈{0,1,…,n} and set for j=1,…,l

where a(ζ), d(ζ) are defined in (29).

The following formula is well known [14].

Proposition 2

Assume that (ξ ₁,…,ξ _l )∈(ℂ^×)^l is a solution of the Bethe equation

(32)

and let (ζ ₁,…,ζ _l )∈(ℂ^×)^l be arbitrary. Then

$$\varOmega_{j,k}=\frac{a(\zeta_k)\prod_{i=1}^l(q^2\xi_i^2-\zeta_k^2)}{(\xi_j^2-\zeta_k^2)(q^2\xi_j^2-\zeta_k^2)} -q^{-2\kappa+n} \frac{d(\zeta_k)\prod_{i=1}^l(\xi_i^2-q^2\zeta_k^2)}{(\xi_j^2-\zeta_k^2)(\xi_j^2-q^2\zeta_k^2)}. $$

We shall consider the specialisation of parameters q,τ=(τ ₁,…,τ _n ) to

Lemma 1

Define x _j (κ) by

Then, for any subset I={i ₁,…,i _l }⊂{1,…,n}, i ₁<⋯<i _l ,

(33)

is a solution of (32) for (q,τ)=(q ₀,τ ₀). If further κ is generic, then we have $\xi^{2}_{j}\neq\pm1$, $\xi^{2}_{j}\neq\pm \xi^{2}_{k}$ (j≠k).

Proof is straightforward.

Hereafter we choose and fix a generic κ ₀. Denote by $\boldsymbol{\xi}_{0}^{(I)}$ the solution (33) at (κ,q,τ)=(κ ₀,q ₀,τ ₀).

Lemma 2

We have

Proof

This follows from the calculation

where (32) is used. □

By Lemma 2 and the implicit function theorem, in a neighborhood of (κ,q,τ)=(κ ₀,q ₀,τ ₀) there exists a unique branch $\boldsymbol{\xi}^{(I)}(\kappa,q,\boldsymbol{\tau})=\{\xi^{2}_{1},\ldots,\xi^{2}_{l}\}$ of solutions to (32) such that $\boldsymbol{\xi}^{(I)}(\kappa_{0},q_{0},\boldsymbol{\tau}_{0})=\boldsymbol{\xi}^{(I)}_{0}$. Denote by

the corresponding Bethe (co)vectors.

Lemma 3

In a neighborhood of (κ ₀,q ₀,τ ₀), we have

for all I,J⊂{1,…,n} with ♯I=♯J=l.

Proof

We apply Proposition 2 at (q,τ)=(q ₀,τ ₀). Setting ξ ^(I)(κ,q ₀,τ ₀)=(ξ ₁,…,ξ _l ) and ξ ^(J)(κ′,q ₀,τ ₀)=(ζ ₁,…,ζ _l ) we find

which is non-zero. Hence the scalar product does not vanish in some neighborhood of (κ ₀,q ₀,τ ₀) and κ′≠κ. □

We finish the proof with the

Proposition 3

For any p,p′≥1 and $X\in \mathcal{W}_{\alpha,0}$ we have

(34)

Proof

Denote the left hand side of (34) by Y. Take (κ,q,τ) in a neighborhood of (κ ₀,q ₀,τ ₀) and α≠0 small enough. Choose 〈Φ|= _I 〈κ+α,q,τ| and |Ψ〉=|κ,q,τ〉 _J , where ♯I=♯J=l and 0≤l≤n. Under the assumption above, we have 〈Φ|Ψ〉≠0 by Lemma 3. Hence Proposition 1 is applicable, and we obtain that

Since the vectors { _I 〈κ+α,q,τ|}, {|κ,q,τ〉 _I } are bases of the spin n/2−l subspace, we find

If we choose n=L−K+1 and τ=τ ₀, then $\mathcal{T}_{[K,L],M}(1)$ becomes a permutation operator and the trace becomes simply $q^{2\kappa S_{[K,L]}}Y$. We conclude that Y=0 provided (q,α) is close enough to (q ₀,0) and α≠0. But Y is rational in q,q ^α, so we must have that Y=0 identically. This completes the proof. □