Weighted Inequalities and Dyadic Harmonic Analysis

Abstract

We survey the recent solution of the so-called A ₂ conjecture, that states: all Calderón–Zygmund singular integral operators are bounded on L ²(w) with a bound that depends linearly on the A ₂ characteristic of the weight w. We also survey corresponding results for commutators. We highlight the interplay of dyadic harmonic analysis in the solution of the A ₂ conjecture, especially Hytönen’s representation theorem for Calderón–Zygmund singular integral operators in terms of Haar shift operators. We describe Chung’s dyadic proof of the corresponding quadratic bound on L ²(w) for the commutator of the Hilbert transform with a BMO function, and we deduce sharpness of the bounds for the dyadic paraproduct on L ^p(w) that were obtained extrapolating Beznosova’s linear bound on L ²(w). We show that if an operator T is bounded on the weighted Lebesgue space L ^r(w) and its operator norm is bounded by a power α of the A _r characteristic of the weight, then its commutator [T,b] with a function b in BMO will be bounded on L ^r(w) with an operator norm bounded by the increased power $\alpha +\max \{ 1, \frac{1} {r-1}\}$ of the A _r characteristic of the weight. The results are sharp in terms of the growth of the operator norm with respect to the A _r characteristic of the weight for all 1<r<∞.

1 Introduction

The main problem of study in this chapter is the weightedL ^p inequalities

$$\|Tf\|_{{L}^{p}(v)} \leq C(u,v)\,\|f\|_{{L}^{p}(u)},$$

(1)

where f ∈ L ^p(u) iff $\|f\|_{{L}^{p}(u)} := {(\int \nolimits \nolimits \vert f(x){\vert }^{p}u(x)\,\mathrm{d}x)}^{1/p} < \infty$, and u, v are locally integrable positive a.e. functions defined on ℝ ⁿ. When u ≡ 1 we denote $\|f\|_{p} :=\| f\|_{{L}^{p}(u)}$.

Two-weight problem: Find necessary and sufficient conditions on the weights so that above inequality holds for a given operator or class of operators T, and find the optimal rate of dependence of the constant C(w) on the weight.

In this survey we will concentrate on one-weight inequalities, u = v, for Calderón–Zygmund singular integral operators, more specifically for the Hilbert transform T = H and for the commutator of the Hilbert transform with a function b in the space BMO of bounded mean oscillation, namely $T = [b,H] := bH - Hb$.

The Hilbert transform is bounded on L ^p(w) if and only if the weight w belongs to the Muckenhoupt A _p class [31]. This is also true for Calderón–Zygmund singular integral operators [11]. A weight w is in the Muckenhoupt  A _p class if

$$[w]_{A_{p}} :=\sup _{I}\left ( \frac{1} {\vert I\vert }\int \nolimits \nolimits _{I}w\right ){\left ( \frac{1} {\vert I\vert }\int \nolimits \nolimits _{I}{w}^{-1/(p-1)}\right )}^{p-1} < \infty.$$

(2)

In the last decade there has been a flurry of activity trying to identify the exact dependence of the operator bound on the A _p characteristic, $[w]_{A_{p}}$, of the weight. This dependence was first proved to be linear in A ₂ for a few dyadic operators [30, 79, 80], then for the Beurling–Ahlfors [70], Hilbert [67], and Riesz transforms [68], and for the dyadic paraproduct [4]. Finally Tuomas Hytönen solved in the positive the A ₂ conjecture [33]: If T is a Calderón–Zygmund singular integral operator, w ∈ A ₂, then the dependence on the A ₂ characteristic of the weight is linear, that is,

$$\|Tf\|_{{L}^{2}(w)} \leq C[w]_{A_{2}}\|f\|_{{L}^{2}(w)}.$$

(3)

Sharp extrapolation [20] then yields the correct L ^p bounds for the class of Calderón–Zygmund singular integral operators:

$$\|Tf\|_{{L}^{p}(w)} \leq C_{p}[w]_{A_{p}}^{\max \{1, \frac{1} {p-1} \}}\|f\|_{{L}^{p }(w)}.$$

Remark.

The long-standing two-weight problem for the Hilbert transform “à la Muckenhoupt” is an outstanding open problem: Characterize the pairs of weights (u, v), in terms of conditions like the A _p condition in the one-weight problem, for which (1) holds. Recently there has been progress due to Lacey, Sawyer, Shen, and Uriarte-Tuero [45]. Note that Cotlar and Sadosky solved, years ago, the two-weight problem “à la Helson-Szëgo,” that is, using complex analysis techniques [13, 14].

In this chapter we want to highlight the interplay with dyadic harmonic analysis [60] in the solution of the A ₂ conjecture. Initially the A ₂ conjecture was shown to hold, one at a time, for dyadic operators and for operators such as the Hilbert transform that have lots of symmetries. Stephanie Petermichl showed, in groundbreaking work in 2000, that the Hilbert transform can be written as an appropriate average of dyadic shift operators [32, 66], and later she showed, in a tour de force using Bellman function techniques, that for the dyadic shift operators the A ₂ conjecture is true and therefore also for the Hilbert transform [67]. This work represented a quantum jump in our understanding of singular integral operators. Until then a simpler dyadic model, the martingale transform, was considered the toy model for singular integrals. One would first try to prove results for this model and then hope to prove them for a genuine singular integral operator, but the transition was by no means automatic [60]. Petermichl’s representation theorem made this transition trivial for the Hilbert transform. For a while it seemed that the miracle of this representation theorem was a consequence of the symmetries of the operator. Similar constructions were found for other symmetric operators: the Riesz transform (n-dimensional analogue of the Hilbert transform) [68], the Beurling–Ahlfors transform [70], and for sufficiently smooth convolution Calderón–Zygmund singular integral operators [76]. The fact that for the Beurling–Ahlfors transform the A ₂ conjecture holds for p > 2 (linear estimate in A _p characteristic in the range of p > 2) had important implications in the theory of quasiconformal mappings [2].

All these operators have a representation as averages of dyadic Haar shift operators of bounded complexity. In 2008, Oleksandra Beznosova showed that the linear bound on L ²(w) also holds for the dyadic paraproduct, an operator not in the above class [4]. Hytönen was able to prove a representation theorem valid for all Calderón–Zygmund singular integral operators (not only convolution) in terms of dyadic Haar shift operators of arbitrary complexity, paraproducts, and adjoints of the paraproducts. Different groups of researchers had already shown that the A ₂ conjecture was true for all these Haar shift operators [17, 18, 44], using techniques other than Bellman function which had dominated the scene until then. However, the dependence of the operator bound on the complexity was exponential and prevented one from deducing the A ₂ conjecture for general Calderón–Zygmund singular operators. Only for those operators that were averages of dyadic shift operators of bounded complexity one could deduce the A ₂ conjecture. Hytönen was able to overcome this obstacle as well, proving a polynomial dependence on the complexity and the linear dependence on the A ₂ characteristic of the weight for Haar shift operators, therefore proving the A ₂ conjecture [33]. Precursors to Petermichl’s and Hytönen’s results can be found in Figiel’s work [24]. Nowadays some of the simpler arguments yielding polynomial and even linear dependence on the complexity use minimally Bellman functions [54, 74], or do not use them at all [37, 42].

The commutator [b, H] is more singular than the operator H, and this is reflected on the nature of its bounds on weighted L ^p spaces. Daewon Chung showed in [8] that

$$\|[b,H]f\|_{{L}^{2}(w)} \leq C[w]_{A_{2}}^{2}\|f\|_{{ L}^{2}(w)}.$$

(4)

That is, the dependence on the A ₂ characteristic of the operator bound is now quadratic as opposed to the linear bound enjoyed by the Hilbert transform. Chung’s proof can be labeled as a dyadic proof. It suffices to consider the commutator with Petermichl’s Haar shift operator [69]. Then known linear bounds for the shift operator [67] and for the dyadic paraproduct [4] can be used, and Bellman function arguments can be invoked as did all of Chung’s predecessors until then. We observe that the sharp bounds for the commutator of the Hilbert transform imply that Beznosova’s bounds [4] are the sharp bounds for the dyadic paraproduct in L ^p(w), which was not known until now. The author in collaboration with Chung and Carlos Pérez established a transference theorem that states that if a linear operator T obeys a linear bound on L ²(w) then its commutator with a BMO function obeys a quadratic bound [10]. In light of Hytönen’s theorem this means that all commutators of Calderón–Zygmund singular operators with BMO functions obey a quadratic bound as in inequality (4). The argument follows the classical Coifman, Rochberg, and Weiss argument [12] exploiting the Cauchy integral formula and some very precise quantitative results in the theory of A ₂ weights and BMO functions. Generalizations of these results to commutators with fractional integrals and to the two-weight setting appear in [16], and weak-type estimates and strong estimates involving instead the A ₁ characteristic of the weight appear in [59]. In this note we present the simple modifications necessary to state a transference theorem that provides bounds on L ^r(w), r≠2, for the commutator given corresponding bounds on L ^r(w) for the initial operator.

The author strongly believes that Petermichl and Hytönen’s representation theorem in terms of dyadic operators could have important consequences in applications, in the same way that the T(1) theorem [19] had repercussions in computational harmonic analysis via the Beylkin, Coifman, and Rokhlin algorithm to decompose singular integral operators [3].

This chapter is organized as follows. In Sect. 2 we define the Hilbert transform and the dyadic Haar shift operators, recall some of their basic properties, state Petermichl’s representation theorem, and show how it provides a straightforward proof of the boundedness of the Hilbert transform on L ^p(ℝ) (Riesz’s theorem). In Sect. 3 we discuss weighted inequalities for the Hilbert transform and recount the prehistory of linear estimates for dyadic operators on L ²(w). We state the sharp extrapolation theorem and deduce L ^p(w) bounds from linear bounds and observe that these bounds are sometimes sharp, but not always, as Buckley’s estimates for the maximal function show. We then define the Haar shift operators of complexity (m, n), discuss their boundedness properties, and state Hytönen’s theorem (the A ₂ conjecture), as well as his representation theorem. In Sect. 4 we define the commutator, state its boundedness properties, and sketch Chung’s dyadic proof of the quadratic estimate on L ²(w). We note that this quadratic estimate is sharp, and we show that Chung’s dyadic method of proof implies that Beznosova’s bound for the dyadic paraproduct is sharp as well. Finally we state a variation of the transference theorem for commutators on L ^r(w) with r≠2 and present its proof in the Appendix.

2 Hilbert Transform Versus Dyadic Shift Operators

We define the Hilbert transform both on Fourier and space domains, and we describe its boundedness and symmetry properties. We introduce the dyadic intervals, the random dyadic grids, and corresponding Haar bases, and we emphasize some of the properties these bases share with wavelets such us being an unconditional basis on L ^p spaces. We define Petermichl’s Haar shift operators and describe their symmetry properties; we state Petermichl’s representation theorem and show how it provides a straightforward proof of the boundedness of the Hilbert transform on L ^p(ℝ).

2.1 Hilbert Transform

In this section we recall the definition of the Hilbert transform on Fourier domain as a Fourier multiplier and on space domain as a convolution with a singular kernel. We also recall how symmetry properties completely characterize the Hilbert transform. These are well-known facts that can be found in any Fourier analysis book such as [21, 26, 73]. You will also find here the definition of BMO, the space of functions of bounded mean oscillation.

2.1.1 Fourier Multiplier

The Fourier transform of a Schwartz function is defined by

$$\widehat{f}(\xi ) := \int \nolimits \nolimits _{\mathbb{R}}f(x)\,{\mathrm{e}}^{-2\pi \mathrm{i}\xi x}\mathrm{d}x.$$

With some work one can define the Fourier transform on L ²(ℝ) and show that it is an isometry, that is, $\|\widehat{f}\|_{2} =\| f\|_{2}$ (Plancherel’s identity).

On Fourier side the Hilbert transform can be defined as a Fourier multiplier:

$$\widehat{Hf}(\xi ) = -i\,\mbox{ sgn}(\xi )\,\widehat{f}(\xi ),$$

(5)

where sgn(ξ) = 1 if ξ > 0, $\mbox{ sgn}(\xi ) = -1$ if ξ < 0, and is zero at ξ = 0.

The absolute value of the symbol $m_{H}(\xi ) := -i\,\mbox{ sgn}(\xi )$ is 1 a.e., and Plancherel’s identity used twice implies that $H : {L}^{2}(\mathbb{R}) \rightarrow {L}^{2}(\mathbb{R})$ and that it is an isometry:

$$\|Hf\|_{2}=\|\widehat{Hf}\|_{2}=\|\widehat{f}\|_{2}=\|f\|_{2}.$$

2.1.2 Singular Integral Operator

Since the Hilbert transform is given on Fourier side by

$$\widehat{Hf}(\xi ) = m_{H}(\xi )\,\widehat{f}(\xi ),$$

multiplication on Fourier side comes from convolution on space with the distributional kernel k _H which is the inverse Fourier transform of the multiplier m _H . A calculation yields

$$k_{H}(x) := {(m_{H})}^{\vee }(x) = \mbox{ p.v.} \frac{1} {\pi x}.$$

For a distributional kernel, the integration must be done in the principal value sense:

$$Hf(x) = k_{H} {_\ast} f(x) = \mbox{ p.v.} \frac{1} {\pi }\int \nolimits \nolimits \frac{f(x - y)} {y} \,\mathrm{d}y :=\lim _{\epsilon \rightarrow 0} \frac{1} {\pi }\int \nolimits \nolimits _{\vert x-y\vert >\epsilon } \frac{f(y)} {x - y}\,\mathrm{d}y.$$

(6)

Had the kernel k _H been integrable, boundedness on L ^p(ℝ) would be a consequence of the Hausdorff–Young’s inequality for p ≥ 1: if g ∈ L ¹(ℝ), f ∈ L ^p(ℝ), then $\|g {_\ast} f\|_{p} \leq \| g\|_{1}\|f\|_{p}$. But k _H is not in L ¹(ℝ); despite this fact, H is bounded on L ^p(ℝ) for all 1 < p < ∞, as Marcel Riesz proved in 1927:

$$\|Hf\|_{p} \leq C_{p}\|f\|_{p}.$$

However, H is not bounded on L ¹(ℝ) nor on L ^∞(ℝ), but there are appropriate substitutes: H is of weak type (1,1) and is bounded on BMO [21, 26, 73]. Recall that a function b : ℝ → ℝ belongs to BMO, the space of bounded mean oscillation, if and only if

$$\|b\|_{BMO} :=\sup _{I} \frac{1} {\vert I\vert }\int \nolimits \nolimits _{I}\vert b(x) - m_{I}b\vert \,\mathrm{d}x < \infty,$$

(7)

where m _I b denotes the integral average of b on the interval I, $m_{I}b = \frac{1} {\vert I\vert }\int \nolimits \nolimits _{I}b(x)\,\mathrm{d}x$. This space was introduced by John and Nirenberg in the 1960s [39]. The space of bounded functions L ^∞(ℝ) is a proper subset of BMO; the canonical example of a function that is not bounded but it is in BMO is log | x | [26].

2.1.3 Symmetries

The Hilbert transform commutes with translations and dilations and anticommutes with reflections, and it is essentially the only bounded linear operator in L ²(ℝ) that has those properties. In what follows h ∈ ℝ and δ > 0.

• Convolution ⇔ H commutes with translations $\tau _{h}f(x) := f(x - h)$

  $$\tau _{h}(Hf) = H(\tau _{h}f).$$

• Homogeneity of kernel ⇔ H commutes with dilationsD _δ f(x) = f(δx)

  $$D_{\delta }(Hf) = H(D_{\delta }f).$$

• Kernel odd ⇔ H anticommutes with reflections $\tilde{f}(x) := f(-x)$

  $$(H\tilde{f}) = -H(\tilde{f}).$$

Theorem 1 ([26, 73]). 

Let T be a linear and bounded operator in L ² (ℝ) that commutes with translations and dilations and anticommutes with reflections, then T must be a constant multiple of the Hilbert transform: T = cH.

Using this principle, Petermichl [66] showed that we can write H as a suitable “average of dyadic operators”; see also [32].

2.2 Dyadic Shift Operators

We first introduce the dyadic intervals and associated Haar basis, as well as random dyadic grids. We recall some important properties of the Haar basis shared with wavelet bases such us being an unconditional system in L ^p spaces and weighted L ^p(w) whenever w ∈ A _p . We then describe Petermichl’s averaging theorem and give some intuition why this should work. We deduce Riesz’s theorem from this representation, that is, the boundedness on L ^p(ℝ) of the Hilbert transform.

2.2.1 Dyadic Intervals

The standard dyadic grid $\mathcal{D}$ is the collection of intervals of the form $[k{2}^{-j},(k + 1){2}^{-j})$, for all integers k, j ∈ ℤ. They are organized by generations: $\mathcal{D} = \cup _{j\in \mathbb{Z}}\mathcal{D}_{j}$, and our labeling is such that $I \in \mathcal{D}_{j}$ iff $\vert I\vert = {2}^{-j}$. They satisfy:

• Trichotomy or nestedness: $\;\;I,J \in \mathcal{D}\;\;$ then   I ∩ J = ∅, I ⊆ J,  orJ ⊂ I. 

• One parent, two children: If $I \in \mathcal{D}_{j}$, then there is a unique interval $\tilde{I} \in \mathcal{D}_{j-1}$ such that $I \subset \tilde{ I}$ and $\vert \tilde{I}\vert = 2\vert I\vert$. There are exactly two disjoint intervals, the right and left children $I_{r},I_{l} \in \mathcal{D}_{j+1}$, such that I = I _r ∪I _l and $\vert I\vert = 2\vert I_{r}\vert = 2\vert I_{l}\vert$.

2.2.2 Random Dyadic Grids

A dyadic grid in ℝ is a collection of intervals, organized in generations, each of them being a partition of ℝ, that have the trichotomy and two children per interval property. For example, the shifted and rescaled regular dyadic grid will be a dyadic grid. However, these are not all possible dyadic grids.

The following parametrization will capture all dyadic grids. Consider the scaling or dilation parameterr with 1 ≤ r < 2 and the random parameter β with $\beta =\{ \beta _{i}\}_{i\in \mathbb{Z}}$, β _i  = 0, 1; let $x_{j} = \sum \nolimits _{i<-j}\beta _{i}{2}^{i}$ and then define

$$\mathcal{D}_{j}^{\beta } := x_{ j} + \mathcal{D}_{j},\quad \quad \mbox{ and}\quad \quad \mathcal{D}_{j}^{r,\beta } := r\mathcal{D}_{ j}^{\beta }.$$

The family of intervals ${\mathcal{D}}^{r,\beta }$ so defined is a dyadic grid. Here r is a dilation parameter, and β a random parameter that encode all possible dyadic grids. Notice that for the standard dyadic grid zero is never an interior point of a dyadic interval, and it is always on the right side of any dyadic interval it belongs to. If we translate $\mathcal{D}$ by a fixed number it will simply shift zero, and it will still have this singular property. The translated grids correspond to parameters β such that β _j is constant for all sufficiently large j. But these are not all the possible grids. Once we have an interval in a dyadic grid its descendants are completely determined, simply subdivide; however, there are two possible choices for the parent, four possible choices for the grandparent, and 2ⁿ choices for the nth-parent. The parameter β captures all of these possibilities. Those β’s that do not become eventually constant eliminate the presence of a singular point such as zero in the standard grid.

The random dyadic grids were introduced by Nazarov, Treil, and Volberg in their study of Calderón–Zygmund singular integrals on nonhomogeneous spaces [56] and are utilized by Hytönen in his representation theorem [32, 33]. The advantage of this parametrization is that there is a very natural probability space, say (Ω, P) associated to the parameters, and averaging here means calculating the expectation in this probability space, that is, $\mathbb{E}f = \int \nolimits \nolimits _{\Omega }f\,\mathrm{d}P$.

2.2.3 Haar Basis

Given an interval I, its associated Haar function is defined to be

$$h_{I}(x) := \vert I{\vert }^{-1/2}(\chi _{ I_{r}}(x) - \chi _{I_{l}}(x)),$$

where χ _I (x) = 1 if x ∈ I, zero otherwise. Note that $\|h_{I}\|_{2} = 1$, and it has zero integral ∫h _I  = 0. One can check, from these integral properties and the nestedness properties of the dyadic intervals, that $\{h_{I}\}_{I\in \mathcal{D}}$ is an orthonormal system in L ²(ℝ). Furthermore, the system is complete, that is, it is an orthonormal basis in L ²(ℝ).

Alfred Haar introduced in 1910 the Haar basis in L ²([0, 1]) and showed that for continuous functions their Haar expansions converge uniformly [28], unlike their expansions in the trigonometric (Fourier) basis [21, 26, 73].

A basis is unconditional inL ^p(ℝ) if and only if changes in the signs of the coefficients of a function keep it in the same space with comparable norms [82]. The trigonometric system $\{{\mathrm{e}}^{2\pi \mathrm{i}nx}\}_{n\in \mathbb{Z}}$ does not form an unconditional basis in L ^p([0, 1)) for p≠2 [26, 82]. On the other hand, the Haar basis $\{h_{I}\}_{I\in \mathcal{D}}$ is an unconditional basis in L ^p(ℝ). More precisely we can define an operator, the martingale transform, given by

$$T_{\sigma }f(x) = \sum \nolimits _{I\in \mathcal{D}}\sigma _{I}\langle f,h_{I}\rangle h_{I},\quad \quad \mbox{ where}\quad \sigma _{I} = \pm 1.$$

(8)

Unconditionality of the Haar basis in L ^p(ℝ) reduces then to show that the martingale transform is bounded in L ^p(ℝ) with norm independent of the choice of signs:

$$\sup _{\sigma }\|T_{\sigma }f\|_{p} \leq C_{p}\|f\|_{p}.$$

This was proved by Burkholder who also found the optimal constant C _p [7].

The Haar system $\{h_{I}\}_{I\in \mathcal{D}}$ is an unconditional basis inL ^p(w) if and only ifw ∈ A _p . This fact is deduced from the boundedness of the martingale transform on L ^p(w) [75]. For sharp linear bounds in L ²(w) for the martingale transform see [79].

The Haar basis is the first example of a wavelet basis, that is, a basis $\{\psi _{j,k}\}_{j,k\in \mathbb{Z}}$, that is found by translating and dilating appropriately a fixed function ψ, the wavelet, more precisely, $\psi _{j,k}(x) := {2}^{-j/2}\psi ({2}^{j}x + k)$. The Haar functions are translates and dyadic dilates of the function $h(x) := \chi _{[0,1/2)}(x) - \chi _{[1/2,1)}(x)$. These unconditionality properties are shared by a large class of wavelets [29, 75, 82].

2.2.4 Petermichl’s Dyadic Shift Operator

Petermichl’s dyadic shift operatorS associated to the standard dyadic grid $\mathcal{D}$ is defined for function f ∈ L ²(ℝ) by

$$Sf(x) := \sum \nolimits _{I\in \mathcal{D}}\langle f,h_{I}\rangle H_{I}(x),\quad \quad \mbox{ where}\quad H_{I} := {2}^{-1/2}(h_{ I_{r}} - h_{I_{l}}).$$

Petermichl’s shift operator is an isometry in L ²(ℝ), that is, it preserves L ²-norms, $\|Sf\|_{2} =\| f\|_{2}$. Notice that if $I \in \mathcal{D}$,  Sh _I (x) = H _I (x). A periodic version of the Hilbert transform that we denote by H _p , has the property that it maps cosines into sines,  H _p cos(x) = sin(x). Draw the profiles of h _I and H _I and you can view them as a localized sine and cosine. This indicates that this shift operator may be a good dyadic model for the Hilbert transform. More evidence comes from the way it interacts with translations, dilations, and reflections.

Denote by S _r, β Petermichl’s shift operator associated to the dyadic grid $\mathcal{D}_{r,\beta }$. Each shift operator S _r, β does not commute with translations and dilations, nor does it anticommute with reflections; however, one can verify that the following symmetries for the family of shift operators {S _r, β}_{(r, β) ∈ Ω} hold:

• Translation: $\tau _{h}(S_{r,\beta }f) = S_{\tau _{h}(r,\beta )}(\tau _{h}f)$, where τ _h (r, β) ∈ Ω.

• Dilation: D _δ(S _r, β f) = $S_{D_{\delta }(r,\beta )}(D_{\delta }f)$, where D _δ(r, β) ∈ Ω.

• Reflection: $\widetilde{S_{r,\beta }f} = S_{r,\tilde{\beta }}(\tilde{f})$, where $\tilde{\beta }_{i} = 1 - \beta _{i}$.

Where the maps τ _h , D _δ : Ω → Ω are bijections. Each shift dyadic operator does not have the symmetries that characterize the Hilbert transform, but the average over all dyadic grids will, therefore,

Theorem 2 (Petermichl’s [32, 66]). 

$$\mathbb{E}S_{r,\beta } = \int \nolimits \nolimits _{\Omega }S_{r,\beta }\mathrm{d}P(r,\beta ) = cH.$$

Petermichl’s result then follows once one verifies that c≠0 (which she did!). Similar trick works for the Beurling–Ahlfors [70] and the Riesz transforms [68]. Vagharshakyan showed that sufficiently smooth one-dimensional Calderón– Zygmund convolution operators are averages of Haar shift operators of bounded complexity [76].

2.2.5 L ^p Boundedness of the Hilbert Transform: A Dyadic Proof

Estimates for the Hilbert transform H follow from uniform estimates for Petermichl’s shift operators.

Lemma 1 (Riesz [17]). 

The Hilbert transform is bounded on L ^p for 1 < p < ∞.

$$\|Hf\|_{p} \leq C_{p}\|f\|_{p}.$$

Proof.

Suffices to check that

$$\sup _{(r,\beta )\in \Omega }\|S_{r,\beta }f\|_{p} \leq C_{p}\|f\|_{p}.$$

Case p = 2 follows from orthonormality of the Haar basis. First rewrite Petermichl’s shift operator in the following manner, where $\tilde{I}$ is the parent of I in the dyadic grid ${\mathcal{D}}^{r,\beta }$:

$$S_{r,\beta }f = \sum \nolimits _{I\in \mathcal{D}_{r,\beta }} \frac{1} {\sqrt{2}}\,\mbox{ sgn}(I,\tilde{I})\langle f,h_{\tilde{I}}\rangle h_{I},$$

where $\mbox{ sgn}(I,\tilde{I}) = 1$ if I is the right child of $\tilde{I}$ and − 1 if I is the left child. We can now use Plancherel to compute the L ² norm, and noticing that each parent has two children,

$$\|S_{r,\beta }f\|_{2}^{2} = \sum \nolimits _{I\in \mathcal{D}_{r,\beta }}\frac{\vert \langle f,h_{\tilde{I}}\rangle {\vert }^{2}} {2} =\| f\|_{2}^{2}.$$

Minkowski integral inequality then shows that

$$\left \|\mathbb{E}S_{r,\beta }f\right \|_{2} \leq \mathbb{E}\|S_{r,\beta }f\|_{2} \leq \| f\|_{2}.$$

Case p≠2 follows from the unconditionality of the Haar basis on L ^p(ℝ).

3 Weighted Inequalities and the A ₂ Conjecture

In this section we discuss weighted inequalities for the Hilbert transform and recount the prehistory of linear estimates for dyadic operators on L ²(w). We state the sharp extrapolation theorem and deduce L ^p(w) bounds from linear bounds and observe that these bounds are sometimes sharp, but not always, as Buckley’s estimates for the maximal function show. We then define the Haar shift operators of complexity (m, n), discuss their boundedness properties, and finally state Hytönen’s theorem (A ₂ conjecture).

3.1 Boundedness on Weighthed L ^p

The Hilbert transform is bounded on weighted L ^p(w); the celebrated 1973 Hunt–Muckenhoupt–Wheeden theorem says:

Theorem 3 (Hunt–Muckenhoupt–Wheeden [31]). 

$$w \in A_{p} \Leftrightarrow \| Hf\|_{{L}^{p}(w)} \leq C_{p}(w)\|f\|_{{L}^{p}(w)}.$$

Dependence of the constant on the A _p characteristic was found 30 years later.

Theorem 4 (Petermichl [67]). 

$$\|Hf\|_{{L}^{p}(w)} \leq C[w]_{A_{p}}^{\max \{1, \frac{1} {p-1} \}}\|f\|_{{L}^{p }(w)}.$$

Proof (Sketch of the proof). 

For p = 2 suffices to find uniform (on the grids) linear estimates for Petermichl’s shift operator (this was the hard part which she did using Bellman functions and a bilinear Carleson embedding theorem due to Nazarov, Treil, and Volberg [55]). For p≠2 a sharp extrapolation theorem [20] that we will discuss in Sect. 3.1.2 automatically gives the result from the linear estimate in L ²(w).

3.1.1 Chronology of First Linear Estimates on L ²(w)

In 1993, Steve Buckley showed that the maximal function obeys a linear bound in L ²(w) [6]. Starting in 2000, one at a time over a span of 10 years, a handful of dyadic operators or operators with enough symmetries that could be written as averages of dyadic operators were shown to obey a linear bound in L ²(w); see (3):

• Martingale transform (Janine Wittwer [79] in 2000)

• Dyadic square function (Sanja Hukovic, Treil, Volberg [30], Wittwer [80] in 2000)

• Beurling transform (Petermichl, Volberg [70] in 2002)

• Hilbert transform (Stephanie Petermichl [67] in 2003, published 2007)

• Riesz transforms (Stephanie Petermichl [68] in 2008)

• Dyadic paraproduct inℝ (Oleksandra Beznosova [4] in 2008)

These estimates were based on Bellman functions and bilinear Carleson estimates by Nazarov, Treil, and Volberg [55]. See [61] for Bellman function extensions of the results for dyadic square functions to homogeneous spaces. See [9] for a neat Bellman function transference lemma that allows to use Bellman functions in ℝ to deduce results in ℝ ⁿ with no sweat, similar considerations are used in [74]. There are now simpler Bellman function proofs that recover the estimates for the dyadic shift operators [54, 74] and for the dyadic paraproduct [52]. The Bellman function method was introduced in harmonic analysis by Nazarov, Treil, and Volberg, and with their students and collaborators, they have been able to use this method to obtain a number of astonishing results not only in this area; see [77, 78] and references.

3.1.2 Estimates in L ^p(w) via Sharp Extrapolation

The L ^p(w) inequalities can be deduced from the linear bounds on L ²(w), thanks to a sharp version of Rubio de Francia’s extrapolation theorem [25].

Theorem 5 (Sharp Extrapolation Theorem [20]). 

If for all w ∈ A _r there is α>0, and C > 0 such that

$$\|Tf\|_{{L}^{r}(w)} \leq C[w]_{A_{r}}^{\alpha }\|f\|_{{ L}^{r}(w)},$$

then for all w ∈ A _p and 1 < p < ∞,

$$\|Tf\|_{{L}^{p}(w)} \leq C_{p,r}[w]_{A_{p}}^{\alpha \max \{1,\frac{r-1} {p-1} \}}\|f\|_{{L}^{p }(w)}.$$

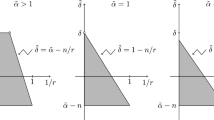
Duoandikoetxea found recently a shorter proof of this theorem [22]. Sharp extrapolation from r = 2 is sharp for the martingale, Hilbert, Beurling–Ahlfors, and Riesz transforms for all 1 < p < ∞ [20]. Therefore the theorem cannot be improved in terms of the power on the A _p characteristic of the weight. However, it is not necessarily sharp for each individual operator. The theorem is sharp for the dyadic square function and 1 < p ≤ 2, see [20], but it is not sharp for p > 2, see [46]. The optimal power for the square function is $\max \{\frac{1} {2}, \frac{1} {p-1}\}$ (see [18]), which corresponds to sharp extrapolation starting at r = 3 with square root power instead of starting at r = 2 with linear power; see also [50]. We conclude that sharp extrapolation is not always sharp. Buckley’s estimates for the maximal function are a more dramatic example of the above statement.

Remember the Hardy–Littlewood maximal function is defined as

$$Mf(x) =\sup _{I\ni x} \frac{1} {\vert I\vert }\int \nolimits \nolimits _{I}\vert f(y)\vert \,\mathrm{d}y.$$

The maximal function is known to be bounded on L ^p(ℝ) for 1 < p; it is not bounded on L ¹(ℝ), but it is of weak type (1, 1) [21, 26, 73]. Muckenhoupt showed in 1972 [53] that the maximal function is bounded on L ^p(w) if and only if w ∈ A _p . The optimal dependence on the A _p characteristic of the weight was discovered by Buckley 20 years later.

Theorem 6 (Buckley [6]). 

Let w ∈ A _p and 1 < p, then

$$\|Mf\|_{{L}^{p}(w)} \leq C_{p}[w]_{A_{p}}^{ \frac{1} {p-1} }\|f\|_{{L}^{p }(w)}.$$

This estimate is key in the proof of the sharp extrapolation theorem. Observe that if we start with Buckley’s estimate on L ^r(w), then sharp extrapolation will give the right power for all 1 < p ≤ r; however, for p > r, it will simply give $\frac{1} {r-1}$ which is bigger than the correct power $\frac{1} {p-1}$.

3.1.3 Estimates for Larger Classes of Operators

Petermichl’s shift operator and the martingale transform are the simplest among a larger class of Haar shift operators that we now define.

A Haar shift operator of complexity (m,n), S _m, n , is defined as follows:

$$S_{m,n}f(x) := \sum \nolimits _{L\in \mathcal{D}}\sum \nolimits _{I\in \mathcal{D}_{m}(L),J\in \mathcal{D}_{n}(L)}c_{I,J}^{L}\langle f,h_{ I}\rangle h_{J}(x),$$

(9)

where the coefficients $\vert c_{I,J}^{L}\vert \leq \frac{\sqrt{\vert I\vert \,\vert J\vert }} {\vert L\vert }$ and $\mathcal{D}_{m}(L)$ denote the dyadic subintervals of L with length 2^− m | L | .

The normalization of the coefficients ensures that $\|S_{m,n}f\|_{2} \leq \| f\|_{2}$. The reader can now check that the martingale transform is a Haar shift operator of complexity (0, 0) and Petermichl’s shift operator is a Haar shift operator of complexity (0, 1). However, the dyadic paraproduct π _b , which is defined for a function b ∈ BMO as

$$\pi _{b}f(x) := \sum \nolimits _{I\in \mathcal{D}}m_{I}f\,\langle b,h_{I}\rangle h_{I}(x),\quad \mbox{ where}\quad m_{I}f = \frac{1} {\vert I\vert }\int \nolimits \nolimits _{I}f(x)\,\mathrm{d}x,$$

is not a Haar shift operator. The Haar shift operators were introduced in [44] and used in [17, 18]. Later, a larger class, the generalized dyadic shift operators, that included the paraproducts was defined [33, 37], where the Haar functions in (9) were replaced by $\vert I{\vert }^{-1/2}\chi _{I}(x)$ and boundedness on L ²(ℝ) is now part of the definition since it will not follow from the normalization of the coefficients. In this setting the dyadic paraproduct, the martingale transform, and Petermichl’s Haar shift operator are generalized dyadic shift operators of complexity (0, 1), (1, 1), and (1, 2), respectively. The adjoint of the dyadic paraproduct, defined by

$$\pi _{b}^{{_\ast}}f(x) = \sum \nolimits _{I\in \mathcal{D}}\langle f,h_{I}\rangle \,\langle b,h_{I}\rangle \frac{\chi _{I}(x)} {\vert I\vert },$$

is a generalized dyadic shift operator of complexity (1, 0), and the composition π _b ^∗π _b is of complexity (0, 0). On the other hand the composition π _b π _b ^∗ is not a generalized dyadic shift operator; localization has been lost.

The following authors either extend to other settings or recover most of the previous known results (the linear bounds on L ²(w)) and can extend them to the larger class of Haar shift operators, and in particular averaging appropriately, they can get Hilbert, Riesz, and Beurling–Ahlfors transforms:

•  Lacey, Moen, Pérez, and Torres [43] obtain sharp bound on weighted L ^p spaces for fractional integral operators.

•  Lacey, Petermichl, and Reguera [44] use a corona decomposition and a two-weight theorem for “well-localized operators” of Nazarov, Treil, and Volberg, to recover linear bounds for Haar shifts operators on L ²(w); they do not use Bellman functions. Dependence on the complexity is exponential. This result does not include dyadic paraproducts.

•   Cruz-Uribe, Martell, and Pérez [17, 18] recover all results for Haar shift operators. No Bellman functions, no two-weight results. Instead they use a local median oscillation introduced by Lerner [47, 48]. The method is very flexible, they can get new results such as the sharp bounds for the square function for p > 2, they can recover also the result for the dyadic paraproduct, they can get results for vector-valued maximal operators and two-weight results as well. Dependence on complexity is exponential.

After these results were posted a lot of activity followed and results covering larger classes of operators appeared:

• Lerner [48, 50] showed that all standard convolution-type operators in arbitrary dimension gave the expected result for p ∈ (1, 3 ∕ 2] ∩ [3, ∞). He also showed sharp estimates on L ^p(w) for all p > 1 and for all sort of square functions. This is based on controlling them with Wilson’s intrinsic square function [81].

• Hytönen, Lacey, Reguera, Sawyer, Uriarte-Tuero, and Vagharshakyan posted a preprint in 2010 which was then replaced by a 2011 preprint with more authors [37]. They obtain the desired result for a general class of Calderón–Zygmund non-convolution operators, still requiring smoothness of the kernels.

• Pérez, Treil, and Volberg [65] showed that all Calderón–Zygmund operators obey an almost linear estimate on L ²(w): $[w]_{A_{2}}\log (1 + [w]_{A_{2}}).$ They identified the obstacle that would remove the log term.

3.1.4 The A ₂ Conjecture (Now Theorem)

The A ₂ conjecture said that all Calderón–Zygmund singular integral operators should obey a linear bound on L ²(w). This was finally proved by Tuomas Hytönen in 2010.

Theorem 7 (Hytönen [33]). 

Let 1 < p < ∞ and let T be any Calderón–Zygmund singular integral operator in ℝ ⁿ ; then there is a constant c _T,n,p > 0 such that

$$\|Tf\|_{{L}^{p}(w)} \leq c_{T,n,p}\,[w]_{A_{p}}^{\max \{1, \frac{1} {p-1} \}}\|f\|_{{L}^{p }(w)}.$$

It is enough to consider the case p = 2 thanks to sharp extrapolation. Hytönen proves the representation theorem, gets linear estimates on L ²(w) with respect to the A ₂ characteristic for Haar shift operators, and gets polynomial dependence in the complexity. Together these imply the theorem for p = 2. We consider the representation theorem to be of independent interest, and we state it here.

Theorem 8 (Hytönen [33]). 

Let T be a Calderón–Zygmund singular integral operator, then

$$Tf = \mathbb{E}\left (\sum \nolimits _{(m,n)\in {\mathbb{N}}^{2}}a_{m,n}S_{m,n}^{r,\beta }f\right ),$$

where the coefficients in the series are of the form $a_{m,n} ={ \mathrm{e}}^{-(m+n)\alpha /2}$ , α is the smoothness parameter of T, and S _m,n ^r,β are Haar shift operators of complexity (m,n) when (m,n)≠(0,0), and when (m,n) = (0,0) they are a linear combination of a Haar shift of complexity (0,0), a dyadic paraproduct, and the adjoint of the dyadic paraproduct, all based on the dyadic grid $\mathcal{D}_{r,\beta }$ , and $\mathbb{E}$ is the expectation in the probability space (Ω,P) associated to the random dyadic grids $\mathcal{D}_{r,\beta }$

Leading to the solution of the A ₂ conjecture were the results of Pérez, Treil, and Volberg [65]. Since the appearance of Hytönen’s theorem several simplifications of the argument have appeared [34, 38, 42, 54, 74], as well as an extension to metric spaces with geometric doubling condition [58]. There is also a very nice survey of the A ₂ conjecture [41].

Can we expect more singular operators to have worst estimates? Yes, for example, the commutators of b ∈ BMO with T a Calderón–Zygmund singular integral operator.

4 Sharp Weighted Inequalities for the Commutator

In this section we define the commutator, state its boundedness properties, and sketch Chung’s dyadic proof of the quadratic estimate on L ²(w). We note that this quadratic estimate is sharp, and we show that Chung’s dyadic method of proof implies that Beznosova’s bounds for the dyadic paraproduct are sharp as well. Finally we state a variation of the transference theorem for commutators on L ^r(w) with r≠2 and present its proof in Appendix.

4.1 The Commutator

The commutator [b, H] of b ∈ BMO and H the Hilbert transform is defined:

$$[b,H]f = b(Hf) - H(bf).$$

It is well known that the commutator [b, H] is bounded on L ^p(ℝ).

Theorem 9 (Coifman et al. [12]). 

Let b ∈ BMO and 1 < p < ∞, then

$$\|[H,b]f\|_{p} \leq C_{p}\|b\|_{BMO}\|f\|_{p}.$$

However, the commutator is not of weak type (1, 1) as Carlos Pérez showed [62]. The commutator [b, H] is more singular than H. Another way to quantify this roughness is to observe that the maximal function M controls H; however, to control the commutator we need M ² [63].

Observe that separately bH and Hb are not bounded on L ^p(ℝ) when b ∈ BMO, simply because multiplication by a BMO function does not preserve L ^p(ℝ) (one needs the multiplier to be bounded and L ^∞(ℝ) ⊊BMO). The commutator introduces some key cancellation. This is very much connected to the celebrated H ¹ - BMO duality by Feffferman and Stein [23] (H ¹ denotes the Hardy space on the line).

Coifman, Rochberg, and Weiss have a beautiful argument in [12] to prove boundedness on L ^p(ℝ) of the commutator based on the boundedness of the Hilbert transform on L ^p(v) for v ∈ A ₂; it is this argument that was exploited to obtain the following weighted inequalities for the commutator in quite a general framework; here we state the estimate for the Hilbert transform.

Theorem 10 (Alvarez et al. [1]). 

If w ∈ A _p and b ∈ BMO, then

$$\|[H,b]f\|_{{L}^{p}(w)} \leq C_{p}(w)\|b\|_{BMO}\|f\|_{{L}^{p}(w)}.$$

4.2 Chung’s Dyadic Argument

Daewon Chung proved the following sharp bound on L ^p(w) for the commutator of the Hilbert transform and a BMO function:

Theorem 11 (Chung [8]). 

$$\|[H,b]f\|_{{L}^{p}(w)} \leq C_{p}\|b\|_{BMO}[w]_{A_{p}}^{2\max \{1, \frac{1} {p-1} \}}\|f\|_{{L}^{p }(w)}.$$

The result is sharp in L ²(w), meaning that in that case the quadratic power cannot be improved. Similar examples show extrapolated bounds are sharp in L ^p(w); see [8].

Chung’s proof is based on a decomposition of the product bf using the dyadic paraproduct π _b f, its adjoint π _b ^∗ f, and a related operator π _f b; this line of argument was suggested in [69]. He works with Petermichl’s dyadic shift operator S instead of H, and Bellman functions. This argument works for dyadic shift operators (hence for Riesz and Beurling transforms, and it is sharp for them as well). We will sketch Chung’s proof after some preliminaries on paraproducts.

4.2.1 Dyadic Paraproduct

Recall that dyadic paraproduct associated to the function b ∈ BMO is defined by

$$\pi _{b}f(x) = \sum \nolimits _{I\in \mathcal{D}}m_{I}f\,\langle b,h_{I}\rangle h_{I}(x),\quad \quad \mbox{ where}\quad m_{I}f = \frac{1} {\vert I\vert }\int \nolimits \nolimits _{I}f(x)\,\mathrm{d}x.$$

The dyadic paraproduct is bounded on L ^p(ℝ) for 1 < p < ∞ and is of weak type (1, 1) [60]. Paraproducts appeared in the work of Bony [5] on paradifferential equations; they also appeared in the proof of the T(1) theorem [19].

Theorem 12 (Beznosova [4]). 

Let b ∈ BMO, w ∈ A ₂ , then for all f ∈ L ² (w)

$$\|\pi _{b}f\|_{{L}^{2}(w)} +\| \pi _{b}^{{_\ast}}f\|_{{ L}^{2}(w)} \leq C\|b\|_{BMO}[w]_{A_{2}}\|f\|_{{L}^{2}(w)}.$$

Ordinary multiplication M _b f = bf is not bounded on L ^p(ℝ) unless b ∈ L ^∞(ℝ). The space BMO includes unbounded functions. Hence the boundedness properties of the paraproduct are better than those of the ordinary product. It is well known that the following decomposition holds:

$$bf = \pi _{b}f + \pi _{b}^{{_\ast}}f + \pi _{ f}b.$$

(10)

The first two terms are not only bounded on L ^p(ℝ) but are also bounded on L ^p(w) (follows by extrapolation from boundedness on L ²(w)) when b ∈ BMO and w ∈ A _p ; the enemy in this decomposition is the third term π _f b. It is because of this relation with the ordinary product that the name “paraproduct” was coined.

Proof (Sketch of Chung’s proof of Theorem 11). 

Apply the decomposition (10) to the commutator with Petermichl’s shift operator S:

$$[S,b]f = [S,\pi _{b}]f + [S,\pi _{b}^{{_\ast}}]f + [{S}(\pi _{ f}b) - \pi _{Sf}(b)].$$

(11)

The first two terms give quadratic bounds from the linear bounds for S, π _b , and π _b ^∗. Boundedness of the commutator on L ^p(w) will be recovered from the uniform boundedness of the third commutator. Surprisingly (at the time this was discovered) the third term is better; it obeys a linear bound, and so do halves of the other two commutators:

$$\begin{array}{rcl} \|S(\pi _{f}b) - \pi _{Sf}(b)\|_{{L}^{2}(w)} +\| S\pi _{b}f\|_{{L}^{2}(w)} +\| \pi _{b}^{{_\ast}}S\|_{{ L}^{2}(w)}& & \\ \leq C\|b\|_{BMO}[w]_{A_{2}}\|f\|_{{L}^{2}(w)}.& & \\ \end{array}$$

Providing uniform quadratic bounds for the commutator [S, b], hence

$$\|[H,b]\|_{{L}^{2}(w)} \leq C\|b\|_{BMO}[w]_{A_{2}}^{2}\|f\|_{{ L}^{2}(w)}.$$

Chung proved his linear estimates using Bellman functions. A posteriori one realizes that the operators [S(π_{. } b) − π _S{. }(b)], Sπ _b , and π _b ^∗ S are generalized Haar shift operators; hence, the linear bound is a particular case of the results in [33, 34, 37, 38]. For the commutator the bad terms are the nonlocal operators π _b S and Sπ _b ^∗.

4.2.2 Commutators Versus Paraproducts

Beznosova proved the linear bound for the dyadic paraproduct, and then sharp extrapolation shows that the following bounds hold in L ^p(w) for w ∈ A _p :

$$\|\pi _{b}f\|_{{L}^{p}(w)} \leq C_{p}\|b\|_{BMO}[w]_{A_{p}}^{\max \{1, \frac{1} {p-1} \}}\|f\|_{{L}^{p }(w)}.$$

It was not known whether these were sharp for some or all 1 < p < ∞.

Theorem 13.

The above estimate is optimal in the power $\max \{1, \frac{1} {p-1}\}$

Proof.

Suppose there is an α < 1 and a p > 1 such that for all b ∈ BMO weights w ∈ A _p and for all f ∈ L ^p(w) the following estimate holds:

$$\|\pi _{b}f\|_{{L}^{p}(w)} \leq C_{p}\|b\|_{BMO}[w]_{A_{p}}^{\alpha \max \{1, \frac{1} {p-1} \}}\|f\|_{{L}^{p }(w)}.$$

One can verify that the same estimate holds for π _b ^∗. Then we will obtain the following bound for the commutator of the Hilbert transform and b:

$$\|[b,H]f\|_{{L}^{p}(w)} \leq C_{p}\|b\|_{BMO}[w]_{A_{p}}^{(1+\alpha )\max \{1, \frac{1} {p-1} \}}\|f\|_{{L}^{p }(w)}.$$

And this is a contradiction because the power $2\max \{1, \frac{1} {p-1}\}$ is optimal for [b, H].

4.3 Transference Theorem in L ^r(w) for Commutators

The following transference theorem holds:

Theorem 14 (Chung et al. [10]). 

If a linear operator T obeys linear bounds in L ² (w) for all w ∈ A ₂

$$\|Tf\|_{{L}^{2}(w)} \leq C[w]_{A_{2}}\|f\|_{{L}^{2}(w)},$$

then its commutator with b ∈ BMO obeys quadratic bounds for all w ∈ A ₂ ,

$$\|[T,b]f\|_{{L}^{2}(w)} \leq C[w]_{A_{2}}^{2}\|b\|_{ BMO}\|f\|_{{L}^{2}(w)}.$$

(12)

Proof follows the beautiful Coifman–Rochberg–Weiss classical argument using the Cauchy integral formula and immediately generalizes to higher-order commutators $T_{b}^{k} := [b,T_{b}^{k-1}]$. Under the same assumptions of Theorem 14,

$$\|T_{b}^{k}f\|_{{ L}^{2}(w)} \leq Ck![w]_{A_{2}}^{k+1}\|b\|_{ BMO}^{k}\|f\|_{{ L}^{2}(w)}.$$

(13)

Extrapolation gives bounds on L ^p(w); they are sharp for all 1 < p < ∞, all k ≥ 1, and all dimensions, as examples involving the Riesz transforms show [10].

As a corollary of these and Hytönen’s theorem we conclude that for each Calderón–Zygmund singular integral operators T there is a constant C > 0 such that for all BMO functions b and for all A ₂ weights w, (12) holds. Sharp extrapolation then shows that for all Calderón–Zygmund singular operators T,

$$\|[T,b]f\|_{{L}^{p}(w)} \leq C_{p}[w]_{A_{p}}^{2\max \{1, \frac{1} {p-1} \}}\|b\|_{BMO}\|f\|_{{L}^{p }(w)}.$$

(14)

A refinement of the argument in [10] shows that

Theorem 15.

If a linear operator T obeys a power bound in L ^r (w) for all w ∈ A _r ,

$$\|Tf\|_{{L}^{r}(w)} \leq C[w]_{A_{r}}^{\alpha }\|f\|_{{ L}^{r}(w)},$$

then its commutator with b ∈ BMO obeys the following bounds for all w ∈ A _r :

$$\|[T,b]f\|_{{L}^{r}(w)} \leq C_{n,r}[w]_{A_{r}}^{\alpha +\max \{1, \frac{1} {r-1} \}}\|b\|_{BMO}\|f\|_{{L}^{r }(w)}.$$

Notice that in the case of T a Calderón–Zygmund singular integral operator, we recover the L ^p(w) norm obtained from sharp extrapolation in [10], because the initial estimate on L ^p(w) corresponds to $\alpha = \max \{1, \frac{1} {p-1}\}$; hence in this case Theorem 15 gives (14). Because this bound is known to be sharp for the Hilbert and Riesz transforms, we deduce that the power obtained in Theorem 15 cannot be improved.

We present the proof of this result in the Appendix.

Generalizations and variations of these results have already appeared. Cruz-Uribe and Moen [16] prove corresponding estimates for commutators with fractional integrals (they also use the classical Coifman–Rochberg–Weiss argument). They use the machinery developed by Cruz-Uribe, Martell, and Pérez [18] and Lerner’s local mean oscillation [48] to obtain two-weight estimates for the commutators with Calderón–Zygmund singular integral operators and fractional integrals. Carmen Ortiz-Caraballo [59] shows the following quadratic estimate for b ∈ BMO, and any Calderón–Zygmund operator T, on L ^p(w) where the weight is in A ₁ ⊂ ∩  _p > 1 A _p , the following estimate was obtained before Hytönen proved the A ₂ conjecture, so it was the first nontrivial bound valid for all commutators of Calderón–Zygmund singular integral operators:

$$\|[T,b]\|_{{L}^{p}(w)} \leq C_{n}\|b\|_{BMO}\,p\,{(p^{\prime})}^{2}[w]_{ A_{1}}^{2}.$$

There are now mixed A _p -A _∞ estimates that hold for all Calderón–Zygmund singular integral operators [34–36, 49]; inequality (15) is an example of such an estimate when p = 2. These estimates can be transferred to the commutators [36].

Theorem 16 (Hytönen and Pérez [36]). 

If a linear operator T obeys the following bounds in L ² (w) for all w ∈ A ₂ :

$$\|Tf\|_{{L}^{2}(w)} \leq C[w]_{A_{2}}^{ \frac{1} {2} }{([w]_{A_{ \infty }} + [{w}^{-1}]_{ A_{\infty }})}^{\frac{1} {2} }\|f\|_{{L}^{2}(w)},$$

(15)

then its commutator of order k ≥ 1 with b ∈ BMO obeys the following bounds for all w ∈ A ₂ :

$$\|T_{b}^{k}f\|_{{ L}^{2}(w)} \leq C[w]_{A_{2}}^{ \frac{1} {2} }{([w]_{A_{ \infty }} + [{w}^{-1}]_{ A_{\infty }})}^{k+\frac{1} {2} }\|b\|_{BMO}\|f\|_{{L}^{2}(w)}.$$

The two-weight problem is still an outstanding open problem for most operators. Necessary and sufficient conditions are known for the maximal function via Sawyer-type conditions [51, 72], for the martingale transform and other dyadic operators [55] (these are of Sawyer type as well with respect to the dyadic operators), and for the dyadic square function (Beznosova, O., personal communication); compare to [81]. As for sufficient conditions many different sets are known, including several sets for the Hilbert transform [15, 40, 45, 57]. In all these cases the conditions are somehow inherent to the operator studied: “Sawyer-type conditions.” An exception being sufficient conditions in terms of “bump conditions” in Orlicz spaces [16, 18]. Lacking are theorems of the nature; operator A is bounded from L ^p(u) into L ^p(v) if and only if operator B is bounded from L ^p(u) into L ^p(v).

5 Appendix

Proof (Sketch the proof of Theorem 15). 

We “conjugate” the operator as follows: if z is any complex number we define

$$T_{z}(f) ={ \mathrm{e}}^{zb}T({\mathrm{e}}^{-zb}f).$$

Then, a computation gives (for instance for “nice” functions)

$$[b,T](f) = \frac{\mathrm{d}} {\mathrm{d}z}T_{z}(f)\vert _{z=0} = \frac{1} {2\pi i}\int \nolimits \nolimits _{\vert z\vert =\epsilon }\frac{T_{z}(f)} {{z}^{2}} \,\mathrm{d}z\,,\quad \quad \epsilon > 0$$

by the Cauchy integral theorem; see [1, 12].

Now, by Minkowski’s inequality,

$$\|[b,T](f)\|_{{L}^{r}(w)} \leq \frac{1} {2\pi \,{\epsilon }^{2}}\, \int \nolimits \nolimits _{\vert z\vert =\epsilon }\|T_{z}(f)\|_{{L}^{r}(w)}\vert \mathrm{d}z\vert \,,\quad \quad \epsilon > 0.$$

The key point is to find the appropriate radius ε. First we look at the inner norm,

$$\|T_{z}(f)\|_{{L}^{r}(w)} =\| T({\mathrm{e}}^{-zb}f)\|_{{ L}^{r}(w{e}^{rRez\,b})}\,,$$

and try to find appropriate bounds on z. To do this we use the main hypothesis, namely that T is bounded on L ^r(v) if v ∈ A _r with

$$\|T\|_{{L}^{r}(v)} \leq C[v]_{A_{r}}^{\alpha }.$$

Let v = we ^{rRez  b}. We must check that if w ∈ A _r then v ∈ A _r for | z | sufficiently small:

$$[v]_{A_{r}} =\sup _{Q}\left ( \frac{1} {\vert Q\vert }\int \nolimits \nolimits _{Q}w{e}^{rRez\,b(x)}\,\mathrm{d}x\right ){\left ( \frac{1} {\vert Q\vert }\int \nolimits \nolimits _{Q}{w}^{- \frac{1} {r-1} }(x){\mathrm{e}}^{- \frac{r} {r-1} Rez\,b(x)}\,\mathrm{d}x\right )}^{r-1}.$$

Now, since w ∈ A _r , then w ∈ RH _q for some q > 1 [11]. Recall that w ∈ RH _q if and only if there is a constant C > 0 such that for all cubes Q,

$${\left ( \frac{1} {\vert Q\vert }\int \nolimits \nolimits _{Q}{w}^{q}\mathrm{d}x\right )}^{\frac{1} {q} } \leq \frac{C} {\vert Q\vert }\int \nolimits \nolimits _{Q}w\,.$$

The following precise reverse Hölder condition for A _r weights holds [64]:

Lemma 2.

If w ∈ A _r and $\,q = 1 + \frac{1} {{2}^{2r+n+1}[w]_{A_{r}}}\;(< 2)$ , then w ∈ RH _q and

$${ \left ( \frac{1} {\vert Q\vert }\int \nolimits \nolimits _{Q}{w}^{q}\mathrm{d}x\right )}^{\frac{1} {q} } \leq \frac{2} {\vert Q\vert }\int \nolimits \nolimits _{Q}w\,.$$

(16)

It is well known that if w ∈ A _r then $\sigma := {w}^{- \frac{1} {r-1} } \in A_{r^\prime}$ with $r^{\prime} = \frac{r} {r-1}$ the dual exponent of r, and $[w]_{A_{r}}^{r^{\prime}} = [\sigma ]_{A_{r^{\prime}}}^{r}$. Applying Lemma 2 to σ and r′ we conclude then that if $\;\;s = 1 + \frac{1} {{2}^{2r^{\prime}+n+1}[\sigma ]_{A_{r^{\prime}}}} < 2\;\;$ then σ ∈ RH _s and

$${ \left ( \frac{1} {\vert Q\vert }\int \nolimits \nolimits _{Q}{\sigma }^{s}\mathrm{d}x\right )}^{\frac{1} {s} } \leq \frac{2} {\vert Q\vert }\int \nolimits \nolimits _{Q}\sigma \,.$$

(17)

Let t = min{q, s}, where q and s are as above, then t ≤ q and t ≤ s. Holder’s inequality with $p = q/t > 1$ and $p = s/t > 1$, respectively, implies that

$${\left ( \frac{1} {\vert Q\vert }\int \nolimits \nolimits _{Q}{w}^{t}\mathrm{d}x\right )}^{\frac{1} {t} } \leq \frac{2} {\vert Q\vert }\int \nolimits \nolimits _{Q}w,\quad \quad \quad {\left ( \frac{1} {\vert Q\vert }\int \nolimits \nolimits _{Q}{\sigma }^{t}\mathrm{d}x\right )}^{\frac{1} {t} } \leq \frac{2} {\vert Q\vert }\int \nolimits \nolimits _{Q}\sigma.$$

Using these and Holder’s inequality twice with p = t, we have for an arbitrary Q

$$\left ( \frac{1} {\vert Q\vert }\int \nolimits \nolimits _{Q}w(x){\mathrm{e}}^{rRez\,b(x)}\,\mathrm{d}x\right ){\left ( \frac{1} {\vert Q\vert }\int \nolimits \nolimits _{Q}\sigma (x){\mathrm{e}}^{-r^{\prime}Rez\,b(x)}\,\mathrm{d}x\right )}^{r-1} \leq 4\,[w]_{ A_{r}}\,[{\mathrm{e}}^{t^{\prime}r\,Rez\,b}]_{ A_{r}}^{\frac{1} {t^{\prime}} }.$$

Now, since b ∈ BMO, it is well known that e^ηb ∈ A _r for η small enough [21, 27]. We need a quantitative version of this result.

Lemma 3.

Given b ∈ BMO then there are 0 < α _n < 1 and β _n > 1 such that if $\eta \leq \min \{ 1,r - 1\} \frac{\alpha _{n}} {\|b\|_{BMO}}$ , then $[{\mathrm{e}}^{\eta b}]_{A_{r}} \leq \beta _{n}^{r}$

This follows from a similar computation to the one done for r = 2 in [10]. In our case, we need to ensure that $\;\vert t^{\prime}r\,Rez\vert \leq \min \{ 1,r - 1\} \frac{\alpha _{n}} {\|b\|_{BMO}}$ to deduce that $[{\mathrm{e}}^{rt^{\prime}Rez\,b}]_{A_{r}} \leq \beta _{n}^{r}$. That is, we are constrained to consider complex numbers z such that $\vert Rez\vert \leq \min \{ \frac{1} {r}, \frac{r-1} {r} \} \frac{\alpha _{n}} {t^{\prime}\|b\|_{BMO}}$.

Recall that $t =\min \{ 1 + \frac{1} {{2}^{2r+n+1}[w]_{A_{r}}},1 + \frac{1} {{2}^{2r^{\prime}+n+1}[w]_{A_{r}}^{ \frac{1} {r-1} }} \}$; a calculation now shows that

$$t^{\prime} = \left \{\begin{array}{lc} 1 + {2}^{2r+n+1}[w]_{A_{r}} & p \geq 2 \\ 1 + {2}^{2r^{\prime}+n+1}[w]_{A_{r}}^{ \frac{1} {r-1} } & p < 2 \end{array} \right..$$

Furthermore $t^{\prime} \sim [w]_{A_{r}}^{\max \{1, \frac{1} {r-1} \}}$ with comparability constant depending exponentially in the dimension n and max{r, r′}.

For | z | ≤ ε, with ${\epsilon }^{-1} \sim \|b\|_{BMO}[w]_{A_{r}}^{\max \{1, \frac{1} {r-1} \}}$, and since 1 < t < 2, thus t′ > 2, we have that

$$[v]_{A_{r}} = [w{e}^{rRez\,b}]_{ A_{r}} \leq 4\,[w]_{A_{r}}\,\beta _{n}^{\frac{r} {t^{\prime}} } \leq 4\,[w]_{A_{ r}}\,\beta _{n}^{r/2}.$$

Observe that $\|{\mathrm{e}}^{-zb}f\|_{{L}^{r}(v)} =\|{ \mathrm{e}}^{-zb}f\|_{{L}^{r}(w{e}^{rRezb})} =\| f\|_{{L}^{r}(w)}$, and if $\vert z\vert \leq \frac{\alpha _{n}} {rt^{\prime}\|b\|_{BMO}},$

$$\|T_{z}(f)\|_{{L}^{r}(w)} =\| T({\mathrm{e}}^{-zb}f)\|_{{ L}^{r}(v)} \leq [v]_{A_{r}}^{\alpha }\|f\|_{{ L}^{r}(w)} \leq 4[w]_{A_{r}}^{\alpha }\,\beta _{ n}^{r/2}\,\|f\|_{{ L}^{r}(w)}.$$

Choose the radius $\epsilon = \frac{\alpha _{n}} {rt^{\prime}\|b\|_{BMO}}$, and we can continue estimating the norm of the commutator

$$\|[b,T](f)\|_{{L}^{r}(w)} \leq \frac{1} {2\pi \,{\epsilon }^{2}}\, \int \nolimits \nolimits _{\vert z\vert =\epsilon }4[w]_{A_{r}}^{\alpha }\,\beta _{ n}^{r/2}\,\|f\|_{{ L}^{r}(w)}\vert \mathrm{d}z\vert =\frac{1} {\epsilon }\,4[w]_{A_{r}}^{\alpha }\,\beta _{ n}^{r/2}\,\|f\|_{{ L}^{r}(w)}.$$

Finally, observe that ε^− 1 is essentially ${[w]_{A_{r}}}^{\max \{1, \frac{1} {r-1} \}}\|b\|_{BMO}$, so we conclude that

$$\|[b,T](f)\|_{{L}^{r}(w)} \leq C_{n,r}\,[w]_{A_{r}}^{\alpha +\max \{1, \frac{1} {r-1} \}}\,\|b\|_{BMO}.$$

This finishes the proof of the theorem.