Optimal Combination of Satellite and Terrestrial Gravity Data for Regional Geoid Determination Using Stokes-Helmert’s Method, the Auvergne Test Case

Abstract

The precise regional geoid modelling requires combination of terrestrial gravity data with satellite-only Earth Gravitational Models (EGMs). In determining the geoid using the Stokes-Helmert approach, the relative contribution of terrestrial and satellite data to the computed geoid can be specified by the Stokes integration cap size defined by the spherical distance ψ ₀ and the maximum degree l ₀ of the EGM-based reference spheroid. Larger values of l ₀ decrease the role of terrestrial gravity data and increase the contribution of satellite data and vice versa for larger values of ψ ₀. The determination of the optimal combination of the parameters l ₀ and ψ ₀ is numerically investigated in this paper. A numerical procedure is proposed to find the best geoid solution by comparing derived gravimetric geoidal heights with those at GNSS/levelling points. The proposed method is tested over the Auvergne geoid computation area. The results show that despite the availability of recent satellite-only EGMs with the maximum degree/order 300, the combination of l ₀ = 160 and ψ ₀ =  45 arc-min yields the best fitting geoid in terms of the standard deviation and the range of the differences between the estimated gravimetric and GNSS/levelling geoidal heights. Depending on the accuracy of available ground gravity data and reference geoidal heights at GNSS/levelling points, the optimal combination of these two parameters may be different in other regions.

1 Introduction

Stokes’s boundary-value problem requires gravity values to be known on the geoid. Moreover, gravity anomalies used as input data must be solid (Vaníček et al. 2004) in order to be continuable from ground down to the geoid. Helmert’s gravity anomalies are solid above the geoid; thus, they can be downward continued. To derive Helmert’s gravity anomalies on the Earth’s surface, the direct topographical effect (DTE) as well as the direct atmospheric effect on gravity must be applied to free-air (FA) gravity anomalies. The latter effect is small and well known and will not be discussed. This gravity reduction, we call it “Helmertization” (see Fig. 1), is the first step in the geoid determination using Stokes-Helmert’s method.

Fig. 1

Three main computational steps of Stokes-Helmert’s technique

The geoidal heights in Helmert’s space (N ^h) can be evaluated by applying the Stokes integral to Helmert’s gravity anomalies (∆g ^h) on the geoid which should be available globally (Stokes 1849). Vaníček and Kleusberg (1987) introduced the idea of splitting the geoidal heights as well as Helmert’s gravity anomalies to reference and residual parts:

$$\begin{aligned} {N}^h\left(\Omega \right)&={N}_{\it ref}^h\left(\Omega \right)+{N}_{\it res}^h\left(\Omega \right),\\{\Delta g}^h\left(\Omega \right)&=\Delta {g}_{\it ref}^h\left(\Omega \right)+\Delta {g}_{\it res}^h\left(\Omega \right)\end{aligned} $$

(1)

where $\Delta {g}_{\it res}^h$ is the residual Helmert gravity anomaly and ${N}_{\it res}^h$ is the residual geoidal height in Helmert’s space. ${\Delta g}_{\it ref}^h\ \mathrm{and}\ {N}_{\it ref}^h$ represent the reference Helmert anomaly and the reference spheroid, respectively; they both can be synthesized from helmertized EGM as (Najafi-Alamadari 1996):

$$ {\displaystyle \begin{array}{l}{T}_{\it ref}^h\left(R,\varOmega \right)=\frac{{\it GM}}{r}\sum \limits_{l=2}^{l_0}{\left(\frac{R}{r}\right)}^l\;\sum \limits_{m=-1}^l{T}_{l,m}^h{Y}_{l,m}\;\left(\lambda, \phi \right)\\ {}{T}_{l,m}^h=\left\{\begin{array}{ll}\hfill {C}_{\it lm}^h\hfill & \hfill m\ge 0\hfill \\ {}\hfill {S}_{\it lm}^h\hfill & \hfill m<0\hfill \end{array}\right.\\[10pt] {}{Y}_{l,m}=\left\{\begin{array}{ll} {P}_{\it lm}\;\left(\cos \phi \right)\;\cos m\lambda \hfill & \hfill m\ge 0\hfill \\ {}\hfill {P}_{\it lm}\;\left(\cos \phi \right)\;\left.\sin \right|\left.m\right|\lambda \hfill & \hfill m<0\hfill \end{array}\right.\end{array}} $$

(2)

where R is the mean Earth’s radius, r is the radius for which helmertized spherical harmonic coefficients (${C}_{\it lm}^h,{S}_{\it lm}^h$) are evaluated; GM is the product of the Newtonian gravitational constant G and the Earth’s mass M. The symbol Ω = (ϕ, λ) represents the geocentric direction of the computation point and λ and ϕ are the geocentric spherical coordinates. The P _lm is the fully normalized associated Legendre function of the degree l and order m. The parameter l ₀ is the maximum degree of the spherical harmonic expansion that defines the maximum contribution of satellite-only EGMs in a spectral way to the Helmert disturbing potential ${T}_{\it ref}^h$. This potential is defined as follows:

$$ \begin{aligned} {T}_{\it ref}^h\left(R,\Omega \right)&={W}_{\it ref}^h\left(R,\Omega \right)-{U}_0\left(\phi \right),\\{W}_{\it ref}^h\left(r,\Omega \right)&={W}_{\it ref}\left(r,\Omega \right)-\delta {V}_{\it ref}^t\left(r,\Omega \right)\end{aligned} $$

(3)

where U ₀ is the latitude-dependent normal gravity potential and W _ref is the actual gravity potential. $\delta {V}_{\it ref}^t\left(r,\varOmega \right)$ is the reference residual gravitational potential of the topographic masses (Novák 2000). By using Eq. (4) the Helmert reference gravity anomaly ${\varDelta g}_{\it ref}^h$ and the reference spheroid ${N}_{\it ref}^h\left(\varOmega \right)$ can be computed using the fundamental equation of physical geodesy and spherical Bruns’s formula, respectively (Heiskanen and Moritz 1967, Eqs. 2-148 and 2-144).

To evaluate the residual geoidal heights in Helmert’s space, i.e., ${N}_{\it res}^h$ in Eq. (3), the Stokes integration is employed. Its integration domain Ω₀ can be split into the near zone ${\Omega}_{\psi_0}$ and the far zone ${\Omega}_0-{\Omega}_{\psi_0}$ (Vaníček and Kleusberg 1987). The size of the near zone dictates the contribution of terrestrial gravity data which reads:

$$ \begin{aligned} {N}_{l>{l}_0,{\varOmega}_{\psi_0}^{\prime}}^h\left(\varOmega \right)=&\frac{R}{4\pi {\gamma}_0\left(\phi \right)}\underset{\varOmega^{\prime}\in {\varOmega}_{\psi_0}}{\iint }{\varDelta g}_{\it res}^h\left(R,{\varOmega}^{\prime}\right)\\ &\times {S}_{n>{l}_0}\left({\psi}_0,\psi \left(\varOmega, {\varOmega}^{\prime}\right)\right)\ d{\varOmega}^{\prime } \end{aligned} $$

(4)

where ${N}_{l>{l}_0,{\Omega}_{\psi_0}^{\prime}}^h$ is the residual geoid height in Helmert’s space computed from the near-zone gravity data. The subscript $l>{l}_0,{\Omega}_{\psi_0}^{\prime }$ indicates that the integration is performed over residual Helmert’s gravity anomalies with frequencies higher than l ₀ and limited to the cap size ${\Omega}_{\psi_0}^{\prime }$. The far-zone contribution (${N}_{l>{l}_0,{\Omega}_0^{\prime }-{\Omega}_{\psi_0}^{\prime}}^h$) reads:

$$ \begin{aligned} {N}_{l>{l}_0,{\varOmega}_0^{\prime }-{\varOmega}_{\psi_0}^{\prime}}^h\left(\varOmega \right)=&\frac{R}{4\pi {\gamma}_0\left(\phi \right)}\underset{\varOmega^{\prime}\in {\varOmega}_0^{\prime }-{\varOmega}_{\psi_0}^{\prime }}{\iint }{\varDelta g}_{\it res}^h\left(R,{\varOmega}^{\prime}\right)\\ &\times {S}_{n>{l}_0}\left({\psi}_0,\psi \left(\varOmega, {\varOmega}^{\prime}\right)\right)\ d{\varOmega}^{\prime} \end{aligned} $$

(5)

where Ω ₀ stands for the geocentric solid angle $\big[\phi \,{\in}\, <-\frac{\pi }{2},\linebreak \frac{\pi }{2}>,\kern0.5em \lambda \,{\in}\, <0,2\pi \,{>}\,\big]$, Ω^′ represents the pair of the integration point coordinates and ψ is the spherical distance between the integration and computation points. The modified version of the spheroidal Stokes function (${S}_{n>{l}_0}$) is used here; the modification minimizes the far-zone contribution in the least square sense. For more details, please refer to (Vaníček and Kleusberg 1987).

The contribution of satellite-only EGMs (in the spectral sense) is given by the maximum degree of the spherical harmonic expansion l ₀ in Eq. (4) while terrestrial gravity data increasingly contributes to the geoidal height with the increasing size of the spherical integration cap ψ ₀ in Eqs. (1) and (2).

The primary indirect topographical effect (PITE) is then added to the co-geoidal heights computed by Eq. (3) to convert them back to the real space; we call this step as “de-helmertization”, see Fig. 1.

Featherstone and Olliver (1994) analyzed the coefficients of the geopotential model along with the terrestrial gravity data to find the optimal Stokes’s integration cap size and the degree of reference field to compute the geoid in the British Isles. In the end they estimated as the maximum degree 257 and the radius of 1 arc-deg 57 arc-min. They did not use any higher degrees than 257 for computing the reference field because according to their analysis the standard errors of the gravity anomalies computed by then-available geopotential models started to exceed the coefficients themselves.

Vella and Featherstone (1999) set the degree of reference field to 360 and changed the Stokes integration cap size to find the optimal contribution of terrestrial gravity data to compute the geoid model of Tasmania. They compared the resulting geoid models with the geoid height from GPS/leveling points in their study area and found out that the cap radius of 18 arc-min gives the smallest STD.

These papers date back to the time when global fields did not have any gravity-dedicated satellite mission data included; thus, they were not as accurate in the low- and mid-wavelengths as they are now because of GRACE and GOCE satellite gravity data (Reigber et al. 2005; Pail et al. 2011).

The methodology proposed in the present study investigates all possible options to find the optimal degree of the reference field and the radius of the integration cap. The optimality is defined according to two criteria: minimum values of STD and range of the differences between the computed geoid model and geoidal heights at GNSS/levelling points described in Sect. 2. Numerical results of the proposed method summarized in Sects. 3 and 4 conclude the paper.

2 Proposed Method

Theoretically if EGMs represent the Earth’s gravity field accurately (for l ₀ going to infinity), the near-zone Stokes integration is not needed, i.e., the radius ψ ₀ can be put equal to 0. If, on the other hand, EGMs were not good, we would have to disregard them and use terrestrial gravity data from the whole world, i.e., ψ ₀ = 180°. As both EGMs and terrestrial gravity data are burdened with position-dependent noise, the optimal combination of l ₀ and ψ ₀ varies from place to place. The pair l ₀ = 90 and ψ ₀ = 2^° has commonly been used in our previous geoid determinations (Ellmann and Vaníček 2007). To find the optimal pair for currently available EGMs in every region, the following algorithm is suggested:

• 1. Vary the degree of the reference field and spheroid and correspondingly the modification degree of Stokes’s kernel function: l ₀  = 90 : 300. Here we shall go only up to l ₀ = 300 as this degree represents the maximum degree of current satellite-only EGMs.

• 2. Remove the helmertized reference field of the degree l ₀ from Helmert’s gravity anomaly on the geoid.

• 3. Vary the near-zone contribution by changing the integration radius ψ ₀ = 30^′ : 2^°.

• 4. Compute the residual co-geoid by Stokes’s integration as the sum of contributions from both near and far zones.

• 5. Add the reference spheroid of the degree l ₀ to the residual co-geoid.

• 6. Compute the geoid in the real space by adding PITE to the co-geoid.

• 7. Evaluate geoidal heights at available GNSS/levelling points in the computation area.

• 8. Find the optimal geoid for the chosen l ₀ in Step 1, the optimal choice can be based on the minimum norm of differences between the computed geoid and GNSS/levelling geoidal heights. The two most reasonable choices among all norms are ‖‖₂ (L ₂ norm), called also the standard deviation (STD) of the differences, and ‖‖_∞(L infinity norm) equal to the maximum absolute value of the differences. The latter is loosely connected to the range of the discrepancies.

• 9. Repeat Steps 1 to 8 for all degrees up to l ₀ < 300.

• 10. Find the “global” optimal pair among the “local” ones which is then the optimal pair (l ₀, ψ ₀) for the computation area.

Depending on the step between degree/order of reference field and integration cap size, the computation of the proposed algorithm can be time demanding. The diagram in Fig. 2 describes how this algorithm works graphically:

Fig. 2

Proposed method to estimate the optimal contributions of near-zone (NZ) and far-zone (FZ) in Stokes’s integration

3 Numerical Results

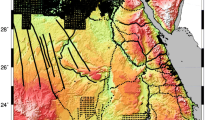
The proposed method was tested in Auvergne, the central area of France, which is limited by (−1^° < λ < 7^°, 43^°< ϕ < 49^°) (Duquenne 2006). The topography of this area is shown in Fig. 3a. This area contains about 240,000 scattered free-air gravity points that have been extracted from the database of the Bureau Gravimetrique International (Fig. 3b). Seventy-five GNSS/levelling points are also available within the central square of the area of interest for the geoid computation (1.5^° < λ < 4.5^°, 45^° < ϕ < 47^°). The data coverage area is larger than the geoid computation area to be able to test the different integration cap radii. Mean gravity anomalies of 1′ resolution were computed from scattered observed gravity using complete spherical Bouguer anomalies, also known as NT anomalies, (they are known to be the smoothest) by means of inverse cubic distance interpolation. It was shown by Kassim (1980) that inverse cubic distance interpolation is superior for predicting gravity anomalies to other tested interpolation techniques. Mean Helmert’s gravity anomalies on the Earth’s surface were obtained by adding the DTE. The secondary indirect topographical effect (SITE), see Vaníček et al. (1999), was added to the predicted anomaly values to prepare them for the downward continuation.

Fig. 3

Topography of the study area (a); distribution of terrestrial gravity data (b)

For computing the DTE at each gravity point, topographical heights over the entire Earth are needed. The integration is done separately in the inner, near and far zones. SITE was also computed for inner, near and far zones separately, but this effect for Helmert’s space is much smaller than DTE. Values of DTE and SITE over the Auvergne area are shown in Fig. 4.

Fig. 4

Direct topographical effect (a); secondary indirect topographical effect on gravity anomalies (b)

Fig. 5

Free-air gravity anomaly with red-cross signs showing GNSS/levelling points (a) and Helmert’s gravity anomalies (b)

Applying DTE and SITE converts the free-air gravity anomalies to Helmert’s gravity anomalies. Figure 5 shows the free-air and mean Helmert’s gravity anomalies in the Auvergne area.

Mean Helmert’s anomalies on the Earth’s surface were then downward continued to mean Helmert’s anomalies on the geoid. This was done using the Poisson integral equation solved by the iterative Jacobi process (Kingdon and Vaníček 2010). The downward continuation was done over 1 arc-deg squared cells augmented by a border strip 30 arc-min wide on all sides. Results from the individual cells were then fused together. On average, seven iterations were needed for the downward continuation in the individual squares. For the purpose of the fusion, an assessment of continuity of Helmert’s gravity anomalies along the borders of two adjacent arc-degree cells on the geoid was done by the technique described by Foroughi et al. (2015b). This assessment showed that discontinuities between the downward continued Helmert anomalies are random within the limits of ±3σ (σ is the standard deviation of observed anomalies) which was assumed acceptable.

Fig. 6

Primary indirect topographical effect on geoidal heights in the Auvergne geoid test area

Fig. 7

Variation of STD and range of differences between resulting geoid and GNSS/levelling. (a) Variation of the range, minimum: (l ₀ = 140, ψ ₀ = 0.75^°), (b) Variation of STD, minimum: (l ₀ = 160, ψ ₀ = 0.75^°)

The next step is the evaluation of Stokes’s integral which starts with removing long wavelengths from gravity anomalies using the reference field. In our case, the satellite-only DIR_R5 EGM (GOCE, GRACE and Lageos) was used for computation of the reference gravity field and the spheroid (Bruinsma et al. 2013). PITE was then computed for the locations of the 1 arc-min grid on the geoid, again separately for the inner, near and far zones (Fig. 6). This resulted in the geoid (in real space) for the pre-selected (l₀, ψ₀). This geoid was then compared against the results from GNSS/levelling.

To find the optimal combination of the degree of the reference field l ₀ and the radius of Stokes’s integration ψ ₀ the above proposed algorithm was repeatedly used. The first computation started with l ₀ = 90 and 0^° < ψ ₀ < 2^°; the maximum integration cap size was chosen 2 arc-deg as commonly used by us with Stokes-Helmert’s technique. This choice meant that we actually needed an extra 2 arc-deg data coverage in latitude direction and around 3 arc-deg in longitude direction outside the geoid computation area which was not covered by the original data. Foroughi et al. (2015a) solved this problem by padding the original data coverage by 3 arc-deg from each side, by using free-air gravity anomalies synthesized from EGM2008 up to the degree/order 2160. They showed this method was accurate enough for the purpose of covering a smaller gap in data coverage. This approach was used here wherever there were coverage gaps.

The proposed method tests all the possible choices of the parameter pair (l ₀, ψ ₀). The optimal geoid is chosen based on the agreement between the resulting gravimetric geoid and geoidal heights derived from GNSS/levelling. STD and ranges of the differences are chosen as tools for finding the optimal combination. Figure 7 shows 2D plots of the range and STD of the differences as functions of ψ ₀ and l ₀.

Figure 7 shows that for all considered degrees l ₀ = 140 is the highest one should go to keep the range as small as possible. In combination with ψ ₀ = 0.75° it gives the smallest range of the differences, 16.3 cm in fact. We note that taking the larger integration cap does not improve the range, but larger ψ ₀ will not make the range significantly larger either. Looking at STD values, it appears that a similar cut-off value should be used for l ₀, i.e., about 160, while the choice of ψ ₀ seems to be even less critical than for the range minimization criterion. The smallest STD = 3.3 cm is obtained for combination l ₀= 160 and ψ ₀ = 0.75°. Generally, it appears that taking l ₀ larger than 160 and ψ ₀ smaller than 0.75° should be avoided. The plots seem to indicate, however, that the deterioration of accuracy is much faster with the increasing degree of EGM than with the increasing radius of the integration cap.

4 Concluding Remarks

A numerical method was proposed to optimally combine terrestrial and satellite gravity data for computing the regional geoid using Stokes-Helmert’s approach. The optimality of the results was measured by the differences between the derived gravimetric and GNSS/levelling geoidal heights in terms of their range and STD. This method was tested over the area of Auvergne and the optimal geoid was derived when the maximum contribution of the DIR-R5 EGM was set to l ₀ = 160 and the near-zone Stokes integration cap size was set to ψ ₀ = 0.75⁰. The resulting optimal geoid of this study showed the 0.3 cm improvement in terms of STD and 2.4 cm improvement in the range with respect to the geoid computed by the standard choice of l ₀ = 90 and ψ ₀ = 2⁰. Comparing the optimal geoid with the geoid computed using the maximum contribution from EGM, i.e., l ₀ = 300 and ψ ₀ = 0.25⁰, showed the improvement of 4 cm in terms of STD and 19 cm in the range. The methodology proposed in this study would have to be tested in other regions as the present results were obtained in the Auvergne study area and might be different for other regions. The choice of the optimal integration cap size depends on the quality and spatial distribution of terrestrial gravity data. However, the estimated optimal degree of reference field (l0 = 160) could also be valid for other regions as Abdalla et al. (2012) found more or less the same number over the Khartoum state. They investigated the validation of all GOCE/GRACE geopotential models and concluded that the models do not show better results beyond degree 150. Due to inherent errors of satellite-only EGM higher-degree coefficients, they are not recommended to be used when reasonably good terrestrial gravity data are available.