Keywords

1 Introduction

A study group under the umbrella of the IAG (International Association of Geodesy)—ICCT (Inter Commission Committee on Theory) between Commission 2 (Gravity Field) and Commission 3 (Earth Rotation and Geodynamics) titled as Joint Study Group JSG0.3 Comparison of Current Methodologies in Regional Gravity Field Modeling was established in 2011 with duration until 2015. The goal of this study group is to compare different regional modeling methodologies and to finally outline standards and conventions for future regional gravity products. One of the activities so far was to provide synthetic test data sets which are used for inter-comparison of regional gravity modeling methodologies. Among the objectives are the choice of the type of basis function, the point grid, an appropriate methodology to solve the adjustment problem, and the consideration of errors.

Details on the study group as well as the test data can be found online at http://jsg03.dgfi.badw.de. Synthetic gravity observations of different types are provided for two different regions in Europe and in South America. For each region satellite-based, aerial, as well as terrestrial observations are provided, along with noise information for each observations type, and validation data sets in terms of disturbing gravity potential on the topography.

We use the test data sets in Europe for our regional gravity modeling approach in spherical radial basis functions. In Chap. 2 we explain the approach, in Chap. 3 we present our results with the individual data sets, and in Chap. 4 their combination. Finally, in Chap. 5 all modeling results are summarized and discussed. Thereby, with this article, we contribute to the goal of the study group of inter-comparison of different regional gravity modeling approaches by presenting our results with the study group’s test data.

2 Regional Gravity Modeling in Spherical Radial Basis Functions

For regional gravity modeling, we use spherical radial basis functions, as presented in Freeden et al. (1998), Holschneider et al. (2003), or Schmidt et al. (2007) and references therein, amongst many others. We follow the approach given in Bentel et al. (2013). A regional residual gravity signal Δ F is represented in a series expansion in spherical radial basis functions according to

$$\displaystyle\begin{array}{rcl} \varDelta F(\mathbf{x}) =\sum _{ k=1}^{K}d_{ k}B(\mathbf{x},\mathbf{x}_{k}).& &{}\end{array}$$
(1)

Thereby, B(x, x k ) are the radial basis functions, which depend only on the spherical distance between their location point x k and the evaluation point x, and are defined as

$$\displaystyle\begin{array}{rcl} B(\mathbf{x},\mathbf{x}_{k}) =\sum _{ n=0}^{N}\frac{2n + 1} {4\pi R^{2}} \left (\frac{R} {r} \right )^{n+1}B_{ n}P_{n}(\mathbf{x},\mathbf{x}_{k}).& &{}\end{array}$$
(2)

P n are the Legendre polynomials, R is the radius of a reference sphere (e.g. mean Earth radius), and r is the radius of the evaluation point x. The coefficients B n define the type of radial basis function. For the computations here, we use cubic polynomial radial basis functions, motivated by the findings in Bentel et al. (2013). They are defined by

$$\displaystyle\begin{array}{rcl} B_{n} = (1 - \frac{1} {N}\,n)^{2}\,( \frac{2} {N}\,n\, + 1),& &{}\end{array}$$
(3)

and can be found in Freeden et al. (1998). The values for N are adjusted according to the signal which is to be modeled. With x, the different types of observations are directly used at the locations at which they are obtained. The points x k , the locations for the radial basis functions, are chosen on a Reuter grid, see Freeden et al. (1998).

To determine the coefficients d k of the regional signal representation, regularization is needed due to the downward continuation problem of gravity which is involved and due to non-uniqueness of the coefficients to be estimated. We use variance component estimation according to Koch and Kusche (2002) to determine the variance components of the data sets and the prior information. The variance components can further be used to determine relative weighting factors between the different data sets as well as the regularization parameter with respect to the prior information. Prior information in terms of the expectation vector for the coefficients to be estimated is added. We set the vector of prior information equal to zero, because a residual signal is modeled after removing a reference field (EGM 96) up to spherical harmonic degree 60. All results presented here are obtained with sets of physically meaningful coefficients, what means they are correlated to the signal to be modeled as well as small on the margins, which are needed beyond the area of observations in order to avoid boundary effects. They are between 2∘ and 3∘ wide.

All modeling approaches are validated with the given validation data sets. From the regional gravity field representation, the disturbing potential is synthesized at the same points where validation data is available, respectively in the area where observations are available after subtracting a margin width. This is necessary to avoid boundary value effects and the margin widths are given together with the results in Table 1. Then the errors in terms of differences in each point are computed as well as a relative RMS error value in terms of percentage of the error RMS from the signal RMS of the full signal up to degree 2,190.

Table 1 Summary of the modeling results
Full size table

3 Different Examples of Gravity Observations in Europe

We use the test data provided by the ICCT study group ready for download at http://jsg03.dgfi.badw.de with the given realistic level of white noise on the observations. For the test region in Europe, two sets of synthetic observations are provided for each observation type. Satellite-based observations are available from GRACE (Tapley et al. 2004) and GOCE (Drinkwater et al. 2007), two sets of aerial observations are available for two different flight campaigns, and the terrestrial observations are available on a regular grid on the topography with two different grid spacings, one with 30′ and the other with 5′ spacing. From all different types of observations, a reference field (EGM 96) up to spherical harmonic degree 60 is removed, and restored later, when the gravity values for validation purposes are synthesized. With the regional gravity modeling approach, only a residual gravity signal is represented. Three different sets of validation data defined on the topography are provided, one in a larger area and two in a smaller area. We use the one which fits best with the area of observations for the different types of observations.

The modeling results, in terms of RMS error after validation, for all data sets are given in the first part of Table 1.

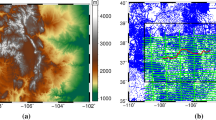
In the following, two examples are presented in more detail. The first example are GRACE-type observations. The observations, potential differences along real GRACE orbits, are given in Fig. 1. Figure 2 shows the modeling results from the GRACE observations in terms of disturbing potential on the topography on the left hand side. The plot in the center shows the validation field, and the plot on the right hand side the difference between the two previous ones, that is, the modeling errors. The second example are aerial observations for one flight campaign. Again, Fig. 3 shows the observations and Fig. 4 the modeling results.

Fig. 1
figure 1

GRACE observations with white noise with a standard deviation of 0.0008 m2/s2, together with validation area (red box)

Full size image
Fig. 2
figure 2

GRACE regional modeling results for a region in Europe; all results given in disturbing potential [m2/s2]; relative error RMS: 2.1%

Full size image
Fig. 3
figure 3

Airborne observations (case I) with white noise with a standard deviation of 1 mGal together with validation area (red box)

Full size image
Fig. 4
figure 4

Regional modeling results for a region in Europe, from aerial observations, case I. All fields are disturbing potential, in [m2/s2]; relative error RMS: 0.40%

Full size image

4 Combination of the Different Data Sets

Investigations in combining heterogenous data sets have already been made, as for example in Panet et al. (2012) with a wavelet approach. We combine different data sets by determining a relative weighting, favourably related to the accuracies of the individual observation sets. For that purpose we use here the method of variance component estimation (VCE) as already mentioned before. To establish our linear model we first transform the observation equation as defined in Eq. (1) into the matrix equation Δ F i +e i  = A i  d where i = 1, …, n means an individual observation set. Then we combine the n single models to the combined model

$$\displaystyle\begin{array}{rcl} & & \left [\begin{array}{*{10}c} \varDelta \mathbf{F}_{1} \\ \varDelta \mathbf{F}_{2}\\ \vdots \\ \varDelta \mathbf{F}_{n}\\ \boldsymbol{\mu } \end{array} \right ] + \left [\begin{array}{*{10}c} \mathbf{e}_{1} \\ \mathbf{e}_{2}\\ \vdots \\ \mathbf{e}_{n} \\ \mathbf{e}_{\boldsymbol{\mu }} \end{array} \right ] = \left [\begin{array}{*{10}c} \mathbf{A}_{1} \\ \mathbf{A}_{2}\\ \vdots \\ \mathbf{A}_{n} \\ \mathbf{I}\end{array} \right ]\mathbf{d}, \\ & & \quad D(\left [\begin{array}{*{10}c} \varDelta \mathbf{F}_{1}\\ \vdots \\ \varDelta \mathbf{F}_{n}\\ \boldsymbol{\mu } \end{array} \right ]) = \left [\begin{array}{*{10}c} \sigma _{1}^{2}\mathbf{I}_{1} & 0 & \cdots & 0 \\ 0 & \ddots & & \vdots \\ \vdots & &\sigma _{n}^{2}\mathbf{I}_{n}& 0 \\ 0 &\cdots & 0 &\sigma _{\boldsymbol{\mu }}^{2}\mathbf{I}_{\boldsymbol{\mu }} \end{array} \right ]\;\quad {}\end{array}$$
(4)

which means a Gauss-Markov model with unknown coefficient vector d and unknown variance components σ i 2 with i = 1, …, n for the n observation sets and \(\sigma _{\boldsymbol{\mu }}^{2}\) for the prior information. In the following we distinguish between two approaches on variance component estimation (according to the Koch and Kusche (2002)):

  1. (a)

    We introduce the assumption \(\sigma _{1}^{2} =\sigma _{ 2}^{2} =\ldots =\sigma _{ n}^{2} =:\sigma _{ 0}^{2}\) for the n variance components σ i 2. Thus, in this approach we determine the estimations of d as well as σ 0 2 and \(\sigma _{\boldsymbol{\mu }}^{2}\). The iteratively determined variance components lead—in the point of convergence—to the solution

    $$\displaystyle\begin{array}{rcl} & \mathbf{\hat{d}} = \left ( \frac{1} {\hat{\sigma }_{0}^{2}}\;\sum _{i=1}^{n}\,\mathbf{A}_{ i}^{T}\mathbf{A}_{ i} + \frac{1} {\hat{\sigma }_{\boldsymbol{\mu }}^{2}}\mathbf{I}_{\boldsymbol{\mu }}\right )^{-1}\;& {}\\ & \quad \left ( \frac{1} {\hat{\sigma }_{0}^{2}}\;\sum _{i=1}^{n}\;\mathbf{A}_{ i}^{T}\varDelta \mathbf{F}_{ i} + \frac{1} {\hat{\sigma }_{\boldsymbol{\mu }}^{2}}\mathbf{I}_{\boldsymbol{\mu }}\boldsymbol{\mu }\right ) & {}\\ \end{array}$$

    for the unknown coefficient vector d.

  2. (b)

    Besides the unknown coefficient vector d we here introduce all n + 1 variance components σ i 2 for i = 1, …, n and \(\sigma _{\boldsymbol{\mu }}^{2}\) defined in the model (4) as unknown parameters. With the estimation of the individual variance components the relative weighting between all observation sets and the prior information is determined. Thus, the VCE yields in the point of convergence the solution

    $$\displaystyle\begin{array}{rcl} & \mathbf{\hat{d}} = \left (\sum _{i=1}^{n}\, \frac{1} {\hat{\sigma }_{i}^{2}}\;\mathbf{A}_{i}^{T}\mathbf{A}_{ i} + \frac{1} {\hat{\sigma }_{\boldsymbol{\mu }}^{2}}\mathbf{I}_{\boldsymbol{\mu }}\right )^{-1}\;& {}\\ & \quad \left (\sum _{i=1}^{n}\, \frac{1} {\hat{\sigma }_{i}^{2}}\;\mathbf{A}_{i}^{T}\varDelta \mathbf{F}_{ i} + \frac{1} {\hat{\sigma }_{\boldsymbol{\mu }}^{2}}\mathbf{I}_{\boldsymbol{\mu }}\boldsymbol{\mu }\right ). & {}\\ \end{array}$$

The different sets of observations are combined according to the two approaches discussed before. The modeling results from these two combinations are presented in the lower part of Table 1. In Fig. 5 the modeling results for one combination example are presented.

Fig. 5
figure 5

Regional modeling results for a simultaneous analysis of GRACE and two sets of aerial observations. The plot shows the difference in the disturbing potential field on the topography synthesized from the modeling approach and the reference field. That is, the modelling errors in [m2/s2]. The red boxes indicate the area of the two flight campaigns (called case I and II). GRACE observations (see Fig. 1) are available throughout the whole area. The relative error RMS is 2.3% and the plot shows that the errors are small in the areas where aerial observations are available, but high outside

Full size image

5 Regional Modeling Results

In Table 1, all modeling results from the ICCT study group test data for the region in Europe are summarized. For each set of observations, the relative RMS error is given in %-values together with the maximum degree in the cubic polynomial basis function and a margin width which is used in order to avoid boundary effects. The values given in [∘] indicate by how much the validation area is smaller than the area of observations. For the results obtained from combination of different data sets the error RMS% values are given for both of the approaches outlined before. The results from satellite based observations lead to slightly worse results than the other observations. This is due to the downward continuation problem of gravity, which is of course included when gravity on the Earth surface is computed from observations at satellite orbit height. Downward continuation is an ill-posed problem by its physical nature, the gravity signal gets attenuated with distance from the masses. The terrestrial observations with 30′ spacing lead as well to an RMS error which is not as low as from the other terrestrial data sets. This is due to the fact that also in the observations with 30′ spacing, information up to spherical harmonic degree 2,190 was included. But the spacing of observations is not dense enough to sample this high frequency signal. Thus, not the full signal content can be recovered from the coarse observations. The very dense sampling of the terrestrial observations with 5′ spacing as well as from the aerial observations lead to very small errors in the recovered signal. The spacing of the sampling is dense enough to recover the maximum frequency in the signal (spherical harmonic degree 2,190). The terrestrial observations lead to even better results than the aerial observations, since in the terrestrial observations no downward continuation of gravity is included, while in the aerial observations it still plays a role.

In the data combination results in the second part of Table 1 approach B, with individual weights for the data sets, generally leads to better results than approach A. The only exception is the combination of GRACE data with the two sets of aerial results. This special case is discussed in the following in more detail.

In the combination of GRACE-type and terrestrial observations with 30′ spacing it can be seen how additional terrestrial observations lead to a better result. The combined error is lower than the individual errors. This also holds for the combination of GRACE and GOCE data, however, when two satellite-based data sets are combined, the result does not improve that much. The combination of aerial and terrestrial observations leads to good results, since the error RMS of the aerial data can be significantly improved by adding terrestrial observations.

The results of combining GRACE-type observations and the two aerial data sets show that even if the two aerial data sets cover a reasonable part of the area of interest (but still less than half of the area), this is not enough to make the solution of the whole area significantly better than from GRACE observations alone. For validation, the data set with spherical harmonic degrees up to 2,190 was chosen. These high degrees can not be recovered in the areas where only GRACE data is available and with a basis function of only degree 350. Therefore, the overall RMS% error is even higher than for GRACE data alone. Furthermore, the results for approach B are even worse than for approach A, since in this non-realistic scenario, no appropriate variances can be assigned to the data sets, and the errors outside the areas of aerial observations get very high.

Finally, the combination of three different types of data sets, namely satellite-based, aerial and terrestrial observations, leads to very good modeling results. The error RMS value is amongst the lowest to be achieved.

6 Summary and Outlook

Different types of gravity observations can be combined in one parameter estimation step in the regional gravity field modeling approach in spherical radial basis functions. The different sets of observations can be directly used in the approach, without prior processing or griding of the observed values. The results presented in this paper are not only useful for comparisons with other methods for the ICCT study group, but they are also a first step towards the analysis of real observations. All results shown above are obtained from simulated observations with a realistic noise level according to the ICCT study group. They lead to modeling errors between 0.2 and 2% for the different scenarios.

Due to more and more available high-resolution gravity observations, regional gravity modeling techniques play an important role, since the common approach of gravity modeling in spherical harmonic basis functions cannot accommodate regional gravity refinements appropriately. However, using real data in the regional modeling approach would be more tricky than this simulation, e.g. due to coloured noise of and correlations between the observations. In order to take the simulation study closer to processing real observations, stochastic properties of the different data types could be considered and improved in the variance component estimation step as well.