Keywords

1 Introduction

The knowledge of the geoid is essential for various geodetic and geophysical applications. For instance, it allows the conversion between GPS-derived and levelled heights. It is also the reference surface for ocean dynamics. The geoid can be computed from an accurate gravity model merging all gravity datasets available over the studied area. With the satellite gravity missions GRACE and GOCE, our knowledge of the long and medium wavelengths of the gravity field is or will be greatly improved (Tapley et al. 2004; Drinkwater et al. 2007). The gravity models derived from those missions need to be locally refined using high resolution surface gravity datasets, to obtain the local high resolution models that will be used for geoid modeling. Such refinements also allow to underline possible biases of the surface gravimetry and to improve the local gravity models, provided that a proper combination with the satellite models is carried out, with an appropriate relative weighting of the datasets. Featherstone et al. (1998) provide an overview of methods developed to realize such combination, using the Stokes integration. Different weighting schemes have been proposed by various authors, see for instance Kern et al. (2003). Local functional representations of the gravity field can also be used (see Tenzer and Klees 2008, for an overview). They can be related to least-squares collocation in reproducing kernel spaces (Sansò and Tscherning 2003).

Here we show that wavelet representations of the gravity field can be very useful for that purpose. Because of their localization properties, the wavelets indeed allow a flexible combination of various datasets. We first explain how to compute a local wavelet model of the gravity field combining different datasets by an iterative domain decomposition approach. Then, we provide an example of application over Japan, an area where significant variations of the gravity field occur in a wide range of spatial scales.

2 Discrete Wavelet Frames

The gravity potential is modeled as a linear combination of wavelets. Wavelets are functions well localized both in space and frequency, which makes them interesting to combine data with different spatial and spectral characteristics. To model a geopotential, harmonic wavelets are well-suited (Freeden et al. 1998, Schmidt et al. 2005). We chose to use axisymmetric Poisson multipole wavelets, introduced by Holschneider et al. (2003). Because they can be identified with equivalent non-central multipolar sources at various depths, they are well-suited to model the gravity potential at a regional scale. A wavelet is described by its scale parameter (defining its width), its position parameter (defining its center in space), and its order (defining the multipoles, as explained in Holschneider et al. 2003). Here we use order three Poisson wavelets, which provide a good compromise between spatial and spectral localization.

A wavelet family is built by an appropriate discretization of the scale and position parameters, as explained in Chambodut et al. (2005), Panet et al. (2004, 2006). First, a sequence of scales is chosen in order to ensure a regular coverage of the spectrum. This leads to a dyadic sequence of scales. Then, for each scale, a set of positions on the mean Earth sphere is chosen, in order to ensure a regular coverage of the sphere. The number of positions increases as the scale decreases, because the dimension of harmonics spaces to be generated by the wavelets increases. The wavelets are thus located at the vertices of spherical meshes that are denser and denser as the scale decreases.

The wavelet family thus obtained forms a frame (Holschneider et al. 2003). It provides a complete and stable representation of the modeled field, that may also be redundant. The redundancy is evaluated by comparing the number of wavelets, approximated with band-limited functions, with the dimension of harmonic spaces to be generated (Holschneider et al. 2003). The wavelet family used in this study (see Table 10.1) is over-complete with a redundancy estimated to 1.4 at 10 km resolution.

Table 10.1 Description of the wavelet frame used in gravity modelling over Japan.
Full size table

Here, we build a wavelet family suitable for local gravity field modeling by refinement of a global geopotential model derived from GRACE data with a surface gravity dataset. We need to combine two datasets: the high resolution surface gravity one, and a dataset created at the ground level from the geopotential model up to degree 120, extending two degrees outside the surface data. We then select the wavelets as follows. First, the largest wavelet scale is limited by the size of the area covered with data. Scales larger than half of the width of the area indeed cannot be reliably constrained by local datasets. Second, wavelet positions, for each scale, are selected in the area covered by data. Potential data are modeled by large scale wavelets, and smaller scales are added to model the surface data. This leads to the wavelet set detailed in Table 10.1. Note that, although the central frequency of the smallest scale wavelets is 20 km, the spectrum is well covered down to 10 to 15 km resolution.

3 Domain Decomposition Methods

The coefficients of the wavelet representation of the gravity potential are computed by least-squares fit of the datasets. Each data type can be related to the potential by a functional relation, leading to the observation equations for each dataset i, with i = 1, …, I. We obtain the following model:

$${b}_{i} = {A}_{i} \cdot x + {\epsilon }_{i}$$

Here, b i is the measurement vector, A i the design matrix relating the observations to the wavelet coefficients of the geopotential, and x the coefficients to be determined. The vector ε i contains the data errors (comprising white noise and correlated errors), with covariance matrix W i  − 1. This matrix is not considered perfectly known a priori, and we will parameterize it with variance factors estimated in the computational process (see below). We then derive the normal system for each dataset: N i ⋅x = f i , where N i  = A i t ⋅W i ⋅A i is the normal matrix, and f i  = A i t ⋅W i ⋅b i is the associated right hand side. Summing the normals for all datasets, and adding a regularization term λK leads to the system to solve:

$$(N + \lambda K) \cdot x = f$$
(10.1)

with N =  ∑ i N i and f =  ∑ i f i . The regularization may be needed if the data distribution leads to an ill-posed problem, and also to stabilize the inversion if the wavelet family is too redundant.

To solve this problem and introduce flexibility, we apply iterative domain decomposition methods (see for instance Chan and Mathew (1994) and Xu (1992)). Here we briefly recall the principle of such approaches. The least-squares computation of a wavelet model can be viewed as a projection of the data vectors on the space H = L 2( ∑) spanned by the wavelets, where ∑stands for the Earth mean sphere. In the domain decomposition approaches, also named Schwarz algorithms, we split H into smaller subspaces named subdomains {H k , k = 1, …, p}, that may be overlapping or not, so that we have \(H\,=\,{\Sigma }_{k=1}^{p}{H}_{k}\). In order for the computation to converge fastly, it is interesting to choose not too correlated subdomains, and we naturally define subdomains spanned by the wavelets at a given scale (hereafter referred to as: scale subdomains). If the scale subdomains still comprise too many wavelets, which is the case at the smaller scales, we split them into smaller subdomains spanned by subsets of wavelets at the given scale. These are referred to as: blocks subdomains. They correspond to a spatial splitting of the area into blocks. To each scale level corresponds a block splitting, with only one block for the larger scales and an increasing number of blocks as the scale decreases. Here we used a simple definition of the blocks, limited by meridians and parallels, but one may consider general shapes, for instance following the physical characteristics of the area. We defined overlapping blocks subdomains, with the size of the overlap area depending on the scale level, in order to speed up the convergency of the computations. On the other hand, our scale subdomains are non-overlapping. Finally, to each subdomain corresponds a subset of the total wavelet coefficient vector x that is to be computed.

Once the subdomains have been defined, the Schwarz algorithms consist in the following steps: (1) project the data vector and the normal systems on each subdomain, (2) compute the local wavelet coefficients by least-squares fit of the datasets for each wavelet subdomain, (3) gather these subsets of coefficients and update the global solution vector x, dropping the coefficients of wavelets located in the overlap areas and reweighting the coefficients, (4) update the right-hand side and iterate the computation. The coefficient weights are defined as the inverse of the number of overlapping blocks to which they belong. The Schwarz algorithms exist in two versions: the sequential one, where the subdomain solutions are computed sequentially, and the parallel one, where they are computed at the same time. In the case of multi-resolution representations based on wavelets, it is interesting to apply a hybrid algorithm, combining sequential Schwarz iterations on the scales subdomains with parallel iterations on the blocks. To design the iteration path over the scales, we followed the iteration sequences of multi-level iterative methods called multigrids. Multigrid methods (Wesseling 1991; Kusche 2001) are based on the resolution of successive projections of the normal system on coarse or fine grids, applying multi-level Schwarz iterations between subdomains corresponding to the grids. They are similar to a multi-scale resolution using wavelets, the wavelet coefficients at a given scale defining the details to add to a coarser grid approximation in order to obtain the finer grid approximation of the signal. We thus applied standard grid iterations schemes (from coarser to finer grids and vice versa) to design the wavelets scales iteration schemes (from larger to finer scales and vice versa). Figure 10.1 summarizes the approach.

Figure 10.1
figure 1

The Schwarz iterative algorithm. Each layer correspond to a scale subdomain, and the solid lines define the spatial blocks. The gray arrows show the iterations over the scales.

Full size image

In such iterative approach, it is possible to reweight the datasets and the regularization subdomain per subdomain. Following ideas by Ditmar et al. (2007) developed in the case of a Fourier analysis of data errors, we model the datasets systematic errors as a linear combination of wavelets, and add a white noise component. To model the systematic errors, we assume here that there exists a discrete orthonormal wavelet basis B sampled at the data points (it may be different from the Poisson wavelets frame). This requires a regular enough data sampling. Then, the covariance matrices of the errors W i  − 1 may be written as:

$${W}_{i}^{-1} = {F}_{ i}^{t} \cdot {D}_{ i}^{-1} \cdot {F}_{ i},$$
(10.2)

where F i and D i are square matrices of size equal to the number of data in the dataset i. F i is an orthogonal matrix containing the basis B wavelets sampled at the data points, and we have: F i t ⋅F i  = I. The weight matrix W i thus verifies:

$${W}_{i} = {F}_{i}^{t} \cdot {D}_{ i} \cdot {F}_{i}.$$
(10.3)

If the datasets errors can be considered locally stationary (without any abrupt variations) over the subdomains, then the projections of D i over these subdomains can be approximated with a white noise of constant subdomain-dependent variance σ k , leading to a block-diagonal structure of D i . Inserting (10.3) into (10.1), and assuming a good enough decorrelation between the Poisson wavelets and the discrete wavelets of basis B for different scales and blocks, leads to a rescaling of the subdomains normals by a factor σ k . In other words, the subdomains normals highlight different components of matrix W i , and the scaling factors σ k are roughly estimated using variance components analysis (Koch 1986; Kusche 2003) of a discrete wavelet transform of the residuals. The regularization may be reweighted in this way too. However, for the convergence of the iterations, a low condition number of the normal system is needed. This may require to increase the regularization weight. Thus, we chose to follow an iterated regularization approach (Engl, 1987), where an initially strong regularization is progressively removed by iterating, the number of iterations finally controlling the amount of regularization.

4 Application Over Japan

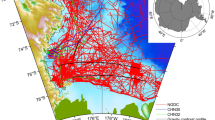
We validated the method on synthetic tests considering white and colored noise models, and then apply it to gravity field modeling over Japan, refining a GRACE-derived global geopotential model (EIGEN-GL04S by Biancale et al. 2005) with a local gravity model by Kuroishi and Keller (2005). We generated 5448 potential values at the Earth’s surface from the EIGEN-GL04S model up to degree and order 120. The cumulative error is estimated to 0. 8 m2 ∕ s2 in rms. The local gravity model is a 3 by 3 min Fayes anomaly grid at the Earth’s surface (103,041 data), merging altimetry-derived, marine and land gravity anomalies (Fig. 10.2). The altimetry-derived gravity anomalies are the KMS2002 ones (Andersen and Knudsen 1998). In order to avoid aliasing from the highest frequencies of the gravity data, we removed the highest frequencies from the local model by applying a 10 km resolution moving average filter, corresponding to the wavelet model resolution. From both datasets, we removed the lower frequencies modeled by the lower degree components of the EIGEN-GL04S model, and the residuals are modeled using wavelets. This allows us to construct a hybrid spherical harmonics/wavelets model, refining locally the global EIGEN-GL04S model using wavelets. For the parametrization of the computation, we use 5 scales subdomains. For the scales 300 km and 150 km, there is only one block. For the scales 75 km, 38 km and 20 km, we split the area into 4, 16 and 36 blocks, respectively. We apply a few iteration cycles over the scale subdomains, and a few hundreds iterations over the blocks. We do not iterate our estimations of the datasets reweightings using variance components estimates, but carry out only one weight estimation at the end of the computation of the wavelet model. Indeed, as the potential data are perfectly harmonic, iterated variance components estimates tend to lead to a perfect fit of these data.

Figure 10.2
figure 2

Surface gravity model by Kuroishi and Keller (2005).

Full size image

The results of a first computation, tightly constrained to the potential data for the large scale wavelets, and with a progressive increase of the weight of the surface data as the scale decreases, highlighted discrepancies between the two datasets, that we attributed to large scale systematic errors in the surface gravity model. Applying a low-pass filter to the residuals to the gravity anomaly data, we defined a corrector model and subtracted it from the surface gravity data. Applying the wavelet method on the corrected datasets allows to progressively improve the resulting wavelet model, and refine our corrector model. The final corrector thus obtained is represented on Fig. 10.3. It is consistent with results from Kuroishi (2009), underlining similar biases in the surface gravity model from a comparison with the GGM02C/EGM96 geopotential model. The residuals of the final wavelet model to the potential and gravity anomaly data are represented on Fig. 10.4, and the final wavelet model on Fig. 10.5. The RMSs of residuals are 0. 80m2 ∕ s2 for the potential data, and 0.50 mGals at 15 km resolution for the corrected anomaly data. This is consistent with our a priori knowledge on the data quality. We also note that these residuals do not show any significant bias. The resolution of the wavelet model may be slightly coarser than that of the surface gravity model, which is why we observe very small scale patterns in the gravity anomaly residuals map. Small edge effects may also be present.

Figure 10.3
figure 3

The final corrector model to the surface gravity anomaly model, derived by low-pass filtering of the residuals of the wavelet model to the gravity anomaly data.

Full size image
Figure 10.4
figure 4

Geographic distribution of residuals in the final combination. Top panel: potential residuals to degree 120. Bottom panel: residuals of corrected gravity anomalies at 15 km resolution.

Full size image
Figure 10.5
figure 5

Surface Fayes gravity anomalies computed from the final wavelet model obtained in the present study.

Full size image

5 Conclusion

We developed an iterative method for regional gravity field modeling by combination of different datasets. It is based on a multi-resolution representation of the gravity potential using Poisson multipole wavelets. We define scale and blocks subdomains, and carry out the computation of the wavelet model subdomain per subdomain. This allows to introduce a flexible reweighting of the datasets in different wavebands and in different areas. Applying this approach to the example of gravity field modeling over Japan, a challenging area with important gravity undulations, allows to derive a hybrid spherical harmonics/wavelet model at about 15 km resolution, refining a global geopotential model with a local high resolution gravity model. Finally, the method can be used to regional modeling of the forthcoming GOCE level 2 gradient data, in combination with surface gravimetry.