Keywords

1 Introduction

The demand for highly effective pharmaceuticals has risen continuously over the past decades [1, 2]. From 2015 to 2018, 129 different biopharmaceuticals have been approved by the EU and the US government, representing the highest number of approvals in a 4-year period since the first biopharmaceuticals were introduced in the end of the twentieth century [3]. In 2018, a total of 374 approved biopharmaceuticals were available, including 316 with different individual active ingredients and current active registrations [4]. Trends for the future indicate a growing market share of up to 50% of the top 100 pharmaceuticals to be bio-based [5], predominantly monoclonal antibody-derived medicinal substances, followed by hormones and blood-related drugs [4]. Simultaneously, the development costs of biopharmaceuticals have increased drastically (620% from 1980 to 2013) [6]. As a result, processes become more complex and intensified, which is further increased by, e.g., changing from simple batch to more complex fed-batch or perfusion processes. The number of process variables to be monitored and their complexity have also increased. Finally, the requirements for quality management and documentation (good manufacturing practice – GMP) have also increased to guarantee quality [7]. For the design of novel bioprocesses, the process analytical technology (PAT) initiative and quality by design (QbD) philosophy require an improved understanding of the drug manufacturing processes [8].

Statistical design of experiments (DoE) methods have become common practice in process development within QbD [9]. However, induced by the explorative approach of DoE, the selection of the experimental design as well as the definition of the boundaries of factors is user-dependent. Furthermore, the definition of the parameter space is particularly critical. This is usually done heuristically, suggesting that non-ideal experimental settings are not necessarily identified and the parameter space has to be iteratively reduced step by step. Narrowing down the design space by using statistical DoE requires a lot of time and experimental effort, especially in cases where a high number of relevant factors are targeted. At the same time, the experiments can be limited in their information content, constraining the outcome of the optimization studies [8,9,10]. This generally results in a small increase in process knowledge only.

To reduce the number of experiments and increase the process understanding during the design and optimization of bioprocesses, a novel model-assisted design of experiments (mDoE) concept was recently introduced [11,12,13]. It combines the benefits of statistical DoE with a mathematical process model as a virtual representation of the bioprocess, called a digital twin. Although the term “digital twin” has not yet been defined across different parts of the industry, in bioprocesses they are intended to be a virtual counterpart of the bioprocess for the entire life cycle of the biopharmaceutical production process. In the context of mDoE, digital twins consist of a mathematical process model, which have gained increased importance in the last decades. They can be applied to design [14,15,16], control [17,18,19], and optimize [20, 21] biopharmaceutical production processes. The main intention of a mathematical model is to find solutions by analyzing the model in order to propose targeted experiments [22]. As they contribute to a scientific understanding of the process variables and their impact on the final product, mathematical process models in the field of biopharmaceutical production processes are now considered to be a sustainable part of QbD [7, 12, 23, 24].

2 Design of Experiments Methods

Even if traditional trial-and-error and one-factor-at-a-time methods are still used, advanced statistical DoE methods are applied more frequently in the field of biopharmaceutical process development [25,26,27]. They can be used for the statistical and systematic planning of experiments for hypothesis testing and/or the optimization of process variables (namely, “factors”) with regard to the desired outcome, called “response” (e.g., product titer, product quality) [7, 28, 29]. In general, the process development based on DoE methods leads to a certain reduction in the number of experiments to be done in practice compared to one-factor-at-a-time approaches. In the context of designing biopharmaceutical production processes, they were used in the upstream as well as in the downstream part. As an example for the design of a bioprocess, Zhang et al. (2013) implemented a screening design to identify active parameters for the development of a serum-free medium for the cultivation of a recombinant CHO cell line. Afterward, the process parameters were optimized, and a fed-batch strategy was designed [30]. As an example for the part of product purification, Horvath et al. (2010) used a screening design with eight experiments to determine the effect of different process parameters on the isoelectric point of a therapeutic antibody expressed in CHO cell culture. The pH, temperature, and the time of the temperature shift were significant. These factors were evaluated in three levels in a concluding response surface design to optimize the isoelectric point [31].

Statistical DoE methods are solely based on user-defined selections of the experimental design and the definition of factor limits, including the definition of experimental variables and their evaluated levels [8, 32, 33]. This can lead to error-prone decisions, iterative re-adjustments of the experimental space with several rounds of costly and time-intensive experiments, and even to a design that simply cannot be implemented [7]. Expert knowledge is required to select suitable boundary values for process development and optimization using DoE [7, 34,35,36]. Therefore, the combination of digital twins with DoE in mDoE offers a novel tool for the knowledge-driven development of bioprocesses.

2.1 Screening Designs

Screening designs are intended to identify the significantly influencing factors from a list of many potential factors [33, 37]. Therefore, different experimental designs can be used. The most commonly used designs, called full factorial, factorial fractional, as well as Plackett-Burman designs, are discussed.

2.1.1 Full Factorial Designs

A full factorial design can be used to examine the main effects and interactions of one or more factors on the respective response. The design consists of two or more factor levels and k-factors, resulting in at least a 2k-design [38, 39]. Exemplary, the full factorial design for three factors is given by a 23-design plan, shown in Fig. 1a.

Fig. 1
figure 1

Geometrical representation for screening (a, b) and optimization designs (c–h) and optimization designs with three factors (Factor a, Factor b, and Factor c). Dots represent the recommended experiments. The gray dots are the star points, and the black dots are the central points. All designs are examined at two levels (+ and -)

Full size image

2.1.2 Reduced Full Factorial Designs

In order to reduce time-consuming and costly experiments in the case of a large number of factors, incomplete designs, like fractional factorial and Plackett-Burman designs, can be chosen. The fractional factorial designs, representing a reduced form of the two-level factorial design, are based on the assumption that higher-value interactions are irrelevant. This results in a 2k-n-design, whereby the 2k-design is reduced by n steps [38, 40, 41]. A reduced form of the previously mentioned 23-design plan, a fractional factorial 23-1-design, is shown in Fig. 1b. Plackett-Burman designs, a special form of the two-level fractional factorial designs, are suitable if the focus is on the investigation of the main effects and interactions can be disregarded [40]. However, a mixing of the effects can occur [38, 41].

2.2 Optimization Designs

In order to maximize a response, the levels of the influencing factors are optimized in so-called optimization designs. Therefore, the most known designs, like the central composite, Box-Behnken, optimal, and space-filling designs, are briefly introduced in the following.

2.2.1 Central Composite Designs

Central composite designs (CCDs) are built from factorial 2k- or fractional factorial 2k-n-designs. Additionally, center and star points (marked gray) are augmented, allowing the estimation of curvature. In general, three variations of CCD exist, which differ in range settings of their factors. Figure 1 C–E illustrates the relationships among these variants. Depending on the variant, the design is spherical, orthogonal, rotatable, or face centered [28, 38, 42].

2.2.2 Box-Behnken Designs

Box-Behnken designs (BBDs; see Fig. 1f) are based on the combination of a two-level factorial design with a balanced incomplete or partial block design [43]. They are nearly rotatable and require an examination on three levels for each factor, resulting in a field with distinct resolution of interactions and quadratic effects [44]. However, for a large number of factors, this implies a poor estimation of the two-factor interactions [43].

2.2.3 Optimal Designs

With optimal experimental designs, the experimental space can be restricted, and user-specific settings can be made. There are a large number of optimization criteria to distribute points in the experimental space. The most frequent representatives are average (A)-, determinant (D)- (shown in Fig. 1g), eigenvalue (E)-, global (G)-, and variance (I)-optimality. If the coefficients of the regression model are of interest, then A-, D-, and E-optimal plans are used. G- and I-optimality, however, refer to the fitted regression model [38].

2.2.4 Space-Filling Designs

Traditional experimental designs, such as the CCDs, BBDs, and the optimal experimental designs, often create experiments close to the factor boundaries. This can cause areas of free space, which are not examined and only minimize noise [45]. However, to minimize bias, space-filling designs can be used. In this case, possible experiments are randomly distributed in the individual spaces. An example of such designs is the Latin Hypercube Sample Design (LHSD), which fills the room evenly, allowing for a large number of factors and levels to be used (Fig. 1h). The experimental space is filled in such a way that there is an even distribution in the entire factor space or the maximum distance between the design points is minimized. However, the corners of the factor space are left out obtaining this information would only be possible by extrapolation [41, 46].

2.3 Examples and Challenges of Conventional DoE

In this part, challenges of conventional DoE are discussed focusing on specific studies. A number of possible applications of screening and optimization designs are shown in Table 1.

Table 1 Different designs for screening and optimization of CHO cultivation processes
Full size table

Plackett-Burman designs are common designs for screening experiments. They are used, e.g., to identify the effects of amino acids and other components in conventional cell culture media formulations. Lee et al. [47] developed a serum-free medium for the production of erythropoietin by suspension culture of recombinant CHO cells, identifying six active determinants (glutamate, serine, methionine, phosphatidycholine, hydrocortisone, and pluronic F68) for cell growth. 79% of the erythropoietin titer achievable in the medium supplemented with 5% dialyzed fetal bovine serum were reached in the serum-free medium. However, 80% confidence levels were used to achieve useful statements, and some of the significant variables are obscure (e.g., pluronic F68) [47]. Chun et al. [48] used a full factorial design to identify effective growth factors in culture medium. Four growth factors were investigated on 2 levels, resulting in the implementation of 16 experiments. Important growth factors were identified. However, no center points were investigated; thus no curvatures could be detected [48]. Rouiller et al. [49] investigated six CHO cell lines in two different cultivation media to which six components were added in three different levels to develop a process for the production of monoclonal antibodies. A two-stage fractionated factorial design with six factors was implemented, and various regression models were used to identify the active variables [49]. This resulted in 384 experiments to be performed, which was only possible by using a deep well plate system. Nevertheless, there were variations in statistical significance, and possible active variables have to be tested on a larger scale [49].

The amount of experiments to be performed can be seen as the main challenge in using optimization designs as well. The most commonly used optimization design is CCD. Yang et al. (2014) used a CCD to optimize the concentration and timing of valproic acid (VPA) addition to the cultivation of three different CHO cell lines [50]. Even the investigation of two factors for one cell line results in eight experiments. Torkashvand et al. (2015) optimized the concentrations of four amino acids (aspartic acid, glutamic acid, arginine, and glycine) in the feed using a BBD. The factors were investigated at 3 levels, resulting in 29 experiments to be implemented [51]. Duvar et al. (2013) developed a feeding protocol for a fed-batch CHO cultivation. The choice of a D-optimal experimental design resulted in 18 experiments with 4 factors (feeding volume, starting point, time of shift in temperature, and osmolality) [34].

For the previously mentioned studies, the planned experiments in statistical DoE result in identifying active parameters and optimization of the bioprocess. However, there are still challenges, and the implementation of statistical DoE can lead to time-consuming and costly rounds of experiments, especially if they are implemented in fed-batch mode. Furthermore, the heuristic selection of, e.g., the parameter settings or the design selection is seen critically. These rely on user-defined settings and mostly require a lot of time and experimental effort. But, as the investigation of various studies has shown, no adequate justification for the choice of an experimental design is provided. In addition, in conventional DoE only the experimental endpoints are examined, and therefore only the integral of it is judged. The entire time trajectory, with, e.g., metabolite formation or substrate uptake, is hardly reflected.

3 Model-Assisted Design of Experiments

The combination of statistical DoE with mathematical process models is a novel tool – enabling a knowledge-driven bioprocess development in the context of QbD. Using this method, the abovementioned limitations of DoE methods can be avoided, and the design as well as the optimization of bioprocesses can be improved. However, in contrast to the chemical industry, bioprocess design on the basis of mathematical models is not yet well established in biopharmaceutical manufacturing processes with mammalian cells [52]. According to experiences of the authors from discussions and projects, the use of model-based innovative methods for process development has so far failed due to different reasons:

  • It is based on the lack of knowledge of the potential and limits of model-based/model-assisted methods and “bad experiences” with them (e.g., due to unrealistic expectations).

  • There is a lack of method integration for a consistent development strategy, which can be adapted to existing work processes, a suspected high (modeling) effort and doubts about the transferability of methods and models to other processes.

  • The qualification profile of the involved personnel does often not fit (required: biotechnology, process technology, modeling, and statistics).

An additional challenge is the application of models on complex metabolic pathways of mammalian cells regarding cell growth and product formation. In addition, models targeting the metabolism of cell cultures demand more effort than those applied in chemical or microbial processes. Even if mathematical models are a promising tool for the development of stable processes that comply with the principles of QbD, examples have so far only been published in the field of product purification and polishing [8]. Nevertheless, Möller et al. (2018) and Abt et al. (2018) showed that model-assisted and model-based DoE methods have great potential for the development of process strategies and makes the process development more knowledge-based [7].

General differences between model-based and model-assisted DoE methods are due to the aim of the recommended experiments. Model-based DoE (MBDoE) [53,54,55] is used to supply valid experimental data for a precise model structure and model parameter identification, where the conventional statistical DoE could fail [56]. Uncertainties are key information in MBDoE, as model and data imperfections cause undesirable variations in model parameters and simulation results. This variation drives the MBDoE methodology, where it manifests itself as optimal experimental settings (e.g., measurement principle, sampling rate, inputs/stimuli) and informative data [55, 57]. However, uncertainties cause a discrepancy between computed and experimental outputs leading to suboptimal or even meaningless experimental designs for model parameter adaptation. To overcome these problems, a sequential approach, as shown in [7], has proven to be very effective by increasing the robustness of the MBDoE against parametric uncertainties [58,59,60].

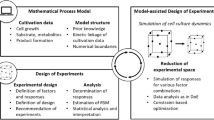
In model-assisted DoE, a process-related target (i.e., product titer) is optimized, and the model supports in the evaluation and recommendation of DoE designs. A structure for a model-assisted DoE concept is shown in Fig. 2. At first, a mathematical process model is used to describe, e.g., the growth, the substrate, and metabolite concentrations as well as the productivity of a specific cell line. Therefore, the model is adapted to first cultivation data (Fig. 2, Box 1), e.g., based on literature and/or existing knowledge. The evaluated data should be used to cover typical known effects, e.g., inhibitions or limitations. Certainly, the number of experiments that can be performed at this stage, preferably in small scale, such as shaking flasks or deep well plates [11,12,13], is usually limited. However, only a few experiments are required to generate the mathematical model, as shown in the case study (see Sect. 4). Accordingly, the number of experiments in mDoE is still less than the number of experiments to be performed in statistical DoE. Based on these data, model parameters are adapted (Fig. 2, Box 2). Afterward, a statistical DoE design (see Sect. 2) is chosen (Fig. 2, Box 3). A scheme to select a design is explained in Sect. 3.2. The model is then used to simulate the responses for each previously planned experiment (Fig. 2, Box 4). Subsequently, the initial DoE is evaluated with respect to the defined factor boundaries as well as the experimental design (see Fig. 2, Box 5). This enables the testing of different designs, boundary conditions, optimization criteria, and factor as well as response combinations in silico before experiments are experimentally performed. This can be used to evaluate the mDoE method as well as boundary conditions and significantly reduce the number of experiments. Additionally, different designs can be chosen and computationally evaluated using the model simulations.

Fig. 2
figure 2

Structure of the model-assisted design of experiments concept [11, 61]

Full size image

3.1 Digital Twins in Model-Assisted Design of Experiments

As already discussed, the term “digital twin” is still not sufficiently defined and has different meanings in different parts of industry. Historically, it is a computational model of a machine tool or a mechanical manufacturing site, and it is used to handle the increased complexity [8]. In the bioprocess industry, digital twins progressively include multiple parts of the manufacturing steps and their interaction [9]. They are intended to be a universal tool for the entire life cycle of a bioprocess, whereby the digital twins are virtual counterparts to the processes. They enable predictive manufacturing, meaning that bioprocesses can be analyzed, optimized, forecasted, and controlled [62]. The complexity of digital twins highly depends on the desired focus of application, and they can be based on a variety of complex structures as data-driven models, artificial neural network, or mathematical process models [22, 24].

With respect to the application of mDoE, the mathematical modeling in the initial phase of process development is, in the author’s opinion, the starting point for knowledge integration into a digital twin for the entire life cycle of the bioprocess. The mathematical process model in the digital twin incorporates the process understanding, for which the degree of model complexity can be increased stepwise throughout the performed studies, as represented in Fig. 3. In this context, the model structure should be kept as simple as possible in the initial process design phase and should then be extended if more data becomes available or novel biological effects are identified.

Fig. 3
figure 3

Usage of the mDoE in bioprocess design and optimization as well as the development of a digital twin from a mathematical model

Full size image

In the application of digital twins within mDoE (see Fig. 3) during process design and optimization with only a low number of available data, they structurally include rather simple mathematical process models. These are based on the formulation of mathematical links (i.e., equations) between cell growth, metabolism, and corresponding product formation [63]. If partial mechanistics are unknown, they can be modeled to gain a systematic understanding, although they might not be measurable (e.g., in systems biology) [17, 41]. Such a mathematical process model mainly works as an initial starting point to obtain a deeper process understanding during the bioprocess life cycle.

3.1.1 Mathematical Model Structures

Mathematical modeling has already been the subject of controversial discussions in recent years, and several models of varying complexity have been described in literature [64,65,66]. In the early phases of bioprocess development, the mathematical models used in mDoE mainly consist of simple model structures and should then be extended stepwise. The model parameters considered should be determinable by simple experiments since these include known mechanistics (e.g., ammonia formation based on glutamine uptake). It is favorable if models used for process optimization are applicable to a broad range of bioreactor scales [12, 64, 67]. Although the application of mathematical process models for the development of sophisticated processes has many advantages, it is still not commonly applied in bioprocess development. Reasons for this include the variety and complexity of mathematical models, e.g., different mechanistics and quality of predictions (recently reviewed in [64]). Due to the complexity of biological processes, simple models might be unsuitable for representing real phenomena. However, it has been suggested that the growth of a cell line follows the same kinetics regardless of the cultivation method, such as batch and fed-batch processes [65]. Nevertheless, even with complex models, the behavior of cells may change, and predictions can differ from observed behavior. Reasons are the inadequate precision of the approximated model coefficients and the complexity during the determination of the model parameters. Therefore, a compromise between the accuracy of the model and the required experimental effort for the determination of the parameters needs to be agreed on for each application [68].

Bioprocess-related mathematical models are either classified according to the description of the biophase, which is seen as an engineering-type approach or based on the implemented model structure (e.g., neural networks, fuzzy logic). This chapter focuses on biophase-classified models, which are historically sorted according to their structural complexity, as shown in Fig. 4. Even if this classification was made in the 1990s, it is still valid for the class of models here discussed.

Fig. 4
figure 4

Classification of mathematical models separated in unstructured, structured, unsegregated, and segregated

Full size image

Unstructured and unsegregated models describe the biophase as one component and use kinetic equations to describe their interaction and response to the environment, e.g., the effect of glucose concentration on bulk cell growth. They are widely applied for industrial applications and are state of the art [69]. It is advantageous that the model parameter estimation is based on only a few measured concentrations [70]. Moreover, a method for their knowledge-driven development was recently reported by Kroll et al. (2017) [23]. With the development of novel analytical methods, structured and unsegregated models were developed. The cellular properties are reflected by average cells with the same physiological, morphological, and genetic identity [71,72,73]. They aim to describe intracellular metabolic pools in otherwise average cells. Most examples try to examine the intrinsic complexity of cell metabolism. Lei et al. (2001) described the growth of Saccharomyces cerevisiae based on glucose and ethanol using two modeled pools, which describes the catabolism and anabolism, respectively [74]. Moreover, a six-compartment model for microbial and mammalian cell culture was recently introduced to reduce the modeling effort as a basis for digital twins [75]. Flux balance analysis, mostly used in systems biology, is additionally associated with the structured model class [76, 77].

In unstructured and segregated models, different separated cell populations are modeled with the description of the metabolism by bulk kinetic equations [78]. The scope of application is broader, leading to the determination of cell culture quality and gaining an understanding of the cell cultivation process. Exemplary, cell-cycle-dependent population balance models were introduced [22, 24, 78, 79]. Therefore, different cell-cycle-dependent growth rates, metabolic activity, and DNA replication rates are modeled, and metabolic regulations were studied, but the degree of complexity and computational power increases significantly from a few seconds to multiple hours. Hence, they require a comprehensive knowledge of the mechanisms and more data to estimate the model parameters. Segregated and structured models describe the nature of cell cultures with individual single-cell metabolism and their interaction with the medium. Sanderson et al. (1999) introduced a single-cell model that describes the interaction of 50 components in the medium, cytoplasm, and mitochondria for an antibody-producing CHO cell line [80]. Other examples could be found for baculovirus-infected insect cell cultures [81] and the amino acid metabolism of HEK293 and CHO cells [82]. However, the computational power and amount of data required to estimate the model parameters are still considerable, which can limit their industrial application.

3.2 Recommendations on the Selection of Designs for mDoE

The choice of an experimental design significantly influences the implementation of DoE and mDoE. Usually, the selection of a design depends on basic settings (number of factors, number of factor steps, the regression model, and the number of test runs) and design-specific properties (block formation, orthogonality, and rotatability). However, as the investigation of various studies has shown, in most references less information for the choice of an experimental design is provided. DoEs are mostly selected based on heuristics within a given scientific field, and there is no guided decision-making workflow yet. Based on the author’s understanding, a scheme (Fig. 5) is presented in the following to assist in the selection of appropriate DoE designs in the field of bioprocess engineering. This scheme was developed based on literature and is seen to assist in the selection of DoE designs within mDoE [8, 11, 12].

Fig. 5
figure 5

Scheme for selection of designs in mDoE

Full size image

Due to their favorable properties, CCDs and BBDs are most frequently used for optimization [39]. If settings are adjusted individually, optimal designs should be used. As a result of the low computational effort, the D-optimal design has become generally accepted among the optimal designs [38]. Therefore, commercial software tools for creating optimal designs are often limited to the D-optimal design [83]. However, the I-optimal designs are sometimes recommended [39, 83]. If a large area of the factor space is to be covered, it is recommended, e.g., to combine the LHSD with an optimal design. This results in a better distribution of points across the factor space and reduces both bias as well as noise [45].

In the first decision-making level, the number of investigated factors k is used. Except for BBDs, which require at least three factors, the number of factors can be selected as desired [38, 41, 84]. Typically, three to six factors are used for processes optimization [38]. In the case of a high number of factors and the use of insignificant factors, the LHSD is recommended. This is enabled by the random distribution of experiments. Hence, if one or more factors appear not to be important, every point in the design still provides some information regarding the influence of the other factors on the response [41]. However, in bioprocesses the number of factors is significantly larger than the observations. Therefore, domain knowledge as used in mDoE is needed, captured on models as additional constraints to the system.

On the next level, the desired regression model is defined. Generally, the use of a quadratic regression model is recommended, since higher-order regression models lead to an increasing number of unknown coefficients and can lead to an overfit [38, 41]. For CCDs und BBDs, a quadratic regression model is used by default, whereas for optimal designs, the regression models can be user-defined. If the regression model cannot be defined, the LHSD can be used [39].

The number of runs is taken into account at the penultimate level. BBD is most efficient with three or four factors. Compared to other designs, they require the least number of runs [44]. However, even with optimal designs, the number of experiments can be user-defined and thus minimized. Only a model-dependent minimum number must be included. For a quadratic regression model with four factors, e.g., the minimum number is 15, one term for the intercept, four linear terms, four purely quadratic terms, and six cross-product terms must be taken into account. In the BBD or CCD, the number of runs varies between 25 and 30, depending on the number of center points [85]. LHSDs, on the other hand, require a large number of experiments to fill the space and are therefore mainly used for computer simulations [86,87,88].

Finally, the choice of factor levels is decisive. In order to evaluate designs optimally, they require at least three levels per factor [43]. In the BBD, the factors are examined at three levels. However, no factor-level combinations are investigated at the corner points, and thus, only a low prediction quality for extrema is available [89]. LHSDs are also not suitable for the investigation of extrema [41]. The CCDs contain five levels per factor [28]. In the optimal designs, the factor levels can also be set user-specifically and combined as desired. However, it can happen that very few test points are generated in the middle of the test area, which means that no statements can be made concerning this area [38].

The selected design can then be implemented experimentally or in the mDoE (see Sect. 4.3). It should be noted that the application of the selection scheme (Fig. 5) is not limited to mDoE solely and it can be generally applied for the selection of DoE designs.

4 Case Study: mDoE for Medium Optimization

As previously mentioned in Sect. 3.1, digital twins are used within the mDoE concept to simulate and evaluate statistical DoE designs in silico. The application of mDoE with a strong reduction in the number of experiments has been shown so far for medium optimization, fed-batch design, and scale-up studies for antibody-producing CHO cells, algae, and yeasts [11, 12, 61, 90]. During these studies, the process understanding is stepwise increased and captured in the digital twin (i.e., mathematical process model). In the following, the application of mDoE is exemplarily discussed for the reduction of the factor boundary values for the optimization of the glucose and glutamine concentrations in an antibody-producing cell culture process. The specific workflow applied in this study is shown in Fig. 6.

Fig. 6
figure 6

Workflow of the upcoming chapters of the medium optimization in the case study

Full size image

In this case study, the dynamics of the bioprocess are modeled first, and the model parameters are based on a few experimental data points. Then, the boundary values of experimental designs are defined, and experimental settings are planned. Each planned experiment is simulated, the responses (e.g., maximal product titer) are calculated, and the response surfaces are determined. Based on these response surfaces, the initially defined factor boundary values and the planned experiments are evaluated, and only a few experiments are recommended to be performed. This results in a significant reduction in the number of experiments to be performed. This example shown in the following is based on our previous publication, and more details can also be found in Möller et al. (2019) [11]. This medium optimization is only a small part of a process development workflow, which could be implemented from medium optimization over fed-batch design to scale-up using mDoE [12]. This resulted in the evolution of the digital twin, as briefly explained in Sect. 4.6.

4.1 Mathematical Process Model

In this case study, an unstructured, non-segregated saturation-type model was used as virtual representation of the bioprocess. The mathematical model from literature [19] was adapted and modified to describe the dynamics of cell growth and metabolism of antibody-producing CHO DP-12 cells in batch mode (see Table 2). This model was chosen due to its simple model structure and the opportunity to estimate all the model parameters from just a few shaking flask cultivations.

Table 2 Mathematical process model in batch mode, modified from [19]
Full size table

4.1.1 Batch Process Model as Digital Twin

According to the mDoE workflow (Fig. 2, Box 1), the mathematical process model is used to simulate the growth of the CHO DP-12 cells. It is based on the linkage of the main substrates glucose (cGlc) and glutamine (cGln) as well as the main metabolites lactate (cLac) and ammonium (cAmm) to describe the behavior of the cells (Xt, total cell density, and Xv, viable cell density). Cell growth is modeled with kinetic parameters KS,i (i = Glc, Gln), a maximal growth rate (μmax), a cell lysis constant (KLys) of dead cells, and a minimal (μd, min) and a maximal death rate (μd, max). Since no inhibition of cell growth could be detected in batch mode, inhibitory components were not considered in the model. Therefore, the calculation of the specific growth rate μ (Eq. 9, in Table 2) and specific death rate μd (Eq. 10, in Table 2) is based on a Monod-like structure of the substrates glucose and glutamine, with only the substrate with the lowest concentration being relevant for growth. The cell-specific uptake rates of glucose and glutamine depend, in contrast to the growth, only on the current glucose and glutamine concentration (Eqs. 4, 5, 11, 12, in Table 2). However, the uptake rate of glucose is reduced at low concentrations. The concentrations of lactate and ammonium are proportional to the uptake rates of glucose (lactate) or glutamine (ammonium) (Eqs. 6, 7, 13, 15, in Table 2) and are linked with the yield coefficients (YAmm/Gln and YLac/Glc). In case of glucose concentrations below 0.5 mmol L−1, a shift of lactate production to lactate uptake was considered (Eq. 14, in Table 2). The antibody production (Eqs. 8, 16, in Table 2), according to Frahm et al. [19], describes the production proportional to the viable cell density. However, glucose concentrations below 1 mmol L−1 stop the antibody production (Eq. 17, in Table 2).

4.1.2 Adaption of Model Parameters

The initial experiments for modeling were based on the previous publications of Beckmann et al. [91] and Wippermann et al. [92] with the same medium and cell line. Biological experiments were performed in quadruplicates, the data were averaged, and the model was adapted as well as model parameters estimated (Fig. 2, Box 2). This initial adaption and the further use of the mathematical model in mDoE can be seen as the starting point into a digital twin. Therefore, the model parameters were adapted. To compare and evaluate the quality of adaption, the modeled simulations and cultivation data were plotted and the coefficient of determination calculated. If the values tend to 1, the behavior of the cells could be represented with high accuracy. However, the area, which should be optimally displayed, should be focused on. The goal could be a high cell density; therefore the representation of the stationary phase and the death phase is not important. This must be taken into account during the evaluation. Alternative measures are detailed explained in literature, e.g., [93, 94].

The simulation with the adapted model parameters is exemplary shown for cell growth and antibody production in Fig. 7. The exponential cell growth, the transition to the stationary phase, and the death phase could be simulated with an accuracy of R2 = 0.96 (Fig. 7a). The antibody concentration increases until Xv decreases after approx. t = 144 h and was estimated with a high accuracy of R2 = 0.98 (Fig. 7b). By this, the previous knowledge is captured into the model structures, and the model parameters reflect the cell behavior, which could further be used in mDoE.

Fig. 7
figure 7

Comparison of experimental data (◊) and simulated data (−), exemplary for viable cell (a) density and antibody (b). Mean and one standard deviation of four parallel batch cultivations. The samples were measured as three technical replicates for each shaking flask, and R2 was calculated compared to the mean experimental data points

Full size image

4.2 Selection of Experimental Design

The determination of a suitable design is essential for the most appropriate evaluation of the mDoE and thus the optimization of the respective process, as can be seen in Fig. 2, Box 3. Therefore, a design for the mDoE was chosen considering the scheme in Fig. 5. In the first decision-making level of the scheme, the number of investigated factors k, which are two in this case study, was examined. Since BBD requires the use of at least three factors and LHSD is recommended for a high number of factors, only the CCD and optimal experimental designs remain. Then, the regression model was considered. For both, CCD and optimal designs, the recommended quadratic regression model can be used, although this is not adjustable for CCD. Therefore, no further restriction has yet been possible on the basis of this level. Finally, the third level can be used to select the design. At this level the number of runs is taken into account. Since the number of runs should be set individually, the CCD was discarded, and an optimal experimental design was chosen.

Experiments were designed with suitable DoE software (in this study, Design-Expert 9, Statcon, USA), and each experimental factor combination of the experimental design was simulated (MATLAB). In the simulated design (20 experiments, D-optimal design), the initial glucose concentration was varied between 20 and 60 mmol L−1. This corresponds to a 50% increase/decrease of the glucose concentrations related to the standard medium formulation as reported in Beckmann et al. [91] and Wippmann et al. [92]. These studies did not focus on the optimization of the batch-medium composition as aimed in this study. Glutamine concentrations typically applied in batch media range from 2 mmol L−1 up to 8 mmol L−1. The factor range of the initial glutamine concentration was, therefore, widely defined between 2 and 12 mmol L−1.

4.3 Simulation of Experiments

Each planned factor combination (Fig. 8a-d) and the corresponding responses (Fig. 8b, c, e, and f) were simulated using the mathematical model (as described in Fig. 2, Box 4). As can be seen in Fig. 8, the concentration range of the substrates (Fig. 8a, d) causes a maximum cell number between 8 × 106 cells mL−1 and 15 × 106 cells mL−1 (Fig. 8b). The maximum antibody concentration lies in a range between 75 mg L−1 and 380 mg L−1 (Fig. 8e). The simulated concentrations for lactate and ammonium range between 12 mmol L−1 to 35 mmol L−1 and 2 mmol L−1 to 11 mmol L−1 (Fig. 8c, f). By simulation, the time course is also determined, which is not the practice in typical experimental DoEs.

Fig. 8
figure 8

Simulation of the growth behavior of CHO DP-12 cells for all initially planned experiments (Fig. 2, Box 3); (a) and (d), dynamic changes of investigated factors; (b), (c), (e), (f), investigated responses

Full size image

4.4 Evaluation of Planned Design

Out of the simulations, the maximal simulated values of Xv, cLac, cmAb, cAmm were exported as responses to generate response surface plots (Design-Expert 9). The simulated responses were treated in the same way as data from experiments. For this purpose, no data transformation was applied, and after analysis of variance (ANOVA, all hierarchical design mode, quadratic process order), an internal RSM was set up with a maximal significance value of 0.05. As can be seen in Fig. 9, different shapes of the response surface plots were determined, and their individual optimum is different, e.g., Xv is maximal for high initial glucose and glutamine, while cmAb is high, regardless of the glutamine concentration. Such interaction could hardly be predicted before and was only possible through the simulations. After defining the RSM for each response, user-defined constraints for medium optimization were chosen (displayed in Fig. 9). The constraints were chosen to maximize Xv above a minimal Xv of 107 cells mL−1. Furthermore, cmAb should be maximized. The constraints for the metabolic waste products were defined based on the literature data with respect to cell growth and product quality. High lactate concentrations were shown to correlate with a reduced integral of viable cell density and a reduced product titer at day 14 in pH-controlled shaking flask cultivation with added sodium lactate [95]. Lactate concentration below 20 mmol L−1 is considered to not harm cell growth and productivity, whereby lactate concentration higher than 40 mmol L−1 was shown to harm CHO cell growth [96]. Therefore, a maximal cLac of 30 mmol L−1 was defined as the upper constraint, and the lactate concentration was minimized below this value to avoid potential lactate inhibition. The ammonium concentration was defined to be minimized. This was motivated based on the following understanding of its impact on product quality, even if it was not measured. Andersen et al. (1995) identified that the sialylation of a granulocyte colony-stimulating factor was significantly reduced by ammonium concentrations over 2 mmol L−1 [97]. Ha et al. (2015) investigated the mRNA expression levels of 52 N-glycosylation-related genes in recombinant CHO cells producing an Fc-fusion protein and observed a decrease of the protein production and the viable cell density after an addition of 10 mmol L−1 ammonium chloride. Simultaneously, the sialic acid content and the acidic isoforms were reduced after 5 days of cultivation [98].

Fig. 9
figure 9

Different shapes of the response surface plots for Xv, cLac, cmAb, and cAmm with different individual optimum. The user-defined constraints for medium optimization were marked red

Full size image

Subsequently, an objective (i.e., desirability) function di was calculated for each response yi individually, based on the user-defined constraints as lower acceptable response Li and the upper acceptable response Ui.

$$ {d}_i\left({y}_i\right)=\left[\begin{array}{cc}0& \mathrm{if}\ {y}_i<{L}_i\\ {}\frac{\left({y}_i-{L}_i\right)}{\left({U}_i-{L}_i\right)}& \mathrm{if}\ {L}_i<{y}_i<{U}_i\\ {}1& \mathrm{if}\ {y}_i>{U}_i\end{array}\right] $$
(18)

di(yi) is 0 if the optimization criteria is not fulfilled, and di(yi) tend toward 1 if the optimization is highly desirable. The multidimensional optimization problem is reduced with the multiplication of the different desirability function values di(yi) to one overall desirability D:

$$ D=\prod \limits_{i=1}^n{d}_i\left({y}_i\right) $$
(19)

The overall desirability function was calculated for the constraints mentioned and is shown in Fig. 10.

Fig. 10
figure 10

Response surface plot for the desirability function of the factors glucose and glutamine. The optimization criteria are fulfilled if the desirability tends toward 1

Full size image

Glutamine concentrations higher than approximately 10.5 mmol L−1 and glucose concentrations above 52 mmol L−1 result in a optimization criteria D = 0. The optimization criteria were also not reached below 4 mmol L−1 glutamine and 21 mmol L−1 glucose. The performance of these experiments would be time- and cost-intensive, without providing sufficient knowledge. In this way, multiple constraints were considered and only a small area (5 of the 20 evaluated factor combinations) results as suggested experimental space with D > 0. Only this 5 factor combinations of the 20 evaluated would increase the process understanding.

4.5 Comparison to Experimentally Performed Design

The usage of mDoE allows the a priori evaluation and reduction of the boundary values if mechanistic links could be formulated beforehand. The reduced experimental space was selected within the estimated desirability function (Fig. 10). Based on the evaluation of Fig. 10, the boundary values for the initial glucose concentration were defined between 52.5 mmol L−1 ≥ cGlc ≥ 32.5 mmol L−1. The initial glutamine concentration has to be between 10 mmol L−1 ≥ cGln ≥ 6 mmol L−1.

After the evaluation of the boundary values of the initially planned design, a new D-optimal design was planned (see Fig. 5) within the reduced design. Therefore, 16 experiments in a D-optimal design based on the reduced boundaries were planned and experimentally performed as well as simulated. The experimentally performed design was realized in 16 parallel shaking flask cultivations (approximately ten samples per cultivation). For the evaluation of the DoE in mDoE, the responses were only simulated. Both designs (experimental performed and simulated) were statistically evaluated, and the response surfaces were estimated. Both desirability functions were calculated due to the maximization of the antibody concentration and the minimization of the ammonium concentration and are shown in Fig. 11.

Fig. 11
figure 11

Reduced simulated (a) and experimentally (b) performed DoEs. Points are the considered factor combinations

Full size image

The evaluation is performed by the executing person, e.g., rely on their individual experience or user-defined constraints (device settings, etc.). Optimal starting concentrations in the upper right corner (high glucose as well as low glutamine concentrations) were recommended with D = 0.87 for the simulated design (Fig. 11a) and nearly the same for the experimentally performed design (D = 0.70). These small differences are typical when comparing the simulated results with uncertainty-based experimental results. No further experiments needs to be performed outside of this area, since the outer experimental space was evaluated beforehand using the digital twin (Sect. 4.4). Compared with the full experimental performed design, mDoE results in a reduction of 75% in the number of experiments (4 experiments for modeling vs. 16 experiments in experimental DoE).

The combination of model-assisted simulations with statistical tools can be used to decrease the experimental effort during medium optimization studies. Furthermore, the modeling study itself leads to an increase of the process understanding, which is part of QbD. No heuristic restrictions with several iterative rounds were necessary, because the mathematical process model incorporates the known factors and interactions and their dynamics in DoE. Furthermore, DoEs are typically based only on endpoints, and different responses and endpoints can be tested using the kinetic model.

4.6 Further Development of the Digital Twin in Process Development Workflow

The evolution of the mathematical process model as digital twin is part of mDoE, as briefly focused in the following. As shown in Fig. 12, an unstructured, unsegregated model was initially adapted and modified to describe the dynamics of cell growth and metabolism of antibody-producing CHO DP-12 cells for the purpose of medium optimization in batch mode (Sect. 4.1). The model incorporated known mechanistic links for CHO cells, and the initial data for modeling was based on just four experiments, and optimal conditions for the medium composition were identified [11].

Fig. 12
figure 12

Process development workflow in context to the digital twin

Full size image

The complexity of the digital twin could be further increased during the process development workflow. The mathematical model was expanded by metabolic inhibition terms to optimize cell growth and productivity in fed-batch mode [11]. Therefore, the digital twin was used to optimize the concentration of glucose as well as glutamine in the feed, the feeding rate, and the start of feeding. After optimizing the medium composition and fed-batch strategy, the digital twin was used in model-assisted scale-up to evaluate the bioprocess dynamics during process transfer and scale-up computationally [12]. Therefore, the mathematical model was extended by model parameter probability distributions, which were determined at different bioreactor scales due to measurement uncertainty. Finally, the quantified parameter distributions were statistically compared to evaluate if the process dynamics have been changed and the former optimized fed-batch strategy was successfully scaled up to 50 L pilot scale. The application in these different processes has deepened the knowledge and thus steadily increased the complexity of the digital twin [11, 12].

5 Conclusion and Outlook

In this chapter, the mDoE concept for the combination of mathematical process models with DoE was described. The most commonly used designs were examined, and one representative study was described in detail. The role of a digital twin was discussed and applied to a medium optimization case study using mDoE. A mathematical process model as a starting point for digital twin was adapted to four experiments, and widely distributed boundary values for a DoE were evaluated using model predictions instead of laboratory experiments. The reduced experimental spaces were experimentally performed (DoE) and compared to the simulated DoE (mDoE). The same optimal conditions were found, and the further development in different steps of a process development workflow was described. Finally, the development of a digital twin and its use in mDoE can be seen as a useful tool in decision-making for process development and optimization with DoE in QbD.

Statistical DoE can still be used for initial screening studies and can also lead to process optimization in several rounds. Compared to conventional DoE, mDoE supplies a more knowledge-based development of bioprocesses. Due to the mathematical model in mDoE, challenges in DoE can be avoided. The mathematical model can be used for simulating the entire time trajectory with, e.g., metabolite formation uptake. Hence, not only endpoints of experiments are examined. Thus the knowledge about the process can be increased. Furthermore, domain knowledge is required and can be captured as additional constraints to the system, leading to a focused screening or optimization of bioprocesses using the mathematical model as a digital twin in mDoE.

Currently, the mDoE approach is tested for algae, yeasts, and cell culture. Further applications of digital twins and mDoE can be seen in the field of cell therapeutics, e.g., in the treatment of previously untreatable diseases as tumor diseases, brain insult, and chronic infections. Since, the production of cells is still mainly performed in static culture systems (e.g., T-flasks), it is difficult to provide a sufficient quantity of patient-specific cells. A digital twin in combination with mDoE could be used to build up an understanding of the process and, e.g., scale-up to enable fast and efficient proliferation of stem and immune cells.