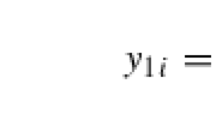Non-parametric Structural Models

Abstract

Nonparametric structural models facilitate the analysis of counterfactuals without making use of parametric assumptions. Such methods make use of the behavioural and equilibrium assumptions specified in economic models to define a mapping between the distribution of the observable variables and the primitive functions and distributions that are used in the model. Using these methods, one can infer elements of the model, such as utility and production functions, that are not directly observed. We review some of the latest works that have dealt with the identification and estimation of nonparametric structural models.

The interplay between economic theory and econometrics comes to its full force when analysing structural models. These models are used in industrial organization, marketing, public finance, labour economics and many other fields in economics. Structural econometric methods make use of the behavioural and equilibrium assumptions specified in economic models to define a mapping between the distribution of the observable variables and the primitive functions and distributions that are used in the model. Using these methods, one can infer elements of the model, such as utility and production functions, that are not directly observed. This allows one to predict behaviour and equilibria outcomes under new environments and to evaluate the welfare of individuals and profits of firms under alternative policies, among other benefits.

To provide an example, suppose that one would like to predict the demand for a new product. Since the product has not previously been available, no direct data exists. However, one could use data on the demand for existent products together with a structural model, as shown and developed by McFadden (1974). Characterize the new product and the existent competing products by vectors of common attributes. Assume that consumers derive utility from the observable and unobservable attributes of the products, and that each chooses the product that maximizes his or her utility of those attributes among the existent products. Then, from the choice of consumers among existent products, one can infer their preferences for the attributes, and then predict what the choice of each of them would be in a situation when a new vector of attributes, corresponding to the new product, is available. Moreover, one could get a measure of the differences in the welfare of the consumers when the new product is available.

Economic theory seldom has implications regarding the parametric structures that functions and distributions may possess. The behavioural and equilibrium specifications made in economic models typically imply shape restrictions, such as monotonicity, concavity, homogeneity, weak separability, and additive separability, and exclusion restrictions, but typically not parametric specifications, such as linearity of conditional expectations, or normal distributions for unobserved variables. Nonparametric methods, which do not require specification of parametric structures for the functions and distributions in a model, are ideally fitted, therefore, to analyse structural models, using as few a priori restrictions as possible. Nonparametric techniques have been applied to many models, such as discrete choice models, tobit models, selection models, and duration models. We will concentrate here, however, on the basic models and on those, indicate some of the latest works that have dealt with identification and estimation.

Nonparametric Structural Econometric Models

As with parametric models, a nonparametric econometric model is characterized by a vector X of variables that are determined outside the model and are observable, a vector ε of variables that are determined outside the model and are unobservable, a vector ϒ of outcome variables, which are determined within the model and are unobservable, and a vector Y of outcome variables that are determined within the model and are observable. These variables are related by functional relationships, which determine the causal structure by which ϒ and Y are determined from X and ε. The functional relationships are characterized by some functions that are known and some that are unknown. Similarly, some distributions may be known, some are unknown, and the others should be derived from the functional relationships and the known and unknown functions and distributions. Let h^* denote the vector of all the unknown functions in the model, F^* denote the vector of all unknown distributions, and ζ^* = (h^*, F^*)-In contrast to parametric models, in nonparametric models, none of the coordinates of ζ^* is assumed known up to a finite dimensional parameter.

Only restrictions such as continuity or values of the conditional expectations are assumed. The specification of the model should be such that from any vector ζ = (h, F), satisfying those same restrictions that ζ^* is assumed to satisfy, one is able to derive a distribution for the observable variables, F_YX(·, ζ).

Nonparametric Identification

When specifying an econometric model, we may be interested in testing it, or we may be interested in estimating ζ^* = (h^*, F^*) or some feature of ζ^*, such as only one of the elements of h^*, or even the value of that element at one point. Suppose that interest lies on estimating a particular feature, ψ(ζ^*) of ζ^*. The first question one must answer is whether that feature is identified. Let Ω denote the set of all possible values that ψ(ζ) may attain, when ζ is restricted to satisfy the properties that ζ^* is assumed to satisfy. Given ψ ∈ Ω, define Γ_Y,X(ψ) to be the set of all probability distributions of (Y, X) that are consistent with ψ. This is the set of all distributions that can be generated by a ζ, satisfying the properties that ζ^* is assumed to satisfy, and with ψ(ζ) = ψ. We say that two values ψ, ψ′∈ Ω are observationally equivalent if

$$ \left[{\Gamma}_{Y,X}\left(\psi \right)\cap {\Gamma}_{Y,X}\left({\psi}^{\prime}\right)\right]\ne \varnothing, $$

that is, they are observationally equivalent if there exist a distribution of the observable variables that could have been generated by two vectors ζ and ζ′ with ψ(ζ) = ψ and ψ(ζ′) = ψ′. The feature ψ* = ψ (ζ*) is said to be identified if there is no ψ ∈ Ω such that ψ ≠ ψ* and ψ is observationally equivalent to ψ*. That is, ψ* = ψ (ζ*) is identified if a change from ψ* to ψ ≠ ψ* cannot be compensated by a change in other unknown elements of ζ, so that a same distribution of observable variables could be generated by both, vectors ζ* and ζ with ψ* = ψ (ζ*) and ψ = ψ (ζ).

When ψ* can be expressed as a continuous functional of the distribution of observable variables (Y, X) one can typically estimate ψ* nonparametrically by substituting the distribution by a nonparametric estimator for it.

Additive and Nonadditive Models with Exogenous Explanatory Variables

The current literature on nonparametric econometrics methods considers additive and nonadditive models. In additive models, the unobservable exogenous variables ε are specified as affecting the value of Y though an additive function. Hence, for some functions m and v and some unobservable η

$$ Y=m(X)+v\left(X,\varepsilon \right)=m(X)+\eta . $$

In these models, the object of interest is typically the function m. Depending on the restrictions that one may impose on η, m may denote a conditional expectation, a conditional quantile, or some other function. Many methods exist to estimate conditional means and conditional quantiles nonparametrically. Prakasa Rao (1983), Härdle and Linton (1994), Matzkin (1994, 2007b), Pagan and Ullah (1999), Koenker (2005), and Chen (2007), among others, survey parts of this literature. Some nonparametric tests for these models include Wooldridge (1992), Yatchew (1992), Hong and White (1995), and Fan and Li (1996).

In nonadditive models, one is interested in analysing the interaction between the unobservable and observable explanatory variables. These models are specified, for some function m as

$$ Y=m\left(X,\varepsilon \right). $$

Nonparametric identification and estimation in models of this type was studied in Roehrig (1988), Olley and Pakes (1996), Brown and Matzkin (1998), Matzkin (1999, 2003, 2004, 2005, 2006), Chesher (2003), Imbens and Newey (2003), and Athey and Imbens (2006), among others.

Dependence Between Observable and Unobservable Explanatory Variables

In econometric models, it is often the case that in an equation of interest, some of the explanatory variables are endogenous; they are not distributed independently of the unobservable explanatory variables in that same equation. This typically occurs when restrictions such as agent’s optimization and equilibrium conditions generate interrelationships among observable variables and unobservable variables, ε, that affect a common observable outcome variable, Y. In such cases, the distribution of the observable outcome and observable explanatory variables does not provide enough information to recover the causal effect of those explanatory variables on the outcome variable, since changes in those explanatory variables do not leave the value of ε fixed. A typical example of this is when Y denotes quantity demanded for a product, X denotes the price of the product, and ε is an unobservable demand shifter. If the price that will make firms produce a certain quantity increases with quantity, this change in ε will generate an increment in the price X. Hence, the observable effect of a change in price in demanded quantity would not correspond to the effect of changing the value of price when the value ε stays constant. Another typical example arises when analysing the effect of years of education on wages. An unobservable variable, such as ability, affects wages and also affects the decision about years of education.

Estimation Techniques for Additive and Nonadditive Functions of Endogenous Variables

The estimation techniques that have been developed to estimate nonparametric models with endogenous explanatory variables typically make use of additional information, which provides some exogenous variation on either the value of the endogenous variable or on the value of the unobservable variable. The common procedures are based on conditional independence methods and on instrumental variable methods. In the first set of procedures, independence between the unobservable and observable explanatory variables in a model is typically achieved by either conditioning on observable variables, or conditioning on unobservable variables. A control function approach (Heckman and Robb 1985) models the unobservable as a function, so that conditioning on that function purges the dependence between the explanatory observable and unobservable variables in the model. Instrumental variable methods derive identification from an independence condition between the unobservable and an external variable (an instrument) or function, which is correlated with the endogenous variable and which might be estimable.

Conditioning on unobservable variables often requires the estimation of those unobservable variables. Two-step procedures, where they are first estimated, and then used as additional regressors in the model of interest have been developed for additive models by Ng and Pinkse (1995), Pinkse (2000), and Newey et al. (1999), among others. Two-step procedures for nonadditive models have been developed by Altonji and Matzkin (2001), Blundell and Powell (2003), Chesher (2003), and Imbens and Newey (2003), among others. Conditional moment estimation methods or quasi-maximum likelihood estimation methods can also be used (see, for example, Ai and Chen 2003). Altonji and Ichimura (2000), Altonji and Matzkin (2001, 2005), and Matzkin (2004), among others, considered conditioning on observables for estimation of nonadditive models with endogenous explanatory variables. Matzkin (2004) provides insight into the sources of exogeneity that are generated when conditioning on either observables or unobservables, and which allow identification and estimation in nonadditive models. In particular, if Y = m(X, ε), with m strictly increasing in ε, and ε is independent of X conditional on W, she shows that there exists functions s(W,η) and r(W, δ) such that δ is independent η conditional on W, X = s(W, η) and ε = r(W, δ). Hence,

$$ Y=m\left(X,\varepsilon \right)=m\left(s\left(W,\eta \right),r\left(W,\delta \right)\right). $$

Instrumental variable methods for additive models were considered by Newey and Powell (1989, 2003), Ai and Chen (2003), Darolles et al. (2003), and Hall and Horowitz (2003), among others. To develop estimators for m in the model

$$ {Y}_1=m\left({Y}_2\right)+\varepsilon \kern0.5em E\left[\varepsilon |Z\right]=0. $$

they use the moment condition

$$ E\left[{Y}_1|Z=z\right]=\int m\left({y}_2\right){f}_{Y_2\mid Z=z}\left({y}_2\right){dy}_2, $$

which depends on the conditional expectation E[Y₁|Z = z] and the conditional density ${f}_{Y_2\mid Z=z}\left({y}_2\right)$, which can be estimated nonparametrically. For nonadditive models, of the form

$$ {Y}_1=m\left({Y}_2,\varepsilon \right)\kern1em \varepsilon \kern1em \mathrm{independent}\ \mathrm{of}\kern0.5em Z $$

where m is strictly increasing in ε, Chernozhukov and Hansen (2005) and Chernozhukov et al. (2007) developed estimation methods using the moment condition that for al τ

$$ \tau =E\left[1\left(\varepsilon <\tau \right)\left]=E\right[1\left(\varepsilon <\tau \right)|Z\right] $$

from which m can be estimated using the conditional moment restriction

$$ E\left[1\left({Y}_1<m\left({Y}_2,\varepsilon \right)\right)\hbox{--} \varepsilon |Z\right]=0. $$

Matzkin (2006) considered the model

$$ {Y}_1={m}_1\left({Y}_2,\varepsilon \right)\ {Y}_2={m}_2\left({Y}_1,\kern0.5em Z,\eta \right) $$

where Z is distributed independently of (ε, η). She established restrictions on the functions m₁ and m₂ and on the distribution of (ε, η, Z) under which

$$ {\left[\frac{\partial {r}_1\left({y}_1,\kern0.5em {y}_2\right)}{\partial {y}_2}\right]}^{-1}\left[\frac{\partial {r}_1\left({y}_1,\kern0.5em {y}_2\right)}{\partial {y}_1}\right] $$

can be expressed as a function of the conditional density ${{f_{Y_1}}_{,{Y}_2}}_{\mid Z={z}^{\ast }}\left({y}_1,{y}_2\right)$, where r₁ is the inverse of m₁ with respect to ε, and the value z* of the instrument Z is easily identified (see also Matzkin 2005, 2007a, b).

Estimation of Averages and Average Derivatives

Nonparametric estimators are notorious by their slow rate of convergence, which worsens as the dimension of the number of arguments of the nonparametric function increases. A remedy for this is to consider averages of the nonparametric function. The average derivative method in Powell et al. (1989) and the partial integration methods of Newey (1994) and Linton and Nielsen (1995), for example, show how rates of convergence can increase by averaging a nonparametric function or its derivatives. This approach has been extended to cases where the explanatory variables are endogenous, using additional variables to deal with the endogeneity, and averaging over them. Examples are Blundell and Powell’s (2003) average structural function, Imbens and Newey’s (2003) average quantile function, and Altonji and Matzkin’s (2001, 2005) local average response function.

Suppose, for example, that the model of interest is

$$ {Y}_1=m\left({Y}_2,\varepsilon \right) $$

and W is such that Y₂ and ε are independent conditional on W. Then, the Blundell and Powell (2003) average structural function is

$$ G\left({y}_2\right)=\int m\left({y}_2,\varepsilon \right){f}_{\varepsilon}\left(\varepsilon \right) d\varepsilon $$

which can be derived from a nonparametric estimator for the distribution of (Y₁, Y₂, W) as

$$ G\left({y}_2\right)=\int E\left({Y}_1|{Y}_2={y}_2,W=w\right){f}_W(w) dw. $$

Imbens and Newey’s (2003) quantile structural function is defined for the τ-th quantile of ε, q_ε(τ), as

$$ r\left({y}_2,{y}_1\right)=\Pr \left(m\left({Y}_2,{q}_{\varepsilon}\left(\tau \right)\right)\le {y}_1|{Y}_2={y}_2\right) $$

which can be estimated by

$$ {\displaystyle \begin{array}{ll}\hfill & r\left({y}_2,{y}_1\right)\\ {}& =\int \Pr \left({Y}_1\le {y}_1|{Y}_2={y}_2,W=w\right){f}_W(w) dv.\hfill \end{array}} $$

Altonji and Matzkin’s (2001, 2005) local average response function is

$$ \beta \left({y}_2\right)=\int \frac{\partial m\left({y}_2,\varepsilon \right)}{\partial {y}_2}{f}_{\varepsilon \mid {Y}_2={y}_2}\left(\varepsilon \right) d\varepsilon $$

which can be derived from a nonparametric estimator for the distribution of (Y₁, Y₂, W) as

$$ {\displaystyle \begin{array}{ll}\beta \left({y}_2\right)=& \int \frac{\partial E\left({Y}_1|{Y}_2={y}_2,W=w\right)}{\partial {y}_2}{f}_{W\mid {Y}_2={y}_2}(w)\hfill \\ {}& \times dw.\hfill \end{array}} $$

Conclusions

The literature on nonparametric structural models has been rapidly developing in recent years. The new methods allow one to analyse counterfactuals without making use of parametric assumptions. Estimation of some features of the model rather than the functions themselves may reduce the curse of dimensionality, therefore providing improved properties and reducing the need for large data-sets.

See Also

• Endogeneity and Exogeneity

• Identification

• Quantile Regression

• Simultaneous Equations Models