Segmented Mirror Telescopes

Abstract

Constructing the primary mirror of a telescope out of segments, rather thanfrom a monolithic piece of glass, can drastically reduce the mass of themirror and its material costs, thereby making possible the construction ofoptical/infrared telescopes with very large diameters. However, segmentation alsointroduces a host of complications, involving the fabrication of off-axis optics,novel diffraction effects, active segment control systems, in situ aberrationcorrection, and the optical alignment of large numbers of degrees of freedom.Progress in these latter areas over the last 25 years has led to the successfuldevelopment of the two Keck telescopes, as well as several other segmentedtelescopes in the 10-m class. Giant segmented telescopes of similar design, butwith mirror diameters of 30–40 m, are now in the planning stages, withfirst light expected around the end of the decade. Segmentation has alsomade possible the 6.5-m James Webb Space Telescope, which is currentlyunder construction. In this work, the technical issues associated withsegmentation are discussed and reviewed in detail. Particular attention ispaid to the properties of arrays of hexagonal segments (the segmentationpattern of choice for these telescopes), including their diffraction patternsand algorithms for their active control. Optical alignment issues are alsodiscussed.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

3.1 Introduction

The motivation for building larger ground-based telescopes has been clear for a very long time: for a telescope of fixed (seeing-limited) resolution, the observing time necessary to reach a given signal-to-noise ratio varies as 1 ∕ D ², where D is the diameter of the primary mirror. However, with the development of adaptive optics (AO), the motivation for building ever larger telescopes is even more powerful. In the first place, with AO, the resolution is no longer set by the atmosphere, independent of the telescope diameter, but rather is given by the diffraction limit λ ∕ D, where λ is the wavelength, so that the angular information content now increases dramatically as the telescope gets larger. In addition, at least for background-limited adaptive optics observations, the benefit of a large telescope grows as D ⁴, not D ²; not only is there the collecting area advantage, according to which the signal grows as D ², but there is less background “behind” the image, so that the noise is reduced by this same factor.

Building a giant telescope from a single monolithic mirror presents many difficulties. These difficulties typically grow rapidly with increasing mirror size and make building monolithic mirrors with diameters of 10 m or more highly impractical. The key issues, briefly stated, are:

• Mirror blank material is expensive and availability may be limited.

• The financial risk associated with breakage increases rapidly with the mirror diameter. The probability of breakage may also increase.

• Passive support of the mirror will result in large optical deflections.

• Larger mirrors are subject to larger deformations and hence large optical aberrations from thermal changes.

• The vacuum chamber for mirror coatings becomes very large and expensive.

• Tool costs for all parts (fabrication and handling) are large.

• Shipping a very large mirror to the observatory site may be impractical.

An obvious solution to these and other problems is to construct the primary mirror from smaller segments, rather than building a single large mirror. Consider problems related to the mass or thickness of the mirror. The gravitational deflection suffered by an optic increases as D ⁴. This means that a monolith must have N times the thickness of a segmented mirror consisting of N equal segments covering the same area. Thus, the 36 segments of each Keck telescope are 7.5 cm thick; an equivalent monolith would be 2.7 m thick! Although many important problems are greatly reduced by building the primary from small segments, there are a number of issues, concerns, and problems that arise with segmentation, and these must be understood and dealt with before one can confidently proceed with building a large telescope having a segmented primary.

The various issues and complications associated with segments can generally be grouped into four categories:

• Because of the large number of segments (36–91 in the current segmented telescopes, 500–1,000 in the extremely large telescopes of the future), the telescope will have a large increase in the number of parts and a proportional increase in complexity.

• Segments are difficult to polish because they are off-axis sections of the parent figure of revolution and are therefore not locally axisymmetric.

• Segments require both active position control and optical alignment. Here and throughout this review, these concepts are distinguished as follows. Optical alignment places the mirror segments in the proper relative positions with respect to one another to within optical tolerances; active position control keeps these relative positions fixed (i.e., it “freezes” the mirror).

• Segment edges and the associated intersegment gaps add to both diffraction and thermal background effects.

The first item, increased complexity, is a general one and is only addressed in a general way in this review. To some extent, the increase in complexity is offset by the advantage, not shared by monolithic systems, that small prototype subsystems, consisting, for example, of a few (full-sized) segments, together with their mechanical supports and associated control electronics, can be built relatively cheaply and used for thorough testing and optimization. In this way, one can engineer components that are highly reliable, so that the probability of failure of critical components can be kept relatively low.

The complexity problem can be further mitigated by providing sufficient spares and by designing the system so that one is able to replace defective components quickly and easily, especially in those cases where the failure of even a single component of a given type (e.g., a segment position actuator) would have serious consequences. It may also be possible to design some aspects of the system so that the failure of a few components of a given type will have little or no effect on the performance of the overall system. Thus, the active control systems of the Keck telescopes are sufficiently robust that the failure of several edge sensors can be tolerated (as long as they can be identified and removed from the control loop). Indeed, neither Keck telescope has ever operated with its full complement of 168 edge sensors all working at the same time. Note that for extremely large telescopes even the temporary loss of an actuator may have little impact on many kinds of science.

The last three items in the above list are specific issues that are discussed in some detail below. A brief history of segmented-mirror telescopes is presented in Sect. 2. General segmentation issues are discussed in Sect. 3, followed by segment asphericity in Sect. 4, segment polishing in Sect. 5, and segment support in Sect. 6. Diffraction and thermal effects are treated in Sects. 7 and 8, respectively. Active control of segments is discussed in Sect. 9 and optical alignment in Sect. 10. Little or no time is spent on those aspects of large (or extremely large) telescopes that are not specifically related to segmentation – for example, telescope drives or dome shutters. However, it is worth noting that adapting the conventional designs of such items to the scale of a 10-m telescope (or larger) can often be a nontrivial problem in itself.

The technical issues listed in the previous paragraph are discussed below in the specific context of the Keck telescopes but with an indication as to how these may be generalized, as, for example, in the discussion of control matrices; alternative approaches to such topics as segment phasing are also described. The review concludes with descriptions of the other segmented-mirror telescopes currently in operation in Sect. 11, as well as those that are under development in Sect. 12.

3.2 History of Segmented-Mirror Telescopes

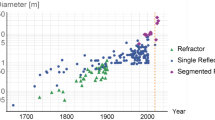
The first recorded use of segmented optics appears to have been by Archimedes, who in 212 BC used an array of mirrors to focus the sun’s rays on the ships of the attacking Roman navy in order to defend Syracuse (although claims that the ships burst into flames as a result may have been exaggerated (Papadogiannis et al. 2009)). More recently, Horn d’Arturo in Italy made a 1.5-m mirror out of 61 hexagonal segments in 1932. However, it was only used vertically and was not actively controlled (Horn D’Arturo  1955). In the 1970s, Pierre Connes in France made a 4.6-m segmented-mirror telescope for infrared astronomy (Chevillard et al. 1977). It was fully steerable and actively controlled, but there were problems with image quality, and the telescope was never put into operation.

A variation on the theme of a segmented-mirror telescope was the Multiple Mirror Telescope (MMT) (Beckers et al. 1982); it consisted of six 1.8-m telescopes in a common mount. The MMT was not a true segmented-mirror telescope and no longer exists in its original multiple mirror configuration, but its advantages and disadvantages compared to a true segmented-mirror telescope are nevertheless worthy of some discussion (see Sect. 3).

The Keck Observatory began as a conceptual design study for a 10-m segmented-mirror telescope (Nelson et al. 1985) in the late 1970s. This project was formally begun in 1984, and full science operations began in 1993. The telescope was quite successful, and as a result, funds were acquired to build a second Keck telescope, 75 m from the first. The close proximity was designed to allow the two Keck telescopes to be used for interferometry as well as for individual telescope observing. Keck 2 was completed in 1996 and began science observations in that year. Each of the telescopes has its own suite of scientific instruments and an adaptive optics system. Interferometric science observations began in 2003. The success of the Keck telescopes led to a Spanish project, the Gran Telescopio Canarias, (GTC) (Rodriguez Espinosa et al. 1999), a 10-m telescope similar to Keck on La Palma in the Canary Islands (see Sect. 11.1).

The Keck telescopes have hyperbolic primary mirrors and this leads to the requirement of polishing off-axis mirror segments. However, this is not the only possible approach to segmentation. Telescopes with spherical primaries can also be designed; these have identical, although not identically spaced, segments, and must contend with a large amount of spherical aberration. A telescope of this latter design, the Hobby-Eberly Telescope, was completed in the late 1990s at the McDonald Observatory in Texas (Barnes et al. 2000). The HET has 91 spherically polished primary mirror segments and is effectively a 9-m telescope. A telescope of very similar design, the Southern African Large Telescope (SALT) (Buckley et al. 2004) saw first light in 2005. The HET and SALT are described in further detail in Sect. 11.2.

Segmented-mirror telescopes as large as 50–100 m have been proposed (Andersen et al. 2004; Dierickx et al. 2002), but the two largest such telescopes currently well into the design stage are the Thirty Meter Telescope (TMT) (Nelson and Sanders 2006), a collaboration of the United States, Canada, and several international partners, and the 42 m European Extremely Large Telescope (E-ELT) (Gilmozzi and Spyromilio 2008), a project of the European Southern Observatory. The Giant Magellan Telescope (circumscribed diameter 24.5 m), although of markedly different design than the other telescopes described in this review, is nevertheless considered a giant segmented-mirror telescope and is discussed briefly in Sect. 12.1. The TMT and E-ELT are described further in Sects. 12.2 and 12.3.

3.3 Segmentation Geometries

There are many ways one can imagine dividing up a primary mirror into smaller optical elements, including:

• Independent telescope arrays

• Independent telescopes on a common mount

• Random subapertures as part of a common primary

• Annular segmentation of a common primary

• Hexagonal segmentation of a common primary

Independent arrays of telescopes have been considered for decades but have generally not been successful, except for radio telescopes, which are aided by the fact that the individual telescope signals can be amplified and combined while preserving phase information. This is not practical in the optical; thus, there are significant inefficiencies associated with coherently combining the light from an array of optical telescopes. Instrumentation for an array of telescopes has also been a cause of difficulty. Perhaps the best known successful array has been the VLT with four 8-m telescopes, each with its own suite of science instruments, and the capacity to combine all telescopes together for interferometric measurements. (The VLT can also be operated as four individual telescopes.)

An alternative to a segmented primary is to put a modest number of independent telescopes into a common mount. The Multiple Mirror Telescope (MMT) (Beckers et al. 1982), consisting of six 1.8-m telescopes, including six separate secondaries, configured in this way (equivalent to a 4.5-m aperture), operated on Mount Hopkins in Arizona, from 1979 to 1998. Although the multiple mirror approach can result in large, well-corrected fields of view, it has many disadvantages compared to a true segmented-mirror telescope. These include the less compact design, which necessitates a larger dome and slit, the difficulty of phasing noncontiguous mirrors, the need for an expensive and complicated beam combiner to bring the light to a common focus, and a generally more complicated diffraction pattern from the sparse aperture. The original six-mirror MMT is no longer in use, having been replaced by a single 6.5-m mirror of honeycomb design (West et al. 1997) in 2000. The proposed Giant Magellan Telescope (Johns 2008) resembles the original MMT in that it has seven circular primary mirror “segments,” each 8 m in diameter, (it includes an on-axis mirror, which the original MMT did not have), but it will have a single secondary so that a beam combiner is not needed.

Special application telescopes have been built with very sparse arrays in order to sample the resolution space with the minimum number of mirrors. Systems like this may give greater angular resolution (longer baseline) but have less sensitivity due to the smaller collecting area. Dense segmentation is generally favored when one is attempting functional replication of the optical properties of a single monolithic mirror. These kinds of mirrors have the best central concentration of light, leading to the smallest instruments and best signal-to-noise ratio, and, for a given collecting area, are generally the most compact and thus the least expensive.

Dense segmentation can be achieved with radial petals (Burgarella et al. 2002), annular patterns, hexagonal patterns, and many others. A regular pattern can only be made of regular polygons (e.g., hexagons) if the mirror is flat, since a curved surface can only be tessellated with nonregular polygons. However, the segments may appear regular when seen in projection. Each of these patterns has its advantages and disadvantages, specific to the fabrication techniques planned. For example, annular rings in general have large numbers of identical segments, so that replication techniques may be utilized and the number of necessary spares is reduced. Hexagons make the best use of the material typically produced in round boules of glass and are easier to polish because the corners are less severe than are four-sided polygons.

In general, for a telescope with N hexagonal segments, there are N ∕ 6 different segment shapes. Having six segments of each shape has not been enough to motivate the use of replication techniques, but at least the number of required spares is reduced by a significant factor. Hexagonal segments also tend to be easier to support against gravity and to attach to position actuators (three per segment) because of their symmetry. Overall, the advantages of hexagonal segments have made this the segmentation pattern of choice for most of the current and planned segmented-mirror telescopes.

Hexagonal segments are naturally arrayed in rings. The Keck telescopes consist of three rings with a total of 36 segments; the central segment, which would be blocked by the secondary mirror, is omitted. For a telescope of n rings, with the central segment omitted, the total number of segments is

$${N}_{\mathrm{seg}} = 3{n}^{2} + 3n$$

(3.1)

and the total number of intersegment edges is

$${N}_{\mathrm{edge}} = 9{n}^{2} + 3n - 6$$

(3.2)

There are three actuators per segment and two sensors per intersegment edge. As the number of segments becomes large, the number of sensors approaches six per segment (two per actuator), since the 12 sensors around a segment are shared with its nearest neighbors. Edge effects, larger for smaller values of n, reduce this ratio somewhat. (Note that, with the central segment missing, a single ring of six segments (n = 1) would have fewer sensors (12) than actuators (18) and thus would not provide a stable configuration for testing a partially completed telescope. However, two rings (72 sensors and 54 actuators) is a stable configuration.) For the extremely large telescopes of the future, with very large numbers of segments, it is advantageous to omit some segments in the outer rings in order to produce a more nearly circular primary.

A significant issue in the segmentation of a telescope mirror is the determination of the optimal segment size. This involves a complicated trade-off: smaller segments are easier and less expensive to fabricate and to support, but there need to be more of them, so alignment and control becomes more difficult. The Keck design study chose a segment side length of 0.9 m, so that 36 segments were required to fill the 10-m aperture; the thickness was 75 mm. In retrospect, for these parameters, the control and alignment of the segments was in some sense easier than the fabrication. As a result, the giant segmented telescopes of the future will have somewhat smaller segments, with a hexagon side length of about 0.7 m.

3.4 Segment Surface Asphericity

Two-mirror telescopes are the most common optical design for ground-based telescopes. These systems require a parabolic or hyperbolic primary mirror. As mentioned above, it is possible to build a segmented-mirror telescope with a primary mirror that is spherical so that the segments are easier to fabricate; however, several additional mirrors are then needed to correct the resultant spherical aberration, and the associated light loss and additional alignment complexity make this configuration less commonly used. In this review, it is assumed that a nonspherical primary is desired and the resulting requirements on the segment figures are discussed.

The primary mirror is typically a figure of revolution, but since it is not spherical, pieces of the primary will not look identical and will not be figures of revolution about their local centers. This basic fact introduces significant complexity for segmented mirrors. The polishing of off-axis segments, which are not figures of revolution, is generally much more difficult than the polishing of spheres. Second, off-axis optics must be carefully aligned in all six rigid body degrees of freedom, and the larger the segment asphericity (deviation from a sphere), the tighter the alignment tolerances become.

This section describes in mathematical detail the surfaces of these segments. The general equation of a conic can be written as

$${r}^{2} - 2kx + (1 + K){z}^{2} = 0$$

(3.3)

where r is the (global) radial coordinate, k is the radius of curvature, and K is the conic constant. It is useful to expand this in powers of r as

$$z(r) = \frac{{r}^{2}} {2k} + (K + 1) \frac{{r}^{4}} {8{k}^{3}} + {(K + 1)}^{2} \frac{{r}^{6}} {16{k}^{5}} + {(K + 1)}^{3} \frac{5{r}^{8}} {128{k}^{7}} + \cdots $$

(3.4)

Expressed in the local segment coordinate system, the symmetry of the equation seen in the global coordinate system is lost, and one will see azimuthal variations. It is useful to express the equation for the segment surface in its local coordinate system:

$$z(\rho,\theta ) =\sum\limits_{n,m}{\alpha }_{nm}{\rho }^{n}\cos m\theta +\sum\limits_{n,m}{\beta }_{nm}{\rho }^{n}\sin m\theta $$

(3.5)

where ρ, θ are the local coordinate system polar coordinates. A suitable rotation of the local coordinate system will cause the β _nm to vanish, and analyticity requires that n, m ≥ 0, n ≥ m, and n − m must be divisible by 2. The expansion has been made (Nelson and Temple-Raston 1982) and yields for the expansion coefficients α _mn :

$$\begin{array}{rcl}{ \alpha }_{20}& =& \frac{{a}^{2}} {k} \left [ \frac{2 - K{\epsilon }^{2}} {4{(1 - K{\epsilon }^{2})}^{3/2}}\right ]\end{array}$$

(3.6)

$$\begin{array}{rcl}{ \alpha }_{22}& =& \frac{{a}^{2}} {k} \left [ \frac{K{\epsilon }^{2}} {4{(1 - K{\epsilon }^{2})}^{3/2}}\right ]\end{array}$$

(3.7)

$$\begin{array}{rcl}{ \alpha }_{31}& =& \frac{{a}^{3}} {{k}^{2}}\left [\frac{K\epsilon {[1 - (K + 1){\epsilon }^{2}]}^{1/2}(4 - K{\epsilon }^{2})} {8{(1 - K{\epsilon }^{2})}^{3}} \right ]\end{array}$$

(3.8)

$$\begin{array}{rcl}{ \alpha }_{33}& =& \frac{{a}^{3}} {{k}^{2}}\left [\frac{{K}^{2}{\epsilon }^{3}{[1 - (K + 1){\epsilon }^{2}]}^{1/2}} {8{(1 - K{\epsilon }^{2})}^{3}} \right ]\end{array}$$

(3.9)

$$\begin{array}{rcl}{ \alpha }_{40}& =& \frac{{a}^{4}} {{k}^{3}}\left [\frac{8(1 + K) - 24K{\epsilon }^{2} + 3{K}^{2}(1 - 3K){\epsilon }^{4} - {K}^{3}(2 - K){\epsilon }^{6}} {64{(1 - K{\epsilon }^{2})}^{9/2}} \right ]\end{array}$$

(3.10)

where a is the segment radius, ε = R ∕ k, and R is the off-axis distance of the segment center. It is useful to expand each of the above equations as a power series in ε:

$$\begin{array}{rcl}{ \alpha }_{20}& =& \frac{{a}^{2}} {2k} + \frac{K{a}^{2}{\epsilon }^{2}} {2k} + \frac{9{K}^{2}{a}^{2}{\epsilon }^{4}} {16k} + \cdots \end{array}$$

(3.11)

$$\begin{array}{rcl}{ \alpha }_{22}& =& \frac{K{a}^{2}{\epsilon }^{2}} {4k} + \frac{3K{a}^{2}{\epsilon }^{4}} {8k} + \cdots \end{array}$$

(3.12)

$$\begin{array}{rcl}{ \alpha }_{31}& =& \frac{K{a}^{3}\epsilon } {2{k}^{2}} + \frac{(9K - 2)K{a}^{3}{\epsilon }^{3}} {8{k}^{2}} + \cdots \ \end{array}$$

(3.13)

$$\begin{array}{rcl}{ \alpha }_{33}& =& \frac{{K}^{2}{a}^{3}{\epsilon }^{3}} {8{k}^{2}} + \cdots \ \end{array}$$

(3.14)

$$\begin{array}{rcl}{ \alpha }_{40}& =& \frac{(1 + K){a}^{4}} {8{k}^{3}} + \cdots \ \end{array}$$

(3.15)

As an explicit example consider the outermost segment (R = 4. 68 m) for the Keck telescopes, which has a = 0.9 m, k = 35 m, K = − 1. 003683, and D = 10.95 m. The segment figures are given in terms of the expansion coefficients in Table  3-1 . Note that the expansion here is in terms of the functions ρ^mcosnθ. These are not the same as Zernike polynomials, but for the lowest orders, they differ only in terms of normalization and in meaningless piston, tip, and tilt (and in defocus for α ₄₀). (They are therefore referred to by the same names.) The former functions are used here for simplicity, for continuity with the literature, and because it is convenient in the present context that the coefficients α _nm give the maximum deviation of the surface directly. Elsewhere in this review, aberrations (as opposed to nominal surface shapes) are expressed in terms of Zernike polynomials. For the latter, the numbering and normalization conventions of Noll (1976) are followed. In the latter convention, the Zernike coefficient gives the rms over the circumscribed circular surface, not the maximum deviation.

Table 3-1 Expansion coefficients for Keck outermost segment shapes

The focus term simply represents the nominally spherical surface. The higher terms quantify the departures from sphericity. As the size of the segments is reduced (for a fixed overall primary mirror area), the higher order terms quickly become smaller, making the segments easier to polish, but more difficult to control, since there are more of them. For the 1.8-m-diameter Keck segments, inspection of Table  3-1 shows that both the astigmatism and coma terms are quite large compared to the ∼ 0.5 μm wavelength of visible light and must therefore be polished out correctly to a fraction of a percent of their nominal values. This represents a unique challenge for segmented optics and requires special polishing techniques.

3.5 Segment Polishing

There are two major areas of concern in polishing segments. The first is the challenge of polishing aspheres. The second is the issue of polishing the surface properly all the way out to the edge of the segment.

Polishing aspheres is difficult because polishing only works well when the polishing tool fits the glass surface to within typical distances of order 1 μm. Polishing tools move in a random motion to produce the desired smoothness, which means that the tool must be spherical in shape, and thus the contact area is limited by the asphericity. There are three main approaches to polishing. The first, the one used for the Keck segments, is stressed mirror polishing (Lubliner and Nelson 1980; Nelson et al. 1980) where the mirror is deformed so that the desired shape is mapped into a sphere. Large tools can then be used to polish a spherical surface, which will relax into the desired shape when the stresses are released. The second approach, stressed lap polishing, is to deform the tool dynamically so that it always fits the mirror as it moves around the surface. The third method is to use suitably small tools so that the tool fit is adequate and make raster scans of the mirror with this small tool.

In addition to these approaches, there are two methods currently in use that do not require a good fit between the tool and the part. These are ion beam figuring and magnetic rheological figuring (MRF). In ion beam figuring, a beam of argon or another rare gas ion is used to remove material from the optical surface, analogous to sandblasting, but at the atomic level (Braunecker et al. 2008). The technique has the advantages of being noncontact, non-iterative, and quite accurate, but it must be done in a vacuum chamber, and the rate of material removal is relatively slow. Ion figuring was used as the final production step in making the Keck segments. The MRF technique exploits the fact that a magneto-rheological fluid greatly increases its viscosity in the presence of a magnetic field, so that its ability to transmit a force can be accurately controlled and rapidly adjusted. Like ion beam figuring, MRF is accurate but relatively slow.

Edge effects must be considered carefully because a significant fraction of the overall area of the primary mirror lies relatively close to at least one intersegment edge. Again, several approaches have been considered. The approach used for the Keck segments was to polish the mirrors as rounds and, when the main polishing was complete, to cut the rounds into the desired hexagonal segments. This introduces no local effects but introduces some global deformations associated with the release of internal stresses. For the Keck segments, the latter deformations were removed by ion figuring. A second approach is to add small “shelves” of material to the edges in order to support the polishing tool when it is near the edge. It is the polishing near the edge that typically rolls the edge in an optically objectionable fashion. The third approach is to polish near the edges with smaller and smaller tools to control the size of the rolled edge. A variant on the first method is to polish spheres with a so-called planetary polisher. In this case, the polishing tool is much larger than the part, and the part is placed face down on the polishing tool in order to produce roll-free edges.

3.6 Segment Support

Supporting the primary mirror segments is a nontrivial problem in mechanical engineering. If a Keck segment were supported on the three actuator points alone, the maximum deflection under gravity due to the weight of the segment itself would be about 1.7 μm when the telescope is pointed at the zenith (Nelson et al. 1985). (A formal study of the deflection of thin plates on point supports has been made by Nelson et al. (1982)). In order to reduce the deflections by the required two orders of magnitude, the axial force of each actuator is distributed over a 12-point whiffletree, so that the segment is supported on a total of 36 points. This reduces the gravitational deflections to 8 nm. To satisfy the high-bandwidth requirements of the active control system, the whiffletrees must be very stiff axially, but they also need to be very flexible radially. The Keck whiffletree design accomplishes this by means of aluminum I-beams with flex pivots and flex rods at each of the 36 points. The flexures also minimize stress on the mirror due to thermal expansion of the whiffletrees.

By attaching springs that extend from the whiffletree to the mirror cell, forces can be applied to the segment in order to warp its surface. These so-called warping harnesses are used at Keck to provide in situ correction to the segment figures. The ability to make warping harness adjustments allows one to correct for the aberrations that segments may acquire as the result of release of internal stresses when the originally circular segments are cut into hexagons, and also allows one to relax the polishing tolerances on the segments, with a resulting cost savings. Adjustment of the Keck warping harnesses is carried out manually immediately after a segment is installed after aluminization. The measurements required for warping harness adjustments at Keck are described in Sect. 10.3 below.

Each Keck segment is supported radially by a thin diaphragm. As the telescope moves from zenith to horizon, the load gradually transfers from the whiffletrees to the diaphragm. The mechanical characteristics of the diaphragm are opposite to those of the whiffletrees: the diaphragm is radially stiff and axially flexible. A thick displacement-limiting disk beneath the diaphragm provides a hard stop that prevents the segment from moving far enough to damage the edge sensors.

3.7 Diffraction Effects

Segment edges will introduce diffractive effects in the image in addition to the diffractive effects caused by the overall aperture itself. Of course, it is desirable to minimize the size of segment gaps, but finite physical and optical gaps are both necessary. Physical (air) gaps provide clearance so that segments do not touch each other during installation and removal. Optical (non-reflective) gaps in the form of bevels are necessary to avoid chipping of edges. Both the physical and optical gaps are typically a few millimeters wide. The Keck segments have 2-mm bevels on the edges and a 3-mm air gap between segments, for a 7-mm total nonoptical strip between segments. The design for the TMT calls for gaps about half this size. By contrast, for a telescope made up of identical segments with spherical surfaces, the gaps are set by geometry, since, as previously noted, it is impossible to tessellate a curved surface with regular polygons. These latter gaps tend to be larger than those mandated by physical and optical considerations, but the concern in this section is primarily with the smaller, Keck-type gaps.

For circular apertures, the simplest of mirrors, the diffraction-limited image is an Airy pattern, and for large angular distances ω the intensity pattern falls as ω^{− 3}, and is azimuthally symmetric. Polygonal mirror segments (such as those of Keck) will concentrate the diffracted energy into lines perpendicular to the segment edges, thus producing a diffraction pattern that is brighter or darker in some places than that of a circular aperture.

The amount of energy in the diffraction pattern and the angular scale of this pattern are set by the size of the segment and the size of the intersegment gaps. In general, diffracted energy is spread out over an angular scale of order $\lambda /\mathcal{l}$ where λ is the wavelength and $\mathcal{l}$ is the appropriate linear scale. This may be the segment gap, the segment diameter, the full diameter of the primary mirror, etc. Furthermore, the fraction of the total intensity that is diffracted out to the angular scale characteristic of the segment gaps will simply be equal to the fraction of the area of the primary mirror that is covered by the gaps (including the associated edge bevels).

The Keck gaps (physical and optical combined) cover about 0.7% of the area of the primary mirror; thus, there is an added diffraction pattern that has about 0.7% of the flux in the central image. At 1 μm, this energy will be diffracted into angular scales of about 30 arcsec. The diffracted energy is small and is spread over a very large region, making its local effects even less significant. For comparison, the structural spiders that typically support the secondary mirror generally block about 1% of the light going to the primary, and since the support widths are typically 1–4 cm, this diffracted energy is larger than that of segment edges and more centrally concentrated by a factor of several. Both of these factors tend to make diffraction from secondary mirror supports more problematic than diffraction from intersegment gaps.

The diffraction pattern for a regular hexagon is proportional to the absolute value squared of the Fourier transform of the hexagon aperture function H. This function is defined by the condition H(x, y) = 1 when the aperture plane coordinates x and y fall within the aperture and H(x, y) = 0 otherwise. Let u and v be the corresponding image plane coordinates (in units of spatial frequency), k = 2π ∕ λ, and s′ be the side length of the hexagon, which is assumed to be centered at the origin, with two sides parallel to the x-axis. The Fourier transform is real and may be obtained analytically (Chanan and Troy 1999) as

$$\begin{array}{rcl} \hat{H}(u,v) = \frac{2\sqrt{3}} {{k}^{2}u} [\hat{{K}}_{+}(u,v) +\hat{ {K}}_{-}(u,v)]& &\end{array}$$

(3.16)

where

$$\begin{array}{rcl} \hat{{K}}_{\pm }(u,v) = \frac{\cos (\sqrt{3}kvs'/2 \pm kus'/2) -\cos (kus')} {u \mp \sqrt{3}v} & &\end{array}$$

(3.17)

For u = v = 0, this expression reduces as expected to the area of the hexagon: $\hat{H}(0,0) = \frac{3\sqrt{3}} {2} {s'}^{2}$.

Now consider an array of hexagons. Let s be the side length of the hexagons which define the array (to be distinguished from the physical side length s′ of the hexagonal segments), and let the vector ${\mathbf{\mathit{\rho }}}_{i}$ specify the position of the center of the ith segment in a nonoverlapping array in the aperture plane. The diffraction pattern from an array of hexagons can then be obtained directly from the pattern for a single hexagon as

$$\hat{f}(\mathbf{\mathit{\omega }}) =\hat{ H}(\mathbf{\mathit{\omega }})\sum\limits_{i}\exp (ik{\mathbf{\mathit{\rho }}}_{i} \cdot \mathbf{\mathit{\omega }})$$

(3.18)

For close-packed arrays of hexagons, the coordinates of ${\mathbf{\mathit{\rho }}}_{i}$ are

$$x = \frac{3} {2}ks, \qquad y = \frac{\sqrt{3}} {2} \mathcal{l}s$$

(3.19)

where k and $\mathcal{l}$ are integers (positive, negative, or zero) such that $k + \mathcal{l}$ is even; for Keck, the 36 segment coordinates are defined by the strict inequality:

$$ 0<3{k}^{2} + {\mathcal{l}}^{2}<48 $$

(3.20)

Because there are physical (and optical) gaps between the segments, s will in general be slightly larger than s′; the gap width is $\sqrt{3}(s - s')$. Plots of monochromatic diffraction patterns for large telescopes are often somewhat misleading because much of the fine structure (of order λ ∕ D) will be washed out for even relatively modest bandwidths Δλ. Note that this same formalism can be applied to the case of circular segments.

Theoretical monochromatic point source profiles for Keck at 1 μm in the directions parallel and perpendicular to the segment edges are shown in Fig.  3-1 , together with the corresponding profiles for a circular aperture of diameter 10 m. On this angular scale, the Keck and circular profiles are quite comparable. Not apparent in these figures are the effects of gaps, which show up on much larger angular scales. The issue of background surface brightness from diffraction effects in general is a complicated one and beyond the scope of this review, involving not only the effects of gaps but also the secondary mirror support structure, optical aberrations, and finite bandwidth effects. Troy and Chanan (2003) have considered this problem in the context of giant segmented-mirror telescopes.

Fig. 3-1

Theoretical diffraction patterns for the Keck telescopes at a wavelength of 1 μm, in the direction parallel (left panel) and perpendicular (right panel) to the segment edges. The diffraction pattern corresponding to a circular aperture, shown for comparison, is quite similar

3.8 Infrared Properties

At infrared wavelengths longer than ∼ 2.2 μm, the thermal emission from the environment (including the telescope and optics) becomes an important source of background. Typical environmental temperatures are of order 300 K, for which the peak emission occurs at wavelengths of about 10 μm. The short wavelength tail of the blackbody spectrum falls off exponentially, which means that the thermal background rises very rapidly from 2 to 10 μm.

All telescopes that are used in the infrared suffer to some degree from this thermal background, depending on the temperature of the telescope and its optics. In practice, telescopes with clean and freshly applied mirror coatings (such as silver) have emissivities of about 1% per surface at wavelengths beyond 1 μm. As the optics degrade with time and the accumulation of contaminants, the emissivity will grow.

The gaps between segments will generally have much higher emissivities, often close to unity. Thus, for a telescope like Keck, the segment edges will add an additional 0.7% thermal background flux in addition to the roughly 3% associated with the three-mirror Nasmyth configuration. When one includes the typical effects of dirt and aging and the backgrounds from the atmosphere and from any additional warm optics in the beam train (such as windows or warm adaptive optics mirrors), the added background from segment edges is a real but nonetheless rather small effect.

3.9 Active Control System

3.9.1 Introduction

At Keck and other segmented-mirror telescopes, the primary mirror segments are actively positioned in their three out-of-plane degrees of freedom by three mechanical actuators, which connect the segment to its supporting subcell (Jared et al. 1990; Mast and Nelson 1982). (Because the optical tolerances on the in-plane degrees of freedom are considerably less restrictive, these three degrees of freedom are positioned passively.) The relative displacements of adjacent mirror segments are sensed by precision electromechanical edge sensors, of which there are two per intersegment edge. The segments are actively controlled (Cohen et al. 1994) by means of a two-step process: (1) initially, the desired readings of the edge sensors are determined by external optical means; (2) subsequently, the mirror is stabilized against perturbations due to gravity and thermal effects by moving the actuators so as to maintain the sensor readings at their desired values. At Keck, the actuators are updated every 0.5 s; for the large segmented telescopes of the future, the update rate is likely to be somewhat higher.

In the following subsections, the actuators and sensors used in the Keck telescopes are discussed first, followed by a description in somewhat general terms of the construction of the control matrix that relates actuator motions to sensor readings. This in turn leads naturally to a discussion of mirror modes and error propagation by the control matrix. One particular mode, focus mode, is singled out for more detailed discussion.

3.9.2 Actuators

In the Keck actuators, a DC motor drives a roller screw with a 1-mm pitch, which in turn supplies axial drive to a slide. The slide drives a small piston into an oil-filled chamber. On the other side of the chamber, a large piston drives an output shaft, which is attached to the mirror. The piston areas are in the ratio 24:1, and the rotary encoders have 10,000 steps per revolution, so that the actuator step size is about 4 nm. The actuator range is 1.1 mm. Each actuator is contained within a cylindrical package 15 cm in diameter and 63 cm long, with a total mass of 11.5 kg. The power dissipation is 0.5 W per actuator, mostly due to the light source in the rotatary encoder (Meng et al. 1990).

3.9.3 Edge Sensors

The Keck edge sensors are interlocking, with one half of the sensor attached to each neighboring mirror segment. To be precise, a drive paddle mounted on one segment fits into the sensor body on a neighboring segment, with a 4-mm clearance both above and below the paddle. (These mechanical parts are mounted on the back of the mirror and do not obscure any of the reflective surface.) The surfaces above and below the nominal 4-mm gaps are conducting so that the gaps and conducting surfaces define two capacitors. When the two segments move relative to each other, the drive paddle moves relative to the sensor body, changing the gaps and hence the capacitance. The difference between the two capacitances is related linearly to the relative displacement of the segments. A sensor preamplifier and analog-to-digital converter measure this difference in capacitance and produce a digital output proportional to the displacement. This output is sent to the control electronics for further processing.

The sensor noise (Minor et al. 1990) is only a few nanometers. The low thermal error (less than 3 nm/K), low drift rate (less than 4 nm/week), and predictable deformation of the sensor under gravity (correctable to better than 7.5 nm rms) make the overall sensor contribution to the optical error budget quite low.

3.9.4 Construction of the Active Control Matrix for Keck-Type Sensors

The linear relationship between the actuators and sensors in the active control system is given by

$$\mathbf{Az = s}$$

(3.21)

where z is a vector containing all of the actuator lengths (with 108 components in the case of Keck) and s is a vector of all of the sensor lengths (168 components). The control matrix A (168 × 108) is determined solely by geometry. The calculation of the precise values of the matrix elements A _ij is described in the following paragraph.

As noted above, the Keck sensors are horizontal, that is, the plates of the differential capacitors which make up the sensors are parallel to the segment surface. The geometrical relationships between the twelve half sensors and the segment which they monitor are defined in Fig.  3-2 ; the placement of the three segment actuators is also indicated. The Keck parameters are given by a = 900 mm, f = 173 mm, g = 55 mm and h = 706 mm. The sensors sense the relative edge height, that is, the height of a segment relative to its neighbor, at the points indicated by the numbered squares in the figure. For the Keck geometry, and for most practical cases, the sensing points for sensors 7 and 12 are both above the line connecting actuators 2 and 3; the simple sign convention below is affected if this is not the case. The values of the ratios f ∕ a, g ∕ a, and h ∕ a for Keck are close to optimal in the sense of minimal noise multiplication (see below), but they also reflect various practical considerations, so that the precise values do not have a fundamental significance. Practical concerns (specifically, the interchangeability of segments) may dictate that the orientation of the actuator triangle will vary from segment to segment, but for simplicity in this discussion, all actuator triangles are taken to have the same orientation. This simplification will not change the basic properties of the associated control matrix; in particular, it will have no effect at all on the error multipliers or other similar quantities derived below.

Fig. 3-2

The geometry of the Keck active control system, showing the locations of the 3 actuators and 12 sensors halves on a typical segment

Now if actuator 1 is pistoned by an amount Δs, the segment will rotate about a line through actuators 2 and 3, so that the reading of each sensor on the segment (in height units) will change by

$$\Delta s = \frac{r\,\Delta z} {h}$$

(3.22)

where r is the perpendicular distance from the sensor to the rotation axis and where the sign of r is positive if the sensor and the actuator are on the same side of the rotation axis and negative if they are on opposite sides.

If actuator 1 is moved by an amount Δz, then from (3.22), the corresponding edge height increment at sensor positions 1–6 will be

$$\begin{array}{rcl} \Delta {s}_{1,1}& =& \Delta z\left [\frac{1} {3}h + f\cos 3{0}^{\circ }- g\sin 3{0}^{\circ }\right ]/h \\ \Delta {s}_{2,1}& =& \Delta z\left [\frac{1} {3}h + (a - f)\cos 3{0}^{\circ } + g\sin 3{0}^{\circ }\right ]/h \\ \Delta {s}_{3,1}& =& \Delta z\left [\frac{1} {3}h + a\cos 3{0}^{\circ }- g\right ]/h \\ \Delta {s}_{4,1}& =& \Delta z\left [\frac{1} {3}h + a\cos 3{0}^{\circ } + g\right ]/h \\ \Delta {s}_{5,1}& =& \Delta z\left [\frac{1} {3}h + (a - f)\cos 3{0}^{\circ }- g\sin 3{0}^{\circ }\right ]/h \\ \end{array}$$

$$\begin{array}{rcl} \Delta {s}_{6,1}& =& \Delta z\left [\frac{1} {3}h + f\cos 3{0}^{\circ } + g\sin 3{0}^{\circ }\right ]/h\end{array}$$

(3.23)

For sensor positions 7–12, Δs _{j, 1} can be obtained from Δs _{j − 6, 1}, but with sin30^∘ and cos30^∘ replaced by − sin30^∘ and − cos30^∘, respectively. A useful check on the signs and normalizations of the above relations is provided by various closure relations, which follow from the symmetries of the system. For example,

$$\Delta {s}_{1,1} + \Delta {s}_{5,1} + \Delta {s}_{9,1} = \Delta z$$

(3.24)

It is a straightforward matter to relate the edge height increments to the readings on the differential capacitors that constitute the edge sensors (Chanan et al. 2004). It is convenient to define the signs of the edge height differences so that all segments are similar. For actuator 1 and the sensors in Fig.  3-2 , one has

$${A}_{j,1} = \pm \Delta {s}_{j,1}/\Delta z$$

(3.25)

where the sign is positive for j = 2, 4, 6, 7, 9, 11 and negative for the remaining values of j. The entire control matrix can readily be filled out in this way. Each actuator affects 12 sensors (or fewer for peripheral segments, since these do not have six nearest neighbors), and each sensor is affected by six actuators (in all cases). Thus, each row of the control matrix has up to 12 nonzero elements, and each column has exactly six nonzero elements, independent of the number or arrangement of segments.

3.9.5 Construction of the Active Control Matrix for Vertical Sensors

For the sake of simplicity and definiteness, the above discussion was presented in the context of Keck-style capacitive edge sensors. In this sensor design, the capacitor plates are horizontal and the two capacitors lie one above the other. Such sensors are interlocking, which complicates segment exchanges, and involve many parts, which makes them expensive to build. By contrast, the sensor design under consideration for the future Thirty Meter Telescope has the capacitors attached directly to the vertical sides of the segments (Mast and Nelson 2000); that is, the capacitor plates are perpendicular to the segment surface. In particular, one half of the sensor consists of a single vertical sense plate bonded or plated directly onto the side of one segment, and the other half consists of two vertical drive plates on the side of its neighbor segment directly across the intersegment gap; in effect, there are again two capacitors, one above the other. Even though there is no physical offset from the segment edge, such sensors still retain a sensitivity to dihedral angle: a change in dihedral angle will affect the two capacitor gaps differently. There is therefore an effective offset, although its geometrical interpretation is not as simple as before, and it tends to be smaller than for the Keck-style sensors. (The TMT sensor design calls for an effective offset of about 25 mm, compared to the actual offset of 55 mm for the Keck sensors.) The construction and properties of the active control matrix for vertical capacitive sensors are similar to those for the horizontal sensors described above (Chanan et al. 2004), and the same is true as well for sensors that utilize induction, not capacitance, to measure relative displacement. For primary mirrors of sufficiently small focal ratio, it may be necessary to take the curvature of the mirror into account explicitly, as opposed to using the planar approximation considered above. However, the planar approximation is adequate for Keck.

3.9.5.1 Singular Value Decomposition

The control equation (3.21) directly gives the sensor values corresponding to the actuator lengths. Implementing the actual control requires solving the inverse problem: what (changes in the) sensor readings are required to produce the desired (changes in the) actuator lengths? If the control matrix could be inverted, the desired solution would be obtained as

$${ \mathbf{s = A}}^{-1}\mathbf{z}$$

(3.26)

However, for an overdetermined system, the matrix A is not square and its inverse does not exist; for that matter, in general, an exact solution does not exist. Nevertheless, the least-squares solution can be constructed from the pseudo-inverse matrix, which does exist and can be constructed by straightforward means and which will still be denoted by A​ ^{− 1}. A particularly useful technique for constructing the pseudo-inverse is singular value decomposition (SVD) (Anderson et al. 1999; Golub and van Loan 1996; Press et al. 1989) of the original control matrix. This technique is briefly reviewed here. In SVD, the m ×n matrix A (where m ≥ n) can be written as the product of three matrices:

$${ \mathbf{A = UWV}}^{T}$$

(3.27)

where U is an m ×n column orthogonal matrix, W is an n ×n diagonal matrix whose diagonal elements w _i are positive or zero and are referred to as the singular values of the matrix A, V is an n ×n orthonormal matrix, and the symbol^T denotes transpose. The pseudo-inverse is then obtained as

$${ \mathbf{A}}^{-1} ={ \mathbf{VW}}^{-1}{\mathbf{U}}^{T}$$

(3.28)

where the jth diagonal element 1 ∕ w _j of W ^{− 1} is replaced by 0 in the event that w _j = 0. The matrix V defines an essentially unique orthonormal basis set of modes of the system, such that any arbitrary configuration of the system can be expressed as a unique linear combination of these modes. In particular, V _ij gives the value of the ith actuator in the jth mode.

For the control matrices considered here, three of the singular values are identically equal to zero; the corresponding singular modes are the three actuator vectors corresponding to rigid body motion (global piston, tip, and tilt) of the primary mirror as a whole (since such motion has no effect on the sensor readings). If there are N segments, there are 3N actuators and 3N − 3 modes of interest in the basis set.

Once the elements of the pseudo-inverse matrix are known, control of the mirror is implemented as follows: The desired sensor readings are defined when the alignment of the telescope is correct as determined by external optical means; actuator lengths are changed further only to maintain these desired sensor readings in the face of deformations due to gravity and temperature changes. The actuator changes that will maintain the desired sensor readings are calculated with the aid of the pseudo-inverse matrix elements ${A}_{ji}^{-1}$ via

$$\Delta {z}_{j} ={ \sum }_{i}{A}_{ji}^{-1}\Delta {s}_{ i}$$

(3.29)

where the symbol Δz _i refers to the difference between the actual and desired actuator values and similarly for the corresponding differences Δs _i in the sensor readings.

In principle, the control matrix only needs to be inverted once and for all time; in practice, it has to be re-inverted every time a sensor is removed from or added to the control loop. At Keck, such changes typically happen every few months or so. By contrast, maintaining the sensor readings at their desired values requires only a simple matrix multiply. This must be done at the frequency of the control loop, 2 Hz for Keck.

The computational power required to support the control algorithm increases rapidly with the size of the telescope. While the Keck active control system uses 168 sensors to control 108 actuators, the Thirty Meter Telescope will require 2,772 sensors to control 1,476 actuators.

3.9.5.2 Error Propagation

The SVD analysis can readily be extended to describe error propagation in the control system. If one were to put random uncorrelated noise equally into all sensors, then the actuators would respond proportionally as determined by the A-matrix:

$$\delta a = \alpha \,\delta s$$

(3.30)

where δs and δa are the rms values of the sensor and actuator errors, and we refer to the dimensionless parameter α as the (overall) noise multiplier. Alternatively, one could put random noise into the sensors and determine the rms amplitude δ α _k for each of the above 3N − 3 modes.

By the orthogonality of the modes, one has

$$\delta {a}^{2} ={ \sum }_{k}\delta {a}_{k}^{2} =\sum\limits_{k}{\alpha }_{k}^{2}\,\delta {s}^{2}$$

(3.31)

It is convenient to order the modes (the columns of the matrix V) according to the magnitude of their error multipliers, from largest to smallest, or – what is the same thing – according to the size of the singular values from smallest to largest. With this ordering, it is convenient to define a residual error multiplier r _k , which includes the error multiplier of the kth mode and all higher modes:

$${r}_{k}^{2} ={ \sum }_{j\geq k}{\alpha }_{j}^{2}$$

(3.32)

(Note that r ₁ is then the same as the overall error multiplier α.) When the modes are ordered in this way, they are also more or less ordered in spatial frequency from lowest to highest. The reason for this correspondence is not hard to understand: low spatial frequency modes have small edge discontinuities that are difficult for the sensors to detect and therefore for the active control system to control; high spatial frequency modes have large edge discontinuities that are easily detected by the edge sensors. The error multiplier α _j associated with the jth mode can be shown to be

$${\alpha }_{j}^{2} = \frac{n} {{w}_{j}^{2}}$$

(3.33)

For a fixed number of segments, the individual error multipliers α _j and the overall error multiplier α are (exactly) independent of the hexagon side length a.

Figure  3-3 shows the two Keck modes with the lowest spatial frequencies (largest error multipliers) and the two highest spatial frequency modes (smallest error multipliers). These results are typical of all sensor geometries. Inspection of the modes shows that there is a close correspondence between the lowest order modes and the Zernike polynomials.

Fig. 3-3

Top panels: the two lowest spatial frequency modes of the Keck telescope active control system. The mode on the upper left is focus mode. This mode has continuous edges and the slope discontinuities are too small to be seen. The mode on the upper right is one of two global astigmatism modes. This mode has small edge discontinuities in addition to the slope discontinuities. The small size of the discontinuities makes these modes the most difficult to control. Bottom panels: the two highest spatial frequency modes. The large edge discontinuities make these modes the easiest to control

The full range of error multipliers for the three-ring Keck telescope, a five-ring telescope similar to the Hobby-Eberly Telescope (HET), and a TMT-type (492 segment) telescope is plotted in Fig.  3-4 . For directness of comparison, the identical sensor geometry has been assumed in each case. Except for focus mode, however, the multipliers are only weakly dependent on sensor geometry. The error multiplier curves scale approximately as the square root of the total number of segments; equivalently, the singular value for a mode of particular spatial frequency is, for low spatial frequencies, virtually independent of the number of segments.

Fig. 3-4

Error multipliers for the control systems for TMT, HET, and Keck. For directness of comparison, the Keck actuator and sensor geometry has been assumed for each control system, together with the actual segment geometry for the telescope

Because of the sharp increase in error multiplier with decreasing mode number, one might worry that for extremely large segmented telescopes, effective mirror control will require optically determined wavefront information to supplement the electromechanical sensors. Although the issue has not yet been completely resolved for the giant telescopes currently in the design stages, it seems likely that little or no supplemental wavefront control for giant segmented telescopes will in fact be necessary (MacMartin and Chanan 2002, 2004). The argument may be summarized as follows. For diffraction-limited (adaptive optics) observing, a wavefront sensor will already be present as a part of the AO system, and it is expected that a reasonable AO system will necessarily have the dynamic range and bandwidth to correct automatically any residual low spatial frequency errors left over from the active control system, without the need for a supplementary alignment wavefront sensor. For seeing-limited observations, one will not have an AO wavefront sensor to correct the misalignments automatically, but the large aberrations from atmospheric turbulence will likely dominate those due to residual misalignments from the control system.

3.9.5.3 Surface Errors from SVD (for Diffraction-Limited Observing)

For diffraction-limited observing, a useful optical figure of merit for the telescope is the rms wavefront error, which is equal to twice the rms surface error. Note that here the averaging should be over the entire surface; the actuator calculation presented above averages the surface only over the discrete points corresponding to the actuator locations. However, one can show that the true rms surface error is very nearly equal to the rms actuator error.

Let z _ij represent the displacement of the ith actuator (i = 1, 2, 3) on the jth segment, let

$${p}_{j} = ({z}_{1j} + {z}_{2j} + {z}_{3j})/3$$

(3.34)

represent the piston error on that segment, and let $\tilde{z}$ represent the continuous height variable over the segment surface, where $\tilde{z} = {z}_{i}$ at the actuator locations. Averaging over all segments and over an ensemble defined by a Gaussian distribution of sensor (not actuator) errors yields

$$\langle \widetilde{{z}}^{2}\rangle \ = \kappa \langle {z}^{2}\rangle + (1 - \kappa )\langle {p}^{2}\rangle$$

(3.35)

where

$$\kappa = \frac{15} {16} \frac{{a}^{2}} {{h}^{2}}$$

(3.36)

and 〈z ²〉 denotes the average over the discrete actuator points only. If the actuators on a given segment were uncorrelated, one would have 〈z ²〉 = 〈p ²〉 and thus $\langle \tilde{{z}}^{2}\rangle =\langle {z}^{2}\rangle$, and there would be no distinction between the rms actuator and the true rms surface. In fact, if the state of the mirror is defined by the sensors, which have a Gaussian distribution of errors, then the actuators will be weakly correlated and there will be a (small) difference between the rms surface and the rms actuator. In general, however, the difference is very small (in theory about 3% for the Keck telescopes), and there is little point in maintaining a distinction between these two quantities. The rms actuator is preferred on the grounds of simplicity.

3.9.5.4 Tip-Tilt Errors from SVD (for Seeing-Limited Observing)

For seeing-limited observations, one is interested not in the rms surface error (as discussed above) but rather in the rms segment tip/tilt, or the rms ray tip/tilt, where the latter includes the factor of two for doubling on reflection. The rms ray tip/tilt may be obtained directly from the SVD formalism (Chanan et al. 2004). The results may be summarized as follows.

While the error multipliers discussed above are independent of the segment size (for a fixed number of segments) and scale as the square root of the total number of segments, the tip/tilt errors scale inversely as the segment size, can vary by 50% or so depending on sensor geometry, and are virtually independent of the number of segments. The typical rms one-dimensional image blur is 2–3 milliarcsec per nm of sensor noise for a segment with a = 0. 500 m or 1–1.5 milliarcsec per nm for a segment with a = 1 m.

3.9.6 Focus Mode

Although it is convenient to think of the edge sensors as responding to the vertical shear of one segment with respect to its neighbor, in general, the sensors will also respond to a change in the dihedral angle between adjacent segments. If all of the segment dihedral angles are changed by the same amount, or (what is essentially the same thing) if a constant is added to all of the sensor readings, this defines a defocus-like configuration of the primary mirror that is referred to as focus mode. In focus mode, the radius of curvature of the surface defined by the segment centers does not match the individual segment radii of curvature. Focus mode corresponds to one of the V-modes of the singular value decomposition, usually the mode with the smallest nonzero singular value and hence the largest error multiplier; that is, it is the least well-controlled mode. (If the dihedral angle sensitivity goes to zero, the singular value of this mode also goes to zero, and it becomes truly unobservable.) The problem may be aggravated by practical considerations. For example, if all sensors had a small but common temperature dependence, then a change in temperature could lead spontaneously to the introduction of focus mode.

However, focus mode can be corrected to first order by pistoning the secondary mirror. This will leave the wavefront with an overall residual scalloping, but since the aberration is quadratic in the coordinates, the scalloping amplitude will be smaller than the original focus mode amplitude by a factor of N, the number of segments. At Keck, this means that focus mode only has to be corrected very occasionally (typically once per month); in the interim, it can be corrected by conventional focusing of the telescope and one simply tolerates the small residual scalloping.

3.10 Optical Alignment

3.10.1 Tip-Tilt Alignment of Segments

The measurement of segment tip/tilt angles is similar to wavefront sensing in adaptive optics but with one important difference. As in adaptive optics, a Shack-Hartmann wavefront sensor is used, with either single or multiple subapertures per segment (Chanan 1988). The difference is that in adaptive optics, one is essentially trying to freeze the atmosphere, so that the exposures need to be very short (typically a few milliseconds); in segment alignment measurements, one is trying to average over local atmospheric tip/tilt errors, so that the exposures need to be quite long, typically tens of seconds.

Although the optical effects of turbulence are well understood theoretically in the short exposure limit, (Fried 1966; Noll 1976) the theoretical situation is much less clear for the long (but not infinitely long) exposures that are typical of alignment measurements. Measurements made at the VLT suggest that the residual atmospheric aberrations (up to Zernike terms of order n ∼ 4) for long exposures are well described by the same statistical distribution of Zernike coefficients as in the theoretical short exposure limit but with an effective atmospheric coherence diameter r ₀ as a single free parameter (Noethe 2002). Although the effective r ₀ for these long exposures may be as much as an order of magnitude larger than the usual “instantaneous” r ₀, residual atmospheric turbulence nevertheless still limits the alignment process at the VLT. Similar results have been found at Keck, for length scales on the order of a segment. Outer scale effects, which tend to become important beyond 10 m (Ziad et al. 2004), may ameliorate this situation somewhat for the extremely large telescopes of the future.

3.10.2 Phasing

The most challenging degrees of freedom to align optically are those associated with segment piston errors. In order that the telescope achieve the diffraction limit corresponding to the full aperture, as opposed to the diffraction limit of the individual segments, the piston errors (or steps between segments) must be small compared to the wavelength of observation. The Strehl ratio for a segmented telescope whose N perfect segments are aligned in tip/tilt but not piston is

$$S = \frac{1 + (N - 1){e}^{-{\sigma }^{2} }} {N}$$

(3.37)

where σ is the standard deviation of the piston errors measured in radians at the wavefront (not at the segment surface) (Chanan and Troy 1999). For a 10-m telescope with adaptive optics in the near-IR, the corresponding segment piston error requirement is less than about 30 nm for high angular resolution imaging; for the giant segmented telescopes of the future, it may be as small as 10 nm.

In principle, a segment with a piston error will produce an out-of-focus image, but this effect is extremely small: at the f/15 focus of the Keck telescope, the individual segment beams have a depth of focus of some 10 mm, which exceeds the dynamic range of the segment pistons by a factor of several. One is instead forced to exploit diffraction effects from misaligned intersegment edges. At Keck, this is accomplished by a physical optics generalization of the traditional geometrical optics Shack-Hartmann test. The Keck technique is described in the Sect. 10.2.1 below. Recently, several other techniques have been developed, and these are described in Sect. 10.2.2.

3.10.2.1 Shack-Hartmann Phasing

The basic idea of Shack-Hartmann phasing is to place the subapertures so that they straddle the intersegment edges of the (reimaged) primary mirror (Chanan 1988). The two halves of the subaperture are analogous to the slits in Young’s two-slit interference experiment. The details of the resulting interference or diffraction pattern are sensitive to the relative piston error between the two segments. (In principle, relative tip/tilt errors between the two segments can also be detected with Shack-Hartmann phasing, but this possibility is not examined here.)

For simplicity, consider the interference pattern from a single subaperture and assume that an adaptive optics system either is not used or is located downstream from the image plane under consideration here. This means that the phasing subimages will be affected by atmospheric turbulence and this limits the phasing subaperture diameter d to less than about r ₀(λ), the atmospheric coherence diameter at the wavelength at which the phasing measurements are made. At Keck, this wavelength is about 0.9 μm, and the subapertures, referred to the primary mirror, are 12 cm in diameter. Atmospheric tip/tilt errors across a subaperture (the dominant atmospheric error for d ≤ r ₀) are generally the limiting factor for geometrical optics Shack-Hartmann tests, but have little effect on phase measurements. As a result, phasing measurements do not require the long exposure times that are necessary to eliminate segment tip/tilt errors. Typical exposure times for phasing measurements at Keck are 15 s, although the question of the minimum exposure time has not been thoroughly explored.

A modest amount of analysis will clarify the basic physics of Shack-Hartmann phasing. Let $\mathbf{\mathit{\rho }} = (\rho,\theta )$ be the position vector in the subaperture plane and let $\mathbf{\mathit{\omega }} = (\omega,\phi )$ be the position vector in the image plane. (It is assumed that the components of $\mathbf{\mathit{\rho }}$ have units of length and components of $\mathbf{\mathit{\omega }}$ have units of radians.) Consider a circular subaperture of radius a straddling two segments separated by the horizontal diameter of the circle, with a physical step height δ between the two. (The corresponding wave-front step height is 2δ.) In the absence of other aberrations, the complex amplitude of the wavefront in the image plane $\hat{f}(\mathbf{\mathit{\omega }};k\delta )$ is the Fourier transform of the complex aperture function $f(\mathbf{\mathit{\rho }};k\delta$):

$$ \begin{array}{rcl} f(\mathbf{\mathit{\rho }};k\delta ) = \left \{\begin{array}{rcl} \exp (+ik\delta )&\mbox{ for}&\rho \leq a; 0 \leq \theta < \pi \\ \exp (-ik\delta )& \mbox{ for}&\rho \leq a; \pi \leq \theta < 2\pi \\ 0&\mbox{ for}& \rho > a \end{array} \right. & &\end{array} $$

(3.38)

where k = 2π ∕ λ and the normalization is chosen such that the integral of the intensity over the image is unity. The intensity in the image plane is then (Chanan et al. 1998)

$$I(\mathbf{\mathit{\omega }};k\delta ) = {[\cos k\delta \hat{f}(\mathbf{\mathit{\omega }};0) +\sin k\delta \hat{f}(\mathbf{\mathit{\omega }};\pi /2)]}^{2}$$

(3.39)

where the in-phase amplitude (kδ = 0) is that corresponding to the familiar Airy disk:

$$\hat{f}(\mathbf{\mathit{\omega }};0) = \frac{2{J}_{1}(ka\omega )} {ka\omega }$$

(3.40)

and the out-of-phase amplitude (kδ = π ∕ 2) is given by

$$\hat{f}(\mathbf{\mathit{\omega }};\pi /2) = \frac{2} {\pi }{\int \nolimits \nolimits }_{0}^{\pi }\frac{u\cos u -\sin u} {{u}^{2}} \mathrm{d}\theta $$

(3.41)

where u = kaωcos(θ − ϕ), with both angles defined as above. This integral can be evaluated explicitly for only a few values of ϕ. For ϕ = 0 or ϕ = π, the integral vanishes; for ϕ = ± π, it reduces to ∓ H ₁(kaω) ∕ (kaω), where H ₁ is the Struve function of order 1. However, these four cases are sufficient to show that for kδ = π ∕ 2, the image splits into two equal subimages, with the intensity vanishing everywhere along the x-axis (see Fig.  3-5 ).

Fig. 3-5

Slices along the y-axis (perpendicular to the intersegment edge) of the phasing diffraction patterns for in-phase (kδ = 0) and (maximally) out-of-phase segments (kδ = π ∕ 2). In the former case, the image is the familiar Airy disk; in the latter, it splits into two equal images. The horizontal units are kaω. The vertical units are arbitrary but the same for both slices

For phase differences other than kδ = 0 and kδ = ± π ∕ 2, the image splits into two unequal subimages; the ratio of the intensities of the subimages provides a measure of the phase difference or step height between the two segments. Figure  3-6 shows the two-dimensional theoretical diffraction patterns for several steps between kδ = 0 and kδ = π. The middle panel (kδ = π ∕ 2) corresponds to a step height of λ ∕ 4, which is the maximal effect. The step height may be extracted from the diffraction pattern via a cross-correlation (Chanan et al. 2000) against a sequence of numerically generated template images. Alternative analytical extraction techniques have been discussed in the literature (Schumacher et al. 2002).

Fig. 3-6

Theoretical diffraction patterns from a single phasing subaperture with relative piston errors of 0, 150, 200, 250, and 400 nm. The wavelength is 800 nm and the subaperture diameter is 120 mm. The figure may be read left to right or right to left, depending on the sign convention for the piston error

It is clear from physical considerations and from the equations that the above monochromatic phasing technique can only give answers for δ in the range 0 to λ ∕ 2 or equivalently (and more conveniently for our purposes) − λ ∕ 4 to λ ∕ 4. All piston errors of larger absolute value will be aliased into this latter interval. There are two different approaches to resolving the resulting piston ambiguity: multiple wavelength measurements and broadband measurements.

In the multiwavelength approach, one makes monochromatic measurements at several discrete wavelengths and looks for a solution that is consistent with all of the measurements. This is also referred to as the artificial wavelength method, since for the case of two wavelengths, the capture range is the same as that for a single effective wavelength λ _a :

$${\lambda }_{a} = \frac{{\lambda }_{1}{\lambda }_{2}} {\vert {\lambda }_{1} - {\lambda }_{2}\vert }$$

(3.42)

where λ₁ and λ₂ are the two individual wavelengths. For large initial piston errors, the technique can be extended to more than two wavelengths. There is an optimal way to choose the individual wavelengths that depends on the initial piston uncertainty as well as on the uncertainty in the individual measurements (Lofdahl and Eriksson 2001).

By contrast, in the broadband approach (Chanan et al. 1998), a continuous range of wavelengths is used. In this case, one is interested in the coherence of the signal. (The precise mathematical definition of coherence is not essential to the present discussion; see Chanan et al. (1998) for one possible definition.) The coherence length of the filter, which sets the wavelength bandwidth, is defined by

$${\lambda }_{c} = \frac{{\lambda }_{1}{\lambda }_{2}} {2\Delta \lambda }$$

(3.43)

The diffraction pattern will then resemble that of the monochromatic case for δ ≪ λ _c . Conversely, if δ ≫ λ _c , the details of the diffraction pattern will be washed out, and the image will be incoherent; the incoherent image can be obtained theoretically by taking the monochromatic result for a nonzero edge step and averaging over all wavelengths in the bandpass or by taking the nominal wavelength and averaging over all possible phases. In broadband phasing, the primary mirror segments are stepped through a series of different configurations such that every intersegment edge changes from its nominal value by 2jλ _c ∕ (n + 1), where j takes on all integer values from − (n − 1) ∕ 2 to + (n − 1) ∕ 2 and n is an odd integer of moderate size; the Keck broadband phasing procedure uses n = 11. The overall capture range is a bit less than ± λ _c . Practical considerations make it difficult to decrease the initial piston error uncertainty by more than about a factor of 30 in a single cycle of 11 measurements with a given filter. At Keck this means that a few cycles are needed to reduce the piston errors from their initial values of order 10 μm to the required 30 nm. Each cycle involves a filter of broader bandwidth, hence shorter coherence length. The detailed characteristics of each cycle used at Keck may be found elsewhere (Chanan et al. 1998).

Although the broadband technique is more time consuming to execute than the multiwavelength technique and the extraction of the edge step from the data is not as straightforward, the former has a distinct advantage: If the initial piston error is underestimated, then the technique will fail in a well-defined and easily recognized way: most or all of the signals from the edge in question will be incoherent. However, if the initial errors or the measurement uncertainties are underestimated in the multiwavelength technique, then it will often converge to the wrong answer, with no easily generated diagnostic. For this reason, the broadband technique has been preferred at Keck.

A variation of the broadband technique called dispersed fringe sensing (DFS) uses a grism (a transmission grating replicated onto a prism) to disperse the light along each intersegment edge, so that a continuum of wavelengths can be observed simultaneously, and there is no need to step through different configurations of the primary mirror. A prototype of this technique was successfully tested at the Keck telescope (Shi et al. 2004). The DFS technique was proposed as the coarse segment phasing technique for the James Webb Space Telescope, but ultimately a different though closely related technique, dispersed Hartmann sensing, was selected instead (see Sect. 11.4).

3.10.2.2 Other Phasing Techniques

In late 2008 and early 2009, the European Southern Observatory mounted an active phasing experiment (APE) at the Very Large Telescope in order to compare three alternative phasing techniques to the Shack-Hartmann approach describe in the preceding section (Gonte et al. 2004). The 8-m aperture of one of the VLTs was reimaged onto a 150 mm mirror with 61 actively controlled segments, so that the testing could be done under conditions of realistic atmospheric turbulence. The three techniques involve variations of curvature sensing and pyramid sensing, as well as a modified Mach-Zehnder interferometer. Unlike Shack-Hartmann sensing, which perturbs the wavefront in the pupil plane, these techniques perturb the wavefront in the focal plane (except for curvature sensing, which effects its wavefront perturbation simply by going out of focus) and relay the pupil plane to the detector. They all therefore eliminate the problem of very tight pupil registration in the Shack-Hartmann approach, although in general the determination of the precise mapping between points on the primary mirror and the corresponding points on the detector is more complicated for these techniques than for Shack-Hartmann phasing. The additional phasing techniques tested by ESO are briefly described as follows:

• Curvature Sensing. Roddier (1988) developed a wavefront sensing technique based on measuring the spatial variation of the intensity of defocused images; this gives a measure of the Laplacian of a continuous wavefront from which, with suitable boundary conditions, the wavefront can be reconstructed. For the discontinuous wavefronts from segmented mirrors, piston errors can be reconstructed using Fresnel diffraction theory (Chueca et al. 2008). A variation of this technique has been implemented at infrared wavelengths at Keck, with some success (Chanan et al. 1999).

• Pyramid Sensing. In this wavefront sensing technique, developed for use in adaptive optics, a four-faceted pyramid in the focal plane splits the beam so that four separate pupil images are formed. It is in some sense a quantitative version of the classical knife edge test but with knife edges in two orthogonal directions at the same time. The signal is a measure of the first derivative of the wavefront and thus again has good piston sensitivity (Esposito et al. 2005).

• Mach-Zehnder Interferometer. In this technique, a spatially filtered beam from the telescope is interfered with a phase-shifted version of itself (Montoya 2004; Surdej et al. 2010; Yaitskova et al. 2005). The output is a measure of the second derivative of the phase, and there is good sensitivity to segment piston errors.

All four techniques (including Shack-Hartmann phasing) tested in the APE experiment were successful to some degree. Each technique has its advantages or disadvantages with respect to pupil registration or determination of the pupil mapping, the fraction of the segment surface which is sampled, ability to determine segment tip/tilt errors simultaneously, sensitivity to rolled edges, and the ability to handle piston errors that are large compared to the wavelength of light. A full discussion of the relevant details may be found in the papers cited above.

3.10.3 Warping Harnesses

It is desirable to be able to adjust the segment figures (at least in the lower spatial frequencies) while the segments are in the telescope. In stressed mirror polishing, when the rounds are cut into hexagons, internal stresses are relieved, which tends to produce low spatial frequency aberrations that are very expensive to polish out at this late stage of the fabrication process. Also, errors in the in-plane positioning of segments cannot be corrected directly, as these degrees of freedom are not actively controlled; however, they can be corrected indirectly by adjusting the segment figures, since the predominant effect of these positioning errors is to cause apparent focus and astigmatism errors in the segments.

The in situ adjustment of segment figures is accomplished at Keck by means of warping harnesses, sets of leaf springs attached to the segment whiffletrees that can apply forces and moments to the backs of the segments so that they can be warped into the correct shapes. Figures  3-7 and 3-8 show the results of two warping harness experiments at Keck. In the first of these, the predicted changes that result from the application of a given force to a single warping beam were accurately confirmed. In the second, the astigmatism of one of the segments was successfully changed by 500 nm, to within the experimental errors of 15 nm.

Fig. 3-7

Theoretical and observed differential response of a Keck telescope segment to the adjustment of a single leaf spring in the warping harness

Fig. 3-8

Results of an experiment to increase the astigmatism (Zernike polynomial 6) of a Keck segment by 200 nm via warping harness adjustment

Keck segments are normally measured and warped immediately after they are installed in the telescope, either initially or after aluminizing (and only at such times). The warping harnesses are typically not adjusted again until after the next aluminization cycle, typically 3 years later. Prior to warping, the Keck segments have a surface error of 98 nm (rms); after warping, this is reduced to 37 nm. The predicted performance for the warping harnesses is for a post-warp rms of 25 nm; this includes both the theoretical performance of the springs and the errors associated with making Shack-Hartmann measurements through atmospheric turbulence. The discrepancy between theory and performance (25 vs. 37 nm) is apparently due to aliasing in the measurements and to the presence of significant non-Zernike aberrations, which the mathematical model for the segment surface error does not readily accommodate. Note that warping a known low spatial frequency aberration into a segment is not the same as (and is in general not as difficult as) flattening a segment with high spatial frequency aberrations present.

The Keck warping harness procedures involve manual adjustment of the warping harnesses. At the Gran Telescopio Canarias, this procedure can be done automatically, and this will also be the case for the giant segmented-mirror telescopes of the future. In principle, such warping harnesses can be exercised as often as several times a night to correct, for example, for temperature variations or gravity. This would require either continuous wavefront sensing or lookup tables to determine the necessary corrections.

3.10.4 Alignment of the Secondary Mirror

As is the case with any two mirror telescope, the secondary mirror of a segmented-mirror telescope must be aligned with respect to the primary in piston, tip, and tilt. (Precise centration of the secondary is typically not required, as the effect of decentering on the image is nearly degenerate with that of tip and tilt.) The complication for a segmented-mirror telescope is that the global rigid body parameters of the primary are not trivial to determine; at best, they can be represented as suitable averages over the corresponding segment quantities.

The basic idea underlying the alignment of the secondary in a segmented-mirror telescope can be understood as follows. In an otherwise perfect telescope, the defocus of the image due to a piston error δz (in microns) of the secondary is

$$AD = \delta {z}{s} ({m}^{2} + 1)/F$$

(3.44)

where AD is the full diameter of image in arcsec, s is the image scale in arcsec per micron, m is the magnification of the secondary, and F is the overall focal ratio of the system. The corresponding global focus error can be expanded locally about the center of each segment. It follows immediately that each segment will have the same focus error to first order. Therefore the piston of the secondary can be adjusted until the average segment focus error is zero. The accuracy of the procedure is limited by atmospheric turbulence. At Keck, the average secondary mirror piston uncertainty is about 4 μm, as determined from the variation in a sequence of measurements.

The idea is similar for secondary tip/tilt. Schroeder (2000) gives the corresponding expression for the coma of the image due to a tilt of the secondary:

$$ATC = 3 \delta \alpha (m - 1) (1 + \beta )/(16{F}^{2})$$

(3.45)

where δ α is the secondary tilt angle, and β is the ratio of back focal distance to the focal length of the primary. Again, expanding the wavefront error about each segment center shows that each segment will have an apparent coma. In this case, each segment will also be astigmatic, with the astigmatism varying from segment to segment; the astigmatism in fact dominates. Thus, the secondary tip/tilt can be reconstructed from the ensemble of segment astigmatisms. The uncertainty in the secondary tip/tilt as determined at Keck is about 3 arcsec each in tip and tilt.

3.11 Other Segmented-Mirror Telescopes

In the last decade or so, several other large segmented-mirror ground-based telescopes have come on line, and the segmented James Webb Space Telescope is currently under construction. These telescopes are briefly described in the following sections.

3.11.1 Gran Telescopio Canarias

The Gran Telescopio Canarias (GTC) (Rodriguez Espinosa et al. 1999) is a 36-segment 10-m telescope with a design very similar to that of the Keck telescopes. The GTC, a project of Spain with the participation of Mexico and the University of Florida, is located on the island of La Palma in the Canary Islands and saw first light in 2007. The GTC incorporates several improvements over Keck, including the capability to continuously monitor the optical alignment and to adjust the segment figures remotely.

3.11.2 Hobby-Eberly Telescope and Southern African Large Telescope

The Hobby-Eberly Telescope (HET) at the McDonald Observatory in Texas (Barnes et al. 2000) is a segmented-mirror telescope designed to do spectroscopy and built for a fraction of the cost (about 20%) of a comparably sized segmented-mirror telescope like Keck or GTC. HET is joint project of the Pennsylvania State University and the University of Texas at Austin. Partner institutions include Stanford University and two German institutions: Ludwig-Maximilians-Universität and Georg-August-Universität. Science operations began in October of 1999.

In order to achieve its dramatic cost reduction, the HET design incorporates a number of design innovations, the most dramatic of which is that the telescope is fixed in elevation and rotates only in azimuth. This means that the primary mirror is fixed with respect to gravity, a fact which greatly simplifies the support structure for the mirror. As the telescope tracks a star in elevation, its image moves with respect to the telescope across the focal surface. A star tracker, which contains a spherical aberration corrector and the science instrument, or the fore optics for fiber-fed instruments that reside below the telescope, follows the image. A large fraction of the sky is covered in this way. Observing times are limited compared to a conventional telescope that can move in altitude as well as azimuth; however, observations as long as 2.5 h are possible. Although the full HET array is 11.1 by 9.8 m, the effective diameter seen by the instruments is 9.2 m.

The HET primary mirror consists of five rings of hexagonal segments, each of which has a circumscribed diameter of 1.15 m. The central segment is included because it is not blocked by a secondary (the telescope is used only at prime focus). Thus, there are 91 segments and 273 actuators (three per segment). Unlike Keck, the HET segments are all spherical and identical, which means that the spacing between adjacent segments varies slightly from the center to the edge of the array. The HET segments are aligned not using starlight but rather using an artificial source and a Shack-Hartmann wavefront sensor located in a tower at the primary mirror center of curvature. The HET was originally designed without edge sensors, so that there was no active control of the primary mirror actuators. The telescope was realigned many times a night by rotating to the center of curvature alignment sensor. However, in the interest of observing efficiency, the telescope was retrofitted with an active control system, similar to the one used at Keck but with inductive, not capacitive, sensors. There are two sensors per intersegment edge for a total of 480, and the system updates once a minute. With the active control system in place, the HET segments only need to be aligned in tip/tilt at the beginning of each night. Because the telescope is not used for imaging, the segment piston tolerances are relatively loose and can be achieved by careful segment installation; the phasing procedures used at Keck are not necessary. A major upgrade to the telescope is planned in order to support an extensive dark-energy study known as HETDEX (Booth et al. 2006).

The Southern African Large Telescope (Buckley et al. 2004) is a southern hemisphere twin of the Hobby-Eberly, built near Sutherland, South Africa, by the South African Astronomical Observatory and a host of international partners. The baseline design was the same as that of the HET, but modifications were introduced to increase the field of view and to incorporate edge sensors and hence active control from the beginning. The telescope was inaugurated in November of 2005.

3.11.3 Large Area Multi-Object Spectrographic Telescope

The Large Sky Area Multi-Object Fibre Spectroscopic Telescope (LAMOST) (Cui et al. 2010) is a Schmidt telescope, built by China and devoted, as the name implies, to spectroscopy. The telescope has two segmented optics: a spherical primary mirror, roughly 6 m in diameter and consisting of 37 hexagonal segments of circumscribed diameter 1.1 m, and a corrector mirror, 5.72 × 4.4 m, consisting of 24 segments of the same size.

3.11.4 James Webb Space Telescope

Although the design considerations for a space-based telescope are much different than for a ground-based one, the James Webb Space Telescope (Gardner et al. 2006; Sabelhaus and Decker 2004), the successor to the Hubble Space Telescope, deserves mention in this review. The 6.5-m primary mirror of JWST will consist of 18 hexagonal segments in two rings. The segments are about the same size as those of Keck but made of light-weighted beryllium, not Zerodur. The motivation for the segmentation of JWST comes not only from fabrication considerations but also from those of launch: it must be both light-weight enough and compact enough to be launched later in this decade by an Ariane 5 rocket. The telescope will be launched in a folded configuration so that it can fit into the 4.5-m-diameter rocket and will be deployed on orbit.

JWST differs from ground-based segmented-mirror telescopes in that the primary mirror will not have an active control system; there are actuators but no sensors. There are several reasons for this. After initial deployment, there is little for the actuators to do since thermal perturbations to the system should be minor and of course the gravitational perturbations are nonexistent. In general, one wants to move actuators in a space-based system as seldom as possible in order to minimize the chance of an actuator failure, even one of which could jeopardize the entire mission. Additionally, a system of segment edge sensors and its electronics could create heat leaks which would compromise the cryogenic environment of this infrared telescope.

As noted in Sect. 10.2, the coarse phasing of the JWST segments will be accomplished with a technique known as dispersed Hartmann sensing (DHS) (Sivaramakrishnan et al. 2003). In DHS, an array of prisms is placed over the intersegment edges at the location of a small image of the primary. The prisms disperse the light so that the wavelengths corresponding to constructive or destructive interference can be identified; the relative piston error can then be reconstructed from this information. The prisms also displace the interference patterns from one another on the detector so that multiple edges can be measured in parallel. Fine phasing will be accomplished using a variation of the Gerchberg-Saxton algorithm (Gerchberg and Saxton 1972; Redding et al. 2000) in which a Fourier transform-based procedure is used to reconstruct the wavefront from an out-of-focus image. Such techniques have not been used for ground-based telescopes because they are severely limited by atmospheric turbulence, but this is clearly not a problem in space.

3.12 Giant Segmented-Mirror Telescopes

There are three extremely large telescope projects currently in the designstages: the Giant Magellan Telescope (GMT), the Thirty Meter Telescope (TMT), and the European Extremely Large Telescope (E-ELT). All three projects involve large international collaborations, all have budgets in the range $1 billion to € 1 billion, and all expect to see first light around the end of the current decade. Because the GMT has only a small number of segments and because these are circular and of the lightweight honeycomb design, a detailed discussion of this telescope is left to Chap. 4 of the current volume; only a brief description is given below. The emphasis here is on the highly segmented TMT and to a lesser extent on the E-ELT. Further information on the E-ELT may be found in Chap. 5 of the current volume.

3.12.1 GMT

The collaboration for the Giant Magellan Telescope (GMT) includes the five partners in the original Magellan project, which built the twin 6.5-m Magellan telescopes: the Carnegie Institution for Science, the University of Arizona, Harvard University, the Massachusetts Institute of Technology, and the University of Michigan, plus several other US universities as well as international partners. The GMT primary mirror will consist of seven circular 8.4-m segments and have an overall diameter of 24.5 m (http://www.gmto.org/science-conceptu.html). The hollow honeycomb segments are similar to those of the Large Binocular Telescope but are somewhat thinner and more flexible in order to accommodate potentially larger aberrations in the six off-axis segments, which are significantly asymmetric. The overall optical design is aplanatic Gregorian, with an exceedingly fast primary mirror focal ratio of f/0.7 and a final focal ratio of f/8.0.

Although the 700-mm-thick primary mirror segments are far stiffer than an 8-m meniscus mirror, some measure of active figure control is nevertheless required; this is supplied by an array of 165 actuators per segment. A ventilating system is used to reduce thermal gradients, since the glass has a nonzero coefficient of thermal expansion. The concave secondary mirror (3.2 m in diameter) is also segmented, with its seven segments conjugated to those of the primary. There will in fact be two secondary mirrors with this geometry: for diffraction-limited aberrations, an adaptive mirror whose segments are deformable thin face sheets, and, for seeing-limited observations, a fast steering mirror with rigid but independently moveable segments.

Wavefront information is supplied by a Shack-Hartmann wavefront sensor. In contrast to the electromechanical edge sensors used on Keck and GTC (and planned for TMT), the active alignment of the GMT segments in tip/tilt will be monitored by two (widely separated) optical sensors on each intersegment edge. According to current plans, the relative piston errors between segments will be measured using a modified phase-diversity scheme (Lloyd-Hart et al. 2006). The fact that the secondary mirror is conjugated to the primary means that the task of phasing the telescope segments can be divided between primary and secondary; for example, piston errors between segments could be sensed at the primary but corrected at the (more agile) secondary.

The GMT enclosure will be a cylinder approximately 65 m high. The telescope will rotate independently of the enclosure and will be able to observe at zenith angles from 0^∘ to 65^∘. The GMT will be built at the existing Las Campanas Observatory in Chile, at an altitude of about 2,500 m. A site testing campaign will determine the optimal peak among several possible candidate sites at LCO.

3.12.2 TMT

TheThirtyMeterTelescope(http://www.tmt.org/sites/default/files/TMT-Construction-Proposal-Public.pdf) represents a merger of three formerly independent segmented-mirror telescope projects: the University of California/Caltech California Extremely Large Telescope (Nelson 2000), the National Observatory’s Giant Segmented-Mirror Telescope (Strom et al. 2002), and Canada’s Very Large Optical Telescope (Roberts et al. 2002). In addition to the University of California and Caltech (the original partners in the development of the Keck Observatory), the collaboration includes the Association of Canadian Universities for Research in Astronomy, and other international partners are expected to join.

For telescopes with monolithic mirrors, the financial rule of thumb is that overall cost scales with primary mirror diameter D as D ^{2. 7}. A TMT study concluded, by contrast, that for a segmented thirty meter telescope, the costs relative to the Keck capital investment should scale far more slowly. This, coupled with the D ⁴ dependence of the figure of merit for background limited observations, makes TMT an extremely good scientific value.

To be precise, 30.0 m is the diameter of the circumscribing circle around the primary mirror, which serves as the entrance pupil of the telescope. The optical design of TMT is Ritchey-Chretien (concave hyperbolic primary mirror and convex hyperbolic secondary), although, unlike most R-C telescopes, there is no Cassegrain focus. This is because an articulated tertiary mirror (2.45 × 3.51 m in diameter) not only folds the telescope beam but also rotates it to direct the light to the science instruments arrayed around the two Nasmyth platforms. This eliminates the need to reposition the very large instruments and also eliminates the need for a conventional (unfolded) Cassegrain focus. Like GMT, TMT will support both diffraction-limited and seeing-limited observations, but unlike GMT, there is only a single secondary mirror, and it is neither active nor adaptive. The primary mirror focal ratio is f/1, converted to f/15 by the 3.02 m diameter secondary mirror.

For adaptive optics observations, TMT will have a facility on the Nasmyth platform capable of feeding a 1 arcmin AO-compensated beam to multiple science instruments. This Narrow Field IR AO System (NFIRAOS) will utilize two deformable mirrors, conjugated to altitudes of 0 and 12 km.

The TMT primary mirror will consist of 492 hexagonal segments, each 0.715 m on a side (somewhat smaller than the 0.9 m Keck segments). There are 492/6 = 82 different types of segments; one spare segment of each type will be provided. The Keck segments are identical regular hexagons when seen in projection. This means that the physical size of the outermost Keck segments is significantly larger than that of the innermost segments. The TMT design, by contrast, utilizes a scaling approach that keeps the physical size of all segments equal to within a few millimeters. As a consequence, the TMT segments are not seen as regular hexagons in projection but appear increasingly foreshortened with increasing radial distance from the center.

As was the case for Keck, the primary mirror control system for TMT will consist of three actuators per segment (a total of 1,476) and two edge sensors per intersegment edge (a total of 2,772). The TMT actuators are considerably more complicated than the Keck actuators in order to provide substantial vibration attenuation and damping in addition to achieving the desired positioning accuracy. Significant geometrical differences between the TMT and Keck edge sensors, described in Sect. 9.3 above, help to reduce the sensor costs and to simplify segment exchanges. The large number of sensors makes it likely that at any given time, several of them will not be functional. At Keck, bad sensors are identified “by hand” and removed from the system. Computer algorithms that will do the identification automatically are being developed for TMT (Chanan and Nelson 2009).

In order to reach the 30-m diffraction limit, the TMT wavefront errors must be a factor of three smaller than the corresponding Keck errors. This presents a significant challenge for both segment fabrication and for optical alignment. The optical alignment system of TMT is still being designed, but it will be based on a Shack-Hartmann approach, similar to that used at Keck.

The TMT enclosure is not of the conventional dome/shutter design but rather involves a calotte configuration, consisting of a base, cap, and shutter. The base and cap form a spherical shell cut by a plane inclined at an angle of θ_cap = 32. 5^∘, with respect to the horizontal. The base rotates about a vertical axis in the azimuth direction, and the cap rotates about an axis perpendicular to the plane that divides cap and base. The cap incorporates a circular aperture that can be positioned for observing at zenith angles from 0^∘ to 2θ_cap = 65^∘. The shutter structure, which rotates about the same axis, but independently of the cap, includes a plug to seal the aperture. Three rows of vents near the bottom of the base structure provide an open area of up to 1,700 m² for natural ventilation of the enclosure during observations.

The TMT site selection process was particularly thorough. On-site measurements with a variety of instruments, including differential image motion monitors and multi-aperture scintillation sensors, were undertaken at five prospective sites: Cerro Tolar, Cerro Armazones, and Cerro Tolonchar in Chile; San Pedro Martir in Mexico (Baja California); and Mauna Kea in Hawaii, for a period of 1–2 years at each site. The atmospheric data were supplemented by existing long-term data sets and also by computational fluid dynamics simulations. Other issues considered in the selection included construction and operating costs; cultural, environmental, and land use issues; labor force issues; proximity to astronomers and to astronomical infrastructure; geological conditions; and other factors. Based on all of these considerations, in July of 2009, the TMT Board selected Mauna Kea as the preferred site for TMT.

3.12.3 E-ELT

The European Extremely Large Telescope (E-ELT) (http://www.eso.org/sci/facilities/eelt/docs/e-elt_constrproposal.pdf) is a project of the 14-member-nation European Southern Observatory. The E-ELT diameter of 42 m will give it twice the area of the Thirty Meter Telescope.

The optical design of the E-ELT is an anastigmat with three powered mirrors and two fold-flats. The f/1 primary mirror (M1) consists of 984 segments with a nominal circumscribed diameter of 1.45 m, very similar to those of TMT. The convex secondary (M2) is 6 m in diameter. A 4.2-m concave and mildly aspheric tertiary (M3) relays light to a flat 2.5-m deformable mirror (M4) with some 5,000 degrees of freedom and then a 2.7-m field stabilizing mirror (M5). The primary mirror focal ratio is f/1 and the final Nasmyth focal ratio is f/17.7. Besides the two Nasmyth foci, there is a gravity-invariant focus that is fed by an additional fold flat (M6) and an f/60 Coude focus.

The enclosure for the E-ELT will be a hemispherical dome with a design that is fairly conventional except for its 100 m diameter; the design for the shutter has not yet been finalized.

In April 2010, the ESO Council selected Cerro Armazones (altitude 3,060 m) as the baseline site for the E-ELT. Cerro Armazones is in the central part of Chile’s Atacama Desert, about 20 km from the VLT on Cerro Paranal.

3.13 Acknowledgments

The preparation of this chapter was supported in part by the Thirty Meter Telescope Corporation. The authors gratefully acknowledge the support of the TMT partner institutions: the Association of Canadian Universities for Research in Astronomy (ACURA), the California Institute of Technology, and the University of California. This work was supported as well by the Gordon and Betty Moore Foundation, the Canada Foundation for Innovation, the Ontario Ministry of Research and Innovation, and the National Research Council of Canada.