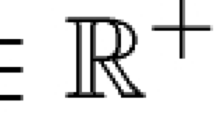Optimal control of the sixth-order convective Cahn-Hilliard equation

Abstract

In this paper, we consider the problem for optimal control of the sixth-order convective Cahn-Hilliard type equation. The optimal control under boundary condition is given, the existence of an optimal solution to the equation is proved and the optimality system is established.

1 Introduction

In past decades, the optimal control of a distributed parameter system has received much more attention in academic field. A wide spectrum of problems in applications can be solved by the methods of optimal control such as chemical engineering and vehicle dynamics. Many papers have already been published to study the control problems for nonlinear parabolic equations, for example, [1]–[9] and so on.

The Cahn-Hilliard (CH) equation is a type of higher order nonlinear parabolic equation, it models many interesting phenomena in mathematical biology, fluid mechanics, phase transition, etc. The fourth-order convective Cahn-Hilliard (FCCH) equation arises naturally as a continuous model for the formation of facets and corners in crystal growth. Many papers have been devoted to CH equation and FCCH equation, see, for example, [10]–[15]. In [16], Savina et al. derived a sixth-order convective Cahn-Hilliard (SCCH) equation

$$u_t-\delta u{u}_x-{(u_{xx}+u-u^3)}_{xxxx}=0$$

(1)

for the description of a growing crystalline surface with small slopes that undergoes faceting. Here, $u=h_x$ is the slope of a $1+1D$ surface $h(x,t)$ and δ is proportional to the deposition strength of an atomic flux. Recently, by an extension of the method of matched asymptotic expansions that retains exponentially small terms, Korzec et al.[17] derived a new type of stationary solutions of the one-dimensional sixth-order Cahn-Hilliard equation. In [18], the existence and uniqueness of weak solutions to equation (1) with periodic boundary conditions were established in $L^2(0,T;{\dot{H}}_{\mathrm{per}}^3)$. Furthermore, a numerical study showed that the solution behave similarly to that for the better known convective Cahn-Hilliard equation. We also noticed that some investigations of SCCH equation were studied, such as in [13], [19].

In this article, suppose that κ is a positive constant, S is a real Hilbert space of observations, $C\in \mathcal{L}(W(0,T;V),S)$ is an operator, which is called the observer. We are concerned with the distributed optimal control problem

$$minJ(u,w)=\frac{1}{2}{\parallel Cu-z_d\parallel }_S^2+\frac{\kappa }{2}{\parallel w\parallel }_{L^2(Q_0)}^2,$$

(2)

subject to

$$\{\begin{array}{c}{u}_t-\delta u{u}_x-{(u_{xx}+u-u^3)}_{xxxx}=Bw,x\in \mathbf{R},\hfill \\ u(x+1,t)=u(x,t),x\in \mathbf{R},\hfill \\ u(x,0)=u_0(x),x\in \mathbf{R},\hfill \end{array}$$

(3)

on an interval $\mathrm{\Omega }=(0,1)$ for $t\in [0,T]$, where $J(u,w)$ is the cost function associated with the control system. The control target is to match the given desired state $z_d$ in $L^2$-sense by adjusting the body force w in a control volume $Q_0\subseteq Q=(0,T)\times \mathrm{\Omega }$ in the $L^2$-sense. On the other hand, we assume that the initial function of (3) has zero mean, i.e., ${\int }_{\mathrm{\Omega }}{u}_0(x)dx=0$, then it follows that ${\int }_{\mathrm{\Omega }}u(x,t)dx=0$ for $t>0$.

Now, we introduce some notations that will be used throughout the paper. For fixed $T>0$, let $Q_0$ be an open set with positive measure, $V={\dot{H}}_{\mathrm{per}}^3(\mathrm{\Omega })$ and $H=L^2(0,1)$, let $V^{\prime }$ and $H^{\prime }$ be dual spaces of V and H. Then we get

$$V\hookrightarrow H=H^{\prime }\hookrightarrow V^{\prime }.$$

Each embedding is dense. The extension operator $B\in \mathcal{L}(L^2(Q_0),L^2(0,T;H))$ which is called the controller is introduced as

$$Bq=\{\begin{array}{cc}q,\hfill & q\in Q_0,\hfill \\ 0,\hfill & q\in Q\setminus Q_0.\hfill \end{array}$$

We supply H with the inner product $(\cdot ,\cdot )$ and the norm $\parallel \cdot \parallel$, and we define a space $W(0,T;V)$ as

$$W(0,T;V)=\{y;y\in L^2(0,T;V),\frac{dy}{dt}\in L^2(0,T;V^{\prime })\},$$

which is a Hilbert space endowed with common inner product.

This paper is organized as follows. In the next section, we give some preparations and establish the existence and uniqueness of a global solution for problem (3). In Section 3, we consider the optimal control problem and prove the existence of an optimal solution. In Section 4, the optimality conditions are showed and the optimality system is derived.

In the following, the letters c, $c_i$ ($i=1,2,\dots$) will always denote positive constants different in various occurrences.

2 Global existence and uniqueness of weak solution

In this section, we prove the existence and uniqueness of a weak solution for problem (3).

Definition 2.1

For all $t\in (0,T)$, a function $y(x,t)\in W(0,T;V)$ is called a weak solution to problem (3), if

$$\frac{d}{dt}(u,\eta )+(u_{xxx},{\eta }_{xxx})-({[u-u^3]}_{xx},{\eta }_{xx})+\frac{\delta }{2}(u^2,{\eta }_x)=(Bw,\eta ),\mathrm{\forall }\eta \in V.$$

(4)

Now, we give Lemma 2.1, which ensures the existence of a unique weak solution to problem (3).

Lemma 2.1

Suppose$u_0\in {\dot{H}}_{\mathrm{per}}^2(\mathrm{\Omega })$, $Bw\in L^2(0,T;H)$, $w\in L^2(Q_0)$. Then problem (3) admits a unique weak solution$u(x,t)\in W(0,T;V)$.

Proof

The Galerkin method is applied to the proof. Denote $\mathbb{A}=-{\partial }_x^6$ as a differential operator, let ${\{{\psi }_i\}}_{i=1}^{\mathrm{\infty }}$ denote the eigenfunctions of the operator $\mathbb{A}=-{\partial }_x^6$. For $n\in N$, define the discrete ansatz space by

$$V_n=span\{{\psi }_1,{\psi }_2,\dots ,{\psi }_n\}\subset V.$$

Let $u_n(t)=u_n(x,t)={\sum }_{i=1}^n{u}_i^n(t){\psi }_i(x)$ require $u_n(0,\cdot )\to u_0$ in H hold true.

By analyzing the limiting behavior of sequences of a smooth function $\{u_n\}$, we can prove the existence of a weak solution to problem (3).

Performing the Galerkin procedure for (3), we obtain

$$\{\begin{array}{c}\frac{d}{dt}{u}_n-\delta u_n{u}_{nx}-{(u_{nxx}+u_n-u_n^3)}_{xxxx}=Bw,x\in \mathbf{R},\hfill \\ u_n(x+1,t)=u_n(x,t),x\in \mathbf{R},\hfill \\ u_n(x,0)=u_{n0}(x),x\in \mathbf{R}.\hfill \end{array}$$

(5)

Obviously, the equation of (5) is an ordinary differential equation, and according to ODE theory, there exists a unique solution to problem (5) in the interval $[0,t_n)$. What we should do is to show that the solution is uniformly bounded when $t_n\to T$. We need also to show that the times $t_n$ there are not decaying to 0 as $n\to \mathrm{\infty }$.

Then, we shall prove the existence of a solution for problem (5). Setting

$$F_n(t)=\frac{1}{2}{\int }_{\mathrm{\Omega }}{|u_{nx}|}^{2}dx-\frac{1}{2}{\int }_{\mathrm{\Omega }}{u}_n^{2}dx+\frac{1}{4}{\int }_{\mathrm{\Omega }}{u}_n^{4}dx,H(s)=s_{xx}+s-s^3.$$

Differentiating $F_n(t)$ with respect to time and integrating by parts, we obtain

$$\begin{array}{rl}\frac{d}{dt}{F}_n(t)=& {\int }_0^1{u}_{nx}{u}_{nxt}dx-{\int }_0^1{u}_n{u}_{nt}dx+{\int }_0^1{u}_n^3{u}_{nt}dx\\ =& {\int }_0^1(-u_{nxx}-u_n+u_n^3)[{(u_{nxx}-u_n+u_n^3)}_{xxxx}+\delta u_n{u}_{nx}+Bw]dx\\ =& -{\int }_0^1{[H(u_n)]}_{xx}^{2}dx+\frac{\delta }{2}{\int }_0^1{[H(u_n)]}_x{u}_n^{2}dx-{\int }_0^{1}H(u_n)Bwdx\\ \le & -{\int }_0^1{[H(u_n)]}_{xx}^{2}dx+{\int }_0^1{[H(u_n)]}_x^{2}dx+\frac{{\delta }^2}{16}{\int }_0^1{u}_n^{4}dx\\ +2{\int }_0^1{[H(u_n)]}^{2}dx+\frac{1}{8}{\int }_0^1{(Bw)}^{2}dx.\end{array}$$

Using Poincaré’s inequality, we have

$${\int }_0^1{[H(u_n)]}^{2}dx\le \frac{1}{2}{\int }_0^1{[H(u_n)]}_x^{2}dx\le \frac{1}{4}{\int }_0^1{[H(u_n)]}_{xx}^{2}dx.$$

Hence

$$\frac{d}{dt}{F}_n(t)\le \frac{{\delta }^2}{16}{\int }_0^1{u}_n^{4}dx+\frac{1}{8}{\parallel Bw\parallel }^2\le \frac{{\delta }^2}{4}{F}_n(t)+\frac{1}{8}{\parallel Bw\parallel }^2.$$

(6)

Since $Bw\in L^2(0,T;H)$ is the control item, we can assume $\parallel Bw\parallel \le M$, where M is a positive constant. Then, by Gronwall’s inequality, we get

$$F_n(t)\le e^{\frac{{\delta }^2}{4}t}(F_n(0)+\frac{M^2}{2{\delta }^2})\le e^{\frac{{\delta }^2}{4}T}(F_n(0)+\frac{M^2}{2{\delta }^2})=c_1,\mathrm{\forall }t\in [0,T].$$

A simple calculation shows that

$${\int }_0^1{|u_{nx}|}^{2}dx\le c_2^2,{\int }_0^1{u}_n^{2}dx\le c_3^2,{\int }_0^1{u}_n^{4}dx\le c_4^4.$$

(7)

Therefore

$${\int }_0^T{\parallel u_n\parallel }_{H^1}^{2}dxdt={\int }_0^T{\int }_0^1(u_n^2+{|u_{nx}|}^2)dxdt=(c_2^2+c_3^2)T=c_5.$$

(8)

By the Sobolev embedding theorem, we get

$${\parallel u_n(x,t)\parallel }_{\mathrm{\infty }}=\underset{x\in [0,1]}{sup}|u_n(x,t)|\le c_6.$$

(9)

Multiplying the equation of (5) by $u_n$, integrating with respect to x on $(0,1)$, we obtain

$$\frac{1}{2}\frac{d}{dt}\parallel u_n^2\parallel +{\parallel u_{nxxx}\parallel }^2=-({(u_n-u_n^3)}_x,u_{nxxx})-\frac{\delta }{2}(u_n^2,u_{nx})+(Bw,u_n).$$

(10)

A simple calculation shows that

$$(u_n^2,u_{nx})={\int }_0^1{u}_n^2{u}_{nx}dx=0.$$

Hence, we have

$$\begin{array}{r}\frac{1}{2}\frac{d}{dt}\parallel u_n^2\parallel +{\parallel u_{nxxx}\parallel }^2\\ ={\parallel u_{nxx}\parallel }^2+(3u_n^2{u}_{nx},u_{nxxx})+(Bw,u_n)\\ \le {\parallel u_{nxx}\parallel }^2+3{\parallel u_n\parallel }_{\mathrm{\infty }}^2\parallel u_{nx}\parallel \parallel u_{nxxx}\parallel +\parallel Bw\parallel \parallel u_n\parallel \\ \le \frac{1}{2}{\parallel u_{nxxx}\parallel }^2+{\parallel u_{nx}\parallel }^2+9c_6^4{\parallel u_{nx}\parallel }^2+\frac{1}{2}{\parallel Bw\parallel }^2+\frac{1}{2}{\parallel u_n\parallel }^2,\end{array}$$

that is,

$$\frac{d}{dt}\parallel u_n^2\parallel +{\parallel u_{nxxx}\parallel }^2\le (2+18c_6^4)c_2^2+c_3^2+{\parallel Bw\parallel }^2\le c_7+{\parallel Bw\parallel }^2.$$

(11)

Therefore

$${\parallel u_n\parallel }^2+{\int }_0^T{\parallel u_{nxxx}\parallel }^{2}dt\le (c_7+M^2)T+{\parallel u_n(0)\parallel }^2.$$

(12)

Multiplying the equation of (5) by $u_{nxxxx}$, integrating with respect to x on $(0,1)$, we deduce that

$$\begin{array}{r}\frac{1}{2}\frac{d}{dt}{\parallel u_{nxx}\parallel }^2+{\parallel u_{nxxxxx}\parallel }^2\\ ={\parallel u_{nxxxx}\parallel }^2+({\left(u_n^3\right)}_{xxx},u_{nxxxxx})-\frac{\delta }{2}(u_n^2,u_{nxxxxx})+(Bw,u_{nxxxx}).\end{array}$$

Note that

$${\left(u_n^3\right)}_{xxx}=3u_n^2{u}_{nxxx}+18u_n{u}_{nx}{u}_{nxx}+6{(u_{nx})}^3.$$

By Nirenberg’s inequality and (7), we have

$$\begin{array}{r}{\parallel u_{nx}\parallel }_4\le c{\parallel u_{nxxxxx}\parallel }^{\frac{1}{16}}{\parallel u_{nx}\parallel }^{\frac{15}{16}},{\parallel u_{nx}\parallel }_6\le c{\parallel u_{nxxxxx}\parallel }^{\frac{1}{12}}{\parallel u_{nx}\parallel }^{\frac{11}{12}},\\ {\parallel u_{nxx}\parallel }_4\le c{\parallel u_{nxxxxx}\parallel }^{\frac{5}{16}}{\parallel u_{nx}\parallel }^{\frac{11}{16}},\parallel u_{nxxx}\parallel \le c{\parallel u_{nxxxxx}\parallel }^{\frac{1}{2}}{\parallel u_{nx}\parallel }^{\frac{1}{2}},\end{array}$$

and

$$\parallel u_{nxxxx}\parallel \le c{\parallel u_{nxxxxx}\parallel }^{\frac{3}{4}}{\parallel u_{nx}\parallel }^{\frac{1}{4}}.$$

Then

$$\begin{array}{r}({\left(u_n^3\right)}_{xxx},u_{nxxxxx})\\ =(3u_n^2{u}_{nxxx}+18u_n{u}_{nx}{u}_{nxx}+6{(u_{nx})}^3,u_{nxxxxx})\\ \le (3{\parallel u_n\parallel }_{\mathrm{\infty }}\parallel u_{nxxx}\parallel +18{\parallel u_n\parallel }_{\mathrm{\infty }}{\parallel u_{nx}\parallel }_4{\parallel u_{nxx}\parallel }_4+6{\parallel u_{nx}\parallel }_6^3)\parallel u_{nxxxxx}\parallel \\ \le [3c_6\left(c{\parallel u_{nxxxxx}\parallel }^{\frac{1}{2}}{\parallel u_{nx}\parallel }^{\frac{1}{2}}\right)+18c_{6}c\left({\parallel u_{nxxxxx}\parallel }^{\frac{1}{16}}{\parallel u_{nx}\parallel }^{\frac{15}{16}}\right)\left({\parallel u_{nxxxxx}\parallel }^{\frac{1}{12}}{\parallel u_{nx}\parallel }^{\frac{11}{12}}\right)\\ +6c{\left({\parallel u_{nxxxxx}\parallel }^{\frac{1}{2}}{\parallel u_{nx}\parallel }^{\frac{1}{2}}\right)}^3]\parallel u_{nxxxxx}\parallel \\ \le \frac{1}{6}{\parallel u_{nxxxxx}\parallel }^2+c_8.\end{array}$$

We also have

$$-\frac{\delta }{2}(u_n^2,u_{nxxxxx})\le \frac{\delta }{2}{\parallel u_n\parallel }_{\mathrm{\infty }}\parallel u_n\parallel \parallel u_{nxxxxx}\parallel \le \frac{1}{6}{\parallel u_{nxxxxx}\parallel }^2+c_9,$$

and

$$\begin{array}{rl}{\parallel u_{nxxxx}\parallel }^2+(Bw,u_{nxxxx})& \le \frac{3}{2}{\parallel u_{nxxxx}\parallel }^2+\frac{1}{2}{\parallel Bw\parallel }^2\\ \le \frac{3}{2}c{\left({\parallel u_{nxxxxx}\parallel }^{\frac{3}{4}}{\parallel u_{nx}\parallel }^{\frac{1}{4}}\right)}^2+\frac{1}{2}{\parallel Bw\parallel }^2\\ \le \frac{1}{6}{\parallel u_{nxxxxx}\parallel }^2+\frac{1}{2}{\parallel Bw\parallel }^2+c_{10}.\end{array}$$

Summing up, we have

$$\frac{d}{dt}{\parallel u_{nxx}\parallel }^2+{\parallel u_{nxxxxx}\parallel }^2\le 2(c_8+c_9+c_{10})+{\parallel Bw\parallel }^2.$$

(13)

Therefore

$${\parallel u_{nxx}\parallel }^2\le 2(c_8+c_9+c_{10})T+M^{2}T=c_{11}^2.$$

(14)

Hence, we have

$${\int }_0^T{\parallel u_n\parallel }_{H^3}^{2}dt={\int }_0^T{\parallel u_n\parallel }_{H^1}^{2}dt+{\int }_0^T{\parallel u_{nxxx}\parallel }^{2}dt+{\int }_0^T{\parallel u_{nxx}\parallel }^{2}dt\le c_{12}.$$

(15)

In addition, we prove a uniform $L^2(0,T;V^{\prime })$ bound on a sequence $\{u_{nt}\}$. Noticing that

$$\begin{array}{r}({(u_n-u_n^3)}_{xxxx},\eta )=-((1-3u_n^2)u_{nx},{\eta }_{xxx})\le {\parallel 1+3u_n^2\parallel }_{\mathrm{\infty }}\parallel u_{nx}\parallel {\parallel \eta \parallel }_V,\\ (u_{nxxxxxx},\eta )=-(u_{nxxx},{\eta }_{xxx})\le \parallel u_{nxxx}\parallel {\parallel \eta \parallel }_V,\\ ({\left(u_n^2\right)}_x,\eta )=-(u_n^2,{\eta }_x)\le \parallel u_n^2\parallel \parallel {\eta }_x\parallel \le \parallel u_n^2\parallel {\parallel \eta \parallel }_V,\\ (Bw,\eta )\le \parallel Bw\parallel \parallel \eta \parallel \le \parallel Bw\parallel {\parallel \eta \parallel }_V.\end{array}$$

By the Sobolev embedding theorem, we have $V\hookrightarrow L^{\mathrm{\infty }}(\mathrm{\Omega })$. Therefore

$${\parallel u_{nt}\parallel }_{V^{\prime }}\le \parallel u_{nxxx}\parallel +{\parallel 1+3u_n^2\parallel }_{\mathrm{\infty }}\parallel u_{nx}\parallel +{\parallel u_n\parallel }_{L^4}^2+\parallel Bw\parallel \le c_{13}.$$

(16)

Then, we immediately conclude

$${\parallel u_{nt}\parallel }_{L^2(0,T;V^{\prime })}^2={\int }_0^T{\parallel u_{nt}\parallel }_{V^{\prime }}^{2}dt\le c_{13}^{2}T.$$

(17)

Based on the above discussion, we obtain $u(x,t)\in W(0,T;V)$. It is easy to check that $W(0,T;V)$ is continuously embedded into $C(0,T;H)$ which denotes the space of continuous functions. We conclude the convergence of a subsequence, denoted by $\{u_n\}$, weak into $W(0,T;V)$, weak-star in $L^{\mathrm{\infty }}(0,T;H)$ (by [20], Lemma 4]) and strong in $L^2(0,T;H)$ to functions $u(x,t)\in W(0,T;V)$. Since the proof of uniqueness is similar as the proof of Theorem 2 of [17], we omit it.

Then, we complete the proof. □

Now, we will discuss the relation among the norm of a weak solution and the initial value and the control item.

Lemma 2.2

Suppose$u_0\in {\dot{H}}_{\mathrm{per}}^2(\mathrm{\Omega })$, $Bw\in L^2(0,T;H)$, $w\in L^2(Q_0)$. Then there exist positive constants$C_1$and$C_2$such that

$${\parallel u\parallel }_{W(0,T;V)}^2\le C_1({\parallel u_0\parallel }^2+{\parallel u_{x0}\parallel }^2+{\parallel u_0\parallel }_{L^4}^4+{\parallel w\parallel }_{L^2(Q_0)}^2)+C_2.$$

(18)

Proof

Setting

$$F(t)=\frac{1}{2}{\parallel u_x\parallel }^2-\frac{1}{2}{\parallel u\parallel }^2+\frac{1}{4}{\parallel u\parallel }_{L^4}^4,$$

passing to the limit in (6), we obtain

$$\frac{d}{dt}F(t)\le \frac{{\delta }^2}{4}F(t)+\frac{1}{8}{\parallel Bw\parallel }^2.$$

Using Gronwall’s inequality, we get

$$F(t)\le e^{\frac{{\delta }^2}{4}t}F(0)+\frac{1}{2{\delta }^2}{\parallel Bw\parallel }^2\le e^{\frac{{\delta }^2}{4}T}F(0)+\frac{1}{2{\delta }^2}{\parallel Bw\parallel }^2,\mathrm{\forall }t\in [0,T].$$

A simple calculation shows that

$${\int }_0^T{\parallel u\parallel }^{2}dt+{\int }_0^T{\parallel u_x\parallel }^{2}dt\le c_{14}F(0)+c_{15}{\parallel Bw\parallel }_{L^2(0,T;H)}^2.$$

(19)

Passing to the limit in (11), we obtain

$$\frac{d}{dt}\parallel u^2\parallel +{\parallel u_{xxx}\parallel }^2\le c_{16}+{\parallel Bw\parallel }^2.$$

Therefore

$${\int }_0^T{\parallel u_{xxx}\parallel }^{2}dt\le c_{17}+c_{18}{\parallel Bw\parallel }_{L^2(0,T;H)}^2+c_{19}{\parallel u_0\parallel }^2.$$

(20)

On the other hand, we have

$${\int }_0^T{\parallel u_{xx}\parallel }^{2}dt=-{\int }_0^T{\int }_{\mathrm{\Omega }}{u}_x{u}_{xxx}dxdt\le \frac{1}{2}{\int }_0^T{\parallel u_x\parallel }^{2}dx+\frac{1}{2}{\int }_0^T{\parallel u_{xxx}\parallel }^{2}dx.$$

(21)

Note that

$$\begin{array}{r}({(u-u^3)}_{xxxx},\eta )=-((1-3u^2)u_x,{\eta }_{xxx})\le {\parallel 1+3u^2\parallel }_{\mathrm{\infty }}\parallel u_x\parallel {\parallel \eta \parallel }_V,\\ (u_{xxxxxx},\eta )=-(u_{xxx},{\eta }_{xxx})\le \parallel u_{xxx}\parallel {\parallel \eta \parallel }_V,\\ ({\left(u^2\right)}_x,\eta )=-(u^2,{\eta }_x)\le \parallel u^2\parallel \parallel {\eta }_x\parallel \le \parallel u^2\parallel {\parallel \eta \parallel }_V,\\ (Bw,\eta )\le \parallel Bw\parallel \parallel \eta \parallel \le \parallel Bw\parallel {\parallel \eta \parallel }_V.\end{array}$$

By the Sobolev embedding theorem, we have $V\hookrightarrow L^{\mathrm{\infty }}(\mathrm{\Omega })$. Therefore

$${\parallel u_t\parallel }_{V^{\prime }}\le \parallel u_{xxx}\parallel +{\parallel 1+3u^2\parallel }_{\mathrm{\infty }}\parallel u_x\parallel +{\parallel u\parallel }_{L^4}^2+\parallel Bw\parallel .$$

Then, we immediately conclude

$$\begin{array}{rl}{\parallel u_t\parallel }_{L^2(0,T;V^{\prime })}^2& ={\int }_0^T{\parallel u_{nt}\parallel }_{V^{\prime }}^{2}dt\\ \le c_{20}+c_{21}{\parallel Bw\parallel }_{L^2(0,T;H)}^2+c_{22}({\parallel u_0\parallel }^2+{\parallel u_{x0}\parallel }^2+{\parallel u_0\parallel }_{L^4}^4).\end{array}$$

(22)

By (19), (20), (21), (22) and the definition of extension operator B, we obtain (18). Hence, Lemma 2.2 is proved. □

3 Optimal control problem

In this section, we consider the optimal control problem associated with the sixth-order convective Cahn-Hilliard equation and prove the existence of an optimal solution.

In the following, we suppose that $L^2(Q_0)$ is a Hilbert space of control variables, we also suppose that $B\in \mathcal{L}(L^2(Q_0),L^2(0,T;H))$ is the controller and a control $w\in L^2(Q_0)$, $u_0\in {\dot{H}}_{\mathrm{per}}^2(\mathrm{\Omega })$. Consider (3), by virtue of Lemma 2.1, we can define the solution map $w\to u(w)$ of $L^2(Q_0)$ into $W(0,T;V)$. The solution $u(w)$ is called the state of control system (3). The observation of the state is assumed to be given by Cu. The cost function associated with control system (3) is given by

$$J(u,w)=\frac{1}{2}{\parallel Cu-z_d\parallel }_S^2+\frac{\kappa }{2}{\parallel w\parallel }_{L^2(Q_0)}^2.$$

(23)

The optimal control problem about (3) is

$$minJ(u,w),$$

(24)

where $(u,w)$ satisfies (3).

Let $X=W(0,T;V)\times L^2(Q_0)$ and $Y=L^2(0,T;V)\times H$. We define an operator $e=e(e_1,e_2):X\to Y$, where

$$\{\begin{array}{c}{e}_1={(-{\mathrm{\Delta }}^3)}^{-1}(u_t-\delta u{u}_x-{(u_{xx}+u-u^3)}_{xxxx}-Bw),\hfill \\ e_2=u(x,0)-u_0.\hfill \end{array}$$

Here ${\mathrm{\Delta }}^3$ is an operator from V to $V^{\prime }$. Hence, we write (24) in the following form:

$$minJ(u,w)\text{subject to }e(u,w)=0.$$

Now, we give Theorem 3.1 on the existence of an optimal solution to the sixth-order convective Cahn-Hilliard equation.

Theorem 3.1

Suppose$Bu\in L^2(0,T;H)$. Then there exists an optimal control solution$(u^{\ast },w^{\ast })$to problem (3).

Proof

Suppose that $(u,w)$ satisfies the equation $e(u,w)=0$. In view of (23), we deduce that

$$J(u,w)\ge \frac{\kappa }{2}{\parallel u\parallel }_{L^2(Q_0)}^2.$$

By Lemma 2.1, we obtain

$${\parallel u\parallel }_{W(0,T;V)}\to \mathrm{\infty }\text{yields }{\parallel w\parallel }_{L^2(Q_0)}\to \mathrm{\infty }.$$

Therefore,

$$J(u,w)\to \mathrm{\infty },\text{when }{\parallel (u,w)\parallel }_X\to \mathrm{\infty }.$$

(25)

As the norm is weakly lower semi-continuous, we achieve that J is weakly lower semi-continuous. Since for all $(u,w)\in X$, $J(u,w)\ge 0$, there exists $\lambda \ge 0$ defined by

$$\lambda =inf\{J(u,w)|(u,w)\in X,e(u,w)=0\},$$

which means the existence of a minimizing sequence ${\{(u^n,w^n)\}}_{n\in N}$ in X such that

$$\lambda =\underset{n\to \mathrm{\infty }}{lim}J(u^n,w^n)\text{and}e(u^n,w^n)=0,\mathrm{\forall }n\in N.$$

From (25), there exists an element $(u^{\ast },w^{\ast })\in X$ such that when $n\to \mathrm{\infty }$,

$$u^n\to u^{\ast }\text{weakly},u^{\ast }\in W(0,T;V),$$

(26)

$$w^n\to w^{\ast }\text{weakly},w^{\ast }\in L^2(Q_0).$$

(27)

Then, using (26), we get

$$\underset{n\to \mathrm{\infty }}{lim}{\int }_0^T{(u_t^n(x,t)-u_t^{\ast },\psi (t))}_{V^{\prime },V}dt=0,\mathrm{\forall }\psi \in L^2(0,T;V).$$

(28)

By the definition of $W(0,T;V)$ and the compactness of embedding $W(0,T;V)\to L^2(0,T;L^{\mathrm{\infty }})$ and $W(0,T;V)\to C(0,T;H_{\mathrm{per}}^1)$, we find from (26) and the results of Lemma 2.1 that $u^n\to u^{\ast }$ strongly in $L^2(0,T;L^{\mathrm{\infty }})$ and $u^n\to u^{\ast }$ strongly in $C(0,T;{\dot{H}}_{\mathrm{per}}^1)$ when $n\to \mathrm{\infty }$.

Since the sequence ${\{u^n\}}_{n\in N}$ converges weakly and $\{u^n\}$ is bounded in $W(0,T;V)$, based on the embedding theorem, we can obtain that ${\{u^n\}}_{L^2(0,T;L^{\mathrm{\infty }})}$ is also bounded.

Because $u^n\to u^{\ast }$ strongly in $L^2(0,T;L^{\mathrm{\infty }})$ as $n\to \mathrm{\infty }$, by [20], Lemma 4], we know that ${\parallel u^{\ast }\parallel }_{L^2(0,T;L^{\mathrm{\infty }})}$ is bounded. Because $u^n\to u^{\ast }$ strongly in $C(0,T;{\dot{H}}_{\mathrm{per}}^1)$ when $n\to \mathrm{\infty }$, we know that ${\parallel u^{\ast }\parallel }_{C(0,T;{\dot{H}}_{\mathrm{per}}^1)}$ is bounded too.

Using (27) again, we derive that

$$\left|{\int }_0^T{\int }_0^1(B{w}^n-B{w}^{\ast })\eta dxdt\right|\to 0,n\to \mathrm{\infty },\mathrm{\forall }\eta \in L^2(0,T;H).$$

By (26), we deduce that

$$\begin{array}{r}\left|{\int }_0^T{\int }_0^1({(u_n-u_n^3)}_{xxxx}-{(u^{\ast }-{\left(u^{\ast }\right)}^3)}_{xxxx})\eta dxdt\right|\\ =\left|{\int }_0^T{\int }_0^1({(u_n-u_n^3)}_x-{(u^{\ast }-{\left(u^{\ast }\right)}^3)}_x){\eta }_{xxx}dxdt\right|\\ \le {\int }_0^T{\int }_0^1(3{\left(u^n\right)}^2{u}_x^n-3{\left(u^{\ast }\right)}^2{u}_x^{\ast }){\eta }_{xxx}dxdt+{\int }_0^T{\int }_0^1(u_x^n-u_x^{\ast }){\eta }_{xxx}dxdt\\ =E_1+E_2.\end{array}$$

For $E_1$, a simple calculation shows that

$$\begin{array}{rl}{E}_1=& {\int }_0^T{\int }_0^1(3{\left(u^n\right)}^2{u}_x^n-3{\left(u^{\ast }\right)}^2{u}_x^{\ast }){\eta }_{xxx}dxdt\\ \le & {\int }_0^T[3{\left(u^n\right)}^2{u}_x^n-3{\left(u^n\right)}^2{u}_x^{\ast }+3{\left(u^n\right)}^2{u}_x^{\ast }-3{\left(u^{\ast }\right)}^2{u}_x^{\ast }]{\eta }_{xxx}dt\\ \le & 3{\int }_0^T{\parallel {\left(u^n\right)}^2\parallel }_{L^{\mathrm{\infty }}}{\parallel u_x^n-u_x^{\ast }\parallel }_H{\parallel {\eta }_{xxx}\parallel }_{H}dt\\ +3{\int }_0^T{\parallel {\left(u^n\right)}^2-{\left(u^{\ast }\right)}^2\parallel }_{L^{\mathrm{\infty }}}{\parallel u_x^{\ast }\parallel }_H{\parallel {\eta }_{xxx}\parallel }_{H}dt\\ \le & 3{\parallel {\left(u^n\right)}^2\parallel }_{L^2(0,T;L^{\mathrm{\infty }})}{\parallel u_x^n-u_x^{\ast }\parallel }_{C(0,T;H)}{\parallel {\eta }_{xxx}\parallel }_{L^2(0,T;H)}\\ +3{\parallel {\left(u^n\right)}^2-{\left(u^{\ast }\right)}^2\parallel }_{L^2(0,T;L^{\mathrm{\infty }})}{\parallel u_x^{\ast }\parallel }_{C(0,T;H)}{\parallel {\eta }_{xxx}\parallel }_{L^2(0,T;H)}\\ \to & 0,n\to \mathrm{\infty },\mathrm{\forall }\eta \in L^2(0,T;V).\end{array}$$

For $E_2$, we get

$$\begin{array}{rl}{E}_2& \le {\int }_0^T{\parallel u_x^n-u_x^{\ast }\parallel }_H{\parallel {\eta }_{xxx}\parallel }_{H}dt\\ \le {\parallel u^n-u^{\ast }\parallel }_{C(0,T;H^1)}{\parallel {\eta }_{xxx}\parallel }_{L^2(0,T;H)}\to 0,n\to \mathrm{\infty },\mathrm{\forall }\eta \in L^2(0,T;V).\end{array}$$

Then, we immediately obtain

$$\left|{\int }_0^T{\int }_0^1({(u_n-u_n^3)}_{xxxx}-{(u^{\ast }-{\left(u^{\ast }\right)}^3)}_{xxxx})\eta dxdt\right|\to 0,\mathrm{\forall }\eta \in L^2(0,T;V).$$

We also have the following inequality:

$$\begin{array}{r}\left|{\int }_0^T{\int }_0^1({\left(u_x^n\right)}^2-{\left(u_x^{\ast }\right)}^2)\eta dxdt\right|\\ =\left|{\int }_0^T{\int }_0^1({\left(u^n\right)}^2-{\left(u^{\ast }\right)}^2){\eta }_{x}dxdt\right|\le {\int }_0^T{\parallel {\left(u^n\right)}^2-{\left(u^{\ast }\right)}^2\parallel }_H{\parallel {\eta }_x\parallel }_{H}dt\\ \le {\parallel {\left(u^n\right)}^2-{\left(u^{\ast }\right)}^2\parallel }_{L^2(0,T;H)}{\parallel {\eta }_x\parallel }_{L^2(0,T;H)}\to 0,n\to \mathrm{\infty },\mathrm{\forall }\eta \in L^2(0,T;V).\end{array}$$

In view of the above discussion, we get

$$e_1(u^{\ast },w^{\ast })=0,\mathrm{\forall }n\in N.$$

As is known, $u^{\ast }\in W(0,T;V)$, we derive that $u^{\ast }(0)\in H$. Since $u^n\to u^{\ast }$ weakly in $W(0,T;V)$, we get $u^n(0)\to u^{\ast }(0)$ weakly when $n\to \mathrm{\infty }$. Thus, we obtain

$$(u^n(0)-u^{\ast }(0),\eta )\to 0,n\to \mathrm{\infty },\mathrm{\forall }\eta \in H,$$

which means $e_2(u^{\ast },w^{\ast })=0$. Therefore, we obtain

$$e(u^{\ast },w^{\ast })=0\text{in }Y.$$

So, there exists an optimal solution $(u^{\ast },w^{\ast })$ to problem (3). Then, we complete the proof of Theorem 3.1. □

4 Optimality conditions

It is well known that the optimality conditions for u are given by the variational inequality

$$J^{\prime }(u,w)(v-w)\ge 0,\text{for all }v\in L^2(Q_0),$$

(29)

where $J^{\prime }(u,w)$ denotes the Gâteaux derivative of $J(u,w)$ at $v=w$.

The following lemma is essential in deriving necessary optimality conditions.

Lemma 4.1

The map$v\to u(v)$of$L^2(Q_0)$into$W(0,T;V)$is weakly Gâteaux differentiable at$v=w$, and such the Gâteaux derivative of$u(v)$at$v=w$in the direction$v-w\in L^2(Q_0)$, say$z=\mathcal{D}u(w)(v-w)$, is a unique weak solution of the following problem:

$$\{\begin{array}{c}{z}_t-z_{xxxxxx}-{[(1-3{(u(w))}^2)z]}_{xxxx}-\delta {(u(w)z)}_x\hfill \\ =B(v-w),0<t\le T,x\in \mathbf{R},\hfill \\ z(x+1,t)=z(x,t),x\in \mathbf{R},\hfill \\ z(x,0)=z_0(x),x\in \mathbf{R}.\hfill \end{array}$$

(30)

Proof

Let $0\le h\le 1$, $u_h$ and u be the solutions of (3) corresponding to $w+h(v-w)$ and w, respectively. Then we prove the lemma in the following two steps.

Step 1, we prove $u_h\to u$ strongly in $C(0,T;H_{\mathrm{per}}^1)$ as $h\to 0$. Let $q=u_h-u$, then

$$\{\begin{array}{c}\frac{d}{dt}q-q_{xxxxxx}-{[(u_h-u_h^3)-(u-u^3)]}_{xxxx}-\frac{\delta }{2}{(u_h^2-u^2)}_x\hfill \\ =hB(v-w),0<t\le T,x\in \mathbf{R},\hfill \\ q(x+1,t)=q(x,t),x\in \mathbf{R},\hfill \\ q(x,0)=q_0(x),x\in \mathbf{R}.\hfill \end{array}$$

(31)

Taking the scalar product of (31) with q, a simple calculation shows that

$$\begin{array}{r}\frac{1}{2}\frac{d}{dt}{\parallel q\parallel }^2+{\parallel q_{xxx}\parallel }^2\\ =-(q_x,q_{xxx})-({(u_h^3-u^3)}_x,q_{xxx})-(u_h^2-u^2,q_x)+(hB(v-w),q).\end{array}$$

By Lemmas 2.1-2.2 and the Sobolev embedding theorem, we get

$$\begin{array}{r}{\parallel u(x,t)\parallel }_{W^{1,\mathrm{\infty }}}=\underset{x\in [0,1]}{sup}(|u(x,t)|+|u_x(x,t)|)\le c,\\ {\parallel u_h(x,t)\parallel }_{W^{1,\mathrm{\infty }}}\underset{x\in [0,1]}{sup}(|u_h(x,t)|+|u_{hx}(x,t)|)\le c.\end{array}$$

In addition, a simple calculation shows that

$${\parallel q_x\parallel }^2\le \frac{2}{3}{\parallel q\parallel }^2+\frac{1}{3}{\parallel q_{xxx}\parallel }^2,{\parallel q_{xx}\parallel }^2\le \frac{1}{3}{\parallel q\parallel }^2+\frac{2}{3}{\parallel q_{xxx}\parallel }^2.$$

Hence

$$\begin{array}{r}\frac{1}{2}\frac{d}{dt}{\parallel q\parallel }^2+{\parallel q_{xxx}\parallel }^2\\ =-(q_x,q_{xxx})-(3u_h^2{u}_{hx}-3u^2{u}_x,q_{xxx})-((u_h+u)q,q_x)+(hB(v-w),q)\\ =-(q_x,q_{xxx})-(3u_h^2{u}_{hx}-3u^2{u}_{hx},q_{xxx})-(3u^2{u}_{hx}-3u^2{u}_x,q_{xxx})\\ -((u_h+u)q,q_x)+(hB(v-w),q)\\ \le \parallel q_x\parallel \parallel q_{xxx}\parallel +3{\parallel u_{hx}\parallel }_{\mathrm{\infty }}{\parallel u_h+u\parallel }_{\mathrm{\infty }}\parallel q\parallel \parallel q_{xxx}\parallel +3{\parallel u\parallel }_{\mathrm{\infty }}^2\parallel q_x\parallel \parallel q_{xxx}\parallel \\ +{\parallel u_h+u\parallel }_{\mathrm{\infty }}\parallel q\parallel \parallel q_x\parallel +h\parallel B(v-w)\parallel \parallel q\parallel \\ \le \frac{1}{2}{\parallel q_{xxx}\parallel }^2+c_1{\parallel q\parallel }^2+h^2{\parallel B(v-w)\parallel }^2,\end{array}$$

that is,

$$\frac{d}{dt}{\parallel q\parallel }^2+{\parallel q_{xxx}\parallel }^2\le 2(c_1{\parallel q\parallel }^2+h^2{\parallel B(v-w)\parallel }^2).$$

(32)

Taking the scalar product of (31) with $q_{xx}$, a simple calculation shows that

$$\begin{array}{r}\frac{1}{2}\frac{d}{dt}{\parallel q_x\parallel }^2+{\parallel q_{xxxx}\parallel }^2\\ =-(q_{xx},q_{xxxx})+({(u_h^3-u^3)}_{xx},q_{xxxx})-(hB(v-w),q_{xx})\\ =-(q_{xx},q_{xxxx})+(3u_h^2{u}_{hxx}-3u^2{u}_{xx},q_{xxxx})\\ +(6u_h{u}_{hx}^2-6u{u}_x^2,q_{xxxx})-(hB(v-w),q_{xx})\\ =-(q_{xx},q_{xxxx})+(3u_h^2{u}_{hxx}-3u^2{u}_{hxx},q_{xxxx})+(3u^2{u}_{hxx}-3u^2{u}_{xx},q_{xxxx})\\ +(6u_h{u}_{hx}^2-6u_h{u}_x^2,q_{xxxx})+(6u_h{u}_x^2-6u{u}_x^2,q_{xxxx})-(hB(v-w),q_{xx})\\ \le \parallel q_{xx}\parallel \parallel q_{xxxx}\parallel +3{\parallel u_h+u\parallel }_{\mathrm{\infty }}{\parallel q\parallel }_{\mathrm{\infty }}\parallel u_{hxx}\parallel \parallel q_{xxxx}\parallel +3{\parallel u\parallel }_{\mathrm{\infty }}^2\parallel q_{xx}\parallel \parallel q_{xxxx}\parallel \\ +6{\parallel u_h\parallel }_{\mathrm{\infty }}{\parallel u_{hx}+u_x\parallel }_{\mathrm{\infty }}\parallel q_x\parallel \parallel q_{xxxx}\parallel +6\parallel q\parallel {\parallel u_x\parallel }_{\mathrm{\infty }}^2\parallel q_{xxxx}\parallel \\ +h{\parallel B(v-w)\parallel }^2\parallel q_{xx}\parallel \\ \le \parallel q_{xx}\parallel \parallel q_{xxxx}\parallel +c_2{\parallel u_h+u\parallel }_{\mathrm{\infty }}\parallel q_x\parallel \parallel u_{hxx}\parallel \parallel q_{xxxx}\parallel +3{\parallel u\parallel }_{\mathrm{\infty }}^2\parallel q_{xx}\parallel \parallel q_{xxxx}\parallel \\ +6{\parallel u_h\parallel }_{\mathrm{\infty }}{\parallel u_{hx}+u_x\parallel }_{\mathrm{\infty }}\parallel q_x\parallel \parallel q_{xxxx}\parallel +6\parallel q\parallel {\parallel u_x\parallel }_{\mathrm{\infty }}^2\parallel q_{xxxx}\parallel \\ +h{\parallel B(v-w)\parallel }^2\parallel q_{xx}\parallel \\ \le \frac{1}{2}{\parallel q_{xxxx}\parallel }^2+c_3{\parallel q\parallel }^2+c_4{\parallel q_x\parallel }^2+h^2{\parallel B(v-w)\parallel }^2,\end{array}$$

that is,

$$\frac{d}{dt}{\parallel q_x\parallel }^2+{\parallel q_{xxxx}\parallel }^2\le 2c_3{\parallel q\parallel }^2+2c_4{\parallel q_x\parallel }^2+2h^2{\parallel B(v-w)\parallel }^2.$$

(33)

Adding (32)-(33) together gives

$$\frac{d}{dt}({\parallel q\parallel }^2+{\parallel q_x\parallel }^2)+({\parallel q_{xxx}\parallel }^2+{\parallel q_{xxxx}\parallel }^2)\le c_5({\parallel q\parallel }^2+{\parallel q_x\parallel }^2)+c_6{h}^2{\parallel B(v-w)\parallel }^2.$$

Using Gronwall’s inequality, it is easy to see that $\parallel q\parallel +{\parallel q_x\parallel }^2\to 0$ as $h\to 0$. Therefore, $u_h\to u$ strongly in $C(0,T;H_{\mathrm{per}}^1)$ as $h\to 0$.

Step 2, we prove that $\frac{u_h-u}{h}\to z$ strongly in $W(0,T;V)$. Now, we rewrite (31) in the following form:

$$\{\begin{array}{c}\frac{d}{dt}(\frac{u_h-u}{h})-{[\frac{u_h-u}{h}]}_{xxxxxx}-\frac{{[(u_h-u_h^3)-(u-u^3)]}_{xxxx}}{h}-\frac{\delta }{2}\frac{{[u_h^2-u^2]}_x}{h}\hfill \\ =B(v-u),0<t\le T,x\in \mathbf{R},\hfill \\ \frac{u_h-u}{h}(x+1,t)=\frac{u_h-u}{h}(x,t),x\in \mathbf{R},\hfill \\ \frac{u_h-u}{h}(x,0)=0,x\in \mathbf{R}.\hfill \end{array}$$

(34)

We can easily verify that the above problem possesses a unique weak solution in $W(0,T;V)$. On the other hand, it is easy to check that the linear problem (30) possesses a unique weak solution $z\in W(0,T;V)$. Let $r=\frac{u_h-u}{h}-z$, thus r satisfies

$$\{\begin{array}{c}\frac{d}{dt}r-r_{xxxxxx}-{(\frac{(u_h-u_h^3)-(u-u^3)}{h}-(1-3u^2)z)}_{xxxx}-\frac{\delta }{2}{(\frac{u_h^2-u^2}{h}-2uz)}_x\hfill \\ =0,0<t\le T,x\in \mathbf{R},\hfill \\ r(x+1,t)=r(x,t),x\in \mathbf{R},\hfill \\ r(0)=0,x\in \mathbf{R}.\hfill \end{array}$$

Taking the scalar product of the equation of the above problem with r, we get

$$\begin{array}{r}\frac{1}{2}\frac{d}{dt}{\parallel r\parallel }^2+{\parallel r_{xxx}\parallel }^2\\ =-({(\frac{(u_h-u_h^3)-(u-u^3)}{h}-(1-3u^2)z)}_x,r_{xxx})+\frac{\delta }{2}({\left(\frac{u_h^2-u^2}{h}\right)}_x-2uz,r).\end{array}$$

Noticing that

$$\begin{array}{r}-({(\frac{u_h-u}{h}-z)}_x-{(\frac{u_h^3-u^3}{h}-3u^{2}z)}_x,r_{xxx})\\ =-(r_x-{[3{(u+\theta (u_h-u))}^2\frac{u_h-u}{h}-3u^{2}z]}_x,D^{3}r)\\ \le 2{\parallel r_x\parallel }^2+2{\parallel {[3{(u+\theta (u_h-u))}^2\frac{u_h-u}{h}-3u^{2}z]}_x\parallel }^2+\frac{1}{8}{\parallel r_{xxx}\parallel }^2,\end{array}$$

where $\theta \in (0,1)$. Taking the scalar product of (34) with $\frac{u_h-u}{h}$ and $\frac{{(u_h-u)}_{xx}}{h}$, respectively, a simple calculation shows that

$$\frac{d}{dt}({\parallel \frac{u_h-u}{h}\parallel }^2+{\parallel \frac{{(u_h-u)}_x}{h}\parallel }^2)\le c_7({\parallel \frac{u_h-u}{h}\parallel }^2+{\parallel \frac{{(u_h-u)}_x}{h}\parallel }^2)+c_8{\parallel B(v-w)\parallel }^2.$$

Using Gronwall’s inequality, we obtain

$${\parallel \frac{u_h-u}{h}\parallel }^2+{\parallel \frac{{(u_h-u)}_x}{h}\parallel }^2\le c_9{\parallel B(v-w)\parallel }^2.$$

On the other hand, we have ${\parallel u\parallel }_{W^{1,\mathrm{\infty }}}\le c_{10}$ and $u_h\to u$ strongly in $C(0,T;H_{\mathrm{per}}^1)$ as $h\to 0$, then

$$\begin{array}{r}{\parallel {[3{(u+\theta (u_h-u))}^2\frac{u_h-u}{h}-3u^{2}z]}_x\parallel }^2\\ ={\parallel {[3{(u+\theta (u_h-u))}^2\frac{u_h-u}{h}-3u^2\frac{u_h-u}{h}]}_x+3{[u^2\frac{u_h-u}{h}-u^{2}z]}_x\parallel }^2\\ \le 2{\parallel {[3{(u+\theta (u_h-u))}^2\frac{u_h-u}{h}-3u^2\frac{u_h-u}{h}]}_x\parallel }^2+2{\parallel 3{[u^2\frac{u_h-u}{h}-u^{2}z]}_x\parallel }^2\\ \le c_{11}[{\parallel ({(u+\theta (u_h-u))}^2-u^2){\left(\frac{u_h-u}{h}\right)}_x\parallel }^2\\ +{\parallel \frac{u_h-u}{h}{({(u+\theta (u_h-u))}^2-u^2)}_x\parallel }^2+{\parallel u^2{r}_x\parallel }^2+{\parallel ur{u}_x\parallel }^2]\\ \le c_{12}(\underset{x\in [0,1]}{sup}\cdot {|{(u+\theta (u_h-u))}^2-u^2|}^2\cdot {\parallel {\left(\frac{u_h-u}{h}\right)}_x\parallel }^2+{\parallel u^2{r}_x\parallel }^2+{\parallel ur{u}_x\parallel }^2\\ +{\parallel {({(u+\theta (u_h-u))}^2-u^2)}_x\parallel }^2\underset{x\in [0,1]}{sup}{\parallel \frac{u_h-u}{h}\parallel }^2)\\ \le c_{13}({\parallel {(u+\theta (u_h-u))}^2-u^2\parallel }_{H^1}^2\cdot {\parallel \frac{u_h-u}{h}\parallel }^2+{\parallel r_x\parallel }^2+{\parallel r\parallel }^2\\ +{\parallel {({(u+\theta (u_h-u))}^2-u^2)}_x\parallel }^2{\parallel \frac{u_h-u}{h}\parallel }_{H^1}^2).\end{array}$$

Noticing that $u_h\to u$ strongly in $C(0,T;H_{\mathrm{per}}^1)$ as $h\to 0$, thus

$${\parallel {[3{(u+\theta (u_h-u))}^2\frac{u_h-u}{h}-3u^{2}z]}_x\parallel }^2\to c_{14}({\parallel r_x\parallel }^2+{\parallel r\parallel }^2)\text{as }h\to 0.$$

Therefore

$$\begin{array}{r}-({(\frac{(u_h-u_h^3)-(u-u^3)}{h}-(1-3u^2)z)}_x,r_{xxx})\\ \le c_{14}({\parallel r_x\parallel }^2+{\parallel r\parallel }^2)+\frac{1}{8}{\parallel D^{3}r\parallel }^2\le \frac{1}{4}{\parallel D^{3}r\parallel }^2+c_{15}{\parallel r\parallel }^2.\end{array}$$

Using the same method as above, we get

$$(\left(\frac{u_h^2-u^2}{h}\right)-2uz,r)\le \frac{1}{4}{\parallel r_{xxx}\parallel }^2+c_{16}{\parallel r\parallel }^2.$$

Summing up, we obtain

$$\frac{d}{dt}{\parallel r\parallel }^2+{\parallel r_{xxx}\parallel }^2\le (c_{15}+c_{16}){\parallel r\parallel }^2.$$

Using Gronwall’s inequality, it is easy to check that $\frac{u_h-u}{h}$ is strongly convergent to z in $W(0,T;V)$. Then, Lemma 4.1 is proved. □

As in [1], [4], we denote Λ= canonical isomorphism of S onto $S^{\ast }$, where $S^{\ast }$ is the dual space of S. By calculating the Gateaux derivative of (25) via Lemma 4.1, we see that the cost $J(v)$ is weakly Gateaux differentiable at u in the direction $v-w$. Then, $\mathrm{\forall }v\in L^2(Q_0)$, (29) can be rewritten as

$${(C^{\ast }\mathrm{\Lambda }(Cu(w)-z_d),z)}_{W{(0,T;V)}^{\ast },W(0,T;V)}+\frac{\kappa }{2}{(w,v-w)}_{L^2(Q_0)}\ge 0,$$

(35)

where z is the solution of (30).

Now we study the necessary conditions of optimality. To avoid the complexity of observation states, we consider the two types of distributive and terminal value observations.

• 1. Case of $C\in \mathcal{L}(L^2(0,T;V);S)$.

In this case, $C^{\ast }\in \mathcal{L}(S^{\ast };L^2(0,T;V^{\ast }))$ and (35) may be written as

$${\int }_0^T{(C^{\ast }\mathrm{\Lambda }(Cu(w)-z_d),z)}_{V^{\ast },V}dt+\frac{\kappa }{2}{(w,v-w)}_{L^2(Q_0)}\ge 0,\mathrm{\forall }v\in L^2(Q_0).$$

(36)

We introduce the adjoint state $p(v)$ by

$$\{\begin{array}{c}-\frac{d}{dt}p(v)-p_{xxxxxx}(v)-(1-3{(u(v))}^2)p_{xxxx}(v)+\delta u(v)p_x(v)\hfill \\ =C^{\ast }\mathrm{\Lambda }(Cu(v)-z_d),0<t\le T,x\in \mathbf{R},\hfill \\ p(x+1,t)=p(x,t),x\in \mathbf{R},\hfill \\ p(x,T;v)=0.\hfill \end{array}$$

(37)

According to Lemma 2.1, the above problem admits a unique solution (after changing t into $T-t$).

Multiplying both sides of (37) (with $v=w$) by z, using Lemma 4.1, we get

$$\begin{array}{r}{\int }_0^T{(-\frac{d}{dt}p(w),z)}_{V^{\ast },V}dt={\int }_0^T(p(w),\frac{d}{dt}z)dt,\\ {\int }_0^T{(p_{xxxxxx}(w),z)}_{V^{\ast },V}dt={\int }_0^T(p(w),z_{xxxxxx})dt,\\ {\int }_0^T{(u(w)p_x(w),z)}_{V^{\ast },V}dt=-{\int }_0^T(p(w),{(u(w)z)}_x)dt\end{array}$$

and

$${\int }_0^T{((1-3{(u(w))}^2)p_{xxxx}(w),z)}_{V^{\ast },V}dt={\int }_0^T(p(w),{\left((1-3{(u(w))}^2)z\right)}_{xxxx})dt.$$

Then, we obtain

$$\begin{array}{r}{\int }_0^T{(C^{\ast }\mathrm{\Lambda }(Cu(w)-z_d),z)}_{V^{\ast },V}dt\\ ={\int }_0^T(p(w),z_t-z_{xxxxxx}-{\left[(1-3{(u(w))}^2)z\right]}_{xxxx}-\delta {(u(w)z)}_x)dt\\ ={\int }_0^T(p(w),Bv-Bw)dt=(B^{\ast }p(w),v-w).\end{array}$$

Hence, (36) may be written as

$${\int }_0^T{\int }_0^1{B}^{\ast }p(w)(v-w)dxdt+\frac{\kappa }{2}{(w,v-w)}_{L^2(Q_0)}\ge 0,\mathrm{\forall }v\in L^2(Q_0).$$

(38)

Therefore we have proved the following theorem.

Theorem 4.1

We assume that all the conditions of Theorem  3.1hold. Let us suppose that$C\in \mathcal{L}(L^2(0,T;V);S)$. The optimal control w is characterized by the system of two PDEs and an inequality: (3), (37) and (38).

• 2. Case of $C\in \mathcal{L}(H;S)$.

In this case, we observe $Cu(v)=Du(T;v)$, $D\in \mathcal{L}(H;H)$. The associated cost function is expressed as

$$J(y,v)={\parallel Du(T;v)-z\parallel }_S^2+\frac{\kappa }{2}{\parallel v\parallel }_{L^2(Q_0)}^2,\mathrm{\forall }v\in L^2(Q_0).$$

(39)

Then, $\mathrm{\forall }v\in L^2(Q_0)$, the optimal control w for (39) is characterized by

$${(Du(T;w)-z,Du(T;v)-Du(T;w))}_{V^{\ast },V}+\frac{\kappa }{2}{(w,v-w)}_{L^2(Q_0)}\ge 0.$$

(40)

We introduce the adjoint state $p(v)$ by

$$\{\begin{array}{c}-\frac{d}{dt}p(v)-p_{xxxxxx}(v)-(1-3{(u(v))}^2)p_{xxxx}(v)+\delta u(v)p_x(v)\hfill \\ =0,0<t\le T,x\in \mathbf{R},\hfill \\ p(x+1,t)=p(x,t),x\in \mathbf{R},\hfill \\ p(T;v)=D^{\ast }(Du(T;v)-z_d).\hfill \end{array}$$

(41)

According to Lemma 2.1, the above problem admits a unique solution (after changing t into $T-t$).

Let us set $v=w$ in the above equations and scalar multiply both sides of the first equation of (41) by $u(v)-u(w)$ and integrate from 0 to T. A simple calculation shows that (40) is equivalent to

$${\int }_0^T{\int }_0^1{B}^{\ast }p(w)(v-w)dxdt+\frac{\kappa }{2}{(w,v-w)}_{L^2(Q_0)}\ge 0,\mathrm{\forall }v\in L^2(Q_0).$$

(42)

Then, we have the following theorem.

Theorem 4.2

We assume that all the conditions of Theorem  3.1hold. Let us suppose that$D\in \mathcal{L}(H;H)$. The optimal control w is characterized by the system of two PDEs and an inequality: (3), (41) and (42).