Introduction

Humans consume protein in different procedures, including animal sources as meat and plant sources as pulses (Lakkakula et al. 2017). Particularly, lentils are a rich source of Protein, Carbohydrates, Fiber, etc. Further, one major benefit of pulse consumption over meat consumption is that pulses contain only tiny amounts of fat compared to meat. Moreover, lentils also can be used for livestock feed. Table 1 shows the nutrition value of 100 g of lentils. Lentils contain a greater amount of protein and carbohydrates, whereas Fat content is low in lentils.

Table 1 Nutritional value for every 100 g of lentils
Full size table

Table 2 exhibits the essential micronutrients and vitamin B9 for each 100 g of lentils. Lentils comprise higher amounts of Iron, Phosphorus, and Copper.

Table 2 Essential micronutrients and B-9 vitamin for every 100 g of lentils
Full size table

Canada is the major producer and exporter of lentils in the world as they export approximately 2.03 million metric tons of lentils in the year 2018/19 to over a hundred countries. They began the lentil production in the 1970s, and currently, there are over 5000 active lentil farmers in Canada. The province of Saskatchewan is the major contributor of 95% of the lentils production in Canada. Typically, lentils are planted in early May and harvested in mid-August in Saskatchewan.

However, the production of red lentils varies due to some influences such as weather, trade wars, and financial policies, etc. As a consequence, the red lentils price fluctuation is volatile, which causes a great impact on the growers, sellers, policymakers, and consumers. There are complex relationships among influential factors. Thus, precise forecasting is challenging. The current methods are mainly focused on qualitative analysis rather than the quantitative forecasting approach in the literature.

One of the most demanded and commonly used time series models is the ARIMA model (Alibuhtto and Ariyarathna 2019; Adebiyi et al. 2014; Esther and Magdaline 2017; Kaur and Ahuja 2019). ARIMA model has autoregressive (AR), moving average (MA), and autoregressive moving average (ARMA) subclasses. The seasonal ARIMA is the completely successful inequality of ARIMA models for forecasting seasonal time series (Box et al. 2015; Kihoro et al. 2004).

Furthermore, the GARCH family models, which are better for volatile data, have a better forecast for price predictions. The GARCH, APARCH, TGARCH, and EGARCH can be used to forecast the linear and nonlinear effects. Moreover, hybrid models are also better for price forecasting (Kumari and Tan 2018; Shetty et al. 2018).

Some studies applied the artificial neural network and genetic algorithm without considering the period of production. Lately, Artificial Neural Networks (ANNs) have slightly increased concentrations in the usage of time series forecasting (Kaur and Ahuja 2019). There are different ANN models, such as multilayered perceptions (MLP), feed forward network (FNN), time lagged neural network (TLNN), and seasonal artificial neural network (SANN) (Hamzacebi 2008; Kamruzzaman et al. 2006).

The red lentils’ price is influenced by the season significantly. Hence, investigating the price fluctuation is needed for the SARIMA model which accounts for the seasonal effect in the time series. The ARIMA and SARIMA model have a stable layout and it is expressly designed for time series data. The ANN needs to make modifications before applying it because it has been designed for cross sectional data. Sometimes ANN is acceptable and does more accurate forecasts, but when adding more data, ANN is ten to overfit. Since the red lentils price forecasting is very important, the researcher used the SARIMA model in this study. Subsequently, this study recommends a quantitative prediction method of red lentils price in Canada by applying the SARIMA model to produce a decision-making tool for each associate. R software was used for this analysis.

Literature review

Many of the studies have been conducted on forecasting future production and price of agricultural commodities specifically pulses based on the historical data by applying time series analysis.

Production of pulses in Kenya was forecasted using the ARIMA model by Esther and Magdaline (2017). The results indicated that ARIMA(1,1,2) model was the appropriate model to forecast the pulses production in Kenya and a decreasing trend in the predicted production by 2030. Therefore, due to the increasing tendency in population growth, the estimated results produce a clue that there won’t be enough pulses to feed the growing population in Kenya by 2030.

One of the agricultural commodities, which is consumed by most of the people can be identified as Cucumber. Forecasting vegetable prices is also a challenging task due to seasonal variation. Hence, Luo et al. (2013) used the SARIMA model which considers the seasonal effect, to investigate an effective model of forecasting Cucumber price. SARIMA(1,0,1)(1,1,1)12 model was selected as the best-fitted model which provides feasible short-term warning of vegetable price.

Bisht and Kumar (2019) focused on estimating the price volatility of major pulses including lentils in India using the GARCH model. The high fluctuation of the production of pulses led to high price variability in the market. Further, the results emphasized that the volatility of price in the current period depends on the previous period.

The ARIMA, SARIMA, and ARIMAX have used in the National Capital Region of the Philippines to identify the movements of fruits and vegetable commodities (Vibas and Raqueno 2019). For vegetables such as pechay and tomato had better forecast for the SARIMA model. That means their price values depend on their prices of the previous season of the same month.

SARIMA model was used to forecast the monthly percentage difference in the wholesale price index value in Nigeria (Otu et al. 2014). The volatility in inflation can be imputed to the money supply, exchange rates reduction, petroleum price rises, and substandard agricultural manufacturing. The predicted outcomes values for policymakers to gain insight into more proper economic.

The forecasting of tomato price is more valuable because tomatoes are highly perishable and seasonality. This forecasting can give essential information to tomato growers for making production and market decisions. Adanacioglu and Yarcan (2012) analyzed the seasonal tomato price variation in Turkey and introduced a model to predict the monthly tomato price. The results specified that SARIMA(1,0,0)(1,1,1)12 was the most accurate model to forecast the tomato prices.

The monthly closing price of soybean has forecasted by Souza et al. (2016) using the SARIMA model. They have mentioned the importance of those predictions for both producers and businesses. It can reduce the risks of soybean economics in the short, medium, and long term.

Mutwiri (2019), has built an analysis tool to give early warning massage of tomatoes wholesale price fluctuations of Nairobi in Kenya using SARIMA. This forecast information is valuable for stakeholders to make options regarding the manufacture, retail, trade, and storage as well as farmers to gain higher profit by storing tomatoes in a cool place and sell in a high market, make tomato paste, souse, and ketchup.

Methodology

Materials and methods

The study aimed to forecast the price of red lentils in Saskatchewan, Canada. The study was carried out using weekly time series data for the period of 2010 to 2018. The data on red lentils was collected from askatchewan.ca, AGR Market Trends, Government of Saskatchewan, Canada. There were 521 observations.

A total number of 469 observations were used for model building and 52 observations among those 469 data points were used for assessing the in-sample performance. Remained 52 observations were used for performing out-sample performance.

Model identification

In the identification stage, the data was tested for stationary and the augmented dickey fuller (ADF) test, and Phillips–Perron (PP) test were applied (Wang and Wu 2012). The seasonal index was calculated to identify the seasonal pattern. Decomposed plots were used to identify the time series components; seasonal, trend, cyclic, and random component in the data over the time. Seasonality is represented by the seasonal component at time. When a time series is influenced by seasonal factors there exists a seasonal pattern. The residual component describes the random or irregular influences at time t.

Non-Stationary time series data has statistical properties, which change with time. So, it is required to change the data into stationary time series data by obtaining the first difference of the time series, before building the predictive model.

SARIMA

The Seasonal ARIMA model (SARIMA) is formed by adding seasonal terms in the ARIMA models:

$$\mathrm{SARIMA}\left(p,d,q\right)\left(P,D,Q\right)\left[S\right],$$
(1)

where p is a non-seasonal autoregressive order, P is a seasonal autoregressive order, q is a non-seasonal moving average order, Q is a seasonal autoregressive order, d and D are the order of common difference and seasonal difference (Pepple and Harrison 2017).

SARIMA(p,d,q)(P,D,Q)[S] models are written as

$$\begin{gathered} \left( {1 - \phi_{1} B^{\omega } - \phi_{2} B^{2\omega } - \cdots - \phi_{p} B^{P\omega } } \right) \times \left( {1 - \varphi_{1} B - \varphi_{2} B^{2} - \cdots - \varphi_{p} B^{p} } \right) \times \left( {1 - B^{\omega } } \right)^{D} \left( {1 - B} \right)^{d} {\mathcal{Q}}_{n} \left( t \right) \hfill \\ = \left( {1 - {\Theta }_{1} B^{\omega } - {\Theta }_{2} B^{2\omega } - \cdots - {\Theta }_{{1{\mathcal{Q}}}} B^{{{\mathcal{Q}}\omega }} } \right) \times \left( {1 - \theta_{1} B - \theta_{2} B^{2} - \cdots - \theta_{q} B^{q} } \right)e\left( t \right), \hfill \\ \end{gathered}$$
(2)

\(\phi\) is the non-seasonal parameter of autoregression and θ is the non-seasonal parameter of moving average, \(\varphi\) is the seasonal parameter of autoregression and Θ is the seasonal parameter of moving average, ω is frequency and B is the differential variable (Pepple and Harrison 2017).

The number of times the series is differenced determines the order of d. The AR and MA signatures are determined using non-seasonal and seasonal autocorrelation function (ACF) and partial autocorrelation function (PACF) plots. A theoretical AR model of order p has an ACF that decays and a PACF that cuts off at lag p while a theoretical MA model of order q consists of a PACF that decays and an ACF that cuts off at lag q. The model with the minimum AIC and BIC values is selected as the model that fits the data best (Pepple and Harrison 2017).

Estimation of parameters and diagnostic checking

Parameters of the best-fitted SARIMA model were estimated using the Akaike information criterion (AIC) and Bayesian information criterion (BIC). Then the significance of the model parameters was assessed using t test statistics. The residuals from the estimated model were generated and tested whether they resemble a white noise series (uncorrelated and have zero mean) by investigating ACF, PACF plots, and performing Ljung–Box statistic test, respectively. Heteroscedasticity of the residuals was detected using the Autoregressive conditional heteroscedasticity Lagrange multiplier (ARCH-LM) test (Bisht and Kumar 2019).

If the parameter estimates were insignificant and the residual was not a white noise then the entire process of model identification, parameter estimation, and diagnostic checking was repeated until the appropriate model was attained.

Forecasting

After the selection of an appropriate model, future values of the time series were forecasted for in-sample and out-sample, and the confidence intervals for the forecasts were generated. Reliability of forecasted values based on the selected model was checked by computing sum of squared errors (SSE), mean absolute error (MAE), mean squared error (MSE), root mean square error (RMSE), and Theil’s inequality coefficient (TIC) (Kumari and Tan 2018):

$${\text{SSE}} = \mathop \sum \limits_{t = 1}^{n} \left( {Y_{t} - \hat{Y}_{t} } \right)^{2} ,$$
(3)
$${\text{MAE}} = n^{ - 1} \mathop \sum \limits_{t = 1}^{n} \left| {\sigma_{t}^{2} - \hat{\sigma }_{t}^{2} } \right|,$$
(4)
$${\text{MSE}} = n^{ - 1} \mathop \sum \limits_{t = 1}^{n} \left( {\sigma_{t}^{2} - \hat{\sigma }_{t}^{2} } \right)^{2} ,$$
(5)
$${\text{RMSE}} = \sqrt {\mathop \sum \limits_{t = 1}^{n} \frac{{\left( {\hat{Y}_{t} - Y_{t} } \right)^{2} }}{n}} ,$$
(6)
$$\mathrm{TIC}=\frac{\sqrt{\frac{1}{h+1}{\sum }_{t=1}^{n}{\left({Y}_{t}-{\widehat{Y}}_{t}\right)}^{2}}}{\sqrt{\frac{1}{h+1} } {\sum }_{t=1}^{n}{\left({Y}_{t}\right)}^{2} - \sqrt{\frac{1}{h+1} {\sum }_{t=1}^{n}{\widehat{Y}}^{2}}},$$
(7)

where n is the number of forecasts, \({{\sigma }_{t}}^{2}\) and \({{\widehat{\sigma }}_{t}}^{2}\) are the actual volatility and the volatility forecasts obtained from SARIMA models respectively.

Results and discussion

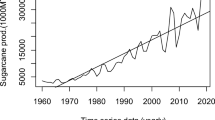
According to the summary statistics in Table 3, the maximum price of red lentils in Saskatchewan was dollar 52.28 per 100 lb in the 2nd week of, 2016 while the lowest red lentils price was dollar 14.25 per 100 lb in the 33rd week, 2018. On average red lentils price in Saskatchewan from 2010 to 2018 was dollar 24.75 per 100 lb. Though a significant increase in red lentils price was realized from the 47th week of 2015 to the 23rd week of 2016, afterward the price was declined as illustrated in Fig. 1. Further, the time series plot indicated that the lentils’ price is highly fluctuating over time.

Table 3 Descriptive statistics of the lentils price during 2010 and 2018
Full size table
Fig. 1
figure 1

Red lentils price in dollars per 100 lb in Saskatchewan (2010–2019)

Full size image

The seasonal indices for weekly red lentils’ price were calculated (Electronic supplementary maerial 1) and plotted. Figure 2 exhibits the maximum price in the 22nd Week and the minimum price in the 37th Week of the year. Further, seasonal indices were negative from 10th week to 14th week and 28th week to 48th week whereas within the first 10 weeks, from 15th week to 27th week and last four weeks in the year seasonal indices were positive. It emphasized that the lentils’ price exhibits seasonality since the price is low during the harvesting period while the price increases through the planting period.

Fig. 2
figure 2

Weekly seasonal index plot for red lentils price from 2010 to 2019

Full size image

ACF and PACF plots for the original red lentils price data were shown in Fig. 3. The results implied that price data was not stationary since the ACF die off slowly. Further, the ADF test and PP test for red lentils price data were performed to confirm whether the data was stationary or not. The p values of ADF and PP tests which were 0.696 and 0.7212, respectively, were greater than 0.05. Therefore, the time series was not stationary at a 5% significance level. Hence, the data was differenced to make it stationary. The p values of the ADF and PP tests were 0.01 which was less than 0.05. It indicates that the differenced data was stationary at a 5% level of significance. The first differencing was sufficient to make the data stationary; hence price was integrated of order one (d = 1). Figure 4 shows a plot of the differenced red lentils price data against time.

Fig. 3
figure 3

ACF and PACF plots for red lentils price

Full size image
Fig. 4
figure 4

Red lentils differenced data

Full size image

The plots of ACF and PACF for the non-seasonal and seasonal differenced price data were used to obtain the order of the non-seasonal and seasonal AR and MA. The results are shown in Figs. 5 and 6. There were insignificant spikes in all plots. Six parsimonious models were selected for the model building purpose using those plots.

Fig. 5
figure 5

ACF and PACF plots for non-seasonal differenced data

Full size image
Fig. 6
figure 6

ACF and PACF plots for seasonal differenced data

Full size image

Table 4 indicates the selected best models according to AIC and BIC values. Accordingly, SARIMA (1,1,1)(0,1,1)[52] has the minimum AIC and BIC value.

Table 4 AIC and BIC values of selected models
Full size table

However, according to the in-sample and out-sample performance, SARIMA(2,1,2)(0,1,1)[52] which had the lowest SSE, MAE, MSE, RMSE, and TIC, was selected as the feasible model (Table 5). Further ACF and PACF plots of residuals and Ljung–Box test statistics indicated that the residuals of the selected model were random, white noise, and independent. Then, the ARCH-LM test was performed to assess the heteroscedasticity of residuals. Since the p value was 0.999 which was greater than 0.05, residuals SARIMA(2,1,2)(0,1,1)[52] model was not heteroscedastic at 5% significance level.

Table 5 Accuracy measurements of SARIMA(2,1,2)(0,1,1)[52]
Full size table

According to the parameter estimation results in Table 6, SARIMA(2,1,2)(0,1,1)[52] model can be expressed as following Eq. (9):

$$\left(1-{\phi }_{1}B\right) \times \left(1- {\varphi }_{2}{B}^{2}\right) \times \left(1- {B}^{52}\right)\left(1-B\right){\mathcal{Q}}_{n}\left(t\right)=\left(1- {\theta }_{2}{B}^{2}\right)e\left(t\right),$$
(8)
$$\left( {1 + 0.9998 \times B} \right) \times \left( {1 + 0.4423 \times B^{2} } \right) \times \left( {1 - B^{52} } \right)\left( {1 - B} \right){\mathcal{Q}}_{n} \left( t \right) = \left( {1 - 0.4882 \times B^{2} } \right)e\left( t \right).$$
(9)
Table 6 Parameter estimation of SARIMA(2,1,2)(0,1,1)[52] model
Full size table

Lentils prices from January to December 2019 were predicted using best-fitted SARIMA (2,1,2)(0,1,1)[52]. The forecasted prices within 80% and 95% prediction intervals are shown in Fig. 7. Forecasted values in 2019 (Electronic supplementary maerial 2) were shown a fluctuating pattern and a decreasing trend concerning the price in the last week of December 2018.

Fig. 7
figure 7

The forecasted red lentils price using SARIMA(2,1,2)(0,1,1)[52] in Canada

Full size image

Conclusion

Red lentils are one of the major pulses that comprise high nutritional value. Therefore, the consumer’s demand is high on lentils in many countries. However, due to the impact of many factors, the price of lentils is fluctuating. Hence, farmers, policymakers, and traders are interested in forecasting lentils prices to attain optimum marketing decisions and to cope with price risk. In this study, Seasonal ARIMA modeling was used to forecast the price of red lentils in Saskatchewan, Canada who is the major contributor in the lentils export market. The best-fitted model for price was identified as SARIMA(2,1,2)(0,1,1)[52]. Consequently, this model can be applied as a short-term decision-making tool on lentils’ price. Since the price is volatile, for long-term forecasting the model should be modified by adding new actual values, and regular monitoring of price should be done by the relevant authorities.